Submitted:
05 October 2025
Posted:
06 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
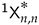 , with * = (1) in the classical case, and * = 0 in the exceptional cases). However, the subbuildings thus obtained are usually smaller than the subbuildings obtained from linear automorphisms (automorphisms acting trivially on the underlying field). Investigating linear polarities of buildings of type reveals indeed large subbuildings, which say a little more about the structure of the ambient building than the smaller ones obtained by Galois descent. For instance, one of the linear polarities that we will encounter, called the “symplectic polarities”, defines a geometric hyperplane of the standard geometry of type .
, with * = (1) in the classical case, and * = 0 in the exceptional cases). However, the subbuildings thus obtained are usually smaller than the subbuildings obtained from linear automorphisms (automorphisms acting trivially on the underlying field). Investigating linear polarities of buildings of type reveals indeed large subbuildings, which say a little more about the structure of the ambient building than the smaller ones obtained by Galois descent. For instance, one of the linear polarities that we will encounter, called the “symplectic polarities”, defines a geometric hyperplane of the standard geometry of type .Structure of the Paper
2. Main Results
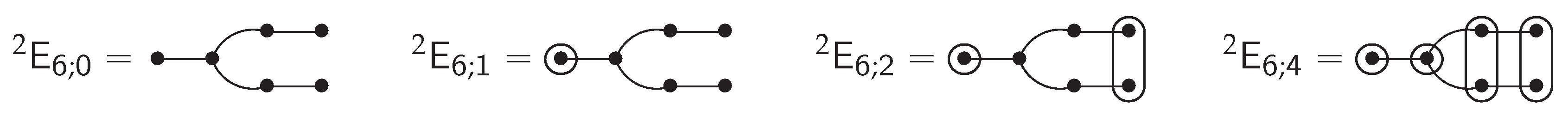
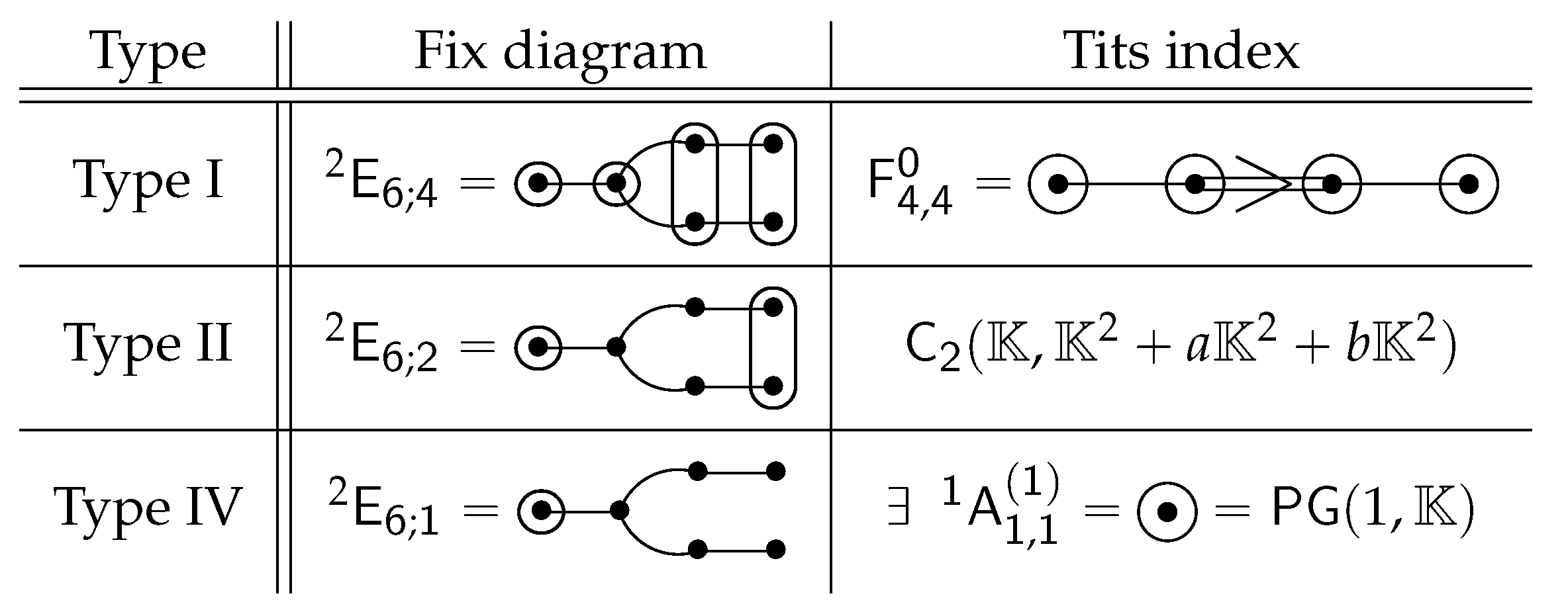
3. Preliminaries
3.1. Buildings and Point-Line Geometries
3.2. Projective Spaces
- , the set of fixed points is a subspace , the set of hyperplanes is the set of hyperplanes containing a given subspace , and .
- and the set of fixed points is the union of two disjoint subspaces U and , with .
3.3. Hyperbolic Quadrics
3.4. Geometries of Type
- Preposition 1. Let be two points of and let be two symps. Then the following properties hold.
- Compactenum 2. []
- Either , or there is a unique line containing both x and y, or x and y are not collinear and there is a unique symp containing both x and y;
- Either , or is a 4-space, or is a point;
- Either , or x is contained in unique 5-space which intersects in a maximal singular subspace distinct from a 4-space, or x is not collinear to any point of .
- The intersection of the unique 5-space with the symp will be referred to as a -space. It follows that 4-spaces and -spaces of a symp belong to different oriflamme classes. The unique symp through x and y in is sometimes denoted as .
- Preposition 2. A point x of is either contained in a given 5-space W of , or it is collinear to all points of a 3-space inside W, or it is collinear to a unique point of W.
- Preposition 3. A symp of is either incident with a given 5-space W of , or it intersects it in a line, or it is disjoint from it.
4. Linear Polarities of the Triality Quadric
- Preposition 4. Let be a linear polarity of , . Then either
- Compactenum 4. []
- is a parabolic polarity;
- The fix structure of is a subquadric of Witt index 1 which is the intersection with of a 4-dimensional subspace of , and no maximal singular subspace is adjacent to its image under ;
- The set of fixed points is the union of a conic and its perp (which is a subspace isomorphic to ).
- (0)
- . If , then and every singular 3-space of Q through U is preserved, implying that is type-preserving, a contradiction. Hence and U does not belong to Q. Then we have situation .
- (1)
- . As in , leads to a contradiction. Hence again. Since , we find that . Suppose first that U intersects Q in two points . Then every singular 3-space of Q through x intersects in a plane and hence is stabilised by . This again implies that is type-preserving, a contradiction. Suppose now that U and Q are disjoint. Set . We claim that is non-degenerate and has Witt index 2. Indeed, is non-degenerate since is empty and hence non-degenerate. Since , the Witt index of is at least 2. Suppose contains a plane . Then . The latter is a 4-space containing the two singular 3-spaces of Q through . Hence U intersects each of these singular 3-spaces, a contradiction. The claim is proved. Now let W be a maximal singular subspace of Q containing a line L of . Since L is fixed pointwise and is a polarity, we deduce that is a plane, stabilised by . Since and pointwise fixes the line L of , it fixes an additional point of , which necessarily has to lie in . But this is impossible as . This shows that this case does not arise.
- (2)
- . As in , leads to a contradiction. Hence and so is a non-degenerate conic. There are two possibilities. The first one is that is empty. Similarly as in , one shows that is a non-degenerate quadric of Witt index 1. We claim that this leads to . Indeed, each maximal singular subspace W of Q intersects in a point. Lemma 3 implies that is either a point or a line. If is a line, is type-preserving and it is always a line. The second possibility is that is a (non-empty) conic. This leads to .
- (3)
- . As in , is non-degenerate. Using similar arguments as above, one shows that the Witt indices of and coincide. If this Witt index is 0, then there are no fixed point, contradicting Lemma 4. If the Witt index is 1, then consider a line L intersecting U and non-trivially, say in the respective points u and . Since L is stabilised by , similarly as above we find a fixed plane, which only contains two fixed points (u and ), contradicting Lemma 2. Finally, if the Witt index of both and were equal to 2, then each maximal singular subspace spanned by a line of and one of , would be fixed, which implies that would be type-preserving, a contradiction.
- Preposition 5. Let be a linear polarity of , . We consider in its ambient projective space . Then either
- is a parabolic polarity, that is, is the unique non-trivial collineation pointwise fixing a given non-degenerate hyperplane of ;
- The fix structure of is a subquadric P of Witt index 1 which is the intersection with of a 4-dimensional subspace of , it has a plane nucleus, and no maximal singular subspace is adjacent to its image under ;
- The set of fixed points is the intersection of with a 4-dimensional subspace U and has the structure of a cone with vertex some point x and base a quadric of Witt index 1 in a hyperplane of U. No maximal singular subspace not through x is mapped onto an adjacent one, whereas each maximal singular subspace through x is mapped onto an adjacent one.
- The set of fixed points is the intersection of with a 4-dimensional subspace U and has the structure of a cone with vertex some line K and base a non-degenerate conic in some plane of U. A maximal singular subspace is mapped onto an adjacent one if, and only if, it is not disjoint from the line K.
- (0)
- . Here, is a point off Q and this leads to situation .
- (1)
- . Here, is a line. Then is 5-dimensional and hence intersects every maximal singular subspace in at least a line, which is consequently fixed by . Hence, since is type-interchanging, corresponding maximal singular subspaces intersect in a plane. Lemma 10 leads to (which, however, cannot occur here; our argument shows would be type-preserving in this case).
- (2)
- . Suppose first . Since , at least one point per maximal singular subspace is fixed. If a singular line L were pointwise fixed, then, since , we would find . The latter is a 5-space intersecting Q in a quadric with radical L. This implies that , and hence is not disjoint from Q, a contradiction. Using Lemma 2, this leads to . Now suppose . Similarly as in the previous case, one shows that no line disjoint from is pointwise fixed by , and hence, also similarly, each maximal singular subspace W not containing x contains exactly one fixed point . Hence, using Lemma 2 again, we deduce that is not a plane. We conclude . Now let W be a maximal singular subspace containing x. Then , with M a line in not through x. This implies some line of W through x is pointwise fixed and so is a plane . That plane cannot be pointwsie fixed as otherwise , which is the union of two hyperplanes, contains , contradicting . This is situation . Similarly, leads to situation .
- (3)
- . Since every maximal singular subspace of Q is also singular with respect to , the intersection is a singular subspace of Q. Hence there exists a maximal singular subspace W of Q disjoint from . This implies that no point of , which is globally stabilised, is fixed. Hence is not a point, and, by Lemma 2, it is not a plane either. This contradicts the fact that is not type-preserving.
5. Proofs of Theorem 1 and Theorem 2
5.1. Fix Diagrams
- Preposition 6. If does not fix any 5-space, then it is anisotropic.
-
is a plane π.Select . Then , since preserves the incidence relation. Hence x is absolute and fixes a 5-space by Lemma 11, a contradiction to our assumptions.
- is a point x. Then clearly x is mapped onto the unique symp incident with both W and , which contains x. Again, Lemma 11 leads to a contradiction.
-
and W is not opposite .Then there is a unique 5-space that intersects both W and in some plane. Clearly, fixes , again a contradiction.
- 1.
- is a symplectic polarity;
- 2.
- and is an orthogonal polarity with absolute geometry ;
- 3.
- and is an orthogonal polarity of Witt index 1, hence with absolute geometry a non-ruled non-degenerate non-empty quadric;
- 4.
- and is a pseudo polarity with absolute point set an absolute hyperplane;
- 5.
- and is a pseudo polarity with absolute point set an absolute 3-space;
- 6.
- and is a pseudo polarity with absolute point set a plane fixed by ;
- 7.
- and is a pseudo polarity with absolute point set a non-absolute line;
- 8.
- and is a pseudo polarity with a unique absolute point;
- (j)
- is an anisotropic polarity.
5.2. Fixing metasymplectic spaces in characteristic different from 2.
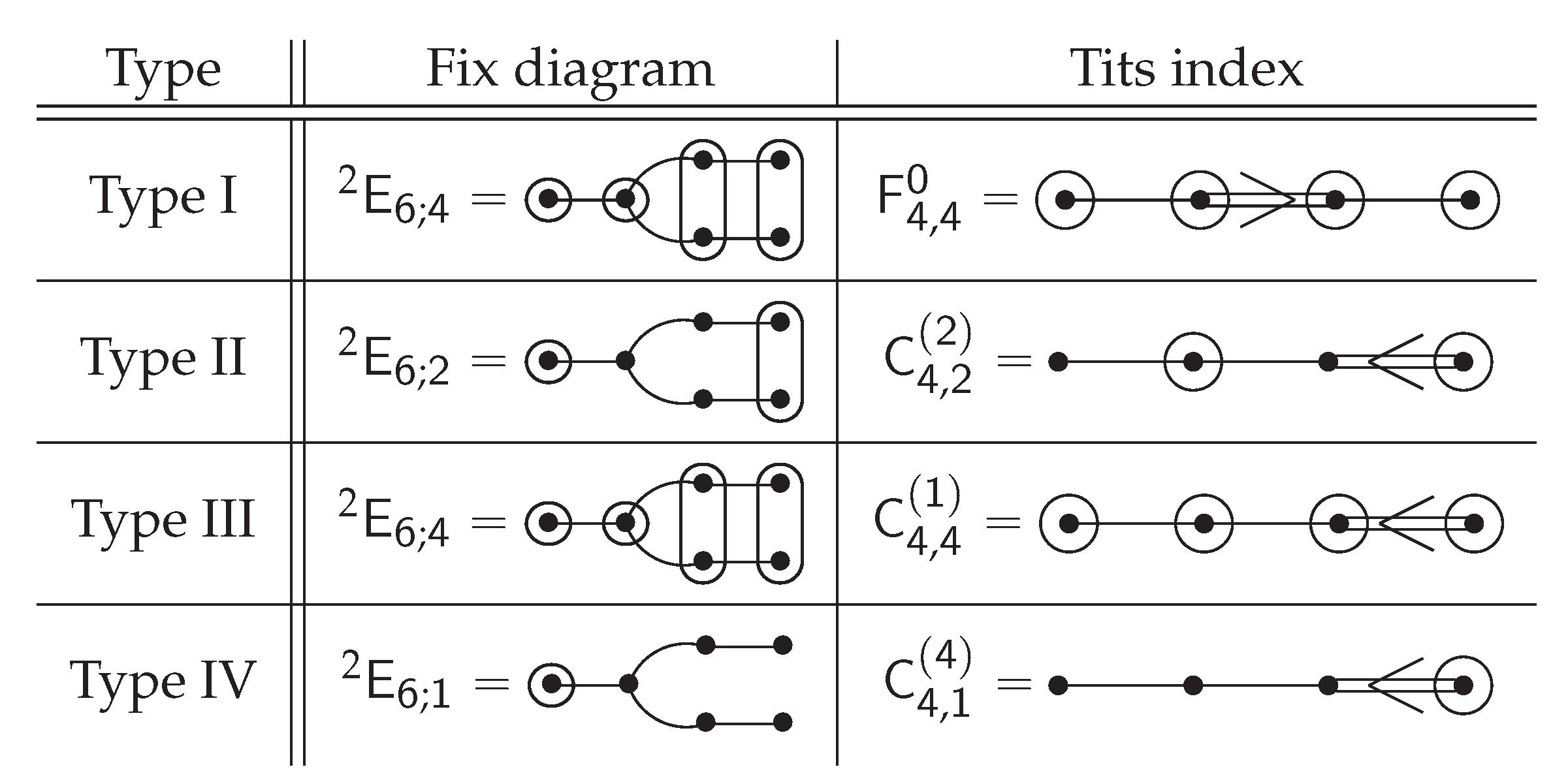
| Type of | Type of |
| Type I | Type A or D |
| Type II | Type C, G or H |
| Type III | Type A, B, D, E or F |
| Type IV | Type A, D, E |
- Preposition 8. Polarities of type I are symplectic polarities.
- Preposition 9. A polarity of type III is characterised by the property that its fixed structure is a non-thick metasymplectic space of type , more precisely, it is the line Grassmannian of a symplectic polar space of rank 4.
5.3. Fixing a Generalised Quadrangle in Characteristic Different from 2
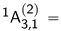
 . Also, the fixed points of in the residue at form a quadric of Witt index 1 in a 4-dimensional space. Hence, over a suitable splitting field, this turns into a parabolic quadric of Witt index 2. Hence the Tits index of the fixed quadric is
. Also, the fixed points of in the residue at form a quadric of Witt index 1 in a 4-dimensional space. Hence, over a suitable splitting field, this turns into a parabolic quadric of Witt index 2. Hence the Tits index of the fixed quadric is 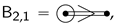 , which coincides with
, which coincides with 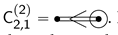 . Note that there is, in fact, also a component of rank 1, type , which is determined by the orthogonal complement of the previously mentioned 4-space. It now follows that, over a common splitting field, becomes of type III and hence is a form of . The above Tits indices paste together as the index :
. Note that there is, in fact, also a component of rank 1, type , which is determined by the orthogonal complement of the previously mentioned 4-space. It now follows that, over a common splitting field, becomes of type III and hence is a form of . The above Tits indices paste together as the index :  and that concludes the proof of the proposition. □
and that concludes the proof of the proposition. □5.4. Fixing a Rank 1 Building in Characteristic Different from 2
5.5. Regular Polarities in Characteristic 2
- Compactenum 10.
- (Type I) The type of is I, for all absolute points x, and the type of is A, for all fixed 5-spaces W;
- (Type II) The type of isII, for all absolute points x, and the type of is G, for all fixed 5-spaces W.
- (Type IV) There are no absolute points, but there are fixed 5-spaces W; all corresponding polarities are anisotropic.
6. Concrete Constructions; Existence
6.1. Representation of Polarities
- Preposition 13. Let be a spread of . Then the permutation of that maps i to j if the line , consists of two disjoint 3-cycles if, and only if, is Hermitian.
6.2. The 9-Space Asociated to a Dual Point
6.3. Explicit Form of Some Polarities of
6.3.1. Polarities of Type I—Symplectic Polarities
6.3.2. Polarities of Type III in Characteristic Unequal to 2
6.3.3. Polarities of Type II in All Characteristics
6.3.4. Polarities of Type IV
References
- P. Abramenko & K. Brown, Buildings: Theory and Applications, Graduate Texts in Mathematics 248, Springer, 2008.
- M. Aschbacher, The 27-dimensional module for E6, I., Invent. Math. 89 (1987), 159–195.
- N. Bourbaki, Lie groups and Lie algebras, Chapters 4–6, Elements of Mathematics, Springer-Verlag, 2002.
- A. E. Brouwer, A. M. Cohen & A. Neumaier, Distance-Regular Graphs, Springer-Verlag, Berlin, New York, 1989.
- I. Cardinali, L. Giuzzi and A. Pasini. Nearly all subspaces of a classical polar space arise from its universal embedding, Lin. Alg. Appl. 627 (2021), 287–207.
- B. N. Cooperstein & E. E. Shult, Frames and bases of Lie incidence geometries, J. Geom. 60, (1997), 17–46.
- A. Devillers, J. Parkinson & H. Van Maldeghem, Automorphisms and opposition in twin buildings, J. Aust. Math. Soc. 94 (2013), 189–201.
- K. J. Dienst, Verallgemeinerte Vierecke in Pappusschen projektiven Räumen, Geom. Dedicata 9 (1980), 199–206. [CrossRef]
- D. R. Hughes & F. C. Piper, Projective Planes, Springer-Verlag, New York Heidelberg Berlin, 1973.
- A. Kasikova and E. E. Shult, Absolute embeddings of point-line geometries, J. Algebra 238 (2001), 265–291.
- B. Mühlherr, H. P. Petersson and R. M. Weiss, Descent in Buildings, Annals of Math. Studies 190, Princeton University Press, Princeton and Oxford, 2015.
- J. Parkinson & H. Van Maldeghem, Automorphisms and opposition in spherical buildings of classical type, Adv. Geom. 24 (2024), 287–321.
- E. E. Shult, Points and Lines: Characterizing the Classical Geometries, Universitext, Springer-Verlag, Berlin Heidelberg, 2011.
- T. A. Springer & F. Veldkamp, On Hjelmslev-Moufang planes, Math. Z. 107 (1968), 249–263.
- J. Tits, Sur la géometrie des R-espaces, J. Math. Pure Appl. (9) 36 (1957), 17–38.
- J. Tits, Les “formes réelles” des groupes de type E6, Séminaire Bourbaki, 10e année : 1957/1958, exp. no 162 (février 1958), 15 p., 2e éd. corrigée, Secrétariat mathématique, Paris 1958; reprinted in Séminaire Bourbaki 4, Société Mathématique de France, Paris (1995), 351–365.
- J. Tits, Classification of simple algebraic groups, in Algebraic groups and discontinuous subgroups, Proc. Summer Mathematical Inst., Boulder, July 5–August 6, 1965, Proc. Symp. Pure Math. 9, Amer. Math. Soc., Providence, RI (1966), 33–62.
- J. Tits, Buildings of Spherical Type and Finite BN-Pairs, Springer Lecture Notes Series 386, Springer-Verlag, 1974.
- J. Tits, Groupes de rang 1 et ensembles de Moufang, Annuaire du Collège de France, 100e année (1999–2000), 93–109.
- J. Tits & R. Weiss, Moufang Polygons, Springer Monographs in Mathematics, Springer, 2002.
- H. Van Maldeghem, Symplectic polarities in buildings of type E6, Des. Codes Cryptogr. 65 (2012), 115–125.
- H. Van Maldeghem & M. Victoor, On Severi varieties as intersections of a minimum number of quadrics, Cubo 24 (2022), 307–331.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




