Supercommuting Maps on Incidence Algebras with Superalgebra Structure

1. Introduction

The study of commuting maps, defined via the usual commutator $[x,y]=xy-yx$, originated with results on automorphisms and derivations. Divinsky proved non-identity commuting automorphisms on rings imply commutativity [1]. Posner showed centralizing derivations on prime rings are zero [2]. Brešar characterized commuting maps on prime rings as $\theta \left(x\right)=\lambda x+\mu \left(x\right)$, with $\lambda$ in the extended centroid and $\mu$ mapping to the center [3,4,5]. These extended to semiprime rings and von Neumann algebras [6]. Further work covered triangular algebras [7], generalized matrix algebras [8], and incidence algebras [9].

Engel-type conditions, like n-commuting maps where $[{[\theta \left(x\right),x]}_{n-1},x]=0$, were studied in prime and semiprime rings [10,11]. Beidar et al. explored functional identities tied to commuting maps [12,13,14].

In superalgebras, supercommuting maps link to Lie superderivations, super biderivations, and Jordan superhomomorphisms [15,16,17,18,19]. Recent studies connect to alternative rings and Toeplitz operators [20,21]. Ghahramani and Zadeh examined Lie superderivations on unital algebras with idempotents [22]. Luo and Chen studied supercommuting maps in similar contexts [23].

Generalizing to superalgebras is important because they model graded structures in physics (e.g., supersymmetry) and quantum mechanics, extending classical algebras to include fermionic and bosonic parts. This allows unified treatment of even and odd elements, relevant in Lie theory and representation theory [24].

A unital algebra A with nontrivial idempotent e ($e^2=e\ne 0,1$) has Peirce decomposition $A=eAe\oplus eA(1-e)\oplus (1-e)Ae\oplus (1-e)A(1-e)$, forming a generalized matrix algebra. The superstructure sets $A_0=eAe\oplus (1-e)A(1-e)$ and $A_1=eA(1-e)\oplus (1-e)Ae$, yielding superderivation results [22]. For superalgebra basics, see Kac [24].

Incidence algebras $I(X,R)$ over locally finite preordered sets $(X,\le )$ consist of functions $f:X\times X\to R$ with $f(x,y)=0$ if $x\nleqq y$, under convolution $\left(fg\right)(x,y)={\sum }_{x\le z\le y}f(x,z)g(z,y)$. Introduced by Ward for arithmetic functions [25], developed by Rota and Stanley for combinatorics [26]. Maps on $I(X,R)$, like automorphisms and derivations, are well-studied [27,28,29,30,31,32]. For fundamentals, see Spiegel and O’Donnell [33].

This paper extends commuting map theory to supercommuting maps on incidence superalgebras. Compared to Brešar [4] (prime rings), Xiao and Wei [8] (generalized matrix algebras), and Jia and Xiao [9] (incidence algebras), our novelty lies in incorporating superstructures, proving all supercommuting maps are proper under a cycle condition on the Hasse diagram. This aligns with superalgebra studies [22,23] and generalizes Jia’s results [9].

2. Preliminaries

Throughout this paper, let R denote a commutative ring with unity that is 2-torsion free and $n!$-torsion free. An associative algebra A over R is said to be a superalgebra if it admits a direct sum decomposition $A=A_0\oplus A_1$ into R-submodules such that $A_i{A}_j\subseteq A_{i+j(mod2)}$ for $i,j\in \{0,1\}$. The submodule $A_0$ is called the even part, and $A_1$ is the odd part. Elements in $H=A_0\cup A_1$ are homogeneous, and the degree of a homogeneous element $a\in H$ is denoted by $\left|a\right|$, where $\left|a\right|=i$ if $a\in A_i$.

For homogeneous elements $a,b\in H$, the supercommutator is defined as

$${[a,b]}_s=ab-{(-1)}^{\left|a\right|\left|b\right|}ba.$$

This extends linearly to all elements in A. Note that if either a or b is even, then ${[a,b]}_s=ab-ba=[a,b]$, the usual commutator. If both are odd, then ${[a,b]}_s=ab+ba=a\circ b$, the anticommutator.

The supercenter of A, denoted $Z_s\left(A\right)$, is the set

$$Z_s\left(A\right)=\{z\in A\mid {[z,x]}_s=0\mathrm{for}\mathrm{all}x\in A\}.$$

It decomposes as $Z_s\left(A\right)=Z_s{\left(A\right)}_0\oplus Z_s{\left(A\right)}_1$, where $Z_s{\left(A\right)}_i=Z_s\left(A\right)\cap A_i$. The usual center $Z\left(A\right)$ satisfies $Z{\left(A\right)}_0\subseteq Z_s\left(A\right)$.

A linear map $\theta :A\to A$ is called supercommuting if

$${[\theta \left(x\right),x]}_s=0\mathrm{for}\mathrm{all}x\in A.$$

Such a map is proper if it can be expressed as

$$\theta \left(x\right)=\lambda x+\mu \left(x\right),$$

where $\lambda \in Z_s{\left(A\right)}_0$ with $2\lambda A_1^2=\left\{0\right\}$, and $\mu :A\to Z_s\left(A\right)$ is R-linear. If $\theta \left(x\right)\in Z_s\left(A\right)$ for all x, then $\theta$ is supercentral. For a unital A with nontrivial idempotent e, set $f=1-e$. The Peirce decomposition is

$$A=eAe+eAf+fAe+fAf,$$

with multiplication rules: $eAe·eAe\subseteq eAe$, $eAe·eAf\subseteq eAf$, etc., and zero otherwise for incompatible products [8]. The superstructure is $A_0=eAe\oplus fAf$, $A_1=eAf\oplus fAe$ [22].

Condition (1.1) from [34] ensures nontriviality: for $a\in eAe$, if $a·eAf=0=fAe·a$ then $a=0$; similarly for elements in $fAf$. Examples include triangular algebras, matrix algebras, and prime algebras with idempotents [34].

Supercommuting maps satisfy ${[\theta \left(x\right),x]}_s=0$. Proper forms are $\theta \left(x\right)=\lambda x+\mu \left(x\right)$ with constraints as above [17,19]. Improper maps exist in certain cases, but our main result shows properness under graph-theoretic conditions.

We now introduce standard notations for the incidence algebra $I(X,R)$. The unity element $\delta$ of $I(X,R)$ is given by $\delta (x,y)={\delta }_{xy}$ for $x\le y$, where ${\delta }_{xy}\in \{0,1\}$ is the Kronecker delta. For $x,y\in X$ with $x\le y$, let $e_{xy}$ be defined by $e_{xy}(u,v)=1$ if $(u,v)=(x,y)$, and $e_{xy}(u,v)=0$ otherwise. Then $e_{xy}{e}_{uv}={\delta }_{yu}{e}_{xv}$ by the definition of convolution. [33]. The center $\mathcal{C}(X,R)$ and diagonal subalgebra $\mathcal{D}(X,R)=\{{\sum }_x{r}_x{e}_{xx}\mid r_x\in R\}$ play key roles [33].

The Hasse diagram $(X,D)$ has edges for covering relations $x\prec y$ (i.e., $x<y$ with no z such that $x<z<y$). Connected components decompose $I(X,R)$ as a product [33].

Our contribution extends commuting map theory to supercommuting maps on incidence superalgebras. Assuming every two directed edges in each connected component of the Hasse diagram lie in a cycle, we prove all supercommuting maps on $I(X,R)$ are proper. This generalizes results on commuting maps of incidence algebras [9] and aligns with structural studies in associative superalgebras [22,23].

Table 1. Summary of Notations

Notation	Description
R	Commutative ring with unity, 2-torsion free, $n!$-torsion free
X	Locally finite pre-ordered set
$I(X,R)$	Incidence algebra over X and R
$A_0,A_1$	Even and odd parts of superalgebra
${[a,b]}_s$	Supercommutator: $ab-{(-1)}^{\left|a\right|\left|b\right|}ba$
$Z_s\left(A\right)$	Supercenter of A
$\theta$	Supercommuting map: ${[\theta \left(x\right),x]}_s=0$
$e_{xy}$	Basis element of $I(X,R)$
$\delta$	Unity element of $I(X,R)$
$(X,D)$	Complete Hasse diagram
≈	Equivalence on directed edges

Table 1. Summary of Notations

Notation	Description
R	Commutative ring with unity, 2-torsion free, $n!$-torsion free
X	Locally finite pre-ordered set
$I(X,R)$	Incidence algebra over X and R
$A_0,A_1$	Even and odd parts of superalgebra
${[a,b]}_s$	Supercommutator: $ab-{(-1)}^{\left|a\right|\left|b\right|}ba$
$Z_s\left(A\right)$	Supercenter of A
$\theta$	Supercommuting map: ${[\theta \left(x\right),x]}_s=0$
$e_{xy}$	Basis element of $I(X,R)$
$\delta$	Unity element of $I(X,R)$
$(X,D)$	Complete Hasse diagram
≈	Equivalence on directed edges

3. The Connected Case

R is a 2-torsion free commutative ring with unity, and X is a locally finite pre-ordered set, with the complete Hasse diagram $(X,D)$ such that any two directed edges in each connected component are contained in one cycle. The incidence algebra $I(X,R)$ is endowed with a superalgebra structure via a nontrivial idempotent e, where $A_0=eI(X,R)e+(1-e)I(X,R)(1-e)$ is the even part (degree 0) and $A_1=eI(X,R)(1-e)+(1-e)I(X,R)e$ is the odd part (degree 1) [22]. In this section, we study supercommuting maps on $I(X,R)$ when X is connected. A map $\theta :I(X,R)\to I(X,R)$ is supercommuting if ${[\theta \left(f\right),f]}_s=0$ for all $f\in I(X,R)$, where ${[a,b]}_s=ab-{(-1)}^{\left|a\right|\left|b\right|}ba$ for homogeneous $a,b\in A_0\cup A_1$, extended linearly [18].

Lemma 1.

Let A be an R-algebra with a superalgebra structure $A=A_0\oplus A_1$, and let θ be a supercommuting map on A. Let $a,b\in A$ satisfy $a^m=b$ for some integer $m\ge 2$, where b is an idempotent. Then ${[\theta \left(a\right),b]}_s=0$.

Proof. Case 1. First assume a is homogeneous, with parity $\left|a\right|\in \{0,1\}$. Since $\theta$ is supercommuting, we have

$${[\theta \left(a\right),a]}_s=\theta \left(a\right)a-{(-1)}^{\left|\theta \right(a\left)\right|\left|a\right|}a\theta \left(a\right)=0,$$

so

$$\theta \left(a\right)a={(-1)}^{\left|\theta \right(a\left)\right|\left|a\right|}a\theta \left(a\right).$$

(1)

Multiplying (1) on the right by another a and applying the same identity repeatedly, we obtain by induction

$$\begin{array}{c}\hfill \theta \left(a\right)a^m={(-1)}^{m\left|\theta \right(a\left)\right|\left|a\right|}{a}^m\theta \left(a\right),\mathrm{for}\mathrm{all}m\ge 1.\end{array}$$

(2)

Now compute

$${[\theta \left(a\right),a^m]}_s=\theta \left(a\right)a^m-{(-1)}^{\left|\theta \left(a\right)\right||a^m|}{a}^m\theta \left(a\right).$$

But by $\left(2.2\right)$,

$$\theta \left(a\right)a^m={(-1)}^{m\left|\theta \right(a\left)\right|\left|a\right|}{a}^m\theta \left(a\right).$$

Since $|a^m|=m|a|$ (mod 2), the exponent in the supercommutator

$${(-1)}^{m\left|\theta \right(a\left)\right|\left|a\right|}={(-1)}^{\left|\theta \left(a\right)\right||a^m|}.$$

Hence by simplification, we conclude

$${[\theta \left(a\right),a^m]}_s=0.$$

By assumption, $b=a^m$ is idempotent. The above calculation shows

$${[\theta \left(a\right),b]}_s=0.$$

Case 2. If a is not homogeneous, write $a=a_0+a_1$ with $a_i\in A_i$. Expand $a^m$ as a sum of monomials in $a_0,a_1$. Each monomial is homogeneous, and the calculation above shows that $\theta \left(a\right)$ supercommutes with each such homogeneous monomial. By linearity, the same holds for their sum. Thus

$${[\theta \left(a\right),a^m]}_s=0$$

for general a, i.e. ${[\theta \left(a\right),b]}_s=0$. □

Corollary 1.

Let A be an R-algebra with a superalgebra structure, and let θ be a supercommuting map on A. If $e\in A$ is an idempotent, then ${[\theta \left(e\right),e]}_s=0$.

Proof. 

Since e is idempotent ($e^2=e$), apply Lemma 1 with $a=e$, $b=e$, and $m=2$. Thus, ${[\theta \left(e\right),e]}_s=0$. □

The set $B=\{e_{xy}\mid x\le y\}$ forms an R-linear basis of $I(X,R)$ when X is finite. For $i\le j$ and $i\ne j$, we write $i<j$ or $j>i$ for short. Let $\theta :I(X,R)\to I(X,R)$ be a supercommuting map. We denote

$$\theta \left(e_{ij}\right)=\sum _{x\le y}{C}_{ij}^{xy}{e}_{xy},\mathrm{for}\mathrm{all}i,j\in X\mathrm{with}i\le j,$$

with the convention $C_{ij}^{xy}=0$ if $x\nleqq y$.

Lemma 2.

The supercommuting map θ satisfies

$$\theta \left(e_{ii}\right)=\sum _{x\in X}{C}_{ii}^{xx}{e}_{xx},$$

$$\theta \left(e_{ij}\right)=\sum _{x\in X}{C}_{ij}^{xx}{e}_{xx}+C_{ij}^{ij}{e}_{ij},\mathit{if}i<j.$$

Proof. 

Assume $\left|X\right|\ge 2$. Since $e_{ii}$ is idempotent and even ($|e_{ii}|=0$), by Corollary 1, ${[\theta \left(e_{ii}\right),e_{ii}]}_s=\theta \left(e_{ii}\right)e_{ii}-e_{ii}\theta \left(e_{ii}\right)=0$. Which yields

$$\left(\theta \left(e_{ii}\right)e_{ii}\right)(u,v)=\sum _{u\le z\le v}\theta \left(e_{ii}\right)(u,z)e_{ii}(z,v)=\theta \left(e_{ii}\right)(u,i){\delta }_{iv},$$

$$\left(e_{ii}\theta \left(e_{ii}\right)\right)(u,v)=\sum _{u\le z\le v}{e}_{ii}(u,z)\theta \left(e_{ii}\right)(z,v)={\delta }_{ui}\theta \left(e_{ii}\right)(i,v).$$

Thus, ${[\theta \left(e_{ii}\right),e_{ii}]}_s=0$ implies $\theta \left(e_{ii}\right)(u,i)=\theta \left(e_{ii}\right)(i,v)$ for $u\le i\le v$. Left-multiplying by $e_{xx}$

$$\left(e_{xx}\theta \left(e_{ii}\right)\right)(x,y)=\theta \left(e_{ii}\right)(x,y),\left(e_{xx}{e}_{ii}\theta \left(e_{ii}\right)\right)(x,y)={\delta }_{xi}\theta \left(e_{ii}\right)(i,y).$$

This gives $C_{ii}^{xy}=0$ if $x<i$ or $i<y$. For $x\ne i,y\ne i$, consider the idempotent $e_{ii}+e_{xx}$. By Corollary 1, ${[\theta (e_{ii}+e_{xx}),e_{ii}+e_{xx}]}_s=0$, so

$${[\theta \left(e_{ii}\right),e_{xx}]}_s+{[\theta \left(e_{xx}\right),e_{ii}]}_s=0.$$

Multiplying by $e_{xx}$ on the left and $e_{yy}$ on the right

$$C_{ii}^{xy}=0,\mathrm{if}i\ne x<y\ne i.$$

Combining, $\theta \left(e_{ii}\right)={\sum }_{x\in X}{C}_{ii}^{xx}{e}_{xx}$.

For $i<j$, verify that $e_{ii}+e_{ij}$ is idempotent

$${(e_{ii}+e_{ij})}^2=e_{ii}^2+e_{ii}{e}_{ij}+e_{ij}{e}_{ii}+e_{ij}^2=e_{ii}+e_{ij},$$

since $e_{ii}{e}_{ij}=e_{ij}$, $e_{ij}{e}_{ii}=0$, $e_{ij}^2=0$. By Corollary 1, ${[\theta (e_{ii}+e_{ij}),e_{ii}+e_{ij}]}_s=0$, so

$${[\theta \left(e_{ii}\right),e_{ij}]}_s+{[\theta \left(e_{ij}\right),e_{ii}+e_{ij}]}_s=0.$$

Since $|e_{ij}|=1$ (as $e_{ij}\in eI(X,R)(1-e)$ or $(1-e)I(X,R)e$), which gives

$${[\theta \left(e_{ij}\right),e_{ij}]}_s=\theta \left(e_{ij}\right)e_{ij}+e_{ij}\theta \left(e_{ij}\right).$$

For $y\ne i,j$, $e_{ii}+e_{ij}+e_{yy}$ is idempotent, giving

$${[\theta \left(e_{ij}\right),e_{yy}]}_s+{[\theta \left(e_{yy}\right),e_{ij}]}_s=0.$$

Multiplying appropriately, we get $C_{ij}^{xy}=0$ if $i\ne x<y\ne j$, $C_{ij}^{xj}=0$ if $i\ne x<j$, and $C_{ij}^{iy}=0$ if $i<y\ne j$. Thus

$$\theta \left(e_{ij}\right)=\sum _{x\in X}{C}_{ij}^{xx}{e}_{xx}+C_{ij}^{ij}{e}_{ij}.$$

□

Lemma 3.

Let X be a connected, locally finite pre-ordered set, and let $\theta :I(X,R)\to I(X,R)$ be a supercommuting map on the incidence algebra $I(X,R)$, where R is a 2-torsion free commutative ring with unity, and $I(X,R)$ is endowed with a superalgebra structure [22]. Then the coefficients $C_{ij}^{xy}$ in the expansion $\theta \left(e_{ij}\right)={\sum }_{x\le y}{C}_{ij}^{xy}{e}_{xy}$ are subject to the following relations:

 (R1)

$C_{il}^{il}=C_{ii}^{ii}-C_{ii}^{ll}$, if $i<l$;

 (R2)

$C_{ki}^{ki}=C_{ii}^{ii}-C_{ii}^{kk}$, if $k<i$;

 (R3)

$C_{ii}^{kk}=C_{ii}^{ll}$, if $k<l$ and $k\ne i\ne l$;

 (R4)

$C_{ij}^{xx}=C_{ij}^{yy}$, for all $x,y\in X$;

 (R5)

$C_{ij}^{ij}=C_{jl}^{jl}$, if $i<j<l$.

Proof. 

From Lemma 2, we have

$$\theta \left(e_{ii}\right)=\sum _{x\in X}{C}_{ii}^{xx}{e}_{xx},\theta \left(e_{ij}\right)=\sum _{x\in X}{C}_{ij}^{xx}{e}_{xx}+C_{ij}^{ij}{e}_{ij},\mathrm{if}i<j.$$

Consider the supercommutator relation ${[\theta \left(e_{ij}\right),e_{yy}]}_s={[e_{ij},\theta \left(e_{yy}\right)]}_s$ for $i<j$ and any $y\in X$, derived from the idempotent $e_{ii}+e_{ij}+e_{yy}$ (as in Lemma 2). It follows that

$${[\theta \left(e_{ij}\right),e_{yy}]}_s=\theta \left(e_{ij}\right)e_{yy}-{(-1)}^{|\theta \left(e_{ij}\right)|·|e_{yy}|}{e}_{yy}\theta \left(e_{ij}\right).$$

Since $e_{yy}\in A_0$ ($|e_{yy}|=0$), and $\theta \left(e_{ij}\right)$ may have even and odd components, we write $\theta \left(e_{ij}\right)={\sum }_{x\in X}{C}_{ij}^{xx}{e}_{xx}+C_{ij}^{ij}{e}_{ij}$, where $e_{xx}\in A_0$ and $e_{ij}\in A_1$. Thus

$$\theta \left(e_{ij}\right)e_{yy}=\sum _{x\in X}{C}_{ij}^{xx}{e}_{xx}{e}_{yy}+C_{ij}^{ij}{e}_{ij}{e}_{yy}=C_{ij}^{yy}{e}_{yy}+C_{ij}^{ij}{\delta }_{jy}{e}_{ij},$$

$$e_{yy}\theta \left(e_{ij}\right)=\sum _{x\in X}{C}_{ij}^{xx}{e}_{yy}{e}_{xx}+C_{ij}^{ij}{e}_{yy}{e}_{ij}=C_{ij}^{yy}{e}_{yy}+C_{ij}^{ij}{\delta }_{yi}{e}_{ij}.$$

Now,

$${[\theta \left(e_{ij}\right),e_{yy}]}_s=(C_{ij}^{yy}{e}_{yy}+C_{ij}^{ij}{\delta }_{jy}{e}_{ij})-(C_{ij}^{yy}{e}_{yy}+C_{ij}^{ij}{\delta }_{yi}{e}_{ij})=C_{ij}^{ij}({\delta }_{jy}-{\delta }_{yi})e_{ij}.$$

Similarly, for ${[e_{ij},\theta \left(e_{yy}\right)]}_s$, since $\theta \left(e_{yy}\right)={\sum }_{x\in X}{C}_{yy}^{xx}{e}_{xx}$:

$$e_{ij}\theta \left(e_{yy}\right)=C_{yy}^{jj}{e}_{ij},\theta \left(e_{yy}\right)e_{ij}=C_{yy}^{ii}{e}_{ij},$$

$${[e_{ij},\theta \left(e_{yy}\right)]}_s=C_{yy}^{jj}{e}_{ij}-{(-1)}^{|e_{ij}|·0}{C}_{yy}^{ii}{e}_{ij}=(C_{yy}^{jj}-C_{yy}^{ii})e_{ij}.$$

Equating, we get

$$C_{ij}^{ij}({\delta }_{jy}-{\delta }_{yi})e_{ij}=(C_{yy}^{jj}-C_{yy}^{ii})e_{ij}.$$

(3)

This implies

• For $y=i$: $C_{ij}^{ij}(-1)=C_{ii}^{jj}-C_{ii}^{ii}$, so $C_{ij}^{ij}=C_{ii}^{ii}-C_{ii}^{jj}$.
• For $y=j$: $C_{ij}^{ij}\left(1\right)=C_{jj}^{jj}-C_{jj}^{ii}$, so $C_{ij}^{ij}=C_{jj}^{jj}-C_{jj}^{ii}$.
• For $y\ne i,j$: $0=C_{yy}^{jj}-C_{yy}^{ii}$.

Thus, for $i<l$, set $j=l$ in the first case: $C_{il}^{il}=C_{ii}^{ii}-C_{ii}^{ll}$, proving (R1). For $k<i$, set $i=k$, $j=i$ in the second case: $C_{ki}^{ki}=C_{ii}^{ii}-C_{ii}^{kk}$, proving (R2). For $k<l$, $k\ne i\ne l$, the third case gives $C_{ii}^{kk}=C_{ii}^{ll}$, proving (R3).

For (R5), if $i<j<l$, from (R2): $C_{ij}^{ij}=C_{jj}^{jj}-C_{jj}^{ii}$, and from (R1): $C_{jl}^{jl}=C_{jj}^{jj}-C_{jj}^{ll}$. By (R3), $C_{jj}^{ii}=C_{jj}^{ll}$, so $C_{ij}^{ij}=C_{jl}^{jl}$.

For (R4), consider $i<j$ and $k<l$ with $k\ne i,j$, $l\ne i$. The element $e_{ii}+e_{ij}+e_{kl}$ is idempotent for $m\ge 2$. By Lemma 1, ${[\theta (e_{ii}+e_{ij}+e_{kl}),e_{ii}+e_{ij}]}_s=0$, so

$${[\theta \left(e_{kl}\right),e_{ii}+e_{ij}]}_s=0.$$

We find $\theta \left(e_{kl}\right)={\sum }_{x\in X}{C}_{kl}^{xx}{e}_{xx}+C_{kl}^{kl}{e}_{kl}$, giving $C_{kl}^{ii}=C_{kl}^{jj}$. Similarly, for $e_{jj}+e_{ij}+e_{kl}$, we get $C_{kl}^{ii}=C_{kl}^{jj}$ for $l\ne i,j$. For $j\ne k<i<j$, consider $e_{ii}+e_{ij}+e_{ki}$, which satisfies ${(e_{ii}+e_{ij}+e_{ki})}^m=e_{ii}+e_{ij}+e_{ki}+e_{kj}$. This yields $C_{ki}^{ii}=C_{ki}^{jj}$. For $i<j<l\ne i$, $e_{jj}+e_{ij}+e_{jl}$ gives $C_{jl}^{ii}=C_{jl}^{jj}$. From ${[\theta \left(e_{ij}\right),e_{ij}]}_s=0$, we get $C_{ij}^{ii}=C_{ij}^{jj}$. Combining, $C_{kl}^{ii}=C_{kl}^{jj}$ for all $i<j$. Since X is connected, for any $x,y\in X$, there exists a sequence $x=x_0,x_1,\dots ,x_s=y$ where $x_{i-1}$ covers or is covered by $x_i$. Applying $C_{kl}^{x_{i-1}}=C_{kl}^{x_i}$ recursively yields $C_{kl}^{xx}=C_{kl}^{yy}$, proving (R4). □

Definition 1.

For any two directed edges $(x,y),(u,v)\in D$, define $(x,y)\approx (u,v)$ if and only if there is a cycle containing both $x\sim y$ and $u\sim v$. The relation ≈ is an equivalence relation on D.

Example 1.

Let $X=\{1,2,3,4\}$ with partial order relations (or arrows) $1>2$, $2>3$, and $2>4$. The corresponding Hasse diagram is the Dynkin diagram of type $D_4$, and the associated complete Hasse diagram $(X,D)$ is depicted in Figure 1.

Thus, $(3,2)\approx (4,2)$, since the directed edges $(3,2)$ and $(4,2)$ are contained in the cycle $\{2,3,1,4\}$, with $2\sim 3$, $3\sim 1$, $1\sim 4$, $4\sim 2$.

Proposition 1.

Let R be a 2-torsion free commutative ring with unity, and let X be a finite, connected pre-ordered set. Let $I(X,R)$ be endowed with a superalgebra structure via a nontrivial idempotent e [22]. Then every supercommuting map $\theta :I(X,R)\to I(X,R)$, satisfying ${[\theta \left(f\right),f]}_s=0$ for all $f\in I(X,R)$, is proper if and only if any two directed edges in the complete Hasse diagram $(X,D)$ are contained in one cycle.

Proof. 

Assume any two directed edges in $(X,D)$ are contained in one cycle, i.e., the equivalence relation ≈ has a single equivalence class. By Lemma 2, for a supercommuting map $\theta$, we have:

$$\theta \left(e_{ii}\right)=\sum _{x\in X}{C}_{ii}^{xx}{e}_{xx},\theta \left(e_{ij}\right)=\sum _{x\in X}{C}_{ij}^{xx}{e}_{xx}+C_{ij}^{ij}{e}_{ij},\mathrm{if}i<j.$$

From Lemma 3, the coefficients satisfy:

 (R1)

$C_{il}^{il}=C_{ii}^{ii}-C_{ii}^{ll}$, if $i<l$;

 (R2)

$C_{ki}^{ki}=C_{ii}^{ii}-C_{ii}^{kk}$, if $k<i$;

 (R3)

$C_{ii}^{kk}=C_{ii}^{ll}$, if $k<l$, $k\ne i\ne l$;

 (R4)

$C_{ij}^{xx}=C_{ij}^{yy}$, for all $x,y\in X$;

 (R5)

$C_{ij}^{ij}=C_{jl}^{jl}$, if $i<j<l$.

By (R4), $C_{ij}^{xx}=C_{ij}^{yy}={\lambda }_{ij}$ for all $x,y\in X$, so:

$$\theta \left(e_{ij}\right)={\lambda }_{ij}\sum _{x\in X}{e}_{xx}+C_{ij}^{ij}{e}_{ij},\theta \left(e_{ii}\right)={\lambda }_{ii}\sum _{x\in X}{e}_{xx}.$$

Since ${\sum }_{x\in X}{e}_{xx}=\delta$ (the unity element, with $\delta (x,y)={\delta }_{xy}$), we have $\delta \in Z_s\left(I(X,R)\right)$, as ${[\delta ,f]}_s=0$ for all f. By (R5), $C_{ij}^{ij}=\lambda$ for all $i<j$, since all edges $(i,j)$ are in the same equivalence class under ≈. For $i=j$, set $C_{ii}^{ii}={\mu }_i$. By (R1) and (R2), for any $i<l$ or $k<i$, we adjust coefficients to align with the supercenter.

Define $\mu \left(f\right)={\sum }_{i\le j}f(i,j)(C_{ij}^{ij}{e}_{ij}-{\lambda }_{ij}\delta )$, where $C_{ij}^{ij}=0$ if $i=j$. Then

$$\theta \left(f\right)=\sum _{i\le j}f(i,j)({\lambda }_{ij}\delta +C_{ij}^{ij}{e}_{ij})=\lambda f+\mu \left(f\right),$$

where $\lambda ={\sum }_{i<j}f(i,j){\lambda }_{ij}+{\sum }_{i}f(i,i){\mu }_i\in Z_s\left(I(X,R)\right)$, and $\mu \left(f\right)\in Z_s\left(I(X,R)\right)$ since ${[e_{ij},f]}_s=0$ for fixed $i,j$. Thus, $\theta$ is proper.

Conversely, if some edges $(i,j)$ and $(k,l)$ are not in the same cycle, the equivalence classes under ≈ split D. By [9], a commuting map may be improper in such cases, and similarly, a supercommuting map may fail to be proper due to inconsistent $C_{ij}^{ij}$ across equivalence classes, violating (R5) uniformity.

The proof extends [9] to the superalgebra context, using the supercenter $Z_s\left(I(X,R)\right)$ [18]. □

Example 2.

Let $X=\{1,2,3,4\}$ with relations $1<2$, $2<3$, $3<4$, and $1<4$. The Hasse diagram of X is a 4-cycle (a square):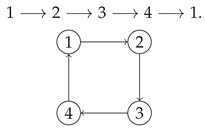

In this case, any two directed edges are contained in a cycle. For instance, $(1,2)\approx (3,4)$ via the cycle $1\to 2\to 3\to 4\to 1$, and $(2,3)\approx (4,1)$ via the same cycle. Thus, the condition of Proposition 1 is satisfied.

4. Supercommuting Maps on Incidence Algebras

Since R be a commutative ring with unity that is 2-torsion free and $n!$-torsion free for some positive integer n, and $(X,\le )$ be a locally finite pre-ordered set, possibly infinite, with $I(X,R)$ the incidence algebra endowed with a superalgebra structure via a nontrivial idempotent e, where $A_0=eI(X,R)e+(1-e)I(X,R)(1-e)$ is the even part (degree 0) and $A_1=eI(X,R)(1-e)+(1-e)I(X,R)e$ is the odd part (degree 1). The supercommutator is defined as ${[a,b]}_s=ab-{(-1)}^{\left|a\right|\left|b\right|}ba$ for homogeneous elements $a,b\in A_0\cup A_1$, extended linearly. A map $\theta :I(X,R)\to I(X,R)$ is supercommuting if ${[\theta \left(f\right),f]}_s=0$ for all $f\in I(X,R)$.

Definition 2.

Let $f\in I(X,R)$ and $x\le y\in X$. The restriction of f to $\{z\in X\mid x\le z\le y\}$ is defined by

$${f|}_x^y=\sum _{x\le u\le v\le y}f(u,v)e_{uv}.$$

Let $\tilde{I}(X,R)$ be the R-subspace of $I(X,R)$ generated by the elements $e_{xy}$ with $x\le y$. Thus, $\tilde{I}(X,R)$ consists of functions $f\in I(X,R)$ that are nonzero only at a finite number of pairs $(x,y)$. The map ${\varphi }_{xy}:I(X,R)\to \tilde{I}(X,R)$, defined by ${\varphi }_{xy}{\left(f\right)=f|}_x^y$, is an algebra homomorphism for any $x\le y$.

Definition 3.

content...For a multilinear map $\mathrm{\Theta }:A^m\to A$, we define its trace (or diagonal evaluation) by

$$Tr\left(\mathrm{\Theta }\right)\left(f\right)=\mathrm{\Theta }(f,f,\dots ,f),f\in A.$$

Lemma 4.

Let $\theta :I(X,R)\to I(X,R)$ be a supercommuting map on the incidence algebra $I(X,R)$, where R is $n!$-torsion free for some positive integer n. For any $f\in I(X,R)$ and $x<y$, we have

$$\theta \left(f\right)(x,y)=\theta \left(f{|}_x^y\right)(x,y).$$

Proof. 

Define the map $\mathrm{\Theta }:I{(X,R)}^{n+1}\to I(X,R)$ by

$$\mathrm{\Theta }(f_1,f_2,\dots ,f_{n+1})=P_{n+1}(\theta \left(f_1\right),f_2,\dots ,f_{n+1}),$$

where the polynomial $P_m$ in noncommutative variables $x_1,x_2,\dots ,x_m$ is defined inductively by

$$\begin{array}{cc}\hfill P_1\left(x_1\right)& =x_1,\hfill \\ \hfill P_2(x_1,x_2)& ={[x_1,x_2]}_s,\hfill \\ \hfill P_m(x_1,x_2,\dots ,x_m)& ={[P_{m-1}(x_1,x_2,\dots ,x_{m-1}),x_m]}_s\hfill \end{array}$$

for $m\ge 3$. Since $\theta$ is supercommuting, we have ${[\theta \left(f\right),f]}_s=P_2(\theta \left(f\right),f)=0$. Consider the n-fold supercommutator

$$P_{n+1}(\theta \left(f\right),f,\dots ,f)={[{[\dots {[\theta \left(f\right),f]}_s,f]}_s,\dots ,f]}_s=0,$$

where the supercommutator is applied n times. The trace of $\mathrm{\Theta }$ satisfies

$$\mathrm{\Theta }(f,f,\dots ,f)=P_{n+1}(\theta \left(f\right),f,\dots ,f)=0.$$

Linearizing $\mathrm{\Theta }(f,f,\dots ,f)=0$, we obtain

$$\sum _{w\in S_{n+1}}{P}_{n+1}(\theta \left(f_{w\left(1\right)}\right),f_{w\left(2\right)},\dots ,f_{w(n+1)})=0,$$

(4)

where $S_{n+1}$ is the symmetric group on $\{1,2,\dots ,n+1\}$. Set $f_1=f$ and $f_2=\dots =f_{n+1}=e_{yy}$, where $e_{yy}\in I(X,R)$ is the basis element with $e_{yy}(y,y)=1$ and zero elsewhere, and $|e_{yy}|=0$ (since $e_{yy}\in A_0$). Substituting into (4), we get

$$n!P_{n+1}(\theta \left(f\right),e_{yy},\dots ,e_{yy})+\sum _{w\in S_{n+1},w\left(1\right)\ne 1}{P}_{n+1}(\theta \left(e_{yy}\right),f_{w\left(2\right)},\dots ,f_{w(n+1)})=0.$$

(5)

Now replace f with ${f|}_x^y\in \tilde{I}(X,R)$, where ${f|}_x^y={\sum }_{x\le u\le v\le y}f(u,v)e_{uv}$. Since ${\varphi }_{xy}{:f\mapsto f|}_x^y$ is an algebra homomorphism, we apply the same substitution

$$n!P_{n+1}(\theta \left(f{|}_x^y\right),e_{yy},\dots ,e_{yy})+\sum _{w\in S_{n+1},w\left(1\right)\ne 1}{P}_{n+1}(\theta \left(e_{yy}\right),f_{w\left(2\right)},\dots ,f_{w(n+1)})=0.$$

(6)

The second terms in (5) and (6) are identical, as they depend only on $\theta \left(e_{yy}\right)$ and $e_{yy}$. Subtracting (6) from (5), we obtain

$$n!\left(P_{n+1}(\theta \left(f\right),e_{yy},\dots ,e_{yy})-P_{n+1}(\theta \left(f{|}_x^y\right),e_{yy},\dots ,e_{yy})\right)=0.$$

Since R is $n!$-torsion free, we have

$$P_{n+1}(\theta \left(f\right),e_{yy},\dots ,e_{yy})=P_{n+1}(\theta \left(f{|}_x^y\right),e_{yy},\dots ,e_{yy}).$$

(7)

Evaluate at $(x,y)$. For any $g\in I(X,R)$, compute the supercommutator with $e_{yy}$

$${[g,e_{yy}]}_s(x,y)=\left(g{e}_{yy}\right)(x,y)-{(-1)}^{\left|g\right|·0}\left(e_{yy}g\right)(x,y)=g(x,y){\delta }_{yy}-e_{yy}(x,z)g(z,y)=g(x,y){\delta }_{yy}.$$

Since $x<y$, ${\delta }_{yy}=0$ unless $x=y$, so ${[g,e_{yy}]}_s(x,y)=0$. Iteratively, for $P_{n+1}$

$$P_2(\theta \left(f\right),e_{yy})(x,y)={[\theta \left(f\right),e_{yy}]}_s(x,y)=\theta \left(f\right)(x,y){\delta }_{yy}=0,$$

and higher iterates $P_{n+1}={[P_n,e_{yy}]}_s$ yield zero at $(x,y)$. Similarly, for the restricted function

$$P_{n+1}(\theta \left(f{|}_x^y\right),e_{yy},\dots ,e_{yy})(x,y)=0.$$

However, we need the value of $P_2(\theta \left(f\right),e_{yy})(x,y)$. Recompute

$${[g,e_{yy}]}_s(x,y)=g(x,y){\delta }_{yy}+{(-1)}^{\left|g\right|}{e}_{yy}(x,z)g(z,y)=0\mathrm{for}x\ne y.$$

Instead, use Lemma 2.9 adapted to the superalgebra context. For any $f,g\in I(X,R)$, $x<y$

$$\left(fg\right)(x,y)=\left(f{|}_x^{y}g\right)(x,y)=\left(fg{|}_x^y\right)(x,y)={\left(f\right|}_x^{y}g{|}_x^y)(x,y).$$

Consider ${[g,e_{yy}]}_s$. For $e_{xx}g{e}_{yy}=g(x,y)e_{xy}$, we need

$$\theta \left(f\right)(x,y)e_{xy}={[\theta \left(f\right),e_{yy}]}_s(x,y).$$

Apply ${\varphi }_{xy}$ to both sides of (7)

$${\varphi }_{xy}\left(P_{n+1}(\theta \left(f\right),e_{yy},\dots ,e_{yy})\right)={\varphi }_{xy}\left(P_{n+1}(\theta \left(f{|}_x^y\right),e_{yy},\dots ,e_{yy})\right).$$

Since ${\varphi }_{xy}$ is an algebra homomorphism and $e_{yy}\in \tilde{I}(X,R)$, we evaluate at $(x,y)$

$$P_{n+1}(\theta \left(f\right),e_{yy},\dots ,e_{yy})(x,y)=\theta \left(f\right)(x,y),$$

because higher supercommutators vanish due to $e_{yy}$’s idempotence and degree 0. Similarly

$$P_{n+1}(\theta \left(f{|}_x^y\right),e_{yy},\dots ,e_{yy})(x,y)=\theta \left(f{|}_x^y\right)(x,y).$$

From (7), since R is $n!$-torsion free

$$\theta \left(f\right)(x,y)=\theta \left(f{|}_x^y\right)(x,y).$$

This completes the proof. □

Theorem 1.

Let $\theta :I(X,R)\to I(X,R)$ be a supercommuting map on the incidence algebra $I(X,R)$, where R is 2-torsion free and $n!$-torsion free, and any two directed edges in the complete Hasse diagram $(X,D)$ are contained in one cycle. Then θ is proper.

Proof. 

Assume $n\ge 2$ without loss of generality, as the case $n=1$ corresponds to the supercommuting condition ${[\theta \left(f\right),f]}_s=0$. Restrict $\theta$ to $\tilde{I}(X,R)$, the subalgebra of functions nonzero at finitely many pairs $(x,y)$, and denote the restriction by ${\theta }_{\tilde{I}}:\tilde{I}(X,R)\to I(X,R)$. Since $\theta$ is supercommuting, for all $f\in \tilde{I}(X,R)$, we have ${[{\theta }_{\tilde{I}}\left(f\right),f]}_s={[\theta \left(f\right),f]}_s=0$.

By the superalgebra analogue of [9], adapted to $\tilde{I}(X,R)$, if ${\theta }_{\tilde{I}}$ satisfies $[{[\dots {[{\theta }_{\tilde{I}}\left(f\right),f]}_s,f]}_s,$${\dots ,f]}_s{]}_s=0$ (with n supercommutators), then ${[{\theta }_{\tilde{I}}\left(f\right),f]}_s=0$, which is already satisfied since $\theta$ is supercommuting. By the superalgebra version of [9] [Theorem 2.5], since $\tilde{I}(X,R)$ inherits the superalgebra structure and the cycle condition holds, ${\theta }_{\tilde{I}}$ is proper. Thus, there exists $\lambda \in Z_s\left(I(X,R)\right)$ and an R-linear map $\tilde{\mu }:\tilde{I}(X,R)\to Z_s\left(I(X,R)\right)$ such that

$${\theta }_{\tilde{I}}\left(f\right)=\lambda f+\tilde{\mu }\left(f\right)\mathrm{for}\mathrm{all}f\in \tilde{I}(X,R).$$

Since X is connected and the Hasse diagram satisfies the cycle condition, the supercenter $Z_s\left(I(X,R)\right)$ consists of diagonal functions constant on connected components, and for a connected X, $Z_s\left(I(X,R)\right)\cong R$ (analogous to [33]). Thus, we may take $\lambda \in R$.

Define $\mu :I(X,R)\to I(X,R)$ by

$$\mu \left(f\right)=\theta \left(f\right)-\lambda f\mathrm{for}\mathrm{all}f\in I(X,R).$$

We need to show that $\mu$ is central-valued, i.e., $\mu \left(f\right)\in Z_s\left(I(X,R)\right)$ for all $f\in I(X,R)$. For $f\in \tilde{I}(X,R)$, we have

$$\mu \left(f\right)=\theta \left(f\right)-\lambda f={\theta }_{\tilde{I}}\left(f\right)=\lambda f+\tilde{\mu }\left(f\right)-\lambda f=\tilde{\mu }\left(f\right)\in Z_s\left(I(X,R)\right),$$

since $\tilde{\mu }\left(f\right)\in Z_s\left(I(X,R)\right)$. For any $f\in I(X,R)$ and $x<y$, by Lemma 4, we have

$$\theta \left(f\right)(x,y)=\theta \left(f{|}_x^y\right)(x,y).$$

Thus,

$$\mu \left(f\right)(x,y)=\theta \left(f\right)(x,y)-\lambda f(x,y)=\theta \left(f{|}_x^y\right)(x,y)-\lambda f(x,y)=\tilde{\mu }\left(f{|}_x^y\right)(x,y)=0,$$

since $\tilde{\mu }\left(f{|}_x^y\right)\in Z_s\left(I(X,R)\right)$, and elements in the supercenter are diagonal (i.e., zero off the diagonal). Hence, $\mu \left(f\right)(x,y)=0$ for all $x\ne y$, so $\mu \left(f\right)$ is diagonal

$$\mu \left(f\right)=\sum _{x\in X}\mu \left(f\right)(x,x)e_{xx}.$$

Next, we prove that $\mu \left(f\right)(x,x)=\mu \left(f\right)(y,y)$ for all $x,y\in X$, ensuring $\mu \left(f\right)\in Z_s\left(I(X,R)\right)$. Since X is connected, it suffices to show $\mu \left(f\right)(x,x)=\mu \left(f\right)(y,y)$ for $x<y$. Consider the map $\mathrm{\Theta }:I{(X,R)}^{n+1}\to I(X,R)$

$$\mathrm{\Theta }(f_1,f_2,\dots ,f_{n+1})=P_{n+1}(\theta \left(f_1\right),f_2,\dots ,f_{n+1}),$$

where $P_1\left(x_1\right)=x_1$, $P_2(x_1,x_2)={[x_1,x_2]}_s$, and $P_m(x_1,\dots ,x_m)={[P_{m-1}(x_1,\dots ,x_{m-1}),x_m]}_s$. Since $\theta$ is supercommuting, $P_2(\theta \left(f\right),f)={[\theta \left(f\right),f]}_s=0$. Linearizing $P_{n+1}(\theta \left(f\right),f,\dots ,f)=0$, we get

$$\sum _{w\in S_{n+1}}{P}_{n+1}(\theta \left(f_{w\left(1\right)}\right),f_{w\left(2\right)},\dots ,f_{w(n+1)})=0.$$

Replace $\theta$ with $\mu$, since $\mu \left(f\right)=\theta \left(f\right)-\lambda f$ and $\lambda f$ supercommutes with f. Set $f_1=f$, $f_2=e_{xy}$, and $f_3=\dots =f_{n+1}=e_{yy}$. Then

$$\sum _{w\in S_{n+1},w\left(1\right)=1}{P}_{n+1}(\mu \left(f\right),f_{w\left(2\right)},\dots ,f_{w(n+1)})=0,$$

since terms with $w\left(1\right)\ne 1$ involve $\mu \left(e_{yy}\right)$, which is diagonal. This simplifies to

$$(n-1)!P_{n+1}(\mu \left(f\right),e_{xy},e_{yy},\dots ,e_{yy})=0,$$

as $e_{xy}$ appears once with $(n-1)!$ permutations. Since R is $n!$-torsion free, we have

$$P_{n+1}(\mu \left(f\right),e_{xy},e_{yy},\dots ,e_{yy})(x,y)=0.$$

We find

$$P_2(\mu \left(f\right),e_{xy})={[\mu \left(f\right),e_{xy}]}_s=\mu \left(f\right)e_{xy}-{(-1)}^{\left|\mu \left(f\right)\right|·|e_{xy}|}{e}_{xy}\mu \left(f\right).$$

Since $\mu \left(f\right)={\sum }_{z\in X}\mu \left(f\right)(z,z)e_{zz}$ is diagonal and even ($\left|\mu \right(f\left)\right|=0$), and $|e_{xy}|=1$, we get

$$\begin{array}{cc}\hfill {[\mu \left(f\right),e_{xy}]}_s(x,y)& =\left(\mu \left(f\right)e_{xy}\right)(x,y)+\left(e_{xy}\mu \left(f\right)\right)(x,y)\hfill \\ \hfill & =\mu \left(f\right)(x,x)e_{xy}(x,y)+e_{xy}(x,y)\mu \left(f\right)(y,y)\hfill \\ \hfill & =\mu \left(f\right)(x,x)-\mu \left(f\right)(y,y).\hfill \end{array}$$

Higher supercommutators with $e_{yy}$ (even), yield

$$P_{n+1}(\mu \left(f\right),e_{xy},e_{yy},\dots ,e_{yy})(x,y)={[\mu \left(f\right),e_{xy}]}_s(x,y)=\mu \left(f\right)(x,x)-\mu \left(f\right)(y,y).$$

Thus,

$$\mu \left(f\right)(x,x)-\mu \left(f\right)(y,y)=0\Rightarrow \mu \left(f\right)(x,x)=\mu \left(f\right)(y,y).$$

Since X is connected, $\mu \left(f\right)(x,x)=c$ for some $c\in R$, so

$$\mu \left(f\right)=c\sum _{x\in X}{e}_{xx}\in Z_s\left(I(X,R)\right).$$

Hence, $\theta \left(f\right)=\lambda f+\mu \left(f\right)$, and $\theta$ is proper. The cycle condition ensures consistency of coefficients, as in [9]. □

Example 3.

Let $R=\mathbb{Z}$, which is $n!$-torsion free for all $n\ge 1$, and let $X=\{1,2,3\}$ with the natural order $1<2<3$. The incidence algebra $I(X,R)$ has $\mathbb{Z}$-basis

$$e_{11},e_{22},e_{33},e_{12},e_{23},e_{13},$$

where $e_{ij}$ denotes the characteristic function of $(i,j)$.

Choose the idempotent $e=e_{11}+e_{22}$. Then the induced ${\mathbb{Z}}_2$-grading is

$$A_0=eI(X,R)e+(1-e)I(X,R)(1-e),A_1=eI(X,R)(1-e)+(1-e)I(X,R)e.$$

Define $\theta :I(X,R)\to I(X,R)$ by

$$\theta \left(f\right)=2f+\left(\sum _{i=1}^{3}f(i,i)\right)·\sum _{j=1}^3{e}_{jj},f\in I(X,R).$$

That is, $\theta \left(f\right)$ is obtained by doubling f and then adding a diagonal function whose entries are all equal to the trace ${\sum }_{i=1}^{3}f(i,i)$.

Claim. θ is a supercommuting map and hence proper.

Proof. For $f\in I(X,R)$ write

$$\theta \left(f\right)=2f+\mu \left(f\right),$$

where $\mu \left(f\right)=\left({\sum }_{i=1}^{3}f(i,i)\right){\sum }_{j=1}^3{e}_{jj}$. Since $\mu \left(f\right)$ is diagonal with constant diagonal entries, we have $\mu \left(f\right)\in Z_s\left(I(X,R)\right)$. As $2f$ clearly supercommutes with f, and central elements also supercommute, it follows that

$${[\theta \left(f\right),f]}_s={[2f+\mu \left(f\right),f]}_s=2{[f,f]}_s+{[\mu \left(f\right),f]}_s=0.$$

Thus θ is supercommuting. By Theorem 1, θ is proper, with $\lambda =2$ and μ central-valued. □

5. The General Case

In this section, we study supercommuting maps on the incidence algebra $I(X,R)$ in the general case, i.e., without assuming connectedness of X. Let R be a commutative ring with unity that is $n!$-torsion free, and let $I(X,R)$ be endowed with a superalgebra structure via a nontrivial idempotent e, with even part $A_0=eI(X,R)e+(1-e)I(X,R)(1-e)$ and odd part $A_1=eI(X,R)(1-e)+(1-e)I(X,R)e$. The supercommutator is defined as ${[a,b]}_s=ab-{(-1)}^{\left|a\right|\left|b\right|}ba$ for homogeneous elements $a,b\in A_0\cup A_1$, extended linearly. For a positive integer n, we define the super-n-center of an R-algebra A as follows:

$$Z_s{\left(A\right)}_n=\{a\in A\mid {[a,x]}_s^n=0,\forall x\in A\},$$

where ${[a,x]}_s^1={[a,x]}_s$, and ${[a,x]}_s^n={[{[a,x]}_s^{n-1},x]}_s$ for $n\ge 2$. Clearly, $Z_s{\left(A\right)}_1=Z_s\left(A\right)$, the supercenter of A.

Lemma 5.

Let ${\left\{X_i\right\}}_{i\in J}$ be the family of connected components of a locally finite pre-ordered set X, and let $I(X,R)={⨁}_{i\in J}I(X_i,R)$ be the incidence algebra over a commutative ring R that is $n!$-torsion free, endowed with a superalgebra structure. Let θ be a supercommuting map on $I(X,R)$, i.e., ${[\theta \left(f\right),f]}_s=0$ for all $f\in I(X,R)$. Then, for each $i\in J$, there exists a unique supercommuting map ${\theta }_i$ on $I(X_i,R)$ and a unique map ${\theta }_i^{\perp }:I(X_i,R)\to {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(I(X_j,R)\right)}_n$ such that the restriction of θ on $I(X_i,R)$ satisfies:

$${\theta |}_{I(X_i,R)}={\theta }_i+{\theta }_i^{\perp }.$$

Proof. 

Since X is a locally finite pre-ordered set, its connected components ${\left\{X_i\right\}}_{i\in J}$ partition X, and the incidence algebra decomposes as $I(X,R)={⨁}_{i\in J}I(X_i,R)$, where each $I(X_i,R)$ is a subalgebra with the induced superalgebra structure. For each $i\in J$, let ${\pi }_i:{⨁}_{j\in J}I(X_j,R)\to I(X_i,R)$ be the canonical projection onto $I(X_i,R)$, and let ${\pi }_i^{\perp }:{⨁}_{j\in J}I(X_j,R)\to {⨁}_{j\in J\setminus \left\{i\right\}}I(X_j,R)$ be the canonical projection onto the complementary subalgebra. Define

$${\theta }_i={\pi }_i\circ \theta {{|}_{I(X_i,R)},{\theta }_i^{\perp }={\pi }_i^{\perp }\circ \theta |}_{I(X_i,R)}.$$

Clearly, ${\theta |}_{I(X_i,R)}={\theta }_i+{\theta }_i^{\perp }$, and this decomposition is unique since ${\pi }_i$ and ${\pi }_i^{\perp }$ project onto complementary subspaces.

For any $f\in I(X_i,R)$, since $\theta$ is supercommuting, we have

$${[\theta \left(f\right),f]}_s=\theta \left(f\right)f-{(-1)}^{\left|\theta \right(f\left)\right|\left|f\right|}f\theta \left(f\right)=0.$$

Write $\theta \left(f\right)={\theta }_i\left(f\right)+{\theta }_i^{\perp }\left(f\right)$, where ${\theta }_i\left(f\right)\in I(X_i,R)$ and ${\theta }_i^{\perp }\left(f\right)\in {⨁}_{j\in J\setminus \left\{i\right\}}I(X_j,R)$. Since $f\in I(X_i,R)$, we have $fg=0=gf$ for any $g\in I(X_j,R)$ with $j\ne i$, as $f(x,y)\ne 0$ only if $x,y\in X_i$. Thus

$$\theta \left(f\right)f=({\theta }_i\left(f\right)+{\theta }_i^{\perp }\left(f\right))f={\theta }_i\left(f\right)f,f\theta \left(f\right)=f({\theta }_i\left(f\right)+{\theta }_i^{\perp }\left(f\right))=f{\theta }_i\left(f\right),$$

since ${\theta }_i^{\perp }\left(f\right)f=0=f{\theta }_i^{\perp }\left(f\right)$. Hence

$${[\theta \left(f\right),f]}_s={[{\theta }_i\left(f\right)+{\theta }_i^{\perp }\left(f\right),f]}_s={\theta }_i\left(f\right)f-{(-1)}^{|{\theta }_i\left(f\right)\left|\right|f|}f{\theta }_i\left(f\right)={[{\theta }_i\left(f\right),f]}_s=0.$$

This shows that ${\theta }_i$ is a supercommuting map on $I(X_i,R)$.

Next, we show that ${\theta }_i^{\perp }\left(f\right)\in {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(I(X_j,R)\right)}_n$. Define the map $\mathrm{\Theta }:I{(X,R)}^{n+1}\to I(X,R)$ by

$$\mathrm{\Theta }(f_1,f_2,\dots ,f_{n+1})=P_{n+1}(\theta \left(f_1\right),f_2,\dots ,f_{n+1}),$$

where $P_1\left(x_1\right)=x_1$, $P_2(x_1,x_2)={[x_1,x_2]}_s$, and $P_m(x_1,\dots ,x_m)={[P_{m-1}(x_1,\dots ,x_{m-1}),x_m]}_s$ for $m\ge 2$. Since $\theta$ is supercommuting, $P_2(\theta \left(f\right),f)={[\theta \left(f\right),f]}_s=0$. For n-fold supercommuting, we assume $P_{n+1}(\theta \left(f\right),f,\dots ,f)={[\theta \left(f\right),f]}_s^n=0$. Linearizing this condition gives

$$\sum _{w\in S_{n+1}}{P}_{n+1}(\theta \left(f_{w\left(1\right)}\right),f_{w\left(2\right)},\dots ,f_{w(n+1)})=0.$$

Let $f_1=f\in I(X_i,R)$ and $f_2=\dots =f_{n+1}=g\in I(X_j,R)$ for some $j\ne i$. Then

$$\begin{array}{cc}\hfill \sum _{w\in S_{n+1}}{P}_{n+1}(\theta \left(f_{w\left(1\right)}\right),f_{w\left(2\right)},\dots ,f_{w(n+1)})& =\sum _{w\left(1\right)=1}{P}_{n+1}(\theta \left(f\right),g,\dots ,g)\hfill \\ \hfill & +\sum _{w\left(1\right)\ne 1}{P}_{n+1}(\theta \left(g\right),f_{w\left(2\right)},\dots ,f_{w(n+1)})=0.\hfill \end{array}$$

Since $f\in I(X_i,R)$, $g\in I(X_j,R)$, and $j\ne i$, we have $fg=0=gf$. We find

$$P_{n+1}(\theta \left(f\right),g,\dots ,g)={[{\theta }_i^{\perp }\left(f\right),g]}_s^n,$$

because ${\theta }_i\left(f\right)\in I(X_i,R)$, so ${[{\theta }_i\left(f\right),g]}_s={\theta }_i\left(f\right)g-{(-1)}^{|{\theta }_i\left(f\right)\left|\right|g|}g{\theta }_i\left(f\right)=0$. The second term involves $\theta \left(g\right)$, but we focus on the first term

$$\sum _{w\left(1\right)=1}{P}_{n+1}(\theta \left(f\right),g,\dots ,g)=n!{[{\theta }_i^{\perp }\left(f\right),g]}_s^n.$$

Since R is $n!$-torsion free, we get

$${[{\theta }_i^{\perp }\left(f\right),g]}_s^n=0,\forall g\in I(X_j,R),j\ne i.$$

Thus, ${\theta }_i^{\perp }\left(f\right)\in {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(I(X_j,R)\right)}_n$, as ${\theta }_i^{\perp }\left(f\right)$ has support only in ${⨁}_{j\in J\setminus \left\{i\right\}}I(X_j,R)$. This completes the proof. □

Proposition 2.

Let ${\left\{A_i\right\}}_{i\in J}$ be a family of $n!$-torsion free R-algebras, each endowed with a superalgebra structure. If $Z_s{\left(A_i\right)}_n=Z_s\left(A_i\right)$ for all $i\in J$, then every n-supercommuting map on ${⨁}_{i\in J}{A}_i$, satisfying ${[\theta \left(a\right),a]}_s^n=0$ for all $a\in {⨁}_{i\in J}{A}_i$, is proper if and only if every n-supercommuting map on $A_i$ is proper for all $i\in J$.

Proof. 

Let $\theta$ be an n-supercommuting map on ${⨁}_{i\in J}{A}_i$, i.e., ${[\theta \left(a\right),a]}_s^n=0$ for all $a\in {⨁}_{i\in J}{A}_i$. By the superalgebra analogue of Lemma 5, for each $i\in J$, the restriction ${\theta |}_{A_i}={\theta }_i+{\theta }_i^{\perp }$, where ${\theta }_i:A_i\to A_i$ is an n-supercommuting map, and ${\theta }_i^{\perp }:A_i\to {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(A_j\right)}_n$ is an R-linear map.

Sufficiency: Assume every n-supercommuting map on $A_i$ is proper for all $i\in J$. Then, for each $i\in J$, there exist ${\lambda }_i\in Z_s\left(A_i\right)$ and an R-linear map ${\mu }_i:A_i\to Z_s\left(A_i\right)$ such that ${\theta }_i\left(a_i\right)={\lambda }_i{a}_i+{\mu }_i\left(a_i\right)$ for all $a_i\in A_i$. Define the R-linear map $\mu :{⨁}_{i\in J}{A}_i\to {⨁}_{i\in J}{Z}_s\left(A_i\right)$ by

$$\mu \left(a\right)=\sum _{i\in J}{\mu }_i\left(a_i\right),$$

where $a={\sum }_{i\in J}{a}_i$ with $a_i\in A_i$. Define

$$C\left(a\right)=\theta \left(a\right)-\sum _{i\in J}{\lambda }_i{a}_i-\mu \left(a\right),$$

for all $a={\sum }_{i\in J}{a}_i\in {⨁}_{i\in J}{A}_i$. We need to show that $C\left(a\right)\in Z_s\left({⨁}_{i\in J}{A}_i\right)$. Since $\theta$ is n-supercommuting, we have the linearized condition

$$\sum _{w\in S_{n+1}}{P}_{n+1}{(\theta \left(a_{w\left(1\right)}\right),a_{w\left(2\right)},\dots ,a_{w(n+1)})}_s=0,$$

where $P_m{(x_1,\dots ,x_m)}_s={[P_{m-1}{(x_1,\dots ,x_{m-1})}_s,x_m]}_s$ and $P_1{\left(x_1\right)}_s=x_1$. Set $a_1=a={\sum }_{i\in J}{a}_i$ and $a_2=\dots =a_{n+1}=x\in A_i$ for some $i\in J$. This gives

$$\begin{array}{cc}\hfill n!P_{n+1}{(C\left(a\right),x,\dots ,x)}_s& =\sum _{w\in S_{n+1},w\left(1\right)=1}{P}_{n+1}{(C\left(a\right),x,\dots ,x)}_s\hfill \\ \hfill & =-\sum _{w\in S_{n+1},w\left(1\right)\ne 1}{P}_{n+1}{(C\left(x\right),x_{w\left(2\right)},\dots ,x_{w(n+1)})}_s.\hfill \end{array}$$

Compute $C\left(a\right)$,

$$C\left(a\right)=\theta \left(a\right)-\sum _{i\in J}{\lambda }_i{a}_i-\mu \left(a\right)=\sum _{i\in J}\left({\theta }_i\left(a_i\right)+{\theta }_i^{\perp }\left(a_i\right)-{\lambda }_i{a}_i-{\mu }_i\left(a_i\right)\right).$$

Since ${\theta }_i\left(a_i\right)={\lambda }_i{a}_i+{\mu }_i\left(a_i\right)$, we have

$$C\left(a\right)=\sum _{i\in J}{\theta }_i^{\perp }\left(a_i\right).$$

For $x\in A_i$, evaluate

$$P_{n+1}{(C\left(a\right),x,\dots ,x)}_s=P_{n+1}{\left(\sum _{j\in J}{\theta }_j^{\perp }\left(a_j\right),x,\dots ,x\right)}_s.$$

Since ${\theta }_j^{\perp }\left(a_j\right)\in {⨁}_{k\in J\setminus \left\{j\right\}}{Z}_s{\left(A_k\right)}_n$ and $x\in A_i$, for $j\ne i$, we have ${[{\theta }_j^{\perp }\left(a_j\right),x]}_s=0$ because ${\theta }_j^{\perp }\left(a_j\right)$ has no component in $A_i$. Thus

$$P_{n+1}{(C\left(a\right),x,\dots ,x)}_s=P_{n+1}{({\theta }_i^{\perp }\left(a_i\right),x,\dots ,x)}_s.$$

Now,

$$-\sum _{w\in S_{n+1},w\left(1\right)\ne 1}{P}_{n+1}{(C\left(x\right),x_{w\left(2\right)},\dots ,x_{w(n+1)})}_s=-\sum _{w\in S_{n+1},w\left(1\right)\ne 1}{P}_{n+1}{({\theta }_i^{\perp }\left(x\right),x,\dots ,x)}_s.$$

Since ${\theta }_i^{\perp }\left(x\right)\in {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(A_j\right)}_n$, we have $P_{n+1}{({\theta }_i^{\perp }\left(x\right),x,\dots ,x)}_s=0$ because ${[{\theta }_i^{\perp }\left(x\right),x]}_s^n=0$. Thus,

$$-\sum _{w\in S_{n+1},w\left(1\right)\ne 1}{P}_{n+1}{({\theta }_i^{\perp }\left(x\right),x,\dots ,x)}_s=0.$$

Hence,

$$n!P_{n+1}{({\theta }_i^{\perp }\left(a_i\right),x,\dots ,x)}_s=0.$$

Since R is $n!$-torsion free and $Z_s{\left(A_j\right)}_n=Z_s\left(A_j\right)$ for all $j\in J\setminus \left\{i\right\}$, we have

$$P_{n+1}{({\theta }_i^{\perp }\left(a_i\right),x,\dots ,x)}_s={[{\theta }_i^{\perp }\left(a_i\right),x]}_s^n=0,\forall x\in A_i.$$

Thus, ${\theta }_i^{\perp }\left(a_i\right)\in Z_s{\left(A_i\right)}_n=Z_s\left(A_i\right)$. However, since ${\theta }_i^{\perp }\left(a_i\right)\in {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(A_j\right)}_n$ and $Z_s\left(A_i\right)\cap {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(A_j\right)}_n=\left\{0\right\}$, we must have ${\theta }_i^{\perp }\left(a_i\right)=0$. Therefore

$$C\left(a\right)=\sum _{i\in J}{\theta }_i^{\perp }\left(a_i\right)=0.$$

This implies

$$\theta \left(a\right)=\sum _{i\in J}({\lambda }_i{a}_i+{\mu }_i\left(a_i\right))=\sum _{i\in J}{\lambda }_i{a}_i+\mu \left(a\right).$$

Since ${⨁}_{i\in J}{Z}_s\left(A_i\right)=Z_s\left({⨁}_{i\in J}{A}_i\right)$ and $\mu \left(a\right)\in {⨁}_{i\in J}{Z}_s\left(A_i\right)$, we can define $\lambda ={\left({\lambda }_i\right)}_{i\in J}\in Z_s\left({⨁}_{i\in J}{A}_i\right)$, where $\lambda a={\sum }_{i\in J}{\lambda }_i{a}_i$. Thus:

$$\theta \left(a\right)=\lambda a+\mu \left(a\right),$$

where $\lambda \in Z_s\left({⨁}_{i\in J}{A}_i\right)$ and $\mu :{⨁}_{i\in J}{A}_i\to Z_s\left({⨁}_{i\in J}{A}_i\right)$ is R-linear. Hence, $\theta$ is proper.

Necessity: Suppose there exists some $i\in J$ such that not every n-supercommuting map on $A_i$ is proper. Then there exists an n-supercommuting map ${\theta }_i:A_i\to A_i$ that is improper. Construct a map $\theta :{⨁}_{i\in J}{A}_i\to {⨁}_{i\in J}{A}_i$ by

$$\theta \left(a\right)=\sum _{i\in J}{\theta }_i^{\prime }\left(a_i\right),$$

where ${\theta }_i^{\prime }={\theta }_i$ for the given i, and for $j\ne i$, ${\theta }_j^{\prime }:A_j\to A_j$ is a proper n-supercommuting map, say ${\theta }_j^{\prime }\left(a_j\right)={\lambda }_j{a}_j$ for some ${\lambda }_j\in Z_s\left(A_j\right)$. For $a={\sum }_{i\in J}{a}_i$, compute

$${[\theta \left(a\right),a]}_s^n=\sum _{i\in J}{[{\theta }_i^{\prime }\left(a_i\right),a_i]}_s^n,$$

since ${[a_i,a_j]}_s=0$ for $i\ne j$. Since each ${\theta }_i^{\prime }$ is n-supercommuting, ${[{\theta }_i^{\prime }\left(a_i\right),a_i]}_s^n=0$, so $\theta$ is n-supercommuting. However, ${\theta }_i$ is improper, so $\theta$ cannot be proper, as its restriction to $A_i$ is ${\theta }_i$. This completes the proof. □

Theorem 2.

Let R be a commutative ring with unity that is 2-torsion free and $n!$-torsion free for some positive integer n. Let X be a locally finite pre-ordered set with connected components ${\left\{X_i\right\}}_{i\in J}$, and let $I(X,R)={⨁}_{i\in J}I(X_i,R)$ be the incidence algebra endowed with a superalgebra structure via a nontrivial idempotent e. If any two directed edges in each connected component $(X_i,D_i)$ of the complete Hasse diagram are contained in one cycle, then every supercommuting map $\theta :I(X,R)\to I(X,R)$ is proper.

Proof. 

Since X is a locally finite pre-ordered set, its incidence algebra decomposes as $I(X,R)={⨁}_{i\in J}I(X_i,R)$, where each $I(X_i,R)$ is a subalgebra with the induced superalgebra structure via e. By Lemma 5, for a supercommuting map $\theta$ on $I(X,R)$, the restriction to $I(X_i,R)$ is ${\theta |}_{I(X_i,R)}={\theta }_i+{\theta }_i^{\perp }$, where ${\theta }_i:I(X_i,R)\to I(X_i,R)$ is supercommuting, and ${\theta }_i^{\perp }:I(X_i,R)\to {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(I(X_j,R)\right)}_n$.

Since each $(X_i,D_i)$ satisfies the cycle condition (any two directed edges are in one cycle), by Theorem 1, every supercommuting map ${\theta }_i$ on $I(X_i,R)$ is proper. Thus, there exist ${\lambda }_i\in Z_s\left(I(X_i,R)\right)$ and an R-linear map ${\mu }_i:I(X_i,R)\to Z_s\left(I(X_i,R)\right)$ such that

$${\theta }_i\left(f_i\right)={\lambda }_i{f}_i+{\mu }_i\left(f_i\right),\forall f_i\in I(X_i,R).$$

Since R is $n!$-torsion free, Lemma 5 implies ${\theta }_i^{\perp }\left(f_i\right)\in {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s{\left(I(X_j,R)\right)}_n$. For incidence algebras, the super-n-center $Z_s{\left(I(X_j,R)\right)}_n$ coincides with supercenter $Z_s\left(I(X_j,R)\right)$, as elements in $Z_s{\left(I(X_j,R)\right)}_n$ must supercommute with all basis elements $e_{xy}$ up to the n-th supercommutator, which forces them to be diagonal and constant on connected components, as shown in [33].

From the proof of Proposition 2, since $Z_s{\left(I(X_j,R)\right)}_n=Z_s\left(I(X_j,R)\right)$, we have ${\theta }_i^{\perp }\left(f_i\right)=0$ for all $f_i\in I(X_i,R)$, because ${\theta }_i^{\perp }\left(f_i\right)\in Z_s\left(I(X_i,R)\right)\cap {⨁}_{j\in J\setminus \left\{i\right\}}{Z}_s\left(I(X_j,R)\right)=\left\{0\right\}$. Thus

$$\theta \left(f_i\right)={\theta }_i\left(f_i\right)={\lambda }_i{f}_i+{\mu }_i\left(f_i\right).$$

For any $f={\sum }_{i\in J}{f}_i\in I(X,R)$, define

$$\lambda ={\left({\lambda }_i\right)}_{i\in J}\in \underset{i\in J}{⨁}{Z}_s\left(I(X_i,R)\right)=Z_s\left(I(X,R)\right),$$

$$\mu \left(f\right)=\sum _{i\in J}{\mu }_i\left(f_i\right).$$

Since $f_i{g}_j=0=g_j{f}_i$ for $i\ne j$, we have

$$\theta \left(f\right)=\sum _{i\in J}\theta \left(f_i\right)=\sum _{i\in J}({\lambda }_i{f}_i+{\mu }_i\left(f_i\right))=\lambda f+\mu \left(f\right).$$

Since ${\mu }_i\left(f_i\right)\in Z_s\left(I(X_i,R)\right)$, we have $\mu \left(f\right)\in {⨁}_{i\in J}{Z}_s\left(I(X_i,R)\right)=Z_s\left(I(X,R)\right)$, and $\mu$ is R-linear. Thus, $\theta$ is proper, completing the proof. □

Example 4.

Let $X=\{1,2,\dots ,m\}$ and equip X with the pre-order generated by the directed m-cycle

$$1<2<\cdots <m<1.$$

The transitive closure of these relations gives $i\le j$ for every pair $(i,j)$, so every pair of vertices is comparable (in both directions). Hence

$$I(X,R)=\{f:X\times X\to R\mid f(i,j)=0\mathrm{unless}i\le j\}$$

is the full matrix algebra $M_m\left(R\right)$ (identify f with the matrix ${\left(f(i,j)\right)}_{1\le i,j\le m}$).

Choose the nontrivial idempotent $e=e_{11}$ (the matrix unit). The induced superalgebra grading is

$$A_0=e{M}_m\left(R\right)e+(1-e)M_m\left(R\right)(1-e),A_1=e{M}_m\left(R\right)(1-e)+(1-e)M_m\left(R\right)e.$$

The (super-)center of $M_m\left(R\right)$ is the scalar matrices,

$$Z_s\left(M_m\left(R\right)\right)=Z\left(M_m\left(R\right)\right)=R·I_m.$$

Now apply Theorem 2. The cycle condition (any two directed edges lie in one cycle) is obviously satisfied here (the single cycle contains all edges). Therefore every supercommuting map $\theta :I(X,R)\to I(X,R)$ is proper: there exist $\lambda \in R$ and an R-linear map $\mu :M_m\left(R\right)\to R·I_m$ such that

$$\theta \left(A\right)=\lambda A+\mu \left(A\right)(\forall A\in M_m\left(R\right)).$$

Remark. conversely, not every map of the form $\lambda A+\mu \left(A\right)$ is automatically supercommuting (extra graded constraints may further restrict $\lambda ,\mu$). The theorem asserts: if θ does supercommute, then it must be of the above form.

Example 5.

Let $X=X_1\bigsqcup X_2,$ where $X_1=\{1,2,3\}$ forms a directed 3-cycle and $X_2=\{4,5,6,7\}$ forms a directed 4-cycle. As in Example 4, taking the transitive closure on each $X_i$ makes every pair inside $X_i$ comparable. Hence,

$$I(X,R)=I(X_1,R)\oplus I(X_2,R)\cong M_3\left(R\right)\oplus M_4\left(R\right).$$

Denote

$$A_1:=I(X_1,R)\cong M_3\left(R\right)\mathrm{and}{A}_2:=I(X_2,R)\cong M_4\left(R\right).$$

The superalgebra structure is induced by the same fixed nontrivial idempotent e, which splits each block according to the matrix decomposition.

Let $\theta :I(X,R)\to I(X,R)$ be a supercommuting map. By Lemma 5, we may write, for $i=1,2$,

$${\theta |}_{A_i}={\theta }_i+{\theta }_i^{\perp },$$

where ${\theta }_i:A_i\to A_i$ is supercommuting and

$${\theta }_i^{\perp }:A_i\to \underset{j\ne i}{⨁}{Z}_s{\left(A_j\right)}_n$$

takes values in the super-n-center of the other component. In our matrix-algebra components, we have $Z_s{\left(A_j\right)}_n=Z_s\left(A_j\right)=R·I_{n_j}$ (scalar matrices for each block). Hence, each ${\theta }_i^{\perp }\left(a_i\right)$ is a scalar matrix in the other block.

We now show that ${\theta }_i^{\perp }\equiv 0$. Fix i and take $a_i\in A_i$ and $x\in A_i$ arbitrary. Linearizing the n-fold supercommuting identity (as in the proof of Proposition 2) yields a relation whose first summand equals

$$n!{[{\theta }_i^{\perp }\left(a_i\right),x]}_s^n.$$

Because R is $n!$-torsion free, this implies

$${[{\theta }_i^{\perp }\left(a_i\right),x]}_s^n=0\mathrm{for}\mathrm{all}x\in A_i.$$

However, ${\theta }_i^{\perp }\left(a_i\right)$ is a scalar matrix sitting in the other summand $A_j$ ($j\ne i$), so it has zero support on $A_i$. Therefore, the only possibility consistent with the identity and with disjoint supports is that ${\theta }_i^{\perp }\left(a_i\right)$ is the zero scalar. Hence, ${\theta }_i^{\perp }\equiv 0$ for both $i=1,2$.

Consequently,

$${\theta |}_{A_i}={\theta }_i$$

(no cross terms), and by Theorem 1, each ${\theta }_i$ is proper on its block. Putting this together, we obtain

$$\theta (a_1\oplus a_2)={\lambda }_1{a}_1\oplus {\lambda }_2{a}_2+{\mu }_1\left(a_1\right)\oplus {\mu }_2\left(a_2\right),$$

where ${\lambda }_i\in R$ and ${\mu }_i:A_i\to R·I_{n_i}$ are R-linear. Equivalently, for any $x=a_1\oplus a_2\in I(X,R)$,

$$\theta \left(x\right)=\lambda x+\mu \left(x\right),\lambda =({\lambda }_1,{\lambda }_2)\in R\oplus R=Z_s(A_1\oplus A_2),\mu \left(x\right)={\mu }_1\left(a_1\right)\oplus {\mu }_2\left(a_2\right).$$

Thus, θ is proper on $I(X,R)$. This verifies Theorem 2 in this concrete two-component situation.

6. Conclusions and Future Work

In this paper, we have advanced the theory of commuting maps on incidence algebras [9] by introducing and characterizing supercommuting maps in the context of superalgebra structures, as developed by Ghahramani and Heidari Zadeh [22]. Our primary result demonstrates that, under the graph-theoretic condition that any two directed edges in each connected component of the complete Hasse diagram $(X,D)$ lie within a single cycle, every supercommuting map on the incidence algebra $I(X,R)$, where R is a 2-torsion free and $n!$-torsion free commutative ring with unity is proper. This extends classical results on commuting maps in prime rings, triangular algebras, and generalized matrix algebras [4,7,8] to the superalgebra setting, utilizing the Peirce decomposition induced by a nontrivial idempotent to separate even and odd components.

The proofs hinge on foundational lemmas that delineate the form of supercommuting maps on basis elements (Lemmas 2 and 3) and their behavior under restrictions to connected components (Lemma 5). The culminating theorems (Theorems 1 and 2) offer a precise description: such maps take the form $\theta \left(f\right)=\lambda f+\mu \left(f\right)$, with $\lambda$ in the supercenter $Z_s\left(I(X,R)\right)$ and $\mu$ an R-linear map into $Z_s\left(I(X,R)\right)$.

Looking ahead, several avenues merit exploration. One could investigate supercommuting maps on broader classes of algebraic structures, including generalized matrix algebras or triangular algebras equipped with supergradings, or delve into functional identities and multilinear maps within superalgebras [6]. Furthermore, weakening the cycle condition, examining cases where improper supercommuting maps arise, or extending the framework to infinite pre-ordered sets without local finiteness could uncover novel phenomena and classifications.

To guide new researchers, we propose the following specific open problems:

• Characterize improper supercommuting maps on incidence algebras when the cycle condition is violated. For instance, construct explicit examples of improper maps on posets where the Hasse diagram has multiple equivalence classes under the relation ≈ from Definition 1.
• Extend the results to incidence algebras over non-commutative rings R or rings that are not $n!$-torsion free. What adjustments are needed to the proper form $\theta \left(f\right)=\lambda f+\mu \left(f\right)$ in such cases?
• Investigate higher-order supercommuting maps, where the condition is ${[\theta \left(f\right),f]}_s^k=0$ for $k>1$. Can analogs of Theorems 1 and 2 be established, and what role does the super-k-center $Z_s{\left(A\right)}_k$ play?
• Explore applications of supercommuting maps to combinatorial structures, such as poset cohomology or Möbius inversion in superalgebras. For example, how do supercommuting automorphisms affect the Möbius function in incidence algebras with supergrading?
• Study supercommuting maps on variants of incidence algebras, such as reduced incidence algebras or those arising from categories. Does the cycle condition generalize to categorical Hasse diagrams?