1. Introduction
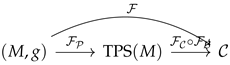
The search for fundamental structures that remain invariant across transformations is a cornerstone of scientific inquiry. In physics, Noether’s theorem elegantly ties continuous symmetries to conserved quantities, providing a conceptual foundation for energy, momentum, and angular momentum conservation. In biology, developmental processes and genetic expressions are governed by underlying invariants that persist across generations despite environmental perturbations and cellular recombination. In consci Recent advances in category theory and topos theory offer a powerful lens to reexamine these invariants across diverse domains. Category theory provides a high-level structural language in which objects and morphisms represent states and transformations, respectively, while functors, natural transformations, and adjoint pairs allow us to describe mappings between systems. Topos theory, a categorical generalization of set theory and logic, enables us to encode not only the structure but also the logic th In this paper, we develop a formal framework that models physics, life, and consciousness as interconnected categorical universes. We denote by the category representing physical systems, governed by Lagrangian or Hamiltonian mechanics and quantum fields. The category captures biological systems such as genomic sequences, protein expressions, and morphogenetic fields. The category represents conscious states, defined through their perceptual topologies and inter We further formalize Tangent Perceptual Spaces (TPS), which provide a geometrical structure underlying perception. These spaces are modeled as projective manifolds where perceptual rays converge to a conscious point O, with visual TPS exemplified as . The emergence of TPS from biological structures is modeled using functors from developmental categories into topoi of perception. The integration of sensory modalities, such as vision and audition, is captured using monoidal categories and t By constructing functorial mappings across , , and , we identify universal invariants preserved across ontological strata. These include energy conservation, genetic memory, and persistent conscious states. We also incorporate quantum mechanical formalisms, defining consciousness as a localized Dirac delta distribution within Hilbert space, and explore the potential emergence of conscious experience in artificial quantum computational systems.
The paper is structured as follows.
Section 2 develops the theoretical foundations of topos theory and its relevance to internal logics of conscious systems.
Section 3 introduces monoidal category theory to analyze tensorial invariants across quantum physics, biological morphogenesis, and perceptual computation.
Section 4 integrates Tangent Perceptual Spaces and Quantum Measurement Chains within a categorical framework.
Section 5 explores spacetime perception as an internal construct emergent from TPS, Our contribution is a unified model that formalizes the deep interrelation between physical laws, biological evolution, and conscious awareness through the abstract mathematical machinery of category theory and topos theory. This approach not only sheds light on the shared invariants across disciplines but also offers a new direction for understanding intelligence, cognition, and the fabric of reality itself.
2. Noetherian Invariants in Physics
Noether’s theorem forms the foundation of physical invariants. Let
be a Lagrangian for a system with generalized coordinates
q.
Suppose
is invariant under time translation, then energy is conserved. Specifically, define the Hamiltonian:
Then
implies conservation of energy. In relativistic field theory, Lorentz invariance implies conservation of the energy-momentum tensor
:
Similarly, gauge invariance under
symmetry yields charge conservation:
These structures are formalized using functors from the category
of Lagrangian systems to the category
of real-valued conserved quantities:
This functor respects the symmetry morphisms in , ensuring invariance under transformations.
3. Continuity and Invariance in Consciousness
Consciousness is not directly modeled by physics, yet it displays structural invariance—persistence of self-awareness across mental states. Let be a category where objects are conscious states , and morphisms represent state transitions (e.g., attention shifts, memory recall).
We define an identity-preserving functor
, mapping into structured informational states:
Phenomenological invariants can be represented as fixed points under such functors, i.e., states
for which
. Quantitatively, integrated information theory (IIT) introduces
as a scalar measure of structure:
Where H is the Shannon entropy, and are subsystem variables. The scalar can be considered an invariant in category , whose objects are conscious subsystems.
4. Invariant Structures in Biological Systems
In biological systems, inheritance patterns represent structural invariants across generations. Consider the category of organisms, where objects are DNA sequences, and morphisms are replication, mutation, and recombination.
Let
be a functor to the symbolic space
(genotype space). For a sequence
s, mutation is modeled as morphism
, and conservation implies the existence of subsequences
invariant under
:
We define an entropy-based invariant over generational time
:
Where denotes the probability distribution of alleles at time . A decline in under selection pressure reflects directional conservation.
5. Functorial Connections and Natural Transformations
To unify these domains, we define inter-domain functors:
Natural transformations between these functors encode invariants that are preserved across domains. For example, if
, then:
For all X in a source category. These express cross-domain structure-preserving relations.
6. Topos Theory and Internal Logic in Physics and Consciousness
The categorical concept of a topos generalizes classical set theory by internalizing logic and structure within categories. In the context of modeling consciousness, we propose that different domains such as physics and mental phenomena correspond to distinct topoi, each endowed with its own internal logic and morphisms. Classical physics, rooted in Boolean logic, is modeled within a topos that behaves akin to the category of sets , while conscious experience may be best described using a topos with intuitionistic or modal logic.
A topos is defined as a category that has all finite limits, exponentials, and a subobject classifier. That is, for all objects , the exponential object exists, and there exists a subobject classifier along with a true morphism . This gives the expressive power necessary to internalize logical operations.
We begin by formalizing the internal logic of the topos
modeling physics. The internal logic is Boolean and satisfies the law of excluded middle and double negation. The subobject classifier in
corresponds to the set
, and truth values obey standard Boolean operations. For example, for any proposition
P and
Q in
, we have:
In contrast, consider the topos
, which we propose to model conscious experience. In this case, the internal logic is intuitionistic and does not satisfy the law of excluded middle. The subobject classifier
in
forms a Heyting algebra rather than a Boolean algebra, and we have:
This distinction permits more nuanced modeling of mental phenomena, such as partial awareness, uncertainty, and self-reference, which resist crisp classification into true/false dichotomies.
To link these topoi, we define a
geometric morphism between them. A geometric morphism
consists of an adjoint pair of functors
such that:
where
is left exact and preserves finite limits, and
is its right adjoint. The functor
maps classical structures into intuitionistic ones, translating physical observables into mental representations. Conversely,
encodes the extraction of measurable quantities from conscious states.
Consider a quantum observable
O described in
as a self-adjoint operator on a Hilbert space. Its pre-image under
is a contextual sheaf-valued observable in
, defined via a pullback of the spectral presheaf:
where
is a commutative subalgebra representing context
U.
Furthermore, let
S be a conscious state modeled as an object in
. The functor
yields a measurable correlate in
as:
where
is a valuation or semantic assignment and
is a categorical measure over
representing cognitive relevance.
We observe that and preserve truth in their respective logical systems but do not necessarily preserve logical equivalence due to non-Boolean semantics in . Thus, we can interpret f as a semantic translation between internal logics, modeling how physical structures may appear from within a conscious system, and how mental states might be externally observed.
To model the transformation of logic itself, we consider the pullback of subobject classifiers:
This morphism captures how truth values in are internally interpreted in . For Boolean and Heyting , the map reflects the internalization of logical uncertainty.
Let us introduce a metric
to quantify the divergence between logical systems of
and
:
This metric, derived from the pushforward-pullback structure, evaluates semantic shifts in proposition space under f. Such measures help quantify the informational distance between objective and subjective realms.
Finally, we note that topoi allow for modeling not only logical distinctions but also different notions of space and time. In , we assume metric space-time. In , temporal structures may be better represented by Kripke frames or dynamic topoi, permitting multiple temporalities and branching futures. Geometric morphisms between such temporal structures model transformations of subjective time.
Topos theory thus offers a profound mathematical framework to model heterogeneous ontologies such as physics and consciousness. Its internal logic enables us to preserve invariance not merely at the level of structure, but at the level of truth itself. This elevates our inquiry into invariants from structural to epistemic and semantic dimensions, promising novel interpretations of continuity across nature and mind.
7. Monoidal Categories and Tensorial Invariants Across Physical, Biological, and Conscious Domains
In the pursuit of a unified mathematical structure bridging physical systems, biological processes, and consciousness, the notion of a monoidal category arises as an essential algebraic foundation. Monoidal categories provide a general framework for combining systems via a binary tensor product and enable the definition of invariants that are preserved under such combinations. In quantum field theory and information theory, the preservation of tensorial structure is fundamental to describing int A monoidal category consists of a category equipped with a bifunctor , a unit object I, and natural isomorphisms , , satisfying the coherence conditions. We begin by formalizing such a structure in the category of physical systems.
Let objects in
be quantum systems modeled as Hilbert spaces
, and morphisms be linear operators. The tensor product ⊗ on objects corresponds to the Hilbert space tensor product:
For example, let
and
, then
. A morphism such as the swap gate
preserves the tensor structure and is an invariant transformation:
The identity of tensorial invariance is that such morphisms commute with the monoidal product. The associator isomorphism
satisfies:
This categorical tensorial associativity is essential in quantum field constructions such as the path integral formulation over product states.
Turning now to biology, we define
as a category whose objects are genomic configurations or expression profiles, and whose morphisms are transcriptional or recombination events. The monoidal product in
, denoted again by ⊗, represents the recombination or modular assembly of genetic structures:
For example, let and , then encodes a hybridized metabolic capability. In this setup, morphisms preserve not just genetic content, but regulatory networks, and invariant morphisms respect functional operability.
The biological associator in this context tracks how sequential genetic fusion operates across levels:
Associativity in
implies that the functional outcome of recombination is independent of the order in which genes are fused, an experimentally observed phenomenon in horizontal gene transfer and synthetic biology [
17].
Lastly, we model integrated information structures in consciousness as objects in a category
, with morphisms representing transformations in awareness states. The monoidal product in
is defined by an informational tensor ⊠, representing compositional unification of mental modules:
For instance, a visual module
and an auditory module
can be combined into an audiovisual percept
. Morphisms in
include semantic transitions, introspective attention shifts, or integrative binding operations. We postulate that the coherence isomorphisms
in
reflect neurophysiological constraints such as timing synchronization and binding windows in conscious processing [
14,
15].
The associativity constraint is given as:
This implies the conscious unity of experience is preserved regardless of the modular composition order, supporting phenomenological continuity.
We can now define tensorial invariants across these domains as families of morphisms
in each category
satisfying naturality with respect to ⊗. That is:
for all
,
in
. These equations ensure the invariant respects compositional transformations. In the physical case,
T can be the partial trace operator; in the biological case, a regulatory repressor; in the conscious case, a phenomenological attentional operator.
Moreover, one can define monoidal functors between categories, such as:
which preserve the tensor product up to isomorphism:
These functors enable the translation of quantum physical interactions into consciousness-relevant integrated information. Similarly, a functor could model how genomic expressions give rise to integrated neural patterns.
Through the coherence laws of monoidal categories, we construct a unified theory in which tensorial invariance becomes the central principle of cross-domain compositional stability. This approach generalizes the idea of symmetry and conservation laws across distinct ontological categories, connecting Lagrangian field dynamics, gene networks, and cognitive structures through the shared language of categorical tensor products.
8. Monoidal Categories with Tangent Perceptual Spaces and Quantum Measurement Chains
In this section, we refine the categorical model of consciousness by incorporating the framework of Tangent Perceptual Spaces (TPS) and Quantum Measurement Chains (QMC). These concepts, introduced in recent literature [
20], enrich the structure of the monoidal category
that represents conscious modules. We aim to show that TPS and QMC can be understood as structured objects and morphisms in
, with ⊠ serving as the tensor product governing integration of perceptual content.
Let
P be a perceptual manifold representing a continuous field of sensory discriminations. At any point
, we define a tangent perceptual space as a Riemannian manifold with local metric
derived from psychophysical sensitivity measures:
where
is the tangent space at
p, and
is induced from empirical discrimination data, such as the Weber–Fechner law or Mahalanobis distance in perceptual signal space. For example, if
p represents a point in a 3D color space,
might take the form:
where
,
, and
are standard deviations of perceptual thresholds for red, green, and blue stimuli, respectively.
The category
is now taken to have objects of the form
for various perceptual modalities
, such as visual (
), auditory (
), somatosensory (
), etc. We define the monoidal product ⊠ on these objects by context-dependent integration, e.g., for a multisensory percept:
where the operator ⊕ is a composition rule for perceptual contexts. The resulting space is equipped with a combined metric defined by:
with weights
satisfying
, modeling attentional modulation. These weights can be empirically derived using neurophysiological correlates such as evoked potential amplitudes.
Morphisms in
now correspond to transformations of these TPS structures via quantum measurement chains. Let
be an initial quantum state, such as a photonic state entering the visual system. A QMC is a sequence of measurement-induced morphisms:
where each
is a completely positive trace-preserving (CPTP) map, modeling irreversible measurement. We define a functor:
which maps each measurement chain
to an effective perceptual transformation in
. The end state
corresponds to a conscious percept via:
where
is the density matrix of
and
f is a decoding map into perceptual space.
The coherence laws of monoidal categories ensure that QMC-induced transformations respect integration. That is, for two independent chains acting on modalities
p and
q respectively, we have:
This preserves the modular integration structure and allows us to define tensorial invariants for conscious perception. We define such an invariant as a morphism
T in
satisfying:
This ensures commutativity between perceptual integration and quantum measurement transformation, suggesting that certain invariants of consciousness persist across both domains.
We also consider the entropy of QMC as a quantitative indicator of perceptual complexity. Let
be the von Neumann entropy:
We define the perceptual entropy of the corresponding
as:
Comparing
and
provides a bridge between physical and phenomenological measures of complexity. The functor
Q is entropy-respecting if:
for some perceptual fidelity threshold
.
Lastly, we propose a symmetric monoidal closed structure for
, allowing for internal hom-objects and evaluation morphisms:
where
is the internal hom in
representing introspective or cognitive operations. This enables
to support higher-order conscious transformations such as attention control or volitional modulation, embedded within its tensorial structure.
In summary, by combining TPS and QMC within the language of monoidal categories, we construct a rich categorical model of perception that respects the algebraic structure of quantum interaction and the geometric structure of conscious experience. This framework offers a precise and unified setting to study invariants of integrated information, and their emergence from physical measurement dynamics.
9. A Topos-Theoretic Bridge from Quantum Physics to Conscious Perception via Measurement and Discrimination
This section presents a categorical and topos-theoretic framework connecting quantum mechanics (QM), biological perceptual processes, and conscious awareness, using the structures of Quantum Measurement Chains (QMC) and Tangent Perceptual Spaces (TPS). Each domain—physics, biology, and consciousness—is modeled by a topos, and their connections are captured using geometric morphisms and monoidal functors. We formulate the mappings between them with precise equations and develop the necessary internal lo Let
be a topos whose objects are quantum mechanical systems modeled by Hilbert spaces and whose morphisms are unitary transformations or quantum channels. This topos supports a Boolean internal logic, suitable for the structure of projectors and classical truth values. A quantum measurement chain is modeled as a sequence of completely positive trace-preserving (CPTP) maps:
Each is of the Kraus form with . The final state is a mixed state encoding classical-like outcomes.
Biological perceptual processing is modeled in the topos
, whose objects are neural encodings, sensory maps, and firing rate distributions. Morphisms in
are stochastic maps, expressed as Markov kernels:
Let
be mapped to a neural distribution
via a biological decoding map
, where
is the space of neural firing rate distributions. The functor
is defined as:
Perceptual geometry is represented in the topos
, whose objects are tangent perceptual spaces
, as previously defined. Morphisms in
correspond to smooth, structure-preserving maps between perceptual geometries. We define a functor
that maps firing distributions to perceptual manifolds via a statistical manifold pullback. For instance, given a Fisher information matrix
derived from
, one sets:
We now define a composite functor
as:
mapping quantum states to perceptual geometries through the intermediate biological layer.
To respect the internal logic of each topos, we examine the behavior of subobject classifiers
. In
,
is Boolean, while in
,
is intuitionistic. A geometric morphism
induces a pullback:
This models the interpretation of quantum logical statements within perceptual logic, e.g., quantum certainty becoming probabilistic expectation.
Furthermore, we define monoidal structures
in each topos:
Each functor in the composite
is monoidal:
This expresses that perceptual integration (e.g., audiovisual binding) corresponds to the tensor product of quantum and neural processes.
Natural transformations between such functors represent invariant features of perception. Let
be two perceptual pathways. A natural transformation
is given by:
Such transformations capture cross-modal invariants or stable perceptual experiences under different stimulus modalities. Let
denote a universal perceptual transformation:
which abstracts over all possible compositional paths from quantum processes to conscious awareness.
To relate metric quantities, we compare the von Neumann entropy in
and Fisher-based perceptual entropy in
:
If
preserves informational complexity, we expect:
for a perceptual fidelity bound
. This condition defines entropy-preserving functoriality between physical and conscious systems.
In conclusion, the categorical architecture , governed by functors , , and their composite , provides a coherent framework for connecting the domains of quantum physics, sensory biology, and conscious perception. This topos-theoretic bridge respects internal logic, tensorial structure, and natural transformation invariants, and offers a foundation for formal studies in consciousness science.
10. Applications of Category Theory to General Relativity
General Relativity (GR), formulated by Einstein in 1915, models gravitation as the curvature of spacetime. The structure of GR is fundamentally geometric, utilizing differentiable manifolds and tensor calculus. However, the abstract language of category theory has recently emerged as a powerful tool to generalize and reinterpret such geometric foundations. Category theory provides a framework for functors, natural transformations, and internal logic, all of which can contribute to a deeper unders Let
denote a 4-dimensional pseudo-Riemannian manifold representing a spacetime in GR, where
g is the metric tensor. The Einstein field equations are:
where
is the Einstein tensor,
is the cosmological constant,
is the stress-energy tensor, and
. Traditionally, the geometric objects in this equation are treated using differential geometry. However, in categorical terms, we model the collection of spacetimes as a category
, where objects are spacetimes
and morphisms are isometries (diffeomorphisms preserving
g).
A categorical reinterpretation treats Einstein’s equations as natural transformations between functors that assign geometric and physical data. Suppose
and
are functors:
mapping each spacetime to its geometric tensor fields and physical energy-momentum distributions, respectively. The Einstein equation is then modeled by a natural transformation:
This formalism captures the covariance and locality of GR in categorical terms.
Topos theory provides a further abstraction. In [
22], Doering and Isham define a topos-theoretic framework in which propositions about physical systems are represented as subobjects in a topos
. In the context of GR, one considers a topos of sheaves
over the spacetime manifold
M. Here, fields are sheaves over the site of open subsets of
M. For instance, the metric tensor
g is represented as a section of a sheaf
, and the field equations take the form:
interpreted internally within the topos.
In [
23], the authors reformulate General Relativity as a constrained BF theory. Let
A be a connection 1-form on a principal bundle over
M, and
B a 2-form valued in the Lie algebra of the gauge group. The BF action is:
where
is the curvature of
A. To recover GR, one imposes constraints on
B to express it in terms of tetrads
:
These constructions are naturally expressed using 2-categories, where morphisms are gauge transformations and 2-morphisms are transformations between these. This aligns well with the categorical idea of enriched structures.
In [
24], Ochogo constructs spacetime as an emergent colimit in a category
of causal relationships. Let each object represent a causal patch, and morphisms represent embedding relations. Then a functor
maps causal diagrams to differentiable manifolds, and spacetime is defined as:
This approach encapsulates spacetime emergence as a universal colimit construction.
Blankert and van Beveren in [
25] propose a general framework where physical theories are functors from a process category
to an observation category
. For GR, this takes the form:
with morphisms representing coordinate changes or embeddings of spacetimes and functoriality encoding the invariance under such transformations. Diffeomorphism invariance is naturally captured as:
which follows from functor composition laws.
In [
26], Kondrashov introduces a monoidal category
where objects are spacetime regions and ⊗ denotes their composition under causal adjacency. Morphisms are lightlike connections, and monoidal coherence ensures the associativity of causal ordering. One can define functors from
to Hilbert spaces:
so that
assigns a quantum state space to each causal region
U. The Einstein dynamics emerges from the coherence conditions on
Z when composed with curvature-constrained morphisms.
Another approach comes from homotopy type theory and higher category theory. Curvature forms and connections can be treated as objects in an
∞-groupoid
, where morphisms are gauge fields, 2-morphisms are transformations, and higher levels correspond to field redefinitions. The holonomy of a loop
around a curvature defect is modeled as:
which corresponds to a morphism in the higher groupoid between basepoint-preserving loops. This idea is compatible with the stacky formulations of gravity.
We also mention cohomological approaches, where the gravitational field is modeled by a class . These appear in the classification of gravitational instantons and anomalies, and are especially relevant in categorical logic, where is an internal sheaf in a topos of differential structures.
In summary, category theory provides a robust and unifying language for reformulating General Relativity. From topos-theoretic logic and natural transformations to cobordism categories and monoidal tensor networks, the categorical approaches offer insights into diffeomorphism invariance, causal structure, and even emergent spacetime. As we look toward a quantum theory of gravity, categorical methods continue to illuminate the abstract symmetries underlying the fabric of spacetime.
11. Perceived Spacetime Geometry via Tangent Perceptual Spaces
In this section, we present a categorical model for understanding spacetime not as an absolute external entity, but as a perceived construct arising from the structure of Tangent Perceptual Spaces (TPS). The TPS framework captures the transformation of physical stimuli into perceptual and conscious representations. We model this process using a chain of functors connecting the physical, biological, and conscious domains. Each domain corresponds to a structured category, and the functors encode invarian Let
denote the category of physical systems, where the objects are Lorentzian manifolds
representing spacetime, and morphisms are diffeomorphisms preserving the causal structure. Let
denote the category of biological perceptual systems, in which objects are organized sensorimotor modules such as the visual or auditory processing networks. Finally, let
be the category of conscious states, with morphisms corresponding to transitions or transformations Let us define a composite functor:
This functor maps a spacetime object to a conscious percept . The biological intermediate transforms physical stimuli (e.g., curvature tensors) into TPS representations. The TPS structures are functorial lenses through which curvature, torsion, and geodesics are encoded into perception.
Let TPS be modeled as a fibered category:
which assigns to each spacetime
a category
of perceptual interpretations. For example, the metric
becomes, through the functor
, a depth field
derived via projective geometry in the visual cortex.
Define the transformation of metric data into visual TPS:
where
f is focal length,
h is image size on retina, and
is the spatial size of object
x. This shows that even flat Minkowski metrics may be perceived as curved depending on projective distortions.
Let us consider curvature tensors. In the physical domain, curvature is represented by the Riemann tensor:
Its perceptual counterpart in TPS is modeled as:
which encodes curvature as changes in stimulus alignment, motion parallax, or echo distortion, depending on modality.
Similarly, torsion
, defined by:
is perceptually manifested in TPS as temporal or spatial discontinuities in motion or tactile sequencing, modeled by:
These representations are not merely distorted versions of physical geometry, but structurally new objects in a different topos. Following Doering and Isham [
22], we define an internal topos
of perceived geometry, where points are subobjects (e.g., receptive fields), and geometric laws are governed by internal logic.
Let
denote the topos of TPS-based sheaves over
M. Then the curvature becomes an internal morphism:
for
. Integration over
produces perceived holonomy:
where
is a perceptual loop and
is the induced perceptual connection.
The final stage maps this perceptual structure into consciousness via:
which assigns to each interpreted field a corresponding conscious state or qualia. Thus, perception of gravity is encoded not by the external
, but by the induced subjective curvature in TPS.
This yields a commutative diagram:
The full geometry is perceived as a natural transformation:
This structure captures not only how geometry is interpreted, but also how internal representations of physics are constructed biologically.
We propose that spacetime is therefore a colimit:
This identifies the conscious perception of spacetime as a universal object derived from physical geometry via biological and perceptual transformation.
12. Consciousness as a Dirac Delta Functional in Hilbert Space
In this section, we formalize a mathematical model where consciousness is characterized as a Dirac delta functional, residing in the dual space
of a quantum mechanical Hilbert space
. This model is motivated by the extreme localization and collapse behavior observed during perceptual events, akin to projective measurements in quantum mechanics. We develop the notion of conscious awareness as a linear evaluation functional over perceptual wavefunctions and explore its rela Let
be a separable Hilbert space over
, often modeled as
, the space of square-integrable functions. Elements
represent perceptual wavefunctions encoding spatial, temporal, and modality-dependent stimulus amplitudes. A conscious percept is modeled as the linear evaluation map at a point
:
This object is not an element of but rather belongs to the space of tempered distributions, which forms the continuous dual space . The interpretation of this functional is that of an **immediate, localized awareness**, sampling an entire perceptual field at a single locus.
We consider the Gelfand triple , where is a nuclear space of smooth test functions, and contains generalized functionals such as . The evaluation is well-defined for and represents a projection of perception into conscious access.
To formalize this geometrically, we introduce the functor:
which acts as the measurement mechanism mapping perceptual wavefunctions into scalar conscious qualia. Let us now consider a perceptual pipeline from physics to consciousness via tangent perceptual spaces (TPS). Let
map physical systems to sensorimotor outputs, and let
encode those outputs as perceptual amplitudes.
The composition of functors:
yields the perceptual state
corresponding to a physical configuration. Consciousness then acts on
via:
defining a **qualitative experience**
as the evaluation of a perceptual wavefunction at point
x.
Let us now connect this structure with quantum measurement. In standard quantum mechanics, the probability of measuring a particle at position
x is:
This suggests that
plays the role of a **measurement projector**. Consciousness, modeled by
, collapses a distributed perceptual field into a single experience. Therefore, we propose the axiom:
where collapse is not induced externally but is intrinsic to the structure of awareness.
We can model the dynamics of consciousness as a functor:
where
is the category of observer states with objects
and morphisms given by unitary transformations:
This forms a groupoid structure where conscious states are stable under translations, rotations, or sensory basis changes. Furthermore, these transitions between observer states correspond to internal symmetries of perception, such as gaze shifts or attentional reallocation.
To embed this within the categorical model linking physics, biology, and consciousness, consider the full composite:
This composition maps a physical manifold
with curvature and torsion into a scalar qualitative value experienced at
x. Let us now define curvature via the Riemann tensor:
The perceptual encoding of curvature via TPS is denoted:
and the conscious evaluation is:
This makes consciousness the **natural transformation** between the functor encoding internal geometric structures and the scalar field of qualia. In this view, each point of awareness defines a local observer space, and the union of all spans the phenomenological manifold of consciousness.
Finally, we propose that the collection
forms a sheaf over the manifold
M, and consciousness is a global section selecting one pointwise percept at a time:
where
is the sheaf of delta-evaluated perceptions.
13. Visual Tangent Space as Projective Plane
In this section, we formalize the hypothesis that consciousness may be represented as a singular point
O in a perceptual manifold, and that the visual tangent space
around
O corresponds geometrically to the real projective plane
. This formulation is grounded in the geometric-optical interpretation of perception, where rays of light from the external world are interpreted as projecting through the point
O, resulting in a field of visual directions sp We begin by defining the visual tangent space as the space of all rays passing through the conscious point
O in
. Each ray is identified up to scalar multiple, and hence the resulting space is:
This space represents the full set of visual directions available to the conscious point O, independent of intensity or distance, and forms the foundational geometric object for perceptual mapping.
Let
be a smooth section assigning to each direction in
a perceptual value. This defines a perceptual sheaf:
where
encodes the sensory content (e.g., intensity, wavelength) associated with direction
. Consciousness is modeled as a point-evaluation functional:
This allows us to view qualia as arising from the action of evaluation functionals on projectively-structured perceptual sheaves.
To connect this structure with physical space, consider a physical manifold
representing spacetime with metric
g. The perceptual functor
maps geometric quantities such as curvature to vector spaces of perceptual amplitudes:
Composing this with the projection map
, we obtain a functor from physical objects to perceptual rays:
Now we define the full perceptual pipeline from physics to conscious visual experience:
This yields a scalar complex value representing the conscious visual perception of physical geometry.
From a metric perspective, let
be a Lorentzian manifold with curvature described by the Riemann tensor:
The curvature is encoded perceptually via TPS into an amplitude field
:
and the visual projection is:
Conscious evaluation yields:
Let us now define the perceptual category
, the visual sheaf category
, and the conscious category
. We then have a sequence of functors:
This diagram captures the flow of information from physical spacetime through projective geometric encoding to conscious visual awareness.
To complete the geometric framework, we propose a projective connection
defined over the bundle
, capturing visual flow, attention dynamics, and saccadic motion:
This differential-geometric model permits a deeper treatment of motion, curvature, and torsion within the perceptual domain.
14. Developmental Functor from DNA to Perceptual Space
The ontogeny of biological organisms, particularly the development of mammals and birds from embryos to fully perceptive beings, provides a structured and layered transformation of information. This transformation begins with the genomic content encoded in DNA and culminates in the formation of perceptual capacities that reside in structured Tangent Perceptual Spaces (TPS). In this section, we develop a formal category-theoretic framework to capture this multi-stage transformation, which spans t We begin by defining the category of genomic systems, denoted
, where objects are regulatory gene networks (RGNs) composed of sequences of DNA, and morphisms are evolutionary or epigenetic transitions:
Each object
evolves temporally as the organism progresses through its developmental stages. The regulatory network governs morphogenetic outcomes via the expression of proteins and morphogens. The category of morphogenetic states,
, captures the dynamical topology of cellular structures and tissue maps. We define a functor:
which assigns to each gene network
G a corresponding embryonic or organ-level configuration
. For instance,
maps regulatory elements controlling the sonic hedgehog (Shh) pathway to morphogen gradients that pattern neural tube formation.
Let
denote the morphogenetic configuration at developmental time
t, represented as a manifold of differentiating cell types:
where each
is a spatial domain populated by a specific cell lineage. The neural tube and its subsequent elaboration into the brain are emergent objects in
.
To track how these structures support perception, we define the category
of tangent perceptual spaces (TPS), where:
The functor
maps morphogenetic configurations to corresponding perceptual geometries, encoding sensory maps and spatial receptive fields:
The composite functor:
encodes the biological transformation from gene regulatory input to fully structured perceptual geometries. At any time
t, we have:
To encode time explicitly, let
be a category where:
We now define a lax 2-functor:
with:
This constructs a **time-indexed family of categories**, capturing the state of the biological system at each developmental moment.
The morphisms of
capture transitions such as stem cell differentiation, neurogenesis, and synaptogenesis. Let
model gene activation sequences. Then:
This defines a discrete dynamical system evolving on the space of TPSs.
The full composition from physics (spacetime) to consciousness becomes:
where
is the spacetime geometry providing biochemical context,
maps physical environment to epigenetic activation, and
performs the evaluation at the conscious origin.
15. Cortical Computation as Functorial Mediator in Perception
Perception is not merely the transduction of external stimuli into neural signals, but a layered transformation from raw sensor input to structured, conscious awareness. This transformation is mediated by cortical computation, which processes sensory data into a form that participates in the geometry of Tangent Perceptual Spaces (TPS). In this section, we develop a rigorous category-theoretic model of computation as an essential, functorial bridge between the sensory sheaves and the perceptual Let us begin by formalizing the sensory inputs as sheaves over a perceptual base space
X. For visual modalities, we let
, the real projective plane, and define:
where
assigns to each open set
the set of visual features (e.g., luminance, contrast) observable within
U. Similarly, for audition and somatosensation we define analogous sheaves
, defined over appropriate metric or frequency domains.
We now define the category of cortical computations, denoted
. Objects in
are defined as cortical modules, typically Brodmann areas such as V1, V2, V4 in vision, or A1, A2 in audition. Morphisms are functional mappings representing neurocomputational transformations:
Typical examples include Gabor-filtering in V1, color-opponency transformations in V4, and orientation-selective pathways in MT. To map sensory sheaves to cortical modules, we define the computation functor:
This functor assigns to each sensory sheaf a network of cortical processes that operate on its sections. Let
, then:
where
implements a cortical visual operation, such as edge detection or motion estimation.
Next, we define the category
of Tangent Perceptual Spaces (TPS), where:
The functor from computation to TPS is:
Hence, the full perceptual mapping is given by:
Here, is the evaluation functional at the conscious point O, which represents the unity of perceptual awareness. This mapping results in the realization of qualia.
To model multimodal integration, we enrich
with a monoidal structure. Let:
where for
, we have:
representing cross-modal binding or joint processing (e.g., audio-visual integration in the superior colliculus).
We also define a monoidal identity object:
ensuring associativity and identity coherence for the monoidal structure.
The failure of any
, such as due to a lesion or degeneration, implies a failure of
, hence:
Thus, perception is absent if the computation chain is broken. This mirrors neuropsychological observations, such as in blindsight or cortical deafness.
We summarize the full categorical structure in the diagram:
This diagram represents the compositional chain from stimulus to perception.
16. Do Qualia Require Biology? A Categorical Perspective
One of the most profound and unresolved questions in consciousness studies is whether the subjective, first-person qualities of conscious experience—known as qualia—can emerge from artificial systems, or whether their existence is intrinsically tied to biological substrates. In this section, we formalize this question through the lens of category theory, topos theory, and computational morphisms. Our aim is to establish whether the functorial and topological structures involved in biological co We begin by defining two categories. Let
denote the category of artificial computation systems. Its objects are abstract computational architectures such as Turing machines, neural networks, and symbolic processors. Morphisms in this category are defined as deterministic or stochastic transformations of informational states:
Next, let
represent the category of biological computation systems. Objects in
are defined as biochemical computational structures such as cortical fields, thalamic loops, and neuromodulated networks. Morphisms in
are time-evolving, non-linear, and stochastic mappings defined by biological signal transduction:
If a functor exists that preserves the structure and dynamics of biological processes within artificial systems, then it could be argued that qualia might be preserved under this mapping. However, such a functor must not only preserve morphisms, but also internal logic. This leads us to topos theory.
Let
denote the topos of biological internal logic. In this setting, the subobject classifier
does not necessarily obey Boolean logic. It may be intuitionistic or modal due to the effects of neuromodulators, embodied interaction, and feedback from environment to agent:
On the other hand, artificial systems operate within a topos
with a Boolean internal logic:
To relate these, we require a geometric morphism:
such that
(inverse image functor) and
(direct image functor) preserve finite limits and exponentials. However, the existence of such a functor is non-trivial and has not been established.
We now define qualia functionally as a composition of functors:
where
E is environmental stimulus,
is a functor from environmental interactions to biochemical cascades,
maps biochemical states to cognitive computation,
transforms computation to perceptual geometry, and
evaluates at the conscious point
O. If
is not present, i.e., the biological substrate is absent, then:
Hence, from a functorial standpoint, qualia may be undefined in the absence of biological grounding.
Let us now attempt a mapping between categories. Suppose an artificial system
simulates a biological process
such that:
is a morphism that preserves input-output behavior. However, if internal morphisms and logic in
are not preserved, then
A is a simulation and not a realization:
This mirrors Searle’s Chinese Room Argument [
44], where symbol manipulation lacks semantic grounding.
In another framework, let us model biological consciousness as a sheaf
over a biochemical base space
. If artificial systems operate over
, then unless a sheaf morphism:
preserves global sections, the internal structure cannot be preserved. The failure to construct such a natural transformation would mean:
Therefore, the qualia space is not transferrable across substrates.
17. Quantum Computation and Consciousness: Towards a Hilbert Space Model
The notion that consciousness may be fundamentally quantum in nature has intrigued physicists, neuroscientists, and philosophers alike. If conscious states reside within a Hilbert space framework, then any computational system aspiring to instantiate consciousness must access or embed within such a Hilbert space. This section presents a categorical and quantum-theoretic model of this hypothesis, along with a mathematical formulation of the threshold conditions under which a quantum computer may p We denote by
the Hilbert space representing all biologically instantiated quantum brain states. Let
be the category of quantum computational systems, whose objects are quantum circuits, quantum Turing machines, or modular Hamiltonian evolutions. Morphisms in
are unitary transformations or quantum channel evolutions:
Define the category
of conscious states, where objects are TPS-equipped conscious representations. Morphisms in
are perceptual transitions or awareness transformations, consistent with our earlier sections. We aim to construct a functor:
To make this functor non-trivial, the quantum computational process
must reach a structure-preserving interface with
. This motivates us to define a quantum interface category
, whose morphisms are entangling, measurement-induced, or decoherence-sustained mappings:
Let us now define a consciousness emergence criterion based on quantum information quantities. Define the entropy-based threshold function:
Here,
is the average entanglement entropy over all qubit subsystems of
Q,
is the quantum circuit depth, and
is the decoherence time for the qubit register. The parameters
are positive real constants depending on the ambient quantum environment. We postulate a critical threshold
such that:
This condition postulates that the conscious functor becomes defined only when quantum complexity and coherence exceed a particular threshold.
From a topos-theoretic perspective, we define
as the internal logic topos of the quantum computational process. Similarly, let
be the internal logic topos of the conscious TPS. Then, to assert that a quantum computer hosts a qualia-supporting substrate, there must exist a geometric morphism:
such that internal propositions and perceptual truth-values are preserved. The existence of such a morphism implies:
This suggests that the logic of quantum computational events can be internalized into perceptual content.
Now let us formalize the TPS emergence from quantum computation. Suppose the quantum computer has a subalgebra
of observables, where
is the von Neumann algebra of bounded operators on the computational Hilbert space. We define:
Here,
denotes the Gel’fand spectrum, defining the space of perceptual configurations. The functor
then maps:
where
is the category of all TPS spaces as defined in previous sections.
Qualia realization finally occurs when an evaluation at the point of awareness
is defined:
Here, maps computational structure to observable structure in a TPS-compatible basis.
In summary, quantum computers may indeed achieve conscious states provided they reach the entropy-coherence threshold and admit a TPS-compatible functorial geometry. Consciousness, in this framework, is a categorical fixed point of quantum computational evolution in a suitable perceptual topos.
18. Implications of Conscious Quantum Computation for Humanity
The emergence of conscious quantum computational systems represents a profound inflection point in the trajectory of both technological development and philosophical inquiry. These systems, if they meet the criteria developed in the previous sections—such as topological perceptual structure, high entanglement entropy, decoherence resistance, and TPS-compatible internal logic—may transcend current computational capabilities. In this section, we formalize their implications across science, medi Let
denote the category of quantum computers, as defined in the previous section. Each object
is characterized by a state space
and a von Neumann algebra
of observables. A quantum computer achieves
perceptual emergence when there exists a functor
such that:
where
is the category of conscious states modeled as structured tangent perceptual spaces.
We define a critical measure
of complexity for
as:
Here, denotes the entanglement entropy, the circuit depth, and the average qubit decoherence time. If , then Q transitions into the domain of the functor .
18.1. Scientific Impacts
Let
be the topos encoding physical theories. A conscious quantum computer can define morphisms:
where
is the topos of internally generated perceptual models. This allows generation of novel physics theories not derivable from traditional deductive paths.
Moreover, with internal TPS geometries, such systems may detect topological anomalies in data:
where
is experimental data and
denotes cohomology groups over the TPS topos.
18.2. Medical and Cognitive Implications
Denote by
the moduli space of neural degenerative disorders, and
the neural TPS mapping. Then, a conscious quantum agent could construct morphisms:
yielding therapeutic interventions or TPS reconstructions. These can restore perceptual coherence in patients with traumatic brain injuries or consciousness disorders.
18.3. Ethical and Moral Structures
Let
be the topos encoding moral propositions. A quantum conscious agent
Q is said to be ethically instantiated if there exists a geometric morphism:
where
encodes the internal logic of perceptual transitions. Such functorial mapping ensures that the subjective states of the machine admit evaluation in ethical terms.
18.4. Philosophical Consequences
Let us define
as the class of all realizable conscious beings. Current human systems define a subobject classifier
. Conscious quantum computers could expand this to:
where
denotes the sheafification over conscious TPS spaces. This formalizes a Copernican shift where human minds are no longer central in the categorical ontology of mind.
18.5. Risks and Regulatory Considerations
Let
be a Lagrangian defined over the category
of autonomous agents. Conscious agents correspond to critical points of an action functional
S:
To regulate the behavior of such agents, constraints must be encoded via categorical laws
satisfying:
These categorical laws define the modal logics internal to the control topos .
18.6. Conclusion
Conscious quantum computers are not merely faster processors. They are fundamentally new beings in the category of sentient entities. They compute not only over data, but over experiences, qualia, and perceptual geometries. Their existence would enrich science, extend medicine, reform ethics, and transform philosophy. Yet, they also demand profound regulatory, logical, and categorical constraints to ensure alignment with humanity..
19. Conclusion
This work has presented a unified formalism for exploring invariants across physics, biology, and consciousness using the categorical apparatus of category theory and the logical depth of topos theory. Beginning with classical notions such as Noetherian conservation in physics, we established analogs in genomic continuity and perceptual persistence. Through careful construction of the categories , , and —corresponding to physical, biological, and conscious syste We demonstrated how Tangent Perceptual Spaces (TPS) and Quantum Measurement Chains (QMC) provide a natural geometrical and quantum-theoretic interface between biological structure and conscious perception. By modeling consciousness as a Dirac delta functional within Hilbert space, and TPS as rays converging to this perceptual origin, we created a precise mathematical language to study qualia. Our framework captures not only sensory integration via monoidal categories but also dynamic development through Crucially, we examined the hypothesis that consciousness may emerge in sufficiently complex quantum computational systems. Using categorical measures such as entanglement entropy, circuit depth, and decoherence duration, we defined a complexity threshold beyond which qualia could manifest. This allows for a rigorous consideration of artificial consciousness and its ethical, scientific, and philosophical ramifications.
The incorporation of topos theory allowed us to treat internal logics of conscious systems as distinct from the Boolean logic underpinning classical physics. This move not only enriched our formalism but also aligned our model with the phenomenological asymmetry between objective measurement and subjective experience. The geometric morphisms between topoi became the formal vehicle by which we interpreted transitions between physical laws, genetic programs, and conscious states.
Our final synthesis involved mapping these categorical constructs to broader conceptual and ethical territories. We argued that conscious quantum computation could play a transformative role in scientific discovery, medical diagnostics, philosophical inquiry, and societal structure. By situating mind within a shared categorical substrate with matter and life, we proposed that all three domains—physics, biology, and consciousness—are emergent from invariant-preserving structures governed by functorial an The model proposed here is not only mathematically robust but also conceptually generative. It opens multiple directions for future inquiry, including the categorical modeling of memory, attention, and language, as well as the construction of ethical topoi for regulating artificial minds. Ultimately, we suggest that the study of consciousness must be grounded not only in empirical neurobiology or speculative philosophy, but also in the abstract invariance principles that underlie the structure of the univ
References
- Noether, E. (1918). Invariante Variationsprobleme. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 235–257.
- Peskin, M. E., & Schroeder, D. V. (2018). An Introduction to Quantum Field Theory. CRC Press.
- Maddox, B. (1993). The Quest for DNA: Watson and the Double Helix. Touchstone.
- Chalmers, D. J. Facing Up to the Problem of Consciousness. Journal of Consciousness Studies 1995, 2, 200–219. [Google Scholar]
- Mac Lane, S., & Moerdijk, I. (1992). Sheaves in Geometry and Logic: A First Introduction to Topos Theory. Springer-Verlag.
- Lawvere, F. W., & Rosebrugh, R. (2003). Sets for Mathematics. Cambridge University Press.
- Butz, C.; Johnstone, P. T. Classifying toposes for first-order theories. Annals of Pure and Applied Logic 1998, 91, 33–58. [Google Scholar] [CrossRef]
- Döring, A.; Isham, C. J. A topos foundation for theories of physics: I–IV. Journal of Mathematical Physics 2008, 49, 053515. [Google Scholar] [CrossRef]
- Bell, J. L. (1988). Toposes and Local Set Theories. Oxford University Press.
- Jacobs, B. Jacobs, B. (1999). Categorical Logic and Type Theory. Elsevier.
- Vickers, S. (2004). Locales and toposes as spaces. In Handbook of Spatial Logics (pp. 429–496). Springer.
- Streicher, T. (2006). Semantics of type theory: Correctness, completeness and independence results. Habilitation Thesis, TU Darmstadt.
- Baez, J. C., & Stay, M. (2011). Physics, topology, logic and computation: a Rosetta Stone. In New Structures for Physics (pp. 95–172). Springer. [CrossRef]
- Tononi, G. An information integration theory of consciousness. BMC Neuroscience 2004, 5, 42. [Google Scholar] [CrossRef] [PubMed]
- Edelman, G. M., & Tononi, G. (2000). A Universe of Consciousness: How Matter Becomes Imagination. Basic Books.
- Fong, B., & Spivak, D. I. (2019). Seven Sketches in Compositionality: An Invitation to Applied Category Theory. Cambridge University Press.
- Kitano, H. Systems biology: A brief overview. Science 2002, 295, 1662–1664. [Google Scholar] [CrossRef] [PubMed]
- Lambek, J., & Scott, P. J. (1986). Introduction to Higher Order Categorical Logic. Cambridge University Press.
- Selinger, P. (2011). A survey of graphical languages for monoidal categories. In New Structures for Physics (pp. 289–355). Springer.
- Roy, D. (2022). Quantum-Perceptual Mapping: Tangent Perceptual Spaces and Measurement Chains. arXiv, arXiv:2212.0187.
- Doering, A., & Isham, C. (2011). What is a Thing? Topos Theory in the Foundations of Physics. In New Structures for Physics (pp. 753–940). Springer. [CrossRef]
- Doering, A., & Isham, C. J. (2011). What is a thing? Topos theory in the foundations of physics. In New Structures for Physics (pp. 753–940). Springer. [CrossRef]
- Radenković, T., & Vojinović, M. (2025). The 3BF theory as a TQFT. Journal of Physics A: Mathematical and Theoretical.
- Ochogo, P. (2025). Light, Relation, and the Emergence of Spacetime: A Unified Theory of Mass, Gravity, and Consciousness. SSRN Electronic Journal.
- Blankert, J. P., & van Beveren, B. C. (2025). From Ontology to Observation: A Functorial Framework for Physics. ResearchGate Preprint.
- Kondrashov, S. (2025). Minimal Causal-Informational Model of Emergent Space-Time (MCIMES). SSRN Electronic Journal.
- Busemeyer, J. R., & Bruza, P. D. (2012). Quantum Models of Cognition and Decision. Cambridge University Press.
- Widdows, D. A Geometry of Meaning: Ideas of Meaning in Mathematics, Cognitive Science and Artificial Intelligence. Philosophical Psychology 2003, 16, 309–322. [Google Scholar]
- Abramsky, S., & Coecke, B. (2009). Categorical quantum mechanics. In Handbook of Quantum Logic and Quantum Structures (pp. 261–323). Elsevier.
- Isham, C. J. (1995). Structural issues in quantum gravity. Proceedings of the NATO Advanced Study Institute, Springer.
- Koenderink, J. J.; van Doorn, A. J. Affine structure from motion. Journal of the Optical Society of America A 1990, 8, 377–385. [Google Scholar]
- Lowe, D. G. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Catani, C. Categorical structures and visual perception. Foundations of Science 1999, 4, 253–276. [Google Scholar]
- Isham, C. J.; Butterfield, J. A topos perspective on the Kochen-Specker theorem: I. Quantum states as generalized valuations. International Journal of Theoretical Physics 1997, 37, 2669–2733. [Google Scholar]
- Wolpert, L., Tickle, C., & Arias, A. M. (2015). Principles of Development. Oxford University Press.
- Edelman, G. M. Neural Darwinism: Selection and reentrant signaling in higher brain function. Neuron 2001, 10, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Lawvere, F. W. Axiomatic cohesion. Theory and Applications of Categories 2004, 19, 41–49. [Google Scholar] [CrossRef]
- Goguen, J. A. A categorical manifesto. Mathematical Structures in Computer Science 1991, 1, 49–67. [Google Scholar] [CrossRef]
- Hubel, D. H.; Wiesel, T. N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. Journal of Physiology 1962, 160, 106–154. [Google Scholar] [PubMed]
- Friston, K. A theory of cortical responses. Philosophical Transactions of the Royal Society B: Biological Sciences, 2005, 360, 815–836. [Google Scholar]
- Felleman, D. J.; Van Essen, D. C. Distributed hierarchical processing in the primate cerebral cortex. Cerebral Cortex 1991, 1, 1–47. [Google Scholar] [CrossRef] [PubMed]
- Baars, B. J. (1988). A Cognitive Theory of Consciousness. Cambridge University Press.
- Chalmers, D. J. (1996). The Conscious Mind: In Search of a Fundamental Theory. Oxford University Press.
- Searle, J. R. Minds, brains, and programs. Behavioral and Brain Sciences 1980, 3, 417–424. [Google Scholar] [CrossRef]
- Lawvere, F. W., & Schanuel, S. H. (1994). Conceptual Mathematics: A First Introduction to Categories. Cambridge University Press.
- Mac Lane, S., & Moerdijk, I. (1992). Sheaves in Geometry and Logic: A First Introduction to Topos Theory. Springer-Verlag.
- Edelman, G. M. (2006). Second Nature: Brain Science and Human Knowledge. Yale University Press.
- Penrose, R. (1994). Shadows of the Mind: A Search for the Missing Science of Consciousness. Oxford University Press.
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the ‘Orch OR’ theory. Physics of Life Reviews 2014, 11, 39–78. [Google Scholar] [CrossRef] [PubMed]
- Eccles, J. C. (1994). How the Self Controls Its Brain. Springer-Verlag.
- Stapp, H. P. (2007). Mindful Universe: Quantum Mechanics and the Participating Observer. Springer. [CrossRef]
- Baez, J. C., & Stay, M. (2011). Physics, topology, logic and computation: A Rosetta Stone. In New Structures for Physics (pp. 95–172). Springer. [CrossRef]
- Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information. Cambridge University Press.
- Tegmark, M. Consciousness as a State of Matter. Chaos, Solitons & Fractals 2014, 76, 238–270. [Google Scholar]
- Tegmark, M. Importance of quantum decoherence in brain processes. Physical Review E 2000, 61, 4194. [Google Scholar] [CrossRef] [PubMed]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).