Prospect Theory-Driven Grey Multi-Attribute Decision-Making with Entropy-Based Weighting

1. Introduction

Multi-attribute decision-making (MADM) serves as a crucial decision-support tool that faces dual challenges of information incompleteness and decision-makers' behavioral preferences in complex environments [1,2,3,4,5,6,7,8] Conventional research often treats information uncertainty processing and behavioral decision analysis as separate domains, failing to adequately address the complexity inherent in real-world decision scenarios. This study develops an innovative decision-making framework by integrating grey system theory, prospect theory, and the entropy weight method to holistically consider both information incompleteness and behavioral characteristics [9,10,11,12,13,14,15].

Grey system theory [3] is particularly suitable for handling incomplete information scenarios. Its fundamental component, interval grey numbers [12,13,14,15], captures both quantitative and qualitative uncertainty through bounded intervals, providing a mathematical foundation for addressing decision information deficiencies. Complementing this, prospect theory [16,17] from behavioral economics reveals three characteristic decision-making patterns under risk: reference dependence, loss aversion, and diminishing sensitivity - features that are particularly prominent in complex decisions. It is noteworthy that while existing literature [18,19,20] has begun exploring prospect theory applications in MADM, most studies remain confined to precise information environments and fail to effectively incorporate uncertainty processing methods.

Regarding weight determination, information entropy [21,22] serves as an effective tool for measuring information uncertainty, yet its integration with interval grey numbers remains an understudied area. Particularly when evaluating significantly different alternatives, traditional fixed-weight approaches [13] cannot adequately reflect decision-makers' differentiated considerations across alternatives.

To address these theoretical gaps, this study constructs a three-phase integrated framework of "grey number representation - behavioral modification - entropy optimization." The framework first preserves original information integrity through the algebraic operation system of interval grey numbers [15], overcoming information distortion in data-deficient situations. Second, it incorporates prospect theory's dynamic reference point mechanism to quantify psychological expectations as value functions within grey intervals, breaking through the limitation of existing research [18,19,20] that only applies to precise numerical values. Specifically, we develop a grey-entropy distance-based algorithm for alternative-specific weighting by establishing a bi-objective optimization model that considers both information entropy and solution deviations, thereby achieving dynamic weight adjustment.

The theoretical innovations of this research manifest in three aspects: (1) establishing mapping relationships between interval grey numbers and prospect value functions to enable behavioral parameter calibration under uncertainty for the first time; (2) proposing an improved grey-entropy coupling weight model that enhances weight interpretability through solution discrimination factors; and (3) developing a cumulative prospect-based grey number ranking method that demonstrates higher cognitive consistency in decision outcomes compared to conventional models [13]. This integrated approach not only remedies the artificial separation of uncertainty processing and behavioral analysis in existing research but also provides novel insights for behavioral decision-making in complex environments.

2. Basic Concepts and Definitions

Definition 1. Suppose the decision scheme set is $A=\left\{\begin{array}{c}{A}_1,A_2,\cdots ,A_m\end{array}\right\}$ and the attribute indicator set is $S=\left\{\begin{array}{c}{S}_1,S_2,\cdots ,S_n\end{array}\right\}$. Because the decision information is not represented by precise values, but rather by interval grey numbers, the attribute value of alternative $A_i$$(i=1,\dots ,m)$ under attribute $S_j$$(j=1,\dots ,n)$ is denoted as a non-negative interval grey number: $u_{ij}(\otimes )\in [u_{ij}^L,u_{ij}^U]$ and $u_{ij}^U\ge u_{ij}^L\ge 0$.

Then, the attribute vector of $A_i$ is denoted as

$u_i(\otimes )=(u_{i1}(\otimes ),u_{i2}(\otimes ),\cdots ,u_{im}(\otimes )),i=1,2,\cdots ,n$.

The decision matrix is expressed as:

$$R={\left(u_{ij}\left(\otimes \right)\right)}_{m\times n}=\left.\left[\begin{array}{cccc}\left[u_{11}^L,u_{11}^U\right]& \left[u_{12}^L,u_{12}^U\right]& \cdots & \left[u_{1n}^L,u_{1n}^U\right]\\ \left[u_{21}^L,u_{21}^U\right]& \left[u_{22}^L,u_{22}^U\right]& \cdots & \left[u_{2n}^L,u_{2n}^U\right]\\ ⋮& ⋮& \ddots & ⋮\\ \left[u_{m1}^L,u_{m1}^U\right]& \left[u_{m2}^L,u_{m2}^U\right]& \cdots & \left[u_{mn}^L,u_{mn}^U\right]\end{array}\right.\right]$$

(1)

Definition 2. Let the weight assigned by the decision-maker to attribute $A_i$ under alternative $S_j$ be an interval grey number $w_{ij}(\otimes )(i=1,2,\cdots ,m$ $,j=1,2,\cdots ,n)$,${\omega }_{ij}(\otimes )\in \left[w_{ij}^L,w_{ij}^U\right]$$0⩽w_{ij}^L⩽w_{ij}^U⩽1$.

Then, the interval grey weight matrix composed of $w_{ij}(\otimes )$ is expressed as:

$$W={\left(w_{ij}\left(\otimes \right)\right)}_{m\times n}=\left[\begin{array}{cccc}\left[w_{11}^L,w_{11}^U\right]& \left[w_{12}^L,w_{12}^U\right]& \cdots & \left[w_{1n}^L,w_{1n}^U\right]\\ \left[w_{21}^L,w_{21}^U\right]& \left[w_{22}^L,w_{22}^U\right]& \cdots & \left[w_{2n}^L,w_{2n}^U\right]\\ ⋮& ⋮& \ddots & ⋮\\ \left[w_{m1}^L,w_{m1}^U\right]& \left[w_{m2}^L,w_{m2}^U\right]& \cdots & \left[w_{mn}^L,w_{mn}^U\right]\end{array}\right]$$

(2)

Definition 3. Given the differing dimensions across attributes, it is necessary to normalize the elements in the interval-valued decision matrix. For benefit-type attributes, normalization was performed as follows:

$$[x_{ij}^L,x_{ij}^U]=\left[u_{ij}^L/\sqrt{\sum _{i=1}^m{\left(u_{ij}^U\right)}^2},u_{ij}^U/\sqrt{\sum _{i=1}^m{\left(u_{ij}^L\right)}^2}\right],i=1,\dots ,m;j=1,\dots ,n$$

(3)

For cost-type attributes, the normalization is performed as follows:

$$[x_{ij}^L,x_{ij}^U]=\left[{\displaystyle \frac{1}{u_{ij}^U}}/\sqrt{\sum _{i=1}^m{\left({\displaystyle \frac{1}{u_{ij}^L}}\right)}^2},{\displaystyle \frac{1}{u_{ij}^L}}/\sqrt{\sum _{i=1}^m{\left({\displaystyle \frac{1}{u_{ij}^U}}\right)}^2}\right],i=1,\dots ,m;j=1,\dots ,n$$

(4)

Let the normalized decision matrix after dimensionless processing be denoted as:

$$X={\left(x_{ij}\left(\otimes \right)\right)}_{m\times n}=\left.\left[\begin{array}{cccc}\left[x_{11}^L,x_{11}^U\right]& \left[x_{12}^L,x_{12}^U\right]& \cdots & \left[x_{1n}^L,x_{1n}^U\right]\\ \left[x_{21}^L,x_{21}^U\right]& \left[x_{22}^L,x_{22}^U\right]& \cdots & \left[x_{2n}^L,x_{2n}^U\right]\\ ⋮& ⋮& \ddots & ⋮\\ \left[x_{m1}^L,x_{m1}^U\right]& \left[x_{m2}^L,x_{m2}^U\right]& \cdots & \left[x_{mn}^L,x_{mn}^U\right]\end{array}\right.\right]$$

(5)

where all elements are non-negative interval grey numbers defined in [0, 1].

The n-dimensional non-negative interval grey number vector:

$$x^{+}(\otimes )=(x_1^{+}(\otimes ),x_2^{+}(\otimes ),\cdots ,x_n^{+}\left(\otimes )\right)$$

(6)

is called the grey positive ideal point and is the n-dimensional non-negative interval grey number vector.

$$x^{-}(\otimes )=(x_1^{-}(\otimes ),x_2^{-}(\otimes ),\cdots ,x_n^{-}\left(\otimes )\right)$$

(7)

is called the grey negative ideal point, where:

$$x_j^{+}(\otimes )=\left[a_j^L,a_j^U\right]=\left[\underset{i}{\max }{x}_{ij}^L,\underset{i}{\max }{x}_{ij}^U\right],(j=1,\cdots ,n)$$

(8)

$$x_j^{-}(\otimes )=\left[b_j^L,b_j^U\right]=\left[\underset{i}{\min }{x}_{ij}^L,\underset{i}{\min }{x}_{ij}^U\right],(j=1,\cdots ,n)$$

(9)

Definition 4. As a valid metric in metric spaces, Euclidean distance satisfies the following three fundamental properties: non-negativity, homogeneity, and triangle inequality. In grey space, when grey numbers degenerate to whitened values, the grey distance reduces to Euclidean distance. Thus, Euclidean distance serves as a special case of grey distance.

Consider two n-dimensional interval grey number vectors:

$a(\otimes )=(a_1(\otimes ),a_2(\otimes ),\cdots ,a_m(\otimes ))$,

$b(\otimes )=(b_1(\otimes ),b_2(\otimes ),\cdots ,b_m(\otimes ))$,

where $a_j(\otimes )\in [a_j^L,a_j^U]$,$b_j(\otimes )\in [b_j^L,b_j^U]$, $(j=1,\dots ,n)$.

The distance between the two n-dimensional interval grey number vectors $a(\otimes )$ and $b(\otimes )$ is defined as follows:

$$d(a(\otimes ),b(\otimes ))={\displaystyle \frac{\sqrt{2}}{2}}\sqrt{\sum _{j=1}^n\left[{\left(a_j^L-b_j^L\right)}^2+{\left(a_j^U-b_j^U\right)}^2\right]}$$

(10)

Then, the distances from each alternative to the positive and negative ideal points are calculated as:

$$D_i^{+}=\left|x_j^{+}-x_{ij}\right|={\displaystyle \frac{\sqrt{2}}{2}}\sqrt{\sum _{j=1}^n\left[{\left(x_{ij}^L-b_j^L\right)}^2+{\left(x_{ij}^U-b_j^U\right)}^2\right]}$$

(11)

$$D_i^{-}=\left|x_{ij}-x_j^{-}\right|={\displaystyle \frac{\sqrt{2}}{2}}\sqrt{\sum _{j=1}^n\left[{\left(x_{ij}^L-a_j^L\right)}^2+{\left(x_{ij}^U-a_j^U\right)}^2\right]}$$

(12)

3. Decision-Making Model Based on Prospect Theory

Prospect Theory

The prospect value is jointly determined by a value function and decision weights, expressed as:

$$V=\sum _{i=1}^{n}v(x_i)\pi (p_i)$$

(13)

Here, $V$ is the prospect value, $v(x)$ is the value function that represents the subjectively perceived value formed by the decision maker, and $\pi (p_i)$ is the decision weight, an evaluative function assigned by the decision maker. If the attribute value provided by the decision maker is greater than the positive ideal point, the decision maker may perceive a gain, where the magnitude of the gain is determined by the distance between the attribute value and the positive ideal point. Similarly, the magnitude of the loss can be determined by the distance between the attribute value and the negative ideal point. Based on the function proposed by Tversky and Kahneman [17] to measure the decision-maker's attitude toward gains and losses, the prospect value function formula for each attribute of the alternative $A_i$ is as follows:

$$v\left(x_{ij}\right)=\left\{\begin{array}{l}{\left(x_{ij}-x_j^{-}\right)}^{\alpha },x_{ij}\ge x_r\hfill \\ -\lambda {\left(x_j^{+}-x_{ij}\right)}^{\beta },x_{ij}<x_r\hfill \end{array}\right.$$

(14)

Let $v^{+}\left(x_{ij}\right)={\left(x_{ij}-x_j^{-}\right)}^{\alpha }$ denote the gain prospect function, representing a positive prospect value, and $v^{-}\left(x_{ij}\right)=-\lambda {\left(x_j^{+}-x_{ij}\right)}^{\beta }$ ($0\le \alpha ,\beta \le 1$) denote the loss prospect function, representing a negative prospect value. Where $\alpha$ and $\beta$ are the gain- and loss-correlation coefficients, respectively. $\lambda$ is a risk-aversion parameter; $\lambda$ > 0. Ensuring that losses are steeper than gains. $\alpha =$0.89, $\beta =$0.92, and $\lambda =$2.25 [16].

3.2. Determining Optimal Attribute Weights

For a MADM problem with partially unknown weight information and interval grey numbers as attribute values, let the decision attribute weight vector for each alternative be $w=(w_1,w_2,\cdots ,w_n)$ or $\sum _{j=1}^n{w}_j=1$.

For each alternative $A_i$, the comprehensive prospect value of each alternative should be maximized. Therefore, the optimal weights can be computed using information entropy.

Based on Definition 2, let:

$$W^L=\left[\begin{array}{cccc}{w}_{11}^L& w_{12}^L& \cdots & w_{1n}^L\\ w_{21}^L& w_{22}^L& \cdots & w_{2n}^L\\ ⋮& ⋮& \ddots & ⋮\\ w_{m1}^L& w_{m2}^L& \cdots & w_{mn}^L\end{array}\right]$$

(15)

$$W^U=\left[\begin{array}{cccc}{w}_{11}^U& w_{12}^U& \cdots & w_{1n}^U\\ w_{21}^U& w_{22}^U& \cdots & w_{2n}^U\\ ⋮& ⋮& \ddots & ⋮\\ w_{m1}^U& w_{m2}^U& \cdots & w_{mn}^U\end{array}\right]$$

(16)

Then:

$$R=W^L\times {\left(diag\left(sum\left(W^L\right)\right)\right)}^{-1}$$

(17)

$$E={\displaystyle \frac{-sum\left(R\times \log \left(R\right)\right)}{\log \left(m\right)}}$$

(18)

$$F=1-E$$

(19)

and:

$${\pi }^{+}\left(w^L\right)={\displaystyle \frac{F}{sum\left(F\right)}}=\left(w_1^{+},w_2^{+},\cdots ,w_n^{+}\right)$$

(20)

and:

$${\pi }^{-}\left(w^U\right)=\left(w_1^{-},w_2^{-},\cdots ,w_n^{-}\right)$$

(21)

Let ${\pi }^{+}\left(w^L\right)=\left(w_1^{+},w_2^{+},\cdots ,w_n^{+}\right)$, ${\pi }^{-}\left(w^U\right)=\left(w_1^{-},w_2^{-},\cdots ,w_n^{-}\right)$ be the optimal solution to be determined, where ${\displaystyle \sum _{j=1}^n}{w}_j^{+}=1$, ${\displaystyle \sum _{j=1}^n}{w}_j^{-}=1$.

Then, the optimal comprehensive prospect value for alternative $A_i$ is given by $V_i={\displaystyle \sum _{j=1}^n}{v}^{+}(x_{ij}){\pi }^{+}(w_j^L)+{\displaystyle \sum _{j=1}^n}{v}^{-}(x_{ij}){\pi }^{-}(w_j^U)$:

By ranking the optimal comprehensive prospect values $V_i$$(i=1,\cdots ,m)$ of all alternatives in descending order, we obtain the complete ranking of alternatives and identify the optimal solution.

4. Procedure

Step 1: Construct the interval grey number decision matrix $R={\left(u_{ij}\left(\otimes \right)\right)}_{m\times n}$ based on the MADM problem, and then normalize it to obtain the standardized decision matrix $X={\left(x_{ij}\left(\otimes \right)\right)}_{m\times n}$.

Step 2: Determine ideal positive and negative points. Calculate the distance between each alternative’s attributes and $x_j^{+}(\otimes )$ and $x^{-}(\otimes )$ using Equations (10) and (11). The positive and negative prospect matrices for each alternative are then computed using (Equation (14)).

Step 3: With the goal of maximizing the comprehensive prospect value, calculate the optimal weights for gains ${\pi }^{+}\left(w^U\right)=\left(w_1^{+},w_2^{+},\cdots ,w_n^{+}\right)$ and losses ${\pi }^{-}\left(w^L\right)=\left(w_1^{-},w_2^{-},\cdots ,w_n^{-}\right)$ using the information entropy method (Equations (17)–(20)).

Step 4: Substitute ${\pi }^{+}\left(w^L\right)=\left(w_1^{+},w_2^{+},\cdots ,w_n^{+}\right)$, ${\pi }^{-}\left(w^U\right)=\left(w_1^{-},w_2^{-},\cdots ,w_n^{-}\right)$ into $V_i={\displaystyle \sum _{j=1}^n}{v}^{+}(x_{ij}){\pi }^{+}(w_j^L)+{\displaystyle \sum _{j=1}^n}{v}^{-}(x_{ij}){\pi }^{-}(w_j^U)$ to compute the optimal comprehensive prospect value $V_i$$(i=1,\cdots ,m)$, for each alternative. All alternatives were ranked in descending order of $V_i$ to obtain the final optimal ranking.

5. Example

Here, we refer to data from Reference [1], considering a venture capital firm evaluating five potential investment projects: $A_1$, $A_2$, $A_3$, $A_4$, and $A_5$. Six risk-based criteria were assessed: market risk ($S_1$); technological risk ($S_2$), management risk ($S_3$), environmental risk ($S_4$), production risk ($S_5$), financial risk ($S_6$).

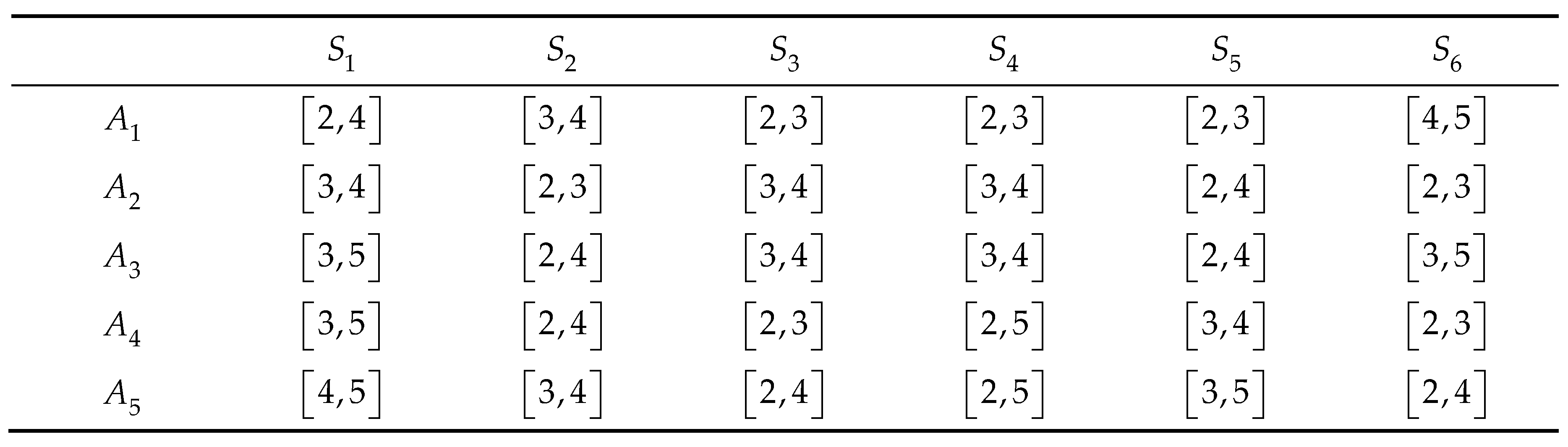
• All six attributes are cost-type criteria, with evaluation scores ranging from one (low risk) to five (high risk). Decision-makers assessed each project against these criteria, providing interval-valued scores for each attribute. The resulting decision matrix is expressed as follows:

Table 1. Information for the decision-making.

Table 1. Information for the decision-making.

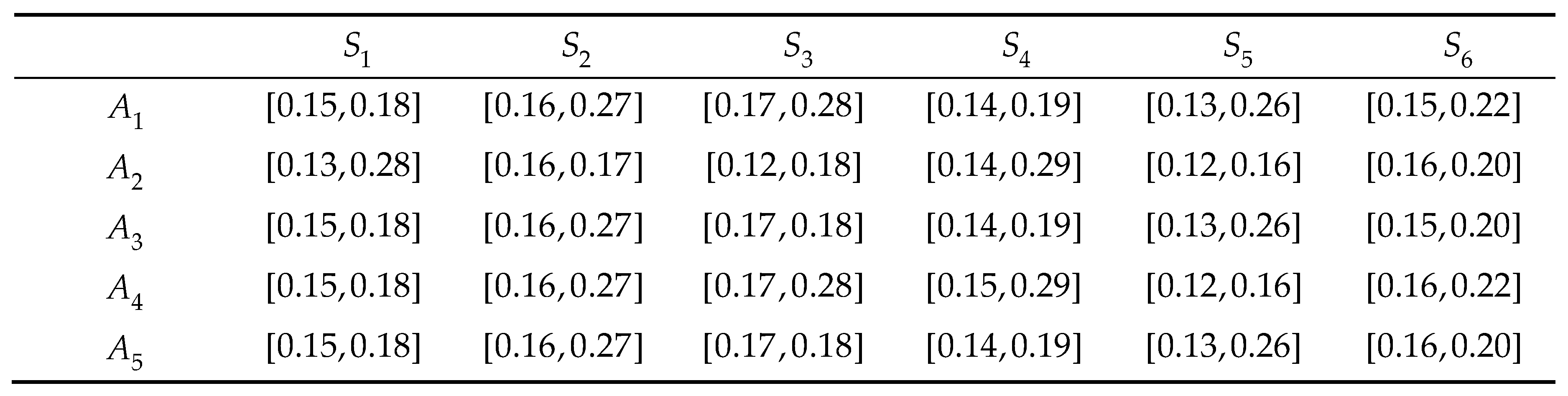
The known attribute weight information is given as:

Table 2. The initial attribute values of decision scheme.

Table 2. The initial attribute values of decision scheme.

The normalized decision matrix is obtained according to Equation (4) as follows:

Table 3. Normalized decision-making information after transformation.

Table 3. Normalized decision-making information after transformation.

2.

From the decision matrix, the positive and negative ideal points are determined as:

Table 4. The grey positive and negative ideal point.

Table 4. The grey positive and negative ideal point.

The distances from each alternative to the positive and negative ideal points were calculated using Equations (11) and (12) respectively.

Table 5. The gain matrix.

Table 5. The gain matrix.

Table 6. The loss matrix.

Table 6. The loss matrix.

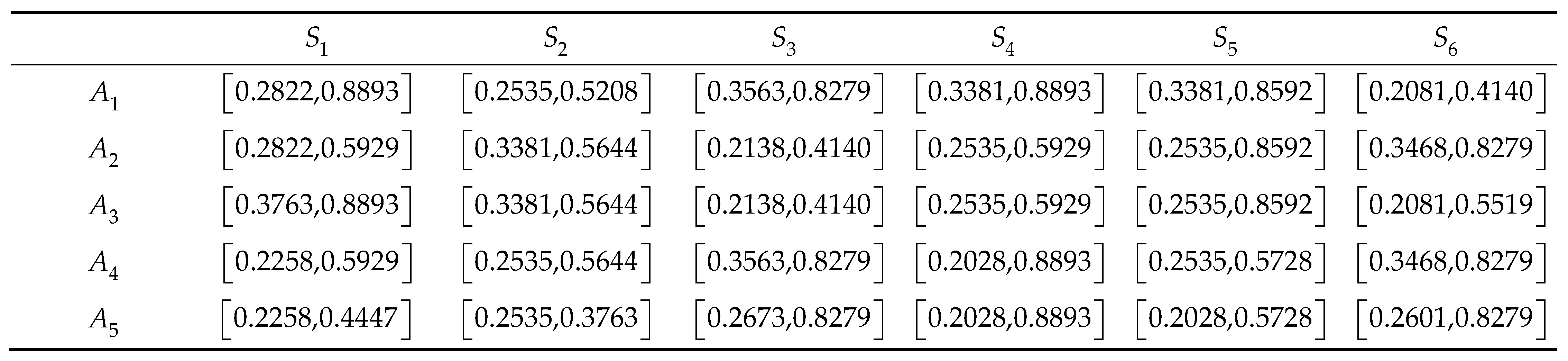
The positive and negative prospect matrices for each alternative are calculated using Equation (14).

Table 7. The positive prospect value matrix.

Table 7. The positive prospect value matrix.

Table 8. The negative prospect value matrix.

Table 8. The negative prospect value matrix.

3.

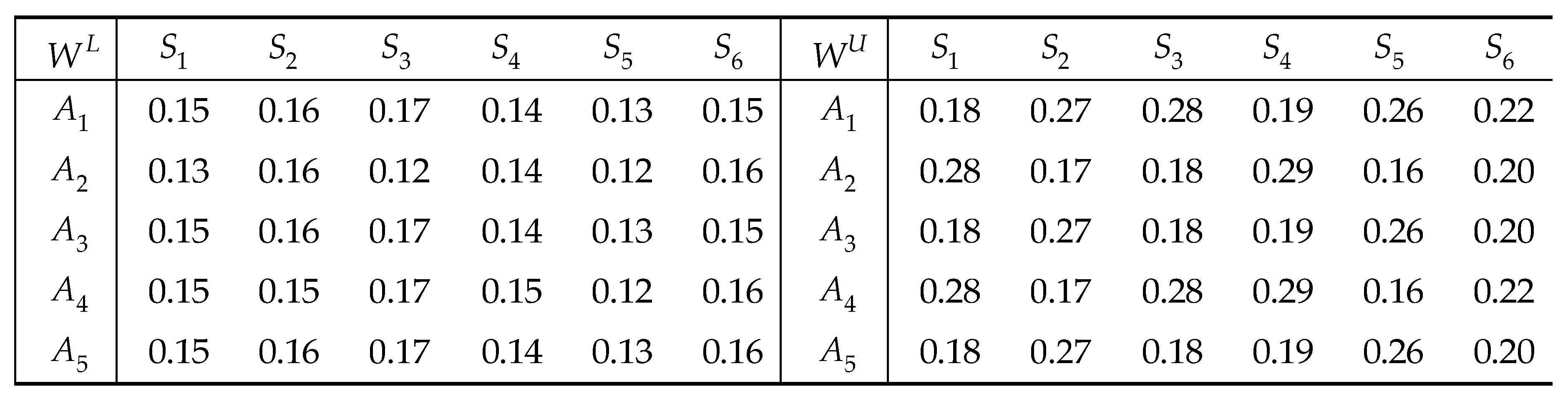
With the objective of maximizing the comprehensive prospect value, an optimization model is established: $\max V_i=\sum _{j=1}^n{v}^{+}(x_{ij}){\pi }^{+}(w_j^L)+\sum _{j=1}^n{v}^{-}(x_{ij}){\pi }^{-}(w_j^U)$

Table 9. The weights for the five attributes.

Table 9. The weights for the five attributes.

The optimal weights for the gains and losses are calculated using the information entropy method (Equations (17)–(20)) as follows:

${\pi }^{+}\left(w^L\right)=\left(w_1^{+},w_2^{+},\cdots ,w_n^{+}\right)=\left(0.1299,0.0273,0.7044,0.0329,0.0639,0.0416\right)$,

${\pi }^{-}\left(w^U\right)=\left(w_1^{-},w_2^{-},\cdots ,w_n^{-}\right)=\left(0.2001,0.1944,0.2001,0.1832,0.2130,0.0091\right)$,

where ${\displaystyle \sum _{j=1}^6}{w}_j^{+}=1,{\displaystyle \sum _{j=1}^6}{w}_j^{-}=1$.

4.

By substituting the optimal weight vectors ${\pi }^{+}\left(w^U\right)=\left(w_1^{+},w_2^{+},\cdots ,w_n^{+}\right)$, ${\pi }^{-}\left(w^L\right)=\left(w_1^{-},w_2^{-},\cdots ,w_n^{-}\right)$ into the comprehensive prospect value function, we obtain the optimal integrated prospect values for each alternative: $A_1\succ A_5\succ A_4\succ A_3\succ A_2$

Table 10. The optimal comprehensive prospect value.

Table 10. The optimal comprehensive prospect value.

The comprehensive prospect values reveal that only $A_1$ yields a positive value, whereas all the others are negative. Consequently, for complex venture capital investments, $A_1$ is the optimal choice for project investment.

6. Conclusion

This study addresses MADM problems in which attribute weights are inconsistent and entirely unknown and attribute values are expressed as interval grey numbers. The proposed framework integrates three key components.

• The interval Grey Number Distance Model: Measures the disparity between alternatives and ideal benchmarks.
• Prospect Value Theory: Quantifies gains/losses based on decision-makers’ psychological preferences.
• Information entropy-based weight optimization: Bijective weights are derived to balance the subjective biases.

Advantages Over Existing Models,

• Behavioral Realism: Explicitly accounts for decision-makers’ varying perceptions of attribute values.
• Adaptability: Suitable for high-uncertainty scenarios with incomplete weight information.
• Practical Utility: The entropy-driven weighting method enhances the reliability of outcomes in complex real-world decisions.

This framework provides a robust tool for venture capital firms and other high-stakes decision environments in which risk perception and data uncertainty play critical roles.