Submitted:
26 September 2025
Posted:
28 September 2025
You are already at the latest version
Abstract
Keywords:
Three Key Points:
- Normative modelling entails quantifying the normative variability of an imaging biomarker in a reference condition and identifying subject-specific pathological deviations.
- Normative modelling addresses the limitations of traditional population-level studies by enabling the detection of subject-level deviations from the normative range, without requiring a shared pattern of abnormalities across multiple individuals.
- The specific application and methodological complexity of the normative modelling framework may vary across studies and imaging methods, depending on several operative choices, including the selection of the modelling approach, the definition of a deviation metric, and the necessity for a data harmonization step.
1. Introduction
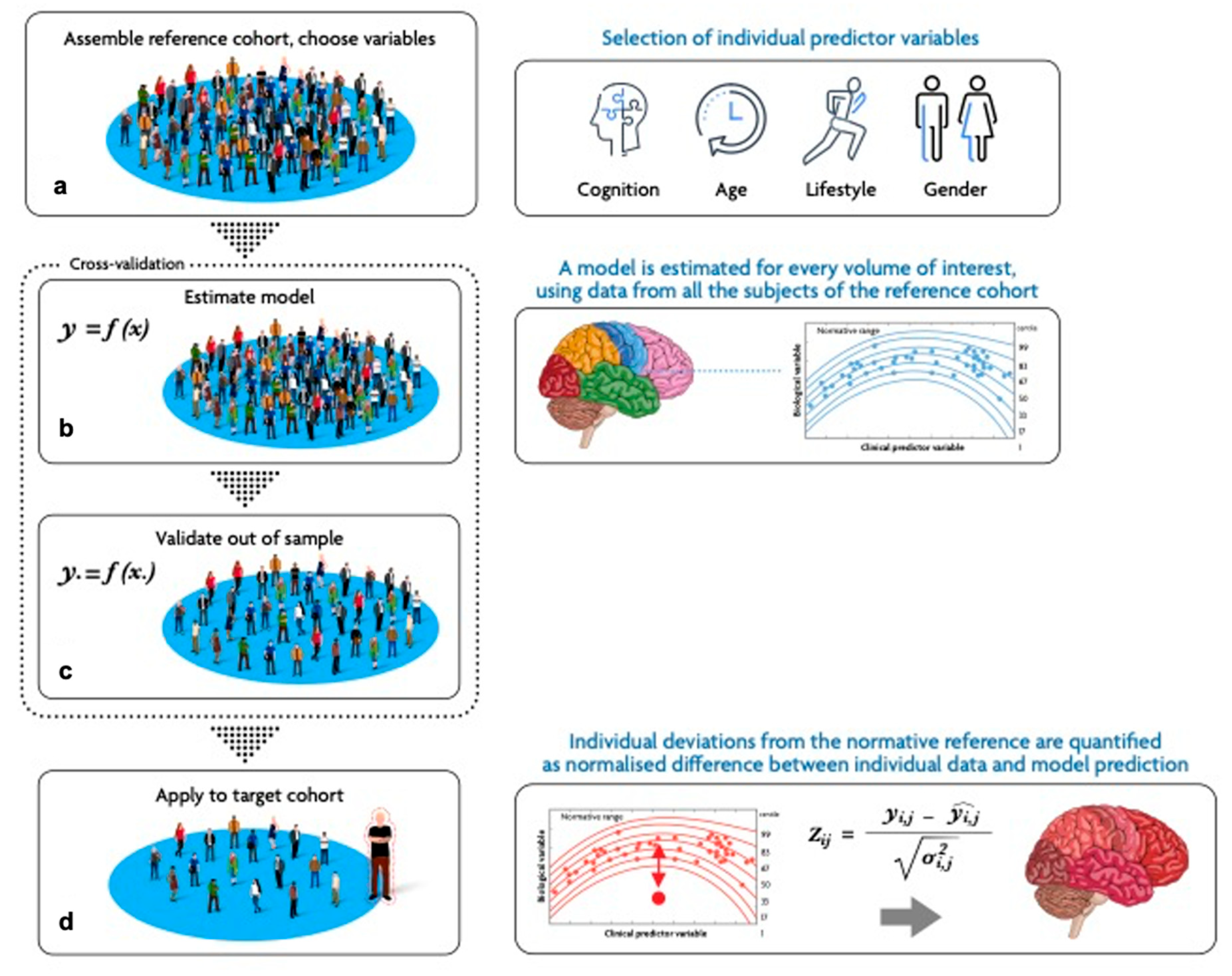
2. The NM Framework in Neuroimaging Studies
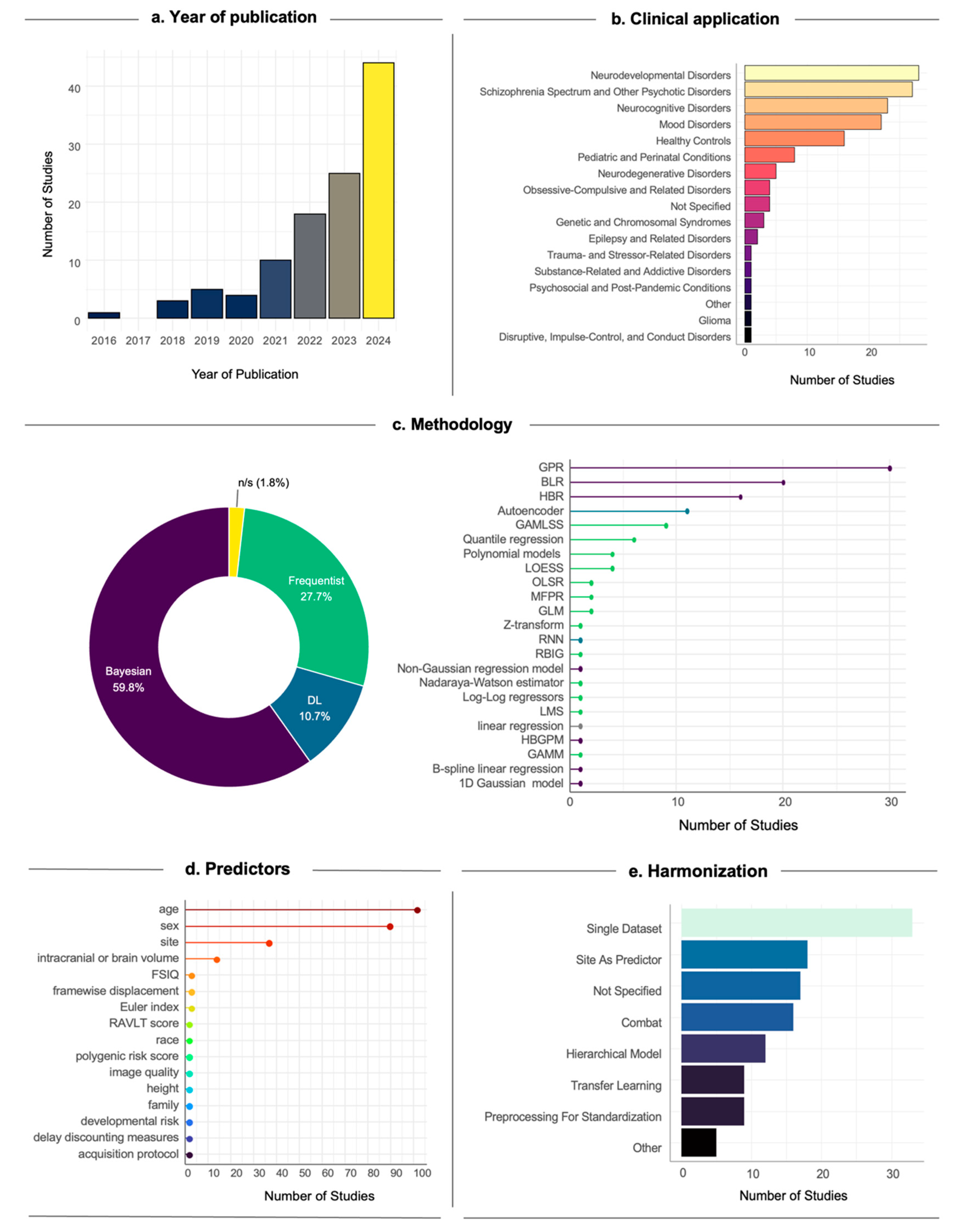
2.1. Study Design: Data Collection, Harmonization, and Covariates Selection
2.2. Model Definition and Identification
Frequentist Methods
Bayesian Methods
DL Methods
2.3. Model Evaluation
2.4. Model Application to the Target Cohort
3. NM Applications to Neuroimaging
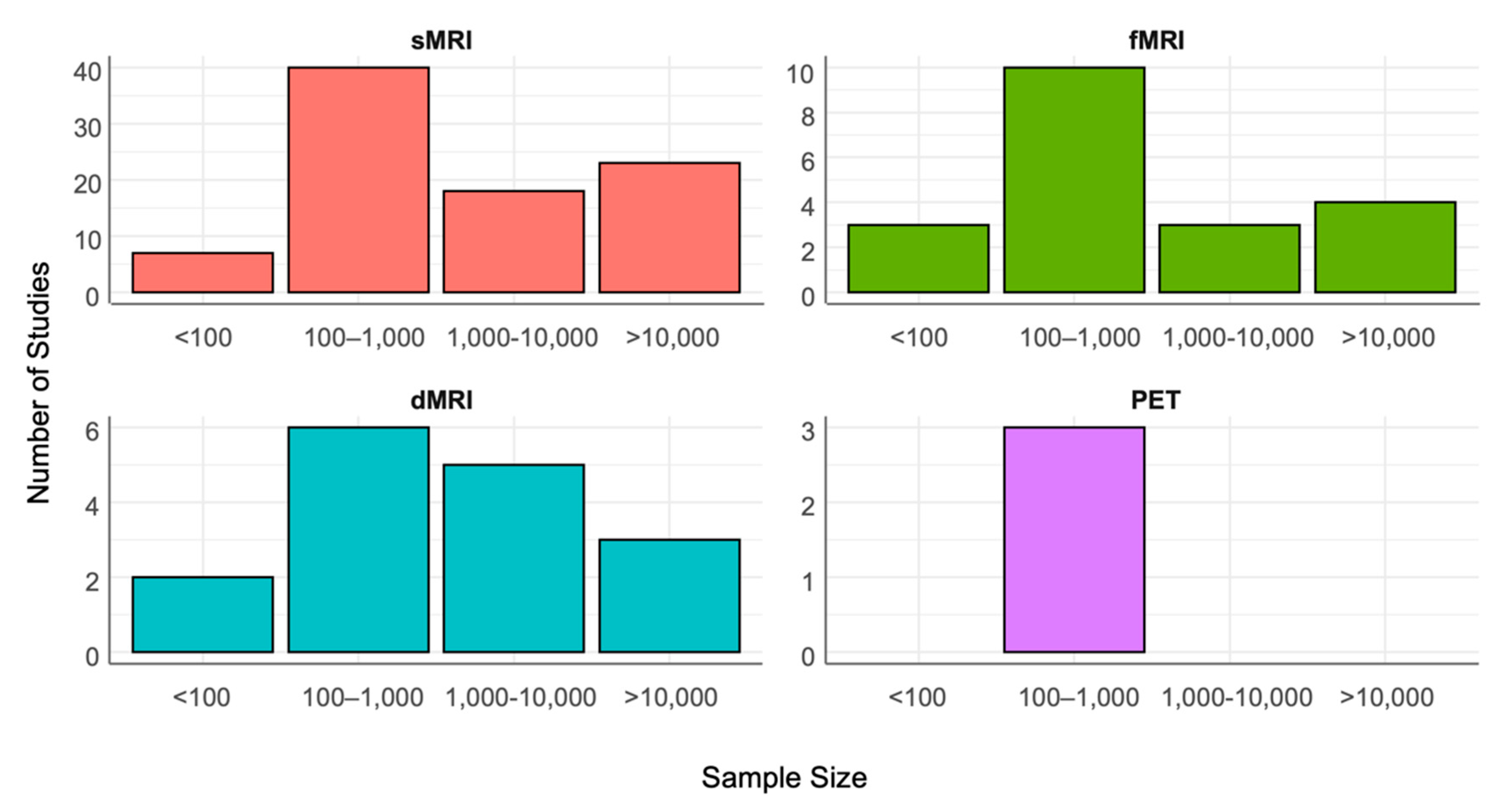
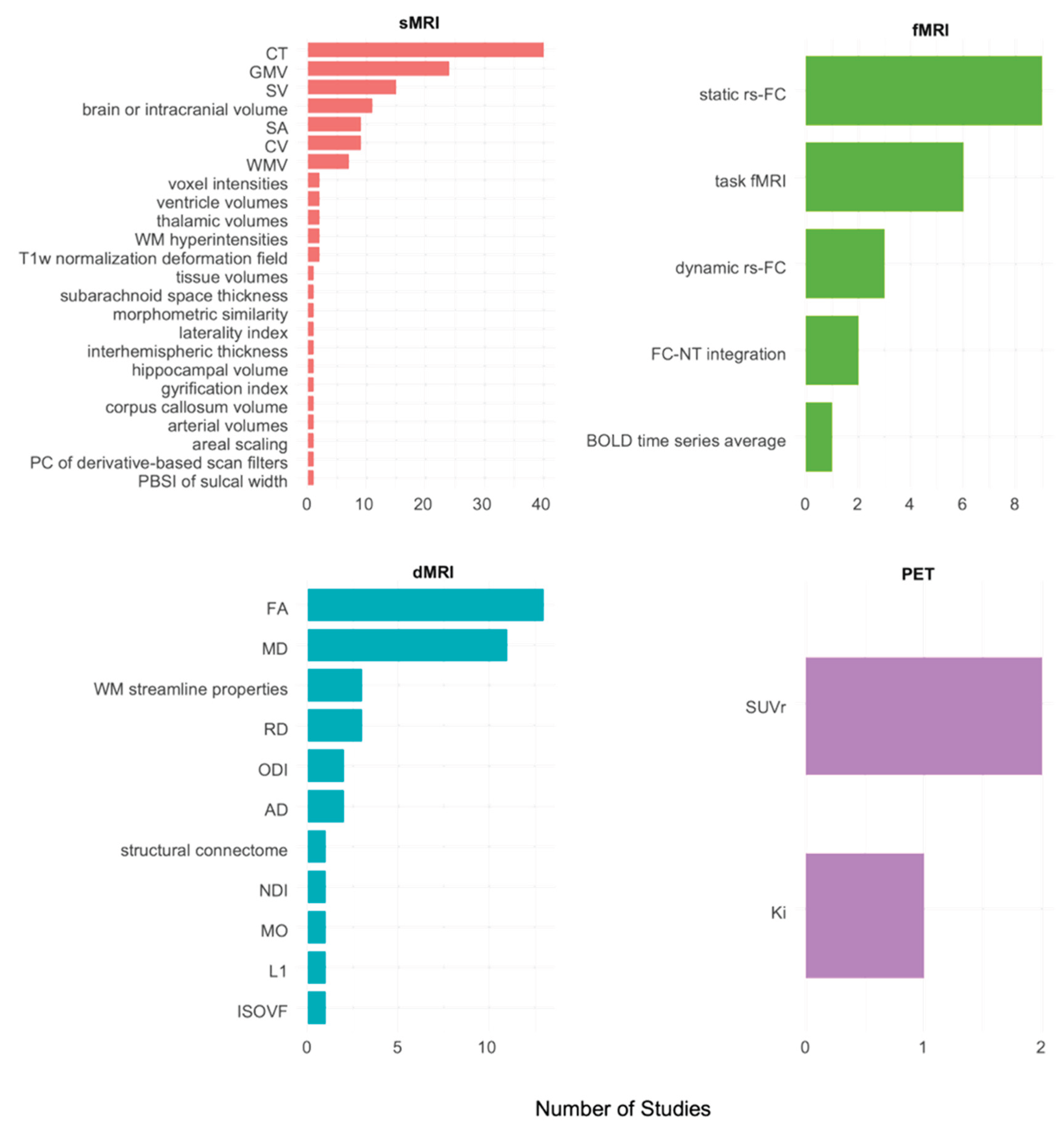
3.1. sMRI
3.2. fMRI
3.3. dMRI
3.4. Molecular Imaging
4. Open-Source Tools to Implement Normative Modelling in Neuroimaging Studies
- Predictive Clinical Neuroscience Toolkit (PCNtoolkit) (Rutherford et al., 2022b): Python package of pipelines for NM estimation and application to neuroimaging data; based on Bayesian approaches, it is highly flexible in handling multi-site data and complex relationships between response and covariates (https://github.com/amarquand/PCNtoolkit).
- Predictive Clinical Neuroscience Portal (PCN Portal) (Barkema et al., 2023): online platform integrated with the PCNtoolkit providing a user-friendly interface where researchers can access pre-trained normative models estimated from large datasets, upload their data, and obtain normative models without requiring local computational resources or programming expertise (https://github.com/predictive-clinical-neuroscience/PCNportal?tab=readme-ov-file).
- PyNM (Harvey and Dumas, 2022): lightweight Python NM implementation designed to facilitate the implementation of NM operative steps (model estimation, comparison, validation, etc) for users with low technical expertise, providing both a Python API and a command-line interface and a comprehensive tutorial (https://github.com/ppsp-team/PyNM?tab=readme-ov-file#readme).
- CentileBrain (Ge et al., 2024a): web portal providing pre-trained models of typical brain trajectories estimated on large multi-site ENIGMA data for their application to users’ datasets (https://centilebrain.org).
5. Discussion
6. Conclusion
Supplementary Materials
Author’s contributions
Acknowledgments
Conflict of interest
References
- Alvarez, I., Parker, A.J., Bridge, H., 2019. Normative cerebral cortical thickness for human visual areas. NeuroImage 201, 116057. [CrossRef]
- Antoniades, M., Haas, S.S., Modabbernia, A., Bykowsky, O., Frangou, S., Borgwardt, S., Schmidt, A., 2021. Personalized Estimates of Brain Structural Variability in Individuals With Early Psychosis. Schizophrenia Bulletin 47, 1029–1038. [CrossRef]
- Baldwin, H., Radua, J., Antoniades, M., Haas, S.S., Frangou, S., Agartz, I., Allen, P., Andreassen, O.A., Atkinson, K., Bachman, P., Baeza, I., Bartholomeusz, C.F., Chee, M.W.L., Colibazzi, T., Cooper, R.E., Corcoran, C.M., Cropley, V.L., Ebdrup, B.H., Fortea, A., Glenthøj, L.B., Hamilton, H.K., Haut, K.M., Hayes, R.A., He, Y., Heekeren, K., Kaess, M., Kasai, K., Katagiri, N., Kim, M., Kindler, J., Klaunig, M.J., Koike, S., Koppel, A., Kristensen, T.D., Bin Kwak, Y., Kwon, J.S., Lawrie, S.M., Lebedeva, I., Lee, J., Lin, A., Loewy, R.L., Mathalon, D.H., Michel, C., Mizrahi, R., Møller, P., Nelson, B., Nemoto, T., Nordholm, D., Omelchenko, M.A., Pantelis, C., Raghava, J.M., Røssberg, J.I., Rössler, W., Salisbury, D.F., Sasabayashi, D., Schall, U., Smigielski, L., Sugranyes, G., Suzuki, M., Takahashi, T., Tamnes, C.K., Tang, J., Theodoridou, A., Thomopoulos, S.I., Tomyshev, A.S., Uhlhaas, P.J., Værnes, T.G., van Amelsvoort, T.A.M.J., Van Erp, T.G.M., Waltz, J.A., Westlye, L.T., Wood, S.J., Zhou, J.H., McGuire, P., Thompson, P.M., Jalbrzikowski, M., Hernaus, D., Fusar-Poli, P., 2022. Neuroanatomical heterogeneity and homogeneity in individuals at clinical high risk for psychosis. Transl Psychiatry 12, 1–11. [CrossRef]
- Baldwin, S.A., Larson, M.J., 2017. An introduction to using Bayesian linear regression with clinical data. Behaviour Research and Therapy 98, 58–75. [CrossRef]
- Bank, D., Koenigstein, N., Giryes, R., 2021. Autoencoders. [CrossRef]
- Barkema, P., Rutherford, S., Lee, H.-C., Kia, S.M., Savage, H., Beckmann, C., Marquand, A., 2023. Predictive Clinical Neuroscience Portal (PCNportal): instant online access to research-grade normative models for clinical neuroscientists. Wellcome Open Res 8, 326. [CrossRef]
- Bayer, J.M.M., Dinga, R., Kia, S.M., Kottaram, A.R., Wolfers, T., Lv, J., Zalesky, A., Schmaal, L., Marquand, A., 2021. Accommodating site variation in neuroimaging data using normative and hierarchical Bayesian models.
- Bayer, J.M.M., Thompson, P.M., Ching, C.R.K., Liu, M., Chen, A., Panzenhagen, A.C., Jahanshad, N., Marquand, A., Schmaal, L., Sämann, P.G., 2022. Site effects how-to and when: An overview of retrospective techniques to accommodate site effects in multi-site neuroimaging analyses. Front. Neurol. 13, 923988. [CrossRef]
- Bedford, S.A., Lai, M.-C., Lombardo, M.V., Chakrabarti, B., Ruigrok, A., Suckling, J., Anagnostou, E., Lerch, J.P., Taylor, M., Nicolson, R., Stelios, G., Crosbie, J., Schachar, R., Kelley, E., Jones, J., Arnold, P.D., Courchesne, E., Pierce, K., Eyler, L.T., Campbell, K., Barnes, C.C., Seidlitz, J., Alexander-Bloch, A.F., Bullmore, E.T., Baron-Cohen, S., Bethlehem, R.A.I., Bailey, A.J., Baron-Cohen, S., Bolton, P.F., Bullmore, E.T., Carrington, S., Catani, M., Chakrabarti, B., Craig, M.C., Daly, E.M., Deoni, S.C.L., Ecker, C., Happé, F., Henty, J., Jezzard, P., Johnston, P., Jones, D.K., Lai, M.-C., Lombardo, M.V., Madden, A., Mullins, D., Murphy, C.M., Murphy, D.G.M., Pasco, G., Ruigrok, A.N.V., Sadek, S.A., Spain, D., Stewart, R., Suckling, J., Wheelwright, S.J., Williams, S.C., 2024. Brain-Charting Autism and Attention-Deficit/Hyperactivity Disorder Reveals Distinct and Overlapping Neurobiology. Biological Psychiatry 0. [CrossRef]
- Berthet, P., Haatveit, B.C., Kjelkenes, R., Worker, A., Kia, S.M., Wolfers, T., Rutherford, S., Alnaes, D., Dinga, R., Pedersen, M.L., Dahl, A., Fernandez-Cabello, S., Dazzan, P., Agartz, I., Nesvåg, R., Ueland, T., Andreassen, O.A., Simonsen, C., Westlye, L.T., Melle, I., Marquand, A., 2024. A 10-Year Longitudinal Study of Brain Cortical Thickness in People with First-Episode Psychosis Using Normative Models. Schizophr Bull 51, 95–107. [CrossRef]
- Bethlehem, R. a. I., Seidlitz, J., White, S.R., Vogel, J.W., Anderson, K.M., Adamson, C., Adler, S., Alexopoulos, G.S., Anagnostou, E., Areces-Gonzalez, A., Astle, D.E., Auyeung, B., Ayub, M., Bae, J., Ball, G., Baron-Cohen, S., Beare, R., Bedford, S.A., Benegal, V., Beyer, F., Blangero, J., Blesa Cábez, M., Boardman, J.P., Borzage, M., Bosch-Bayard, J.F., Bourke, N., Calhoun, V.D., Chakravarty, M.M., Chen, C., Chertavian, C., Chetelat, G., Chong, Y.S., Cole, J.H., Corvin, A., Costantino, M., Courchesne, E., Crivello, F., Cropley, V.L., Crosbie, J., Crossley, N., Delarue, M., Delorme, R., Desrivieres, S., Devenyi, G.A., Di Biase, M.A., Dolan, R., Donald, K.A., Donohoe, G., Dunlop, K., Edwards, A.D., Elison, J.T., Ellis, C.T., Elman, J.A., Eyler, L., Fair, D.A., Feczko, E., Fletcher, P.C., Fonagy, P., Franz, C.E., Galan-Garcia, L., Gholipour, A., Giedd, J., Gilmore, J.H., Glahn, D.C., Goodyer, I.M., Grant, P.E., Groenewold, N.A., Gunning, F.M., Gur, R.E., Gur, R.C., Hammill, C.F., Hansson, O., Hedden, T., Heinz, A., Henson, R.N., Heuer, K., Hoare, J., Holla, B., Holmes, A.J., Holt, R., Huang, H., Im, K., Ipser, J., Jack, C.R., Jackowski, A.P., Jia, T., Johnson, K.A., Jones, P.B., Jones, D.T., Kahn, R.S., Karlsson, H., Karlsson, L., Kawashima, R., Kelley, E.A., Kern, S., Kim, K.W., Kitzbichler, M.G., Kremen, W.S., Lalonde, F., Landeau, B., Lee, S., Lerch, J., Lewis, J.D., Li, J., Liao, W., Liston, C., Lombardo, M.V., Lv, J., Lynch, C., Mallard, T.T., Marcelis, M., Markello, R.D., Mathias, S.R., Mazoyer, B., McGuire, P., Meaney, M.J., Mechelli, A., Medic, N., Misic, B., Morgan, S.E., Mothersill, D., Nigg, J., Ong, M.Q.W., Ortinau, C., Ossenkoppele, R., Ouyang, M., Palaniyappan, L., Paly, L., Pan, P.M., Pantelis, C., Park, M.M., Paus, T., Pausova, Z., Paz-Linares, D., Pichet Binette, A., Pierce, K., Qian, X., Qiu, J., Qiu, A., Raznahan, A., Rittman, T., Rodrigue, A., Rollins, C.K., Romero-Garcia, R., Ronan, L., Rosenberg, M.D., Rowitch, D.H., Salum, G.A., Satterthwaite, T.D., Schaare, H.L., Schachar, R.J., Schultz, A.P., Schumann, G., Schöll, M., Sharp, D., Shinohara, R.T., Skoog, I., Smyser, C.D., Sperling, R.A., Stein, D.J., Stolicyn, A., Suckling, J., Sullivan, G., Taki, Y., Thyreau, B., Toro, R., Traut, N., Tsvetanov, K.A., Turk-Browne, N.B., Tuulari, J.J., Tzourio, C., Vachon-Presseau, É., Valdes-Sosa, M.J., Valdes-Sosa, P.A., Valk, S.L., van Amelsvoort, T., Vandekar, S.N., Vasung, L., Victoria, L.W., Villeneuve, S., Villringer, A., Vértes, P.E., Wagstyl, K., Wang, Y.S., Warfield, S.K., Warrier, V., Westman, E., Westwater, M.L., Whalley, H.C., Witte, A.V., Yang, N., Yeo, B., Yun, H., Zalesky, A., Zar, H.J., Zettergren, A., Zhou, J.H., Ziauddeen, H., Zugman, A., Zuo, X.N., Bullmore, E.T., Alexander-Bloch, A.F., 2022. Brain charts for the human lifespan. Nature 604, 525–533. [CrossRef]
- Bethlehem, R.A.I., Seidlitz, J., Romero-Garcia, R., Dumas, G., Lombardo, M.V., 2019. Normative age modelling of cortical thickness in autistic males. [CrossRef]
- Bhome, R., Verdi, S., Martin, S.A., Hannaway, N., Dobreva, I., Oxtoby, N.P., Castro Leal, G., Rutherford, S., Marquand, A.F., Weil, R.S., Cole, J.H., 2024. A neuroimaging measure to capture heterogeneous patterns of atrophy in Parkinson’s disease and dementia with Lewy bodies. NeuroImage: Clinical 42, 103596. [CrossRef]
- Bigler, E.D., 1994. Neuroimaging and Neuropsychological Assessment, in: Reynolds, C.R. (Ed.), Cognitive Assessment: A Multidisciplinary Perspective. Springer US, Boston, MA, pp. 1–34. [CrossRef]
- Blok, E., Geenjaar, E.P.T., Geenjaar, E.A.W., Calhoun, V.D., White, T., 2022. Neurodevelopmental Trajectories in Children With Internalizing, Externalizing and Emotion Dysregulation Symptoms. Front. Psychiatry 13, 846201. [CrossRef]
- Bozek, J., Griffanti, L., Lau, S., Jenkinson, M., 2023. Normative models for neuroimaging markers: Impact of model selection, sample size and evaluation criteria. NeuroImage 268, 119864. [CrossRef]
- Brammer, M., 2009. The role of neuroimaging in diagnosis and personalized medicine--current position and likely future directions. Dialogues Clin Neurosci 11, 389–396. [CrossRef]
- Bremner, J.D., 2005. Brain imaging handbook, Brain imaging handbook. W W Norton & Co, New York, NY, US.
- Chen, C.-L., Hwang, T., Tung, Y.-H., Yang, L.-Y., Hsu, Y.-C., Liu, C., Lin, Y.-T., Hsieh, M.-H., Liu, C.-C., Chien, Y.-L., Hwu, H., Tseng, W.-Y.I., 2022a. Detection of advanced brain aging in schizophrenia and its structural underpinning by using normative brain age metrics. Neuroimage Clin 34, 103003. [CrossRef]
- Chen, C.-L., Kuo, M.-C., Wu, W.-C., Hsu, Y.-C., Wu, R.-M., Tseng, W.-Y.I., 2022b. Advanced brain aging in multiple system atrophy compared to Parkinson’s disease. NeuroImage: Clinical 34, 102997. [CrossRef]
- Cole, J.H., Franke, K., 2017. Predicting Age Using Neuroimaging: Innovative Brain Ageing Biomarkers. Trends Neurosci 40, 681–690. [CrossRef]
- Cole, T.J., 2012. The development of growth references and growth charts. Annals of Human Biology 39, 382–394. [CrossRef]
- Corrigan, N.M., Rokem, A., Kuhl, P.K., 2024. COVID-19 lockdown effects on adolescent brain structure suggest accelerated maturation that is more pronounced in females than in males. Proceedings of the National Academy of Sciences 121, e2403200121. [CrossRef]
- Cotter, J., 2006. Extreme Value Estimation of Boom and Crash Statistics. The European Journal of Finance 12, 553–566. [CrossRef]
- Coupé, P., Manjón, J.V., Mansencal, B., Tourdias, T., Catheline, G., Planche, V., 2022. Hippocampal-amygdalo-ventricular atrophy score: Alzheimer disease detection using normative and pathological lifespan models. Hum Brain Mapp 43, 3270–3282. [CrossRef]
- Cromb, D., Wilson, S., Bonthrone, A.F., Chew, A., Kelly, C., Kumar, M., Cawley, P., Dimitrova, R., Arichi, T., Tournier, J.D., Pushparajah, K., Simpson, J., Rutherford, M., Hajnal, J.V., Edwards, A.D., Nosarti, C., O’Muircheartaigh, J., Counsell, S.J., 2024. Individualized cortical gyrification in neonates with congenital heart disease. Brain Commun 6, fcae356. [CrossRef]
- Cropley, V.L., Tian, Y., Fernando, K., Mansour L, S., Pantelis, C., Cocchi, L., Zalesky, A., 2021. Brain-Predicted Age Associates With Psychopathology Dimensions in Youths. Biol Psychiatry Cogn Neurosci Neuroimaging 6, 410–419. [CrossRef]
- D’Ambrosio, E., Pergola, G., Pardiñas, A.F., Dahoun, T., Veronese, M., Sportelli, L., Taurisano, P., Griffiths, K., Jauhar, S., Rogdaki, M., Bloomfield, M.A.P., Froudist-Walsh, S., Bonoldi, I., Walters, J.T.R., Blasi, G., Bertolino, A., Howes, O.D., 2022. A polygenic score indexing a DRD2-related co-expression network is associated with striatal dopamine function. Scientific reports 12, 12610. [CrossRef]
- Di Biase, M.A., Tian, Y.E., Bethlehem, R.A.I., Seidlitz, J., Alexander-Bloch, A.F., Yeo, B.T.T., Zalesky, A., 2023. Mapping human brain charts cross-sectionally and longitudinally. Proc Natl Acad Sci U S A 120, e2216798120. [CrossRef]
- Dimitrova, R., Arulkumaran, S., Carney, O., Chew, A., Falconer, S., Ciarrusta, J., Wolfers, T., Batalle, D., Cordero-Grande, L., Price, A.N., Teixeira, R.P.A.G., Hughes, E., Egloff, A., Hutter, J., Makropoulos, A., Robinson, E.C., Schuh, A., Vecchiato, K., Steinweg, J.K., Macleod, R., Marquand, A.F., McAlonan, G., Rutherford, M.A., Counsell, S.J., Smith, S.M., Rueckert, D., Hajnal, J.V., O’Muircheartaigh, J., Edwards, A.D., 2021. Phenotyping the Preterm Brain: Characterizing Individual Deviations From Normative Volumetric Development in Two Large Infant Cohorts. Cerebral Cortex 31, 3665–3677. [CrossRef]
- Dinga, R., Fraza, C.J., Bayer, J.M.M., Kia, S.M., Beckmann, C.F., Marquand, A.F., 2021. Normative modeling of neuroimaging data using generalized additive models of location scale and shape (preprint). Neuroscience. [CrossRef]
- Dipasquale, O., Selvaggi, P., Veronese, M., Gabay, A.S., Turkheimer, F., Mehta, M.A., 2019. Receptor-Enriched Analysis of functional connectivity by targets (REACT): A novel, multimodal analytical approach informed by PET to study the pharmacodynamic response of the brain under MDMA. Neuroimage 195, 252–260. [CrossRef]
- Doucet, G.E., Glahn, D.C., Frangou, S., 2020. Person-based similarity in brain structure and functional connectivity in bipolar disorder. J Affect Disord 276, 38–44. [CrossRef]
- Duan, X., Shan, X., Uddin, L.Q., Chen, H., 2024. The Future of Disentangling the Heterogeneity of Autism With Neuroimaging Studies. Biological Psychiatry S0006322324015361. [CrossRef]
- Elad, D., Cetin-Karayumak, S., Zhang, F., Cho, K.I.K., Lyall, A.E., Seitz-Holland, J., Ben-Ari, R., Pearlson, G.D., Tamminga, C.A., Sweeney, J.A., Clementz, B.A., Schretlen, D.J., Viher, P.V., Stegmayer, K., Walther, S., Lee, J., Crow, T.J., James, A., Voineskos, A.N., Buchanan, R.W., Szeszko, P.R., Malhotra, A.K., Keshavan, M.S., Shenton, M.E., Rathi, Y., Bouix, S., Sochen, N., Kubicki, M.R., Pasternak, O., 2021. Improving the predictive potential of diffusion MRI in schizophrenia using normative models—Towards subject-level classification. Human Brain Mapping 42, 4658–4670. [CrossRef]
- ENIGMA Clinical High Risk for Psychosis Working Group, Haas, S.S., Ge, R., Agartz, I., Amminger, G.P., Andreassen, O.A., Bachman, P., Baeza, I., Choi, S., Colibazzi, T., Cropley, V.L., de la Fuente-Sandoval, C., Ebdrup, B.H., Fortea, A., Fusar-Poli, P., Glenthøj, B.Y., Glenthøj, L.B., Haut, K.M., Hayes, R.A., Heekeren, K., Hooker, C.I., Hwang, W.J., Jahanshad, N., Kaess, M., Kasai, K., Katagiri, N., Kim, M., Kindler, J., Koike, S., Kristensen, T.D., Kwon, J.S., Lawrie, S.M., Lebedeva, I., Lee, J., Lemmers-Jansen, I.L.J., Lin, A., Ma, X., Mathalon, D.H., McGuire, P., Michel, C., Mizrahi, R., Mizuno, M., Møller, P., Mora-Durán, R., Nelson, B., Nemoto, T., Nordentoft, M., Nordholm, D., Omelchenko, M.A., Pantelis, C., Pariente, J.C., Raghava, J.M., Reyes-Madrigal, F., Røssberg, J.I., Rössler, W., Salisbury, D.F., Sasabayashi, D., Schall, U., Smigielski, L., Sugranyes, G., Suzuki, M., Takahashi, T., Tamnes, C.K., Theodoridou, A., Thomopoulos, S.I., Thompson, P.M., Tomyshev, A.S., Uhlhaas, P.J., Værnes, T.G., van Amelsvoort, T.A.M.J., van Erp, T.G.M., Waltz, J.A., Wenneberg, C., Westlye, L.T., Wood, S.J., Zhou, J.H., Hernaus, D., Jalbrzikowski, M., Kahn, R.S., Corcoran, C.M., Frangou, S., 2024. Normative Modeling of Brain Morphometry in Clinical High Risk for Psychosis. JAMA Psychiatry 81, 77–88. [CrossRef]
- Erus, G., Battapady, H., Satterthwaite, T.D., Hakonarson, H., Gur, R.E., Davatzikos, C., Gur, R.C., 2015. Imaging Patterns of Brain Development and their Relationship to Cognition. Cerebral Cortex 25, 1676–1684. [CrossRef]
- Fang, K., Hou, Y., Niu, L., Han, S., Zhang, W., 2024. Individualized gray matter morphological abnormalities uncover two robust transdiagnostic biotypes. Journal of Affective Disorders 365, 193–204. [CrossRef]
- Feng, Y., Chandio, B.Q., Villalon-Reina, J.E., Benavidez, S., Chattopadhyay, T., Chehrzadeh, S., Laltoo, E., Thomopoulos, S.I., Joshi, H., Venkatasubramanian, G., John, J.P., Jahanshad, N., Thompson, P.M., 2024a. Deep Normative Tractometry for Identifying Joint White Matter Macro- and Micro-structural Abnormalities in Alzheimer’s Disease. bioRxiv 2024.02.05.578943. [CrossRef]
- Feng, Y., Chandio, B.Q., Villalon-Reina, J.E., Thomopoulos, S.I., Nir, T.M., Benavidez, S., Laltoo, E., Chattopadhyay, T., Joshi, H., Venkatasubramanian, G., John, J.P., Jahanshad, N., Reid, R.I., Jack, C.R., Weiner, M.W., Thompson, P.M., Alzheimers Disease Neuroimaging Initiative, 2024b. Microstructural Mapping of Neural Pathways in Alzheimer’s Disease using Macrostructure-Informed Normative Tractometry. bioRxiv 2024.04.25.591183. [CrossRef]
- Floris, D., Llera, A., Zabihi, M., Jones, E., Mason, L., Haartsen, R., Holz, N., Mei, T., Elleaume, C., Hebling Vieira, B., Pretzsch, C., Forde, N., Baumeister, S., Dell’Acqua, F., Durston, S., Banaschewski, T., Ecker, C., Holt, R., Baron-Cohen, S., Langer, N., 2024. A multimodal neural signature of face processing in autism within the fusiform gyrus. [CrossRef]
- Floris, D.L., Wolfers, T., Zabihi, M., Holz, N.E., Zwiers, M.P., Charman, T., Tillmann, J., Ecker, C., Dell’Acqua, F., Banaschewski, T., Moessnang, C., Baron-Cohen, S., Holt, R., Durston, S., Loth, E., Murphy, D.G.M., Marquand, A., Buitelaar, J.K., Beckmann, C.F., Ahmad, J., Ambrosino, S., Auyeung, B., Banaschewski, T., Baron-Cohen, S., Baumeister, S., Beckmann, C.F., Bölte, S., Bourgeron, T., Bours, C., Brammer, M., Brandeis, D., Brogna, C., De Bruijn, Y., Buitelaar, J.K., Chakrabarti, B., Charman, T., Cornelissen, I., Crawley, D., Dell’Acqua, F., Dumas, G., Durston, S., Ecker, C., Faulkner, J., Frouin, V., Garcés, P., Goyard, D., Ham, L., Hayward, H., Hipp, J., Holt, R., Johnson, M.H., Jones, E.J.H., Kundu, P., Lai, M.-C., Liogier d’Ardhuy, X., Lombardo, M.V., Loth, E., Lythgoe, D.J., Mandl, R., Marquand, A., Mason, L., Mennes, M., Meyer-Lindenberg, A., Moessnang, C., Mueller, N., Murphy, D.G.M., Oakley, B., O’Dwyer, L., Oldehinkel, M., Oranje, B., Pandina, G., Persico, A.M., Ruggeri, B., Ruigrok, A., Sabet, J., Sacco, R., San José Cáceres, A., Simonoff, E., Spooren, W., Tillmann, J., Toro, R., Tost, H., Waldman, J., Williams, S.C.R., Wooldridge, C., Zwiers, M.P., 2021. Atypical Brain Asymmetry in Autism—A Candidate for Clinically Meaningful Stratification. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging 6, 802–812. [CrossRef]
- Fortin, J.-P., Cullen, N., Sheline, Y.I., Taylor, W.D., Aselcioglu, I., Cook, P.A., Adams, P., Cooper, C., Fava, M., McGrath, P.J., McInnis, M., Phillips, M.L., Trivedi, M.H., Weissman, M.M., Shinohara, R.T., 2018. Harmonization of cortical thickness measurements across scanners and sites. Neuroimage 167, 104–120. [CrossRef]
- Fraza, C., Zabihi, M., Beckmann, C.F., Marquand, A.F., 2022. The Extremes of Normative Modelling. [CrossRef]
- Fraza, C.J., Dinga, R., Beckmann, C.F., Marquand, A.F., 2021. Warped Bayesian linear regression for normative modelling of big data. Neuroimage 245, 118715. [CrossRef]
- Frisoni, G.B., Prestia, A., Zanetti, O., Galluzzi, S., Romano, M., Cotelli, M., Gennarelli, M., Binetti, G., Bocchio, L., Paghera, B., Amicucci, G., Bonetti, M., Benussi, L., Ghidoni, R., Geroldi, C., 2009. Markers of Alzheimer’s disease in a population attending a memory clinic. Alzheimer’s & Dementia 5, 307–317. [CrossRef]
- Fukami-Gartner, A., Baburamani, A.A., Dimitrova, R., Patkee, P.A., Ojinaga-Alfageme, O., Bonthrone, A.F., Cromb, D., Uus, A.U., Counsell, S.J., Hajnal, J.V., O’Muircheartaigh, J., Rutherford, M.A., 2023. Comprehensive volumetric phenotyping of the neonatal brain in Down syndrome. Cereb Cortex 33, 8921–8941. [CrossRef]
- Gage, A.T., Stone, J.R., Wilde, E.A., McCauley, S.R., Welsh, R.C., Mugler, J.P., Tustison, N., Avants, B., Whitlow, C.T., Lancashire, L., Bhatt, S.D., Haas, M., 2024. Normative Neuroimaging Library: Designing a Comprehensive and Demographically Diverse Dataset of Healthy Controls to Support Traumatic Brain Injury Diagnostic and Therapeutic Development. J Neurotrauma 41, 2497–2512. [CrossRef]
- Gaiser, C., Berthet, P., Kia, S.M., Frens, M.A., Beckmann, C.F., Muetzel, R.L., Marquand, A.F., 2024. Estimating cortical thickness trajectories in children across different scanners using transfer learning from normative models. Hum Brain Mapp 45, e26565. [CrossRef]
- García-San-Martín, N., Bethlehem, R.A.I., Mihalik, A., Seidlitz, J., Sebenius, I., Alemán-Morillo, C., Dorfschmidt, L., Shafiei, G., Ortiz-García de la Foz, V., Merritt, K., David, A., Morgan, S.E., Ruiz-Veguilla, M., Ayesa-Arriola, R., Vázquez-Bourgon, J., Alexander-Bloch, A., Misic, B., Bullmore, E.T., Suckling, J., Crespo-Facorro, B., Romero-García, R., 2024. Molecular and micro-architectural mapping of gray matter alterations in psychosis. Mol Psychiatry 30, 1287–1296. [CrossRef]
- Ge, R., Yu, Y., Qi, Y.X., Fan, Y., Chen, S., Gao, C., Haas, S.S., New, F., Boomsma, D.I., Brodaty, H., Brouwer, R.M., Buckner, R., Caseras, X., Crivello, F., Crone, E.A., Erk, S., Fisher, S.E., Franke, B., Glahn, D.C., Dannlowski, U., Grotegerd, D., Gruber, O., Hulshoff Pol, H.E., Schumann, G., Tamnes, C.K., Walter, H., Wierenga, L.M., Jahanshad, N., Thompson, P.M., Frangou, S., Agartz, I., Asherson, P., Ayesa-Arriola, R., Banaj, N., Banaschewski, T., Baumeister, S., Bertolino, A., Borgwardt, S., Bourque, J., Brandeis, D., Breier, A., Buitelaar, J.K., Cannon, D.M., Cervenka, S., Conrod, P.J., Crespo-Facorro, B., Davey, C.G., De Haan, L., De Zubicaray, G.I., Di Giorgio, A., Frodl, T., Gruner, P., Gur, R.E., Gur, R.C., Harrison, B.J., Hatton, S.N., Hickie, I., Howells, F.M., Huyser, C., Jernigan, T.L., Jiang, J., Joska, J.A., Kahn, R.S., Kalnin, A.J., Kochan, N.A., Koops, S., Kuntsi, J., Lagopoulos, J., Lazaro, L., Lebedeva, I.S., Lochner, C., Martin, N.G., Mazoyer, B., McDonald, B.C., McDonald, C., McMahon, K.L., Medland, S., Modabbernia, A., Mwangi, B., Nakao, T., Nyberg, L., Piras, F., Portella, M.J., Qiu, J., Roffman, J.L., Sachdev, P.S., Sanford, N., Satterthwaite, T.D., Saykin, A.J., Sellgren, C.M., Sim, K., Smoller, J.W., Soares, J.C., Sommer, I.E., Spalletta, G., Stein, D.J., Thomopoulos, S.I., Tomyshev, A.S., Tordesillas-Gutiérrez, D., Trollor, J.N., Van ’T Ent, D., Van Den Heuvel, O.A., Van Erp, T.G., Van Haren, N.E., Vecchio, D., Veltman, D.J., Wang, Y., Weber, B., Wei, D., Wen, W., Westlye, L.T., Williams, S.C., Wright, M.J., Wu, M.-J., Yu, K., 2024a. Normative modelling of brain morphometry across the lifespan with CentileBrain: algorithm benchmarking and model optimisation. The Lancet Digital Health 6, e211–e221. [CrossRef]
- Ge, R., Yu, Y., Qi, Y.X., Fan, Y.-N., Chen, S., Gao, C., Haas, S.S., New, F., Boomsma, D.I., Brodaty, H., Brouwer, R.M., Buckner, R., Caseras, X., Crivello, F., Crone, E.A., Erk, S., Fisher, S.E., Franke, B., Glahn, D.C., Dannlowski, U., Grotegerd, D., Gruber, O., Hulshoff Pol, H.E., Schumann, G., Tamnes, C.K., Walter, H., Wierenga, L.M., Jahanshad, N., Thompson, P.M., Frangou, S., ENIGMA Lifespan Working Group, 2024b. Normative modelling of brain morphometry across the lifespan with CentileBrain: algorithm benchmarking and model optimisation. Lancet Digit Health 6, e211–e221. [CrossRef]
- Giacomel, A., Martins, D., Nordio, G., Easmin, R., Howes, O., Selvaggi, P., Williams, S.C.R., Turkheimer, F., De Groot, M., Dipasquale, O., Veronese, M., 2025. Investigating dopaminergic abnormalities in schizophrenia and first-episode psychosis with normative modelling and multisite molecular neuroimaging. Mol Psychiatry. [CrossRef]
- Ginsburg, G.S., Phillips, K.A., 2018. Precision Medicine: From Science To Value. Health Aff (Millwood) 37, 694–701. [CrossRef]
- Gomes, M.I., Guillou, A., 2015. Extreme Value Theory and Statistics of Univariate Extremes: A Review. International Statistical Review / Revue Internationale de Statistique 83, 263–292.
- Gorgolewski, K.J., Auer, T., Calhoun, V.D., Craddock, R.C., Das, S., Duff, E.P., Flandin, G., Ghosh, S.S., Glatard, T., Halchenko, Y.O., Handwerker, D.A., Hanke, M., Keator, D., Li, X., Michael, Z., Maumet, C., Nichols, B.N., Nichols, T.E., Pellman, J., Poline, J.-B., Rokem, A., Schaefer, G., Sochat, V., Triplett, W., Turner, J.A., Varoquaux, G., Poldrack, R.A., 2016. The brain imaging data structure, a format for organizing and describing outputs of neuroimaging experiments. Sci Data 3, 160044. [CrossRef]
- Guedj, E., Varrone, A., Boellaard, R., Albert, N.L., Barthel, H., van Berckel, B., Brendel, M., Cecchin, D., Ekmekcioglu, O., Garibotto, V., Lammertsma, A.A., Law, I., Peñuelas, I., Semah, F., Traub-Weidinger, T., van de Giessen, E., Van Weehaeghe, D., Morbelli, S., 2022. EANM procedure guidelines for brain PET imaging using [18F]FDG, version 3. Eur J Nucl Med Mol Imaging 49, 632–651. [CrossRef]
- Gunn, R.N., Slifstein, M., Searle, G.E., Price, J.C., 2015. Quantitative imaging of protein targets in the human brain with PET. Phys Med Biol 60, R363-411. [CrossRef]
- Guo, B., Chen, Y., Lin, J., Huang, B., Bai, Xiangzhuo, Guo, C., Gao, B., Gong, Q., Bai, Xiangzhi, 2024. Self-supervised learning for accurately modelling hierarchical evolutionary patterns of cerebrovasculature. Nat Commun 15, 9235. [CrossRef]
- Hamdi, Y., Haigh, I.D., Parey, S., Wahl, T., 2021. Preface: Advances in extreme value analysis and application to natural hazards. Natural Hazards and Earth System Sciences 21, 1461–1465. [CrossRef]
- Han, S., Cui, Q., Zheng, R., Li, S., Zhou, B., Fang, K., Sheng, W., Wen, B., Liu, L., Wei, Y., Chen, H., Chen, Y., Cheng, J., Zhang, Y., 2023a. Parsing altered gray matter morphology of depression using a framework integrating the normative model and non-negative matrix factorization. Nat Commun 14, 4053. [CrossRef]
- Han, S., Fang, K., Zheng, R., Li, S., Zhou, B., Sheng, W., Wen, B., Liu, L., Wei, Y., Chen, Y., Chen, H., Cui, Q., Cheng, J., Zhang, Y., 2024. Gray matter atrophy is constrained by normal structural brain network architecture in depression. Psychol Med 54, 1318–1328. [CrossRef]
- Han, S., Xu, Y., Fang, K., Guo, H.-R., Wei, Y., Liu, L., Wen, B., Liu, H., Zhang, Y., Cheng, J., 2023b. Mapping the neuroanatomical heterogeneity of OCD using a framework integrating normative model and non-negative matrix factorization. Cereb Cortex 33, 8667–8678. [CrossRef]
- Harnett, N.G., Fani, N., Rowland, G., Kumar, P., Rutherford, S., Nickerson, L.D., 2024. Population-level normative models reveal race- and socioeconomic-related variability in cortical thickness of threat neurocircuitry. Commun Biol 7, 745. [CrossRef]
- Harvey, A., Dumas, G., 2022. PyNM: a Lightweight Python implementation of Normative Modeling. Journal of Open Source Software 7, 4321. [CrossRef]
- Holdgraf, C., Appelhoff, S., Bickel, S., Bouchard, K., D’Ambrosio, S., David, O., Devinsky, O., Dichter, B., Flinker, A., Foster, B.L., Gorgolewski, K.J., Groen, I., Groppe, D., Gunduz, A., Hamilton, L., Honey, C.J., Jas, M., Knight, R., Lachaux, J., Lau, J.C., Lee-Messer, C., Lundstrom, B.N., Miller, K.J., Ojemann, J.G., Oostenveld, R., Petridou, N., Piantoni, G., Pigorini, A., Pouratian, N., Ramsey, N.F., Stolk, A., Swann, N.C., Tadel, F., Voytek, B., Wandell, B.A., Winawer, J., Whitaker, K., Zehl, L., Hermes, D., 2019. iEEG-BIDS, extending the Brain Imaging Data Structure specification to human intracranial electrophysiology. [CrossRef]
- Huizinga, W., Poot, D.H.J., Vernooij, M.W., Roshchupkin, G.V., Bron, E.E., Ikram, M.A., Rueckert, D., Niessen, W.J., Klein, S., 2018. A spatio-temporal reference model of the aging brain. NeuroImage 169, 11–22. [CrossRef]
- Huo, Y., Jing, R., Li, P., Chen, P., Si, J., Liu, G., Liu, Y., 2025. Delineating the Heterogeneity of Alzheimer’s Disease and Mild Cognitive Impairment Using Normative Models of Dynamic Brain Functional Networks. Biological Psychiatry, Cortical Connectivity in Alzheimer’s Disease 97, 1034–1044. [CrossRef]
- Janahi, M., Aksman, L., Schott, J.M., Mokrab, Y., Altmann, A., Alzheimer’s Disease Neuroimaging Initiative, 2022. Nomograms of human hippocampal volume shifted by polygenic scores. Elife 11, e78232. [CrossRef]
- Janssen, J., Díaz-Caneja, C.M., Alloza, C., Schippers, A., De Hoyos, L., Santonja, J., Gordaliza, P.M., Buimer, E.E.L., Van Haren, N.E.M., Cahn, W., Arango, C., Kahn, R.S., Hulshoff Pol, H.E., Schnack, H.G., 2021. Dissimilarity in Sulcal Width Patterns in the Cortex can be Used to Identify Patients With Schizophrenia With Extreme Deficits in Cognitive Performance. Schizophrenia Bulletin 47, 552–561. [CrossRef]
- Janssen, J., Guil Gallego, A., Díaz-Caneja, C.M., Gonzalez Lois, N., Janssen, N., González-Peñas, J., Macias Gordaliza, P., Buimer, E., van Haren, N., Arango, C., Kahn, R., Pol, H.E.H., Schnack, H.G., 2025. Heterogeneity of morphometric similarity networks in health and schizophrenia. Schizophr 11, 70. [CrossRef]
- Ji, G.-J., Zalesky, A., Wang, Y., He, K., Wang, L., Du, R., Sun, J., Bai, T., Chen, X., Tian, Y., Zhu, C., Wang, K., 2023. Linking Personalized Brain Atrophy to Schizophrenia Network and Treatment Response. Schizophr Bull 49, 43–52. [CrossRef]
- Jiang, A., Ma, X., Li, S., Wang, L., Yang, B., Wang, S., Li, M., Dong, G., 2024. Age-atypical brain functional networks in autism spectrum disorder: a normative modeling approach. Psychol Med 54, 2042–2053. [CrossRef]
- Jiang, J., Zhou, H., Duan, H., Liu, X., Zuo, C., Huang, Z., Yu, Z., Yan, Z., 2017. A novel individual-level morphological brain networks constructing method and its evaluation in PET and MR images. Heliyon 3, e00475. [CrossRef]
- Jing, R., Lin, X., Ding, Z., Chang, S., Shi, L., Liu, L., Wang, Q., Si, J., Yu, M., Zhuo, C., Shi, J., Li, P., Fan, Y., Lu, L., 2023. Heterogeneous brain dynamic functional connectivity patterns in first-episode drug-naive patients with major depressive disorder. Hum Brain Mapp 44, 3112–3122. [CrossRef]
- Jirsa, V.K., McIntosh, A. (Eds.), 2007. Handbook of Brain Connectivity, Understanding Complex Systems. Springer, Berlin, Heidelberg. [CrossRef]
- Kapur, S., Phillips, A.G., Insel, T.R., 2012. Why has it taken so long for biological psychiatry to develop clinical tests and what to do about it? Mol Psychiatry 17, 1174–1179. [CrossRef]
- Kasper, J., Caspers, S., Lotter, L.D., Hoffstaedter, F., Eickhoff, S.B., Dukart, J., 2024. Resting-State Changes in Aging and Parkinson’s Disease Are Shaped by Underlying Neurotransmission: A Normative Modeling Study. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging 9, 986–997. [CrossRef]
- Kia, S.M., Huijsdens, H., Dinga, R., Wolfers, T., Mennes, M., Andreassen, O.A., Westlye, L.T., Beckmann, C.F., Marquand, A.F., 2020. Hierarchical Bayesian Regression for Multi-Site Normative Modeling of Neuroimaging Data.
- Kia, S.M., Huijsdens, H., Rutherford, S., De Boer, A., Dinga, R., Wolfers, T., Berthet, P., Mennes, M., Andreassen, O.A., Westlye, L.T., Beckmann, C.F., Marquand, A.F., 2022. Closing the life-cycle of normative modeling using federated hierarchical Bayesian regression. PLoS ONE 17, e0278776. [CrossRef]
- Kia, S.M., Marquand, A., 2018. Normative Modeling of Neuroimaging Data Using Scalable Multi-task Gaussian Processes, in: Frangi, A.F., Schnabel, J.A., Davatzikos, C., Alberola-López, C., Fichtinger, G. (Eds.), Medical Image Computing and Computer Assisted Intervention – MICCAI 2018. Springer International Publishing, Cham, pp. 127–135. [CrossRef]
- Klunk, W.E., Koeppe, R.A., Price, J.C., Benzinger, T.L., Devous, M.D., Jagust, W.J., Johnson, K.A., Mathis, C.A., Minhas, D., Pontecorvo, M.J., Rowe, C.C., Skovronsky, D.M., Mintun, M.A., 2015. The Centiloid Project: Standardizing quantitative amyloid plaque estimation by PET. Alzheimer’s & Dementia 11, 1-15.e4. [CrossRef]
- Koenker, R., Hallock, K.F., 2001. Quantile Regression. Journal of Economic Perspectives 15, 143–156. [CrossRef]
- Kumar, S., Earnest, T., Yang, B., Kothapalli, D., Aschenbrenner, A.J., Hassenstab, J., Xiong, C., Ances, B., Morris, J., Benzinger, T.L.S., Gordon, B.A., Payne, P., Sotiras, A., Alzheimer’s Disease Neuroimaging Initiative, 2024. Analyzing heterogeneity in Alzheimer Disease using multimodal normative modeling on imaging-based ATN biomarkers. bioRxiv 2023.08.15.553412. [CrossRef]
- Kumar, S., Payne, P., Sotiras, A., 2023a. Improving Normative Modeling for Multi-modal Neuroimaging Data using mixture-of-product-of-experts variational autoencoders. [CrossRef]
- Kumar, S., Payne, P.R.O., Sotiras, A., 2023b. Normative Modeling using Multimodal Variational Autoencoders to Identify Abnormal Brain Volume Deviations in Alzheimer’s Disease. Proc SPIE Int Soc Opt Eng 12465, 1246503. [CrossRef]
- Laidi, C., Floris, D.L., Tillmann, J., Elandaloussi, Y., Zabihi, M., Charman, T., Wolfers, T., Durston, S., Moessnang, C., Dell’Acqua, F., Ecker, C., Loth, E., Murphy, D., Baron-Cohen, S., Buitelaar, J.K., Marquand, A.F., Beckmann, C.F., Frouin, V., Leboyer, M., Duchesnay, E., Coupé, P., Houenou, J., Tobias Banaschewski, Persico, A., San Jose Caceres, A., Hayward, H., Crawley, D., Faulkner, J., Sabet, J., Ellis, C., Oakley, B., Holt, R., Ambrosino, S., Bast, N., Baumeister, S., Rausch, A., Bours, C., Cornelissen, I., von Rhein, D., O’Dwyer, L., Ahmad, J., Simonoff, E., 2022. Cerebellar Atypicalities in Autism? Biological Psychiatry, Brain Development and Communication in Autism Spectrum Disorder 92, 674–682. [CrossRef]
- Lawn, T., Giacomel, A., Martins, D., Veronese, M., Howard, M., Turkheimer, F.E., Dipasquale, O., 2024. Normative modelling of molecular-based functional circuits captures clinical heterogeneity transdiagnostically in psychiatric patients. Commun Biol 7, 689. [CrossRef]
- Lawry Aguila, A., Chapman, J., Janahi, M., Altmann, A., 2022. Conditional VAEs for Confound Removal and Normative Modelling of Neurodegenerative Diseases [WWW Document]. In: Wang, L and Dou, Q and Fletcher, PT and Speidel, S and Li, S, (eds.) Medical Image Computing and Computer Assisted Intervention – MICCAI 2022. (pp. pp. 430-440). Springer: Cham, Switzerland. (2022). [CrossRef]
- Lin, X., Huo, Y., Wang, Q., Liu, G., Shi, J., Fan, Y., Lu, L., Jing, R., Li, P., 2024. Using normative modeling to assess pharmacological treatment effect on brain state in patients with schizophrenia. Cerebral Cortex 34, bhae003. [CrossRef]
- Lin, X., Jing, R., Chang, S., Liu, L., Wang, Q., Zhuo, C., Shi, J., Fan, Y., Lu, L., Li, P., 2023. Understanding the heterogeneity of dynamic functional connectivity patterns in first-episode drug naïve depression using normative models. Journal of Affective Disorders 327, 217–225. [CrossRef]
- Liu, L., Jia, D., He, Z., Wen, B., Zhang, X., Han, S., 2024. Individualized functional connectome abnormalities obtained using two normative model unveil neurophysiological subtypes of obsessive compulsive disorder. Progress in Neuro-Psychopharmacology and Biological Psychiatry 135, 111122. [CrossRef]
- Looden, T., Floris, D.L., Llera, A., Chauvin, R.J., Charman, T., Banaschewski, T., Murphy, D., Marquand, Andre.F., Buitelaar, J.K., Beckmann, C.F., Ahmad, J., Ambrosino, S., Auyeung, B., Banaschewski, T., Baron-Cohen, S., Baumeister, S., Beckmann, C.F., Bölte, S., Bourgeron, T., Bours, C., Brammer, M., Brandeis, D., Brogna, C., de Bruijn, Y., Buitelaar, J.K., Chakrabarti, B., Charman, T., Cornelissen, I., Crawley, D., Acqua, F.D., Dumas, G., Durston, S., Ecker, C., Faulkner, J., Frouin, V., Garcés, P., Goyard, D., Ham, L., Hayward, H., Hipp, J., Holt, R., Johnson, M.H., Jones, E.J.H., Kundu, P., Lai, M.-C., D’ardhuy, X.L., Lombardo, M.V., Loth, E., Lythgoe, D.J., Mandl, R., Marquand, A., Mason, L., Mennes, M., Meyer-Lindenberg, A., Moessnang, C., Mueller, N., Murphy, D.G.M., Oakley, B., O’Dwyer, L., Oldehinkel, M., Oranje, B., Pandina, G., Persico, A.M., Rausch, A., Ruggeri, B., Ruigrok, A., Sabet, J., Sacco, R., Cáceres, A.S.J., Simonoff, E., Spooren, W., Tillmann, J., Toro, R., Tost, H., Waldman, J., Williams, S.C.R., Wooldridge, C., Ilioska, I., Mei, T., Zwiers, M.P., the AIMS-2-TRIALS group, 2022. Patterns of connectome variability in autism across five functional activation tasks: findings from the LEAP project. Molecular Autism 13, 53. [CrossRef]
- Lopez Pinaya, W.H., Vieira, S., Garcia-Dias, R., Mechelli, A., 2020. Chapter 11 - Autoencoders, in: Mechelli, A., Vieira, S. (Eds.), Machine Learning. Academic Press, pp. 193–208. [CrossRef]
- Lotter, L.D., Saberi, A., Hansen, J.Y., Misic, B., Paquola, C., Barker, G.J., Bokde, A.L.W., Desrivières, S., Flor, H., Grigis, A., Garavan, H., Gowland, P., Heinz, A., Brühl, R., Martinot, J.-L., Paillère, M.-L., Artiges, E., Papadopoulos Orfanos, D., Paus, T., Poustka, L., Hohmann, S., Fröhner, J.H., Smolka, M.N., Vaidya, N., Walter, H., Whelan, R., Schumann, G., Nees, F., Banaschewski, T., Eickhoff, S.B., Dukart, J., 2024. Regional patterns of human cortex development correlate with underlying neurobiology. Nat Commun 15, 7987. [CrossRef]
- Lv, J., Di Biase, M., Cash, R.F.H., Cocchi, L., Cropley, V.L., Klauser, P., Tian, Y., Bayer, J., Schmaal, L., Cetin-Karayumak, S., Rathi, Y., Pasternak, O., Bousman, C., Pantelis, C., Calamante, F., Zalesky, A., 2021. Individual deviations from normative models of brain structure in a large cross-sectional schizophrenia cohort. Mol Psychiatry 26, 3512–3523. [CrossRef]
- Macleod, R., O’Muircheartaigh, J., Edwards, A.D., Carmichael, D., Rutherford, M., Counsell, S.J., 2020. Automatic Detection of Neonatal Brain Injury on MRI, in: Hu, Y., Licandro, R., Noble, J.A., Hutter, J., Aylward, S., Melbourne, A., Abaci Turk, E., Torrents Barrena, J. (Eds.), Medical Ultrasound, and Preterm, Perinatal and Paediatric Image Analysis, Lecture Notes in Computer Science. Springer International Publishing, Cham, pp. 324–333. [CrossRef]
- Marcus, D.S., Wang, T.H., Parker, J., Csernansky, J.G., Morris, J.C., Buckner, R.L., 2007. Open Access Series of Imaging Studies (OASIS): cross-sectional MRI data in young, middle aged, nondemented, and demented older adults. J Cogn Neurosci 19, 1498–1507. [CrossRef]
- Marquand, A.F., Kia, S.M., Zabihi, M., Wolfers, T., Buitelaar, J.K., Beckmann, C.F., 2019. Conceptualizing mental disorders as deviations from normative functioning. Mol Psychiatry 24, 1415–1424. [CrossRef]
- Marquand, A.F., Rezek, I., Buitelaar, J., Beckmann, C.F., 2016a. Understanding Heterogeneity in Clinical Cohorts Using Normative Models: Beyond Case-Control Studies. Biological Psychiatry 80, 552–561. [CrossRef]
- Marquand, A.F., Wolfers, T., Mennes, M., Buitelaar, J., Beckmann, C.F., 2016b. Beyond Lumping and Splitting: A Review of Computational Approaches for Stratifying Psychiatric Disorders. Biol Psychiatry Cogn Neurosci Neuroimaging 1, 433–447. [CrossRef]
- Marzi, C., Giannelli, M., Barucci, A., Tessa, C., Mascalchi, M., Diciotti, S., 2024. Efficacy of MRI data harmonization in the age of machine learning: a multicenter study across 36 datasets. Sci Data 11, 115. [CrossRef]
- Mechelli, A., Price, C.J., Friston, K.J., Ashburner, J., 2005. Voxel-based morphometry of the human brain: Methods and applications. CURRENT MEDICAL IMAGING REVIEWS 1, 105–113.
- Meijer, J., Hebling Vieira, B., Elleaume, C., Baranczuk-Turska, Z., Langer, N., Floris, D.L., 2024. Toward understanding autism heterogeneity: Identifying clinical subgroups and neuroanatomical deviations. Journal of Psychopathology and Clinical Science 133, 667–677. [CrossRef]
- Meyer-Lindenberg, A., 2023. The non-ergodic nature of mental health and psychiatric disorders: implications for biomarker and diagnostic research. World Psychiatry 22, 272–274. [CrossRef]
- Mishra, S.K., Singh, P., 2010. History of Neuroimaging: The Legacy of William Oldendorf. J Child Neurol 25, 508–517. [CrossRef]
- Mueller, S.G., Weiner, M.W., Thal, L.J., Petersen, R.C., Jack, C.R., Jagust, W., Trojanowski, J.Q., Toga, A.W., Beckett, L., 2005. Ways toward an early diagnosis in Alzheimer’s disease: the Alzheimer’s Disease Neuroimaging Initiative (ADNI). Alzheimers Dement 1, 55–66. [CrossRef]
- Muili, A.O., Olalekan, A.A., Kuol, P.P., Moradeyo, A., Phiri, E.C., Habibat, S., Adekemi, A.A., Mustapha, M.J., 2024. Advancing brain health: harnessing the centilebrain model for enhanced diagnosis of mental health disorders. Ann Med Surg (Lond) 86, 4944–4946. [CrossRef]
- Narang, K.S., Jha, A.N., 2017. Intraoperative Imaging in Neurosurgery. JP Medical Ltd.
- Niso, G., Gorgolewski, K.J., Bock, E., Brooks, T.L., Flandin, G., Gramfort, A., Henson, R.N., Jas, M., Litvak, V., T. Moreau, J., Oostenveld, R., Schoffelen, J.-M., Tadel, F., Wexler, J., Baillet, S., 2018. MEG-BIDS, the brain imaging data structure extended to magnetoencephalography. Sci Data 5, 180110. [CrossRef]
- Norgaard, M., Matheson, G.J., Hansen, H.D., Thomas, A., Searle, G., Rizzo, G., Veronese, M., Giacomel, A., Yaqub, M., Tonietto, M., Funck, T., Gillman, A., Boniface, H., Routier, A., Dalenberg, J.R., Betthauser, T., Feingold, F., Markiewicz, C.J., Gorgolewski, K.J., Blair, R.W., Appelhoff, S., Gau, R., Salo, T., Niso, G., Pernet, C., Phillips, C., Oostenveld, R., Gallezot, J.-D., Carson, R.E., Knudsen, G.M., Innis, R.B., Ganz, M., 2021. PET-BIDS, an extension to the brain imaging data structure for positron emission tomography. [CrossRef]
- Nunes, A., Trappenberg, T., Alda, M., 2020. Measuring heterogeneity in normative models as the effective number of deviation patterns. PLoS ONE 15, e0242320. [CrossRef]
- Oliveira-Saraiva, D., Ferreira, H.A., 2023. Normative model detects abnormal functional connectivity in psychiatric disorders. Front. Psychiatry 14, 1068397. [CrossRef]
- Pernet, C.R., Appelhoff, S., Gorgolewski, K.J., Flandin, G., Phillips, C., Delorme, A., Oostenveld, R., 2019. EEG-BIDS, an extension to the brain imaging data structure for electroencephalography. Sci Data 6, 103. [CrossRef]
- Petersen, R.C., Aisen, P.S., Beckett, L.A., Donohue, M.C., Gamst, A.C., Harvey, D.J., Jack, C.R., Jagust, W.J., Shaw, L.M., Toga, A.W., Trojanowski, J.Q., Weiner, M.W., 2010. Alzheimer’s Disease Neuroimaging Initiative (ADNI): clinical characterization. Neurology 74, 201–209. [CrossRef]
- Pinaya, W.H.L., Mechelli, A., Sato, J.R., 2019. Using deep autoencoders to identify abnormal brain structural patterns in neuropsychiatric disorders: A large-scale multi-sample study. Human Brain Mapping 40, 944–954. [CrossRef]
- Pinaya, W.H.L., Scarpazza, C., Garcia-Dias, R., Vieira, S., Baecker, L., F Da Costa, P., Redolfi, A., Frisoni, G.B., Pievani, M., Calhoun, V.D., Sato, J.R., Mechelli, A., 2021. Using normative modelling to detect disease progression in mild cognitive impairment and Alzheimer’s disease in a cross-sectional multi-cohort study. Sci Rep 11, 15746. [CrossRef]
- Pinto, M.S., Anania, V., Paolella, R., Smekens, C., Billiet, T., Janssens, T., den Dekker, A.J., Sijbers, J., Guns, P.-J., Van Dyck, P., 2025. Harmonization of diffusion MRI on healthy subjects using NeuroCombat and LongCombat: a B-Q MINDED brain intra- and inter-scanner study. Front Neurosci 19, 1591169. [CrossRef]
- Rasmussen, C.E., Williams, C.K.I., 2006. Gaussian processes for machine learning, Adaptive computation and machine learning. MIT Press, Cambridge, Mass.
- Reardon, P.K., Seidlitz, J., Vandekar, S., Liu, S., Patel, R., Park, M.T.M., Alexander-Bloch, A., Clasen, L.S., Blumenthal, J.D., Lalonde, F.M., Giedd, J.N., Gur, R.C., Gur, R.E., Lerch, J.P., Chakravarty, M.M., Satterthwaite, T.D., Shinohara, R.T., Raznahan, A., 2018. Normative brain size variation and brain shape diversity in humans. Science 360, 1222–1227. [CrossRef]
- Romascano, D., Rebsamen, M., Radojewski, P., Blattner, T., McKinley, R., Wiest, R., Rummel, C., 2024. Cortical thickness and grey-matter volume anomaly detection in individual MRI scans: Comparison of two methods. NeuroImage: Clinical 43, 103624. [CrossRef]
- Rutherford, S., Barkema, P., Tso, I.F., Sripada, C., Beckmann, C.F., Ruhe, H.G., Marquand, A.F., 2023. Evidence for embracing normative modeling. eLife 12, e85082. [CrossRef]
- Rutherford, S., Fraza, C., Dinga, R., Kia, S.M., Wolfers, T., Zabihi, M., Berthet, P., Worker, A., Verdi, S., Andrews, D., Han, L.K., Bayer, J.M., Dazzan, P., McGuire, P., Mocking, R.T., Schene, A., Sripada, C., Tso, I.F., Duval, E.R., Chang, S.-E., Penninx, B.W., Heitzeg, M.M., Burt, S.A., Hyde, L.W., Amaral, D., Wu Nordahl, C., Andreasssen, O.A., Westlye, L.T., Zahn, R., Ruhe, H.G., Beckmann, C., Marquand, A.F., 2022a. Charting brain growth and aging at high spatial precision. eLife 11, e72904. [CrossRef]
- Rutherford, S., Kia, S.M., Wolfers, T., Fraza, C., Zabihi, M., Dinga, R., Berthet, P., Worker, A., Verdi, S., Ruhe, H.G., Beckmann, C.F., Marquand, A.F., 2022b. The normative modeling framework for computational psychiatry. Nat Protoc 17, 1711–1734. [CrossRef]
- Sampaio, I.W., Tassi, E., Bellani, M., Benedetti, F., Nenadic, I., Phillips, M., Piras, F., Yatham, L., Bianchi, A.M., Brambilla, P., Maggioni, E., 2024. A generalizable normative deep autoencoder for brain morphological anomaly detection: application to the multi-site StratiBip dataset on bipolar disorder in an external validation framework. bioRxiv 2024.09.04.611239. [CrossRef]
- Savage, H.S., Mulders, P.C.R., van Eijndhoven, P.F.P., van Oort, J., Tendolkar, I., Vrijsen, J.N., Beckmann, C.F., Marquand, A.F., 2024. Dissecting task-based fMRI activity using normative modelling: an application to the Emotional Face Matching Task. Commun Biol 7, 1–14. [CrossRef]
- Schulz, E., Speekenbrink, M., Krause, A., 2018. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. Journal of Mathematical Psychology 85, 1–16. [CrossRef]
- Segal, A., Parkes, L., Aquino, K., Kia, S.M., Wolfers, T., Franke, B., Hoogman, M., Beckmann, C.F., Westlye, L.T., Andreassen, O.A., Zalesky, A., Harrison, B.J., Davey, C.G., Soriano-Mas, C., Cardoner, N., Tiego, J., Yücel, M., Braganza, L., Suo, C., Berk, M., Cotton, S., Bellgrove, M.A., Marquand, A.F., Fornito, A., 2023. Regional, circuit and network heterogeneity of brain abnormalities in psychiatric disorders. Nat Neurosci 26, 1613–1629. [CrossRef]
- Segal, A., Smith, R.E., Chopra, S., Oldham, S., Parkes, L., Aquino, K.M., Kia, S.M., Wolfers, T., Franke, B., Hoogman, M., Beckmann, C.F., Westlye, L.T., Andreassen, O.A., Zaleskey, A., Ben, H.J., Davey, C.G., Soriano-Mas, C., Cardoner, N., Tiego, J., Yucel, M., Braganza, L., Suo, C., Berk, M., Cotton, S., Bellgrove, M.A., Marquand, A.F., Fornito, A., 2024. Multiscale heterogeneity of white matter morphometry in psychiatric disorders. [CrossRef]
- Segal, A., Tiego, J., Parkes, L., Holmes, A.J., Marquand, A.F., Fornito, A., 2025. Embracing variability in the search for biological mechanisms of psychiatric illness. Trends Cogn Sci 29, 85–99. [CrossRef]
- Shan, X., Uddin, L.Q., Xiao, J., He, C., Ling, Z., Li, L., Huang, X., Chen, H., Duan, X., 2022. Mapping the Heterogeneous Brain Structural Phenotype of Autism Spectrum Disorder Using the Normative Model. Biological Psychiatry 91, 967–976. [CrossRef]
- Shao, J., Qin, J., Wang, H., Sun, Y., Zhang, W., Wang, X., Wang, T., Xue, L., Yao, Z., Lu, Q., 2024. Capturing the Individual Deviations From Normative Models of Brain Structure for Depression Diagnosis and Treatment. Biological Psychiatry 95, 403–413. [CrossRef]
- Shen, R.S., Osmanlıoğlu, Y., Parker, D., Aunapu, D., Yerys, B.E., Tunç, B., Verma, R., 2024. Parsing altered brain connectivity in neurodevelopmental disorders by integrating graph-based normative modeling and deep generative networks. [CrossRef]
- Sima, D., Phan, T.V., Van Eyndhoven, S., Vercruyssen, S., Magalhães, R., Maes, C., Khan, R., Guo, J., Hughes, R., Gabr, R., Saha-Chaudhuri, P., Curiale, G., Belachew, S., Van Hecke, W., Ribbens, A., Smeets, D., 2024. Validation of Icobrain Aria - An AI-based Software Tool for Automated Detection and Quantification of Amyloid-related Imaging Abnormalities (S1.005). Neurology 102, 6102. [CrossRef]
- Smola, A.J., Schölkopf, B., 2004. A tutorial on support vector regression. Statistics and Computing 14, 199–222. [CrossRef]
- Snyder, K., Whitehead, E.P., Theodore, W.H., Zaghloul, K.A., Inati, S.J., Inati, S.K., 2021. Distinguishing type II focal cortical dysplasias from normal cortex: A novel normative modeling approach. NeuroImage: Clinical 30, 102565. [CrossRef]
- Sokoloff, L., Reivich, M., Kennedy, C., Des Rosiers, M.H., Patlak, C.S., Pettigrew, K.D., Sakurada, O., Shinohara, M., 1977. The [14C]deoxyglucose method for the measurement of local cerebral glucose utilization: theory, procedure, and normal values in the conscious and anesthetized albino rat. J Neurochem 28, 897–916. [CrossRef]
- Sun, L., Zhao, T., Liang, X., Xia, M., Li, Q., Liao, X., Gong, G., Wang, Q., Pang, C., Yu, Q., Bi, Y., Chen, P., Chen, R., Chen, Y., Chen, T., Cheng, J., Cheng, Y., Cui, Z., Dai, Z., Deng, Y., Ding, Y., Dong, Q., Duan, D., Gao, J.-H., Gong, Q., Han, Y., Han, Z., Huang, C.-C., Huang, R., Huo, R., Li, L., Lin, C.-P., Lin, Q., Liu, B., Liu, C., Liu, N., Liu, Ying, Liu, Yong, Lu, J., Ma, L., Men, W., Qin, S., Qiu, J., Qiu, S., Si, T., Tan, S., Tang, Y., Tao, S., Wang, D., Wang, F., Wang, J., Wang, P., Wang, X., Wang, Y., Wei, D., Wu, Y., Xie, P., Xu, X., Xu, Y., Xu, Z., Yang, L., Yuan, H., Zeng, Z., Zhang, H., Zhang, X., Zhao, G., Zheng, Y., Zhong, S., Alzheimer’s Disease Neuroimaging Initiative, Cam-CAN, Developing Human Connectome Project, DIDA-MDD Working Group, MCADI, NSPN, He, Y., 2024. Functional connectome through the human life span. bioRxiv 2023.09.12.557193. [CrossRef]
- Sun, X., Sun, J., Lu, X., Dong, Q., Zhang, L., Wang, W., Liu, J., Ma, Q., Wang, X., Wei, D., Chen, Y., Liu, B., Huang, C.-C., Zheng, Y., Wu, Y., Chen, T., Cheng, Y., Xu, X., Gong, Q., Si, T., Qiu, S., Lin, C.-P., Cheng, J., Tang, Y., Wang, F., Qiu, J., Xie, P., Li, L., He, Y., Xia, M., He, Y., Li, L., Cheng, J., Gong, Q., Lin, C.-P., Qiu, J., Qiu, S., Si, T., Tang, Y., Wang, F., Xie, P., Xu, X., Xia, M., 2023. Mapping Neurophysiological Subtypes of Major Depressive Disorder Using Normative Models of the Functional Connectome. Biological Psychiatry 94, 936–947. [CrossRef]
- Thomas, M., Lemaitre, M., Wilson, M.L., Viboud, C., Yordanov, Y., Wackernagel, H., Carrat, F., 2016. Applications of Extreme Value Theory in Public Health. PLOS ONE 11, e0159312. [CrossRef]
- Thompson, P.M., Stein, J.L., Medland, S.E., Hibar, D.P., Vasquez, A.A., Renteria, M.E., Toro, R., Jahanshad, N., Schumann, G., Franke, B., Wright, M.J., Martin, N.G., Agartz, I., Alda, M., Alhusaini, S., Almasy, L., Almeida, J., Alpert, K., Andreasen, N.C., Andreassen, O.A., Apostolova, L.G., Appel, K., Armstrong, N.J., Aribisala, B., Bastin, M.E., Bauer, M., Bearden, C.E., Bergmann, Ø., Binder, E.B., Blangero, J., Bockholt, H.J., Bøen, E., Bois, C., Boomsma, D.I., Booth, T., Bowman, I.J., Bralten, J., Brouwer, R.M., Brunner, H.G., Brohawn, D.G., Buckner, R.L., Buitelaar, J., Bulayeva, K., Bustillo, J.R., Calhoun, V.D., Cannon, D.M., Cantor, R.M., Carless, M.A., Caseras, X., Cavalleri, G.L., Chakravarty, M.M., Chang, K.D., Ching, C.R.K., Christoforou, A., Cichon, S., Clark, V.P., Conrod, P., Coppola, G., Crespo-Facorro, B., Curran, J.E., Czisch, M., Deary, I.J., de Geus, E.J.C., den Braber, A., Delvecchio, G., Depondt, C., de Haan, L., de Zubicaray, G.I., Dima, D., Dimitrova, R., Djurovic, S., Dong, H., Donohoe, G., Duggirala, R., Dyer, T.D., Ehrlich, S., Ekman, C.J., Elvsåshagen, T., Emsell, L., Erk, S., Espeseth, T., Fagerness, J., Fears, S., Fedko, I., Fernández, G., Fisher, S.E., Foroud, T., Fox, P.T., Francks, C., Frangou, S., Frey, E.M., Frodl, T., Frouin, V., Garavan, H., Giddaluru, S., Glahn, D.C., Godlewska, B., Goldstein, R.Z., Gollub, R.L., Grabe, H.J., Grimm, O., Gruber, O., Guadalupe, T., Gur, R.E., Gur, R.C., Göring, H.H.H., Hagenaars, S., Hajek, T., Hall, G.B., Hall, J., Hardy, J., Hartman, C.A., Hass, J., Hatton, S.N., Haukvik, U.K., Hegenscheid, K., Heinz, A., Hickie, I.B., Ho, B.-C., Hoehn, D., Hoekstra, P.J., Hollinshead, M., Holmes, A.J., Homuth, G., Hoogman, M., Hong, L.E., Hosten, N., Hottenga, J.-J., Hulshoff Pol, H.E., Hwang, K.S., Jack, C.R., Jenkinson, M., Johnston, C., Jönsson, E.G., Kahn, R.S., Kasperaviciute, D., Kelly, S., Kim, S., Kochunov, P., Koenders, L., Krämer, B., Kwok, J.B.J., Lagopoulos, J., Laje, G., Landen, M., Landman, B.A., Lauriello, J., Lawrie, S.M., Lee, P.H., Le Hellard, S., Lemaître, H., Leonardo, C.D., Li, C., Liberg, B., Liewald, D.C., Liu, X., Lopez, L.M., Loth, E., Lourdusamy, A., Luciano, M., Macciardi, F., Machielsen, M.W.J., MacQueen, G.M., Malt, U.F., Mandl, R., Manoach, D.S., Martinot, J.-L., Matarin, M., Mather, K.A., Mattheisen, M., Mattingsdal, M., Meyer-Lindenberg, A., McDonald, C., McIntosh, A.M., McMahon, F.J., McMahon, K.L., Meisenzahl, E., Melle, I., Milaneschi, Y., Mohnke, S., Montgomery, G.W., Morris, D.W., Moses, E.K., Mueller, B.A., Muñoz Maniega, S., Mühleisen, T.W., Müller-Myhsok, B., Mwangi, B., Nauck, M., Nho, K., Nichols, T.E., Nilsson, L.-G., Nugent, A.C., Nyberg, L., Olvera, R.L., Oosterlaan, J., Ophoff, R.A., Pandolfo, M., Papalampropoulou-Tsiridou, M., Papmeyer, M., Paus, T., Pausova, Z., Pearlson, G.D., Penninx, B.W., Peterson, C.P., Pfennig, A., Phillips, M., Pike, G.B., Poline, J.-B., Potkin, S.G., Pütz, B., Ramasamy, A., Rasmussen, J., Rietschel, M., Rijpkema, M., Risacher, S.L., Roffman, J.L., Roiz-Santiañez, R., Romanczuk-Seiferth, N., Rose, E.J., Royle, N.A., Rujescu, D., Ryten, M., Sachdev, P.S., Salami, A., Satterthwaite, T.D., Savitz, J., Saykin, A.J., Scanlon, C., Schmaal, L., Schnack, H.G., Schork, A.J., Schulz, S.C., Schür, R., Seidman, L., Shen, L., Shoemaker, J.M., Simmons, A., Sisodiya, S.M., Smith, C., Smoller, J.W., Soares, J.C., Sponheim, S.R., Sprooten, E., Starr, J.M., Steen, V.M., Strakowski, S., Strike, L., Sussmann, J., Sämann, P.G., Teumer, A., Toga, A.W., Tordesillas-Gutierrez, D., Trabzuni, D., Trost, S., Turner, J., Van den Heuvel, M., van der Wee, N.J., van Eijk, K., van Erp, T.G.M., van Haren, N.E.M., van ‘t Ent, D., van Tol, M.-J., Valdés Hernández, M.C., Veltman, D.J., Versace, A., Völzke, H., Walker, R., Walter, H., Wang, L., Wardlaw, J.M., Weale, M.E., Weiner, M.W., Wen, W., Westlye, L.T., Whalley, H.C., Whelan, C.D., White, T., Winkler, A.M., Wittfeld, K., Woldehawariat, G., Wolf, C., Zilles, D., Zwiers, M.P., Thalamuthu, A., Schofield, P.R., Freimer, N.B., Lawrence, N.S., Drevets, W., the Alzheimer’s Disease Neuroimaging Initiative, E.C., IMAGEN Consortium, Saguenay Youth Study (SYS) Group, 2014. The ENIGMA Consortium: large-scale collaborative analyses of neuroimaging and genetic data. Brain Imaging and Behavior 8, 153–182. [CrossRef]
- Varrone, A., Dickson, J.C., Tossici-Bolt, L., Sera, T., Asenbaum, S., Booij, J., Kapucu, O.L., Kluge, A., Knudsen, G.M., Koulibaly, P.M., Nobili, F., Pagani, M., Sabri, O., Vander Borght, T., Van Laere, K., Tatsch, K., 2013. European multicentre database of healthy controls for [123I]FP-CIT SPECT (ENC-DAT): age-related effects, gender differences and evaluation of different methods of analysis. Eur J Nucl Med Mol Imaging 40, 213–227. [CrossRef]
- Verdi, S., Marquand, A.F., Schott, J.M., Cole, J.H., 2021. Beyond the average patient: how neuroimaging models can address heterogeneity in dementia. Brain 144, 2946–2953. [CrossRef]
- Villalón-Reina, J.E., Moreau, C.A., Nir, T.M., Jahanshad, N., Simons Variation in Individuals Project Consortium, Maillard, A., Romascano, D., Draganski, B., Lippé, S., Bearden, C.E., Kia, S.M., Marquand, A.F., Jacquemont, S., Thompson, P.M., 2022. Multi-site Normative Modeling of Diffusion Tensor Imaging Metrics Using Hierarchical Bayesian Regression, in: Wang, L., Dou, Q., Fletcher, P.T., Speidel, S., Li, S. (Eds.), Medical Image Computing and Computer Assisted Intervention – MICCAI 2022, Lecture Notes in Computer Science. Springer Nature Switzerland, Cham, pp. 207–217. [CrossRef]
- Villalón-Reina, J.E., Zhu, A.H., Nir, T.M., Thomopoulos, S.I., Laltoo, E., Kushan, L., Bearden, C.E., Jahanshad, N., Thompson, P.M., 2023. Large-scale Normative Modeling of Brain Microstructure, in: 2023 19th International Symposium on Medical Information Processing and Analysis (SIPAIM). Presented at the 2023 19th International Symposium on Medical Information Processing and Analysis (SIPAIM), IEEE, Mexico City, Mexico, pp. 1–5. [CrossRef]
- Wang, J., 2023. An Intuitive Tutorial to Gaussian Process Regression. Comput. Sci. Eng. 25, 4–11. [CrossRef]
- Wang, X., Zhao, K., Zhou, R., Leow, A., Osorio, R., Zhang, Y., He, L., 2022. Normative Modeling via Conditional Variational Autoencoder and Adversarial Learning to Identify Brain Dysfunction in Alzheimer’s Disease. [CrossRef]
- Williams, L.M., Whitfield Gabrieli, S., 2025. Neuroimaging for precision medicine in psychiatry. Neuropsychopharmacol. 50, 246–257. [CrossRef]
- Wolfers, T., Beckmann, C.F., Hoogman, M., Buitelaar, J.K., Franke, B., Marquand, A.F., 2020. Individual differences v. the average patient: mapping the heterogeneity in ADHD using normative models. Psychol. Med. 50, 314–323. [CrossRef]
- Wolfers, T., Doan, N.T., Kaufmann, T., Alnæs, D., Moberget, T., Agartz, I., Buitelaar, J.K., Ueland, T., Melle, I., Franke, B., Andreassen, O.A., Beckmann, C.F., Westlye, L.T., Marquand, A.F., 2018. Mapping the Heterogeneous Phenotype of Schizophrenia and Bipolar Disorder Using Normative Models. JAMA Psychiatry 75, 1146. [CrossRef]
- Wolfers, T., Rokicki, J., Alnæs, D., Berthet, P., Agartz, I., Kia, S.M., Kaufmann, T., Zabihi, M., Moberget, T., Melle, I., Beckmann, C.F., Andreassen, O.A., Marquand, A.F., Westlye, L.T., 2021. Replicating extensive brain structural heterogeneity in individuals with schizophrenia and bipolar disorder. Human Brain Mapping 42, 2546–2555. [CrossRef]
- Wong, T.Y., Moore, T.M., Seidlitz, J., Yuen, K.S.L., Ruparel, K., Barzilay, R., Calkins, M.E., Alexander-Bloch, A.F., Satterthwaite, T.D., Gur, R.E., Gur, R.C., 2023. Traumatic stress load and stressor reactivity score associated with accelerated gray matter maturation in youths indexed by normative models. Mol Psychiatry 28, 1137–1145. [CrossRef]
- Wüthrich, M.V., Merz, M., 2023. Generalized Linear Models, in: Wüthrich, M.V., Merz, M. (Eds.), Statistical Foundations of Actuarial Learning and Its Applications. Springer International Publishing, Cham, pp. 111–205. [CrossRef]
- Xu, B., Kuplicki, R., Sen, S., Paulus, M.P., 2021. The pitfalls of using Gaussian Process Regression for normative modeling.
- Yamashita, M., Yoshihara, Y., Hashimoto, R., Yahata, N., Ichikawa, N., Sakai, Y., Yamada, T., Matsukawa, N., Okada, G., Tanaka, S.C., Kasai, K., Kato, N., Okamoto, Y., Seymour, B., Takahashi, H., Kawato, M., Imamizu, H., 2018. A prediction model of working memory across health and psychiatric disease using whole-brain functional connectivity. eLife 7, e38844. [CrossRef]
- Yang, Z., Wu, J., Xu, L., Deng, Z., Tang, Y., Gao, J., Hu, Y., Zhang, Y., Qin, S., Li, C., Wang, J., 2020. Individualized psychiatric imaging based on inter-subject neural synchronization in movie watching. NeuroImage 216, 116227. [CrossRef]
- Zabihi, M., Floris, D.L., Kia, S.M., Wolfers, T., Tillmann, J., Arenas, A.L., Moessnang, C., Banaschewski, T., Holt, R., Baron-Cohen, S., Loth, E., Charman, T., Bourgeron, T., Murphy, D., Ecker, C., Buitelaar, J.K., Beckmann, C.F., Marquand, A., The EU-AIMS LEAP Group, 2020. Fractionating autism based on neuroanatomical normative modeling. Transl Psychiatry 10, 384. [CrossRef]
- Zabihi, M., Kia, S.M., Wolfers, T., De Boer, S., Fraza, C., Dinga, R., Arenas, A.L., Bzdok, D., Beckmann, C.F., Marquand, A., 2024. Nonlinear latent representations of high-dimensional task-fMRI data: Unveiling cognitive and behavioral insights in heterogeneous spatial maps. PLoS ONE 19, e0308329. [CrossRef]
- Zabihi, M., Oldehinkel, M., Wolfers, T., Frouin, V., Goyard, D., Loth, E., Charman, T., Tillmann, J., Banaschewski, T., Dumas, G., Holt, R., Baron-Cohen, S., Durston, S., Bölte, S., Murphy, D., Ecker, C., Buitelaar, J.K., Beckmann, C.F., Marquand, A.F., 2019. Dissecting the Heterogeneous Cortical Anatomy of Autism Spectrum Disorder Using Normative Models. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging 4, 567–578. [CrossRef]
- Zhang, G., Zhang, X., Huang, H., Wang, Y., Li, H., Duan, Y., Chen, H., Liu, Y., Jing, B., Tie, Y., Lin, S., 2022. Probing individual-level structural atrophy in frontal glioma patients. Neurosurg Rev 45, 2845–2855. [CrossRef]
- Zhang, J., Fang, S., Yao, Y., Li, F., Luo, Q., 2023. Parsing the heterogeneity of brain-symptom associations in autism spectrum disorder via random forest with homogeneous canonical correlation. Journal of Affective Disorders 335, 36–43. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




