High Frequency Induction Motor Analysis for Common Mode and Differential Mode Impedance Characteristics

1. Introduction

Induction motors (IMs) are known for high performance in diverse industrial environments. The IM’s smooth operational characteristics without core or insulation damage are maintained by thermal protection and winding failure associated with motor components maintaining better dynamic performance [1]. Variable frequency drive-based IM applications are common in daily life applications. IMs exhibit exceptional reliability, robustness, and efficient operation in complex situations. These motors are subjected to Electro-Magnetic Interference (EMI) issues by higher frequency content due to instant transients in power supply parameters. The pulses generated after pulse width modulation (PWM) contribute to leakage and bearing currents as well as the machine’s body losses. The transients in voltage cause insulation failure, which can cause short circuit currents leading to contact failures [2,3]. Furthermore, the EMI waves are capable to affect the machine drive components and severely affect the performance of key components involved in feedback loops [4]. Motor bearings are distressed by the flow of leakage current due to winding insulation failure caused by stress developed by voltage transient, this, in turn, reduces the life span and reliable operation of the motor drive [5,6]. The high frequency models used to represent the behavior of machines are electrical equivalent circuits. The circuits are developed to mirror the machine behavior at higher frequency bands. These equivalent models are based on impedance values depending upon resistance and reactance offered by resistance (R), inductance (L), and conductance (C) of the stator, rotor, and magnetizing components respectively. The value of RLC based impedance can be measured by calculations based on motor design parameters for the EMI testing environment [7,8,9,10,11,12,13]. The resistance and inductance of the motor remain constant at lower frequencies, Hence the value remains the same for lower frequency bands. Whereas, at higher frequencies, the value of stator, rotor, and magnetizing impedance deviates from existing values. This behavior is observed due to the dependency of reactance in both inductance or capacitance forms on the frequency of supply parameters. The EMI standards are measured over the frequency band of 150 KHz to 30 MHz [12,13]. Moreover, models operating beyond 10 MHz are deviating from the accurate handling of design parameters [14,15,16].

The high frequency phenomenon lies in the magnetic core of IMs that can significantly influence the motor’s performance. The rotor and stator magnetic cores are laminated with steel sheets to reduce the flow of eddy currents generated during alternating magnetic fields created by alternating supply voltages. But, after a certain frequency range, the eddy current factor becomes prominent despite the presence of insulation, as the skin depth of conducting path becomes smaller than the overall thickness of the insulation sheet. Therefore, the eddy currents induced by magnetic field create a shielding effect in the lamination sheet which in turn changes the value of inductance [17,18].

The impact of parasitic capacitance at low frequency is neglectable as the impedance offered in the form of capacitive reactance is large. Whereas, if the frequency rises then capacitive reactance decreases. It creates new current paths inside the motor body due to the lower impedance offered by parasitic capacitors. Therefore, due to higher frequency multiple current paths are created due to lesser opposition offered by parasitic capacitance [14,17,19]. There are multiple ways to visualize the behavior of IM over a wide range of frequencies. The equivalent circuit model of IM for electromagnetic field analysis is derived from the design parameters of the motor by using the finite element method (FEM). The FEM analysis is capable to find the resistance, inductance, and capacitance of each turn in winding [20,21,22,23,24]. On the other hand, lumped parameter model (LPM) measures the parameters of IM experimentally. This approach demands the physical presence of the motor for measurements, hence it cannot facilitate the design stage as a manufactured motor cannot be altered instantly [25,26,27,28]. Some hybrid approaches are used for the measurement of constant motor parameters [19,29].

Measurement based approach takes CM and DM impedance and calculates Impedance parameters from measured values to model a high frequency IM. While, obtaining CM and DM impedance curves concerning frequency separate connection schemes are employed [7,8,25,26,28,30].

The paper objectives presented in this paper are as follows:

• To develop high frequency model of induction motor per phase model for common mode and differential mode impedance characteristics.
• The High frequency model of the IM drive for common mode characteristics was tested by the POWERSIM simulation model.
• Analyze common mode and differential mode impedance (magnitude and phase) frequency response bode plots of high frequency induction motors.

The paper was arranged in the following order: Section 2 highlights the background of studies related to the high frequency behavior of induction motors and state-of-the-art simulation approaches to visualize the variation of IM behavior at higher frequencies. Section 3 gives a detailed parameter as well as an FFT analysis of high frequency IM drive model simulated in POWERSIM for various electrical parameters. Section 4 presents two different high frequency IM Matlab models that are investigated for CM and DM impedance characteristics at higher frequencies. Both models were analyzed under the same equivalent per phase high frequency CM and DM impedance models. Conclusion and prospects are discussed in Section 5.

2. Materials and Methods

An induction motor (IM) can withstand interference from the outside environment and has a reasonable price tag. By tracking a rotating magnetic field, the IM’s rotor induces a voltage in the rotor bar that is proportional to the rotation's angular velocity [31]. The adjustable speed drive (ASD) inverter of the IM switches multiples times on or off, it subjects the power lines and the IM to a significant dV/dt. High-frequency currents can flow as a result of these voltage variations, both between the motor's windings and the ground through stray capacitive contacts creating common mode currents and across the phases of the motor. Common mode current is a source of electromagnetic interference and can cause other problems by coupling to surrounding systems. It causes the bearings to wear down, the lubrication to evaporate, and the conduit housing the three-phase wires to overheat. It also decreases the motor insulation lifespan [32].

High-frequency (HF) voltage injection is used to estimate the rotor winding temperature in current-regulated squirrel-cage induction motors (IMs). The test result displays that the estimator works well under the initial situation, load variations, and cooling state of the motor. The newly presented technique not only helps in predicting faults but it can also be used to remedy the effects of changes in an IM controller [33]. To generate the switching pulses, hysteresis current control (HCC) is used. HCC is more popular due to its simplicity, remarkable stability, lack of tracking error, very fast transient response, inherent limiting maximum current, and intrinsic robustness to variations in load parameters. It is the job of the hysteretic controller to send the appropriate switching signal to the VSI to deliver the reference current if the error is greater than either the higher or lower hysteresis limit [34].

The digital adaptive hysteresis current control is particularly simple and effective at controlling the switching frequency and the phase of the inverter's voltage pulses, which are naturally centered in the modulation period. This mode of regulation has proven better switching frequency and phase control [35]. A high frequency power converter module for recharging batteries is developed for use in plug-in hybrid electric vehicle (EV) systems. The suggested 3-phase semi-controlled rectification topology significantly reduces switching and conduction losses in contrast to the fully-controlled topology. Under varying situations, such as a shift in the dc-reference step and load changes, a swift control dynamic response of 0.1 seconds is observed. The collected information supports the validity of the proposed system for PHEVs [36]. Current and vibration transients are examined using cutting-edge signal processing techniques including the discrete wavelet transform (DWT) and a multiresolution Fourier transform (MFT). Vibrational transients are recorded during the load withdrawal process provide evidence that it occurs at a very high frequency. As the defect grows worse, frequency of the defective gear mesh gain energy, but a large amount of impact energy is also generated in low-frequency regions. Load release in current transients, on the other hand, happens at low frequencies, albeit a tiny transient might be observed in high-frequency regions due to faulty equipment [37].

Hysteresis controllers are used in many applications due to their high dynamic responsiveness, ease of setup, and high overload current safety. Hysteresis current control has been proven to be efficient for two-level inverters. Dynamic responsiveness, implementation simplicity, and current overload prevention are all strong suits of the multiband hysteresis current controller (MHCC). As the torque output of a three-stage brushless DC motor drive is smoothed down as much as possible by the design [38]. The DTC method is used to minimize torque ripples and control the switching frequency of a motor. The simulations are ranging from transient to steady-state activities. At a constant reference speed, an induction motor's transient response is examined at starting, accelerating, and slowing down phases [39]. Space-vector pulse-width modulation-based switching sequence for a three-level neutral-point clamped inverter (SV-PWM) helps to reduce the number of switching sequences and keeps the difference in voltage between the two dc-link capacitors at the desired level, both are improvements over the standard SV-PWM strategy. In addition, the technique aids in maintaining the specified voltage differential between the capacitors. There is a limited range of switching patterns that are employed uniformly across all industries. It keeps the system's switching frequency constant [40].

A user-friendly high frequency model of IM presents the variation in parameters for EMI examination. The circuit elements are determined by a multilayer perceptron neural network for time-domain simulation of variable frequency drive systems [41]. An IM drive high frequency performance is observed for EMI for a frequency range of 100 Hz to 30 Mhz. The high frequency model can be modified to predict the EMC problems and implements adequate filter operation to enhance susceptibility in cable-fed motor-drive system [42,43]. High frequency induction machine model parameters are converted into state-space model illustration and motor impedance is estimated for a frequency range of 150 kHz to 30 MHz [44]. Common mode and bearing currents supplied by the inverter are investigated for the Spice-based high frequency electric motor model. The simulated model is suitable to present model behavior for a frequency range of 50 kHz to 3 MHz [45].

In an induction machine drive system, Inverter’s switching operation generates a higher rate of change in voltage, this abrupt change is the main cause of leakage and bearing currents, due to the formation of stray and parasitic capacitances in high frequency drive operation. The analysis of high frequency model is beneficial to evaluate model performance under EMC recommendations [46]. The motor speed and bearing-key frequency are used to detect the failure and guide for diagnosis of the electric motor. Estimation algorithms are used for the detection of bearing faults during high frequency demodulation. The motor vibration model is simulated to generate vibration data. The algorithm performance is validated by comparison with the vibration dataset [47]. The star-connected high-frequency model of IM with defined parameters is being analyzed for EMI analysis. The IM model consists of a simple structure and nine circuit elements per phase. The element values are calculated by using a multilayer perceptron (MLP) neural network, with phase-to-frame motor impedance acquired for model training. The analysis suggests that common mode and differential mode impedance are accurately measured for the frequency range 150 kHz to 30 MHz [48]. IM high frequency model is developed to predict terminal overvoltage, common mode, and differential mode impedance of AC motor. The model is derived based on a mathematical model of IM’s transfer function simulated in Matlab to visualize the high frequency behavior of IM under the frequency range of 40 Hz to 110 MHz [49].

High frequency IM’s impedance is measured in CM and DM configurations. The impedance values are taken for state-space representation and the HF model structure is developed. The genetic algorithm is used for tuning real impedance as per the configuration of High frequency IM model [50]. IM models powered by inverters ranging from 1.5 and 240 kW are modeled for the calculation of common-mode current and bearing voltage to investigate bearing failure. The model parameters are calculated to accurately predict IM’s bearing fault [51]. A six-port star and delta model of three-phase IM is derived from CM and DM equivalent RLC impedances. The model predicts impedance with high precision to 100 MHz and highlights six port CM and DM multi-mode noise [52].

The high frequency behavior of IM over a wider frequency range from 10 Hz to 10 MHz is examined. The equivalent circuit model is presented for bearing, common mode, and differential mode models developed under a single universal three-phase model [53]. The high frequency IM models are examined to summarize motor behavior at high frequency. The model forecasts EMI noise disturbances in motor drive applications [54]. The IM model parameters are determined by the least-square curve fitting approach. Magnitude and phase plots of CM and DM impedance curves are used to calculate IM model parameters. This approach indicates the suitable value of high frequency parameters concerning the model and size of the motor [55]. In the IM-based variable speed drive powered by PWM, impedance parameters are measured by RLC bridges in the laboratory, the parameters are measured at rated and high frequencies to monitor the effect of EMI in CM and DM configurations [56]. The high frequency motor impedance of stator winding is measured by per unit length (PUL) transmission line equivalent circuit. The PUL circuit consists of both high and low-frequency components, able to measure high frequency behavior of IM. Moreover, the same procedure can be employed to simulate high frequency motor’s magnitude and phase response accurately [57].

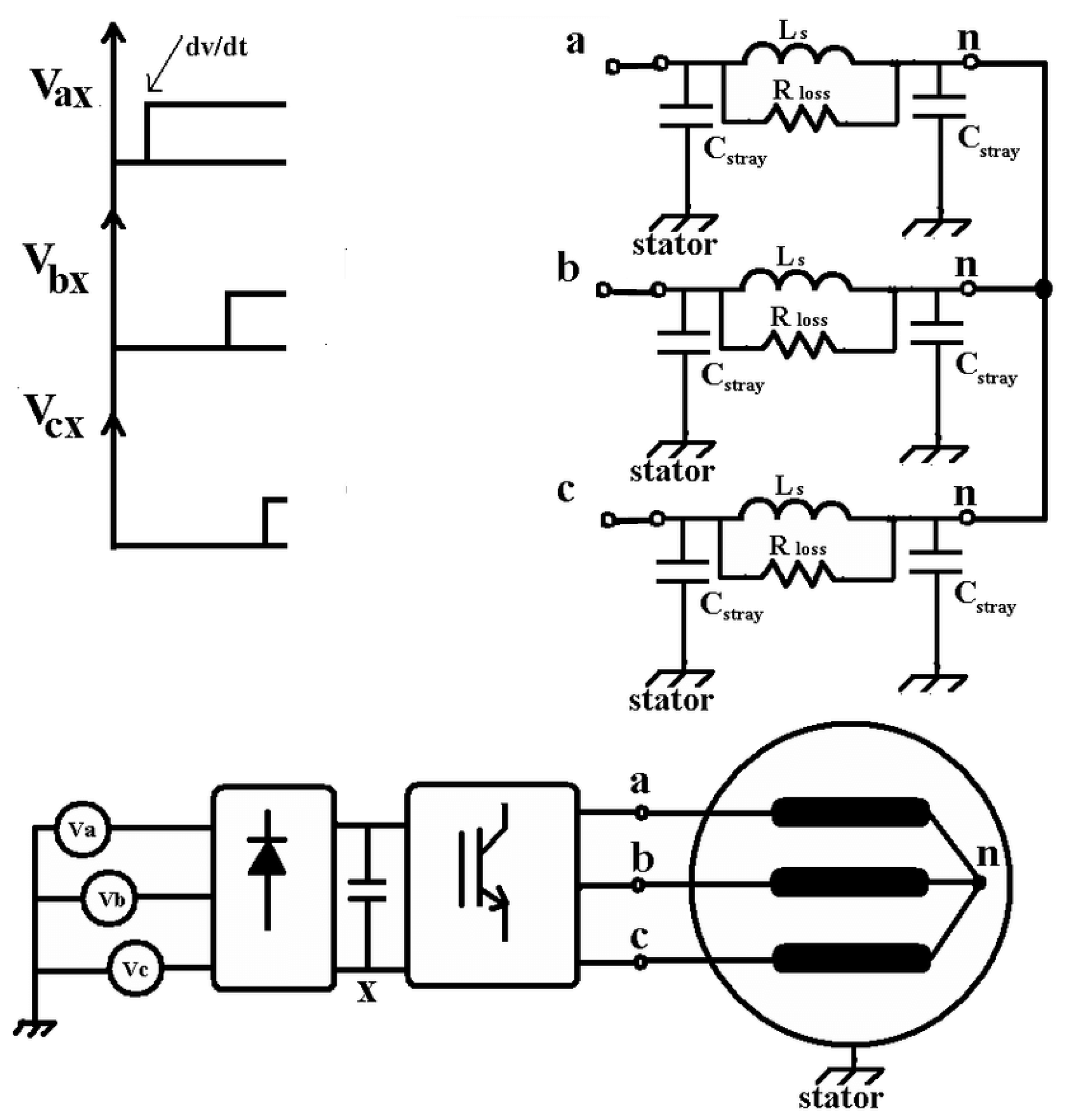
2.1. High Frequency Model for Induction Motor

The asynchronous motor, often known as an induction motor, is the type of motor that is most commonly used in commercial settings. The proposed models are developed by the calculation of the CM and DM impedances. The impedance model is employed to get a behavioral interpretation of the induction machine.

Electromagnetic interference (EMI) can be broken down into two distinct types: common mode interference (CM) and differential mode interference (DM). Motor impedance analysis requires the simultaneous observation of two sets of curves, one for the common mode and one for the differential mode, revealing the variations in motor impedance concerning frequency. An electric motor model at high frequency can be broken down into three main parts. These include inductance, losses, and stray capacitance between the windings and the stator. The key difficulty is an analysis of high dv/dt between the motor's terminals in Figure 1, which is caused by a common mode current generated by high-speed switching devices such as insulated gate bipolar transistors (IGBTs). The switching time and dv/dt are controlled by the IGBTs and their gate drivers [58,59].

The equivalent per-phase model of high frequency IM is presented in Figure 2.

Where,

L_d : Phase Leakage Inductance

R : Winding Resistance

R_e : Eddy current resistance inside the magnetic core and motor frame

C_p : Turn-to-turn distributive coupling capacitance

C_g : Winding to turn distributive coupling capacitance

The high frequency three-phase model of an induction motor consists of three differential mode impedances denoted by Z_DM, as well as three common mode impedances denoted by Z_CM, all of which are connected to the ground terminal. Figure 2 shows per phase common mode impedance ${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}$ of high frequency induction motor model.

The following equations (1-5) are used to derive the common mode impedance ${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}$ of induction motor:

$${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}={\displaystyle \frac{\mathrm{V}\left(\mathrm{C}\mathrm{M}\right)}{\mathrm{I}\left(\mathrm{C}\mathrm{M}\right)}}$$

(1)

$${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}=\left[\right((\mathrm{R}+\mathrm{sL}|\left|{\mathrm{R}}_{\mathrm{e}}\right||{\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{p}}})+({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}}\left)\right)\left|\right|({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}}\left)\right]$$

(2)

$${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}={\displaystyle \frac{\mathrm{R}\mathrm{R}\mathrm{e}+\mathrm{s}\mathrm{L}\mathrm{R}\mathrm{e}}{{\mathrm{s}}^2\mathrm{R}\mathrm{e}\mathrm{L}{\mathrm{C}}_{\mathrm{p}}+\mathrm{s}\left(\mathrm{L}+\mathrm{R}\mathrm{R}\mathrm{e}{\mathrm{C}}_{\mathrm{p}}\right)+\mathrm{R}+\mathrm{R}\mathrm{e}}}+({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}}\left)\right|\left|\right({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}}\left)\right]$$

(3)

$${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}={\displaystyle \frac{{\mathrm{s}}^2\mathrm{R}\mathrm{e}\mathrm{L}\left({\mathrm{C}}_{\mathrm{g}}+{\mathrm{C}}_{\mathrm{p}}\right)+\mathrm{s}\left(\mathrm{L}+\mathrm{R}\mathrm{r}\mathrm{R}\mathrm{e}+\mathrm{R}\mathrm{R}\mathrm{e}{\mathrm{C}}_{\mathrm{g}}\right)+\mathrm{R}+\mathrm{R}\mathrm{e}}{{(\mathrm{s}}^2\mathrm{R}\mathrm{e}\mathrm{L}{\mathrm{C}}_{\mathrm{p}}+\mathrm{s}\left(\mathrm{L}+\mathrm{R}\mathrm{R}\mathrm{e}{\mathrm{C}}_{\mathrm{p}}\right)+\mathrm{R}+\mathrm{R}\mathrm{e}\left)\right(\mathrm{s}\mathrm{C}\mathrm{g})}}\left|\right|({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}}\left)\right]$$

(4)

$${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}={\displaystyle \frac{{\mathrm{s}}^2\frac{\mathrm{R}\mathrm{e}.\mathrm{L}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\left({\mathrm{C}}_{\mathrm{g}}+{\mathrm{C}}_{\mathrm{p}}\right)+\mathrm{s}\left(\frac{\mathrm{R}.\mathrm{R}\mathrm{e}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\left({\mathrm{C}}_{\mathrm{g}}+{\mathrm{C}}_{\mathrm{p}}\right)+\frac{\mathrm{L}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\right)+1}{2{{\mathrm{C}}_{\mathrm{g}}\mathrm{s}(\mathrm{s}}^2\frac{\mathrm{R}\mathrm{e}.\mathrm{L}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\left({\mathrm{C}}_{\mathrm{p}}+\frac{{\mathrm{C}}_{\mathrm{g}}}{2}\right)+\mathrm{s}\left(\frac{\mathrm{R}.\mathrm{R}\mathrm{e}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\left({\mathrm{C}}_{\mathrm{p}}+\frac{{\mathrm{C}}_{\mathrm{g}}}{2}\right)+\frac{\mathrm{L}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\right)+1)}}$$

(5)

An equivalent per-phase circuit for a differential mode induction motor is presented in Figure 3. The following equations (6-10) are used to derive the differential mode impedance ${\mathrm{Z}}_{\mathrm{p}{\mathrm{p}}^{\prime }}$ of induction motor:

$${\mathrm{Z}}_{\mathrm{p}{\mathrm{p}}^{\prime }}={\displaystyle \frac{\mathrm{V}\left(\mathrm{D}\mathrm{M}\right)}{\mathrm{I}\left(\mathrm{D}\mathrm{M}\right)}}$$

(6)

$${\mathrm{Z}}_{\mathrm{p}{\mathrm{p}}^{\prime }}=\left[\right(\mathrm{R}+\mathrm{sL}\left|\right|{\mathrm{R}}_{\mathrm{e}}\left|\right|{\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{p}}}\left)\right|\left|\right(({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}})+({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}}\left)\right)]$$

(7)

$${\mathrm{Z}}_{\mathrm{p}{\mathrm{p}}^{\prime }}={\displaystyle \frac{\mathrm{R}\mathrm{R}\mathrm{e}+\mathrm{s}\mathrm{L}\mathrm{R}\mathrm{e}}{{\mathrm{s}}^2\mathrm{R}\mathrm{e}\mathrm{L}{\mathrm{C}}_{\mathrm{p}}+\mathrm{s}\left(\mathrm{L}+\mathrm{R}\mathrm{R}\mathrm{e}{\mathrm{C}}_{\mathrm{p}}\right)+\mathrm{R}+\mathrm{R}\mathrm{e}}}\left|\right|\left(\right({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}})+({\displaystyle \frac{1}{\mathrm{s}\mathrm{C}\mathrm{g}}}\left)\right)]$$

(8)

$${\mathrm{Z}}_{\mathrm{p}{\mathrm{p}}^{\prime }}={\displaystyle \frac{\mathrm{R}\mathrm{R}\mathrm{e}+\mathrm{s}\mathrm{L}\mathrm{R}\mathrm{e}}{{\mathrm{s}}^2\mathrm{R}\mathrm{e}\mathrm{L}{\mathrm{C}}_{\mathrm{p}}+\mathrm{s}\left(\mathrm{L}+\mathrm{R}\mathrm{R}\mathrm{e}{\mathrm{C}}_{\mathrm{p}}\right)+\mathrm{R}+\mathrm{R}\mathrm{e}}}\left|\right|({\displaystyle \frac{2}{\mathrm{s}\mathrm{C}\mathrm{g}}}\left)\right]$$

(9)

$${\mathrm{Z}}_{\mathrm{p}{\mathrm{p}}^{\prime }}={\displaystyle \frac{\mathrm{R}\mathrm{R}\mathrm{e}(\frac{\mathrm{L}}{\mathrm{R}}\mathrm{s}+1)}{{(\mathrm{s}}^2\frac{\mathrm{R}\mathrm{e}.\mathrm{L}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\left({\mathrm{C}}_{\mathrm{p}}+\frac{{\mathrm{C}}_{\mathrm{g}}}{2}\right)+\mathrm{s}\left(\frac{\mathrm{R}.\mathrm{R}\mathrm{e}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\left({\mathrm{C}}_{\mathrm{p}}+\frac{{\mathrm{C}}_{\mathrm{g}}}{2}\right)+\frac{\mathrm{L}}{\mathrm{R}+\mathrm{R}\mathrm{e}}\right)+1)}}$$

(10)

Figure 4 presents the arrangement of motor terminals for the measurement of CM and DM impedance. The impedance ${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}$ is representing CM impedance and ${\mathrm{Z}}_{\mathrm{p}{\mathrm{p}}^{\prime }}$ is serving as DM impedance. The phase resistance R is much smaller than the reactance of the leakage inductance L throughout the high frequency range. For this reason, the stator resistance will be ignored in all subsequent analyses. Both the Z_CM and Z_DM impedances can be simplified in equations (11-12) as follows:

$${\mathrm{Z}}_{\mathrm{p}\mathrm{g}}={\displaystyle \frac{{\mathrm{s}}^2\mathrm{L}\left({\mathrm{C}}_{\mathrm{g}}+{\mathrm{C}}_{\mathrm{p}}\right)+\mathrm{s}\left(\frac{\mathrm{L}}{\mathrm{R}}\right)+1}{2{{\mathrm{C}}_{\mathrm{g}}\mathrm{s}(\mathrm{s}}^2\mathrm{L}\left({\mathrm{C}}_{\mathrm{p}}+\frac{{\mathrm{C}}_{\mathrm{g}}}{2}\right)+\mathrm{s}\left(\frac{\mathrm{L}}{\mathrm{R}}\right)+1)}}$$

(11)

$${\mathrm{Z}}_{\mathrm{p}{\mathrm{p}}^{\prime }}={\displaystyle \frac{\mathrm{L}\mathrm{s}}{{(\mathrm{s}}^2\mathrm{L}\left({\mathrm{C}}_{\mathrm{p}}+\frac{{\mathrm{C}}_{\mathrm{g}}}{2}\right)+\mathrm{s}\left(\frac{\mathrm{L}}{\mathrm{R}}\right)+1)}}$$

(12)

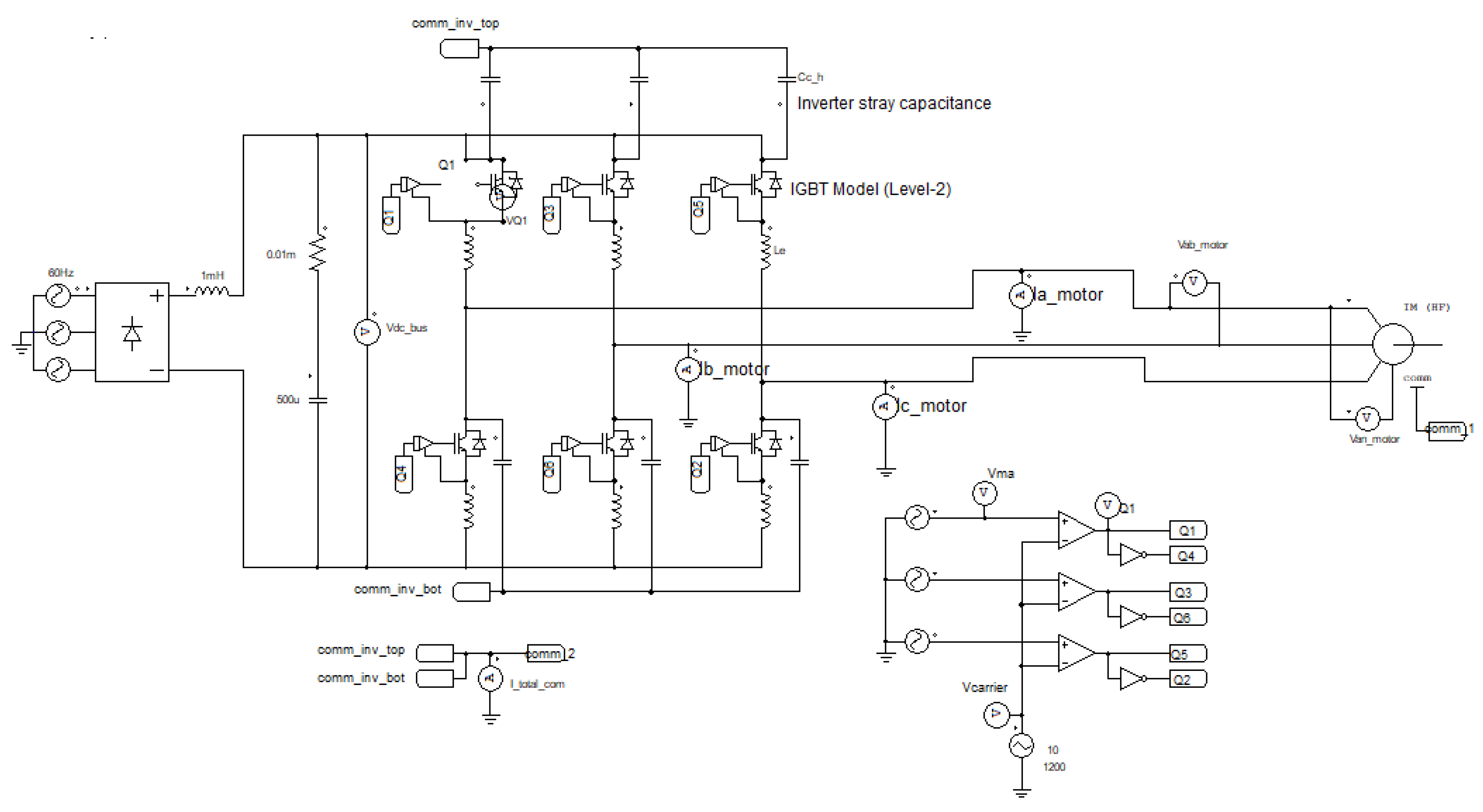
2. Simulation of High Frequency Induction Motor Drive

A high frequency induction motor drive model based on an IGBT inverter is being analyzed in POWERSIM. The three-phase windings are connected as a Y-network as shown in Figure 5. Phase A, B, and C stator winding terminals are placed at nodes a, b, and c, respectively. Node n is the neutral point in a circuit, while the comm terminal is the common connection for a common-mode circuit. The mechanical shaft’s node houses the shaft's connection terminal. Parameters associated with high frequency responses are intended to be used for analyzing transient responses caused by the reflecting effect. Iron losses, Re, are caused by eddy currents in the magnetic core. The composite circuit of Rt, Lt, and Ct captures the second resonance in the frequency response. The skin effect and the inter-turn capacitance of the stator winding contributed to the development of second resonance. Parasitic components of each phase and the stator neutral relative to the motor frame (common point) are represented graphically by the Rg and Cg network. The dissipative effect is denoted by Rg, and the winding-to-ground capacitance is denoted by Cg.

The high frequency Induction Motor parameters are:

• Rs: Stator Resistance;
• Ls: Stator winding leakage inductance;
• Rr: Rotor winding resistance with respect to stator side;
• Lr: Rotor winding leakage inductance with respect to stator side;
• Lm: Magnetizing inductance;
• P: Total number of poles;
• J: Moment of inertia

High frequency model EMC parameters are:

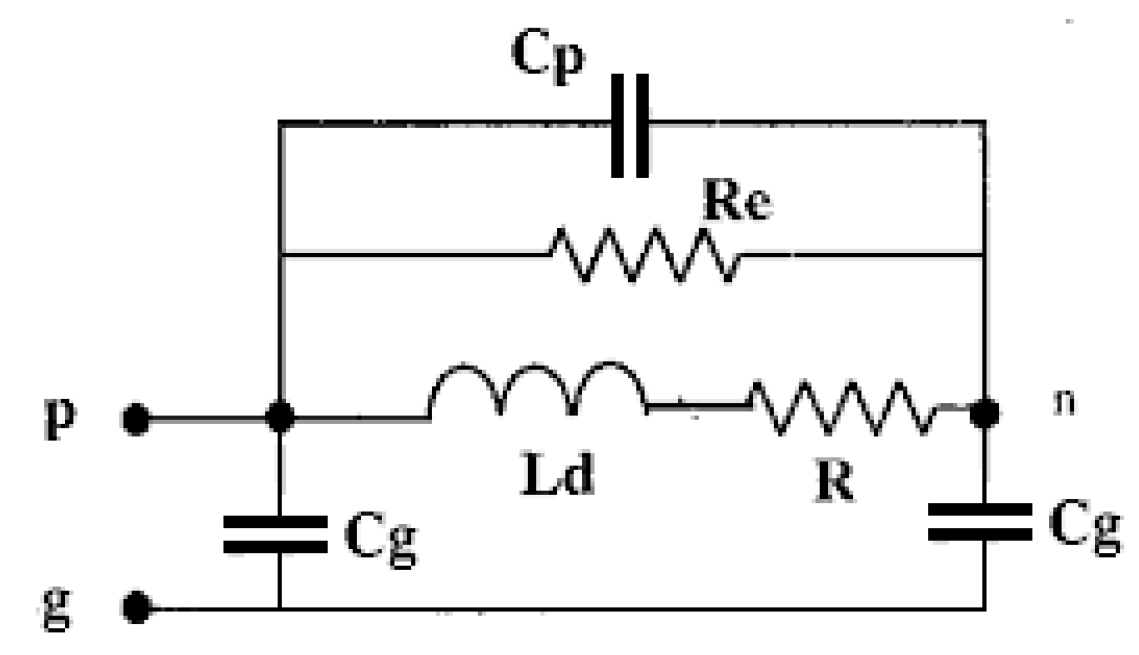
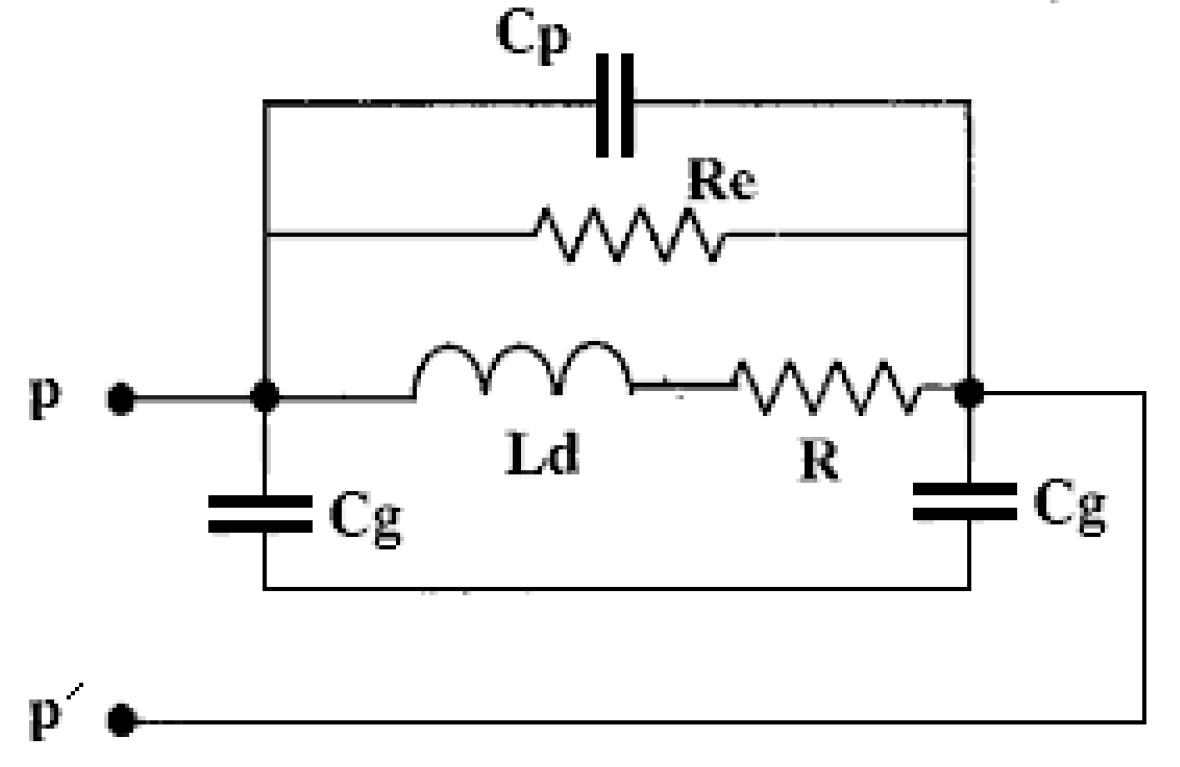
• Cg: Winding to ground capacitance;
• Rg: Resistance due to motor frame;
• Re: Eddy current resistance in the motor core;
• Rt: Skin effect resistance at high-frequency;
• Lt: Skin effect inductance at high-frequency;
• Ct: Skin effect capacitance at high frequency;

Common mode electromagnetic interference (EMI) is produced on the three-phase output lines of a power inverter as a result of hard switching with higher change in voltage concerning time, it is dependent on the rise time of IGBTs and the system voltage. Due to the existence of parasitic components and operational factors, electromagnetic compatibility (EMC) issues become easily apparent. The high frequency IM drive model in Figure 6 is used to analyze the EMI effect caused by the inverter, AC cable, and induction motor at higher frequencies. While, L_e represents the emitter’s parasitic inductance, and C_ch represents the stray capacitance between the collector terminal and the grounded heatsink of each IGBT. Table 1 presents the parameters considered for the high frequency model.

The three-phase voltage supply is rectified from three phase diode bridge rectifier. Then the rectified output is applied on a three-phase IGBT inverter for a three-phase high frequency induction motor supply. The switching operation of the IGBT inverter is controlled by comparing the sinusoidal wave voltage source with a triangular wave voltage source.

The comparison generates pulses for IGBT switches. The pulses are applied directly to IGBT numbers 1, 3, and 5. Whereas, then inverted pulses are applied on IGBT numbers 4, 6, and 2 respectively.

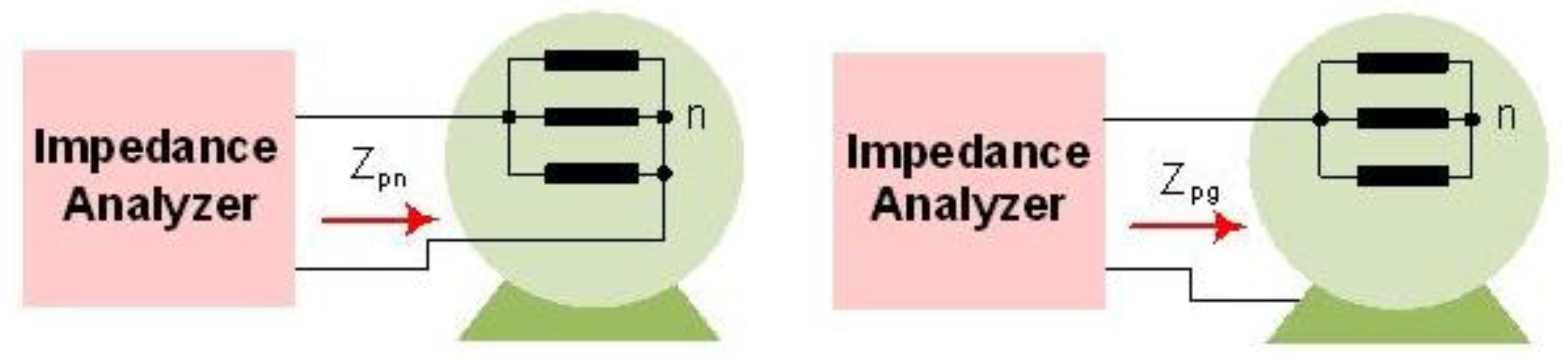
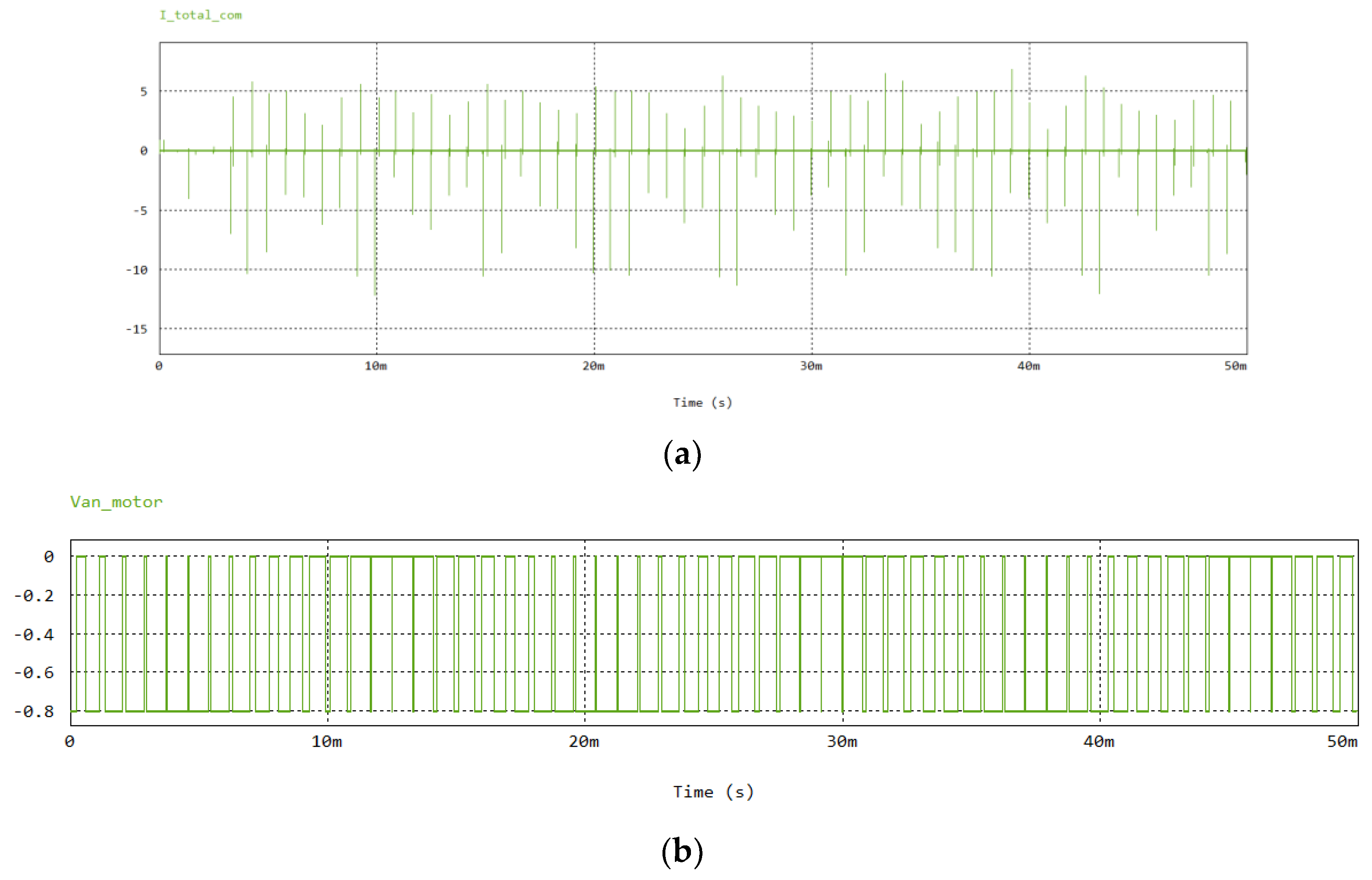
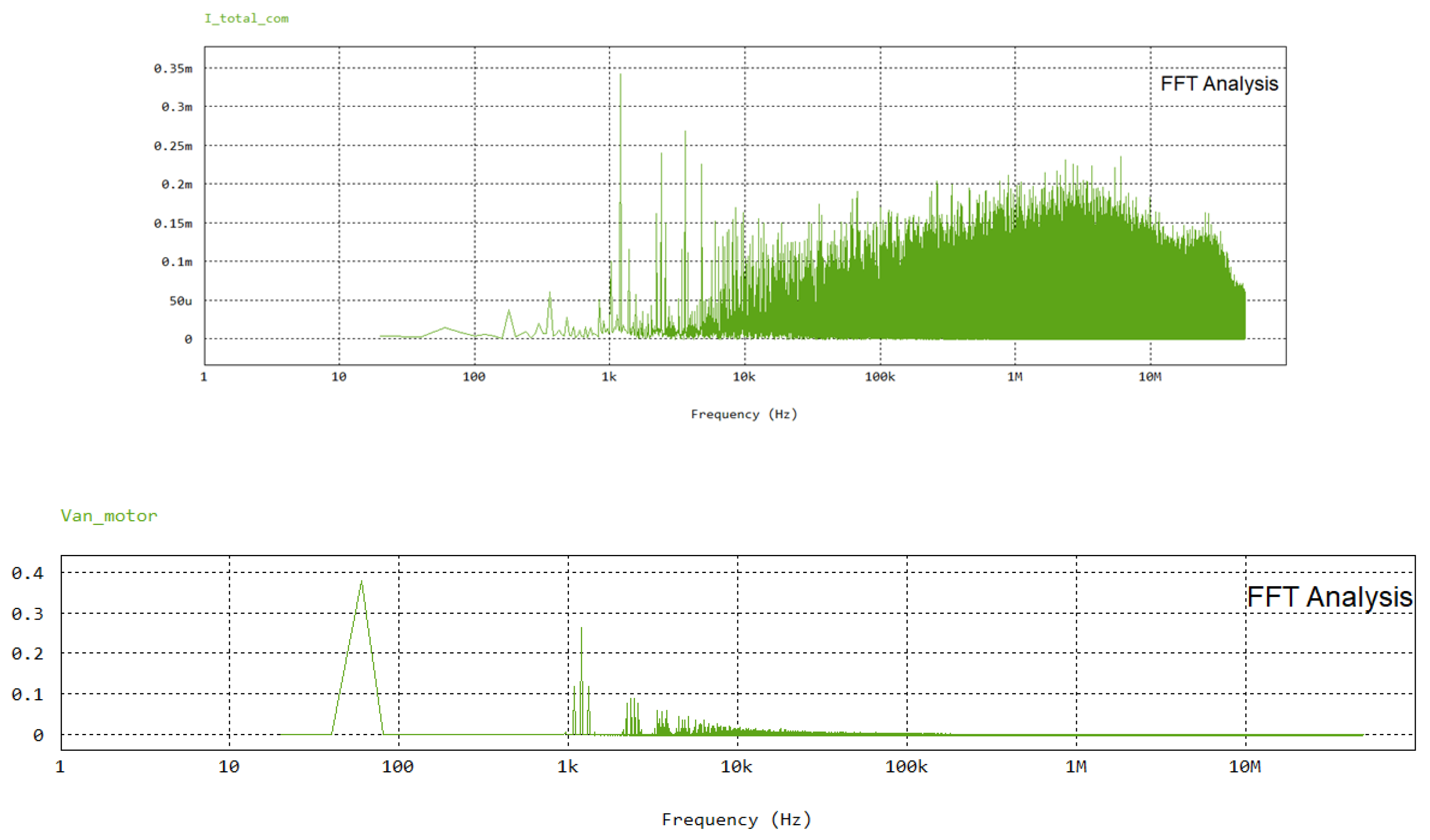
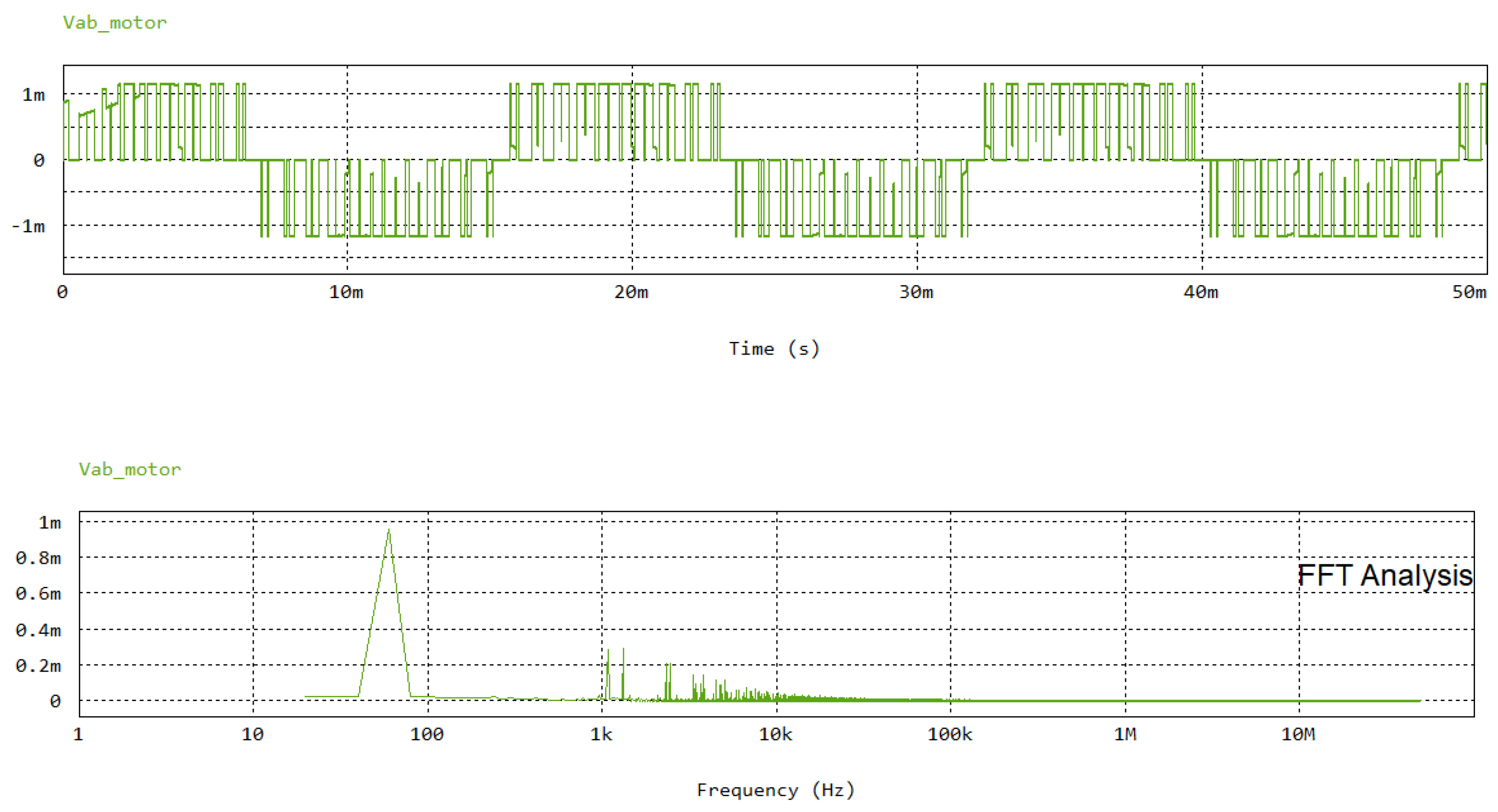
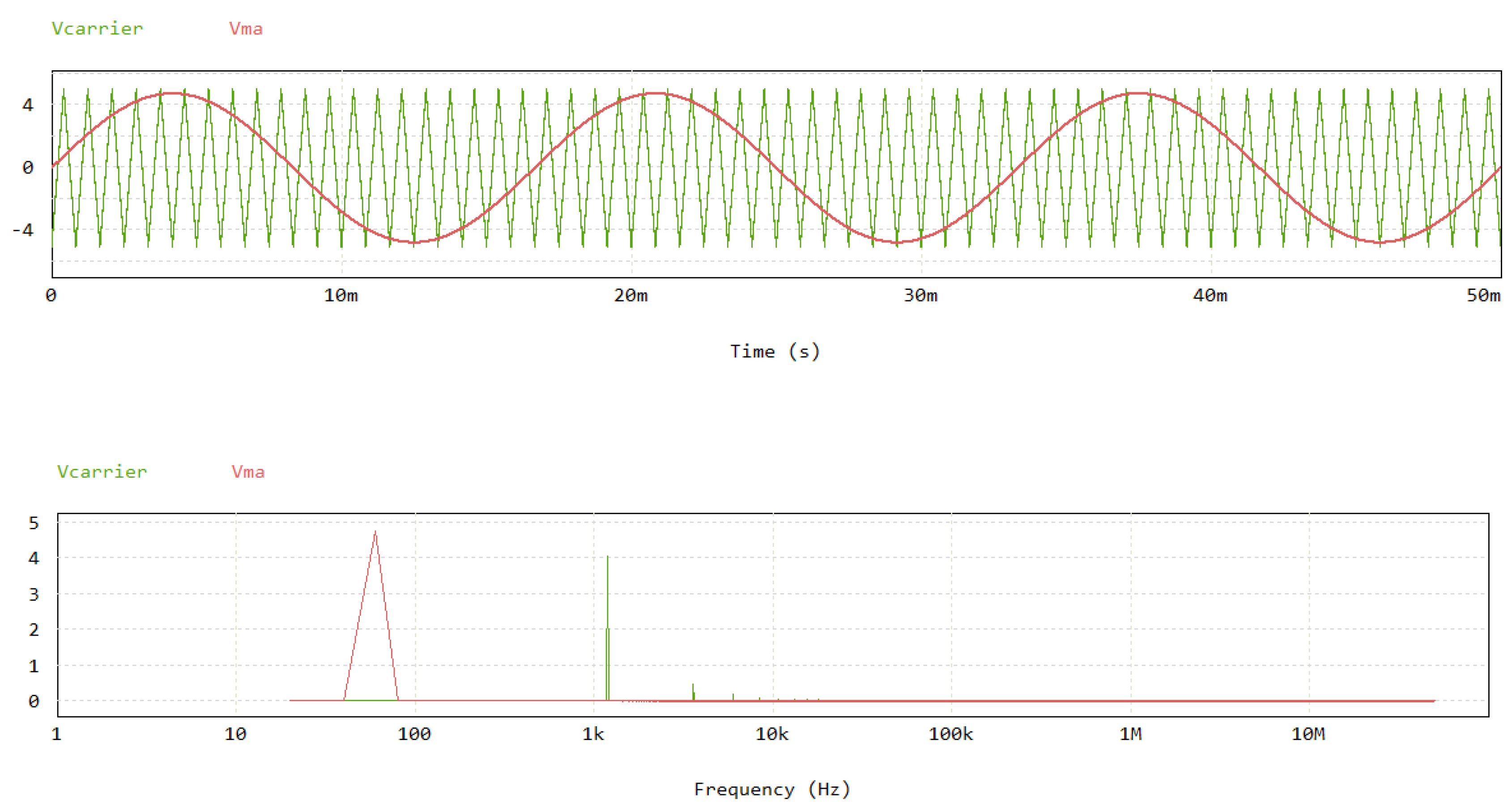
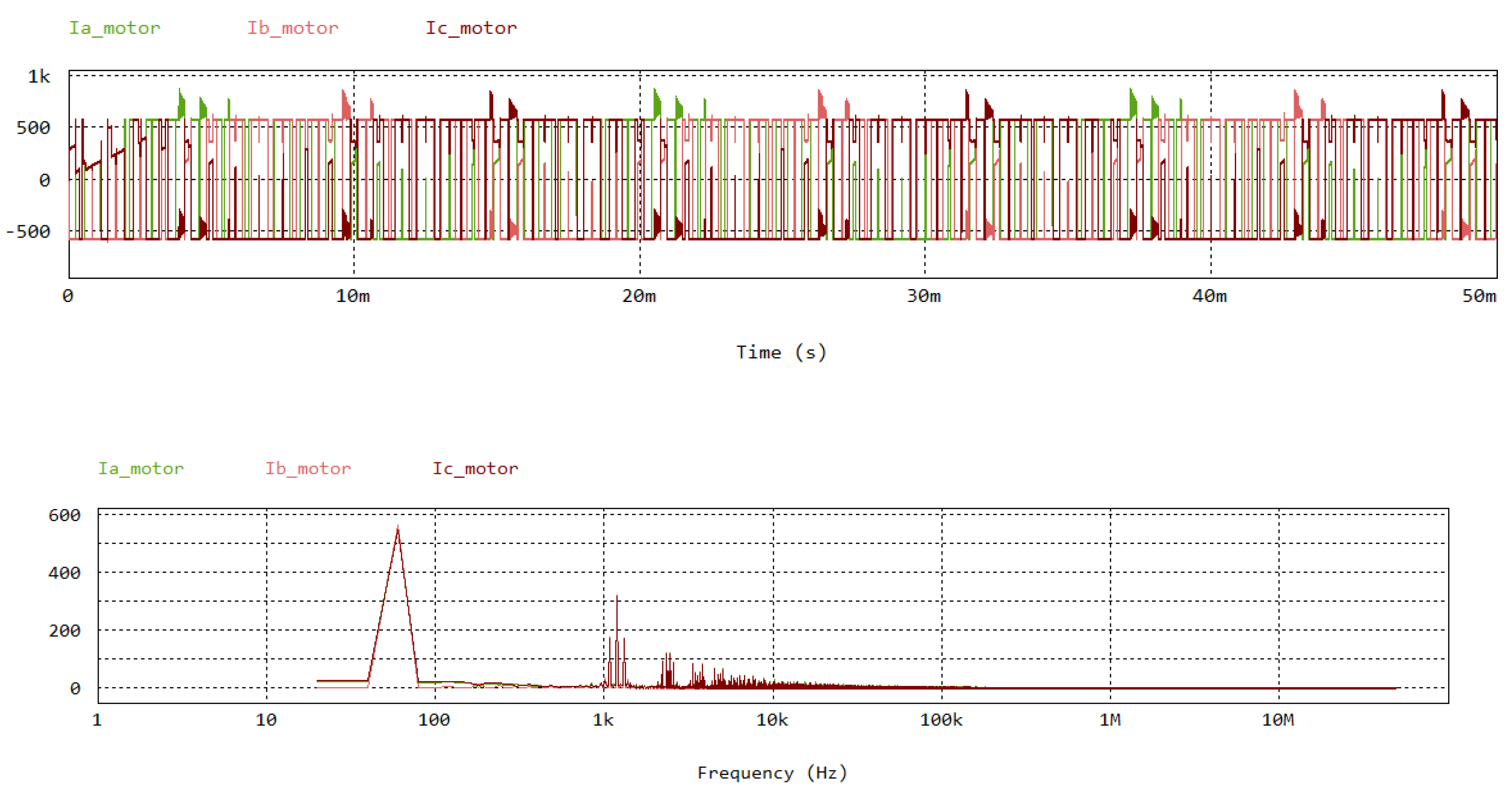
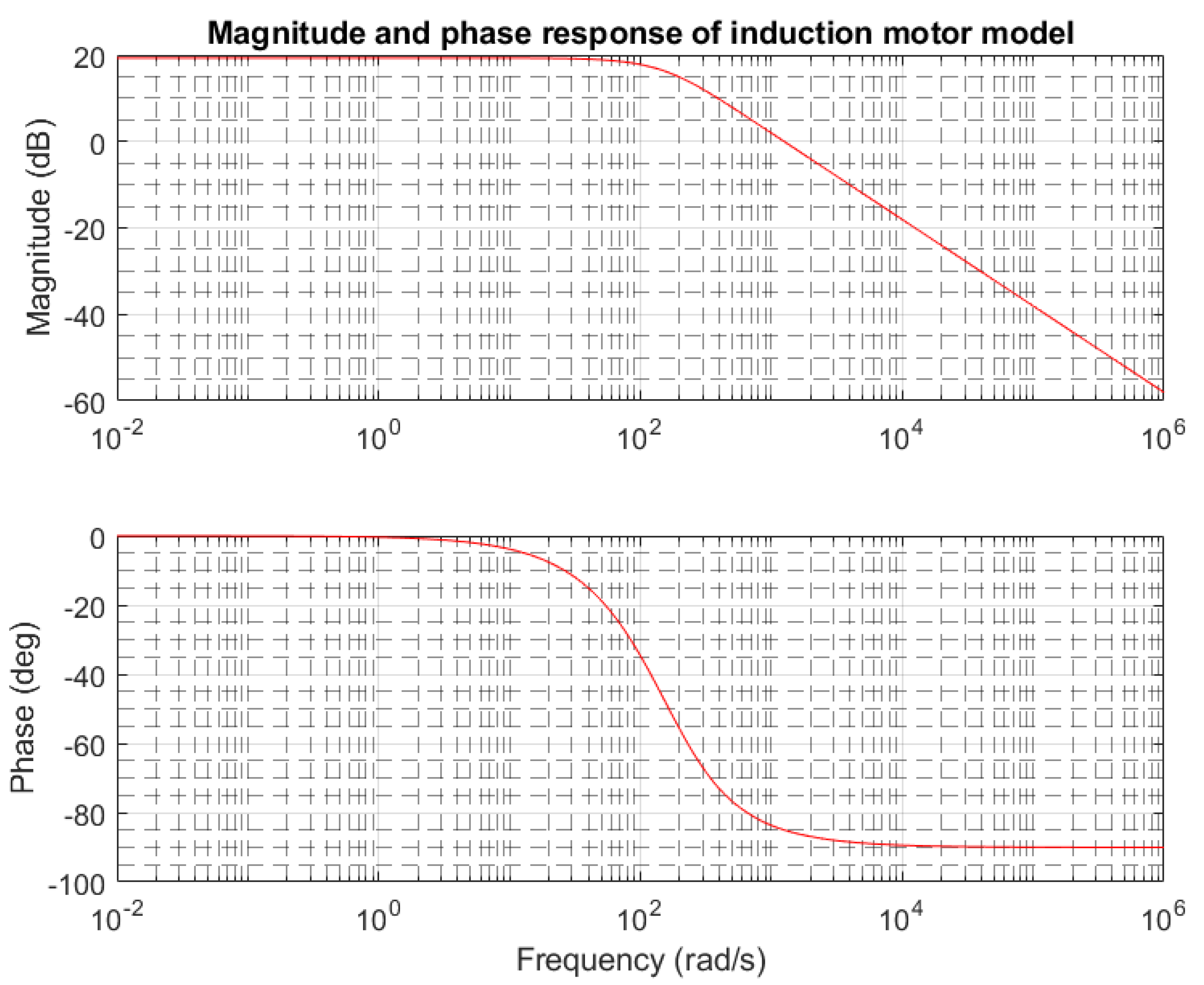
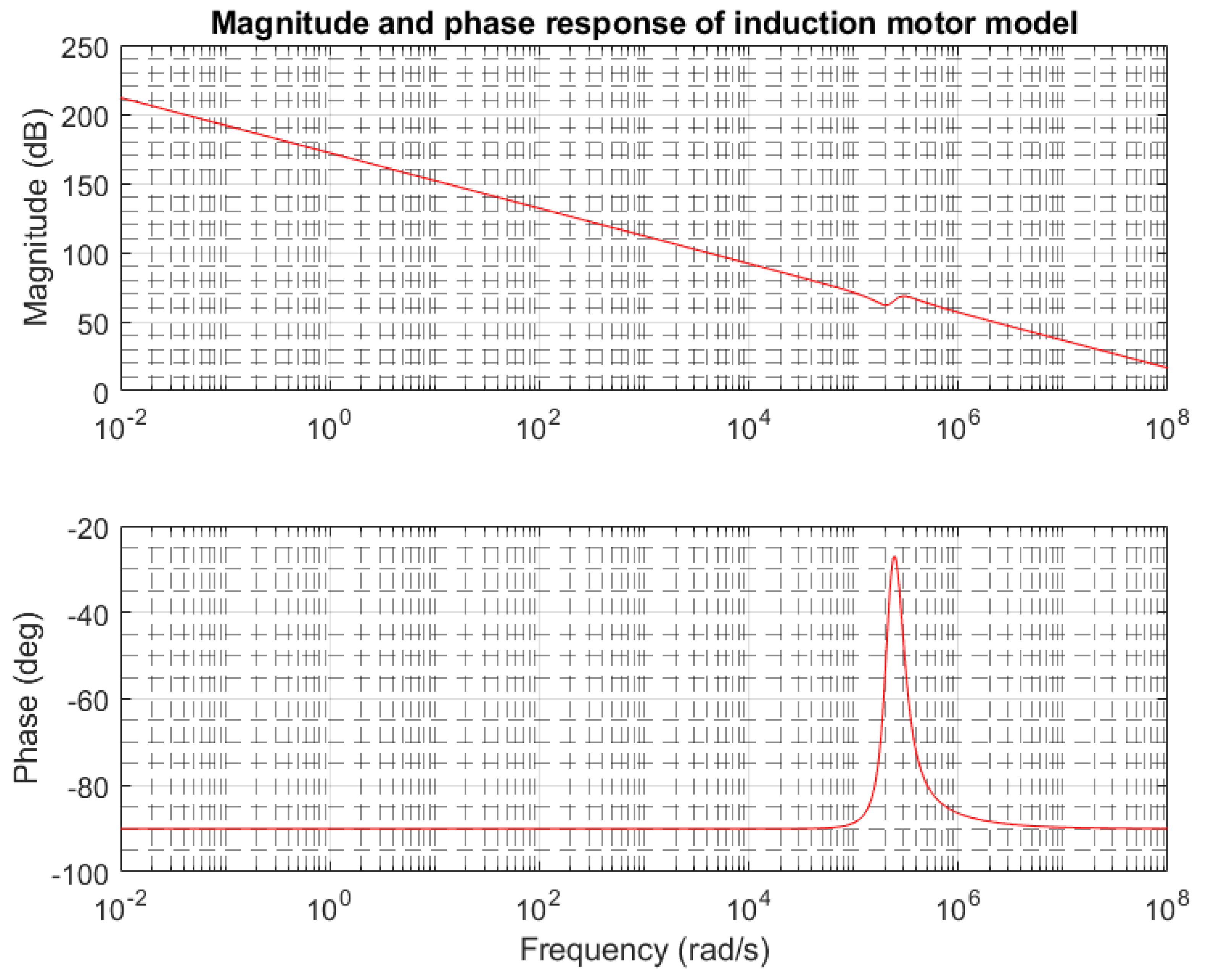
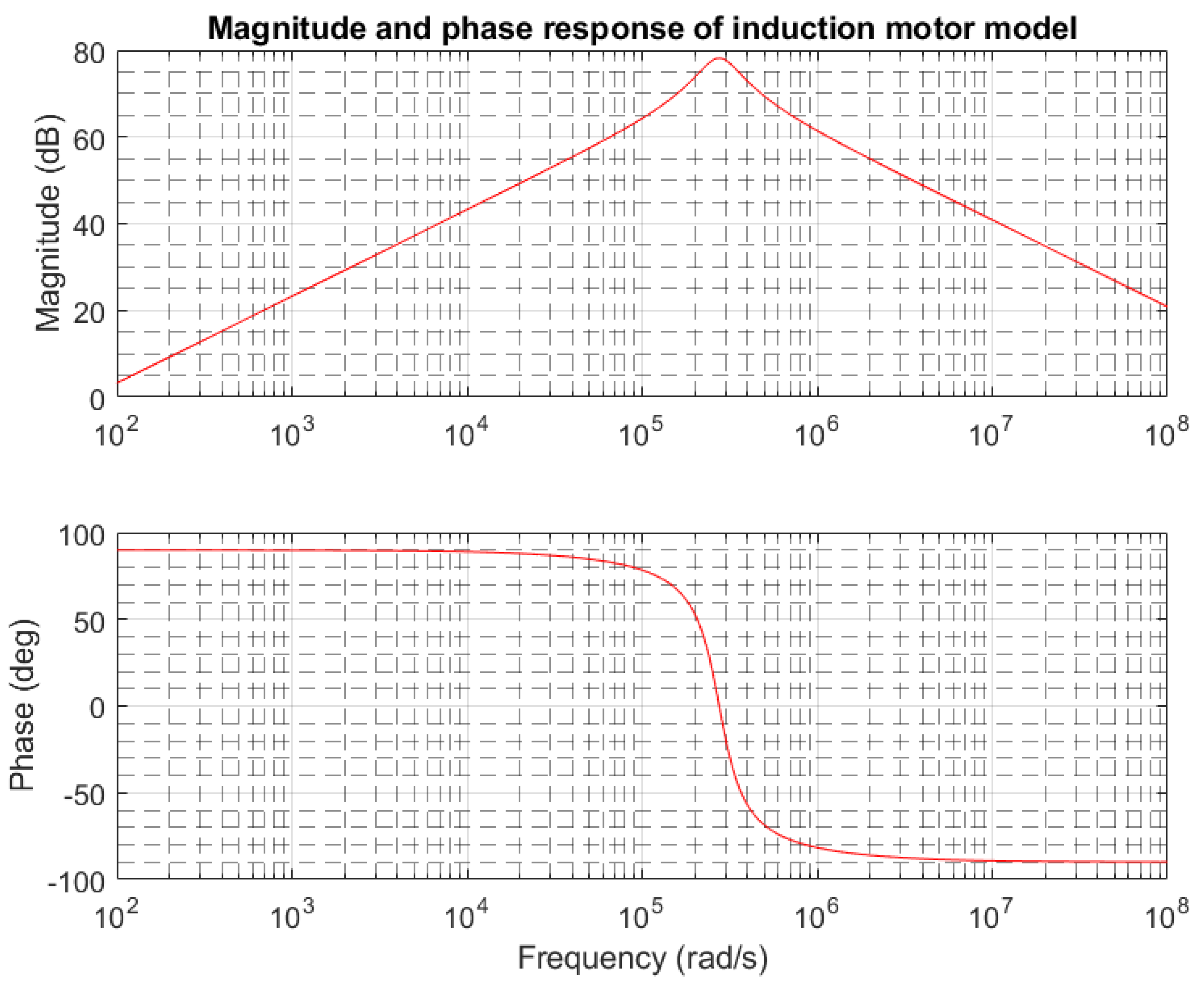
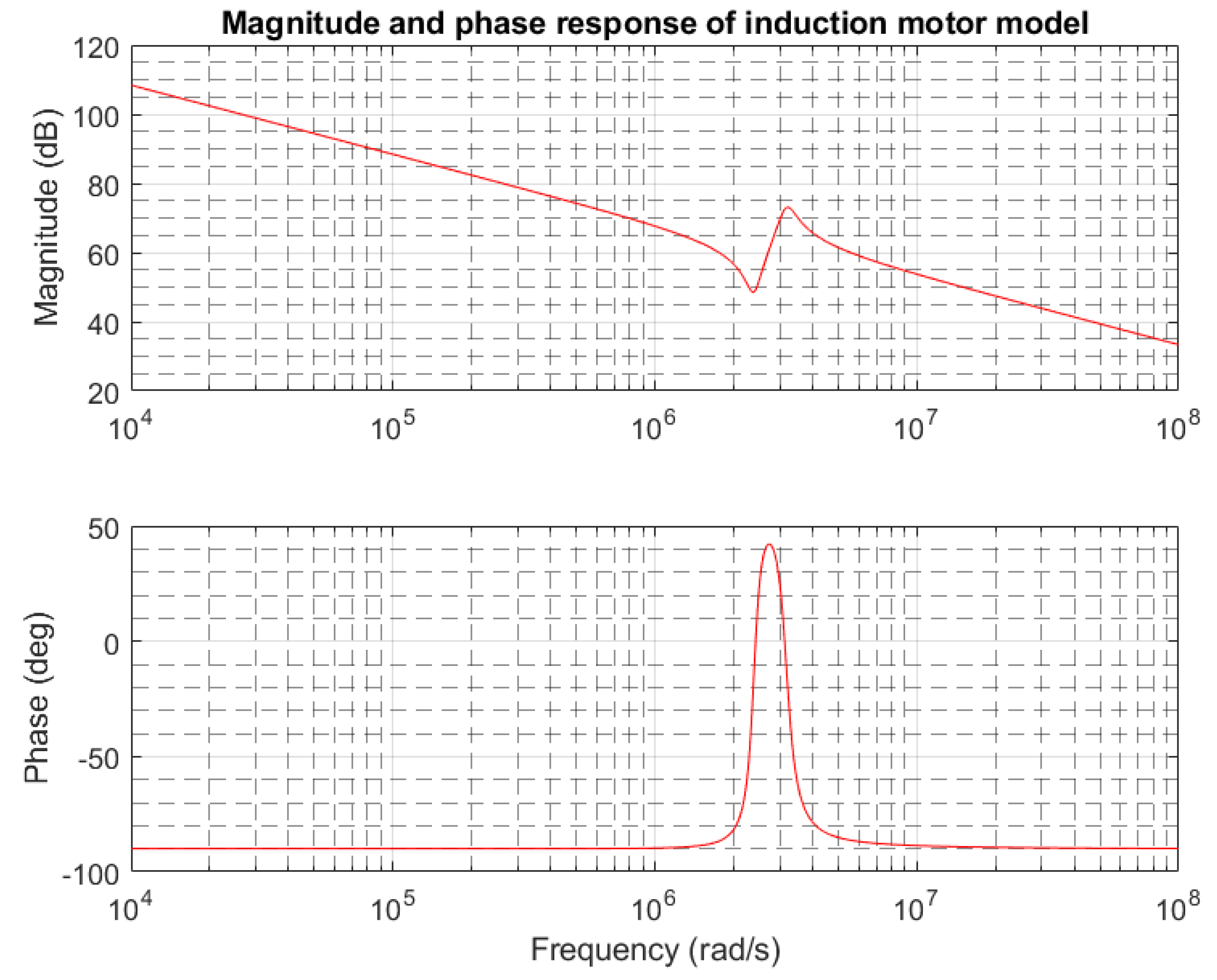
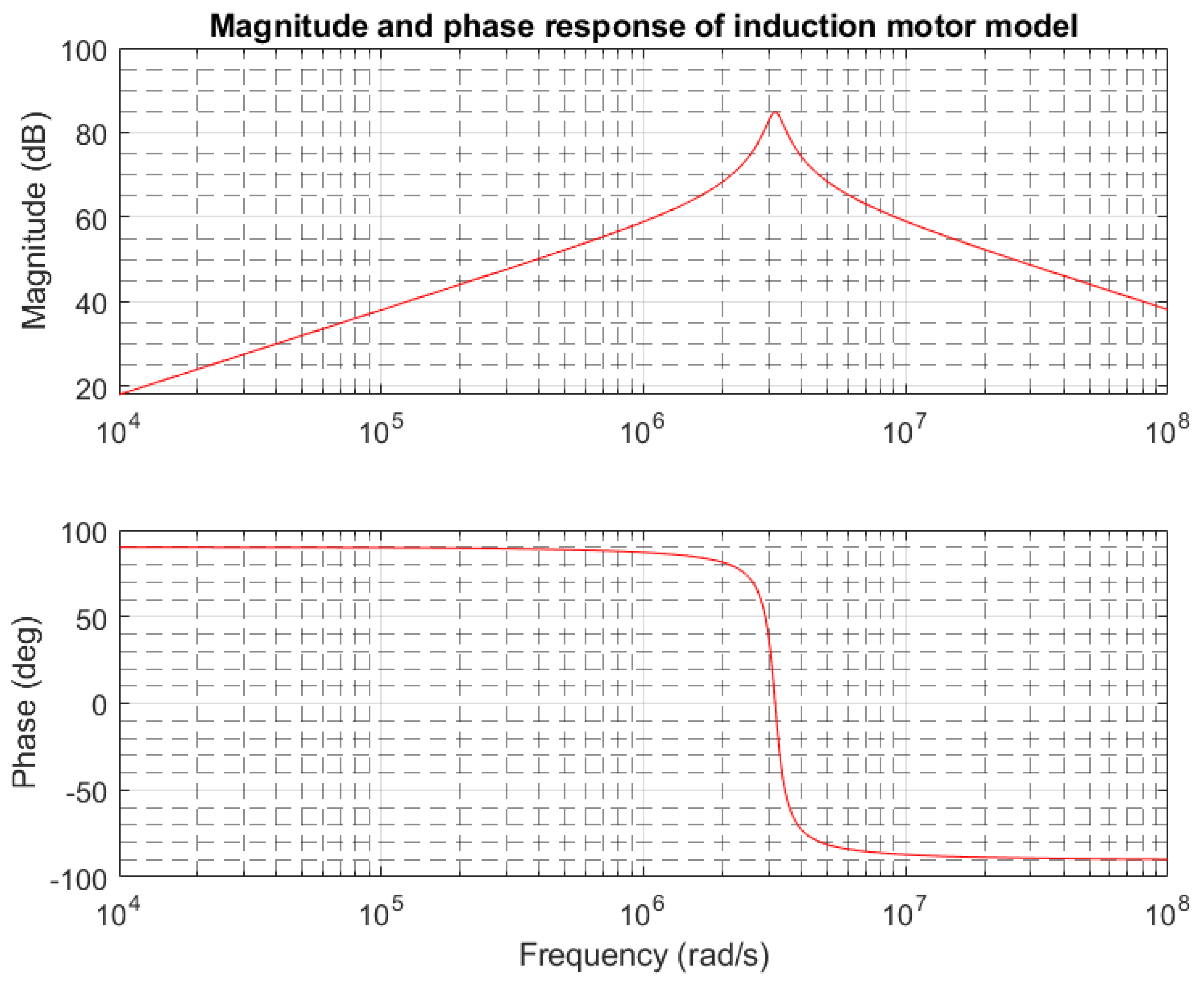
3. Results and Discussion

The simulation of high frequency induction motor drive model is implemented with stray capacitance and parasitic impedance to visualize high frequency behavior of the induction motor connected in a common mode configuration. Figure 7a shows the existence of high-frequency transients in the common-mode current due to the presence of stray capacitance and parasitic inductance connected with six IGBT switches of three phase inverter. The common-mode current is taken by adding stray capacitance currents from upper and lower switches connected as a pair to even and odd values. The current waveform is further investigated in Figure 7b by taking the Fast Fourier Transform (FFT) of common mode current signal frequency analysis till megahertz frequency. The FFT analysis interprets multiple peaks presenting high frequency components in the current signal. The log scale enables visualization of the high frequency range to highlight the model performance under EMI effects caused by high frequency components introduced in the high frequency induction motor drive model. The waveform indicates the occurrence of high frequency content in current taken from inverter switches.

Figure 8a shows the terminal voltage V_an applied at terminal A of high frequency induction motor drive. While Figure 8b presents an FFT analysis of terminal voltage (V_an). Figure 9a displays phase-phase voltage V_ab and Figure 9b is an FFT analysis of phase-phase voltage (V_ab). Figure 10a compares carrier and modulation waves to generate upper output level and lower output level signals respectively. Whereas, Figure 10b highlights the FFT analysis used to indicate the fundamental frequency and harmonic frequency of both waves. Figure 11a presents a three-phase current supplied to the induction motor drive. Figure 11b compares FFT analysis of frequency harmonics for a three-phase current supply fed by an IGBT inverter.

4. Discussion of High Frequency IM Impedance

The high-frequency 50 Hp IM model has been visualized by performing frequency domain studies by developing the MATLAB program. Figure 12 presents the frequency response of the induction motor without considering EMC compatibility specifications. The switching operation performed in power devices in the inverter is the main cause of the abrupt change in voltage of the induction motor. As a result of this voltage variation, high-frequency differential mode currents flow between the motor phases due to the emergence of parasitic capacitance, while high-frequency common mode currents flow across the motor windings and the ground by means of stray capacitance. The common mode and differential mode characteristics of induction motor high frequency models presented in Figure 2 and Figure 3 have been validated by generating magnitude and phase plots in the frequency domain. The simulation results of CM and DM magnitude and phase response of 0.3 kW IM are presented in Figure 13 and Figure 14. Table 2 presents high frequency parameters of 0.3 kW IM presented in [60] Whereas 38 kW IM magnitude and phase frequency response of CM and DM impedance characteristics are displayed in Figure 15 and Figure 16.

Figure 13 CM bode plot indicates that a pole is located at the origin and two complex conjugate poles are located at the same distance on the imaginary axis. Moreover, two complex conjugate zeros are contributing to the frequency response of impedance in equation 11. The natural frequencies f₁ and f₂ are representing zeros and poles in equations (13-14).

$$f_1={\displaystyle \frac{1}{2\pi \sqrt{L(C_p+C_g}}}$$

(13)

$$f_2={\displaystyle \frac{1}{2\pi \sqrt{L\left(C_p+\raisebox{1ex}{$C_g$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}}}$$

(14)

The parameters in Table 3 are taken from high frequency induction motor model connected in a common mode configuration with stray and parasitic components in POWERSIM. The induction motor parameters are further matched with the 38 kW IM model in Simulink MATLAB. The common mode impedance bode plots of Figure 13 and Figure 15 indicate that the reactance of capacitor C_g dominates with the rise in frequency and it decreases linearly at a rate of -20dB per decade as frequency increases concerning the logarithmic scale. Until it reaches the first resonance point where the phase angle equals -90$°$ degrees. Identical behavior is observed in Figure 13 and Figure 15 for the first resonant point f₁ occurrence at -90$°$ degrees.

The differential mode impedance bode plots in Figure 14 and Figure 16 indicate the dominance of inductive behavior with a rise of +20 dB in magnitude plot per decade till before resonant frequency point f₁, while the phase plot indicates an angle of +90$°$ degrees. At resonant frequency point f₁, the inductive reactance of the inductor (L) becomes equal to the sum of capacitive reactance (C_p + C_g). With further upsurge in frequency the capacitive reactance of $\left(C_p+{\displaystyle \raisebox{1ex}{$C_g$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)$ decays further until it becomes equal to the magnitude of the reactance of inductor (L) where second resonant frequency point f₂ occurs. At this point, the reactance of both the capacitive and inductive sides becomes equal and cancels out each other.

After the second resonance frequency point f₂ the parasitic capacitive reactance starts dominating and increases at a rate of -20 dB per decade. Whereas phase angle suddenly

reaches -90$°$ degrees due to the dominance of parasitic capacitance after an increase in frequency beyond the second resonance frequency. One zero and two poles that are complex conjugates of each other constitute the differential mode impedance. Figure 14 and Figure 16 show good resemblance in simulated magnitude and phase frequency response behavior. The common mode impedance has two separate characteristic frequencies, based on the characteristic frequency of the magnitude. The first frequency f₁, is the natural frequency of the common mode impedance Z_pg numerator that occurs at the lowest impedance in the magnitude curve. The second frequency f₂, is accomplished when the inductive and capacitive impedances in equation 14 are equal. The denominator of equation 14 specifies the differential mode resonance impedance. After crossing the second resonance frequency parasitic capacitance dominates for higher frequencies.

5. Conclusions

The study presents an equivalent per-phase mathematical model of induction motor for high frequency analysis of electrical parameters. The high frequency induction motor drive model is being analyzed for the effects of stray and parasitic by consideration of electrical parameters with FFT analysis. A correlation was found between computed models of 0.3 kW and 38 kW IM for frequency response curves. The proposed models are simulated by MATLAB program to visualize impedance characteristics beyond megahertz frequencies. The variation of common mode and differential mode impedance of IM models is quite comparable to each other. This research work provides a worthwhile visualization of EMI analysis for the design and modeling of induction motor drives at higher frequencies, in future EMI filters can be designed based on the high frequency behavior of induction motor drives.