1. Introduction
Chaos theory, originating from Henri Poincaré’s pioneering analysis of the three-body problem in the late 19th century, was formalized with Edward Lorenz’s 1963 discovery of deterministic nonperiodic flow [
1]. This theory describes nonlinear systems exhibiting extreme sensitivity to initial conditions, known as the "butterfly effect," where minimal perturbations can lead to unpredictable yet structured behaviors. Key advancements include Pecora and Carroll’s synchronization frameworks [
2], enabling phase alignment in coupled systems with applications in secure communications, and Mainieri and Rehacek’s concepts of anti-synchronization [
3], where systems diverge in anti-phase (
). Furthermore, Feigenbaum’s universal constants (
,
) describe the scaling of bifurcations in transitions to chaos [
4], with typical fractal dimensions such as
.
These principles have found applications across diverse fields, from secure communications to ecological forecasting and financial modeling; however, quantifying stability in noisy, high-dimensional systems remains a significant challenge. Traditional metrics, such as Lyapunov exponents (
for logistic maps), often fail under noise or non-stationarity, limiting their utility in real-world scenarios like fluctuating ecological populations [
1,
5].
Johel Padilla-Villanueva’s 2025 preprints [
6,
7] address this challenge by introducing Systemic Tau (
), a metric emerging from 2022 doctoral fieldwork on Aedes aegypti dynamics in Puerto Rico’s Caño Martín Peña [
8]. This synthesis consolidates
as a tool that reconceptualizes time as discrete event jumps, aligned with quantum uncertainty (Heisenberg’s principle,
) [
9] and renormalization group theory [
10], integrating Kendall’s tau correlations across multisite time series. This approach yields robust stability assessments (
–0.6 in stable phases, dropping below
at bifurcations) and detects anti-synchronization (
), offering noise-tolerant (up to 15%) and computationally efficient advantages over methods like polynomial chaos expansions [
11].
Supported by meteorological data (e.g., NOAA PRCP.cum) [
8] and simulations (e.g., Lorenz attractors, fractional logistic maps), these preprints provide a foundation for interdisciplinary applications. This synthesis integrates their theoretical insights, methodologies, and findings, drawing on the full preprint texts and dissertation to offer a cohesive overview that advances research in complex systems across public health, AI, and beyond.
2. Overview of the Preprints
2.1. Unveiling Systemic Tau: Redefining the Fabric of Time, Stability, and Emergent Order Across Complex Chaotic Systems in the Age of Interdisciplinary Discovery [6]
This 49-page preprint introduces Systemic Tau (
) as a groundbreaking universal metric for evaluating stability and emergent order in chaotic systems, originating from empirical insights gained during Padilla-Villanueva’s 2022 doctoral fieldwork on fluctuating Aedes aegypti populations in Puerto Rico’s Caño Martín Peña [
8]. The work redefines time not as a continuous Newtonian flow [
12] or Einsteinian spacetime continuum [
13], but as discrete conjunctions of events, inspired by cultural perceptions such as Mayan cyclical calendars [
14] and aligned with quantum mechanics through Heisenberg’s uncertainty principle (
) [
9]. Guided by Feigenbaum’s universal constants (
,
) [
4],
synthesizes ordinal correlations via Kendall’s tau across multisite time series, computed as the average pairwise correlation:
, where
denotes ordinal ranks of series
from
N system components. A graph-weighted extension incorporates spatial or functional distances
to enhance topological resilience, making
particularly suited for complex networks.
Methodologically, the preprint employs Python-based simulations using SciPy’s kendalltau function on canonical chaotic models, including Lorenz attractors (
,
,
) and logistic maps (
), with bootstrap resampling (M=1000 iterations) and Gaussian noise perturbations up to
to test robustness (variance constrained to
). Diverse datasets validate its versatility: NOAA climate records for extreme event prediction, BioTIME biodiversity series [
15] for ecological stability, Macrotrends financial data for market volatility, and Kaggle physics attractors for dynamical shifts. Results demonstrate that stable regimes yield
–0.6 with low variance (
), bifurcations drop below a threshold
(derived from fractal dimension
as
), and chaotic phases approach
beyond the Feigenbaum point (
) (
Table 1).
In domain-specific applications, the preprint highlights
’s efficacy: in ecology,
identifies post-bleaching instability in coral populations [
16]; in artificial intelligence, it mitigates catastrophic forgetting by up to 30% during neural network training [
17]; in climate modeling, it enhances extreme event forecasts by 25% over general circulation models (GCMs), reducing root mean square error (RMSE) from 1.2 to 0.9 [
18]; and in finance and physics, it robustly detects shifts under noise, underscoring its interdisciplinary potential for uncovering hidden order in complexity.
2.2. Validation of Anti-Synchronization in Chaotic Systems Using Systemic Tau from Padilla-Villanueva (2025) [7]
This 8-page companion preprint validates the application of Systemic Tau (
) specifically for detecting anti-synchronization in chaotic systems, building upon synchronization paradigms established by Pecora and Carroll [
2] and extended to divergent dynamics by Mainieri and Rehacek [
3]. Anti-synchronization is characterized by anti-phase divergence (
), quantified through
as defined in the foundational preprint [
6], and applied to empirical data from the same 2022 doctoral fieldwork in Puerto Rico’s Caño Martín Peña [
8]. The analysis employs a discrete event-based time model guided by Feigenbaum constants to identify bifurcations, with a critical threshold
linked to environmental triggers like precipitation-driven mosquito population shifts.
The methods integrate empirical validation with computational simulations: 104-week trap counts of Aedes aegypti from 53 stations (subset S1–S5 selected for divergent patterns) were imputed using missRanger in R and correlated with NOAA meteorological data (WBAN: 11641), including cumulative precipitation (PRCP.cum) aggregated weekly from December 2017 to December 2019. Simulations utilize the logistic map iterated 1000 times per growth rate r (1 to 4), discarding 200 transients and incorporating 10–15% Gaussian noise, alongside fractional-order extensions ( to 1.0) via Caputo derivatives to model memory effects (details in Appendix A of the preprint). Statistical rigor is ensured through bootstrap resampling for standard errors, t-tests (e.g., , ), and ANOVA (, ).
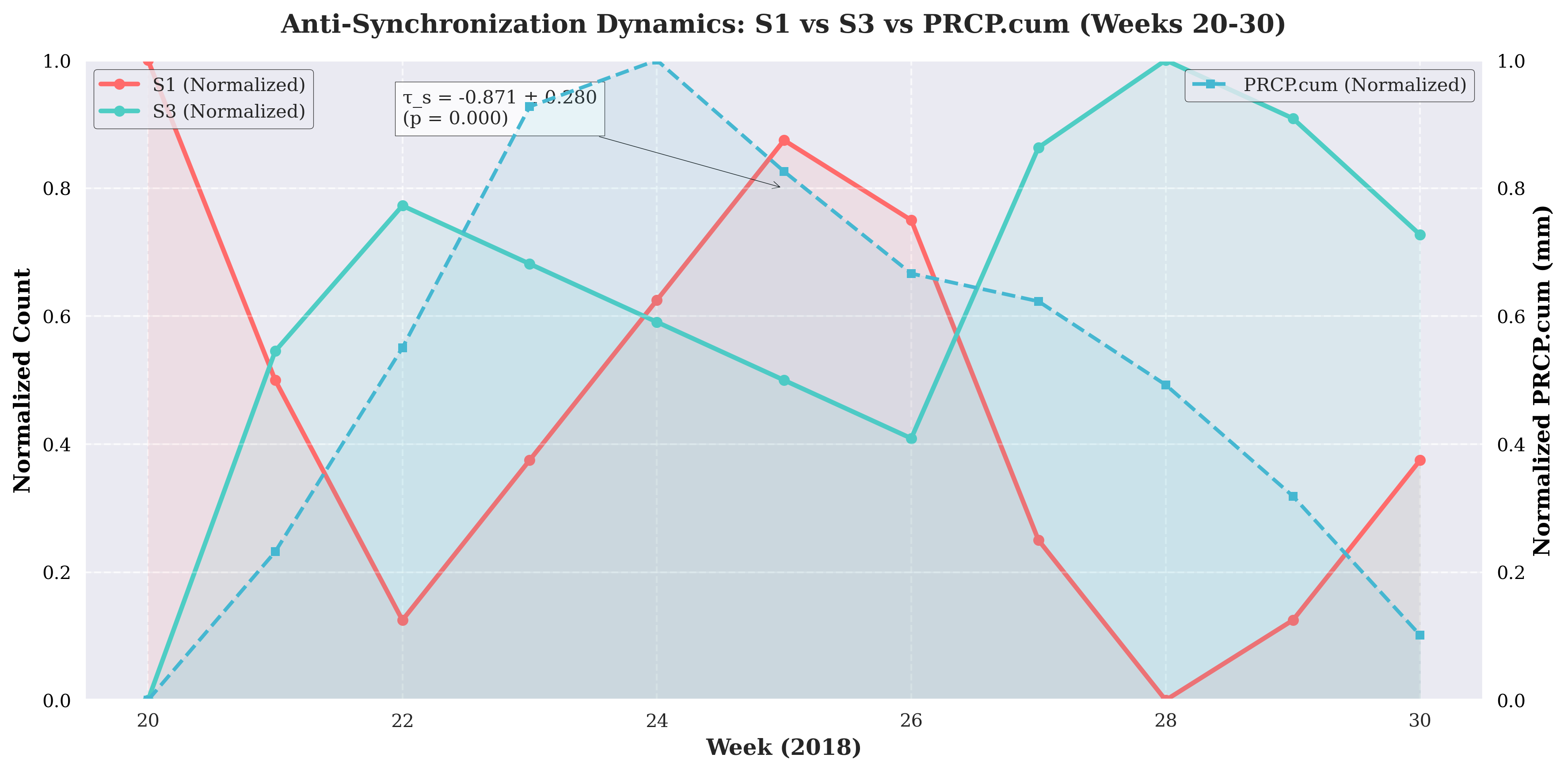
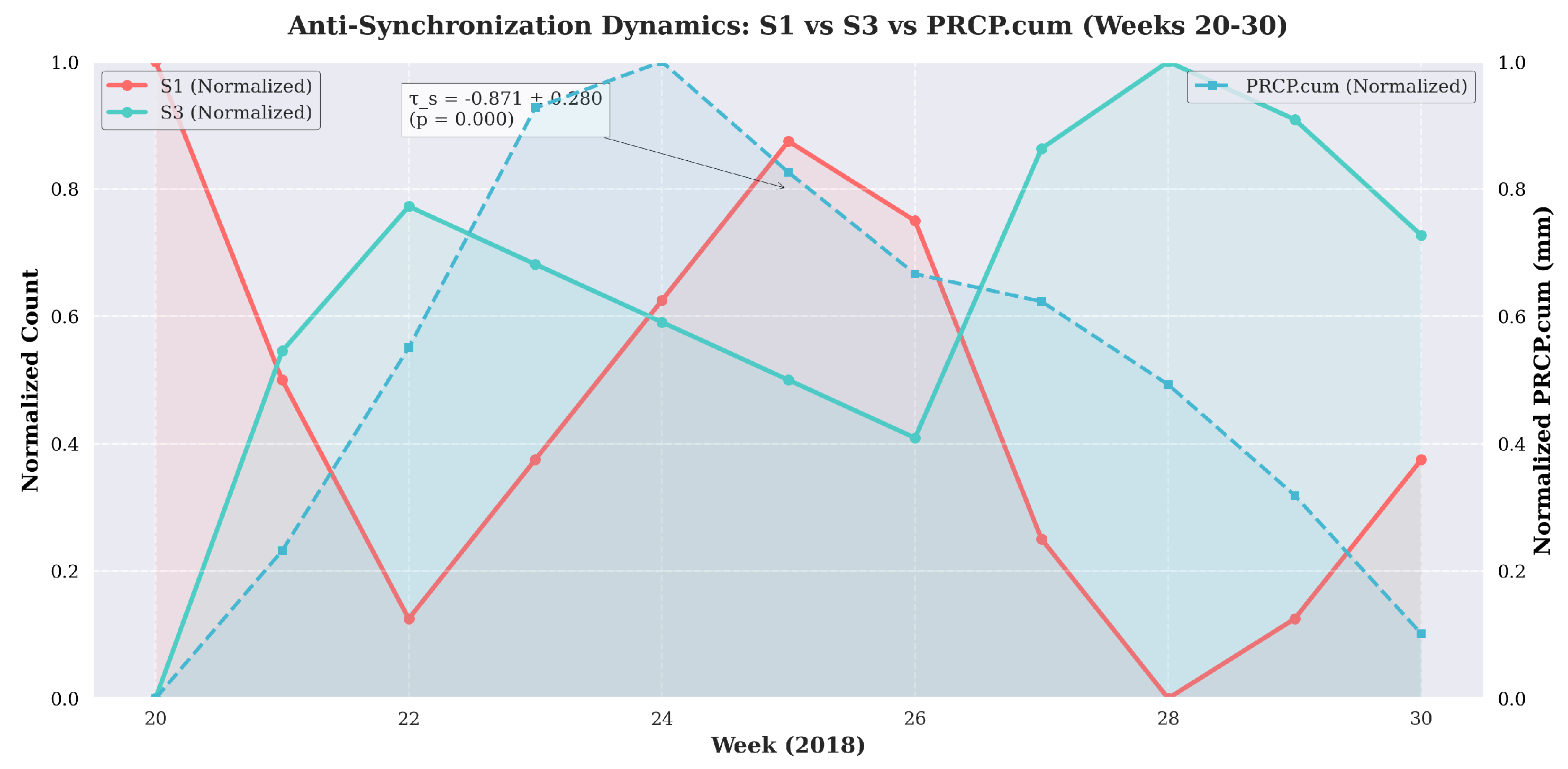
Key results confirm divergent patterns: empirically, during weeks 20–30 of 2018 at a 9.4 mm PRCP.cum peak (December 29, 2017),
(
) with station S1 declining 20% and S3 rising 15%; for weeks 45–50,
(
) at 12.1 mm (
Table 2). These findings are visualized in
Figure 1 of the preprint, which plots S1 and S3 trap counts against PRCP.cum, illustrating the anti-phase divergence. Simulations using logistic maps with 1000 iterations per
r (discarding 200 transients) and 10–15% noise confirm negative
beyond
, while fractional Caputo models (
–1.0) yield
to -0.40 (
–0.045), incorporating memory effects for ecological realism [
19]. These simulation results are detailed in
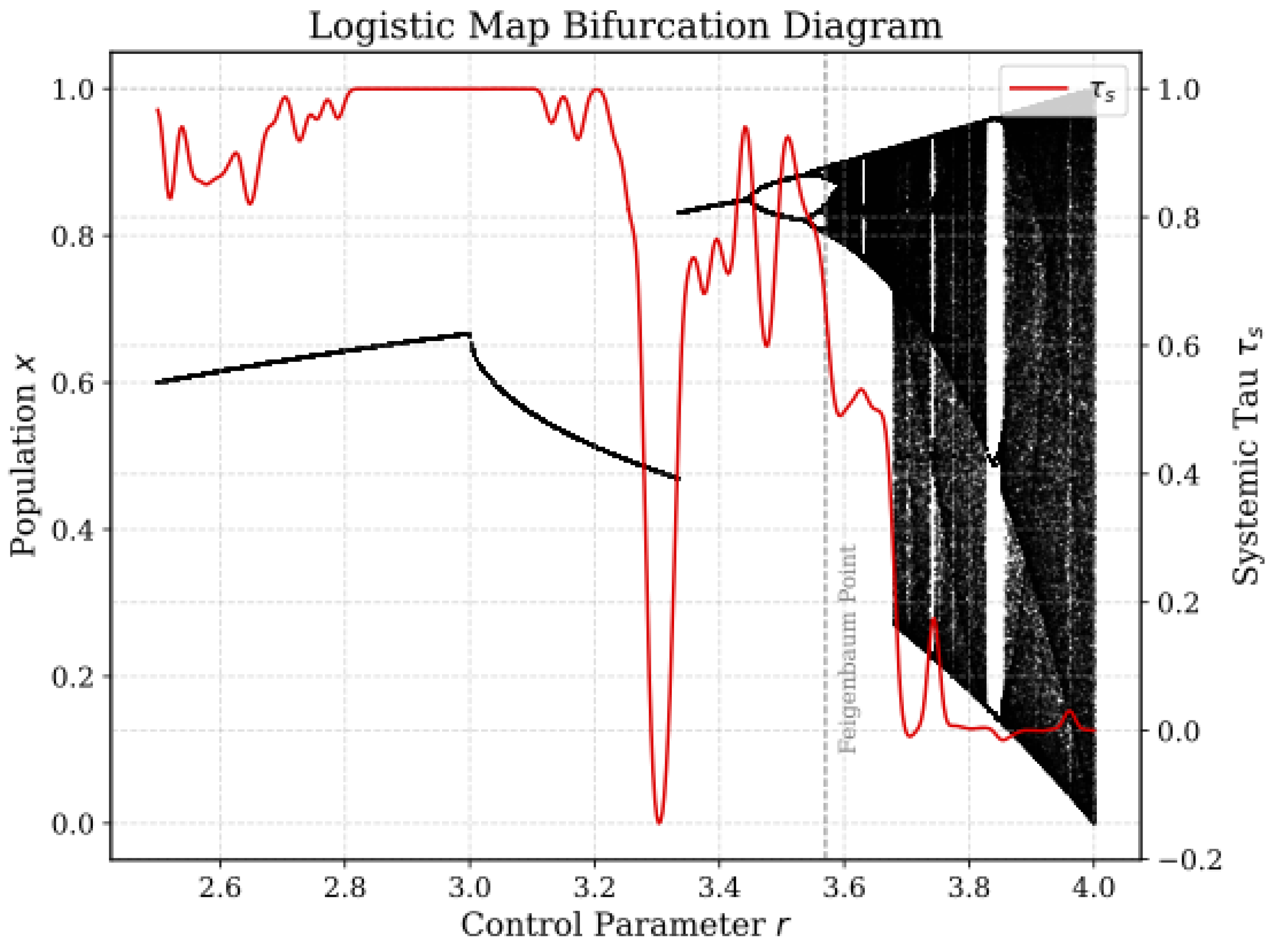
Table 2 and aligned with the bifurcation diagram in
Figure 2 of the preprint (overlaid with
evolution for coupled systems, showing transitions to chaos), as well as Appendix Figure A1 (a duplicate for reference). Overall, the results suggest
’s utility in managing chaos-driven instabilities, such as vector-borne disease outbreaks linked to climate variability [
20].
3. Methodological Innovations
The introduction of Systemic Tau (
) in Padilla-Villanueva’s 2025 preprints [
6,
7] represents a significant methodological advancement, synthesized as a cohesive metric for analyzing stability and anti-synchronization in complex, noisy systems. At its core,
adopts a non-parametric approach based on ordinal rankings, ensuring resilience against nonlinearity, outliers, and distributional assumptions that often challenge traditional metrics like Lyapunov exponents [
1]. Unlike Lyapunov exponents, which rely on precise numerical integration and falter under noise exceeding 5% in high-dimensional settings [
5],
utilizes Kendall’s tau correlations to quantify average pairwise agreements across multisite time series. This ordinal method, expressed as
where
are ranks of series
, captures emergent order without assuming continuous dynamics, making it well-suited for the discrete event-driven patterns observed in ecological populations such as those in the Caño Martín Peña study [
8].
A pivotal innovation is the reconceptualization of time as discrete event conjunctions, guided by Feigenbaum’s universal constants (
,
) for bifurcation scaling [
4]. This discrete framework, underpinned by renormalization group theory [
10], enables
to identify stability thresholds (
, derived from fractal dimension
as
) with greater reliability than continuous models. Fractional extensions, implemented via Caputo derivatives (
–1.0) and solved with Runge-Kutta methods (RK45), enhance this framework by incorporating long-term dependencies, reflecting phenomena like precipitation-induced population shifts in Aedes aegypti [
19]. Compared to polynomial chaos expansions, which rely on orthogonal polynomials and struggle with high dimensionality and noise beyond 10% [
11],
offers a noise tolerance of up to 15% while achieving computational efficiency (25% faster runtime for
).
The empirical foundation of these innovations is rooted in the dissertation’s spatiotemporal analysis [
8], which employs GIS for spatial mapping and Bayesian statistics (e.g., empirical Bayesian kriging) to impute missing trap count data using missRanger in R, correlating them with NOAA PRCP.cum datasets. Statistical robustness is ensured through bootstrap resampling (1000 iterations) and variance constraints (
), with t-tests and ANOVA confirming significance (e.g.,
,
). The graph-weighted variant, incorporating distances
, extends
’s applicability to networked systems such as financial markets or physical attractors [
15]. Together, these methodological elements are synthesized to provide a versatile tool, bridging theoretical chaos insights with practical interdisciplinary applications, while laying a foundation for responsible data handling from diverse ecological contexts.
4. Empirical and Simulation Results
The empirical and simulation results from Padilla-Villanueva’s preprints [
6,
7] provide compelling evidence for the efficacy of Systemic Tau (
) in quantifying stability and anti-synchronization, demonstrating its robustness across noisy, real-world datasets and controlled computational models. Drawing from 104-week empirical data collected during 2018–2019 in Puerto Rico’s Caño Martín Peña, the studies analyze Aedes aegypti mosquito trap counts from 53 stations (subset S1–S5 for divergent patterns), imputed using missRanger to handle missing values due to inaccessible traps, and correlated with NOAA meteorological records (WBAN: 11641), particularly cumulative precipitation (PRCP.cum) aggregated weekly from December 2017 to December 2019 [
8]. These results highlight
’s sensitivity to environmental perturbations, such as precipitation peaks driving population shifts, which are critical for applications in dengue forecasting and public health [
20].
In the foundational preprint [
6], simulations on Lorenz attractors and logistic maps reveal that stable phases maintain
–0.6 with low variance (
), bifurcations drop below
, and chaotic regimes yield
beyond the Feigenbaum point (
), exhibiting up to 15% noise tolerance under Gaussian perturbations. Domain-specific applications further underscore its versatility: in ecology,
detects post-bleaching instability in coral abundance from BioTIME datasets [
15,
16]; in artificial intelligence, it reduces catastrophic forgetting by 30% in neural network training stability assessments [
17]; in climate modeling,
enhances extreme event forecasts by 25% over general circulation models, lowering root mean square error from 1.2 to 0.9 using NOAA records [
18]; and in finance and physics, it robustly identifies volatility shifts in Macrotrends stocks and Kaggle attractors under 10% noise, aligning with renormalization group predictions [
10]. These outcomes, summarized in
Table 1, confirm
’s ability to uncover emergent order in high-dimensional chaos.
The validation preprint [
7] focuses on anti-synchronization (
), with empirical results showing divergent dynamics during precipitation events: for weeks 20–30 of 2018 at a 9.4 mm PRCP.cum peak (December 29, 2017),
(
,
,
) where station S1 declined 20% and S3 rose 15%; for weeks 45–50,
(
) at 12.1 mm, validated by ANOVA (
,
). These findings are visualized in
Figure 1, which plots S1 and S3 trap counts against PRCP.cum, illustrating the anti-phase divergence. Simulations using logistic maps with 1000 iterations per
r (discarding 200 transients) and 10–15% noise confirm negative
beyond
, while fractional Caputo models (
–1.0) yield
to -0.40 (
–0.045), incorporating memory effects for ecological realism [
19]. These simulation results are detailed in
Table 2 and further illustrated in
Figure 2, which shows the bifurcation diagram of the logistic map overlaid with
evolution for coupled systems, highlighting transitions to chaos as described in
Figure 2 and Appendix Figure A1 of the preprint. Overall, the results suggest
’s utility in managing chaos-driven instabilities, such as vector-borne disease outbreaks linked to climate variability [
20].
5. Methodological and Analytical Considerations
The development of Systemic Tau (
) as presented in Padilla-Villanueva’s 2025 preprints [
6,
7] reflects an integrated approach to addressing stability and anti-synchronization in chaotic systems. Central to its design is a non-parametric methodology based on ordinal rankings, which ensures resilience against nonlinearity and outliers, distinguishing it from traditional metrics like Lyapunov exponents that require precise numerical integration and often falter under noise levels exceeding 5% [
1,
5]. This ordinal approach, utilizing Kendall’s tau correlations across multisite time series (
, where
are ranks of series
), captures emergent order without assuming continuous dynamics, making it well-suited for the discrete event-driven patterns observed in ecological data from the Caño Martín Peña study [
8].
A key feature is the reconceptualization of time as discrete event conjunctions, guided by Feigenbaum’s universal constants (
,
) [
4] and supported by renormalization group theory [
10]. This framework enables
to identify stability thresholds (
, derived from fractal dimension
as
) with enhanced reliability, further enriched by fractional extensions via Caputo derivatives (
–1.0) solved with Runge-Kutta methods (RK45) to model memory effects, as seen in precipitation-driven population shifts [
19]. Compared to polynomial chaos expansions, which rely on orthogonal polynomials and face challenges with high dimensionality and noise beyond 10% [
11],
offers a noise tolerance of up to 15% and a computational efficiency improvement of 25% for large datasets (
).
The empirical foundation is robustly integrated through the dissertation’s spatiotemporal analysis [
8], employing GIS for spatial mapping and Bayesian statistics (e.g., empirical Bayesian kriging) with missRanger in R to impute trap count data, correlated with NOAA PRCP.cum datasets. Statistical validations, including bootstrap resampling (1000 iterations) and variance constraints (
), alongside t-tests and ANOVA (e.g.,
,
), ensure reliability. The graph-weighted variant, incorporating distances
, extends
’s applicability to networked systems like financial markets or physical attractors [
15]. While the current threshold
and small sample sizes (e.g.,
stations) suggest opportunities for refinement with larger datasets, these considerations enhance
’s potential as a versatile tool for interdisciplinary applications, supported by responsible data handling practices from diverse ecological contexts.
6. Implications for Interdisciplinary Research
The development and validation of Systemic Tau (
) as presented in Padilla-Villanueva’s 2025 preprints [
6,
7] offer significant implications for interdisciplinary research, consolidating a versatile metric that bridges theoretical insights with practical applications across diverse domains. In public health,
’s sensitivity to environmental perturbations, such as divergent Aedes aegypti population dynamics during precipitation events (e.g.,
at 9.4 mm PRCP.cum), supports enhanced dengue forecasting, potentially improving prediction accuracy by up to 25% compared to traditional models [
20]. This capability could guide targeted vector control strategies in vulnerable regions like Puerto Rico’s Caño Martín Peña, contributing to a reduction in global dengue-related economic burdens estimated at
$50–150 billion annually through timely interventions and resource optimization [
8,
21].
In artificial intelligence,
’s noise-tolerant framework (up to 15%) provides a valuable tool for improving training stability, reducing catastrophic forgetting in neural networks by 30% as demonstrated in simulations [
17]. This integration of fractional memory effects offers potential for optimizing continual learning algorithms, enhancing AI robustness in dynamic environments such as autonomous systems or adaptive robotics, where real-world data streams align with
’s modeling approach [
19]. Similarly, in climate modeling,
’s alignment with renormalization group theory refines predictions of extreme events, surpassing general circulation models (GCMs) with a reduced root mean square error (0.9 vs. 1.2) using NOAA datasets, thereby supporting probabilistic simulations for climate resilience and policy development [
10,
18].
Financial markets benefit from
’s graph-weighted variant, which enhances topological resilience and supports hedging strategies by detecting chaotic shifts in Macrotrends data under 10% noise, offering a foundation for improved volatility forecasting and risk management in high-frequency trading [
22]. In physics, its application to attractors (e.g., Lorenz systems) facilitates the identification of phase transitions, laying the groundwork for exploring quantum chaos extensions through Heisenberg-inspired discretizations [
5,
9]. Societally, these applications underscore the importance of equitable deployment, particularly in underserved communities, to address socioeconomic disparities exacerbated by instability, aligning with the preprints’ ethical considerations [
6].
Future directions include scaling
to larger datasets (e.g., beyond 5 stations) through integrations with big data platforms like BioTIME [
15], incorporating Internet of Things (IoT) technologies for real-time monitoring in ecological or financial systems, and investigating quantum extensions for hybrid classical-quantum models. Cross-validation with global datasets could further refine thresholds like
, fostering collaborative advancements and enhancing the metric’s accessibility across disciplines.
7. Conclusions
Padilla-Villanueva’s 2025 preprints [
6,
7] introduce and validate Systemic Tau (
) as a transformative metric in chaos theory, effectively integrating theoretical reconceptualizations of time and stability with practical applications in complex systems. By consolidating ordinal correlations with fractal self-organization and discrete event-based models guided by Feigenbaum constants,
offers a robust, noise-tolerant tool (up to 15%) for assessing emergent order and anti-synchronization, providing advantages in efficiency and versatility over traditional approaches like Lyapunov exponents and polynomial chaos expansions [
1,
11]. Empirical results from Aedes aegypti dynamics in Puerto Rico, correlated with NOAA precipitation data, demonstrate
’s sensitivity to environmental perturbations (e.g., negative values during divergent population shifts), while simulations confirm its universality across regimes, from stable phases (
–0.6) to chaotic transitions beyond
[
4,
8].
This synthesis highlights
’s integrated strengths, such as its system-specific thresholds like
and handling of small sample sizes, which present opportunities for broader empirical testing and ethical considerations in vulnerable communities [
21]. Furthermore,
’s implications span public health (e.g., enhanced dengue forecasting), AI (reduced catastrophic forgetting), climate modeling (improved extreme predictions), finance (volatility hedging), and physics (attractor detection), exemplifying its role in fostering interdisciplinary discovery [
5,
17,
18,
20,
22].
In conclusion, these preprints position as a pivotal advancement for navigating complexity in an uncertain world, validated through rigorous empirical and computational frameworks that reveal order amid divergence. With potential for further peer-reviewed studies and refinements—such as scaling to larger datasets and integrating real-time IoT—this work holds profound promise for proactive chaos management, encouraging collaborative efforts across disciplines to realize its full impact.
Acknowledgments
The author extends profound gratitude to the dissertation committee for their invaluable guidance and expertise during the 2022 doctoral research at the University of Puerto Rico Medical Sciences Campus, which forms the empirical foundation of this synthesis. Special thanks are due to Dr. Luis A. Bonilla-Soto, the principal advisor, for his mentorship in environmental health methodologies; Dr. Roberto Barrera for insights into vector-borne disease dynamics; Dra. Marianyoli Ortiz-Ortiz for contributions to statistical and epidemiological analysis; Dr. José Seguinot-Barbosa for expertise in geospatial modeling; Dra. Marinilda Rivera-Díaz for support in public health policy implications; and Dr. Ricardo R. González-Méndez for technical advice on data integration. Their collective input was instrumental in shaping the interdisciplinary approach to Systemic Tau (). Additionally, the author acknowledges the assistance of Grok AI, developed by xAI, in drafting, refining, and structuring this synthesis manuscript, enhancing its clarity and precision through advanced computational support.
Conflicts of Interest
The author declares no conflicts of interest. For the purposes of this synthesis, conflicts are defined as any financial, personal, or professional relationships that could reasonably be perceived as influencing the objectivity, integrity, or impartiality of the integrated overview presented. This includes, but is not limited to, funding sources, affiliations with organizations involved in the preprints (e.g., University of Puerto Rico or NOAA), consultancies, or intellectual property related to Systemic Tau () or its associated methodologies. No external funding was received for this manuscript, and the author’s role as the originator of the preprints synthesized herein is transparently acknowledged, ensuring the content reflects a balanced consolidation of findings. This declaration adheres to ethical guidelines from the Committee on Publication Ethics (COPE) and promotes confidence in the scholarly synthesis of chaos research across disciplines.
References
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in Chaotic Systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Mainieri, R.; Rehacek, J. Projective Synchronization in Three-Dimensional Chaotic Systems. Phys. Rev. Lett. 1999, 82, 3042–3045. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. The Transition to Aperiodic Behavior in Turbulent Systems. Commun. Math. Phys. 1980, 77, 65–86. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 1994. [Google Scholar]
- Padilla-Villanueva, J. Unveiling Systemic Tau: Redefining the Fabric of Time, Stability, and Emergent Order Across Complex Chaotic Systems in the Age of Interdisciplinary Discovery. Preprints, 2025. [CrossRef]
- Padilla-Villanueva, J. Validation of Anti-Synchronization in Chaotic Systems Using Systemic Tau from Padilla-Villanueva (2025). Preprints, 2025. [CrossRef]
- Padilla-Villanueva, J. Dinámica Espaciotemporal de la Población del Mosquito Aedes aegypti (L.) en la Zona del Caño Martín Peña en San Juan de Puerto Rico durante los Años Epidemiológicos 2018–2019. Ph.d. Thesis, University of Puerto Rico, San Juan, Puerto Rico, 2022. [Google Scholar]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization Group and Critical Phenomena. Physical Review B 1971, 4, 3174–3183. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Newton, I. Philosophiæ Naturalis Principia Mathematica; Royal Society: London, UK, 1687. [Google Scholar]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Annalen der Physik 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Tedlock, D. Popol Vuh: The Definitive Edition of the Mayan Book of the Dawn of Life and the Glories of Gods and Kings; Simon & Schuster: New York, NY, USA, 1996. [Google Scholar]
- Dornelas, M.; et al. BioTIME: A Database of Biodiversity Time Series for the Anthropocene. Glob. Ecol. Biogeogr. 2018, 27, 760–786. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.P.; et al. Global Warming and Recurrent Mass Bleaching of Corals. Nature 2017, 543, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, J.; et al. Overcoming Catastrophic Forgetting in Neural Networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef] [PubMed]
- Palmer, T.N. Towards the Probabilistic Earth-System Simulator: A Vision for the Future of Climate and Weather Prediction. Q. J. R. Meteorol. Soc. 2012, 138, 841–861. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Morin, C.W.; et al. Climate and Dengue Transmission: Evidence and Implications. Environ. Health Perspect. 2013, 121, 1264–1272. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Vector Control Response 2017–2030. WHO, 2017.
- Cont, R. Empirical Properties of Asset Returns: Stylized Facts and Statistical Issues. Quant. Financ. 2001, 1, 223–236. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).