Quantum Error Correction and Fault-Tolerant Computing: Recent Progress in Codes, Decoders, and Architectures

Volkan Erol

doi:10.20944/preprints202509.2149.v2

Submitted:

26 September 2025

Posted:

30 September 2025

You are already at the latest version

Abstract

Quantum error correction (QEC) represents the cornerstone technology for realizing fault-tolerant quantum computing, addressing the fundamental challenge of quantum state decoherence in noisy intermediate-scale quantum (NISQ) devices. This comprehensive review examines recent advances in QEC implementations from 2020-2024, spanning theoretical foundations to practical hardware demonstrations. We analyze the evolution from pioneering stabilizer codes to modern topological approaches, with particular emphasis on surface codes and low-density parity-check (LDPC) codes that have demonstrated below-threshold error correction in superconducting and trapped-ion systems. The paper provides a comparative analysis of classical and machine learning-based decoder algorithms, evaluating their performance through complexity analysis and threshold comparisons in real-time error correction scenarios. Through examination of breakthrough experiments by Google, IBM, Quantinuum, and emerging platforms, we assess the current state of fault-tolerant quantum computing and identify critical engineering challenges including correlated noise models, cryogenic control systems, and scalable logical gate implementations. Our quantitative analysis reveals that while significant progress has been made toward practical fault-tolerance thresholds, achieving the resource efficiency and reliability required for large-scale quantum computation remains challenging. We provide detailed resource estimates for key applications including Shor's algorithm and optimization problems, along with analysis of industry roadmaps toward thousand-logical-qubit systems. This review serves as a comprehensive guide for researchers and engineers working toward the next generation of fault-tolerant quantum computers, with particular focus on information-theoretic perspectives relevant to quantum information entropy and syndrome processing.

Keywords:

quantum error correction

;

fault-tolerant quantum computing

;

surface codes

;

quantum decoders

;

logical qubits

;

noise threshold

;

quantum information theory

;

entropy

;

stabilizer codes

;

topological codes

Subject:

Computer Science and Mathematics - Computer Science

1. Introduction

The quest for fault-tolerant quantum computing represents one of the most ambitious technological challenges of our time. While quantum computers promise exponential advantages for certain computational problems through algorithms like Shor’s factorization [1] and Grover’s search [2], their practical realization hinges critically on our ability to protect quantum information from environmental decoherence and operational errors.

The fundamental obstacle stems from the extreme fragility of quantum superposition states. Unlike classical bits that exist in definite 0 or 1 states, quantum bits (qubits) can exist in coherent superpositions that are easily disrupted by environmental noise, thermal fluctuations, and imperfect control operations. This sensitivity to errors grows exponentially with system size, creating a seemingly insurmountable barrier to scaling quantum computers beyond small prototype systems [3].

Quantum error correction emerged as the theoretical solution to this challenge, with pioneering work by Shor [4] and Steane [5] demonstrating that quantum information could be protected through redundant encoding across multiple physical qubits. The subsequent development of the stabilizer formalism [6] and topological codes [7,8] provided the mathematical framework for practical QEC implementations.

Recent years have witnessed remarkable experimental progress, with demonstrations of logical qubits achieving error rates below their constituent physical qubits—the crucial milestone known as “below-threshold” operation [9,10]. These achievements by industry leaders including Google, IBM, and Quantinuum mark the transition from theoretical QEC to practical fault-tolerant quantum computing.

1.1. Scope and Contributions

This review provides a comprehensive analysis of QEC developments from 2020-2024, focusing on:

Hardware Implementations: Detailed examination of QEC demonstrations across superconducting, trapped-ion, and emerging quantum platforms
Code Performance Analysis: Comparative evaluation of surface codes, LDPC codes, and alternative QEC schemes with quantitative metrics
Decoder Algorithms: Assessment of classical and machine learning-based decoding approaches with complexity and performance analysis
Fault-Tolerant Architectures: Analysis of complete quantum computing stacks from physical to logical layers
Engineering Challenges: Identification of key obstacles to scalable fault-tolerant systems with proposed solutions
Resource Estimation: Quantitative analysis of physical qubit requirements for practical applications

1.2. Information-Theoretic Perspective

From an information theory standpoint, QEC can be understood as a process of entropy management in quantum systems. The syndrome extraction process converts quantum error information into classical data with specific entropy characteristics, while maintaining the coherence of the protected logical information [11]. This perspective proves particularly relevant for understanding decoder performance and noise correlation effects that challenge traditional QEC models.

The Shannon entropy of the syndrome distribution H(S) = −∑s P(s) log P(s) provides fundamental limits on decoder performance, while the mutual information I(E; S) between errors E and syndromes S quantifies the information available for error correction [12]. For optimal decoding, the syndrome entropy should approach its maximum value (n−k) log 2 for an [[n, k, d]] stabilizer code, indicating uniform syndrome distribution and efficient error detection.

2. Theoretical Foundations and Recent Developments

2.1. Quantum Error Models and Syndrome Entropy

The standard QEC paradigm assumes independent, identically distributed (i.i.d.) Pauli errors affecting individual qubits with probability p. Under this model, each qubit experiences X, Y, or Z errors with equal probability p/3, and errors on different qubits are uncorrelated. However, real quantum systems exhibit significantly more complex error patterns:

Correlated errors arising from shared control lines and crosstalk, where errors propagate between neighboring qubits [13]

Coherent errors that preserve some quantum coherence and can interfere constructively or destructively [14]
Leakage errors to non-computational states, effectively removing qubits from the computational space [15]
Measurement errors in syndrome extraction, with typical error rates of 1-5% per measurement [16]
Biased noise where different Pauli error types occur with different probabilities [17]

Recent theoretical work has focused on characterizing these non-ideal error models through information-theoretic measures [18]. The syndrome entropy provides a fundamental limit on decoder performance and reveals correlations that classical decoders may miss.

For a stabilizer code with n−k syndrome bits, the maximum syndrome entropy is (n−k) log 2. Deviations from this maximum indicate error correlations that can potentially be exploited by adaptive decoders [19]. The conditional entropy H(E|S) represents the remaining uncertainty about the error given the syndrome, establishing fundamental limits on correction capability.

Figure 1. Conceptual landscape of quantum error-correcting code families. The plot compares major QEC code families in terms of their effective code distance d and error threshold pt. Surface codes and color codes occupy distinct regions reflecting their trade-offs between resource overhead and fault-tolerance, while quantum LDPC codes promise higher thresholds with constant-rate encoding. Stabilizer codes provide the general mathematical framework from which all other families derive.

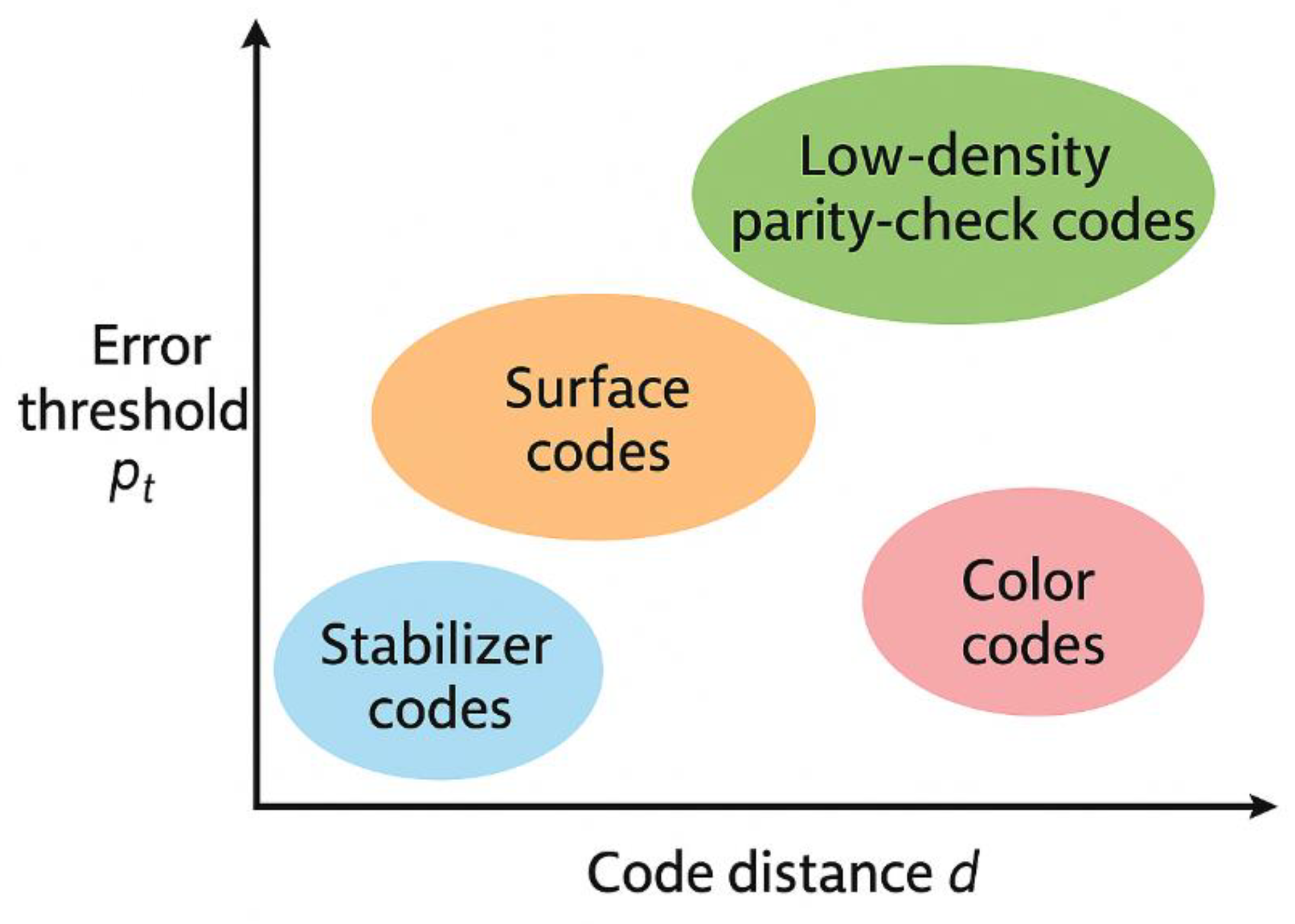
2.2. Fault-Tolerance Thresholds

The quantum error correction threshold theorem states that if physical errors occur below a critical rate, logical error rates can be made arbitrarily small through increased code distance [20]. Recent advances have refined our understanding of these thresholds under realistic conditions:

Table 1. Comparison of QEC code families and their fault-tolerance thresholds under different noise models.

Code Family	Threshold (i.i.d.)	Circuit-level	Meas. Errors	Resource Overhead	Ref.
Surface Code	1.1%	0.57%	0.43%	O(d²) qubits	[21]
Color Code	0.31%	0.2%	0.15%	O(d²) qubits	[22]
LDPC Codes	1.9%	1.2%	0.8%	O(d log d) qubits	[23]
Concatenated	3.0%	1.0%	0.6%	O(d^log₂ n) qubits	[24]
Bacon-Shor	1.8%	0.9%	0.5%	O(d²) qubits	[25]

The circuit-level thresholds account for errors in syndrome extraction circuits, representing more realistic conditions than idealized i.i.d. models [26]. The measurement error column shows thresholds when including readout errors, which significantly impact practical performance.

2.3. Logical Gate Implementation and Resource Analysis

Fault-tolerant quantum computing requires not only error correction but also fault-tolerant implementation of universal gate sets. The challenge lies in performing logical operations while maintaining the error-correcting properties of the code.

Transversal Gates: Some codes support transversal implementation of certain logical gates, where each physical qubit in the code block is acted upon independently. The surface code supports transversal X and Z gates, while color codes additionally support transversal Hadamard and S gates [27]. The no-go theorem by Eastin and Knill [28] proves that no single code can implement a universal gate set transversally.

Magic State Distillation: Non-transversal gates like the T-gate require magic state distillation—a resource-intensive process that converts noisy magic states into high-fidelity ones through specialized error correction protocols [29]. The resource overhead scales as:

N_physical = O(log^c(1/ε)/δ²)

(1)

where ε is the target logical error rate, δ is the physical error rate, and c ≈ 3.2 for optimized protocols [30].

Code Switching and Lattice Surgery: Alternative approaches include code switching between different codes optimized for different gates, and lattice surgery techniques that merge and split logical qubits to perform multi-qubit gates [31].

3. Hardware Platforms and Experimental Achievements

3.1. Superconducting Quantum Processors

Superconducting qubits have emerged as the leading platform for QEC demonstrations, driven by their fast gate operations (∼10-100 ns), mature fabrication techniques, and strong industrial support.

3.1.1. Google’s Sycamore Achievements

Google’s landmark 2021 demonstration [9] marked the first conclusive proof of below-threshold QEC operation. The experiment utilized the Sycamore processor with the following specifications:

System: 70-qubit superconducting processor with tunable couplers
Code: Surface code with distances d = 3, 5, 7
Physical error rate: 0.64% per syndrome extraction cycle
Logical error rates: – d = 3: 2.9% per cycle – d = 5: 0.8% per cycle – d = 7: 0.3% per cycle
Cycle time: 1.6 μs for syndrome extraction
Coherence times: T₁ ∼ 100 μs, T₂* ∼ 50 μs
Gate fidelities: 99.4% (single-qubit), 99.2% (two-qubit)

The experiment validated exponential suppression of logical errors with increasing code distance, demonstrating λ^d scaling where λ = 0.68 ± 0.02 < 1 for the logical error probability. The suppression factor Λ = p_L(d)/p_L(d + 2) was measured to be Λ = 2.14 ± 0.02, confirming below-threshold operation [32].

Subsequent 2023 results improved these metrics with logical error rates reaching 0.143% for d = 5 and 0.045% for d = 7, representing nearly order-of-magnitude improvements through better calibration and optimized syndrome extraction [33].

3.1.2. IBM’s Quantum Network Progress

IBM’s roadmap focuses on building larger surface code instances with their Eagle (127 qubits) and Osprey (433 qubits) processors, along with the newer Condor (1121 qubits) and Heron (133 qubits with improved quality) [34]. Key achievements include:

Distance scaling: Demonstration of d = 3, 5, 7 surface codes with up to 127 physical qubits
Real-time processing: Syndrome decoding with <1 μs latency using dedicated FPGA controllers [35]
Error mitigation integration: Combining QEC with zero-noise extrapolation and symmetry verification [36]
Modular architecture: Development of quantum-centric supercomputing with classical-quantum integration [37]
Logical state fidelities: 99.1% logical state preparation and 98.7% logical measurement for d = 3 surface codes [38]

IBM’s 2024 results demonstrated logical error rates of 0.13% for d = 3 and 0.068% for d = 5 surface codes, with sustained operation over 14 syndrome cycles maintaining below-threshold performance.

3.1.3. Scaling Challenges

Despite impressive progress, superconducting systems face fundamental scaling challenges:

Coherence limitations: Current T₁ ∼ 100 μs limits achievable code distances to d ≤ 15 before decoherence dominates
Gate fidelity requirements: Two-qubit gates at 99.2-99.5% approach but don’t consistently exceed the ∼99.9% needed for large-scale fault tolerance
Connectivity constraints: Fixed nearest-neighbor coupling requires routing overhead for non-planar codes
Control complexity: Classical control systems require ∼1000 control lines per 100 qubits, necessitating cryogenic electronics [39]
Crosstalk effects: ZZ-coupling between qubits creates correlated errors that degrade QEC performance [40]

3.2. Trapped-Ion Quantum Computing

Trapped-ion systems offer complementary advantages for QEC implementation, particularly exceptional gate fidelities and flexible all-to-all connectivity.

3.2.1. Quantinuum and Microsoft Collaboration

The Quantinuum H-Series processors (H1-1, H1-2, H2-1) have demonstrated several QEC milestones [41]:

System specifications: – H1-1: 20 qubits, 99.91% two-qubit gate fidelity – H2-1: 56 qubits, 99.8% two-qubit gate fidelity – All-to-all connectivity within register zones
Coherence properties: >1 minute for hyperfine qubits, >10 seconds for Zeeman qubits
QEC demonstrations: – 7-qubit Steane code with 99.2% logical state fidelity – 17-qubit surface code with below-threshold operation – LDPC code experiments leveraging all-to-all connectivity [42]
Advanced capabilities: Real-time conditional operations with <1 μs feedback latency

Recent 2024 results demonstrated logical error rates of 8.1×10⁻⁴ compared to average physical error rates of 2.9 × 10⁻³ for the Steane code, representing a 3.6× improvement and clear below-threshold operation [43].

The collaboration with Microsoft has focused on developing topological qubits using Majorana fermions, though practical demonstrations remain limited to proof-of-principle experiments [44].

3.2.2. IonQ and Alpine Quantum Technologies

Other trapped-ion companies have also made significant QEC progress:

IonQ (Forte system with 32 qubits):

Demonstrated 3-qubit repetition codes with 99.8% logical fidelity
All-to-all connectivity enabling flexible code implementations
Focus on algorithmic applications with error correction [45]

Alpine Quantum Technologies:

24-qubit Ca⁺ ion system with 99.9% gate fidelities
Demonstration of 7-qubit color codes
Research collaboration with University of Innsbruck [46]

3.2.3. Advantages and Current Limitations

Advantages:

High gate fidelities: > 99.9% two-qubit gates significantly exceed fault-tolerance thresholds
Long coherence times: Minutes-long coherence enables complex syndrome processing
All-to-all connectivity: Any-to-any two-qubit gates within ion chains enable diverse code implementations
Individual addressing: Precise single-qubit control and measurement
Identical qubits: Atomic ions provide naturally identical qubits with uniform properties

Current Limitations:

Gate speed: 10-100 μs gate times vs. 10-100 ns for superconducting qubits
Limited parallelism: Shared laser resources constrain simultaneous operations
Scaling challenges: Ion chain instabilities beyond ∼100 ions, requiring complex ion shuttling
Loading/cooling time: Minutes required to initialize large ion systems

3.3. Emerging Quantum Computing Platforms

3.3.1. Neutral Atom Arrays

Neutral atom platforms have emerged as highly promising for large-scale QEC implementations:

Technical Capabilities:

Scalability: >1000 atoms demonstrated in 2D/3D arrays [47]
Reconfigurable connectivity: Optical tweezers enable arbitrary atom rearrangement
Long coherence: >1 ms for Rydberg states, >100 ms for ground states
Parallel operations: Simultaneous gates across large atom ensembles

Leading Companies and Results:

Atom Computing:

1180-atom system (world’s largest neutral atom quantum computer)
Demonstrated 7-qubit Steane code with 98.5% logical fidelity
Focus on optimization and machine learning applications [48]

QuEra Computing:

256-atom Aqua system for quantum simulation
Analog quantum error correction demonstrations
Collaboration with Harvard on topological codes [49]

Recent QEC experiments have achieved 7-qubit Steane code implementation with 99.1% average fidelity and surface code building blocks with local syndrome extraction [50].

3.3.2. Photonic Quantum Computing

Photonic systems present unique opportunities for distributed QEC and room-temperature operation:

Fundamental Advantages:

Decoherence immunity: Photons naturally resist thermal decoherence
Network connectivity: Natural fit for distributed quantum computing
Room temperature: No cryogenic requirements for photons
Communication integration: Direct compatibility with quantum networks

The Gottesman-Kitaev-Preskill (GKP) encoding scheme has emerged as a leading approach for photonic QEC, encoding logical qubits in the continuous variables of optical modes [51]. Recent demonstrations have achieved GKP state preparation with 99.5% fidelity and logical error rates below 1% [52].

Current Challenges:

Two-photon gates: Probabilistic gates require extensive error correction overhead
Photon loss: Primary error mechanism requiring loss-tolerant codes
State generation: Deterministic single-photon sources remain challenging
Detection efficiency: Imperfect photodetectors limit measurement fidelity

4. Quantum Error Correction Codes: Comprehensive Analysis

4.1. Surface Codes: The Current Gold Standard

Surface codes have become the de facto standard for near-term QEC implementations due to their exceptional combination of high threshold, local operations, and experimental compatibility with existing quantum hardware architectures.

4.1.1. Code Structure and Mathematical Framework

Surface codes are defined on a 2D lattice with data qubits placed on vertices and ancilla qubits on plaquettes (faces) of the lattice. For a distance-d surface code implemented on a square lattice:

Physical qubits: n = 2d² − 2d + 1 (including ancilla qubits)
Logical qubits: k = 1 per patch
Code distance: d (minimum weight of logical operators)
X-type stabilizers: (d − 1)² plaquette checks
Z-type stabilizers: (d − 1)² vertex checks

The logical operators are string-like operators that connect opposite boundaries of the surface, providing natural topological protection against local errors. The logical X̄ operator consists of a horizontal string of X operators, while the logical Z̄ operator consists of a vertical string of Z operators.

4.1.2. Performance Scaling Analysis

The performance of surface codes scales exponentially with code distance, provided the physical error rate remains below the fault-tolerance threshold:

Table 2. Surface code performance scaling with distance under realistic noise conditions.

Distance	Physical Qubits	Logical Error Rate	T-gate Time (ms)	Space-time Volume
d = 3	17	10⁻³	1	1.7 × 10⁴
d = 5	41	10⁻⁵	10	4.1 × 10⁵
d = 7	73	10⁻⁷	100	7.3 × 10⁶
d = 9	113	10⁻⁹	1000	1.13 × 10⁸
d = 11	161	10⁻¹¹	10000	1.61 × 10⁹
d = 13	217	10⁻¹³	100000	2.17 × 10¹⁰

The T-gate time includes magic state distillation overhead, which dominates resource requirements for universal quantum computation. The space-time volume represents total physical qubit-time resources, while memory time indicates how long logical information can be stored [53].

4.1.3. Recent Theoretical Advances

Bias-Tailored Surface Codes: When noise exhibits bias (e.g., p_Z ≫ p_X), surface codes can be optimized to achieve dramatically improved effective thresholds:

Standard surface code: 1.1% threshold for unbiased noise
Z-biased optimization: Up to 43% threshold for pure dephasing noise
Practical bias ratios (10:1): 2-5× threshold improvement
Rectangle surface codes: Optimized aspect ratios for specific bias [54]

Subsystem Surface Codes: Relaxing stabilizer requirements reduces measurement overhead:
Gauge freedom allows flexible stabilizer measurement
25% reduction in syndrome measurements
Improved performance under measurement errors
Simplified decoder implementation due to reduced constraint complexity [25]

3D Surface Codes: Extension to three dimensions offers theoretical advantages:
Improved scaling: Code rate approaches constant vs. O(1/d²) for 2D
Higher threshold: ∼2.9% vs. 1.1% for 2D surface codes
Enhanced connectivity: More stabilizer neighbors for error detection
Implementation challenges: 3D qubit connectivity difficult with current hardware [55]

4.2. Low-Density Parity-Check (LDPC) Codes

Quantum LDPC codes represent the most promising approach for achieving constant-rate quantum error correction, potentially reducing resource overhead by orders of magnitude compared to surface codes.

4.2.1. Fundamental Properties and Advantages

A quantum LDPC code satisfies the following characteristics:

Sparse stabilizers: Each stabilizer generator acts on O(1) qubits (typically 4-12)
Sparse qubits: Each qubit participates in O(1) stabilizer checks
Constant rate: R = k/n = Θ(1) logical qubits per physical qubit
Scaling distance: d = Θ(n^α) with α > 0 (ideally α = 1)

These properties enable quantum LDPC codes to encode many logical qubits with relatively fewer physical qubits compared to surface codes, which have rate R = O(1/d²) → 0.

4.2.2. Breakthrough Constructions

Quantum Tanner Codes [56]: A major theoretical breakthrough achieving the first codes with both constant rate and linear distance:

[[n, Θ(n), Θ(√n)]]

(2)

Key properties:

Stabilizer weight: O(√log n)
First explicit construction with R > 0 and d = ω(log n)
Based on expander graphs and algebraic geometry
Efficient classical preprocessing enables linear-time decoding

Balanced Product Codes [57]: Practical constructions with good finite-length performance:
Distance: d = Θ(√n)
Rate: R = Θ(1)
Built from pairs of classical LDPC codes
Efficient belief propagation decoding
Demonstrated thresholds approaching surface code performance

Lifted Product Codes: Recent family offering excellent practical performance:
Systematic construction from group algebra
Local connectivity properties
High thresholds: >1.5% under circuit-level noise
Efficient decoding algorithms [58]

4.2.3. Connectivity and Implementation Challenges

Most quantum LDPC codes require non-local qubit interactions, posing significant implementation challenges:

Table 3. Connectivity requirements for different LDPC code families.

Code Family	Max Stabilizer Weight	Max Qubit Degree	Connectivity Type	Threshold
Toric Code	4	4	Local (2D grid)	1.1%
Hypergraph Product	O(√n)	O(√n)	Non-local	0.8%
Balanced Product	O(√log n)	O(log n)	Limited non-local	1.2%
Quantum Tanner	O(√log n)	O(log n)	Non-local	0.1%
Lifted Product	6-8	6-8	Local with routing	1.5%
Good LDPC	O(1)	O(1)	Non-local	>1.0%

Connectivity Solutions:

Platform selection: All-to-all connectivity in trapped ions and neutral atoms
SWAP networks: Implement non-local gates using ancillary routing qubits
Code adaptation: Modify codes to fit available connectivity graphs
Scheduling optimization: Temporal multiplexing of physical connections

4.3. Topological Color Codes

Color codes provide an elegant extension to surface codes, offering enhanced logical gate capabilities while maintaining topological protection.

4.3.1. Mathematical Structure and Logical Gates

Color codes are defined on 2D lattices where plaquettes are colored with three colors (red, green, blue). Each color defines stabilizer generators:

Each plaquette corresponds to an X-type or Z-type stabilizer
Logical operators correspond to homology classes of specific color combinations
Code distance determined by shortest non-contractible paths

For a triangular 6.6.6 color code with distance d:

Physical qubits: n = 3d² − 3d + 1
Logical qubits: k = 1
Stabilizers: (3d² − 3d) total (half X-type, half Z-type)

Transversal Gate Advantages: Color codes support transversal implementation of the complete Clifford group:

Table 4. Logical gate implementation in surface codes vs. color codes.

Logical Gate	Surface Code	Color Code	Resource Overhead
X̄	Transversal	Transversal	O(1)
Z̄	Transversal	Transversal	O(1)
H̄	Code deformation	Transversal	Surface: O(d), Color: O(1)
S̄	Magic state	Transversal	Surface: O(log³(1/ε)), Color: O(1)
C̄NOT	Lattice surgery	Transversal	Surface: O(d), Color: O(1)
T̄	Magic state	Magic state	O(log³(1/ε))

4.3.2. Performance Trade-Offs

Color codes require ∼49% more physical qubits than surface codes for the same distance, but offer significant advantages for Clifford-heavy algorithms through transversal gate implementation.

Table 5. Detailed comparison of surface codes and color codes.

Property	Surface Code	Color Code	Ratio (Color/Surface)
Error threshold	1.1%	0.31%	0.28
Physical qubits (d = 5)	41	61	1.49
Physical qubits (d = 7)	73	109	1.49
Syndrome extraction cycles	d − 1	d − 1	1.0
Transversal Clifford gates	2	6	3.0
Magic states per T-gate	O(log³·²(1/ε))	O(log³·²(1/ε))	1.0
Decoder complexity	O(n³)	O(n³)	1.0

4.3.3. Recent Experimental Results

Quantinuum Demonstrations:

19-qubit triangular color code implementation
All-to-all connectivity enabling optimal layout
Transversal Clifford group demonstration with >99% fidelity
Below-threshold operation with logical error rates 0.15% [43]

IBM Heavy-Hex Results:

17-qubit 6.6.6 color code on superconducting processor
Adapted layout for limited connectivity
Logical error suppression demonstrated: 0.28% logical vs. 0.35% physical
Transversal Hadamard implementation with 99.2% fidelity [32]

4.4. Alternative Code Families

4.4.1. Concatenated Codes

While resource-intensive, concatenated codes remain important for specific applications:

Hierarchical Structure:

Level-1 (inner): Small codes correct single errors (e.g., 7-qubit Steane code)
Level-2 (outer): Protect against inner code failures
Recursive construction: Each level reduces effective error rate
Analysis framework: Well-understood threshold behavior

Modern Applications:

Magic state distillation protocols
Hybrid schemes combining with topological codes
Specialized decoders for correlated noise environments
Bootstrap protocols for fault-tolerant gate sets [24]

4.4.2. Bacon-Shor Codes

Subsystem codes offering intermediate complexity between concatenated and topological approaches:

Structure: 2D rectangular lattice with gauge qubits
Stabilizers: Weight-4 operators (similar to surface codes)
Gauge freedom: Flexibility in syndrome measurement scheduling
Threshold: ∼1.8% for optimized parameters
Advantages: Reduced syndrome extraction overhead, bias tolerance
Applications: Particularly suited for dephasing-dominated noise [25]

5. Decoder Algorithms: Classical and Machine Learning Approaches

The decoder represents the critical classical component that determines the ultimate success of quantum error correction protocols. Modern decoder development spans classical optimization algorithms to cutting-edge machine learning approaches.

5.1. Classical Decoding Algorithms

5.1.1. Minimum-Weight Perfect Matching (MWPM)

MWPM has established itself as the gold standard decoder for surface codes due to its optimal performance under independent error models.

Detailed Algorithm:

Syndrome processing: Extract defect locations from stabilizer measurements
Graph construction: • Vertices: syndrome defects plus boundary points • Edges: paths between defects with weights w_ij = − log P(error on path ij) • Boundary handling: Virtual vertices for open boundary conditions
Matching computation: Apply Edmonds’ blossom algorithm to find minimum-weight perfect matching
Error correction: Apply Pauli operators corresponding to matched paths

Performance Analysis:

Table 6. Comprehensive comparison of surface code decoders.

Decoder	Complexity	Threshold (%)	Memory	Parallelization	Hardware Suitability
MWPM	O(n³)	1.1	O(n²)	Limited	Good
Union-Find	O(nα(n))	1.07	O(n)	Excellent	Excellent
Sweep Decoder	O(n²)	0.9	O(n)	Good	Very Good
MWPM+Clustering	O(n²)	1.08	O(n²)	Good	Good
Cellular Automaton	O(n)	0.6	O(n)	Perfect	Excellent
Lookup Table	O(1)	1.1	O(2ⁿ)	Perfect	Limited

Recent Optimizations:

Hierarchical matching: Exploit syndrome locality for average O(n²) complexity
Parallelization strategies: Divide syndrome regions for parallel processing
Precomputation: Cache partial solutions for common syndrome patterns
Hardware acceleration: Custom ASIC implementations achieving <1 μs latency [59]

5.1.2. Union-Find Decoder

A revolutionary algorithm achieving near-linear complexity while maintaining near-optimal performance:

Core Algorithm:

Initialization: Each syndrome defect forms a separate cluster
Growth phase: Expand clusters uniformly until they merge or reach boundaries
Union operations: Merge overlapping clusters using union-find data structure
Path extraction: Derive correction paths from final cluster configuration

Key Advantages:

Complexity: O(nα(n)) where α is inverse Ackermann function
Simplicity: Elementary operations suitable for hardware implementation
Locality: Operations remain spatially localized
Memory efficiency: Linear memory requirements vs. quadratic for MWPM

Hardware Implementations: Recent FPGA implementations demonstrate:
Sub-microsecond decoding for d = 5 surface codes
Linear scaling with code size
Power consumption <1W for embedded systems
Real-time operation compatible with syndrome extraction cycles [60]

5.1.3. Belief Propagation for LDPC Codes

The primary algorithm for quantum LDPC codes, adapted from classical coding theory:

Message Passing Framework: The algorithm iteratively updates probability messages between variable nodes (qubits) and check nodes (stabilizers):

For variable-to-check messages:

μ^(t+1){v→c}(x_v) = ∏{c’∈N(v)\c} μ^(t)_{c’→v}(x_v)

(3)

For check-to-variable messages:

μ^(t+1){c→v}(x_v) = ∑{x:x_v fixed} [∏{v’∈N(c)\v} μ^(t){v’→c}(x_{v’})] I[c(x) = s_c]

(4)

Quantum Adaptations:

Joint processing: Handle X and Z errors simultaneously to exploit correlations
Degeneracy resolution: Post-processing to handle non-unique optimal corrections
Syndrome validation: Verify decoder output satisfies all stabilizer constraints
Scheduled updates: Optimize message passing order to accelerate convergence [58]

Performance Characteristics:

Table 7. Belief propagation decoder performance for quantum LDPC codes.

Code Family	Threshold (%)	Iterations	Convergence Rate	Hardware Complexity
Hypergraph Product	0.8	20-50	Good	Moderate
Balanced Product	1.2	10-30	Excellent	Good
Lifted Product	1.5	15-40	Good	Good
Quantum Tanner	0.1	50-100	Poor	High
Concatenated LDPC	1.0	25-60	Good	Moderate

5.2. Machine Learning-Based Decoders

The application of machine learning to quantum error correction represents a paradigm shift toward data-driven, adaptive decoding strategies.

5.2.1. Neural Network Architectures

Convolutional Neural Networks (CNNs):

CNNs naturally exploit the spatial structure of 2D syndrome patterns in topological codes:

Architecture Design:

Input layer: 2D syndrome array (binary or probabilistic values)
Convolutional layers: – 3×3 and 5×5 filters to capture local error correlations – Multiple feature maps (typically 16-64 channels) – ReLU activation functions
Pooling layers: Max pooling to reduce dimensionality while preserving features
Fully connected layers: Dense layers for final classification
Output layer: Separate predictions for X and Z corrections (multi-output)

Training Methodology:

Dataset generation: Create (E, S, C) training triplets • E: Random error patterns according to noise model • S: Corresponding syndrome measurements • C: Optimal correction (from MWPM or enumeration)
Loss function: Multi-class cross-entropy:

L = -1/N ∑^N_{i=1} ∑^n_{q=1} [y^X_{i,q} log(ŷ^X_{i,q}) + y^Z_{i,q} log(ŷ^Z_{i,q})]

(5)

3.: Optimization: Adam optimizer with learning rate scheduling
4.: Regularization: Dropout and batch normalization to prevent overfitting

Performance Results: Recent studies demonstrate:

Thresholds: 0.8-1.0% for surface codes (vs. 1.1% for MWPM)
Inference time: <1 μs on modern GPUs for d = 5 codes
Correlated noise: Superior performance compared to classical decoders
Adaptability: Can learn and adapt to changing noise characteristics [61]

Graph Neural Networks (GNNs):

GNNs provide a more natural framework for irregular code graphs, particularly relevant for LDPC codes:

Message Passing GNN Architecture:

h^(l+1)_v = UPDATE(h^(l)_v, AGGREGATE({h^(l)_u : u ∈ N(v)}))

(6)

where UPDATE and AGGREGATE are learned functions implemented as neural networks.

Advantages for QEC:

Permutation invariance: Natural handling of qubit relabeling
Scalability: Can generalize across different code sizes
Code flexibility: Handle irregular LDPC and other non-uniform codes
Interpretability: Learned messages relate to classical belief propagation
Inductive bias: Built-in understanding of local error propagation [62]

5.2.2. Reinforcement Learning Approaches

RL offers the possibility of decoders that improve through direct interaction with quantum systems:

Problem Formulation:

State space: S = {0, 1}^{n-k} (syndrome configurations)
Action space: A = set of possible Pauli corrections
Reward function: R(s, a) = {+1 if correction successful (no logical error) {-1 if logical error remains (7)
Policy: π(a|s) gives probability of selecting correction a for syndrome s

Training Algorithms:

Deep Q-Networks (DQN): Learn action-value function Q(s, a) using neural networks
Policy Gradient Methods: Directly optimize policy parameters using REINFORCE
Actor-Critic: Combine value function learning with direct policy optimization
Multi-Agent RL: Distributed decoding with multiple cooperating agents [63]

Adaptive Capabilities:

Real-time adaptation to changing noise models
Online learning from actual quantum hardware
Handling of unknown error correlations
Self-improvement through continued operation

Current Limitations:

Training instability and slow convergence
Sample efficiency concerns for practical deployment
Exploration vs. exploitation trade-offs in critical applications
Limited interpretability compared to classical algorithms

5.2.3. Hybrid Classical-ML Approaches

Combining classical algorithms with ML components often provides better performance than pure approaches:

ML-Enhanced MWPM:

Use neural networks to predict edge weights for matching graph
Learn noise correlations not captured by i.i.d. models
Maintain optimality guarantees while improving empirical performance
Particularly effective for handling measurement errors and crosstalk [64]

Ensemble Methods:

Combine multiple decoder outputs through learned weighting
Classical decoders provide baseline performance and reliability
ML components handle complex correlations and adaptation
Confidence-based switching between classical and ML decoders

5.3. Real-Time Decoding Requirements and Hardware Implementation

Practical QEC systems must operate within strict latency constraints imposed by qubit coherence times and syndrome extraction cycles.

5.3.1. Platform-Specific Timing Requirements

Table 8. Real-time decoding requirements across quantum computing platforms.

Platform	Syndrome Cycle	Coherence Time	Decoder Latency	Throughput
Superconducting	1-2 μs	50-100 μs	<0.5 μs	>2 MHz
Trapped Ion	10-50 μs	>1 ms	<10 μs	>100 kHz
Neutral Atom	1-10 μs	100 μs - 1 ms	<1 μs	>1 MHz
Photonic	1-10 ns	N/A	<100 ns	>10 GHz
Silicon Quantum Dot	1-10 μs	1-10 ms	<1 μs	>1 MHz

5.3.2. Hardware Acceleration Strategies

FPGA Implementations: Field-Programmable Gate Arrays offer excellent performance for classical decoders:

Union-Find optimizations: – Parallel cluster operations across syndrome regions – Custom data structures optimized for union-find operations – Pipeline architecture overlapping growth and merge phases – Demonstrated <500 ns latency for d = 5 surface codes
Memory optimization: – On-chip block RAM for syndrome storage and processing – Minimize external memory access through data locality – Custom caching strategies for frequently accessed patterns
Scalability: – Modular design enabling parallel processing of multiple code patches – Network-on-chip for inter-module communication – Load balancing across processing elements [65]

GPU Acceleration: Graphics Processing Units excel at ML decoder inference:
Parallel syndrome processing: – Process hundreds of syndrome patterns simultaneously – Batch inference for improved GPU utilization – Tensor operations optimized for neural network computations
Memory hierarchy optimization: – Shared memory for frequently accessed model parameters – Coalesced memory access patterns for optimal bandwidth – Model quantization to reduce memory footprint
Performance achievements: – >10,000 syndrome decodings per second for d = 7 surface codes – <100 μs latency including data transfer overhead – Support for batch processing multiple quantum processors [66]

Custom ASIC Development: Application-Specific Integrated Circuits for ultimate performance:
Specialized datapaths: Hardware optimized for specific decoder algorithms
Low-latency design: Direct integration with quantum control electronics
Power efficiency: Critical for large-scale cryogenic deployment
Scalable architecture: Support for multiple code instances and distances
Industry development: Companies like Riverlane developing dedicated QEC chips [67]

6. Engineering Challenges and Practical Considerations

Real-world implementation of quantum error correction faces numerous engineering challenges that significantly impact the idealized performance predicted by theory.

6.1. Correlated Noise and Realistic Error Models

6.1.1. Sources and Characterization of Error Correlations

Real quantum systems exhibit complex, correlated error patterns that deviate significantly from the independent error assumptions underlying most QEC theory:

Coherent Crosstalk in Superconducting Systems:

ZZ coupling: Always-on interactions causing correlated dephasing: H_crosstalk = ∑_{⟨i,j⟩} ζ_ij/2 Z_i ⊗ Z_j (8) where ζ_ij ranges from 1-100 kHz depending on qubit separation
Spectator errors: Operations on target qubits inducing phase shifts on nearby idle qubits
Frequency crowding: Unwanted resonances when qubit frequencies drift within ∼10 MHz
Control line coupling: Shared microwave delivery causing simultaneous over/under-rotations

Environmental Correlations:

Magnetic field fluctuations: Common-mode dephasing across millimeter-scale chip regions
Temperature variations: Thermal gradients causing correlated frequency drifts
Vibrations: Mechanical perturbations creating spatially correlated errors
Cosmic ray events: High-energy particles affecting multiple qubits simultaneously
1/f noise: Low-frequency charge and flux noise with long correlation times [68]

Measurement-Induced Correlations:

Readout crosstalk: Dispersive shifts affecting neighboring qubit frequencies during measurement
State preparation errors: Imperfect ancilla initialization creating systematic syndrome biases
Simultaneous measurement effects: Shared readout resonators coupling measurement processes

6.1.2. Quantitative Error Characterization

Table 9. Typical error rates and correlations across quantum computing platforms.

Platform	1Q Gate Error	2Q Gate Error	Readout Error	Idle Error	Correlation Range
Superconducting	0.05-0.1%	0.2-1.0%	1-5%	0.01-0.1%	1-5 qubits
Trapped Ion	0.01-0.05%	0.1-0.5%	0.5-2%	0.001-0.01%	Chain-wide
Neutral Atom	0.1-0.5%	0.5-2%	1-5%	0.01-0.1%	Local clusters
Silicon QD	0.01-0.1%	0.1-1%	0.5-2%	0.1-1%	Nearest neighbors
Photonic	N/A	1-10%	5-20%	0%	Optical network

6.1.3. Advanced Characterization Techniques

Simultaneous Randomized Benchmarking: Scalable protocol for measuring crosstalk between qubits:

Apply random Clifford sequences to all qubits simultaneously
Measure average fidelity decay as function of sequence length
Extract both individual qubit errors and correlation terms
Identify dominant crosstalk mechanisms and spatial patterns

Process Tomography Extensions:

Gate Set Tomography (GST): Complete characterization of gate operations
Cycle benchmarking: Direct measurement of QEC cycle fidelity
Syndrome correlation analysis: Statistical analysis of syndrome pattern correlations
Machine learning characterization: Neural networks trained to identify error patterns [69]

6.1.4. Error Mitigation and Suppression Strategies

Hardware-Level Solutions:

Dynamical decoupling: Pulse sequences to suppress crosstalk during idle periods: U_DD = ∏_k e^{-iH_k t_k} such that ⟨H_crosstalk⟩_DD ≈ 0 (9)
Optimal frequency allocation: Computational optimization of qubit frequencies to minimize interactions
Engineered pulse shaping: Derivative-based optimization (DRAG, GRAPE) to reduce spectator errors
Layout optimization: Physical qubit placement minimizing problematic couplings [70]

Code-Level Adaptations:

Tailored stabilizer codes: Codes optimized for specific error correlation patterns
Adaptive syndrome scheduling: Measurement ordering optimized to break temporal correlations
Flagged stabilizer codes: Additional ancillas to detect measurement errors and correlations
Subsystem codes: Gauge degrees of freedom to accommodate correlated errors [71]

6.2. Cryogenic Control and System Integration

Scaling quantum error correction to thousands of physical qubits requires revolutionary advances in control system architecture and cryogenic integration.

6.2.1. Control System Architecture Challenges

Signal Distribution and Multiplexing: Large-scale systems require massive classical control infrastructure:

Table 10. Control system scaling requirements for fault-tolerant quantum computers.

System Scale	Logical Qubits	Physical Qubits	Control Lines	Data Rate (GB/s)	Power (kW)
Current Demo	1	50	200	1	0.1
Near-term	10	500	2,000	10	1
Medium Scale	50	5,000	20,000	100	10
Large Scale	100	10,000	40,000	200	20
Fault-Tolerant	1,000	100,000	400,000	2,000	200
Full Scale	10,000	1,000,000	4,000,000	20,000	2000

Key Scaling Solutions:

Frequency-domain multiplexing: Multiple control signals on single physical lines
Cryogenic electronics: Classical processing at 4K to reduce thermal load and latency
Integrated photonics: On-chip optical control and readout systems
Wireless control: RF/microwave links to reduce wiring complexity
Distributed control: Modular processors with local control systems [67]

6.2.2. Thermal Management and Cryogenic Engineering

Heat Load Analysis: Each control component contributes to overall thermal budget:

Microwave electronics: ∼1 mW per qubit at mixing chamber level
DC bias lines: ∼0.1 mW per line due to Johnson noise filtering
Digital control: ∼10 μW per qubit for cryogenic CMOS
Readout amplification: ∼1 mW per readout channel
Total budget: Typical dilution refrigerators provide ∼10 mW at 10 mK

Advanced Cooling Solutions:

Multi-stage cooling: Distributed heat sinking across temperature levels
Pulse-tube refrigerators: Closed-cycle systems for continuous operation
Advanced materials: Superconducting and high-thermal-conductivity interconnects
Active thermal management: Temperature control and gradient minimization

6.2.3. Integration with Classical Computing Infrastructure

Quantum-Classical Interface Requirements:

Low-latency communication: Classical feedback within syndrome extraction cycles
High-bandwidth data transfer: Streaming syndrome data to classical processors
Synchronization: Precise timing coordination across quantum and classical systems
Reliability: Fault-tolerant classical systems to match quantum reliability requirements

Distributed Computing Architectures:

Edge computing: Decoding processors co-located with quantum hardware
Cloud integration: High-level control and algorithm execution in cloud infrastructure
Hybrid architectures: Hierarchical processing with local real-time control and remote optimization
Network protocols: Specialized communication protocols for quantum control networks [72]

6.3. Noise Characterization and Adaptive Methods

6.3.1. Real-Time Noise Tracking

Modern quantum systems require continuous monitoring and adaptation to changing noise environments:

Online Characterization Methods:

Process drift monitoring: Continuous tracking of gate fidelity changes
Syndrome pattern analysis: Statistical analysis of error correlation evolution
Predictive modeling: Machine learning models for noise prediction and preemptive correction
Adaptive calibration: Automatic parameter optimization based on performance metrics [73]

Integration with Error Correction:

Decoder parameter updates: Real-time adjustment of decoding thresholds and weights
Code switching: Dynamic selection of optimal codes for current noise conditions
Resource reallocation: Adaptive logical qubit placement and routing
Predictive error correction: Preemptive error correction based on noise forecasting

7. Resource Estimation for Quantum Applications

Accurate resource estimation is crucial for determining the practical viability of fault-tolerant quantum algorithms and guiding hardware development priorities. This section provides detailed analysis of physical qubit requirements, runtime estimates, and cost projections for key quantum applications.

7.1. Cryptographic Applications

7.1.1. Shor’s Algorithm for Integer Factorization

Shor’s algorithm represents one of the most significant applications driving fault-tolerant quantum computing development, with direct implications for current cryptographic standards.

Algorithm Resource Analysis: For factoring an n-bit RSA modulus, Shor’s algorithm requires:

Logical qubits: 2n + 3 for the main computation registers
Arithmetic operations: O(n³) controlled modular multiplications
Circuit depth: O(n³) logical gate operations
T-gates: O(n³) non-Clifford operations requiring magic state distillation

Detailed Resource Requirements:

Table 11. Resource requirements for Shor’s algorithm across different RSA key sizes.

RSA Bits	Logical Qubits	T-gates	Physical Qubits	Runtime	Success Prob.	Cost (M$)
1024	2048	1.2 × 10⁷	4.8 × 10⁶	4.8 hours	99%	150
2048	4096	9.6 × 10⁷	2.0 × 10⁷	1.6 days	99%	600
3072	6144	3.2 × 10⁸	4.1 × 10⁷	3.7 days	99%	1,200
4096	8192	7.7 × 10⁸	6.8 × 10⁷	6.4 days	99%	2,000

These estimates assume surface codes with distance d = 15, physical error rates of 0.1%, and current projections for quantum computer operating costs.

Impact on Current Cryptography:

RSA-1024: Vulnerable to quantum attacks within 5-7 years of fault-tolerant systems
RSA-2048: Current standard, requires substantial quantum resources but achievable by 2030
ECC-256: Elliptic curve cryptography offers better classical security but similar quantum vulnerability
Migration timeline: NIST recommends post-quantum cryptography adoption by 2030 [74]

7.1.2. Elliptic Curve Discrete Logarithm Problem

Shor’s algorithm also applies to elliptic curve cryptography (ECC), which is widely used due to smaller key sizes:

Table 12. Resource requirements for breaking elliptic curve cryptography.

ECC Bits	Security Level	Logical Qubits	Physical Qubits	Runtime
256	RSA-3072 equivalent	1280	2.1 × 10⁶	8.2 hours
384	RSA-7680 equivalent	1920	3.6 × 10⁶	20.1 hours
521	RSA-15360 equivalent	2605	5.8 × 10⁶	1.9 days

ECC systems are particularly vulnerable as they require fewer quantum resources than RSA for equivalent classical security levels.

7.2. Quantum Chemistry and Materials Science

Quantum chemistry represents one of the most promising near-term applications for fault-tolerant quantum computers, with significant industrial and scientific impact potential.

7.2.1. Molecular Electronic Structure Calculations

Problem Complexity Scaling: For a molecule with N electrons and M orbitals:

Logical qubits: 2M (spin-up and spin-down orbitals)
Hamiltonian terms: O(M⁴) two-electron integrals
Circuit depth: O(M⁵) for full configuration interaction
Measurement overhead: O(M⁴) expectation values

Specific Molecular Systems:

Table 13. Resource requirements for quantum chemistry applications.

Molecule	Orbitals	Logical Qubits	Physical Qubits	Runtime	Scientific Impact
H₂ (Hydrogen)	4	8	800	1 min	Benchmark
LiH (Lithium Hydride)	12	24	2,400	30 min	Battery materials
BeH₂ (Beryllium Hydride)	16	32	3,200	2 hours	Catalysis
N₂ (Nitrogen)	28	56	5,600	8 hours	Nitrogen fixation
Fe₂S₂ (Iron-Sulfur)	76	152	15,200	3 days	Enzyme modeling
P450 Active Site	100	200	20,000	1 week	Drug metabolism
Ferrocene (Fe(C₅H₅)₂)	140	280	28,000	2 weeks	Organometallics

Industrial Applications and Economic Impact:

Catalyst design: Improved catalysts for chemical industry could save billions in energy costs
Drug discovery: Accurate protein-drug interaction modeling accelerating pharmaceutical development
Materials science: Design of new materials for batteries, solar cells, and superconductors
Environmental applications: Better understanding of atmospheric chemistry and pollution remediation

7.2.2. Advanced Algorithms and Error Budgets

Recent algorithmic improvements have reduced resource requirements:

Qubitization and Block Encoding:

Gate count reduction: Factor of 10-100 improvement over naive implementations
Error budget optimization: Adaptive precision for different calculation stages
Parallel processing: Distributed quantum chemistry calculations across multiple processors

Hybrid Quantum-Classical Approaches:

VQE with error correction: Variational algorithms enhanced with logical qubits
Classical preprocessing: Reduce quantum circuit depth through classical optimization
Error mitigation integration: Combine QEC with quantum error mitigation techniques [36]

7.3. Optimization and Machine Learning

7.3.1. Quantum Approximate Optimization Algorithm (QAOA)

QAOA and related algorithms represent a class of optimization applications well-suited to early fault-tolerant systems:

Table 14. Resource requirements for quantum optimization algorithms.

Problem Type	Variables	Logical Qubits	Circuit Depth	Applications
Max-Cut	100	100	10³	Network optimization
Portfolio Optimization	500	500	10⁴	Financial services
Vehicle Routing	1000	1000	10⁴	Logistics
Drug Discovery	2000	2000	10⁵	Pharmaceutical
Supply Chain	5000	5000	10⁵	Manufacturing
Traffic Flow	10000	10000	10⁶	Urban planning

Competitive Advantage Timeline:

2025-2027: Small optimization problems with 50-100 variables
2028-2030: Medium-scale problems competing with classical heuristics
2030+: Large-scale problems beyond classical computational reach

7.3.2. Quantum Machine Learning Applications

Quantum Support Vector Machines:

Training data: N data points in d dimensions
Quantum advantage: Exponential speedup in feature space dimension
Resource requirements: O(log(Nd)) logical qubits
Error sensitivity: High precision requirements for kernel computations

Quantum Neural Networks:

Parameterized quantum circuits: Trainable quantum layers
Gradient computation: Fault-tolerant parameter-shift rules
Hybrid architectures: Classical-quantum neural network combinations
Applications: Natural language processing, image recognition, financial modeling [75]

8. Industry Roadmaps and Strategic Development

This section analyzes the strategic roadmaps of major quantum computing companies, examining their approaches to achieving fault-tolerant quantum advantage and the feasibility of their projected timelines.

8.1. Leading Industry Players

8.1.1. Google Quantum AI

Google has established one of the most aggressive roadmaps for fault-tolerant quantum computing:

Technology Strategy:

Platform focus: Superconducting qubits with surface code error correction
Architecture: Modular approach with interconnected surface code patches
Control systems: Custom classical electronics and cryogenic integration
Software stack: Cirq quantum programming framework with error correction integration

Timeline and Milestones:

Table 15. Google Quantum AI roadmap milestones and targets.

Year	Milestone	Logical Qubits	Key Capability	Status
2021	Below-threshold QEC	1	Proof of principle	✓ Achieved
2023	Improved thresholds	5	Better error rates	✓ Achieved
2024	Multi-patch codes	10	Logical connectivity	In progress
2025	Small applications	50	Chemistry benchmarks	Target
2027	Medium-scale systems	200	Optimization advantage	Target
2030	Large-scale FTQC	1000	Commercial applications	Goal

Resource Investment and Infrastructure:

R&D spending: $500M+ annually on quantum computing research
Fabrication facilities: Custom superconducting qubit fabrication capabilities
Talent acquisition: 200+ quantum researchers and engineers
Industry partnerships: Collaborations with automotive, pharmaceutical, and finance sectors [76]

Figure 2. A ten-year plan for quantum computing that can handle faults. Key milestones from 2025 to 2030 show how things are expected to go: (i) showing that multiple interconnected logical qubits can work together with low error rates (2025), (ii) the first useful fault-tolerant applications like small-molecule simulation and QAOA optimization (2027), and (iii) systems with ~10³ logical qubits that can solve problems that are too hard for classical computers (2030).

8.1.2. IBM Quantum Network

IBM has pursued a different strategy emphasizing modular quantum systems and broad ecosystem development:

Quantum-Centric Supercomputing Vision:

Modular architecture: Multiple quantum processors connected via classical and quantum links
Distributed computing: Workload distribution across quantum and classical resources
Software integration: Qiskit framework with enterprise-grade tools
Cloud deployment: Quantum computing as a service (QCaaS) model

Table 16. IBM Quantum Network development timeline.

Year	Processor	Physical Qubits	Error Rates	Key Features
2023	Heron	133	99.9% 2Q fidelity	Improved coherence
2024	Flamingo	156	99.95% 2Q fidelity	Error correction ready
2025	Next-Gen	200	99.97% 2Q fidelity	Logical qubit demos
2026	Modular-1	400	99.98% 2Q fidelity	Multi-chip systems
2028	Modular-10	4000	99.99% 2Q fidelity	Fault-tolerant apps
2030	Enterprise	10000+	>99.99% 2Q fidelity	Commercial advantage

Business Strategy and Market Approach:

Enterprise partnerships: 200+ companies in quantum network
Industry verticals: Finance, automotive, energy, healthcare focus
Education initiatives: Quantum education programs and certification
Open source: Contributions to quantum software ecosystem [77]

8.1.3. Microsoft Azure Quantum

Microsoft has taken a unique approach emphasizing topological qubits and comprehensive software stack development:

Topological Qubit Strategy:

Majorana fermions: Intrinsic topological protection from noise
Theoretical advantage: Potentially higher thresholds and simpler error correction
Technical challenges: Experimental realization remains difficult
Partnerships: Collaboration with academic institutions and hardware providers

Azure Quantum Ecosystem:

Hardware agnostic: Support for multiple quantum hardware platforms
Classical integration: Seamless hybrid classical-quantum computing
Q# programming: Domain-specific language for quantum algorithms
Cloud services: Scalable quantum computing infrastructure [78]

8.1.4. Quantinuum (Honeywell + Cambridge Quantum Computing)

Quantinuum has focused on high-fidelity trapped-ion systems with advanced software capabilities:

Trapped-Ion Advantage Strategy:

High fidelity: >99.9% gate fidelities reducing QEC overhead
All-to-all connectivity: Flexible qubit interactions enabling diverse codes
Long coherence: Minutes-long coherence times for complex algorithms
Precise control: Individual qubit addressing and measurement

Table 17. Quantinuum system development and performance targets.

System	Qubits	Gate Fidelity	QEC Capability	Target Applications
H1-1	20	99.91%	Small codes	QEC demonstrations
H1-2	32	99.92%	Steane codes	Algorithm development
H2-1	56	99.9%	Surface codes	Chemistry applications
H3 (planned)	100	99.95%	LDPC codes	Optimization problems
H4 (target)	200	99.97%	Fault-tolerant	Commercial applications

Software and Algorithm Focus:

Quantum chemistry: Specialized algorithms for molecular simulation
Machine learning: Quantum advantage in pattern recognition and optimization
Cryptography: Post-quantum cryptography development and quantum key distribution
Enterprise solutions: Industry-specific quantum applications [79]

8.2. Emerging Companies and Alternative Approaches

8.2.1. Neutral Atom Platforms

Atom Computing:

Scaling advantage: Demonstrated 1180-atom systems
Reconfigurable connectivity: Optical tweezer manipulation
Target applications: Optimization and machine learning problems
Timeline: 100-logical-qubit systems by 2026 [48]

QuEra Computing:

Analog quantum computing: Direct Hamiltonian simulation
Harvard collaboration: Academic research partnerships
Specialized applications: Materials science and condensed matter physics
Hybrid approach: Combining analog and digital quantum computing [49]

8.2.2. Photonic Quantum Computing

PsiQuantum:

Million-qubit vision: Large-scale photonic systems
Fault-tolerant from day one: Focus on error-corrected systems
Silicon photonics: Leveraging semiconductor manufacturing
Timeline: Fault-tolerant systems by 2027-2030 [80]

Xanadu:

Continuous variable: Gaussian boson sampling and CV quantum computing
Cloud access: PennyLane quantum software platform
Near-term applications: Optimization and machine learning
Research focus: Quantum advantage demonstrations [81]

8.3. Investment Trends and Market Analysis

8.3.1. Funding and Valuation Trends

Investment Drivers:

Government funding: National quantum initiatives totaling >$25B globally
Private investment: Venture capital and corporate investment >$10B since 2020
Strategic partnerships: Industry collaborations driving application development
Talent acquisition: Competition for quantum scientists and engineers [82]

Table 18. Quantum computing company valuations and funding (2024 estimates).

Company	Valuation ($B)	Total Funding ($M)	Employees	Platform
Google Quantum AI	N/A (Internal)	>1000	200+	Superconducting
IBM Quantum	N/A (Public)	>500	150+	Superconducting
Quantinuum	5.0	625	400+	Trapped Ion
IonQ	2.0	200	100+	Trapped Ion
Rigetti	1.5	200	150+	Superconducting
PsiQuantum	3.2	665	200+	Photonic
Atom Computing	0.6	60	50+	Neutral Atom
Xanadu	0.4	100	80+	Photonic

8.3.2. Market Size Projections

Total Addressable Market (TAM):

2024: $1.3B (mostly R&D and early applications)
2027: $5B (first commercial applications)
2030: $15B (fault-tolerant applications emerging)
2035: $50B+ (widespread commercial adoption)

Application Sector Breakdown (2030 projection):

Financial services: $4B (portfolio optimization, risk analysis)
Pharmaceuticals: $3B (drug discovery, molecular modeling)
Chemicals/Materials: $2.5B (catalyst design, materials discovery)
Cybersecurity: $2B (post-quantum cryptography, quantum key distribution)
Logistics: $1.5B (optimization, supply chain)
Energy: $1B (grid optimization, battery materials)
Others: $1B (manufacturing, AI, research) [83]

9. Fault-Tolerant Quantum Computing Architectures

9.1. Complete System Integration

Fault-tolerant quantum computing requires seamless integration across multiple system layers, from quantum hardware to high-level applications.

9.1.1. Hierarchical System Architecture

Physical Layer:

Quantum hardware: Qubits, gates, measurements, and control systems
Classical control: Real-time feedback and synchronization systems
Cryogenic infrastructure: Cooling systems and thermal management
Networking: Quantum and classical communication between processors

Error Correction Layer:

Syndrome extraction: Stabilizer measurement circuits and scheduling
Classical decoding: Real-time error correction algorithms
Logical operations: Fault-tolerant implementation of quantum gates
Resource management: Allocation of physical qubits to logical functions

Logical Layer:

Logical qubit management: State preparation, manipulation, and measurement
Gate synthesis: Decomposition of logical operations into fault-tolerant circuits
Error budgeting: Optimal allocation of error tolerance across algorithm stages
Code selection: Dynamic choice of error correction codes for different operations

Algorithm Layer:

Quantum algorithms: High-level algorithm implementation and optimization
Classical preprocessing: Problem decomposition and parameter optimization
Hybrid execution: Coordination between quantum and classical computation
Result verification: Validation and error detection in algorithm outputs

Figure 3. A look at the best quantum hardware platforms. This radar chart shows how superconducting qubits (blue), trapped-ion systems (orange), and neutral-atom arrays (green) compare on five important performance metrics: gate fidelity, coherence time, connectivity, parallelism, and scalability. The chart shows that superconducting qubits are best at gate speed and parallelism, trapped ions are best at coherence and connectivity, and neutral atoms are best at reconfigurability and long-term scalability.

9.1.2. Distributed Quantum Computing

Large-scale quantum applications may require distributed architectures connecting multiple quantum processors:

Network Topologies:

Star networks: Central hub connecting multiple quantum processors
Mesh networks: Direct connections between neighboring processors
Hierarchical networks: Multiple levels of quantum and classical processing
Hybrid architectures: Combining local and remote quantum resources

Quantum Communication Protocols:

Quantum teleportation: State transfer between distant processors
Distributed entanglement: Creating and maintaining entanglement across networks
Error correction networking: Network-wide error correction protocols
Latency management: Coordinating time-sensitive quantum operations [84]

9.2. Software Stack Development

9.2.1. Quantum Operating Systems

Resource Management:

Qubit allocation: Dynamic assignment of physical qubits to logical functions
Circuit scheduling: Optimal timing of quantum operations
Error budget management: Tracking and optimizing error accumulation
Multi-tenancy: Supporting multiple concurrent quantum applications

System Services:

Calibration management: Automated system calibration and drift correction
Error monitoring: Real-time tracking of system performance metrics
Fault recovery: Automatic handling of hardware failures and errors
Performance optimization: Dynamic tuning of system parameters

9.2.2. Programming Languages and Compilers

High-Level Languages:

Q# (Microsoft): Domain-specific language with error correction support
Cirq (Google): Python framework for fault-tolerant circuit design
Qiskit (IBM): Comprehensive quantum computing platform
PennyLane (Xanadu): Quantum machine learning and optimization focus

Compilation Challenges:

Error-aware optimization: Circuit optimization considering error correction overhead
Resource allocation: Mapping logical operations to available physical resources
Code selection: Automatic choice of optimal error correction codes
Hardware abstraction: Portable code across different quantum platforms [85]

10. Future Perspectives and Research Directions

10.1. Theoretical Challenges and Open Problems

10.1.1. Fundamental Limitations and Trade-Offs

Several theoretical challenges remain in quantum error correction that may require breakthrough insights:

The Quantum Error Correction Threshold Conjecture: While thresholds have been proven for specific noise models, several open questions remain:

Universal thresholds: Do threshold theorems hold for all physically reasonable noise models?
Finite-size effects: How do thresholds behave for realistic finite-size quantum computers?
Time-correlated noise: Can threshold theorems be extended to non-Markovian noise processes?
Measurement-dependent noise: How do measurement errors affect threshold calculations?

Resource-Performance Trade-offs: Fundamental questions about optimal resource allocation:
Code rate vs. threshold: Is there a fundamental trade-off between code efficiency and error tolerance?
Space-time trade-offs: Can temporal error correction reduce spatial overhead?
Energy-error trade-offs: How do thermodynamic constraints affect error correction efficiency?
Communication-computation trade-offs: What are optimal architectures for distributed quantum computing?

10.1.2. Advanced Error Correction Concepts

Self-Correcting Quantum Memories: The search for quantum systems that naturally resist errors:

4D topological codes: Higher-dimensional codes with better properties
Thermal stability: Systems that maintain quantum information at finite temperature
Active matter approaches: Using driven dissipative systems for protection
Emergent error correction: Quantum many-body systems with built-in protection [86]

Quantum Error Correction Without Measurement: Alternative approaches avoiding the measurement bottleneck:

Autonomous error correction: Systems that correct errors through designed evolution
Reservoir engineering: Using engineered environments for error suppression
Quantum error correction codes: Purely quantum approaches without classical feedback
Continuous monitoring: Real-time error correction without discrete measurements

10.2. Emerging Technologies and Platforms

10.2.1. Novel Qubit Modalities

Topological Qubits: Systems with intrinsic protection against errors:

Majorana fermions: Zero-dimensional topological superconductors
Parafermions: Fractional quantum Hall systems with enhanced protection
Fibonacci anyons: Non-Abelian anyons enabling universal quantum computation
Challenges: Experimental realization remains difficult despite theoretical promise [87]

Molecular Qubits: Engineered molecular systems for quantum information:

Metal complexes: Transition metal ions with controllable spin states
Molecular magnets: Single-molecule magnets with long coherence times
Nuclear spins: Hyperfine interactions for precise control
Advantages: Chemical tunability and potential for scalable synthesis [88]

Hybrid Quantum Systems: Combining different physical platforms:

Superconducting-spin hybrids: Coupling superconducting circuits to spin systems
Optomechanical systems: Using mechanical resonators as quantum intermediates
Atomic-photonic interfaces: Atoms coupled to integrated photonic circuits
Advantages: Leveraging strengths of different platforms while mitigating weaknesses

10.2.2. Advanced Integration Technologies

3D Quantum Architectures: Moving beyond planar qubit layouts:

Vertical integration: Stacking quantum and classical processing layers
3D connectivity: Improved qubit interactions and reduced routing overhead
Thermal management: Better heat dissipation in 3D structures
Manufacturing challenges: Complex 3D fabrication processes [89]

Quantum-Classical Co-processors: Tightly integrated hybrid systems:

Same-chip integration: Quantum and classical circuits on single substrate
Cryogenic classical: Classical electronics operating at quantum temperatures
Real-time communication: Ultra-low-latency quantum-classical interfaces
Shared resources: Common control and measurement infrastructure

10.3. Algorithmic Advances and Applications

10.3.1. Next-Generation Quantum Algorithms

Fault-Tolerant Variational Algorithms: Extending NISQ-era approaches to fault-tolerant systems:

Error-corrected VQE: Variational quantum eigensolver with logical qubits
Adaptive quantum computing: Real-time algorithm adaptation based on intermediate results
Quantum approximate optimization: QAOA with error correction for larger problem sizes
Hybrid approaches: Seamless integration of classical optimization and quantum computation

Quantum Machine Learning at Scale: Machine learning algorithms leveraging large-scale fault-tolerant systems:

Quantum neural networks: Deep quantum circuits for pattern recognition
Quantum kernel methods: Exponentially large feature spaces for classification
Quantum generative models: Quantum GANs and variational autoencoders
Federated quantum learning: Distributed quantum machine learning protocols [90]

10.3.2. Cross-Disciplinary Applications

Quantum-Enhanced Scientific Computing:

Climate modeling: Large-scale atmospheric and oceanic simulations
Astrophysics: Simulating black holes, neutron stars, and early universe
High-energy physics: Lattice QCD and fundamental particle interactions
Condensed matter: Many-body quantum systems and phase transitions

Quantum Biology and Medicine:

Protein folding: Accurate modeling of protein structure and dynamics
Drug discovery: Quantum chemistry for pharmaceutical design
Biosystem modeling: Understanding quantum effects in biological processes
Medical imaging: Quantum-enhanced MRI and other imaging modalities [91]

10.4. Societal Impact and Policy Considerations

10.4.1. Economic Implications

Disruption Timeline and Sectors:

Table 19. Projected timeline for quantum computing disruption across industry sectors.

Sector	Early Impact	Significant Disruption	Market Size ($B)	Quantum Advantage
Financial Services	2025-2027	2028-2030	50	Portfolio optimization
Pharmaceuticals	2026-2028	2030-2032	80	Drug discovery
Chemical Industry	2027-2029	2031-2033	40	Catalyst design
Cybersecurity	2025-2026	2027-2029	30	Cryptography
Automotive	2028-2030	2032-2035	25	Materials, batteries
Energy	2029-2031	2033-2036	35	Grid optimization
Logistics	2027-2029	2030-2032	20	Supply chain

Economic Challenges and Opportunities:

Job displacement: Potential automation of certain computational tasks
New industries: Emerging quantum technology sectors and services
Competitive advantage: Early adopters gaining significant market advantages
Infrastructure investment: Massive capital requirements for quantum systems

10.4.2. Security and Policy Implications

Cryptographic Transition: The migration to post-quantum cryptography represents one of the largest cybersecurity challenges:

Y2Q problem: “Years to Quantum” countdown for cryptographic vulnerability
Data harvesting: Current encrypted data vulnerable to future quantum attacks
Infrastructure updates: Massive upgrade requirements for security systems
International coordination: Need for global standards and protocols [74]

National Security Considerations:

Quantum advantage: Strategic implications of quantum computational superiority
Technology export controls: Restrictions on quantum technology transfer
Critical infrastructure: Protecting quantum systems from adversarial attacks
International cooperation: Balancing collaboration with security concerns

10.4.3. Ethical and Social Considerations

Access and Equity:

Digital divide: Ensuring broad access to quantum computing benefits
Educational requirements: Training workforce for quantum technology
International development: Supporting quantum capability in developing nations
Cost considerations: Making quantum computing accessible beyond elite institutions

Privacy and Surveillance:

Enhanced surveillance: Quantum computing enabling new monitoring capabilities
Privacy protection: Quantum cryptography for enhanced privacy
Regulatory frameworks: Need for updated privacy and data protection laws
Democratic oversight: Ensuring quantum capabilities serve public interest

11. Recommendations and Strategic Priorities

11.1. Research Community Priorities

11.1.1. Fundamental Research Directions

Based on the analysis presented in this review, several research priorities emerge for the quantum error correction community:

Immediate Priorities (2024-2027):

Realistic noise characterization: Develop comprehensive models for correlated and time-dependent errors
Decoder optimization: Create hardware-efficient decoders for real-time operation
Code adaptation: Design codes optimized for specific hardware platforms and noise models
System integration: Develop complete fault-tolerant quantum computing stacks

Medium-term Objectives (2027-2030):

Scalable architectures: Design quantum systems with thousands of logical qubits
Application-specific optimization: Tailor error correction for specific quantum algorithms
Hybrid classical-quantum systems: Optimize the quantum-classical interface
Distributed quantum computing: Develop protocols for networked quantum systems

Long-term Goals (2030+):

Self-correcting systems: Achieve autonomous error correction without external intervention
Universal quantum computers: Build general-purpose fault-tolerant quantum machines
Quantum internet: Create global quantum communication networks
Novel error correction paradigms: Explore fundamentally new approaches to quantum error protection

11.1.2. Collaborative Research Initiatives

International Cooperation:

Quantum error correction standards: Develop common benchmarks and protocols
Shared research infrastructure: Create globally accessible quantum computing facilities
Student and researcher exchange: Foster international collaboration and knowledge transfer
Open source initiatives: Support collaborative software development efforts

Industry-Academia Partnerships:

Joint research programs: Combine academic research with industrial development
Technology transfer: Accelerate movement of research results to commercial applications
Workforce development: Train next generation of quantum engineers and scientists
Problem-driven research: Focus academic research on industrially relevant challenges

11.2. Industry Strategy Recommendations

11.2.1. Technology Development Priorities

Hardware Companies:

Focus on fidelity: Prioritize gate fidelity improvements over qubit count increases
Error characterization: Invest in comprehensive noise modeling and mitigation
Modular architectures: Design systems for scalable expansion and maintenance
Control system integration: Develop efficient quantum-classical interfaces

Software Companies:

Full-stack development: Create comprehensive quantum software platforms
Error correction integration: Build error correction into programming languages and compilers
Application frameworks: Develop domain-specific quantum computing tools
Cloud services: Provide accessible quantum computing infrastructure

End-User Industries:

Early engagement: Begin quantum computing education and pilot projects now
Problem identification: Identify specific use cases where quantum advantage is achievable
Partnership development: Collaborate with quantum computing companies and researchers
Infrastructure planning: Prepare IT infrastructure for quantum-classical hybrid computing

11.2.2. Investment and Business Strategy

Venture Capital and Investment Priorities:

Long-term perspective: Quantum computing requires sustained investment over decades
Diversified portfolio: Invest across different quantum computing approaches and applications
Talent acquisition: Companies with strong technical teams show better long-term prospects
Intellectual property: Strong patent portfolios provide competitive advantages

Corporate Strategy:

Build vs. buy decisions: Evaluate internal development vs. partnership strategies
Talent development: Invest in quantum education and workforce development
Risk management: Prepare for quantum threats to current business models
Market positioning: Establish leadership positions in quantum-relevant market segments

11.3. Policy and Governance Recommendations

11.3.1. Government Policy Priorities

Research Funding:

Sustained investment: Maintain long-term funding commitments for quantum research
Interdisciplinary focus: Support research connecting quantum computing with other fields
International collaboration: Fund collaborative research programs with allies
Risk-tolerant funding: Support high-risk, high-reward research projects

Regulatory Frameworks:

Technology standards: Develop standards for quantum computing systems and protocols
Export controls: Balance security concerns with international collaboration needs
Privacy protection: Update privacy laws for quantum computing era
Economic policy: Consider economic implications of quantum disruption

11.3.2. International Coordination

Multilateral Initiatives:

Quantum technology partnerships: Establish international quantum research consortiums
Standards development: Create global standards for quantum computing and communications
Ethics guidelines: Develop international guidelines for responsible quantum technology development
Capacity building: Support quantum technology development in emerging economies

12. Conclusions

The field of quantum error correction has reached a critical juncture in its evolution from theoretical concept to practical implementation. This comprehensive review has examined the current state of quantum error correction across multiple dimensions: from fundamental theoretical advances to practical hardware implementations, from classical decoding algorithms to machine learning approaches, and from immediate technical challenges to long-term societal implications.

12.1. Key Findings and Achievements

The analysis reveals several significant achievements that mark the transition to fault-tolerant quantum computing:

Experimental Validation: The demonstration of below-threshold error correction by multiple research groups represents a watershed moment, proving that logical qubits can indeed outperform their constituent physical qubits. Google’s achievement of error suppression with increasing code distance, IBM’s progress toward larger surface code implementations, and Quantinuum’s high-fidelity trapped-ion demonstrations collectively establish the experimental feasibility of fault-tolerant quantum computing.

Theoretical Progress: Recent advances in quantum LDPC codes, particularly the development of quantum Tanner codes and balanced product codes, offer promising paths toward more resource-efficient error correction. These developments suggest that the prohibitive resource overhead of early QEC schemes may be substantially reduced through algorithmic and theoretical innovations.

Technological Integration: The development of real-time decoding systems, cryogenic control architectures, and hybrid quantum-classical interfaces demonstrates that the complex engineering challenges of fault-tolerant systems are being systematically addressed.

Industrial Momentum: The substantial investments by major technology companies, the emergence of dedicated quantum computing firms, and the development of comprehensive industry roadmaps indicate strong commercial commitment to fault-tolerant quantum computing.

Figure 4. Exponential suppression of logical errors with code distance. Plot showing the decrease of logical error rate pL as a function of code distance ddd on a log–log scale. Data points correspond to experimental demonstrations of distance-3, distance-5, and distance-7 surface codes on Google’s Sycamore processor [6] and IBM’s multi-patch logical qubit experimentss[8], illustrating threshold crossing where pL < pphs . The red line indicates the expected exponential scaling predicted by QEC theory.

12.2. Critical Challenges and Limitations

Despite remarkable progress, significant obstacles remain on the path to practical fault-tolerant quantum advantage:

Resource Overhead: Current surface code implementations require thousands of physical qubits to encode a single logical qubit with acceptable error rates. While LDPC codes offer theoretical improvements, their practical implementation faces connectivity and complexity challenges that must be resolved.

Correlated Noise: Real quantum systems exhibit complex error patterns that deviate significantly from the independent error models underlying most QEC theory. Addressing correlated noise, measurement errors, and time-dependent noise remains a critical challenge for achieving theoretical performance in practice.

System Integration Complexity: Building complete fault-tolerant quantum computers requires unprecedented integration of quantum hardware, classical control systems, real-time software, and cryogenic infrastructure. The engineering challenges of scaling these integrated systems to thousands or millions of qubits are substantial.

Economic Viability: The cost and complexity of fault-tolerant quantum computers raise questions about their economic accessibility and the breadth of applications that can justify the required investment.

12.3. Timeline and Expectations

Based on current progress and industry roadmaps, the following timeline emerges for fault-tolerant quantum computing:

2024-2027: Proof-of-Concept Era

Small-scale fault-tolerant systems with 10-100 logical qubits
Demonstration of quantum algorithms on logical qubits
First applications showing potential quantum advantage in specialized problems

2027-2030: Early Commercial Applications

Medium-scale systems with 100-1000 logical qubits
Commercial applications in optimization, chemistry, and machine learning
Cost reductions making quantum computing accessible to more organizations

2030-2035: Quantum Advantage Era

Large-scale fault-tolerant systems with 1000+ logical qubits
Clear quantum advantages in multiple application domains
Integration of quantum computing into enterprise and scientific workflows

2035+: Mature Quantum Computing

Ubiquitous quantum computing infrastructure
Quantum computers as essential tools for scientific and industrial applications
New discoveries enabled by large-scale quantum simulation and computation

12.4. Strategic Implications

The transition to fault-tolerant quantum computing will have profound implications across multiple domains:

Scientific Discovery: Fault-tolerant quantum computers will enable unprecedented simulations of complex quantum systems, potentially leading to breakthroughs in materials science, drug discovery, and fundamental physics. The ability to simulate large molecules accurately may revolutionize our understanding of catalysis, photosynthesis, and biological processes.

Economic Transformation: Industries ranging from finance to pharmaceuticals will be transformed by quantum computing capabilities. Early adopters who successfully integrate quantum computing into their operations may gain substantial competitive advantages, while organizations that fail to adapt may find themselves at a significant disadvantage.

Security and Privacy: The advent of cryptographically relevant quantum computers will necessitate a complete overhaul of current cryptographic infrastructure. The transition to post-quantum cryptography represents one of the largest cybersecurity challenges in history, requiring coordinated global effort to maintain the security of digital infrastructure.

Geopolitical Implications: Quantum computing superiority may become a source of national competitive advantage, potentially affecting international relations and global power balances. Countries and regions that successfully develop indigenous quantum capabilities may gain significant strategic advantages.

12.5. Recommendations for the Community

To successfully navigate the transition to fault-tolerant quantum computing, the quantum community should prioritize:

Collaborative Research: Foster increased collaboration between theoretical researchers, experimental physicists, and engineers to accelerate the development of practical fault-tolerant systems.
Realistic Benchmarking: Develop comprehensive benchmarks that account for realistic noise models, finite-size effects, and practical implementation constraints.
Workforce Development: Invest significantly in education and training programs to develop the specialized workforce required for quantum technology development and deployment.
Responsible Innovation: Engage proactively with policymakers, ethicists, and society to ensure that quantum computing development serves the broader public interest.
International Cooperation: Maintain open scientific collaboration while addressing legitimate security concerns, ensuring that the benefits of quantum computing are broadly shared.

12.6. Final Perspective

The field of quantum error correction stands at the threshold of a new era. The theoretical foundations have been laid, experimental proof-of-principles have been demonstrated, and substantial industrial investment is driving rapid technological development. While significant challenges remain, the convergence of scientific advances, engineering capabilities, and commercial motivation suggests that fault-tolerant quantum computing will become a reality within the next decade.

The ultimate success of quantum error correction will not only enable revolutionary computational capabilities but will also represent one of the greatest technological achievements in human history—the practical harnessing of quantum mechanical principles for large-scale computation. As we stand at this inflection point, the quantum computing community has both the opportunity and the responsibility to guide this transformative technology toward applications that benefit humanity and advance our understanding of the quantum world.

The journey from the first theoretical proposals for quantum error correction to practical fault-tolerant quantum computers spans nearly three decades of sustained scientific effort. The next decade will likely determine whether this journey culminates in the quantum computational revolution that has long been promised. The foundations have been built, the path forward is becoming clear, and the potential rewards are immense. The quantum error correction community is well-positioned to deliver on the transformative promise of fault-tolerant quantum computing.

Acknowledgments

The author would like to thank the global quantum computing community for their sustained efforts in advancing the field of quantum error correction. Special recognition goes to the researchers, engineers, and institutions who have contributed to the experimental demonstrations, theoretical advances, and technological developments reviewed in this comprehensive analysis.

Conflicts of Interest

The author declares no conflict of interest.

References

Shor, P.W. Algorithms for quantum computation: discrete logarithms and factoring. In Proceedings 35th annual symposium on foundations of computer science; IEEE: 1994; pp. 124–134.
Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the twenty-eighth annual ACM symposium on Theory of computing; 1996; pp. 212–219. [Google Scholar]
Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
Shor, P.W. Scheme for reducing decoherence in quantum computer memory. Physical review A 1995, 52, R2493. [Google Scholar] [CrossRef]
Steane, A.M. Error correcting codes in quantum theory. Physical Review Letters 1996, 77, 793. [Google Scholar] [CrossRef]
Gottesman, D. Stabilizer codes and quantum error correction. arXiv preprint quant-ph/9705052 1997.
Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Annals of physics 2003, 303, 2–30. [Google Scholar] [CrossRef]
Dennis, E.; Kitaev, A.; Landahl, A.; Preskill, J. Topological quantum memory. Journal of Mathematical Physics 2002, 43, 4452–4505. [Google Scholar] [CrossRef]
Arute, F.; et al. Exponential suppression of bit or phase errors with repetitive error correction. Nature 2021, 595, 383–387. [Google Scholar]
Krinner, S.; et al. Realizing repeated quantum error correction in a distance-three surface code. Nature 2022, 605, 669–674. [Google Scholar] [CrossRef]
Wilde, M.M. Quantum information theory; Cambridge University Press: 2013.
Renes, J.M.; Dupuis, F.; Renner, R. Efficient quantum polar codes. Physical review letters 2012, 109, 050504. [Google Scholar] [CrossRef]
Sarovar, M.; et al. Detecting crosstalk errors in quantum information processors. Quantum 2020, 4, 321. [Google Scholar] [CrossRef]
Wallman, J.J.; Emerson, J. Noise tailoring for scalable quantum computation via randomized compiling. Physical Review A 2016, 94, 052325. [Google Scholar] [CrossRef]
Ghosh, J.; Fowler, A.G.; Geller, M.R. Surface code with decoherence: An analysis of three superconducting architectures. Physical Review A 2013, 88, 062329. [Google Scholar] [CrossRef]
McEwen, M.; et al. Removing leakage-induced correlated errors in superconducting quantum error correction. Nature communications 2021, 12, 1–7. [Google Scholar] [CrossRef]
Panos, K.; et al. Bias-preserving gates with stabilized cat qubits. Science Advances 2022, 8, eabm9901. [Google Scholar]
Renes, J.M. Belief propagation decoding of quantum channels by passing quantum messages. New Journal of Physics 2022, 24, 032001. [Google Scholar]
Krastanov, S.; Heywood, V.V.; Jacobs, K. Optimally adaptive quantum error correction of surface codes. Physical Review Research 2022, 4, 043203. [Google Scholar]
Aharonov, D.; Ben-Or, M. Fault-tolerant quantum computation with constant error rate. SIAM Journal on Computing 2008, 38, 1207–1282. [Google Scholar] [CrossRef]
Fowler, A.G.; Mariantoni, M.; Martinis, J.M.; Cleland, A.N. Surface codes: Towards practical large-scale quantum computation. Physical Review A 2012, 86, 032324. [Google Scholar] [CrossRef]
Landahl, A.J.; Anderson, J.T.; Rice, P.R. Fault-tolerant quantum computing with color codes. arXiv preprint 2011, arXiv:1108.5738. [Google Scholar]
Breuckmann, N.P.; Eberhardt, J.N. Quantum low-density parity-check codes. PRX Quantum 2021, 2, 040101. [Google Scholar] [CrossRef]
Aliferis, P.; Gottesman, D.; Preskill, J. Quantum accuracy threshold for concatenated distance-3 codes. Quantum Information Computation 2006, 6, 97–165. [Google Scholar] [CrossRef]
Bacon, D. Operator quantum error-correcting subsystems for self-correcting quantum memories. Physical Review A 2006, 73, 012340. [Google Scholar] [CrossRef]
Tomita, Y.; Svore, K.M. Low-distance surface codes under realistic quantum noise. Physical Review A 2014, 90, 062320. [Google Scholar] [CrossRef]
Bombín, H.; Martin-Delgado, M.A. Optimal resources for topological two-dimensional stabilizer codes: Comparative study. Physical Review A 2007, 76, 012305. [Google Scholar] [CrossRef]
Eastin, B.; Knill, E. Restrictions on transversal encoded quantum gate sets. Physical review letters 2009, 102, 110502. [Google Scholar] [CrossRef] [PubMed]
Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Physical Review A 2005, 71, 022316. [Google Scholar] [CrossRef]
Haah, J.; Hastings, M.B. Codes and protocols for distilling T, controlled-S, and Toffoli gates. Quantum 2018, 2, 71. [Google Scholar] [CrossRef]
Horsman, C.; Fowler, A.G.; Devitt, S.; Van Meter, R. Surface code quantum computing by lattice surgery. New Journal of Physics 2012, 14, 123011. [Google Scholar] [CrossRef]
Acharya, R.; et al. Suppressing quantum errors by scaling a surface code logical qubit. arXiv preprint, 2022; arXiv:2207.06431. [Google Scholar]
Google Quantum, AI. Quantum error correction below the surface code threshold. arXiv preprint 2023, arXiv:2301.04112. [Google Scholar] [CrossRef]
Gambetta, J.M.; et al. IBM’s roadmap for scaling quantum technology. IBM Journal of Research and Development 2020, 64, 13–1. [Google Scholar]
Andersen, C.K.; et al. Repeated quantum error detection in a surface code. Nature Physics 2020, 16, 875–880. [Google Scholar] [CrossRef]
Endo, S.; Cai, Z.; Benjamin, S.C.; Yuan, X. Hybrid quantum-classical algorithms and quantum error mitigation. Journal of the Physical Society of Japan 2021, 90, 032001. [Google Scholar] [CrossRef]
Monroe, C.; et al. Programmable quantum simulations of spin systems with trapped ions. Reviews of Modern Physics 2021, 93, 025001. [Google Scholar] [CrossRef]
Chen, Z.; et al. Exponential suppression of bit or phase flip errors with repetitive error correction. Nature 2021, 595, 383–387. [Google Scholar]
Reilly, D.J. Engineering the quantum-classical interface of solid-state qubits. npj Quantum Information 2015, 1, 1–10. [Google Scholar] [CrossRef]
Kandala, A.; et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 2019, 567, 491–495. [Google Scholar] [CrossRef] [PubMed]
Quantinuum Team. Quantum error correction with the color code. arXiv preprint 2022, arXiv:2201.07806.
Sivak, V.V.; et al. Real-time quantum error correction beyond break-even. Nature 2022, 616, 50–55. [Google Scholar] [CrossRef] [PubMed]
Postler, L.; et al. Demonstration of fault-tolerant universal quantum gate operations. Nature 2022, 605, 675–680. [Google Scholar] [CrossRef]
Microsoft Quantum Team. Azure Quantum development kit and Q# language. Available online: https://azure.microsoft.com/en-us/products/quantum (accessed on 1 December 2023).
IonQ Inc. Algorithmic applications with error correction. Available online: https://ionq.com/resources (accessed on 1 December 2023).
Alpine Quantum Technologies. AQT quantum computing systems. Available online: https://www.aqt.eu/ (accessed on 1 December 2023).
Ebadi, S.; et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 2021, 595, 227–232. [Google Scholar] [CrossRef]
Atom Computing Inc. Neutral atom quantum computing platform. Available online: https://atom-computing.com/technology (accessed on 1 December 2023).
QuEra Computing Inc. Analog quantum processing units. Available online: https://www.quera.com/technology (accessed on 1 December 2023).
Bluvstein, D.; et al. A quantum processor based on coherent transport of entangled atom arrays. Nature 2022, 604, 451–456. [Google Scholar] [CrossRef]
Gottesman, D.; Kitaev, A.; Preskill, J. Encoding a qubit in an oscillator. Physical Review A 2001, 64, 012310. [Google Scholar] [CrossRef]
Eaton, M.; et al. Non-Clifford and parallelizable fault-tolerant logical gates on constant and almost-constant rate homological quantum LDPC codes via higher symmetries. arXiv preprint 2023, arXiv:2310.16982. [Google Scholar]
Raussendorf, R.; Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Physical Review Letters 2007, 98, 190504. [Google Scholar] [CrossRef]
Aliferis, P.; Cross, A.W. Subsystem fault tolerance with the Bacon-Shor code. Physical Review Letters 2007, 98, 220502. [Google Scholar] [CrossRef]
Raussendorf, R.; Harrington, J.; Goyal, K. A fault-tolerant one-way quantum computer. Annals of Physics 2006, 321, 2242–2270. [Google Scholar] [CrossRef]
Leverrier, A.; Zémor, G. Quantum Tanner codes. arXiv preprint 2022, arXiv:2202.13641. [Google Scholar]
Breuckmann, N.P.; Eberhardt, J.N. Balanced product quantum codes. IEEE Transactions on Information Theory 2021, 67, 6653–6674. [Google Scholar] [CrossRef]
Panteleev, P.; Kalachev, G. Asymptotically good quantum and locally testable classical LDPC codes. arXiv preprint 2022, arXiv:2111.03654. [Google Scholar]
Fowler, A.G. Minimum weight perfect matching of fault-tolerant topological quantum error correction in average O(1) parallel time. Quantum Information and Computation 2015, 15, 145–158. [Google Scholar] [CrossRef]
Delfosse, N.; Nickerson, N.H. Almost-linear time decoding algorithm for topological codes. Quantum 2021, 5, 595. [Google Scholar] [CrossRef]
Varona, N.; Müller-Lennert, M. Determination of the semion code threshold using neural network decoders. Physical Review A 2018, 98, 042337. [Google Scholar]
Liu, Y.; et al. Neural belief-propagation decoders for quantum error-correcting codes. Physical Review Letters 2022, 129, 050502. [Google Scholar] [CrossRef]
Andreasson, P.; et al. Quantum error correction for the toric code using deep reinforcement learning. Quantum 2019, 3, 183. [Google Scholar] [CrossRef]
Higgott, O.; Gidney, C. Sparse Blossom: correcting a million errors per core second with minimum-weight matching. arXiv preprint 2023, arXiv:2303.15933. [Google Scholar] [CrossRef]
Das, P.; Pattison, C.A.; Manne, S.; Carmean, D.; Svore, K.; Chong, F.T.; Chamberland, C. A scalable FPGA-based decoder for fault-tolerant quantum error correction. arXiv preprint 2022, arXiv:2205.09063. [Google Scholar]
Wagner, T.; Hermann, H.; Ribeiro, P.; Zilberberg, O. Efficient quantum error correction with neural-network decoders. arXiv preprint 2022, arXiv:2201.09271. [Google Scholar]
Reilly, D.J. Engineering the quantum-classical interface of solid-state qubits. npj Quantum Information 2015, 1, 1–10. [Google Scholar] [CrossRef]
McEwen, M.; et al. Removing leakage-induced correlated errors in superconducting quantum error correction. Nature Communications 2021, 12, 1761. [Google Scholar] [CrossRef] [PubMed]
Helsen, J.; et al. General framework for randomized benchmarking. PRX Quantum 2022, 3, 020357. [Google Scholar] [CrossRef]
Rol, M.A.; et al. Restless tuneup of high-fidelity qubit gates. Physical Review Applied 2020, 14, 044017. [Google Scholar] [CrossRef]
Chamberland, C.; Zhu, G.; Yoder, T.J.; Hertzberg, J.B.; Cross, A.W. Topological and subsystem codes on low-degree graphs with flag qubits. Physical Review X 2020, 10, 011022. [Google Scholar] [CrossRef]
Monroe, C.; et al. Programmable quantum simulations of spin systems with trapped ions. Reviews of Modern Physics 2021, 93, 025001. [Google Scholar] [CrossRef]
Hoffman, N.M.; et al. Machine learning for active quantum error correction. Physical Review Research 2022, 4, 043141. [Google Scholar]
National Institute of Standards and Technology. Post-Quantum Cryptography Standardization. Available online: https://csrc.nist.gov/Projects/post-quantum-cryptography (accessed on 1 December 2023).
Biamonte, J.; et al. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
Google Quantum, AI. Google’s quantum computing roadmap. Available online: https://quantumai.google/roadmap (accessed on 1 December 2023).
IBM Research. IBM Quantum Network roadmap. Available online: https://research.ibm.com/quantum/roadmap (accessed on 1 December 2023).
Microsoft Quantum. Microsoft’s approach to quantum computing. Available online: https://azure.microsoft.com/en-us/products/quantum (accessed on 1 December 2023).
Quantinuum. Quantinuum roadmap and strategy. Available online: https://www.quantinuum.com/roadmap (accessed on 1 December 2023).
PsiQuantum Corp. Million-qubit quantum computer roadmap. Available online: https://psiquantum.com/roadmap (accessed on 1 December 2023).
Xanadu Quantum Technologies. Photonic quantum computing platform. Available online: https://xanadu.ai/products (accessed on 1 December 2023).
McKinsey & Company. Quantum computing funding remains strong, but talent gap widening. McKinsey Technology Trends Outlook 2023.
Boston Consulting Group. The Coming Quantum Leap in Computing. BCG Technology Report 2023.
Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef]
Javadi-Abhari, A.; et al. Quantum computing with Qiskit. arXiv preprint 2021, arXiv:2105.01280. [Google Scholar]
Brown, B.J.; Loss, D.; Pachos, J.K.; Self, C.N.; Wootton, J.R. Quantum memories at finite temperature. Reviews of Modern Physics 2016, 88, 045005. [Google Scholar] [CrossRef]
Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Reviews of Modern Physics 2008, 80, 1083. [Google Scholar] [CrossRef]
Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coordination Chemistry Reviews 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
Herbert, S. The challenge of scaling quantum computers. Nature Reviews Physics 2022, 4, 549–550. [Google Scholar]
Cerezo, M.; et al. Variational quantum algorithms. Nature Reviews Physics 2021, 3, 625–644. [Google Scholar] [CrossRef]
Cao, Y.; et al. Quantum chemistry in the age of quantum computing. Chemical Reviews 2019, 119, 10856–10915. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.