An Adaptive Test for Two-Sample Accelerated Life Models

1. Introduction

In clinical trials, comparing the lifetimes of different groups, such as treatment and control groups, is crucial for evaluating therapeutic efficacy. The proportional hazards model ([2]), also referred to as the Cox model, has been widely adopted for such studies, particularly when data are censored. However, the proportional hazards assumption underlying the Cox model is restrictive and often difficult to satisfy in practice. An alternative approach is the accelerated life model ([5]), which models the direct relationship between lifetime and covariates. In this model, covariates act as acceleration or deceleration factors on the lifetime, making parameter interpretation more straightforward. For example, taking the logarithm of survival time yields a linear relationship between them. Despite this interpretational advantage, the accelerated life model presents obstacles in variance estimation because the asymptotic variance involves unknown densities, especially when censored data are present. The difficulty of estimating variance has hindered the development of model-checking procedures, necessitating the use of non-parametric methods. To address this issue, many authors have studied this model, including [10,13,15], among others.

To assess differences in variability between two groups through the cumulative hazard function in the accelerated life model, Yang ([15]) employed a weighting scheme that eliminates the density function from the variance expression through the hazard function. [15] further developed a corresponding test to validate the two-sample accelerated life model. This lack-of-fit test utilizes methodologies developed by [4]. The underlying approach is based on the idea that under $H_0$ (correct model specification) the scale estimators should converge, while under $H_1$ (model misspecification) these estimates diverge significantly. Thus, the test construction necessitates deriving multiple parameter estimates through the estimating function, which substantially increases computational complexity.

In addition, Yang’s method presents several practical challenges. First, it requires selecting an appropriate weight function that may vary depending on specific alternatives, a common issue in dealing with survival data. The careful selection of weight functions is crucial to obtain accurate results, which is not an easy process. Although various forms of weight functions have been proposed in the literature, including those by [11], the a priori selection of the optimal weight function remains a challenge. Second, both the derivation of the statistic and its practical implementation are also difficult due to the complexity of its mathematical expression. These difficulties can limit the practical applicability of the method in practice.

To address the limitations inherent in existing testing methods for accelerated life models, especially those associated with Yang’s method, this paper presents a novel procedure that dynamically determines optimal weight functions without requiring prespecified alternative hypotheses. Following [12], the proposed method adaptively determines optimal weighting schemes based on observed differences between cumulative hazard functions of the two samples. Unlike conventional testing procedures that depend heavily on assumed alternative hypotheses, this method offers enhanced flexibility and broader applicability. The proposed test statistic overcomes a limiting of existing weighted testing methods by not relying on specific alternatives, making it well-suited for developing robust testing procedures for two-sample accelerated life models.

The remainder of this paper proceeds as follows. Section 2 reviews Yang’s estimating function for accelerated life models. Section 3 and Section 4 develop proposed testing procedures. Section 5 presents numerical studies, including simulation results and a real-data example. Finally, Section 6 provides concluding remarks and directions for future research.

2. Estimating Function

Consider two censored samples with sample sizes $n_1$ and $n_2$. Let $X_{ij},i=1,2,j=1,\dots ,n_i$, be independent, positive lifetimes with absolutely continuous distributions $F_i$ that are also independent of the corresponding censoring variables $C_{ij}$. The observed data are $T_{ij}=\min (X_{ij},C_{ij})$, and ${\Delta }_{ij}=I(X_{ij}\le C_{ij})$, where $I(·)$ is the indicator function. Let $f_i\left(t\right)$ be the density of $F_i\left(t\right)$. Then the hazard function ${\lambda }_i\left(t\right)$ and the cumulative hazard function ${\mathsf{\Lambda }}_i\left(t\right)$ are defined as ${\lambda }_i\left(t\right)={\displaystyle \frac{f_i\left(t\right)}{1-F_i\left(t\right)}}$ and ${\mathsf{\Lambda }}_i\left(t\right)={\int }_0^t{\lambda }_i\left(u\right)du=-log(1-F_i\left(t\right))$, respectively.

We are interested in testing the null hypothesis $H_0$ that two samples exhibit a scale factor relationship. To this end, consider the accelerated life model, which assumes that ${\mathsf{\Lambda }}_1$ and ${\mathsf{\Lambda }}_2$ are related by

$${\mathsf{\Lambda }}_2\left(t\right)={\mathsf{\Lambda }}_1\left({\displaystyle \frac{t}{\theta }}\right)$$

for $\theta >0$, but otherwise unspecified. Equivalently, the random variables $X_{1j}$, $j=1,\dots ,n_1$, have the same distribution as the random variables $X_{2j}/\theta$, $j=1,\dots ,n_2$. Therefore, $\theta$ serves as the scale factor for acceleration or deceleration, depending on whether $\theta >1$ or $\theta <1$.

We assess the validity of the two-sample accelerated life model by using the available data $T_{ij}$ and ${\Delta }_{ij}$, assuming the censoring distributions are unknown. That is, we test $H_0$ that the accelerated life model holds. Let $N_{ij}\left(t\right)=I(T_{ij}\le t,{\Delta }_{ij}=1)$, $Y_{ij}\left(t\right)=I(T_{ij}\ge t)$, $N_i\left(t\right)={\sum }_j{N}_{ij}\left(t\right)$, and $Y_i\left(t\right)={\sum }_j{Y}_{ij}\left(t\right)$. The Nelson-Aalen estimator ([1]) of ${\mathsf{\Lambda }}_i(·)$ is

$${\widehat{\mathsf{\Lambda }}}_i\left(t\right)={\int }_0^{\min (t,{\max }_i{T}_{ij})}{\displaystyle \frac{1}{Y_i\left(s\right)}}d{N}_i\left(s\right).$$

Let $n=n_1+n_2$. [15] defined a scale estimator $\widehat{\theta }$ for the accelerated life model above as the solution to $S_n\left(a\right)=0$, for

$$S_n\left(a\right)=n^{1/2}{\int }_u^v{W}_n(t;a)\{{\widehat{\mathsf{\Lambda }}}_1\left(t\right)-{\widehat{\mathsf{\Lambda }}}_2\left(at\right)\}dt,$$

(1)

where $W_n(t;a)$ is a data-dependent weight function. [15] showed that choosing the weight function $W_n(t;a)=\eta \left\{\widehat{F}\left(t\right)\right\}/t$ for some function $\eta$, where $\widehat{F}$ is the product-limit estimator ([6]), eliminates the unknown density from the variance expression, thus simplifying the variance estimation procedures. Furthermore, [15] showed that $\widehat{\theta }$ is a consistent estimator for $\theta$ and follows a normal distribution under $H_0$. It is important to note that a finite integration range, $[u,v]$, containing sufficient data is used instead of $(0,\infty )$. This adjustment addresses the potential for explosive behavior near 0 or ∞, a challenge that can be mitigated by truncating the integration range. We use this estimating function to develop testing procedures for the accelerated life model.

3. Test Statistic

Let $D\left(t\right)={\mathsf{\Lambda }}_1\left(t\right)-{\mathsf{\Lambda }}_2\left(\theta t\right)$. Our primary aim is to evaluate the null hypothesis that two samples are related by a scale factor, $\theta$, consistent with the accelerated life model. Testing the null hypothesis $H_0$ is equivalent to verifying whether $D\left(t\right)=0$ for all t in $[u,v]$. To assess this, let $\widehat{D}\left(t\right)={\widehat{\mathsf{\Lambda }}}_1\left(t\right)-{\widehat{\mathsf{\Lambda }}}_2\left(\theta t\right)$ be the empirical counterpart, where ${\widehat{\mathsf{\Lambda }}}_i(·)$ represents the Nelson-Aalen estimator of the cumulative hazard function ${\mathsf{\Lambda }}_i(·)$. To standardize the difference at each time point t, define

$$Z\left(t\right)={\displaystyle \frac{\widehat{D}\left(t\right)}{{\widehat{\sigma }}_{NA}\left(t\right)}},$$

where the estimated variance, ${\widehat{\sigma }}_{NA}\left(t\right)$, under the assumption of independence is given by

$${\widehat{\sigma }}_{NA}^2\left(t\right)=\widehat{\mathrm{Var}}\left\{{\widehat{\mathsf{\Lambda }}}_1\left(t\right)\right\}+\widehat{\mathrm{Var}}\left\{{\widehat{\mathsf{\Lambda }}}_2\left(\theta t\right)\right\}.$$

Note ${\widehat{\sigma }}_{NA}^2(·)$ denotes its (approximately) estimated variance. Specifically,

$$\widehat{\mathrm{var}}\left\{{\widehat{\mathsf{\Lambda }}}_i\left({\theta }^{i-1}t\right)\right\}={\int }_0^t{\displaystyle \frac{d{N}_i(u;{\theta }^{i-1})}{Y_i^2(u;{\theta }^{i-1})}},i=1,2.$$

Following [12] associated with the estimating function in (1), consider the following statistic that is an integrated cumulative hazard difference on the integration range,

$$S_Z={\int }_u^v{W}_n\left(t\right)Z\left(t\right)dt,$$

where $W_n\left(t\right)$ is a data-dependent weight function. It is clear that the test statistic $S_Z$ is expected to perform well when the weight function $W_n\left(t\right)$ is proportional to the expected value of $Z\left(t\right)$ under $H_1$, as mentioned in [12]. This is because, in this case, a larger $Z\left(t\right)$ corresponds to a larger $W_n\left(t\right)$. Thus, one potential class of test statistics can be expressed as

$$S_Z={\int }_u^v{Z}^2\left(t\right)dt,$$

which results in a right tail distribution under $H_0$. However, this chi-squared distributed statistic might underperform for certain alternatives due to the extended right tail of its distribution. This issue could be resolved by choosing the weight function $W_n\left(t\right)$ that produces a statistic with a short right tail under $H_0$ and a pronounced right tail under $H_1$. Refer to [12] for more details. Based on [12] and [14], a convenient choice is to define $W_n(t;c)$ as $W_n(t;c)=\max \{Z\left(t\right),c\}$, where c is a specified value on $[u,v]$, such as 1.65. Let

$$S_Z\left(c\right)={\int }_u^v{W}_n(t;c)Z\left(t\right)dt.$$

Note that $S_Z$ would not show a long right tail under $H_0$ for a fixed value of c, such as 1.65. In contrast, under $H_1$, $S_Z\left(c\right)$ would yield a large value. Therefore, selecting an appropriate value for c is based on circumstance and can be challenging. To test the two-sample scale model, we adopt the adaptive approach to select the value of c in [12]. This approach is based on the development of a process with respect to c. To construct a robust testing procedure for the two-sample accelerated life model, we incorporate this process into the approximation procedures presented in Section 4.

4. Approximation Procedures

Let $N_{2j}(t;\theta )=I(T_{2j}/\theta \le t,{\Delta }_j=1)$ and $Y_{2j}(t;\theta )=I(T_{2j}/\theta \ge t)$ for $j=1,\dots ,n_2$. By the standard martingale theory, the processes

$$\begin{array}{cc}\hfill M_{1j}\left(t\right)& =N_{1j}\left(t\right)-{\int }_0^t{Y}_{1j}\left(s\right)d{\mathsf{\Lambda }}_1\left(s\right),\hfill \\ \hfill M_{2j}(t;\theta )& =N_{2j}(t;\theta )-{\int }_0^t{Y}_{2j}(s;\theta )d{\mathsf{\Lambda }}_2\left(\theta s\right)\hfill \end{array}$$

are mean-zero martingales ([3]). From these, we have

$$\begin{array}{cc}\hfill {\widehat{\mathsf{\Lambda }}}_1\left(t\right)-{\mathsf{\Lambda }}_1\left(t\right)& ={\int }_0^t{\displaystyle \frac{d{M}_1\left(s\right)}{Y_1\left(s\right)}},\hfill \\ \hfill {\widehat{\mathsf{\Lambda }}}_2\left(\theta t\right)-{\mathsf{\Lambda }}_2\left(\theta t\right)& ={\int }_0^t{\displaystyle \frac{d{M}_2(s;\theta )}{Y_2(s;\theta )}},\hfill \end{array}$$

where $M_1\left(s\right)={\sum }_{j=1}^{n_1}{M}_{1j}\left(s\right)$, $M_2(s;\theta )={\sum }_{j=1}^{n_2}{M}_{2j}(s;\theta )$, $Y_1\left(s\right)={\sum }_{j=1}^{n_1}{Y}_{1j}\left(s\right)$, and $Y_2(s;\theta )={\sum }_{j=1}^{n_2}{Y}_{2j}(s;\theta )$. Let

$$S_Z(c,\theta )={\int }_u^v{W}_n(t;c)Z_M\left(t\right)dt,$$

(2)

where $Z_M\left(t\right)=\{{\widehat{\mathsf{\Lambda }}}_1\left(t\right)-{\widehat{\mathsf{\Lambda }}}_2\left(\theta t\right)\}/{\widehat{\sigma }}_{NA}$. Note that the distribution $S_Z(c,\theta )$ is determined by $M_{1j}$ and $M_{2j}$ due to it being a sum of integrable martingales. However, its distribution remains analytically intractable. One approach to overcome this challenge is to substitute $M_{ij}$ with suitable approximations. Motivated by this, we derive an approximation process with respect to c that is formulated in terms of martingales $M_{1j}$ and $M_{2j}$. This serves as a fundamental component for developing robust testing procedures. A key property of martingales $M_{ij}\left(t\right)$ is that they have zero expectations, $E\left\{M_{ij\left(t\right)}\right\}=0$, with variance $Var\left\{M_{ij}\left(t\right)\right\}=E\left\{N_{ij}\left(t\right)\right\}$. See [9] for details. This approximation framework allows us to establish asymptotic properties and optimize the power performance of our proposed tests under various configurations.

We now derive an approximation process, $S_Z^{*}(c,\widehat{\theta })$, from $S_Z(c,\theta )$ associated with $\widehat{\theta }$. As mentioned in [8] and [9], the distribution of $S_z(c,\theta )$ can be approximated by the normal multiplier. Let $\{G_{ij}:i=1,2,j=1,\dots ,n_i\}$ be independent random samples from the standard normal distribution. By the martingale properties of $M_{ij}\left(t\right)$ specified above, $M_{ij}\left(t\right)$ can be replaced by $N_{ij}\left(t\right)G_{ij}$. Applying this substitution to $S_Z(c,\theta )$ yields an approximation process $S_Z^{*}(c,\widehat{\theta })$, where $\widehat{\theta }$ is the estimator $\widehat{\theta }$. Specifically,

$$S_Z^{*}(c,\widehat{\theta })={\int }_u^v{W}_n^{*}(t;c)Z_M^{*}(t;\widehat{\theta })dt,$$

(3)

where

$$\begin{array}{cc}\hfill W_n^{*}(t;c)& =\max \{Z_M^{*}(t;\widehat{\theta }),c\},\hfill \\ \hfill Z_M^{*}(t;\widehat{\theta })& =\{{\widehat{\mathsf{\Lambda }}}_1^{*}\left(t\right)-{\widehat{\mathsf{\Lambda }}}_2^{*}\left(\widehat{\theta }t\right)\}/{\widehat{\sigma }}_{NA}\left(t\right),\hfill \end{array}$$

with

$${\widehat{\mathsf{\Lambda }}}_i^{*}\left({\widehat{\theta }}^{i-1}t\right)={\displaystyle \frac{{\sum }_{i=1}^2{\sum }_{j=1}^{n_i}{(-1)}^{i-1}{G}_{ij}{\Delta }_{ij}I(u\le T_{ij}/{\widehat{\theta }}^{i-1}\le v)}{Y^{2-i}\left(T_{1j}\right)Y_2^{i-1}(T_{2j};\widehat{\theta })}},i=1,2.$$

Note that $S_Z^{*}(c,\widehat{\theta })$ in (3) can be expressed as

$$S_Z^{*}(c,\widehat{\theta })=\sum _{i=1}^2\sum _{j=1}^{n_i}{(-1)}^{i-1}{G}_{ij}{\Delta }_{ij}I(u\le T_{ij}/{\widehat{\theta }}^{i-1}\le v){\displaystyle \frac{\left\{{\int }_{T_{ij}/{\widehat{\theta }}^{i-1}}^{\infty }{W}_n^{*}(s;c)ds\right\}}{Y^{2-i}\left(T_{1j}\right)Y_2^{i-1}(T_{2j};\widehat{\theta })}}.$$

Following [9], the conditional distribution of the process $S_Z^{*}(c,\widehat{\theta })$ given the data is asymtotically equivalent to the unconditional distribution of the process $S_Z(c,\widehat{\theta })$. The only random component in $S_Z^{*}(c,\widehat{\theta })$ is $G_{ij}$, so this formulation facilitates computation in numerical studies.

To validate the two-sample accelerated life model, we obtain a large number of realizations of $S_Z^{*}(c,\widehat{\theta })$ by generating $G_{ij}$, creating a reference distribution against which test statistics can be compared. Note that it is generated such that they maintain complete statistical independence from the observed data set. This approach enables robust assessment of the model’s validity under various conditions.

The procedures consists of two stages. First, we choose an optimum value of c from the null distribution approximation of the process $S_Z(c,\widehat{\theta })$ with respect to c. Note that although an ideal test would consider the entire range of c throughout $(0,\infty )$, we deliberately restrict the range to $[u,v]$ to circumvent computational challenges and theoretical complexities. In practical situations, we select $[u,v]$ to include all observed data. Then, model validation proceeds through analysis of the p-value corresponding to the adaptively selected c, providing a statistical foundation for assessing the model’s empirical fit.

Let $s_Z(c,\widehat{\theta })$ be the observed value of $S_Z(c,\widehat{\theta })$. We calculate the corresponding p-value $p\left(c\right)$ to $s_Z(c,\widehat{\theta })$ through the approximation distribution of $S_Z(c,\widehat{\theta })$ under $H_0$. This procedure generates the null distribution of $P_c=\min \{P\left(c\right):c\mathrm{in}[u,v]\}$, where $P\left(c\right)$ is the random counterpart of $p\left(c\right)$. Note that the distribution of $P_c$ is based on the minimum value of $P\left(c\right)$, as this represents the most statistical significance, thereby offering the most reliable criterion for evaluation. We then adaptively identify the optimal value of c that yields the minimum p-value of $p\left(c\right)$, i.e., $p_c=\min \{p\left(c\right):c\mathrm{in}[u,v]\}$. Among evaluated p-values, smaller p-values provide stronger evidence against the null hypothesis, supporting the alternative hypothesis.

By arguments in [12], $Z_M(·)$ asymptotically converges to a zero-mean process, which we denote as $Z_G(·)$. Thus, as demonstrated by [12], the process over c given by ${\int }_u^v\max \{Z_M(t;\widehat{\theta }),c\}{Z}_M\left(t\right)dt$ converges to ${\int }_u^v\max \{Z_G(t;\widehat{\theta }),c\}{Z}_G\left(t\right)dt$. It follows that $P\left(c\right)$ converges to the survival function evaluated at this integral involving $Z_G$. For further details, refer to [12]. Similar arguments were previously presented by [8].

We utilize simulation-based approaches to estimate the asymptotic distribution of the process. To approximate the distribution of $S_Z\left(c\right)$ under $H_0$, we generate multiple realizations of $S_Z^{*}(c,\widehat{\theta })$ by simulating normal random samples $G_{ij}$ the only source of randomness in $S_Z^{*}(c,\widehat{\theta })$. From a collection of realizations of $S_Z^{*}(c,\widehat{\theta })$, we obtain the corresponding p-value, denoted by $P^{*}\left(c\right)$. Subsequently, the null distribution of $P_c$ is approximated based on multiple sets of realizations, from which $P_c^{*}=\min \{P^{*}\left(c\right):c\mathrm{in}[u,v]\}$ is derived. This enables empirical estimation of the null distribution of $P_c$ using $P_c^{*}$. Notably, the asymptotic equivalence between the conditional distribution of $S_Z^{*}(c,\widehat{\theta })$ given the data and unconditional distribution of $S_Z(c,\widehat{\theta })$ justifies the simulation approach as a robust method for testing. Finally, as in [9] and [12], the p-value of the test, which is given by P($P_c<p_c$), can be empirically approximated by P($P_c^{*}<p_c$).

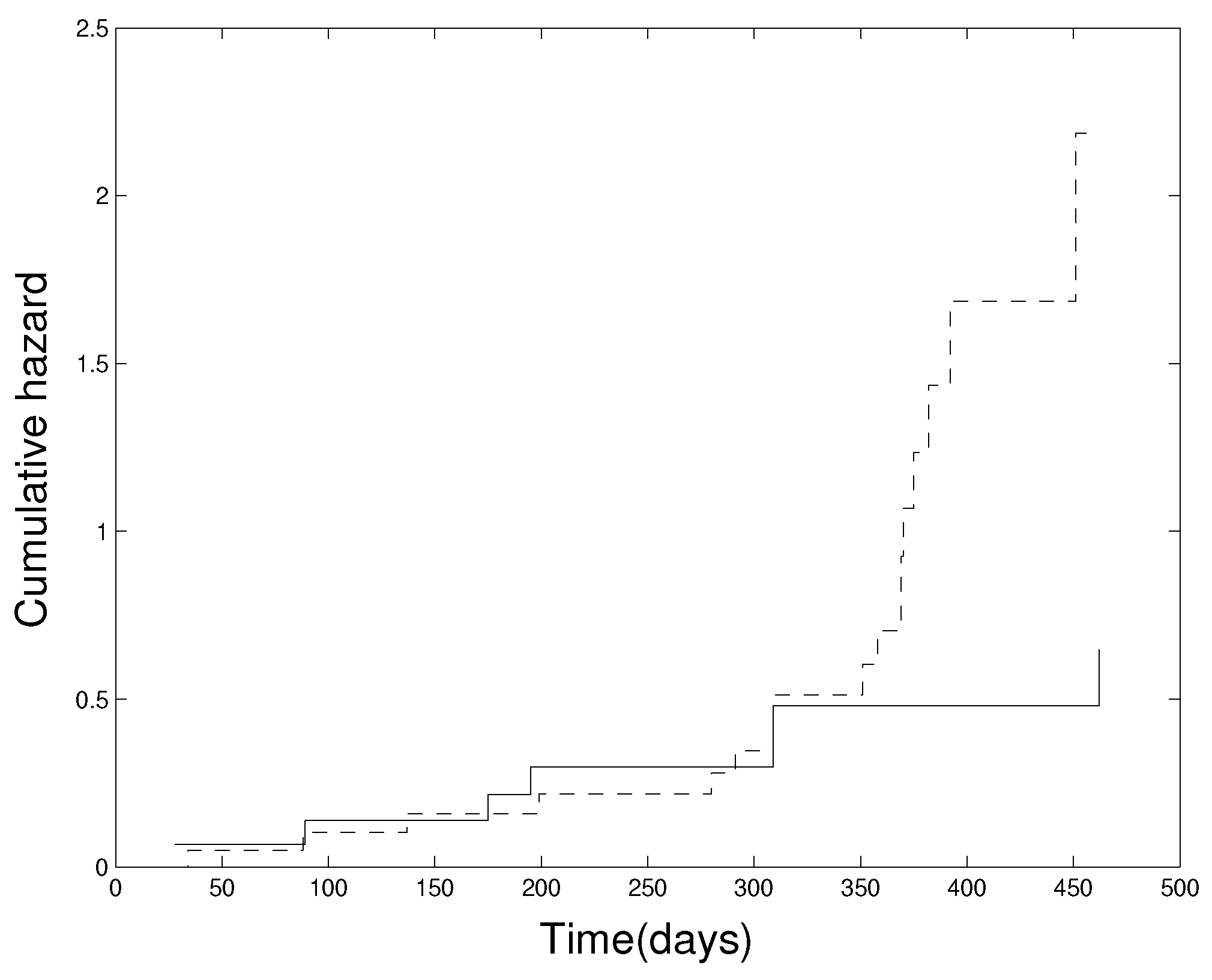
5. Numerical Study

To assess the statistical properties and performance of the proposed test, we conducted comprehensive simulations using several commonly used survival functions. These simulations evaluate the statistical power and reliability of the test in the varying sample sizes and censoring proportions. Similar to [8], the simulation incorporates several configurations: the log-logistic family and Weibull distributions with the scale parameter $\theta =$ 2 (scenario where the accelerated life model holds), as well as the lognormal survival distribution with the location (shift) parameter $\theta$ = 2 (scenarios where the accelerated life model is violated). Including both compatible and incompatible models enables examination of the test’s validity under correct model specification and its robustness to model misspecification. The specific simulation cases are outlined below.

• Case (a). We examine the case where $2^{1-i}{X}_{ij}$ follows the log-logistic density function $2t{(1+t^2)}^{-2}),t>0$, while the censoring variable $C_{ij}$ is characterized by density $2h^{2}t(1+h^2{t}^2)$, $t>0$, with some constant h.
• Case (b). We also investigate conditions where $2^{1-i}{X}_{ij}$ has Weibull density $2t{e}^{-t^2}$, $t>0$, with $log\left(C_{ij}\right)$ following a normal distribution with mean h and unit standard deviation.
• Case (c). Lastly, we consider scenarios where $log(X_{ij}-2^{i-1})$ is distributed as standard normal, while $log\left(C_{ij}\right)$ follows a uniform distribution on interval $[h,1+h]$. In contrast to cases (a) and (b), where the accelerated life model holds, this configurations represents the location shift model defined by the relationship ${\mathsf{\Lambda }}_2\left(t\right)={\mathsf{\Lambda }}_1(t-\theta )$. This setup enables evaluation of the test performance under conditions that violate the assumption of the accelerated life model.
• The constant h was chosen in each scenario to achieve the desired censoring proportions, allowing an evaluation of test performance under varying censoring proportions. In addition, the integration limits u and v in (1) define the temporal intersection of observations between the two groups. In survival analysis, explosive behavior is often observed near the endpoints of the estimating function. So, this setup is necessary to appropriately capture and account for such boundary effects. Specifically, u and v represent the lower and upper bounds of the shared observation times, where u is the maximum of the minimum observation times across the groups, and v is the minimum of the maximum observation times. Thus, the interval $[u,v]$ represents the time period in which observations from both groups coexist.

Table 1 and Table 2 present the power and type I error rates of the proposed test for the cases (a), (b), and (c), based on 500 repetitions. For each case, the simulations were conducted for censoring proportions of 25% and 50%, with sample sizes of 25 and 50. The simulations used the weight $W_n={(1-\widehat{F}\left(t\right))}^2{\widehat{F}}^2\left(t\right)/t$ for the estimating function defined in (1), which corresponds to a form of $\eta \widehat{F}\left(t\right)/t$. The results show that the test performs well overall, showing adequate power under both modest (25%) and heavy (50%) censoring proportions across all sample sizes considered, while maintaining Type I error rates close to the nominal level of $\alpha =0.05$ under $H_0$. The simulation results show the effectiveness of the proposed method in testing two-sample accelerated life models across various scenarios. To further demonstrate its practical utility, we applied the procedure to a real-world dataset.

The dataset comprises clinical data from 35 patients diagnosed with limited stage II or IIIA ovarian carcinoma at the Mayo Clinic and has become a benchmark for methodological validation in survival analysis. It stratifies patients into two cohorts based on tumor differentiation (low-grade versus well-differentiated). Many researchers have examined this dataset. Examples include [7,15] and Gill and [4]. They demonstrated the inadequacy of the accelerated life model. In line with them, this study further demonstrates that the relationship between disease grade and progression cannot be adequately captured by the two-sample scale modeling approach.

Specifically, the sample has a censoring percentage $13/35=0.37\%$, and the estimated scale parameter is $\widehat{\theta }=0.56$ using the same weight function as in the simulations. The observed $p-$value is 0.0075, obtained at $c=0$. The reference set for the test was constructed using the 5000 realized samples $G_{ij}$ drawn from $N(0,1)$. This reference set generates the null distribution of $P_c$ from which the approximate $P(P_c^{*}<p_c)=0.0077$ is calculated. These results provide strong evidence against the adequacy of the two-sample accelerated life model. Figure 1, which displays the estimated cumulative hazard functions for both groups in the dataset, supports this conclusion graphically. These results underscores the need for more flexible or nonparametric approaches to accurately characterize outcomes.

6. Concluding Remarks

Motivated by [12], we have proposed an adaptive and robust model-checking method for two-sample accelerated life models. The procedures use an estimating function that incorporates the integrated cumulative hazard difference developed by [15]. Following the approach in [12], our test employs a simple simulation-based approach to determine optimal critical values, yielding versatility that performs well across diverse scenarios without assuming specific alternative hypotheses. Simulation results demonstrate that the proposed approach provides comprehensive evaluation of statistical power and reliability under various conditions. Real-world data analysis validated the proposed method. Although developed specifically for accelerated life models, the methodology extends to other survival models, such as the accelerated hazards model, providing a flexible framework that maintains statistical power across diverse lifetime distributions.