The Orthogonal Formulation of Thales' Theorem A note on the Foundation of Geometry

1. Introduction

Thales’ theorem (VI century B.C.), in one of its usual formulations, says that given two lines $r_1,r_2$ having a common point A, when intersected by two parallel lines, they determine correspondent segments over them: $A{P}_1,A{P}_2$ and $A{P}_1^{\prime },A{P}_2^{\prime }$, respectively, that are in the same ratio: $A{P}_1/A{P}_1^{\prime }=A{P}_2/A{P}_2^{\prime }$.

It is one of the oldest achievements in Greek geometry. Thales did not prove it, but used it for evaluating distances by angles, as it will clearly appear from the definitions that we give of segment multiplication. It is a formidable method for evaluating great distances (Eratosthenes used it to calculate Earth’s circumference). Later, Thales’ intuition was transformed into a theorem on segment proportions. Euclid postpones it to the sixth book of his thirteen books of Elements [3] (Proposition VI, 2). Namely, the proof is simple when corresponding segments have a rational ratio; if they are not commensurable, then very often certain kinds of arguments require some forms of Eudoxus’ hexaustion method, considering infinite sequences of rational ratios (Euclid VI, 1 in [3] and Proposition III, 3 in [8]). Segment multiplication is a key point in Hilbert’s book on the foundations of geometry [5]. In this paper, we consider a segment multiplication based on a particular case of Thales’ theorem, from which the general case easily follows. Then, the “correctness" of this segment multiplication is proved, and Thales’ theorem is related to the parallel axiom and to other fundamental concepts and theorems of Euclidean geometry.

2. Segment Multiplication

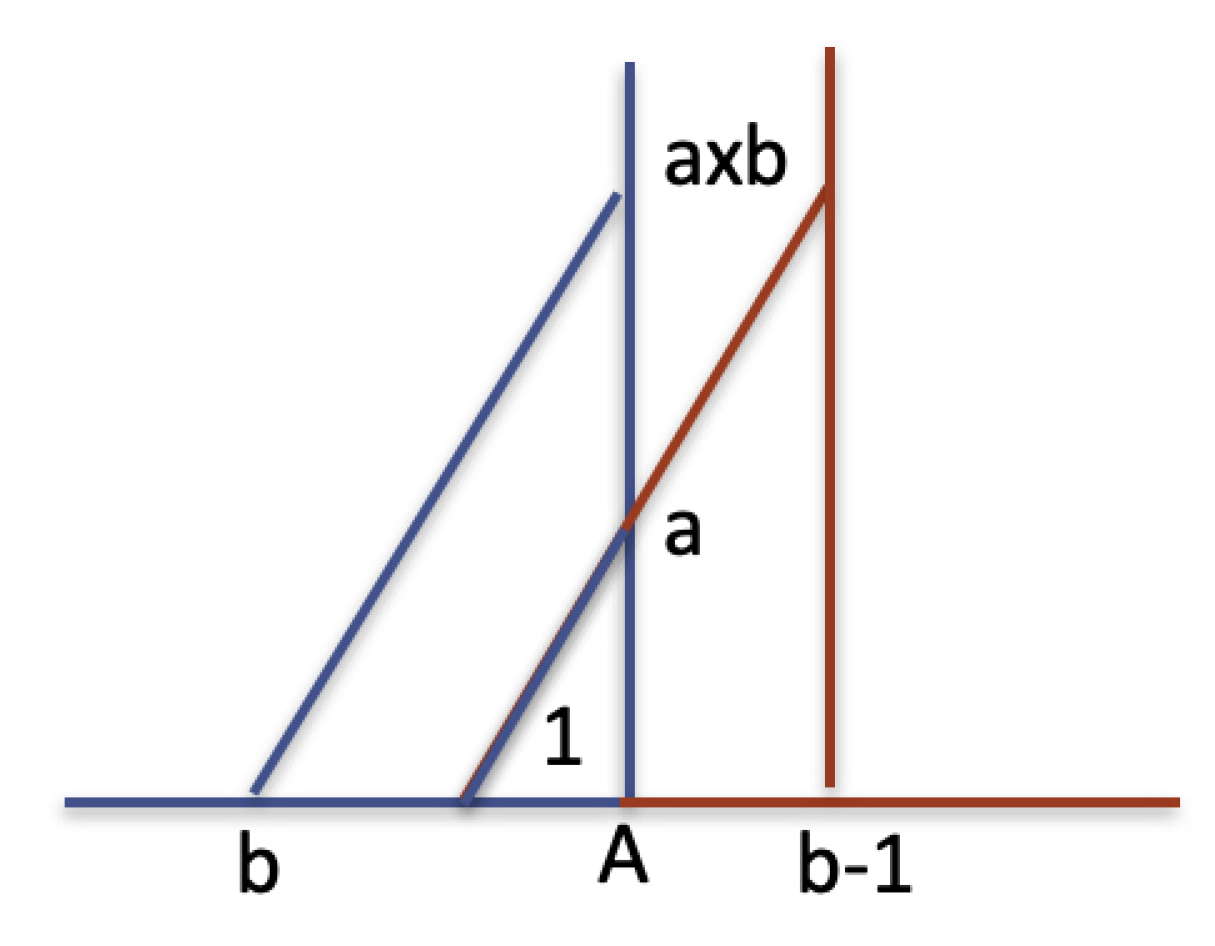
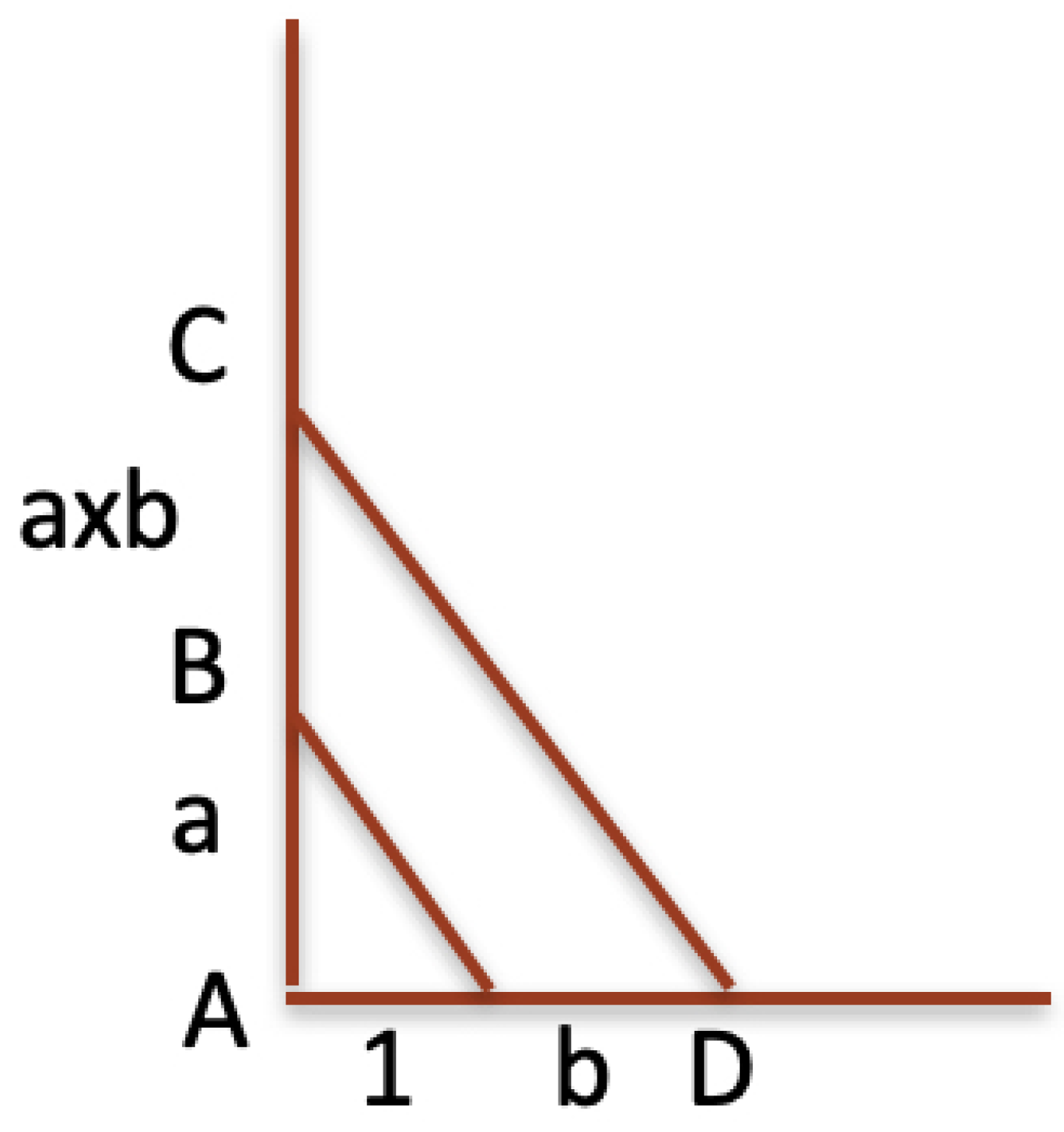
In Grundlagen der Geometrie [5], a classic book on the foundations of geometry (the first edition in 1899, the last one in 1971), Hilbert reformulates the theory of proportions of Euclidean geometry in equational form by defining the sum and product of segments. Figure 1 illustrates Hilbert’s definition of multiplication between two segments. It is based on parallel lines, but the proof that his segment multiplication is correct, that is, satisfies all the properties of multiplication on real numbers, is given by using a particular form of a theorem proved by Blaise Pascal in the context of the conic section curves [5].

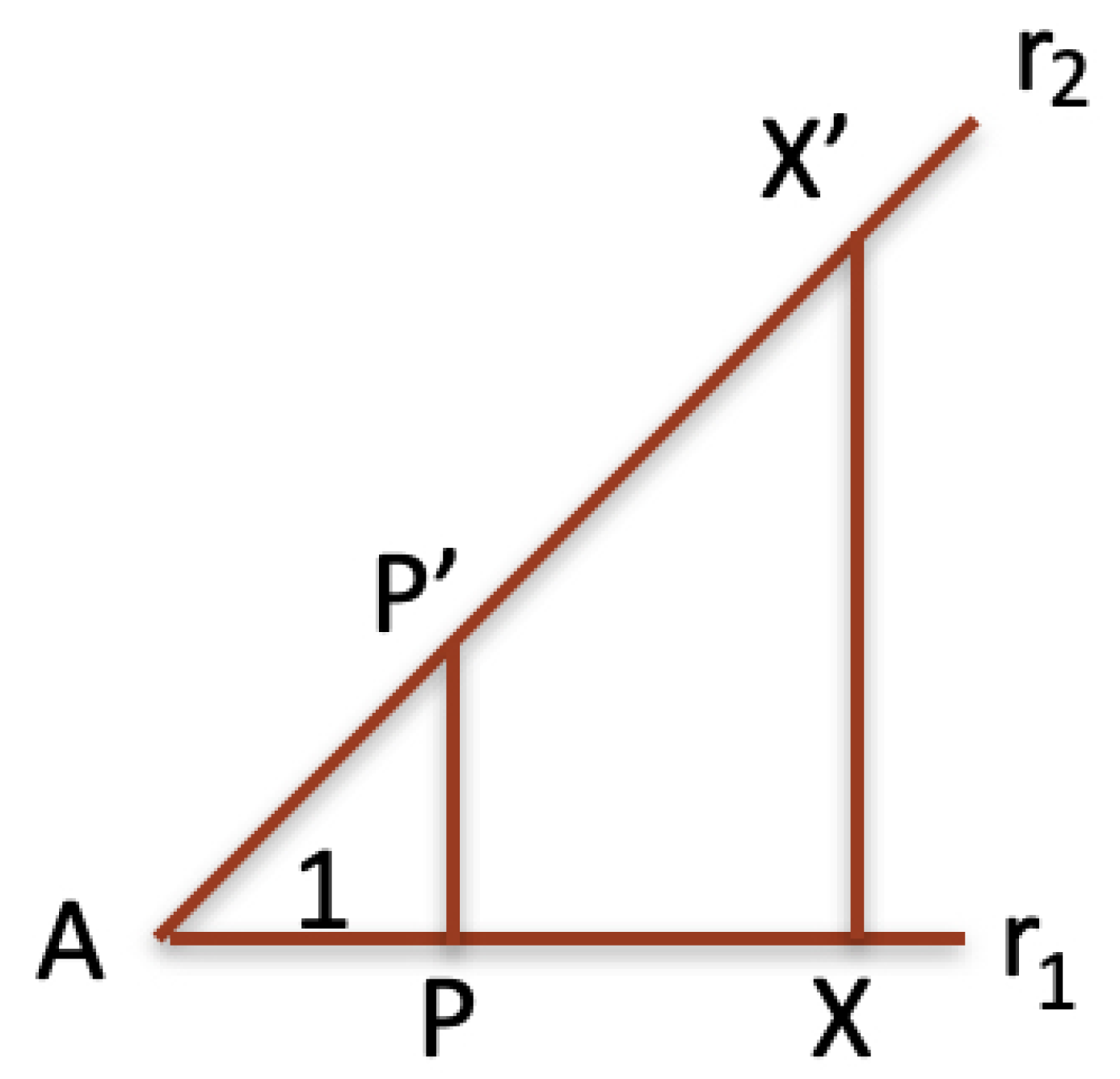
Let us provide a different definition of segment multiplication related to Thales’ theorem. In the following, a line will always be considered a straight line. Let $\alpha =(A,r_1,r_2)<\pi /2$ be an angle of two half-lines $r_1,r_2$ with common origin A. Let P be any point of $r_1$ and $P^{\prime }\in r_2$, the point where the orthogonal line to $r_1$ in P intersects $r_2$. We denote by $P{\mapsto }_{\alpha }{P}^{\prime }$ this orthogonal correspondence, omitting the subscript $\alpha$ when it is arguable by the context. If $OP=\mathbf{1}$, with $\mathbf{1}$ unitary segment, and X a point in $r_1$, we set $\left|\alpha \right|=A{P}^{\prime }$ (see Figure 2), and the orthogonal multiplication of $\left|\alpha \right|$ by $AX$ is given by:

$$\left|\alpha \right|{\times }_{\angle }AX=A{X}^{\prime }$$

The following algorithm computes the orthogonal segment multiplication.

Thales’ Orthogonal Multiplication Algorithm

1. Let $a\le b$ be two numbers for which $a\times b$ has to be calculated, and $\mathbf{1}$ a fixed unitary length;

2. Let $P,Q$ be the points on a half-line r with origin A, such that $AP,AQ$ have lengths $a,b$;

3. Let H be any point on r before P, draw the line h orthogonal to r in H;

4. Let $P^{\prime }$ be the point of h such that $A{P}^{\prime }=AP$ ($AH=\mathbf{1}$, $\alpha =HA{P}^{\prime }$, and $H{\mapsto }_{\alpha }{P}^{\prime }$);

5. Let $Q^{\prime }$ be the point on the line $A{P}^{\prime }$ such that $Q\mapsto Q^{\prime }$, then $ab=l\left(A{Q}^{\prime }\right)$.

Remark 2.1.

In the previous algorithm, the angle $P^{\prime }A{Q}^{\prime }$ is constructed such that the length of $A{Q}^{\prime }$ provides ab. Alternatively, we can fix an angle $\alpha =(A,r_1,r_2)$ and determine the point X of $r_2$ such that $AX$ has length a. Then, we search for the point $X^{\prime }$ of $r_2$ such that: 1) X is in $r_1$, 2) $X{\mapsto }_{\alpha }{X}^{\prime }$, and 3) $AX$ has length b. This point $X^{\prime }$ provides the segment $A{X}^{\prime }$ of length ab. The two methods correspond to different choices of the unitary length.

Now we state the orthogonal version of Thales’ theorem as a direct consequence of orthogonal segment multiplication. Let us define the length multiplication of a segment s by a number k, denoted by $k·s$, as the segment such that $l(k·s)=kl\left(s\right)$, where l is a function from segments to numbers giving the length (with respect to a unitary segment 1). The existence of a length function with this property is not obvious. Namely, it means that segments with length multiplication satisfy the Archimedean axiom (Euclid X, 1), holding on real numbers (given two numbers $p<q$, there always exists a positive integer such that $np>q$). This means that if $l\left(s\right)<l\left(s^{\prime }\right)$, then $l(n·s)>l\left(s^{\prime }\right)$, for some positive integer n.

Segments are identified by their length and extremities, which may change when they are moved. For this reason, very often, when no confusion can arise, segments and lengths (numbers) are denoted in the same way.

Theorem 2.2

(Thales VI B.C., orthogonal version). Given an angle $\alpha =(A,r_1,r_2)$, for any pair of segments $s,s^{\prime }$ of $r_1,r_2$, respectively:

$$s\mapsto s^{\prime }\iff l\left(s^{\prime }\right)/l\left(s\right)=l\left(\right|\alpha \left|\right).$$

Proof. 

According to the definition of ${\times }_{\angle }$, in $\alpha$ the correspondence $\mathbf{1}\mapsto \left|\alpha \right|$ holds. By the definition of segment length multiplication, the ratio between the lengths of two segments $l\left(s_1\right)/l\left(s_2\right)$ does not change if they are multiplied by the same number, that is, $l\left(s_1\right)/l\left(s_2\right)=l(k·s_1)/l(k·s_2)$. Therefore, changing the unitary length by a suitable factor $l\left(s\right)$, from $\mathbf{1}\mapsto \left|\alpha \right|$ we derive $s\mapsto l\left(s\right)·\left|\alpha \right|$, that is, $s\mapsto s^{\prime }$ with $s^{\prime }=l\left(s\right)·\left|\alpha \right|$. Whence, $l\left(s^{\prime }\right)=l\left(s\right)l\left(\right|\alpha \left|\right)$, and $l\left(s^{\prime }\right)/l\left(s\right)=l\left(\right|\alpha \left|\right)$. □

Remark 2.3.

According to the previous theorem, in an angle $\alpha =(A,r_1,r_2)$, the ratio between the lengths of orthogonally corresponding segments is always the same. This implies that the angle intrinsically determines the number $\left|\alpha \right|$ independently of any choice of the unitary length. Therefore, a “poetic" formulation of Thales’ theorem could be: Angles are pure numbers. □

Theorem 2.4.

The segment multiplication ${\times }_{\angle }$ commutes with the length function l:

$$l\left(s_1{\times }_{\angle }{s}_2\right)=l\left(s_1\right)l\left(s_2\right)$$

Proof. 

According to the proof of the previous theorem, for a suitable angle such that $s_1=\left|\alpha \right|$: $s_1{\times }_{\angle }{s}_2=l\left(s_2\right)·s_1$, therefore $l\left(s_1{\times }_{\angle }{s}_2\right)=l(s_2·l\left(s_1\right))=l\left(s_2\right)l\left(s_1\right)=l\left(s_1\right)l\left(s_2\right)$ □

The previous theorem tells us that Thales’ orthogonal theorem can be paraphrased by saying that the orthogonal segment multiplication ${\times }_{\angle }$ coincides with the segment length multiplication, or equivalently, that, for any angle $\alpha$ and number k, the orthogonal correspondence ${\mapsto }_{\alpha }$ preserves the segment length multiplication:

$$s{\mapsto }_{\alpha }{s}^{\prime }\iff k·s{\mapsto }_{\alpha }k·s^{\prime }.$$

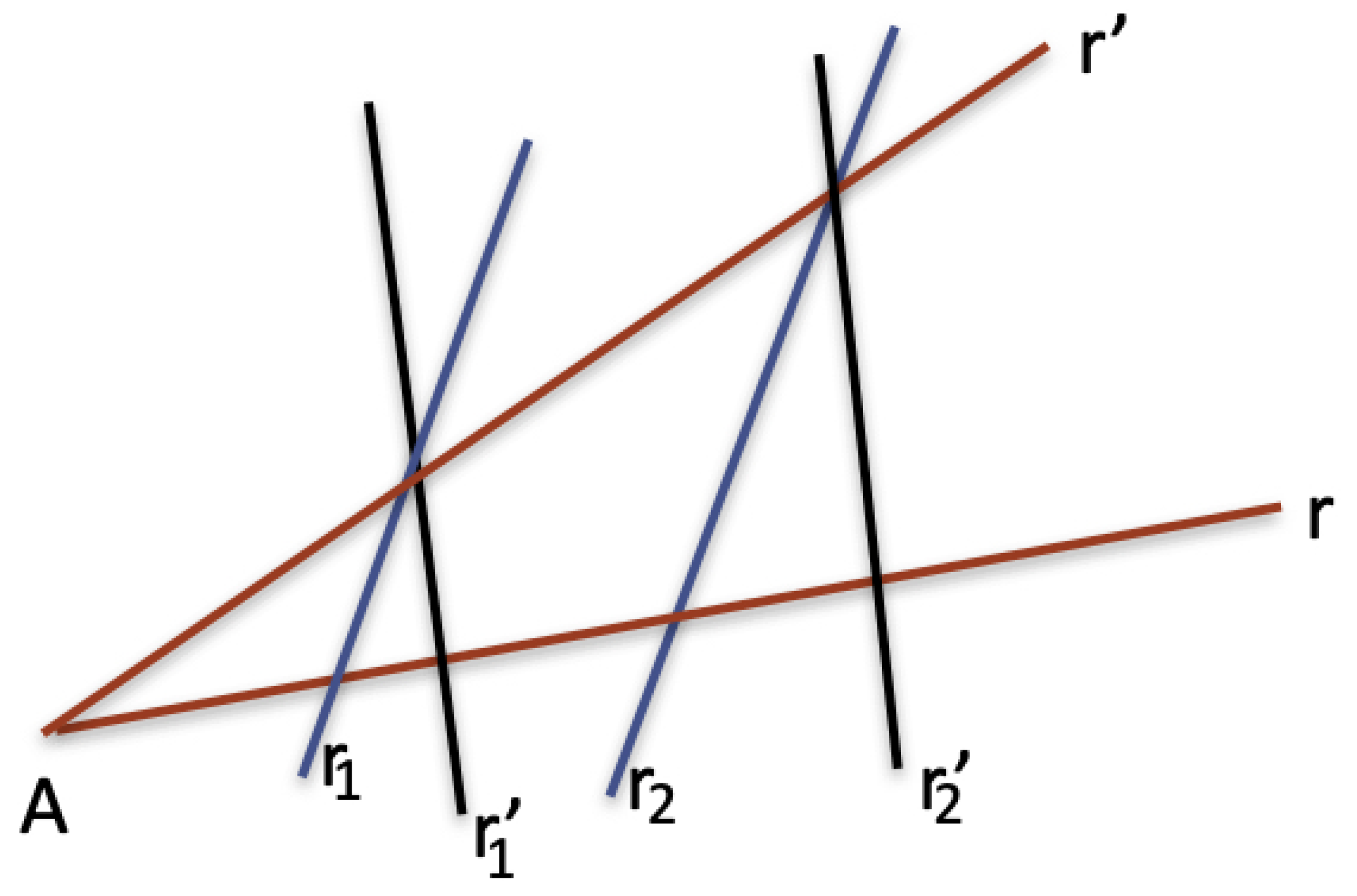
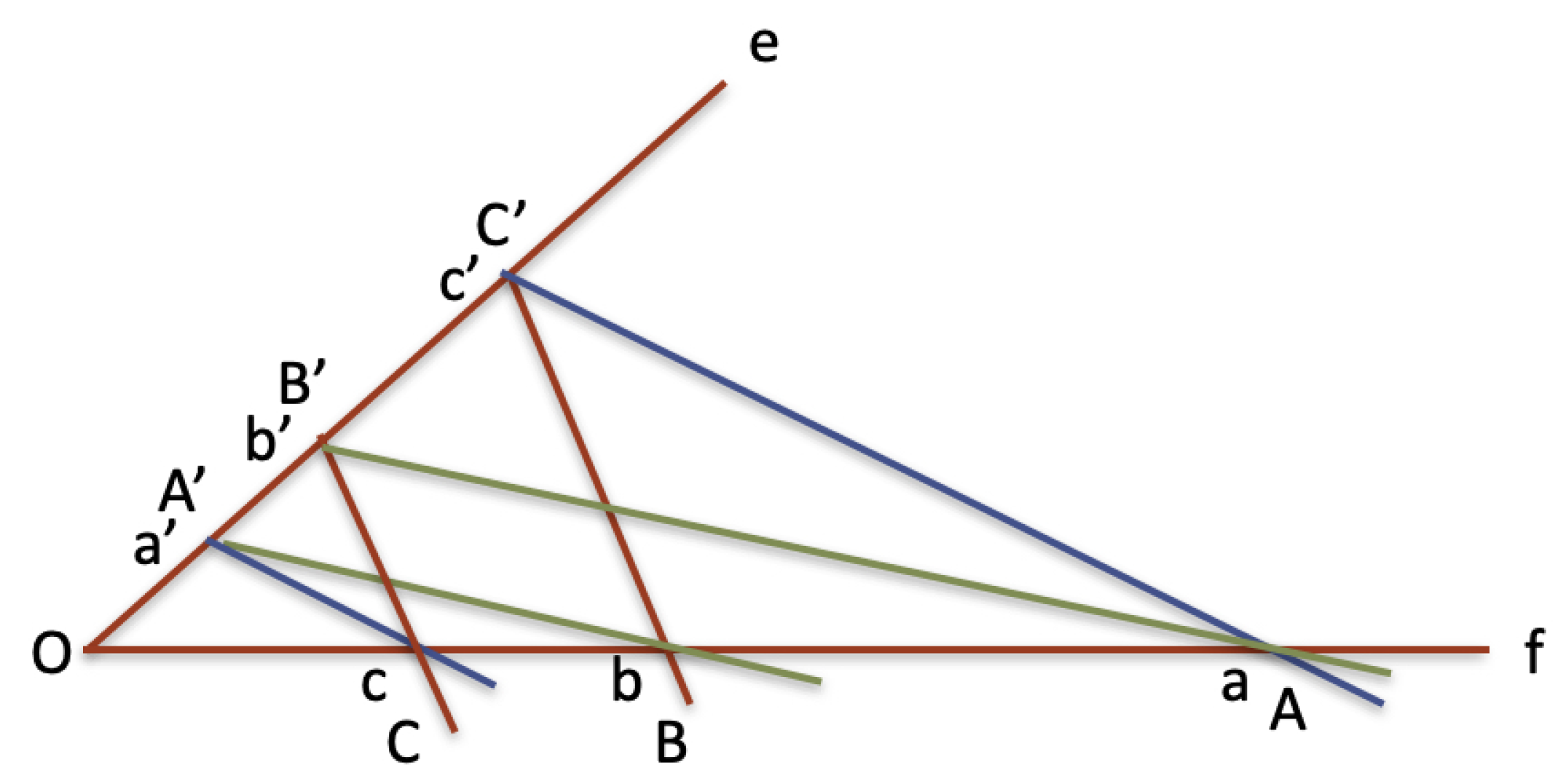
In general, Thales’ theorem is formulated in terms of parallel lines that are not necessarily orthogonal to one line of the angle. However, this more general formulation follows directly from the orthogonal version of the theorem by combining two applications of the orthogonal version. Figure 3 suggests clearly how to do it (the ratio between segments of lines $r_1,r_2$ with $r,r^{\prime }$ can be obtained from the ratios of $r_1^{\prime },r_2^{\prime }$ with $r,r^{\prime }$ and $r_1,r_2$. The formulation based on orthogonality also has the advantage of being generalized to non-Euclidean geometries, as we suggest in a following section.

Thales’ theorem, in its general form, can be inverted, as shown by the following theorem.

Theorem 2.5.

If the lines $r_1$ and $r_2$ of angle $(A,r_1,r_2)$ are cut by two distinct lines $r,r^{\prime }$ producing on them corresponding segments that are in the same ratio, then lines r and $r^{\prime }$ are parallel.

Proof. 

Lines $r,r^{\prime }$ can join outside of the angle either externally to $r_1$ or externally to $r_2$ (otherwise $r=r^{\prime }$). Let $r_1$ be the line where no intersection external to $\alpha$ exists. Then, reporting the angle $\alpha$ by the line $r_1^{\prime }$, such that $(A,r_2,r_1^{\prime })=\alpha$, we should have on $r_1^{\prime }$ corresponding segments that are equal to those formed on $r_1$; therefore, if $r,r^{\prime }$ join externally to $r_2$, they also join externally to $r_1$ against the hypothesis. □

Figure 3. Thales’ theorem obtained from its orthogonal version.

Figure 3. Thales’ theorem obtained from its orthogonal version.

According to Theorem 2.4, segment orthogonal multiplication ${\times }_{\angle }$ is commutative, associative, and distributive with respect to the segment addition.

Theorem 2.6.

The orthogonal segment multiplication ${\times }_{\angle }$ is correct and complete with respect to number multiplication.

Proof. 

Completeness follows when we assume the completeness of line: any real number x corresponds to a point $X\in r$ such that, if we fix a point A in r, then $x·l\left(1\right)=l\left(AX\right)$, where 1 is a unitary segment. □

Hilbert in [5] states the continuity of lines by using a completeness axiom that is more properly a meta-axiom, stating that no other system of axioms can exist that extends to a wider class of geometrical entities the properties following from the other 19 axioms (divided into five groups: Axioms of connection, Axioms of order, Axiom of parallels, Axioms of congruence, Archimedes’s axiom). Euclid investigates continuity in Book X on commensurability and uncommensurability. Modern classical approaches to continuity are due to Augustine Cauchy, Kari Weierstrass, Richard Dedekind, and Georg Cantor. They are all strictly related, in analytical or algebraic settings, to Eudoxus’ hexaustion method, on which Euclid builds his arguments, widely used and extended by Archimedes [3,4]. However, the birth of differential analysis, since its prodromes (related to Archimedes’ Method), before Newton and Leibniz (Bonaventura Cavalieri, Pierre de Fermat, Evangelista Torricelli, John Wallis, Blaise Pascal, Christiaan Huygens, James Gregory) belongs to an interrupted line of thought strictly related to continuity and incommensurability [7].

For Greeks, the completeness of lines was an implicit assumption, because they identified numbers with ratios of segments. The discovery of pairs of segments with ratios that are not fractions was the origin of the difficulty in stating general assertions about ratios between segments. For this reason, Euclid postpones proportions to the end of the geometry of the plane.

3. Euclid’s and Pythagoras’ Theorems on Right Triangles

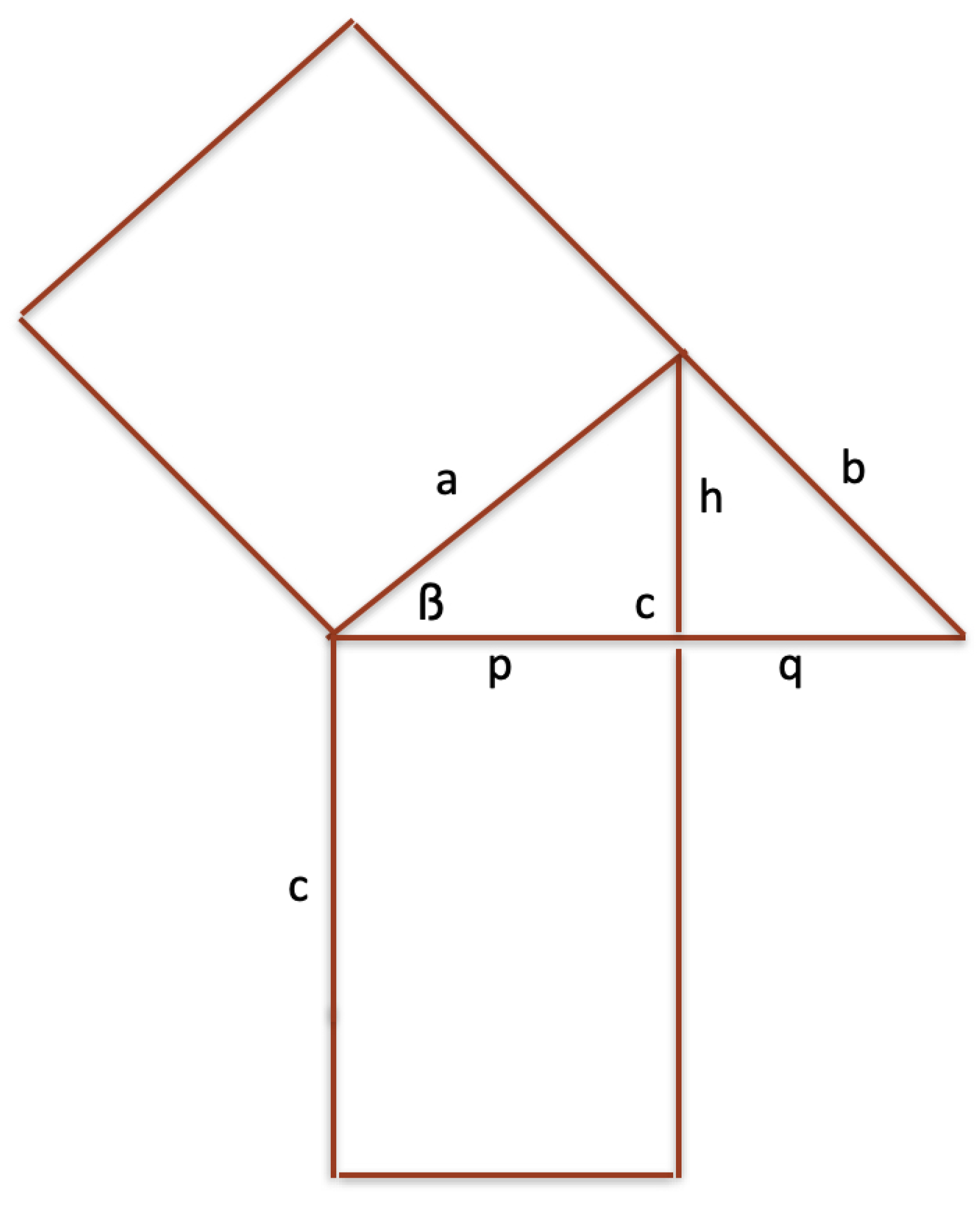
Euclid’s first theorem on right triangles says that the square over a cathete is equal to the product of the hypotenuse and the projection of a cathete over the hypotenuse (see Figure 4).

This theorem follows directly from Thales’ theorem, because if $\beta$ is the angle opposite to cathete b, and segments p, q the orthogonal projections of a and b in the hypotenuse, respectively, then $a=l\left(\right|\beta \left|\right)·p$ and $p+q=l\left(\right|\beta \left|\right)·a$. Therefore, we derive $a/p=p+q/a$, that is, $a^2=pc$.

From Euclid’s first theorem, we have $a^2=pc$, but even $b^2=qc$, therefore, summing:

$$a^2+b^2=pc+qc=(p+c)c=c^2$$

This proof is reported by Erwin Schöredinger [11] as the shortest proof of Pythagoras’ theorem.

Figure 4. Euclid’s first theorem: $pc=a^2$.

Figure 4. Euclid’s first theorem: $pc=a^2$.

Euclid’s second theorem says that the square of the height with respect to the hypotenuse is equivalent to the rectangle of the two projections of the catheti over the hypotenuse. From Figure 5, it is easy to realize that the two angles marked by $\beta$ are equal (both summed to the angle $\mu$ give a right angle). Therefore, from Thales’ theorem, the equation $p/h=h/q$ follows, whence $h^2=pq$.

In conclusion, Euclid’s and Pythagoras’ theorems on right triangles directly follow from Thales’ theorem in orthogonal formulation.

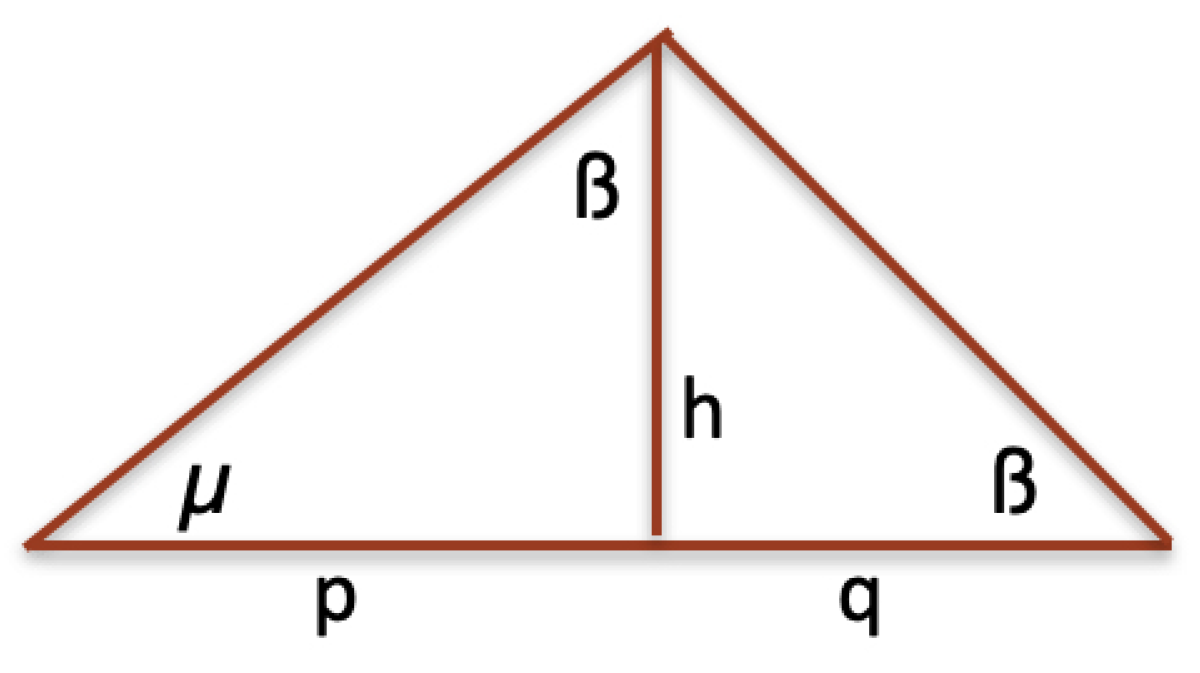
Let us consider another segment multiplication defined over an angle $\alpha =(A,r_1,r_2)$, say it vertical multiplication, as indicated in Figure 6.

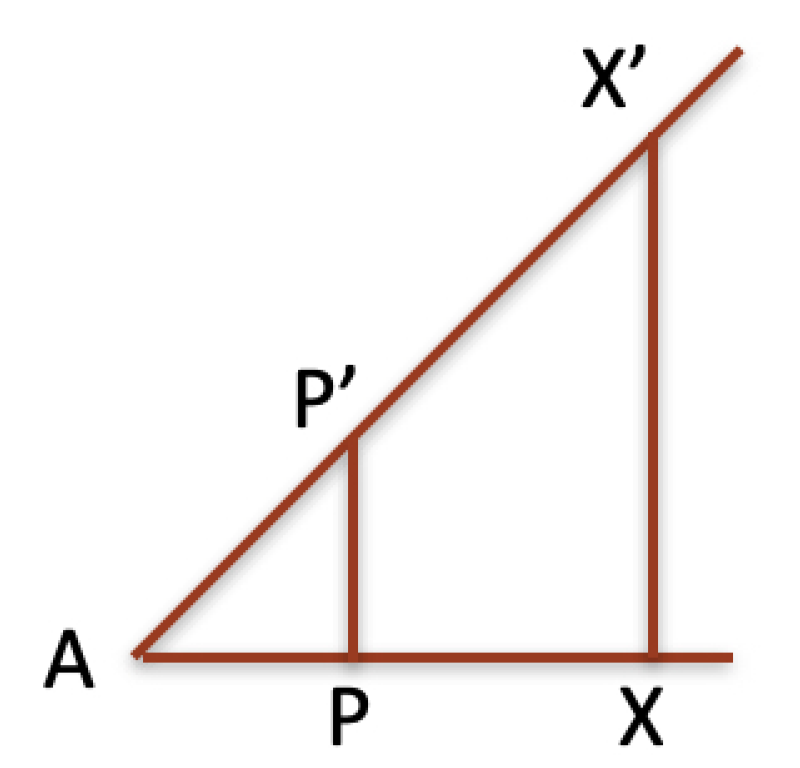
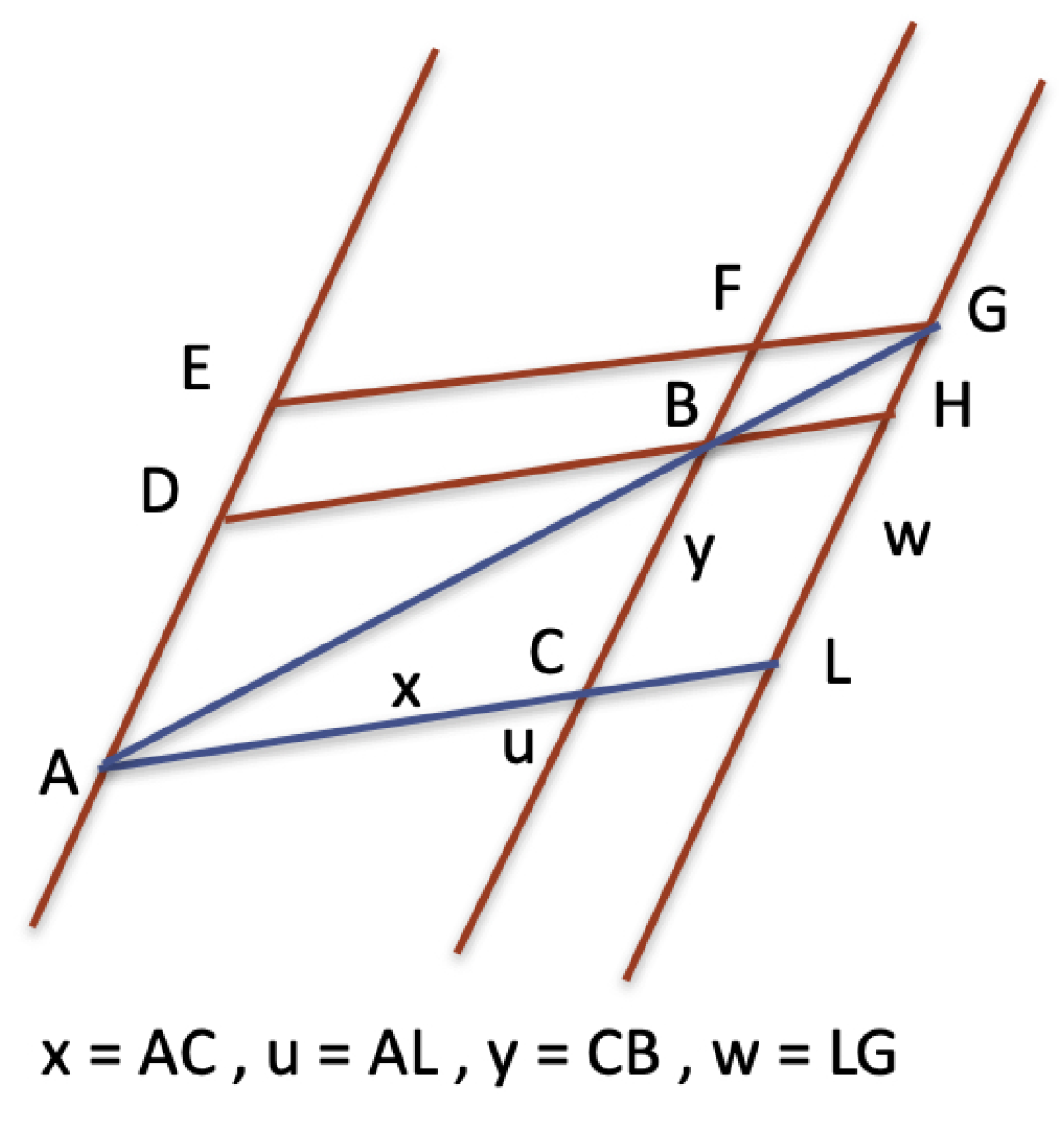
Theorem 3.1.

Vertical segment multiplication is equivalent to Hilbert’s segment multiplication, and it is also equivalent to the orthogonal multiplication.

Proof. 

The first equivalence is proved by Figure 7. The second equivalence follows from Pythagoras’ according to which vertical segments are all in the ratio $\sqrt{\left|\alpha \right|-1}$ with the corresponding horizontal segments. □

At the end of the third chapter of [5], where Hilbert uses Pascal’s theorem for proving the correctness of his segment multiplication, from this correctness, he derives Thales’ theorem, which is called Fundamental theorem of proportions. Now we prove Pascal’s theorem by using Thales’ theorem. Parallelism between lines will be denoted by $\left|\right|$.

Theorem 3.2

(Pascal). Let $A,B,C$ be three points internal to the edge e of an angle $(O,e,f)$, and $A^{\prime },B^{\prime },C^{\prime }$ be points internal to the edge f of angle (see Figure 8). If $C{B}^{\prime }\left|\right|B{C}^{\prime }$ and $C{A}^{\prime }\left|\right|A{C}^{\prime }$, then $B{A}^{\prime }\left|\right|A{B}^{\prime }$.

Proof. 

Let $a,b,c$ be the segments $OA,OB,OC$ respectively, and $a^{\prime },b^{\prime },c^{\prime }$ the segments $O{A}^{\prime },O{B}^{\prime },O{C}^{\prime }$ respectively. By the parallelism conditions $C{B}^{\prime }\left|\right|B{C}^{\prime }$ and $C{A}^{\prime }\left|\right|A{C}^{\prime }$ of the hypothesis we have:

$$a^{\prime }/c=c^{\prime }/a$$

(1)

$$b^{\prime }/c=c^{\prime }/b$$

(2)

Equation (1) implies the following equation:

$$c/a=a^{\prime }/c^{\prime }$$

(3)

By multiplying the corresponding members of Equations (2) and (3), we obtain the equation:

$$b^{\prime }/a=a^{\prime }/b$$

(4)

which implies, by Theorem 2.4, $B{A}^{\prime }\left|\right|A{B}^{\prime }$. □

We mention that Paul Bernays, in his Second Supplement to [5], proves Thales’ theorem by using the incenters (where bisectors of a triangle meet, but an implicitly restricted form of Thales’ is used).

Finally, another theorem equivalent to Thales’ theorem is the Gnomon Theorem (Euclid I, 43), saying that in any parallelogram the complements about the diagonal are equal (see Figure 9). Namely, $DEFB=BHLC$ because they are the difference of equal triangles $DEFB=EAG-FBG-DBA$, $BHLC=AGL-BGH-BCA$. Then $AEFC=ADHL$, therefore, $x·w=u·y$, which implies Thales’ theorem $x/y=u/w$.

4. Equiangularity

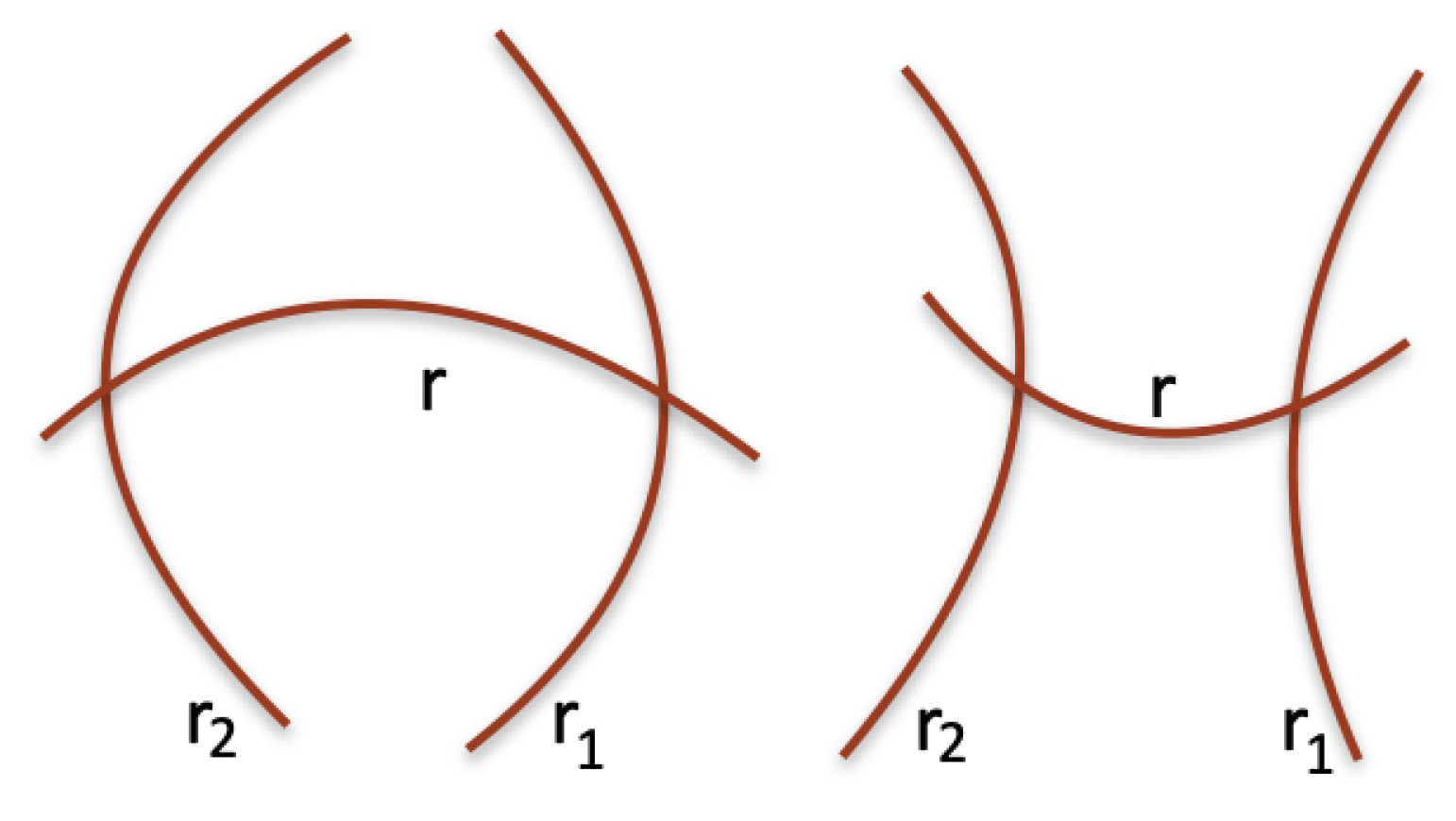
As we have already noticed, in the above orthogonal multiplications, we did not use parallel lines, but only orthogonality. This suggests to us a notion more general than parallelism. Two lines with a common point $r_1,r_2$ are equiangular when they form four equal angles. In Euclidean geometry, equiangular lines are orthogonal, and the angles they form are right angles. However, in the non-Euclidean geometries [2,6], orthogonality does not coincide with equiangularity, because two lines can form equal angles that are not right angles (see Figure 10). Equiangularity is important because it allows us to extend Thales’ angle multiplication to non-Euclidean geometries.

We say that a segment s of a line $r_1$ is equiangular with another line $r_2$ if $r_1$ is equiangular with $r_2$. The following theorem gives a property of equiangularity that enables us to define a restricted form of parallelism.

Theorem 4.1.

A segment $AP$ is equiangular with a line r if it is the shortest segment joining the point A with the line r. Conversely, the shortest segment joining A with r has to be equiangular with r.

Proof. 

Only one equiangular segment can join A with r in the shortest way, because if A segment $A{P}^{\prime }$ joins A with r and $P\ne P$, triangle $AP{P}^{\prime }$ can be formed and $AP=A{P}^{\prime }$, therefore the triangle is isoscele, therefore a point of the segment $P{P}^{\prime }$ there exists that is shorter than $AP$ and $A{P}^{\prime }$, then both these segments cannot be the shortest segments joining A with r. Conversely, if $AP$ is the shortest segment joining P with r, then the line including $AP$ has to be equiangular with r. Namely, if it forms with r angles that are not equal, then a triangle $PA{P}^{\prime }$ can be formed with $P^{\prime }$ placed in the smaller angle $APr$, and $A{P}^{\prime }$ should be smaller than $AP$, against the hypothesis that $AP$ is the shortest segment joining A with r. □

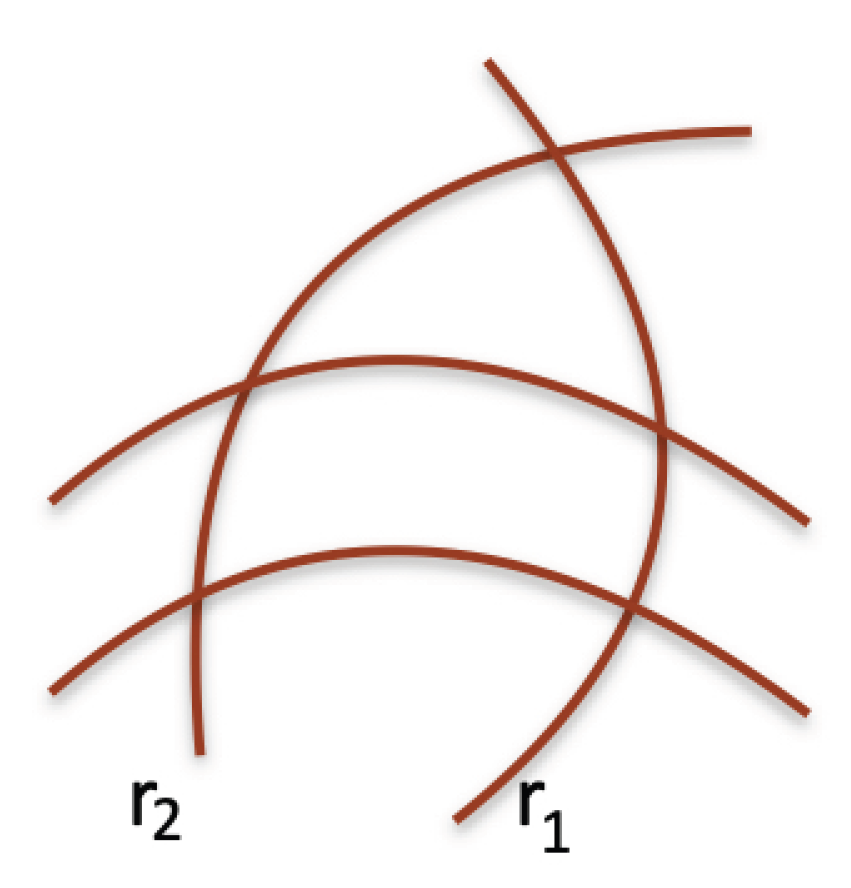
The notion of equiangularity enables us to extend the angle multiplication by using the equiangular correspondence in place of the orthogonal one. Moreover, we can introduce a notion weaker than parallelism. Two lines are quasi-parallel if a segment exists joining them that is equiangular with both lines. In this case, given a line r and a point A that does not belong to r, if $AP$ with $P\in r$ is the equiangular segment of r in P, the line r such that $AP$ is equiangular with $r^{\prime }$ in A is the quasi-parallel to r including the point A. A “curve" version of Thales’ theorem can be developed in cases as shown in Figure 11.

Figure 10. Equiangular and quasi-parallel (curve) lines in non-Euclidean geometries. The equiangular lines intersect by providing four angles that are not right angles.

Figure 10. Equiangular and quasi-parallel (curve) lines in non-Euclidean geometries. The equiangular lines intersect by providing four angles that are not right angles.

Figure 11. Two quasi-parallel (curve) lines intersecting a curve angle.

Figure 11. Two quasi-parallel (curve) lines intersecting a curve angle.

5. Conclusions

We developed an analysis of Thales’ theorem that has demonstrated its cruciality by considering a particular form of it, without any loss of generality, and thereby restoring its historical genesis and its special role in the correspondence between real numbers and lines. This correspondence is a cornerstone in the development of Greek mathematics and in the transition from it to post-Cartesian mathematics, as part of the general aritmetization process from which modern mathematical theories emerged.

In conclusion, we mention that another important theorem on the bisector of triangles states that, in any triangle, the bisector of an angle divides the opposite side into two parts that are proportional to the adjacent sides. (Euclid VI, 3). This theorem, which is an easy consequence of Thales’ theorem, is the basis of the cord bisection method discovered by Archimedes [9] in determining the (approximate) value of $\pi$ ($3+10/71<\pi <3+1/7$). In modern algebraic notation, it provides the recurrent formulae for the ledges $l_{n+1}=l_n/\sqrt{2+\sqrt{4-l_n^2}}$ and $L_{n+1}=L_n/(\sqrt{L_n^2+1}+1)$ (with $l_0=L_0=1$) for the edge of inscribed and circumscibed poligons, respectively (with $6·2^n$ number of edges) [9]. Archimedes’ cord bisection was the seed of trigonometry, later developed by Indian and Arab mathematicians [9,12].