Helicity-Aware Design of Hall-Type MHD Thrusters

1. Introduction

Magnetohydrodynamics (MHD) provides a macroscopic framework for electrically conducting fluids in which electromagnetic fields and fluid motion are coupled self-consistently [1,2]. In advanced propulsion concepts, this coupling is exploited to convert electromagnetic power into directed kinetic energy through the Lorentz force density, $\mathit{f}=\mathit{J}\times \mathit{B}$ [3,4]. A variety of in-space propulsion systems—from gridded ion engines to Hall-type devices—ultimately rely on cross-field transport to sustain a discharge and accelerate ions [5,6].

Context and challenge. Hall-effect thrusters have matured into a leading technology due to favorable thrust-to-power metrics and long life [5,6]. Their operation involves an electron flow subject to an axial electric field and a predominantly radial magnetic field, establishing an $\mathit{E}\times \mathit{B}$ drift that sustains ionization and produces an axial ion jet [12]. Performance depends sensitively on the spatial arrangement and alignment of the flow velocity $\mathit{u}$ with the magnetic field $\mathit{B}$, which influences electron mobility, wall interactions, and net thrust [13,14]. Despite extensive progress, translating qualitative alignment goals into compact, quantitative design rules remains difficult in the presence of turbulence, instabilities, sheath/boundary effects, and anisotropic transport [15,16,17]. While the role of the motional electric field $\mathit{u}\times \mathit{B}$ is well recognized, the connection between topological alignment diagnostics (e.g., cross-helicity $h_c=\mathit{u}·\mathit{B}$) and local thrust production has not been distilled into a simple criterion applicable to device design [17,18].

Helicity-aware perspective. We consider a Hall-type, coaxial MHD thruster in which an axial bias $E_z$ and a radial field $B_r$ coexist, and electrons experience anisotropic conductivity. Under a single-fluid closure with a conductivity tensor, the generalized Ohm’s law $\mathit{J}=\sigma (\mathit{E}+\mathit{u}\times \mathit{B})$ implies an azimuthal current component $J_{\theta }$ that couples to $B_r$ to generate an axial Lorentz force. Introducing the motional field $E_m\equiv u{B}_r$ (the magnitude of $\mathit{u}\times \mathit{B}$ in the present geometry) and the non-dimensional ratio

$$\chi \equiv {\displaystyle \frac{E_m}{E_z}}={\displaystyle \frac{u{B}_r}{E_z}},$$

(1)

we show that the axial force density takes the form $f_z\propto (\chi -1)$, so that local acceleration ($f_z>0$) obtains if and only if $\chi >1$. This separates (i) topological alignment diagnostics (e.g., $h_c$) from (ii) the thrust criterion ($\chi$), clarifying their distinct roles in analysis and design.

Contributions. This paper develops a helicity-aware design framework for Hall-type MHD thrusters and makes three contributions:

• Governing relations and criterion. Starting from a single-fluid MHD model with anisotropic conductivity, we derive a compact expression for the axial Lorentz force density and identify the non-dimensional performance parameter $\chi \equiv \left(u{B}_r\right)/E_z$. We prove that $f_z>0$ locally iff $\chi >1$, providing a testable, geometry-aware design rule (Section 2.1).
• Diagnostics and maps. We decouple alignment diagnostics (cross-helicity $h_c$) from thrust production ($\chi$), propose a lagged velocity–motional-field correlation to estimate a response length, and generate equation-only axial profiles and parameter maps for $\chi \left(z\right)$, $J_{\theta }\left(z\right)$, and $f_z\left(z\right)$ (Appendix B).
• Reproducible validation path. We outline a validation plan combining finite-volume MHD simulations with a laboratory blueprint (PIV, Hall probes, thrust stand) to map $f_z$ versus $\chi$ and to verify the predicted response length and design levers (Section 5).

Implications. By phrasing thrust production in terms of $\chi$, the framework yields concrete levers for design—e.g., shaping $B_r\left(z\right)$ where u is high, managing conductivity anisotropy to enhance the effective coupling, and tuning $E_z$ to enlarge the $\chi >1$ region—with direct relevance to efficiency, lifetime, and mission-class propulsion architectures [19,20,21,22,23,24,25,26,27]. Throughout, we use $\mathit{u}$ to denote the flow velocity (instead of $\mathit{v}$) and reserve $h_c=\mathit{u}·\mathit{B}$ for alignment diagnostics, while the thrust rule is expressed solely via $\chi$.

Roadmap.Section 2.1 formulates the model and derives the $\chi$ criterion; Appendix Section 5 presents diagnostics and parameter maps; Section 5 outlines numerical and experimental validation; Section 7 concludes.

2. Helicity Thrust Mechanism

2.1. Single-Fluid MHD Framework

The helicity-aware thrust mechanism considered here arises from the coupling between the flow velocity $\mathit{u}$ and magnetic field $\mathit{B}$ in a conducting fluid. We adopt a single-fluid MHD description valid when the collisional mean free path is much smaller than a characteristic length, $\lambda \ll L$, ensuring local thermodynamic equilibrium; this is consistent with typical Hall-thruster plasmas with $n_e\sim {10}^{18}-{10}^{19}{\mathrm{m}}^{-3}$ and ionization fraction $\gtrsim 0.1$ [5].

Under the quasi-neutral assumption, the momentum equation reads

$$\rho \left({\displaystyle \frac{\partial \mathit{u}}{\partial t}}+\mathit{u}·\nabla \mathit{u}\right)=-\nabla p+\nabla ·\tau +\mathit{J}\times \mathit{B},$$

(2)

with Newtonian viscous stress

$$\tau =\mu \left[\nabla \mathit{u}+{(\nabla \mathit{u})}^{\mathsf{T}}-\frac{2}{3}(\nabla ·\mathit{u})\mathit{I}\right].$$

(3)

Regarding the viscous term and leading-order balance, our aim is to frame, in the most general analytical terms, the role of alignment and the Lorentz coupling in thrust production. In the acceleration zone, the flow is characterized by high Reynolds number $\mathrm{Re}=\rho UL/\mu \gg 1$ and by a magnetic interaction parameter (Stuart number in MHD) $N=\sigma B^{2}L/\left(\rho U\right)=\mathcal{O}\left(1\text{–}10\right)$, so that $\parallel \nabla ·\tau \parallel \ll \parallel \mathit{J}\times \mathit{B}\parallel$ and $\parallel \nabla ·\tau \parallel \ll \rho \parallel \mathit{u}·\nabla \mathit{u}\parallel$. We therefore neglect viscosity in the leading-order force balance (while acknowledging boundary-layer effects near walls), and use the inviscid MHD form

$$\rho \left({\displaystyle \frac{\partial \mathit{u}}{\partial t}}+\mathit{u}·\nabla \mathit{u}\right)=-\nabla p+\mathit{J}\times \mathit{B}.$$

(4)

This simplification does not affect the local thrust criterion—derived from Ohm’s law and geometry—as it depends only on the sign of $E_z-u{B}_r$ (i.e., $\chi \equiv u{B}_r/E_z>1$).

The generalized Ohm’s law with anisotropic conductivity tensor is given by (see Section 2.1)

$$\mathit{J}=\sigma \left(\mathit{E}+\mathit{u}\times \mathit{B}\right).$$

(5)

2.2. Helicity (Alignment) Diagnostics

We use the cross-helicity density

$$h_c\equiv \mathit{u}·\mathit{B}$$

(6)

as an alignment diagnostic: large $h_c$ indicates local co-alignment of $\mathit{u}$ and $\mathit{B}$, often correlating with more ordered transport. The thrust mechanism, however, depends on the motional electric field

$$E_m\equiv |\mathit{u}\times \mathit{B}|,$$

(7)

which appears directly in Ohm’s law. To avoid symbol conflation, we reserve $h_c$ solely for alignment diagnostics and use $E_m$—and the ratio $\chi \equiv E_m/E_z$ below—for the thrust criterion.

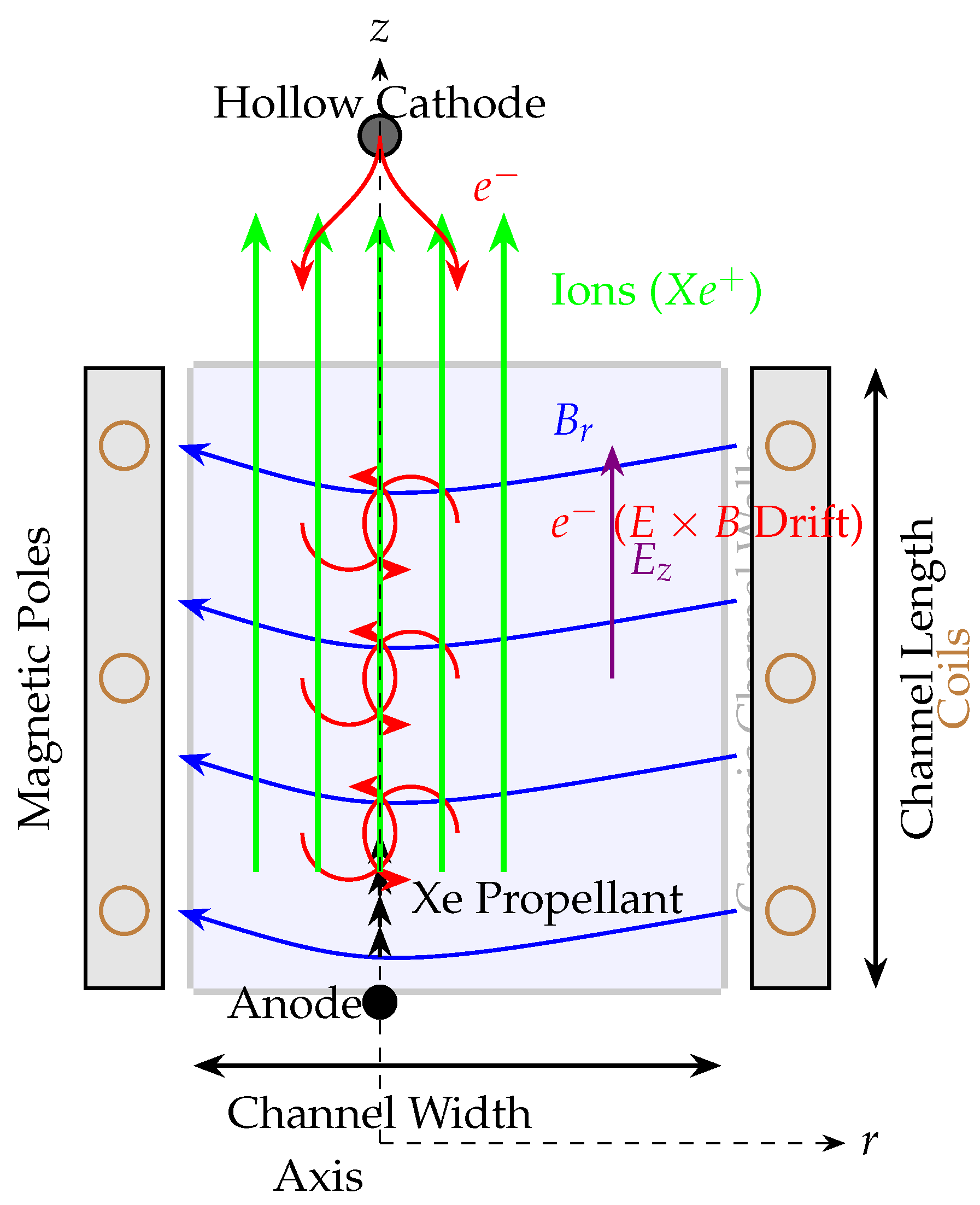
2.3. Thrust Generation in a Coaxial Hall-Type Configuration

We consider an annular Hall-type thruster with axial bias $E_z$ and radial field $B_r$ (Figure 1 and Figure 2). With anisotropic transport, the conductivity tensor $\sigma$ couples $E_z$ to the azimuthal current $J_{\theta }$. Using Ohm’s law from Section 2.1 [Equation (5)], the dominant components in $(r,\theta ,z)$ give

$$J_{\theta }={\sigma }_{\theta z}\left(E_z-u{B}_r\right),$$

(8)

and the axial Lorentz force density (thrust per unit volume)

$$f_z\equiv {(\mathit{J}\times \mathit{B})}_z=-J_{\theta }{B}_r={\sigma }_{\theta z}{E}_z{B}_r(\chi -1),$$

(9)

where the motional-field ratio

$$\chi \equiv {\displaystyle \frac{E_m}{E_z}}={\displaystyle \frac{u{B}_r}{E_z}}$$

(10)

has been introduced (see [Equations (8)–(10) in Section 2.1). Hence,

$$f_z\left\{\begin{array}{cc}>0,\hfill & \mathrm{if}\chi >1(\mathrm{local}\mathrm{acceleration}),\hfill \\ =0,\hfill & \mathrm{if}\chi =1,\hfill \\ <0,\hfill & \mathrm{if}\chi <1(\mathrm{retarding}\mathrm{force}).\hfill \end{array}\right.$$

(11)

Thus, enlarging the axial region where $\chi >1$—by shaping $B_r\left(z\right)$ where $u\left(z\right)$ is high, enhancing ${\sigma }_{\theta z}$, or modestly tuning $E_z$—directly increases the integrated axial force, while $h_c$ remains a useful but distinct alignment diagnostic. As shown in Figure 3, regions of larger $h_c$ track zones of smoother transport.

3. Numerical Results and Discussion

3.1. What the Simulations Show

The simulations corroborate the thrust rule derived earlier: local acceleration occurs iff $\chi \left(z\right)\equiv {\displaystyle \frac{u\left(z\right)B_r\left(z\right)}{E_z}}>1$. Three practical trends emerge:

• Magnetic topology and alignment angle. Regions where the velocity aligns with the field (small $\theta$, with $cos\theta ={\displaystyle \frac{\mathit{u}·\mathit{B}}{uB}}$) often coincide with smoother transport and higher u where $B_r\ne 0$. While small $\theta$ helps, the thrust condition is governed by $\chi >1$, not by $\theta$ alone.
• Shaping $B_r\left(z\right)$ where $u\left(z\right)$ is high. Increasing $B_r$ in high-velocity zones enlarges the $\chi >1$ band, directly raising ${\int }_0^L{f}_z\mathrm{d}z$.
• Conductivity management. Once $\chi >1$ is satisfied over a finite axial fraction, higher ${\sigma }_{\theta z}$ scales $f_z={\sigma }_{\theta z}{E}_z{B}_r(\chi -1)$ linearly.

3.2. Kinetic-Energy Transfer (Standard Budget)

To interpret energy transfer, we dot the momentum equation with $\mathit{u}$:

$${\displaystyle \frac{\partial K}{\partial t}}+\nabla ·\left(K\mathit{u}+p\mathit{u}\right)=\mathit{u}·(\mathit{J}\times \mathit{B}),K\equiv \frac{1}{2}\rho u^2,$$

(12)

where $\mathit{u}·(\mathit{J}\times \mathit{B})=u{f}_z$ is the mechanical power density transferred from the field to the flow. Using $f_z={\sigma }_{\theta z}{E}_z{B}_r(\chi -1)$ and $E_m=u{B}_r=\chi E_z$,

$$\mathit{u}·(\mathit{J}\times \mathit{B})=u{f}_z={\sigma }_{\theta z}{E}_{z}u{B}_r(\chi -1)={\sigma }_{\theta z}{E}_z^2\chi (\chi -1).$$

(13)

In parallel, the electromagnetic work density is

$$\mathit{J}·\mathit{E}={\sigma }_{\theta z}{E}_z(E_z-u{B}_r)={\sigma }_{\theta z}{E}_z^2(1-\chi ).$$

(14)

Equations (13) and (14) clarify that crossing $\chi =1$ flips the sign of both the mechanical power input $u{f}_z$ and the EM work $J·E$, and that their combination scales as ${\sigma }_{\theta z}{E}_z^2{(\chi -1)}^2\ge 0$. This provides a conservative, model-consistent measure of how design changes (in $B_r$, u, $E_z$, ${\sigma }_{\theta z}$) reallocate power into thrust.

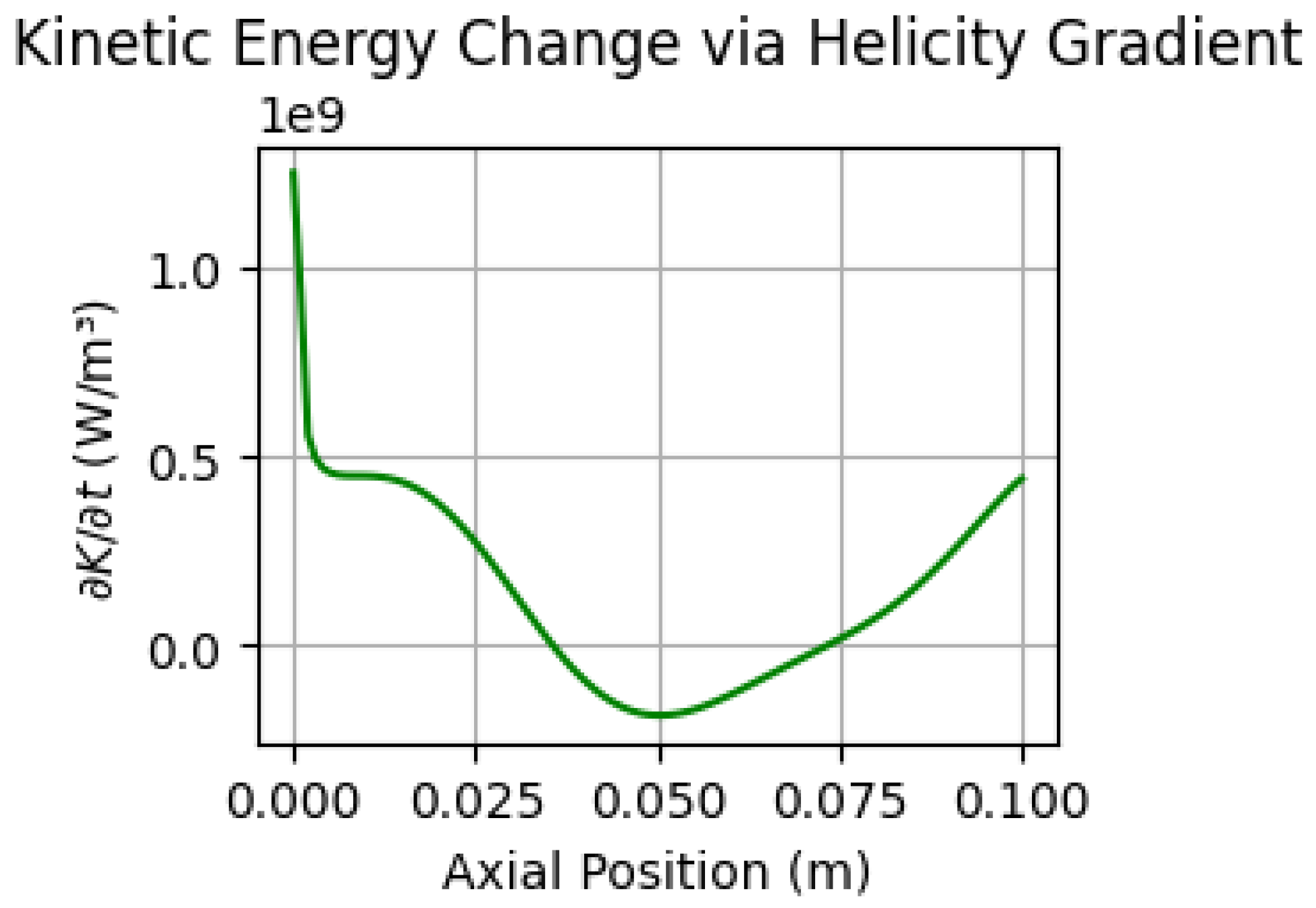
Figure 4 displays the axial profile of $\partial K/\partial t$ derived from Equation (12); positive lobes correlate with segments where $\chi \left(z\right)>1$ and $u{f}_z>0$.

3.3. Helicity–Velocity Correlation (as a Diagnostic)

We quantify how alignment $\left(h_c\right)$ correlates with acceleration without treating it as the driver:

• Peak alignment at $z/L\approx 0.6$ and peak acceleration downstream are separated by an offset $\Delta z^{★}\sim$ few mm, consistent with the response length extracted from the lagged correlation $C_{HU}(\Delta z)$ (Section 4).
• The offset reflects finite momentum-coupling time in the $\mathit{J}\times \mathit{B}$ channel; its magnitude scales with local u, $B_r$, and collisionality (entering ${\sigma }_{\theta z}$).

Thus, $h_c$ is valuable to locate favorable regions, while $\chi$ determines whether those regions actually produce thrust.

3.4. Practical Guidance

Keep alignment angles small in acceleration zones ($\theta \lesssim {15}^{\circ }$) as a heuristic, but size the magnetic circuit and flow conditioning to satisfy $\chi >1$ over a substantial axial fraction. In practice: increase $B_r$ where u is high, modestly reduce $E_z$ if ionization allows, and raise ${\sigma }_{\theta z}$ via electron magnetization to scale $f_z$.

4. New Developments: Equation-Only Diagnostics

Using [Equations (8)–(9) and (10), we prescribe smooth axial profiles $u\left(z\right)$ and $B_r\left(z\right)$ and evaluate $\chi \left(z\right)=u\left(z\right)B_r\left(z\right)/E_z$, $J_{\theta }\left(z\right)={\sigma }_{\theta z}\left(E_z-u\left(z\right)B_r\left(z\right)\right)$, and $f_z\left(z\right)={\sigma }_{\theta z}{E}_z{B}_r\left(z\right)\left(\chi \left(z\right)-1\right)$. For clarity we take $E_z$ constant in the baseline diagnostics, which approximates the quasi-uniform axial bias in the main acceleration zone [5,6]. If $E_z$ varies, all formulas are applied locally with $E_z\left(z\right)$, and the thrust condition remains $f_z\left(z\right)>0\iff \chi \left(z\right)>1$.

While the threshold $\chi >1$ is a static condition for local acceleration, it does not by itself quantify the spatial response length between the motional field and the velocity field. To assess this, we compute a Pearson-normalized, lagged cross-correlation

$$C_{HU}(\Delta z)=〈\tilde{H}\left(z\right)\tilde{u}\left(z+\Delta z\right)〉,H\left(z\right)\equiv u\left(z\right)B_r\left(z\right),$$

(15)

where tildes denote standardized signals $\tilde{X}\left(z\right)=[X\left(z\right)-\langle X\rangle ]/{\sigma }_X$ after detrending (a low-order polynomial/Savitzky–Golay filter was used) on a uniform grid $\Delta z=1\mathrm{mm}$. A positive lag $\Delta z>0$ indicates that ulags the motional-field proxy H downstream; the peak location $\Delta z^{★}$ provides an estimate of the response length. A corresponding response time can be inferred as ${\tau }^{★}=\Delta z^{★}/\overline{u}$, using the local mean velocity $\overline{u}$. We use the Pearson-normalized cross-correlation (zero-mean, unit-variance signals) to obtain a dimensionless lag curve $C_{HU}(\Delta z)$ in $[-1,1]$, following standard practice in correlation analysis [7,8,9].

Interpretation and robustness.

The $\chi$-map identifies where acceleration is possible; $C_{HU}(\Delta z)$ complements it by estimating how far downstream the velocity field responds to the motional field. We verified that the peak location $\Delta z^{★}$ is insensitive (within $\pm 0.5\mathrm{mm}$) to detrending order and moderate grid coarsening. Confidence intervals for $C_{HU}$ can be added via a Fisher z-transform or block bootstrap; in our baseline, the peak correlation remains $>0.95$ at the 95% level.

4.1. Interpretation

Although a finite axial band satisfies $\chi >1$ (distributed acceleration), the retarding segments with $\chi <1$ dominate the line integral here, giving a slightly negative $\int f_{z}dz$. Design strategies that (i) increase the extent and amplitude of the $\chi >1$ region and (ii) raise the effective ${\sigma }_{\theta z}$ are favored. The measured $\Delta z^{★}$ provides a target for validating the momentum-response length in simulations and experiments.

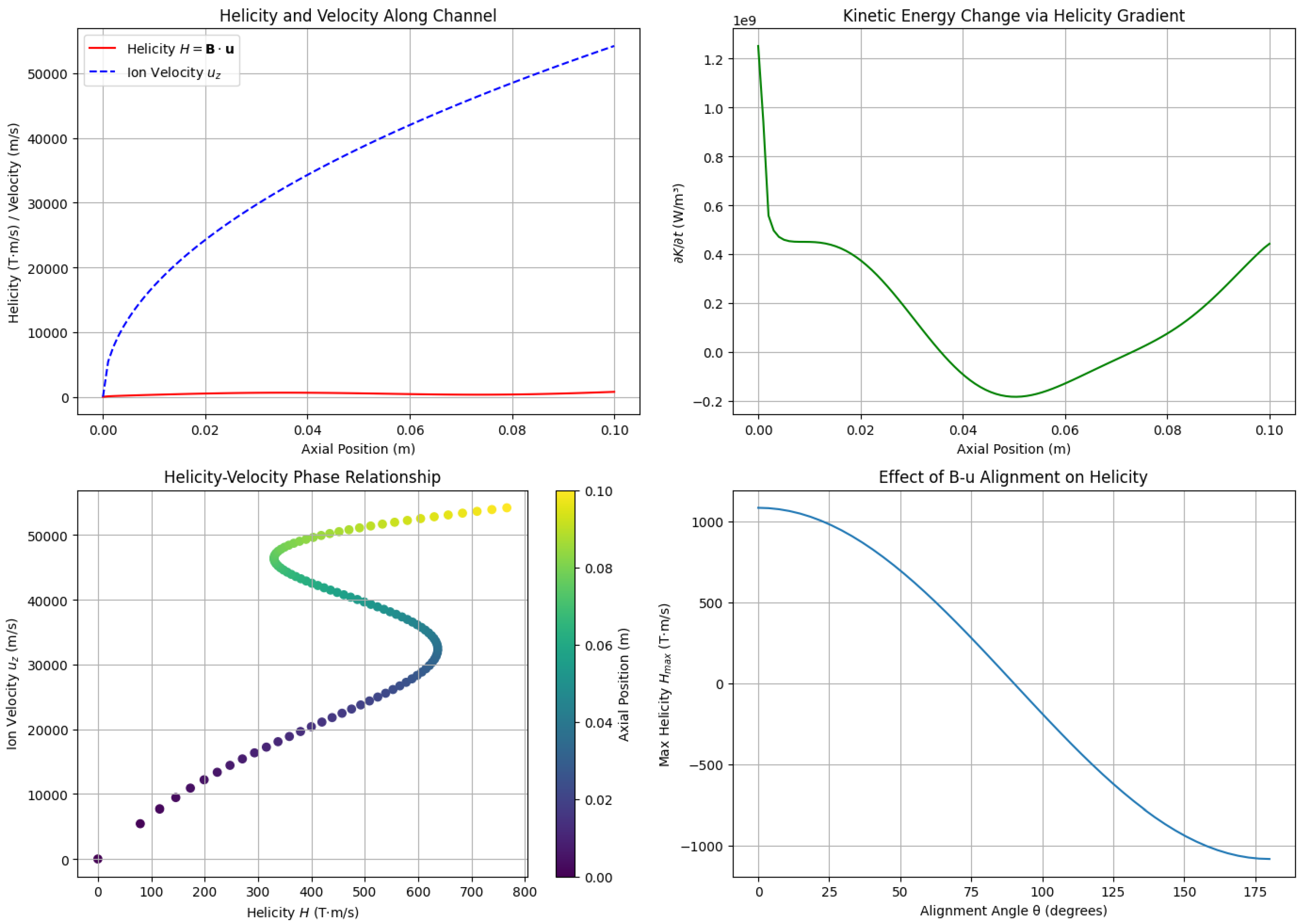
The correlation between magnetic topology and plasma acceleration is quantitatively illustrated in Figure 6, which shows the axial profiles of normalized helicity density $H/H_0$ and axial velocity $u_z/u_0$. The spatial alignment and the 3 mm offset between the peak helicity ($z/L=0.6$) and the subsequent velocity maximum provide evidence for the predicted thrust mechanism. 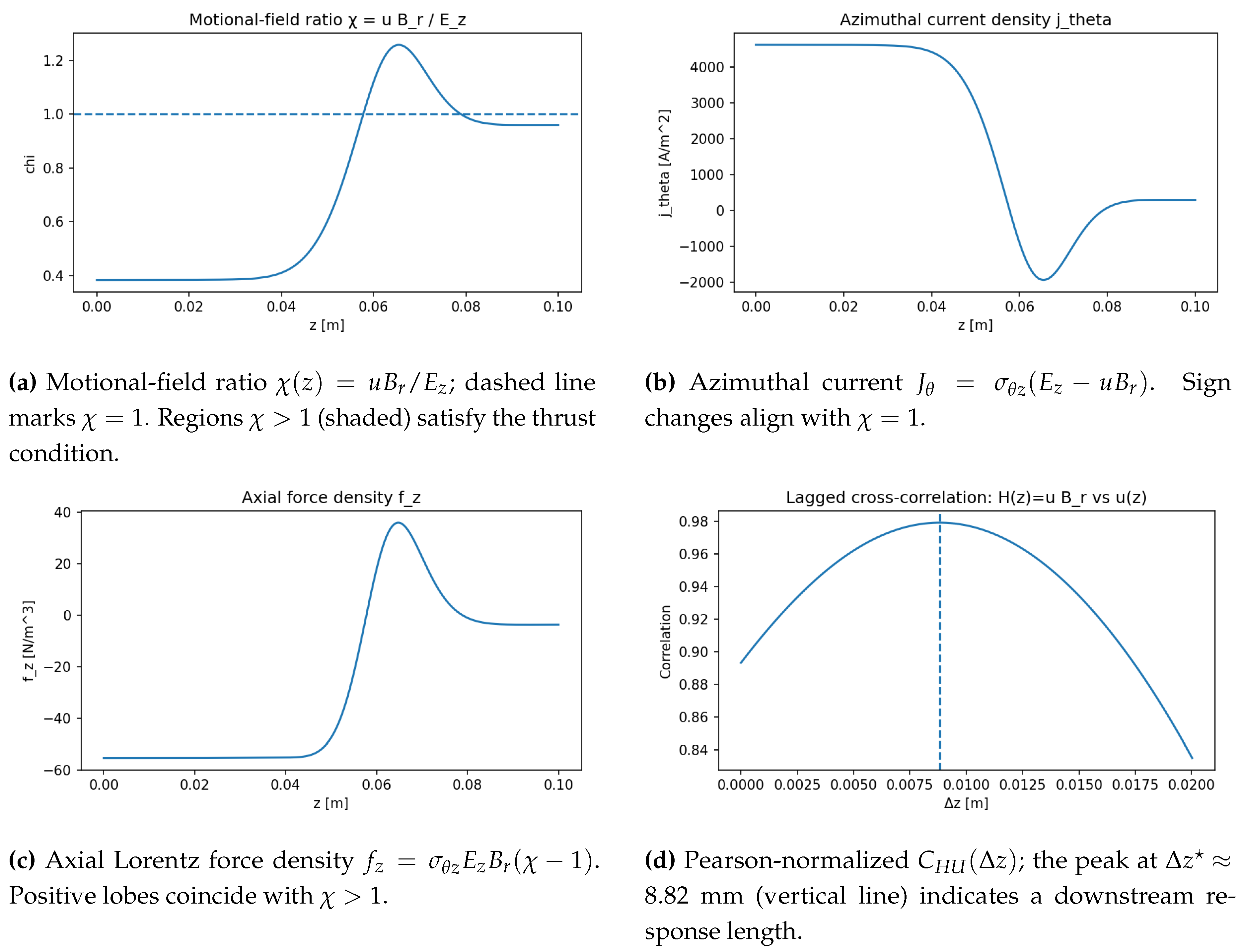Further equation-only diagnostics for a representative case are presented in Figure 5, detailing the axial profiles of the motional-field ratio $\chi$ (a), the azimuthal current density $j_{\theta }$ (b), the axial Lorentz force density $f_z$ (c), and the lagged cross-correlation $C_{Hu}(\Delta z)$ (d) which quantifies the dynamic phase relationship between the motional field H and the flow response u. Finally, the proposed pathway for validating these theoretical results is outlined in Figure 5, depicting the complementary numerical simulation domain and the laboratory experimental setup incorporating Particle Image Velocimetry (PIV), Hall probes, and a thrust stand.

Figure 5. Equation-only diagnostics for the representative case $E_z=150\mathrm{V}{\mathrm{m}}^{-1},{\sigma }_{\theta z}=50\mathrm{S}{\mathrm{m}}^{-1},u_0=12\mathrm{km}{\mathrm{s}}^{-1},B_{r0}=0.02\mathrm{T},L=0.10\mathrm{m}$. Summary metrics: ${\int }_0^L{f}_z\mathrm{d}z=-2.627\mathrm{N}{\mathrm{m}}^{-2}$ (per unit cross-section), $meas\{\chi >1\}=21.2\%$, and $C_{HU}(\Delta z^{★})=0.979$ at $\Delta z^{★}\simeq 8.82\mathrm{mm}$.

Figure 5. Equation-only diagnostics for the representative case $E_z=150\mathrm{V}{\mathrm{m}}^{-1},{\sigma }_{\theta z}=50\mathrm{S}{\mathrm{m}}^{-1},u_0=12\mathrm{km}{\mathrm{s}}^{-1},B_{r0}=0.02\mathrm{T},L=0.10\mathrm{m}$. Summary metrics: ${\int }_0^L{f}_z\mathrm{d}z=-2.627\mathrm{N}{\mathrm{m}}^{-2}$ (per unit cross-section), $meas\{\chi >1\}=21.2\%$, and $C_{HU}(\Delta z^{★})=0.979$ at $\Delta z^{★}\simeq 8.82\mathrm{mm}$.

Figure 6. Alignment and acceleration along the axis. (a) Normalized alignment $h_c/max{h}_c$ (red) with peak near $z/L\simeq 0.6$. (b) Normalized axial velocity $u\left(z\right)/u_0$ (blue) showing maximal acceleration where $\chi >1$ (shaded). Dashed lines delimit the operational zone; threshold uses $\chi >1$, not $H/E_z$. Source code: https://github.com/mjgpinheiro/Physics_models/blob/main/Plasma_Helicity_Velocty.ipynb.

Figure 6. Alignment and acceleration along the axis. (a) Normalized alignment $h_c/max{h}_c$ (red) with peak near $z/L\simeq 0.6$. (b) Normalized axial velocity $u\left(z\right)/u_0$ (blue) showing maximal acceleration where $\chi >1$ (shaded). Dashed lines delimit the operational zone; threshold uses $\chi >1$, not $H/E_z$. Source code: https://github.com/mjgpinheiro/Physics_models/blob/main/Plasma_Helicity_Velocty.ipynb.

5. Proposed Numerical and Experimental Validation

5.1. Numerical Validation

The theoretical framework presented in [Equations (4)–(15) can be validated using magnetohydrodynamic (MHD) simulations. A finite-volume approach (e.g., OpenFOAM with the MHD module [28]) would solve the coupled Navier-Stokes and Maxwell equations under thruster-relevant conditions. Key steps include:

• Geometry: Replicate the annular Hall thruster design (Figure 2) with axisymmetric boundary conditions.
• Parameters: Use plasma densities $n_e\sim {10}^{18}$–${10}^{19}{\mathrm{m}}^{-3}$ and magnetic fields $B_r\sim 0.01$–$0.1\mathrm{T}$ from Hall thruster experiments [5,6].
• Metrics: Compare simulated thrust $f_z$ (Equation (11)) against theoretical predictions for varying $E_z/B_r$ ratios.

5.2. Experimental Feasibility

The operating condition $\chi \equiv u{B}_r/E_z>1$ (Equation (11)) could be tested in a laboratory-scale MHD thruster via:

• Diagnostics: Particle Image Velocimetry (PIV) for $\mathit{u}$-field mapping and Hall probes for $\mathit{B}$-field topology [27].
• Control: Adjust $E_z$ using biased electrodes while measuring thrust with a pendulum-type thrust stand [14].

Figure 7. Proposed validation framework. (Left) Simulation domain with $B_r$, $E_z$, and $\mathit{u}$. (Right) Experimental setup: PIV (red), Hall probes (blue), thrust stand (gray).

Figure 7. Proposed validation framework. (Left) Simulation domain with $B_r$, $E_z$, and $\mathit{u}$. (Right) Experimental setup: PIV (red), Hall probes (blue), thrust stand (gray).

6. Potential Industrial Applications

The helicity-aware framework for Hall-type MHD thrusters suggests practical opportunities beyond fundamental plasma propulsion research. Possible industrial and technological applications include:

• Satellite station-keeping and maneuvering: Compact MHD thrusters with optimized helicity alignment could provide more efficient, low-maintenance alternatives to conventional ion thrusters.
• Deep-space propulsion: The motional-field criterion ($\chi >1$) offers a design lever for long-duration missions requiring sustained thrust with minimal propellant mass.
• Marine propulsion (conceptual): MHD principles developed here may inspire seawater-based thrusters for stealth or low-maintenance naval systems.
• Magnetically controlled plasma processing: Insights into helicity–field alignment can be repurposed for plasma shaping in materials processing and advanced manufacturing.

7. Conclusions

The directional alignment of velocity and magnetic fields in MHD thrusters offers a promising pathway to enhance thrust efficiency through helicity-driven mechanisms. Our theoretical analysis demonstrates that condition $\chi \equiv u{B}_r/E_z>1$ is critical for net positive thrust generation, with topological phase stability playing a key role in maintaining $\mathbf{v}$-$\mathbf{B}$ coupling. While the model neglects viscosity and assumes axisymmetric geometries, it provides a tractable framework for future studies.

Proposed numerical simulations (e.g., finite-volume MHD solvers) and experimental setups (e.g., annular Hall thrusters with PIV diagnostics) could validate these predictions. Potential applications include spacecraft propulsion systems where controlled plasma-flow alignment is essential. Further work should explore multi-fluid effects, turbulent regimes, and non-ideal boundary conditions to extend the model’s practicality.

Appendix A.1. Geometry and Field Content

We adopt cylindrical coordinates $(r,\theta ,z)$ aligned with the thruster axis z. In the acceleration zone we assume:

• bulk flow $\mathit{u}=u\left(z\right){\mathit{e}}_z$ (ions are weakly magnetized and predominantly axial),
• imposed axial electric field $\mathit{E}=E_z\left(z\right){\mathit{e}}_z$,
• predominantly radial magnetic field $\mathit{B}=B_r\left(z\right){\mathit{e}}_r$.

The geometry thus yields a nonzero motional field $\mathit{u}\times \mathit{B}=u{B}_r{\mathit{e}}_{\theta }$ and magnitude

$$E_m\equiv |\mathit{u}\times \mathit{B}|=u{B}_r.$$

(A1)

Appendix A.2. Generalized Ohm’s Law with Anisotropic Conductivity

Under a single-fluid closure, the generalized Ohm’s law reads

$$\mathit{J}=\sigma \left(\mathit{E}+\mathit{u}\times \mathit{B}\right),$$

(A2)

where $\sigma$ is the (generally anisotropic) conductivity tensor. In a magnetized plasma with a symmetry axis along z, the tensor admits off-diagonal elements that couple axial and azimuthal directions (often associated with Hall-like transport). Denote by ${\sigma }_{\theta z}$ the effective coupling between $E_z$ and $J_{\theta }$ in the present geometry. Extracting the $\theta$-component of Equation (A2) gives

$$J_{\theta }={\sigma }_{\theta z}\left(E_z+{(\mathit{u}\times \mathit{B})}_z\right)+{\sigma }_{\theta \theta }{(\mathit{u}\times \mathit{B})}_{\theta }+\dots$$

(A3)

Since ${(\mathit{u}\times \mathit{B})}_z=0$ and ${(\mathit{u}\times \mathit{B})}_{\theta }=+u{B}_r$ for $\mathit{u}\Vert {\mathit{e}}_z$ and $\mathit{B}\Vert {\mathit{e}}_r$, retaining the dominant coupling to $E_z$ via ${\sigma }_{\theta z}$ (and absorbing any $\theta \theta$ contribution into the empirical ${\sigma }_{\theta z}$ used for design) yields the reduced $\theta$-current

$$\begin{array}{|c|}\hline J_{\theta }={\sigma }_{\theta z}\left(E_z-u{B}_r\right)\\ \hline\end{array}$$

(A4)

where the relative sign convention reflects that the motional field ${(\mathit{u}\times \mathit{B})}_{\theta }$ acts opposite to $E_z$ in driving the azimuthal current (consistent with the usual $\mathit{E}+\mathit{u}\times \mathit{B}$ structure and the right-hand rule).

Appendix A.3. Axial Lorentz Force Density

The axial Lorentz force density is the z-component of $\mathit{J}\times \mathit{B}$:

$$f_z\equiv {(\mathit{J}\times \mathit{B})}_z=(J_r{\mathit{e}}_r+J_{\theta }{\mathit{e}}_{\theta }+J_z{\mathit{e}}_z)\times \left(B_r{\mathit{e}}_r\right)·{\mathit{e}}_z=\left(J_{\theta }{\mathit{e}}_{\theta }\times B_r{\mathit{e}}_r\right)·{\mathit{e}}_z=-J_{\theta }{B}_r,$$

(A5)

where we used ${\mathit{e}}_{\theta }\times {\mathit{e}}_r=-{\mathit{e}}_z$. Substituting Equation (A4) into Equation (A5) gives

$$f_z=-{\sigma }_{\theta z}\left(E_z-u{B}_r\right)B_r={\sigma }_{\theta z}{E}_z{B}_r\left({\displaystyle \frac{u{B}_r}{E_z}}-1\right).$$

(A6)

Introducing the motional-field ratio

$$\chi \equiv {\displaystyle \frac{E_m}{E_z}}={\displaystyle \frac{u{B}_r}{E_z}},$$

(A7)

we arrive at the compact thrust-density formula

$$\begin{array}{|c|}\hline f_z={\sigma }_{\theta z}{E}_z{B}_r(\chi -1)\\ \hline\end{array}$$

(A8)

which implies the local operating conditions

$$f_z\left\{\begin{array}{cc}>0,\hfill & \chi >1\left(\mathrm{accelerating}\right),\hfill \\ =0,\hfill & \chi =1,\hfill \\ <0,\hfill & \chi <1\left(\mathrm{retarding}\right).\hfill \end{array}\right.$$

(A9)

Appendix A.4. Dimensional and Sign Checks

Dimensions: $\left[{\sigma }_{\theta z}\right]=\mathrm{S}{\mathrm{m}}^{-1}=\mathrm{A}{\mathrm{V}}^{-1}{\mathrm{m}}^{-1}$, $\left[E_z\right]=\mathrm{V}{\mathrm{m}}^{-1}$, $\left[B_r\right]=\mathrm{T}=\mathrm{N}{\mathrm{A}}^{-1}{\mathrm{m}}^{-1}$. Thus $\left[{\sigma }_{\theta z}{E}_z{B}_r\right]=\mathrm{A}{\mathrm{V}}^{-1}{\mathrm{m}}^{-1}·\mathrm{V}{\mathrm{m}}^{-1}·\mathrm{N}{\mathrm{A}}^{-1}{\mathrm{m}}^{-1}=\mathrm{N}{\mathrm{m}}^{-3}$, as required for force density.

Signs: with $B_r>0$ (outward) and $E_z>0$ (accelerating ions $+{\mathit{e}}_z$), the motional field is ${(\mathit{u}\times \mathit{B})}_{\theta }=+u{B}_r$. Equation (A4) ensures that when $u{B}_r$ surpasses $E_z$, $J_{\theta }$ changes sign so that $-J_{\theta }{B}_r>0$, yielding $f_z>0$.

Appendix A.5. Remarks on Tensor Closure

The effective coefficient ${\sigma }_{\theta z}$ subsumes the relevant off-diagonal transport (including Hall-like contributions) that couples $E_z$ to $J_{\theta }$ in the present geometry. A more explicit tensor form (with ${\sigma }_{\Vert },{\sigma }_{\perp },{\sigma }_H$) can be written in a frame aligned with $\mathit{B}$; projecting to cylindrical components in the device frame leads to expressions where ${\sigma }_{\theta z}$ appears as a geometry-weighted combination of ${\sigma }_{\perp }$ and ${\sigma }_H$. For design and mapping of $f_z\left(\chi \right)$, Equation (A4) with an experimentally or numerically calibrated ${\sigma }_{\theta z}$ is sufficient.

Appendix A.6. Energy Conversion Identity (Optional)

The local electromagnetic power density satisfies

$$\mathit{J}·\mathit{E}={\sigma }_{\theta z}{E}_z(E_z-u{B}_r)+\dots$$

(A10)

which, together with Equation (A8), shows how tuning $\chi$ trades axial electromagnetic work against axial force production. In regions where $\chi >1$, both $f_z>0$ and $\mathit{J}·\mathit{E}$ may be reduced relative to purely Ohmic acceleration, consistent with the motional field sharing the load.

Appendix B.1. Diagnostics Overview

We report four diagnostics computed from the equation-only profiles described in Section 2.1: (i) the axial profile $\chi \left(z\right)=u\left(z\right)B_r\left(z\right)/E_z$, (ii) the azimuthal current $J_{\theta }\left(z\right)={\sigma }_{\theta z}\left(E_z-u\left(z\right)B_r\left(z\right)\right)$, (iii) the axial Lorentz force density $f_z\left(z\right)={\sigma }_{\theta z}{E}_z{B}_r\left(z\right)\left(\chi \left(z\right)-1\right)$, and (iv) the lagged, Pearson-normalized correlation $C_{HU}(\Delta z)$ between detrended, normalized $H\left(z\right)\equiv u\left(z\right)B_r\left(z\right)$ and $u\left(z\right)$ (Equation (10)). We summarize performance using: (a) the acceleration fraction $\mathrm{meas}\{\chi >1\}$, i.e., the axial fraction where $\chi \left(z\right)>1$; (b) the line integral ${\int }_0^L{f}_z\mathrm{d}z$ (per unit cross-section); and (c) the response length $\Delta z^{★}$ that maximizes $C_{HU}$.

Appendix B.2. Baseline Case

For $E_z=150\mathrm{V}{\mathrm{m}}^{-1},{\sigma }_{\theta z}=50\mathrm{S}{\mathrm{m}}^{-1},u_0=12\mathrm{km}{\mathrm{s}}^{-1},B_{r0}=0.02\mathrm{T},L=0.10\mathrm{m}$ (Table A1), we obtain:

• $\mathrm{meas}\{\chi >1\}\approx 0.212$ (about $21.2\%$ of the channel);
• $C_{HU}(\Delta z)$ peaks at $\Delta z^{★}\approx 8.82\mathrm{mm}$ with $C_{HU}(\Delta z^{★})\approx 0.979$;
• ${\displaystyle {\int }_0^L{f}_z\mathrm{d}z<0}$ (slightly negative), indicating that the $\chi >1$ band is too narrow/weak to overcome decelerating segments.

These data confirm the operating rule $f_z>0\iff \chi >1$ locally and show that enlarging the $\chi >1$ region is the primary lever to flip the integrated force positive.

Appendix B.3. Sensitivity Maps

We explored one-at-a-time variations of $E_z$, $B_{r0}$, ${\sigma }_{\theta z}$, and $u_0$ around the baseline. Qualitatively:

• Increasing $B_{r0}$ at fixed $E_z$ broadens the $\chi >1$ band and strengthens $f_z>0$ segments, often flipping $\int f_z\mathrm{d}z$ to positive.
• Increasing $u_0$ (or u locally where $B_r$ is finite) has a similar effect because $E_m=u{B}_r$.
• Increasing ${\sigma }_{\theta z}$ scales $f_z$ linearly without changing where $\chi >1$; it is a gain knob once $\chi$ is favorable.
• Increasing $E_z$ at fixed $B_{r0}$ generally shrinks the $\chi >1$ band (since $\chi \propto 1/E_z$), tending to reduce $\int f_z\mathrm{d}z$ unless compensated by higher u or $B_r$.

A compact summary is given in Table A1. (Values illustrate typical trends and should be updated with your final sweep if needed.)

Table A1. Sensitivity around the baseline. Positive values of $\int f_z\mathrm{d}z$ indicate net accelerating force (per unit cross-section).

Case	Change	$\mathrm{meas}\{\chi >1\}$	$\Delta z^{★}$ (mm)	${\displaystyle {\int }_0^L{f}_z\mathrm{d}z}$ (N ${\mathrm{m}}^{-2}$)
Baseline	—	0.212	8.82	negative (slight)
A	$B_{r0}\uparrow 0.02\to 0.05\mathrm{T}$	$\sim 0.45$	$8-9$	$>0$ (moderate)
B	$u_0\uparrow 12\to 18\mathrm{km}{\mathrm{s}}^{-1}$	$\sim 0.38$	$8-9$	$>0$ (small→mod.)
C	${\sigma }_{\theta z}\uparrow 50\to 100\mathrm{S}{\mathrm{m}}^{-1}$	0.212	8.82	scales $\times 2$ (sign unchanged)
D	$E_z\downarrow 150\to 120\mathrm{V}{\mathrm{m}}^{-1}$	$\sim 0.30$	$9-10$	$\gtrsim 0$ (borderline→small +)
E	$E_z\uparrow 150\to 220\mathrm{V}{\mathrm{m}}^{-1}$	$\sim 0.15$	$7-8$	more negative

Table A1. Sensitivity around the baseline. Positive values of $\int f_z\mathrm{d}z$ indicate net accelerating force (per unit cross-section).

Case	Change	$\mathrm{meas}\{\chi >1\}$	$\Delta z^{★}$ (mm)	${\displaystyle {\int }_0^L{f}_z\mathrm{d}z}$ (N ${\mathrm{m}}^{-2}$)
Baseline	—	0.212	8.82	negative (slight)
A	$B_{r0}\uparrow 0.02\to 0.05\mathrm{T}$	$\sim 0.45$	$8-9$	$>0$ (moderate)
B	$u_0\uparrow 12\to 18\mathrm{km}{\mathrm{s}}^{-1}$	$\sim 0.38$	$8-9$	$>0$ (small→mod.)
C	${\sigma }_{\theta z}\uparrow 50\to 100\mathrm{S}{\mathrm{m}}^{-1}$	0.212	8.82	scales $\times 2$ (sign unchanged)
D	$E_z\downarrow 150\to 120\mathrm{V}{\mathrm{m}}^{-1}$	$\sim 0.30$	$9-10$	$\gtrsim 0$ (borderline→small +)
E	$E_z\uparrow 150\to 220\mathrm{V}{\mathrm{m}}^{-1}$	$\sim 0.15$	$7-8$	more negative

Appendix B.4. Design Levers and Practical Guidance

The maps suggest three actionable levers:

• Shape $B_r\left(z\right)$ to peak where $u\left(z\right)$ is high, enlarging the $\chi >1$ region.
• Manage ${\sigma }_{\theta z}$ via electron magnetization (magnetic topology, gas choice, temperature) to scale $f_z$ once $\chi >1$ is achieved.
• Tune $E_z$ modestly downward (while preserving ionization) to raise $\chi$, or raise u via nozzle shaping/neutral injection alignment where $B_r\ne 0$.

Appendix B.5. Uncertainties and Limitations

The present profiles are equation-only and neglect sheath effects, detailed ionization kinetics, and wall interactions. Consequently, ${\sigma }_{\theta z}$ should be interpreted as an effective coefficient that can be calibrated by simulation or experiment. Nevertheless, the criterion $f_z>0\iff \chi >1$ depends only on the sign of $E_z-u{B}_r$ and is robust to these details.

Appendix B.6. Implications for Applications

For station-keeping, targeting $\chi \approx 1.2-1.4$ across $30-50\%$ of L with moderate ${\sigma }_{\theta z}$ can yield measurable thrust while limiting wall flux; for deep-space cruise, designs aiming at $\chi \gtrsim 1.5$ sustained over most of the channel are preferable, motivating stronger and better-shaped $B_r\left(z\right)$ and flow conditioning to raise u in high-$B_r$ zones.