High Interfacial Adsorption/Low Solubility of Light Gases on Pristine Nano-Thin Molten Polyethylene Films

1. Introduction

Polymer-based coatings solve multiple technological problems beyond surface insulation. In addition to protecting commercial products [1,2,3] or large surfaces like building components, these coatings also provide specialized functions such as waterproofing, fire resistance, and thermal insulation [4,5,6].

Polymeric structures are also employed as adsorbent materials. Specifically, bulk polyethylene (PE) in its linear (HDPE and LLDPE) and branched (LDPE) structures, has been extensively studied for its ability to store and separate various gases of industrial interest, such as H₂, CO₂, ethylene, and light alkanes [7,8,9], as well as environmental pollutants like CO₂, polycyclic aromatic hydrocarbons, and polychlorinated biphenyls [10,11,12]. PE is widely used due to a combination of low cost, excellent processability, high chemical inertness, remarkable durability and flexibility, low moisture absorption, biocompatibility, and electrical insulation properties [13,14,15].

Experimental studies, corroborated by the Statistical Associating Fluid Theory (SAFT), have investigated the capacity of bulk LLDPE to adsorb and dissolve light gases such as ethylene, propene, but-1-ene, and propane [16,17]. At temperatures where LLDPE is in a molten state (413.15−473.15K), the dissolution capacity for these gases is considerable and increases with the gas's molecular weight. At 413.5 K, the solubility slightly exceeds 200 g per 1000 g of LLDPE at gas phase pressures of approximately 25.0 MPa (ethene), 5.3 MPa (propene), and 2.5 MPa (but-1-ene). For propane, the only alkane studied, achieving the same solubility required a slightly higher pressure (~ 6.5 MPa), which suggests that smaller alkenes like ethylene may be more soluble than its corresponding alkane (ethane). This trend of solubility as a function of gas molecular weight has also been reported in experimental studies comparing the solubilities of n-pentane at 423.65 K [18] and propane at 443.15 K [16], which has been corroborated by close SAFT predictions [19]. Studies on the solubility of ethylene in different bulk PE structures at temperatures between 333.15 and 423.15 K have found that the degree of crystallinity plays a significant role: higher crystallinity leads to lower solubility [20].

Experimental investigations of PE films have shown that the solubility of pure ethylene increases exponentially with gas pressure, while the solubility of methane and nitrogen increases asymptotically. Methane / ethylene mixtures at 50% by weight behave similarly to pure ethylene [9]. The maximum observed solubility was low, at approximately 67 g of ethylene per 1000 g of PE, at 9 MPa and 298.15 K. The PE films used in these studies were pre-treated with n-heptane, and their thickness was not determined, potentially influencing the reported solubilities [21]. The solubility of CO₂ and H₂ has also been studied experimentally in HDPE films without determining their thickness, finding high CO₂ solubilities (624.3g / 1000g of HDPE) at 0.3 MPa and 303.15 K, while H₂ reached only 36.1g / 1000g of HDPE [7].

In previous work, we used classical Molecular Dynamics (MD) simulations to characterize linear PE films of 200 monomers at their stability limit [22,23]. This allowed us to determine the critical thickness at which a PE film becomes unstable by developing pores. Above this critical thickness, large pores of instability develop and typically self-heal within picoseconds. Below it, they grow, causing the film to fragment into aerosol droplets [24,25]. The limiting thicknesses obtained with MD are a few nanometers, slightly lower than those obtained in subsequent state-of-the-art experimental studies where PE films are produced through careful stretching processes to prevent rupture [26]. The pores that destabilize the PE film become more pronounced as the thickness approaches the critical stability value. These pores can be filled with smaller species that are affine to PE, with the goal of increasing stability and potentially further reducing the critical thickness. Alternatively, they can be used as storage sites for problematic light gases or for those of specific commercial interest.

Here, we study the storage capacity of supercritical ethane adsorbed in very thin, self-standing molten PE films at thicknesses at their stability limit. The following sections detail the classical MD methodology used and present the results and their discussion. We include analyses of the total storage capacity, estimates of ethane solubility in the PE film, the large adsorption of ethane at the interfaces, the volumetric properties of the ethane gas, the interfacial properties of the film with dissolved and adsorbed ethane gas, and their dependence on gas pressure and system temperature. The article concludes with a summary of the main findings and future work.

2. Methodology

Classical MD simulations were used to study the interfacial adsorption and solubility of supercritical ethane in thin films formed by molten PE chains. The study focused on films at their mechanical stability limit and at temperatures of 298.15 K, 373.15 K, and 448.15 K. This method is commonly used to simulate various properties of polymeric systems [27,28,29]. We used the MD code implemented in the Large-scale Atomic / Molecular Massively Parallel Simulator (LAMMPS) [30]. The simulations were performed within a periodic simulation cell with a rectangular parallelepiped shape. The film was positioned in the center of the simulation cell, oriented along the smallest square face of the parallelepiped. The sides of this face were long enough to contain a PE chain of 200 monomers, stretched in each square direction. Previous simulations have demonstrated that this designated interfacial area is large enough to accurately predict the density and interfacial properties of molten polyethylene at temperatures between 373.15 K and 673.15 K [22,23]. The initial conformation of the chains formed a film that completely covered the face of the simulation cell and evolved into a cohesive, self-standing film. The periodicity along the normal direction resulted in a central film that is periodically repeated along the normal axis.

A molten PE film in contact with 938 to 7938 ethane molecules was placed in a rectangular parallelepiped simulation cell with dimensions A = 14.5 × 14.5 nm² and L_z = 48.4 nm. This setup allowed us to simulate a thin layer of polyethylene in contact with different ethane gas phase densities (ρ_et,g) ranging from 4.10 × 10^-3 to 7.97 × 10^-2 g/ml at 373.15 K. Additional simulations were conducted by progressively reducing L_z to 12.4 nm while keeping the number of ethane molecules constant (7938), which allowed us to reach ρ_et,g values of 1.36 × 10^-1 g/ml. The reduction of L_z was performed in stages, at a rate of 0.2 nm every 100 ps, with remapping of the coordinates of the entire system, which prevented the system from losing stability. The varying L_z values ensured sufficient separation between the central layer and its periodic images to render inter-layer interactions negligible. The systems were also simulated at 298.15 K and 448.15 K starting from equilibrated configurations at 373.15 K and changing the temperature of the system in several steps. The ethane - PE systems were simulated using the NVT ensemble, where the number of particles and the volume of the simulation cell were kept constant while the temperature fluctuated around a constant value, for which the Nosé thermostat [31] was used with a time step of 1 fs.

The inter-chain interactions (van der Waals) and those due to intra-chain vibrations (bond distance, bond angles, and dihedral angles) were calculated using the Transferable Potentials for Phase Equilibria (TraPPE) force field [32]. This force field uses sites that represent the different monomers along with the Lennard-Jones potential to calculate interaction forces between sites of different chains and also for interactions between sites of the same chain but separated by more than four bonds. Coarse-grained force fields have been widely used to describe the structural properties of polymers [33,34], but the resolution of the components of the pressure profiles $P_{\alpha \beta }\left(z\right)$, $\alpha \beta =\{xx,yy,zz\}$, is in the range of a few Å [35], which is difficult to resolve when the interaction sites have diameters of several Å. Bond distance and angle vibrations were calculated using harmonic potentials, while dihedral angle vibrations were calculated using a cosine function [36]. Interactions between sites of different chains were calculated using a large cutoff radius, 7.5 times the value of σ_CH3−CH3. The parameter σ_CH3−CH3 is a Lennard-Jones potential parameter specific for interactions between two terminal -CH₃ groups of two different chains. This radius was wide enough to consider all significant inter-chain interactions, reproduce experimental interfacial properties (tension), and avoid the use of long-range corrections during and after simulations in systems fully described only with Lennard-Jones potentials [24,37] or even in more complex systems with partial electric charges (ionic) [38,39]. The TraPPE potential has been used to simulate C₅₀ and C₁₉₂ PE chains, and these simulations have reproduced their experimental properties, such as melting temperature [40] and glass transition temperature [41].

We calculated the density profiles, ρ(z), and the components of $P_{\alpha \beta }\left(z\right)$), using sub-cells with a thickness of 0.1 Å along the normal direction. The pressure tensor components were calculated using the Harasima contours [42], a function available in LAMMPS [30], which arbitrarily distributes the tension of two interacting sites between the two sub-cells in the normal direction that originate the interactions. Although local pressure lacks a unique definition, the Harasima contours accurately describe interfacial pressures in flat interfaces for systems at thermodynamic equilibrium [35]. From the total pressure profiles, we calculated the interfacial tension, γ, using its mechanical definition:

$$\gamma ={\displaystyle \frac{1}{2}}{\int }_{-\infty }^{\infty }\left\{P_{zz}\left(z\right)-0.5\left[P_{xx}\left(z\right)+P_{yy}\left(z\right)\right]\right\}$$

(1)

where $P_{zz}\left(z\right)$ is the component in the normal direction, while the other two are the components lateral to the surfaces that form the interfaces. Equation 1 considers the existence of two interfaces.

3. Results and Discussion

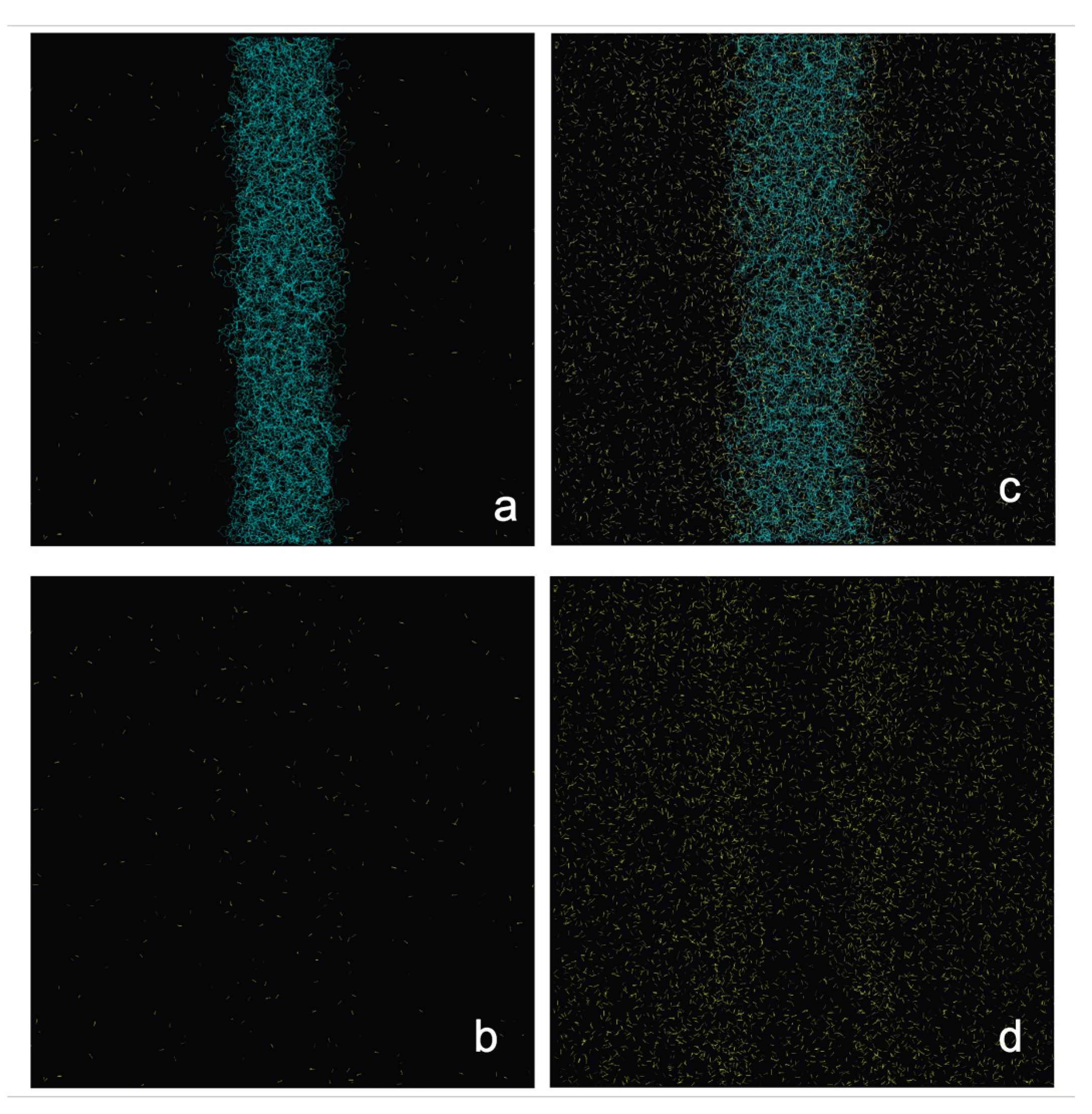
Figure 1 shows the equilibrium conformations of the molten PE films in contact with supercritical ethane at 373.15 K. The visualizations correspond to the low and high ρ_et,g studied in this work. These conformations were taken after 10 ns of initial simulation to reach equilibrium conformations. The thin polyethylene layer widens as ρ_et,g increases, a phenomenon that likely reduces the PE film density. At high ρ_et,g, ethane molecules accumulate at the polymer / gas interfaces at densities greater than those in the center of the film.

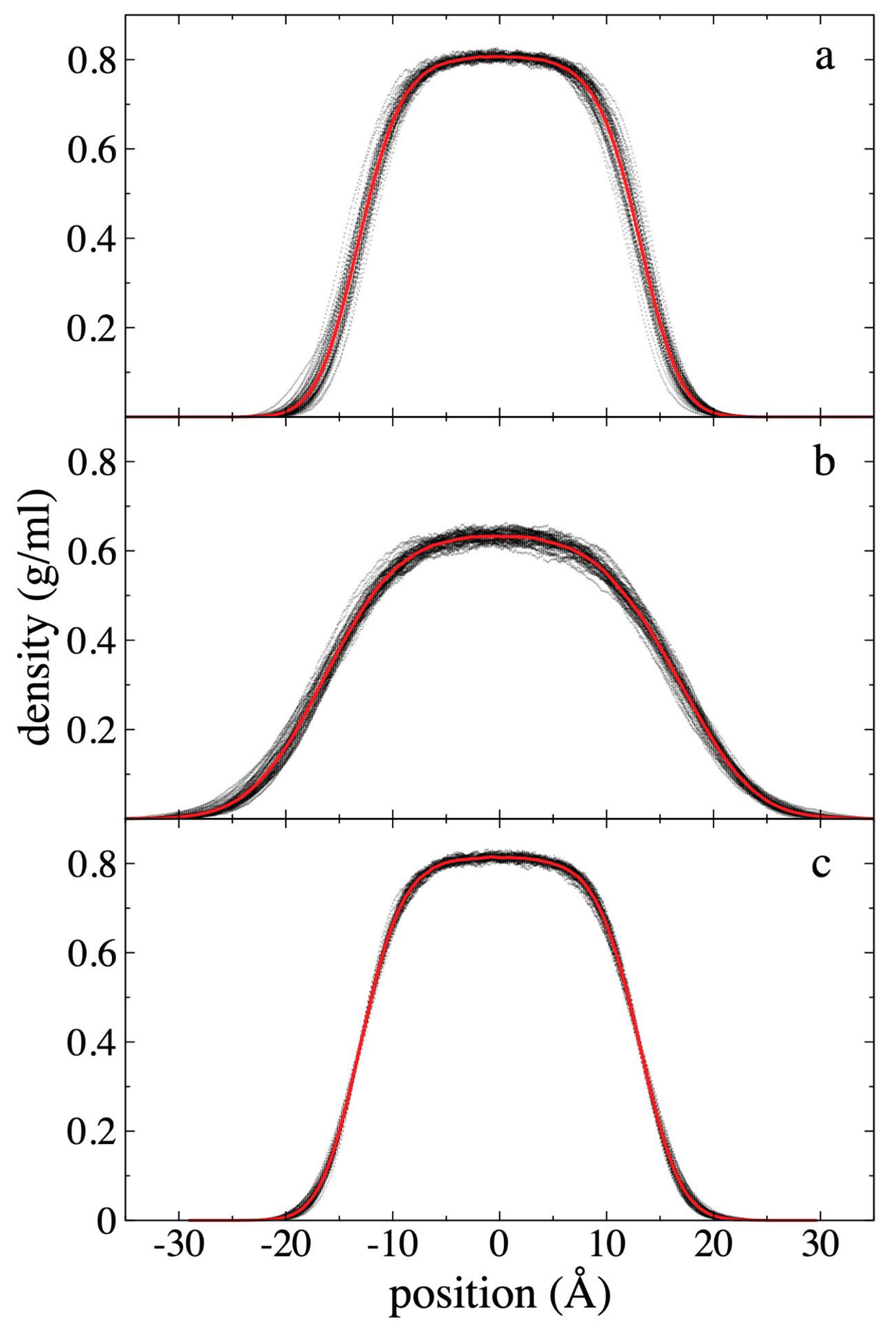
3.1. Density Profiles

The ρ(z) for each component (PE and ethane) and the sum of both (total) along the axis normal to the interfacial surfaces, were calculated over a period of 5 ns after an initial 10 ns of equilibration. The density profiles for the 94 PE chains at 373.15 K are shown in Figure 2, while the density profiles for ethane are shown in Figure 3. To show the data dispersion, Figure 2 and Figure 3 also show the ρ(z) averaged every 0.1 ns and the overall average over 5 ns. The PE profiles (Figure 2) generally show low data dispersion, with maximum differences in the center of the layer of up to 0.015, 0.020, and 0.030 g/ml for the system without ethane molecules, and the systems with ethane at ρ_et,g of 4.10 × 10^-3 g/ml and  1.36 × 10^-1 g/ml, respectively. Figure 2 also shows the density profile of the PE chains before coming into contact with supercritical ethane at the same temperature. In previous reports we show that the maximum value for the density is almost independent of the width of the film for systems dominated by van der Waals forces [22,25]. The ρ(z) show that the molten film widens in the presence of ethane, and that the film’s central density decreases as ρ_et,g increases, similar to a surfactant effect. Similar effects have been found in phase equilibrium systems of binary mixtures of long-chain alkanes like n-decane in thermodynamic equilibrium with short-chain alkanes like methane and ethane [44,45,46].

We defined the layer thickness formed only by PE chains, as the separation between interfacial points where the PE density (Figure 2) was half its maximum central value. Using this criterion, we found that the PE film did not widen when it was put in contact with ethane at the lowest ρ_et,g studied (4.10 × 10^-3 g/ml). However, it did widen by approximately 30% when it was put in contact with the gas phase with the highest ρ_et,g studied (1.36 × 10^-1 g/ml). Considering also only the PE chains, the maximum density at the center of the layer is reduced by less than 1% for the lowest ρ_et,g studied and approximately 22% for the highest ρ_et,g studied.

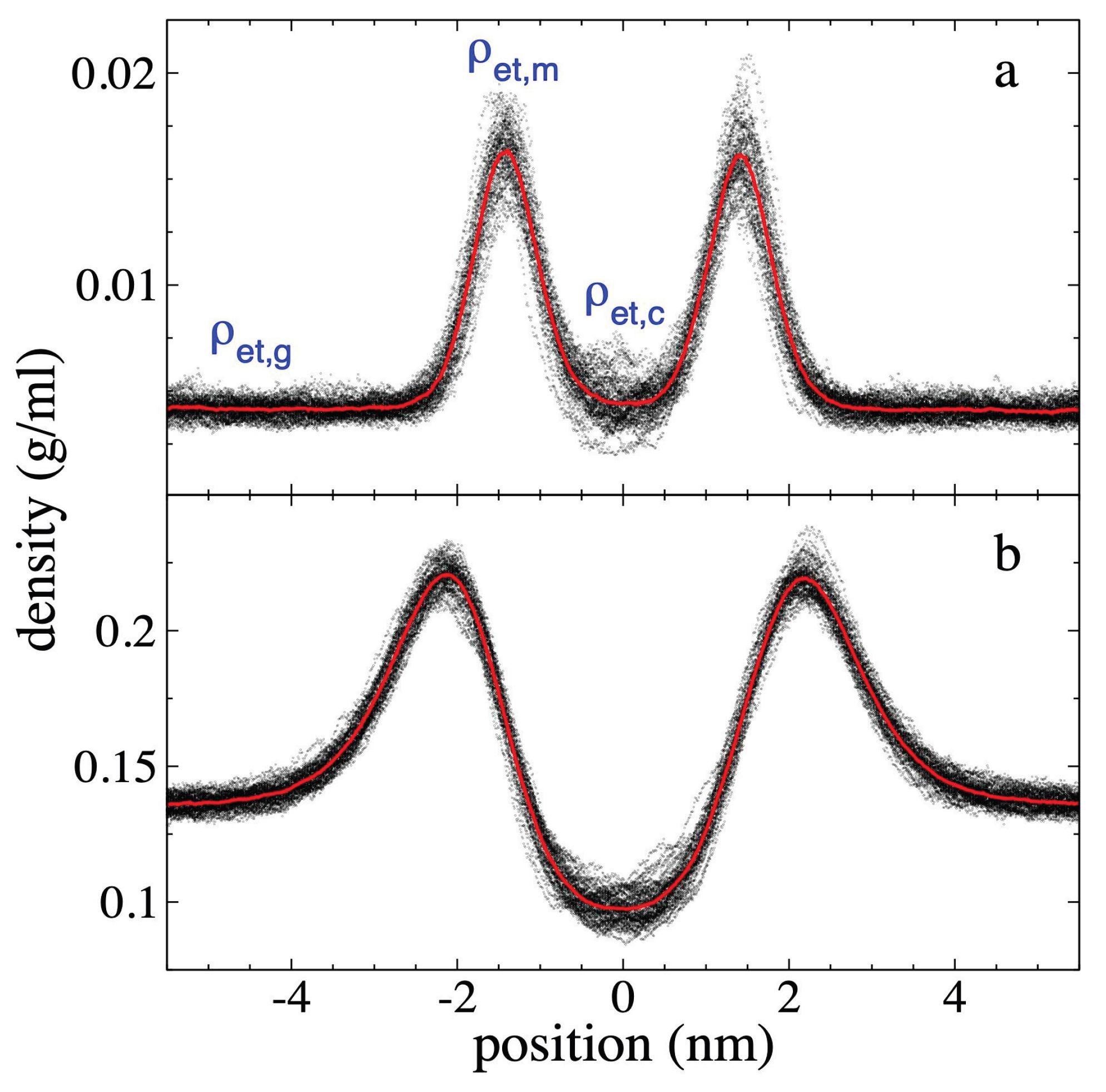
The ρ(z) corresponding to ethane (Figure 3) shows a pronounced adsorption of ethane at the interfaces, which manifests as adsorption peaks near the surfaces of the PE film. Similar adsorption peaks have also been reported in previous studies of low molecular weight gases in liquid / vapor equilibrium with long alkane chains [47,48,49], and are also present in many systems with polar and non-polar components [50]. The ρ(z) show that as ρ_et,g increases, the maximum density of the ethane adsorption peaks, ρ_et,m, also grows, and can reach values as high as approximately ⅓ of the density values of the PE chains in the center of the PE film. The widening of the polyethylene film as ρ_et,g increases is also reflected in the separation of the ethane adsorption peaks at the interfaces. This separation widens from approximately 2.82 nm (ρ_et,g = 4.10 × 10-3 g/ml) to approximately 4.31 nm (ρ_et,g = 1.36 × 10-1 g/ml), representing an increase of approximately 52%. In the center of the film, the average ethane density, ρ_et,c, reaches values similar to ρ_et,g for the system with the lowest ρ_et,g studied at 373.15 K. In the system with the highest ρ_et,g studied, ρ_et,c decreases to approximately ⅔ of the ρ_et,g value, which could indicate that a saturation process for ethane adsorption is in progress  in the center of the PE layer, but not in the adsorption peaks, which continue to grow as ρ_et,g increases.

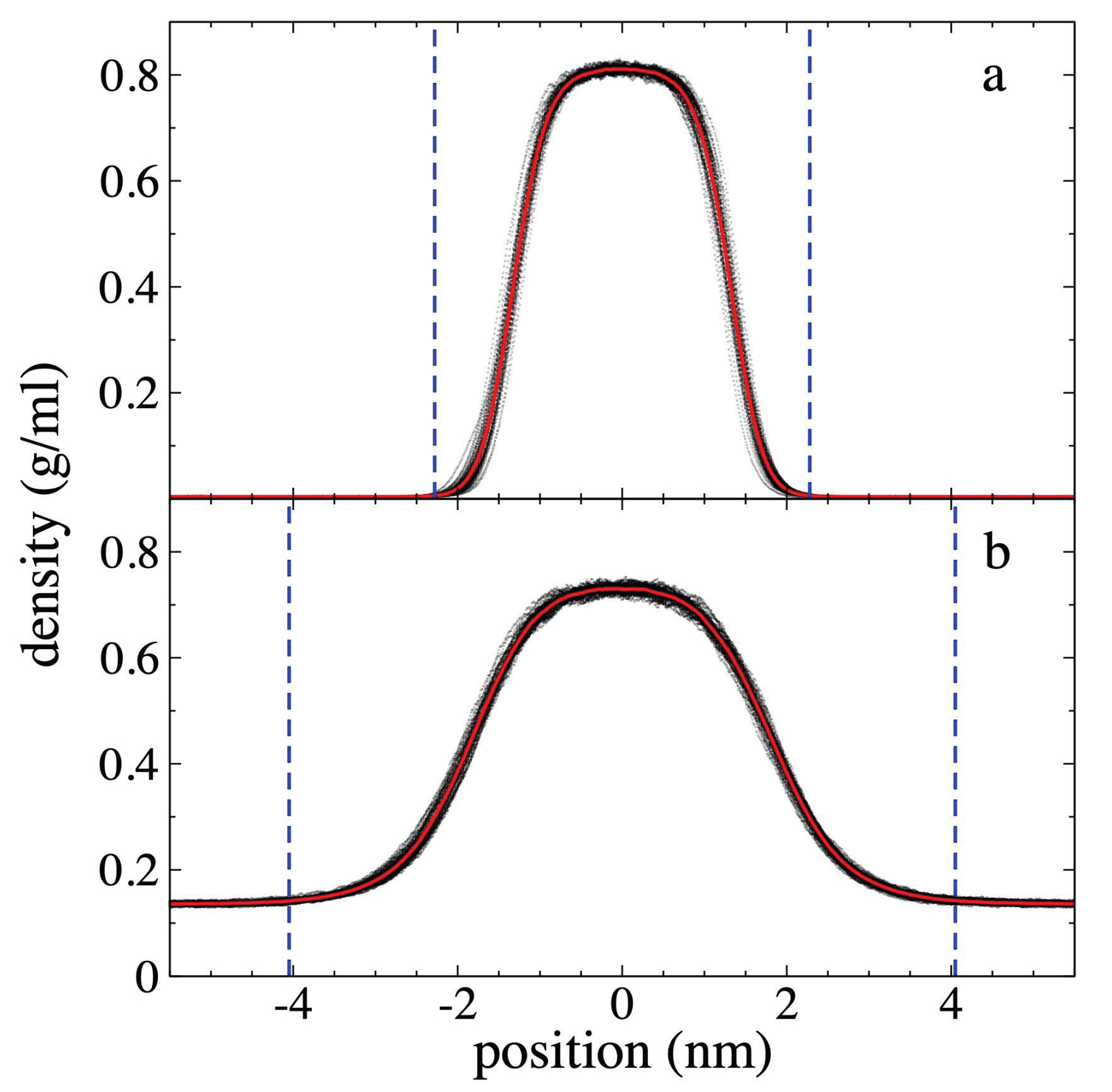
The total ρ(z), including both components of the system, are shown in Figure 4. Compared to the PE profiles, a less pronounced decrease in density is observed in the center of the layers. For the system with ρ_et,g = 4.10 × 10^-3 g/ml, there is no density reduction. However, for the system with ρ_et,g = 1.36 × 10^-1 g/ml, the reduction is only 8.8%, which is probably due to the solubility of ethane molecules in the PE film. The widening of the layer, is due to the progressive widening of the adsorbed ethane layers at the interfaces, but is also due to a reduction in the PE chains density, we find that for the system with the lowest ρ_et,g studied, the widening is insignificant, but for the system with the highest ρ_et,g studied, the widening is significant, approximately 60%, estimated from the total ρ(z) positions where the density begins to deviate from the average ρ_et,g.

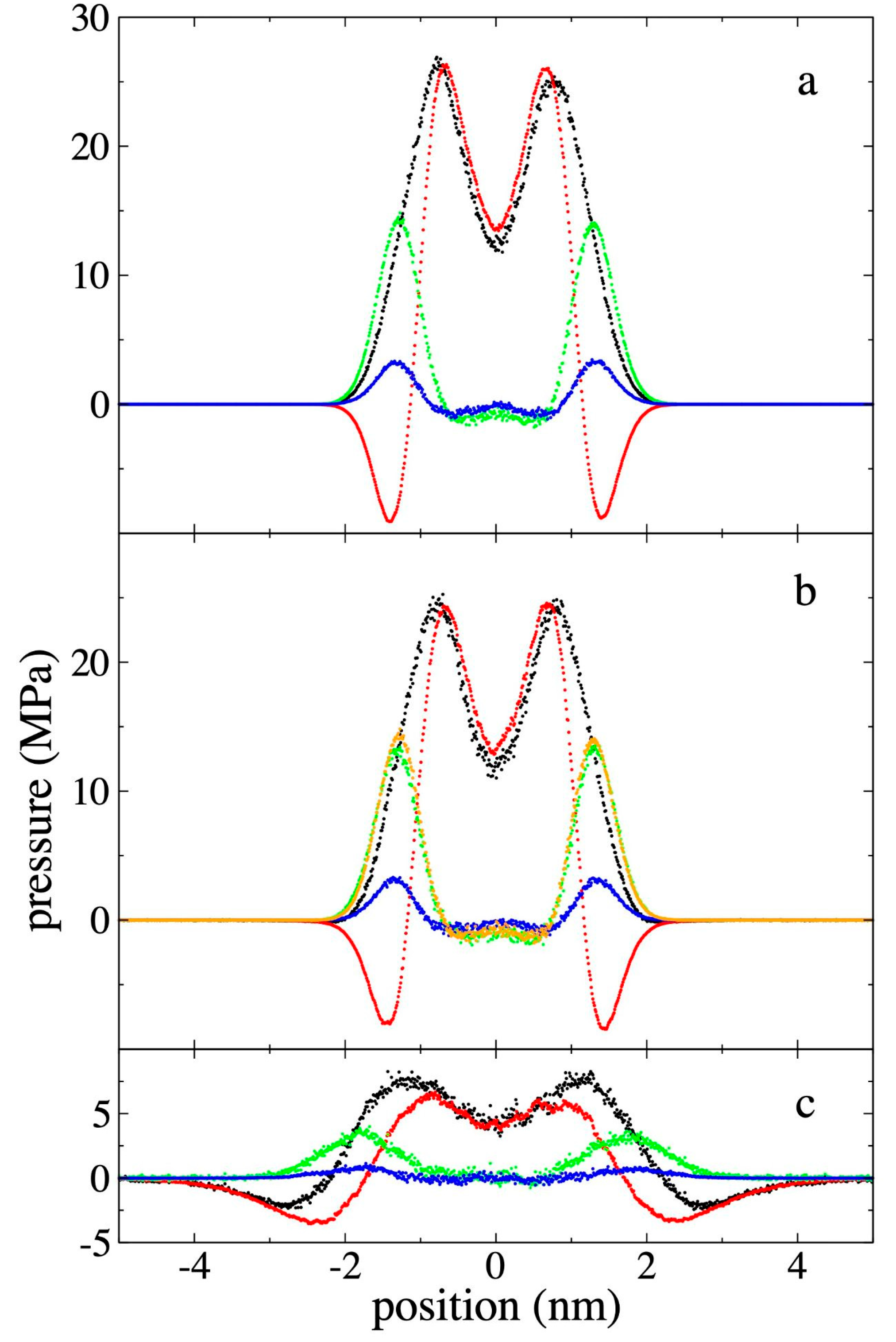
3.2. Pressure Profiles

The $P_{\alpha \beta }\left(z\right)$ in the normal ($zz$) and lateral ($xx$ and $yy$) directions were calculated for all systems, and with them, we estimated the average pressure in the ethane gas phase, $P_{T,g}$, and calculated the interfacial tension, γ. The pressure component profiles from the simulations at 373.15 K, at the limit values of the ρ_et,g range studied, are shown in Figure 5. These profiles are compared with those obtained for the pristine PE film, without being exposed to ethane molecules. The effect of ethane in the PE film reduces the magnitude of the peaks and valleys of the 3 pressure components. The presence of ethane makes the PE film less cohesive. This might seem counterintuitive, as one might expect a small molecule like ethane to fill the natural pores in the films [22] and increase stability. For comparison, interstitial carbon atoms in steel form a solid solution, creating a harder but more fragile system [51]. However, in our simulations, ethane appears to have the opposite effect, suggesting its main influence is at the interfaces, making the film more 'fragile'.

The $P_{\alpha \beta }\left(z\right)$ show a behavior corresponding to a metastable system. At the ethane gas phase, the pressure is in equilibrium and is isotropic. Its 3 components have equal average values, which is not the case in the center of the PE layer, where one would expect the development of an isotropic phase similar to a liquid. However, this isotropy is not achieved. The lateral pressure components $P_{xx}\left(z\right)$ and $P_{yy}\left(z\right)$ are equal and indicate cohesive conformations, but they differ from the normal component $P_{zz}\left(z\right)$, which has positive, non-cohesive values. This pressure difference causes the system not to be in mechanical equilibrium. The mechanical imbalance will eventually cause these systems to transform into more stable systems, which could occur through the film breaking and the formation of an aerosol [24,52,53]. The stability of these molten films depends on many external factors. Although classical MD simulations without external perturbations have shown long periods of stability, up to 0.1 $\mu$s, with potentials based on interaction sites of -CH₂- and -CH₃ functional groups [22], and with mesoscale simulations [54].

The $P_{\alpha \beta }\left(z\right)$ in the interfacial region show more cohesive states in the lateral directions than in the normal direction, which is natural and gives rise to the development of γ. This difference is a result of the inhomogeneity of the system in the normal direction. The studied self-standing PE film is basically interfacial; there is no region that we can identify as a bulk liquid, in which the three pressure components should develop with isotropic and positive values to maintain mechanical equilibrium with the ethane gas phase. If we compare the change in pressures between the minimum value at the interfaces and its corresponding maximum in the center of the layer, we see that the magnitude of the change is the same in the three components. Such large changes in the normal direction are not expected in wider layers [38], which probably indicates interference of the opposite interfaces. In wider layers, the expected deviations from a constant $P_{zz}\left(z\right)$ are considerably lower than those observed in the lateral directions, and the small deviations are due to the way the interactions in the $P_{zz}\left(z\right)$ are accumulated in the Harasima profiles.

Based on the $P_{\alpha \beta }\left(z\right)$ obtained, we calculated the profiles of the function $P_{zz}\left(z\right)-0.5\left[P_{xx}\right(z)+P_{yy}(z\left)\right]$. These profiles, which are shown in Figure 5d, once integrated, are used to calculate γ (Eq. 1). Compared to the profiles of the pristine PE film without ethane, the presence of ethane causes the maximums of the interfacial peaks to reduce their magnitude. Furthermore, when ρ_et,g is high enough, non-cohesive regions appear in the outermost part of the interfaces, which could be investigated in the future using a code implemented in such a way that it allows for the separate calculation of the contributions of each component to the profiles, and in this way determine if these values are due to the PE chains or the ethane molecules. This is not possible today with the MD implementation used [30]. Figure 5d also shows that the system is composed of two overlapping interfacial regions, with no central bulk liquid exhibiting isotropic pressures. This is because the influence tails of the two interfacial peaks overlap in the center of the layer.

Figure 6 shows the profiles of the main contributions (van der Waals inter-chain interactions, bond distance vibrations, and bond angle vibrations) to the function $P_{zz}\left(z\right)-0.5\left[P_{xx}\right(z)+P_{yy}(z\left)\right]$, along with the total profile and the profiles for the pristine PE film. In the pristine film, it is shown that the vibrations contribute mainly in the outermost parts of the interfaces, while the inter-chain interactions (van der Waals forces) are divided between regions that have positive and negative contributions. The negative contributions, like the vibrations, are located in the outermost part of the interfaces, followed by the positive regions in the center of the film. The positive contributions due to vibrations are greater than the effect of the negative contributions due to inter-chain interactions in the outermost regions of the interfaces. The $P_{\alpha \beta }\left(z\right)$ due to bond distance and bond angle vibrations do show an isotropic region that develops in an internal sub-layer located at the center of the film, with a thickness of ~1.4 nm. The thickness of this isotropic region increases slightly at higher ρ_et,g. The contributions due to inter-chain interactions do not show any isotropic region at the center of the film.

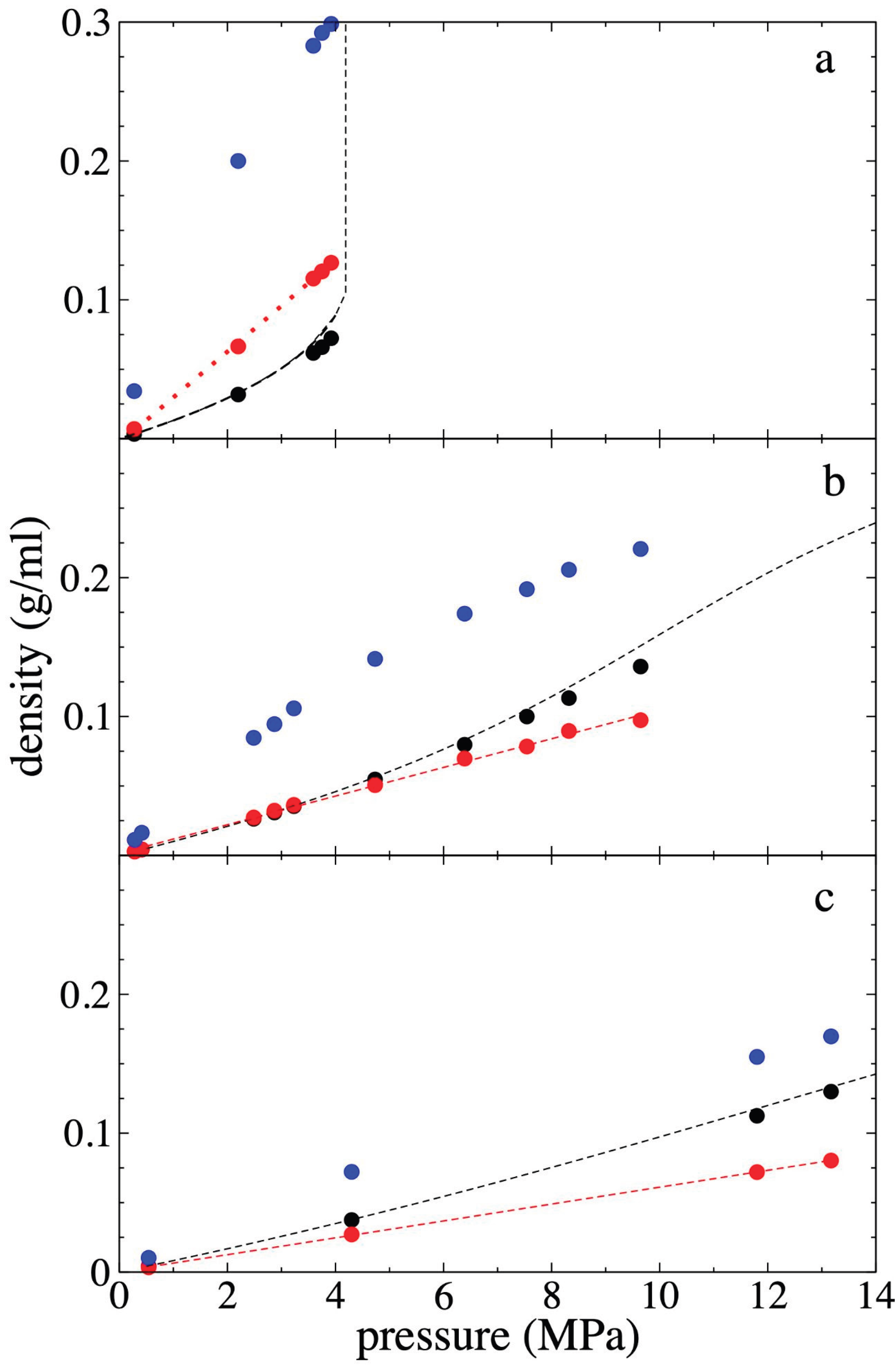
3.3. Pressure - Density of Supercritical Gas Ethane

We related $P_{T,g}$, which represents the average value of the three $P_{\alpha \beta }\left(z\right)$ components in the homogeneous regions away from the film and its interfaces, where the density varies around a constant value. Figure 7 shows the values obtained for $P_{T,g}$ along with its corresponding ρ_et,g, as well as the corresponding values for ρ_et,c and ρ_et,m. The results are also shown at temperatures of 298.15 K and 448.15 K, to have a more global view of the behavior of these systems. Previous work with pristine PE films had shown that at higher temperatures, a greater number of chains was needed to keep the film stable for long simulation periods (100 ns). We found that the systems at 448.15 K remained stable, during the short simulation period studied (15 ns), probably because we started from configurations with the ethane molecules, which gives some sort of ‘strength’ to the film.

Figure 7 also shows experimental isotherms [55] of the $P_{T,g}$ - ρ_et,g relationship for pure supercritical ethane at the 3 studied temperatures. The used potential reproduces the experimental ethane $P_{T,g}$ - ρ_et,g relationship well. There are slight over-predictions at high ρ_et,g, with maximum errors of 6.25% within the $P_{T,g}$ - ρ_et,g region studied. The behavior between these variables is monotonically increasing, although at 298.15 K, and slightly higher ρ_et,g, the experimental $P_{T,g}$ increases exponentially, or viewed another way, there is a saturation of $P_{T,g}$ at higher ρ_et,g. ρ_et,m and ρ_et,c grow with ρ_et,g, although ρ_et,m grows asymptotically and ρ_et,c grows linearly, which could indicate that the phenomenon that is entering a saturation behavior in this studied density range is the phenomenon of ethane adsorption at the interfaces, while the solubility in the center of the film has not really started a saturation process. ρ_et,m presents magnitudes up to 2.4 times greater than ρ_et,c, although it is not clear if the isotherms could connect at higher ρ_et,g. At 298.15 K, the densities of ρ_et,c are greater than ρ_et,g, but at higher temperatures, there is an inversion in this relationship that also becomes more pronounced as the temperature increases, which is probably related to the melting temperature for pure PE occurring in this range of temperatures [56].

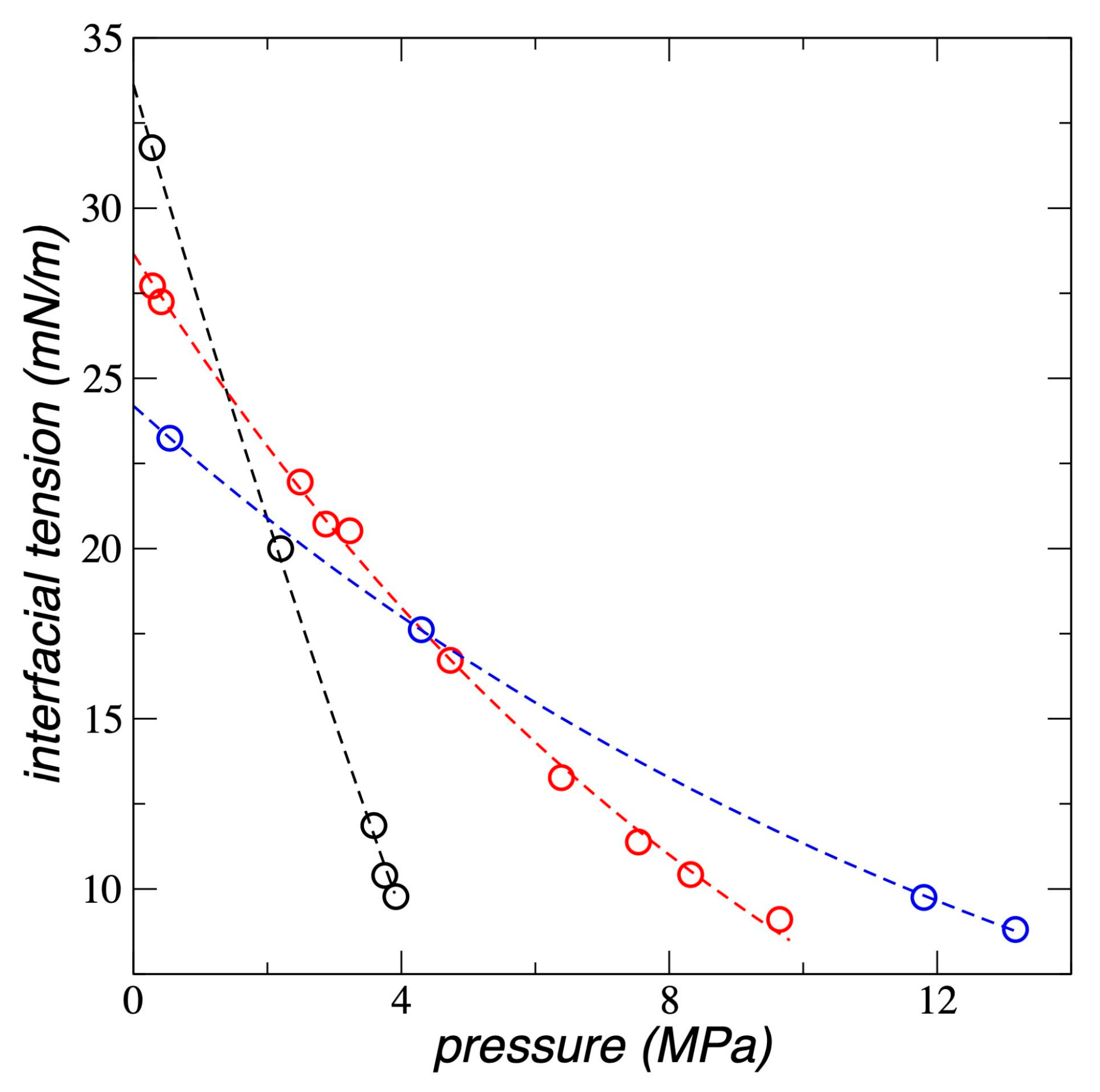
3.4. Interfacial Tension

We calculated γ by integrating the profiles of the function $P_{zz}\left(z\right)-0.5\left[P_{xx}\right(z)+P_{yy}(z)$. For this, we used the total values of $P_{\alpha \beta }\left(z\right)$. The γ values obtained are reported in Figure 8 for the 3 temperatures studied. We found that as $P_{T,g}$ increases, γ decreases, and this negative growth fits well to the behavior of an exponential decay function. It has been previously reported that this potential reproduces the experimental γ of pure PE films [23], finding an independence of γ with the thickness of the PE film. Therefore, γ is independent of whether the film is metastable or stable. Ethane has the effect of a surfactant on the metastable molten PE film, and its effect is more pronounced at low temperatures. At 298.15 K, γ drops on average by 17.5% with each MPa increase in $P_{T,g}$, while at 448.15 K the decrease is ~4.8% for each MPa.

The three isotherms reach similar γ values at high $P_{T,g}$, while at the lowest $P_{T,g}$, the curves behave as expected; γ values at zero $P_{T,g}$ depend only on the temperature of the pristine PE film. The literature has widely documented that in liquid / vapor thermodynamic equilibrium systems, γ is minimally affected by pressure but greatly influenced by liquid density [57]. Given that at the highest $P_{T,g}$ studied, the only difference between the 3 systems is the temperature (the cell volume and the overall density are the same), we compared the average PE densities at the different temperatures and the change they underwent from the pristine systems at $P_{T,g}$ = 0 MPa. Compared to the pristine PE films, the films in contact with methane at high $P_{T,g}$ take lower total densities of 0.768 (298.15 K), 0.7383 (373.15 K), and 0.694 g/ml (448.15 K), while the corresponding percentage reductions were more or less constant, of 9.49 %, 8.99 %, and 10.23 %, respectively. This probably indicates that the dependence of γ should probably be related to the change in the magnitude and not to the total value of the film PE density, as commonly occurs in bulk phases under thermodynamic equilibrium.

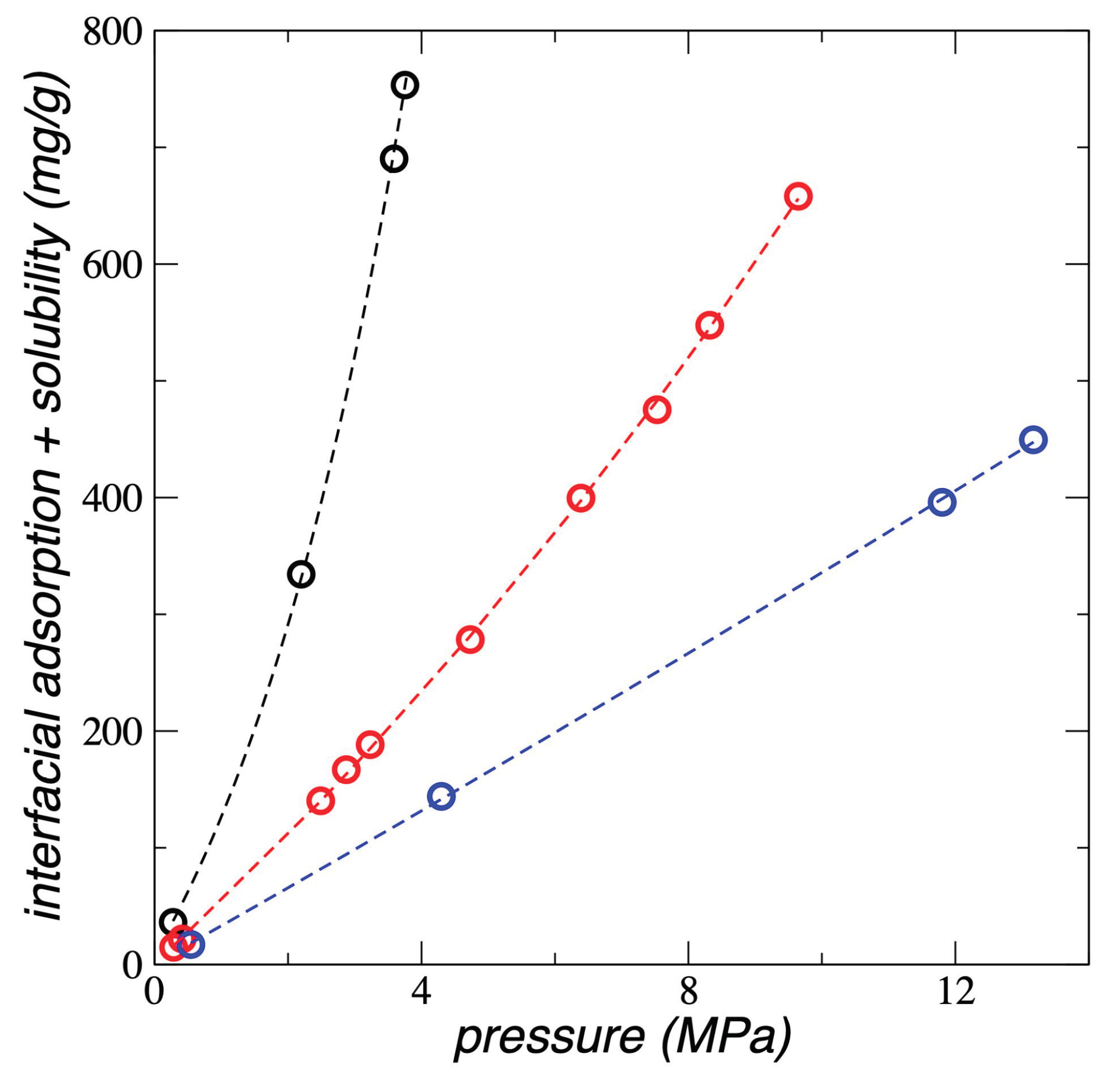
3.5. Interfacial and Soluble Load

We calculated how much ethane the PE film can accumulate, $q_T$, sum of both what is dissolved in the center of the film, $q_S$, and what is adsorbed at the interfaces, $q_I$, and the results are shown in Figure 9 for all the temperatures studied. $q_T$ at all temperatures studied grows exponentially with $P_{T,g}$, and the growth rate decreases as the temperature increases. Experimental studies [16] and numerical calculations using SAFT [17,19,20], have found a similar behavior for $q_S$ in systems composed of different forms of PE exposed to supercritical gases like n-pentane, propane, ethene, propene, but-1-ene, and ethylene. These studies were carried out with bulk PE where the interfacial adsorption part plays an insignificant role. However, for PE in film form, interfacial adsorption is very significant, as can be seen in the $\rho \left(z\right)$ of ethane (Figure 3). No reported studies were found in the literature of ethane adsorbed in any form of PE.

Studies with PE films at 298.15 K have also found that the $q_T$ - $P_{T,g}$ trend reported in this work is the same when the PE film was in contact with supercritical ethylene, but the trend changed to an asymptotic behavior when the PE was exposed to a lighter gas like supercritical methane [9]; this has also been reported for combinations of heavier supercritical alkanes in bulk PE [19]. The experimental results reported in the literature with PE films [9,21] cannot be directly compared with the results of this work, since in the experiments the PE films are pre-treated with n-heptane and the thickness of the experimental films was not reported, which can affect the degree of adsorption and solubility of ethane. The values obtained in this work using pristine, untreated PE films at the stability limit thickness accumulated up to 40 times what was observed experimentally at 4 MPa with films pre-treated with n-heptane and without knowledge of their thickness [9].

We estimated the solubility of ethane in the PE films by considering that there is a region in the center of the liquid that exhibits mechanical stability, at least in terms of the vibrations of the chain sites (Figure 6), but not in their inter-chain interactions due to van der Waals forces. We found that $q_S$ reaches values of 2.94 and 74.8 g per 1000 g of PE for the systems at 373.15 K and $P_{T,g}$ of 0.29 and 9.65 MPa, respectively. These values show that $q_T$ varies between 4.8 and 8.6 times the $q_S$ value when $P_{T,g}$ varies between 0.29 and 9.65 MPa, at 373.15 K.

4. Conclusions

We carried out classical Molecular Dynamics simulations to understand how supercritical ethane molecules accumulate, distinguishing between the ethane that dissolves and that which accumulates at the polymer / gas interface of a polyethylene film at its stability limit thickness. Results at temperatures of 298.15 K, 373.15 K, and 448.15 K, and pressures up to 13.17 MPa, show that the total ethane load grows exponentially as the pressure of the ethane in the gas phase increases. This is similar to what has been found in experiments with polyethylene in film and bulk form in equilibrium with light gases in supercritical state. No experimental studies on ethane were found that would allow us to compare our results, not even with bulk polyethylene. The accumulation capacity of ethane in these two regions decreases as the system temperature increases. We estimate that the increase due to interfacial ethane adsorption can be between 4.8 and 8.6 times the solubility that ethane naturally exhibits when absorbed in bulk polyethylene at 373.15 K and pressures up to 9.65 MPa. The high adsorption at the interfaces, compared to its solubility in the bulk, suggests the development of multiple polyethylene film arrangements as a promising strategy for developing adsorbents for problematic light gases in various industrial and environmental processes.

The films at thei mechanical limit of stability are metastable; while contributions to surface tension from chain vibrations exhibit mechanical stability and the systems remain stable for up to 15 ns, they are not mechanically stable with respect to inter-chain van der Waals interactions. This is likely because these systems are mainly composed of two interfaces whose influence tails overlap in the center of the film. Thicker films are necessary to prevent the interfaces from interacting and make the systems mechanically stable. The interfacial tension exhibits an exponential decay with the pressure of the gas phase, and the rate of decay slows as temperature increases.

The solubility of ethane in the polyethylene film changes with the temperature. At 298.15 K, the density of dissolved ethane is greater than that of the gas phase. This relationship reverses at 373.15 K and becomes more pronounced with increasing temperature, which is probably related to the melting temperature of polyethylene films. It will be interesting to investigate if both transitions occur at the same temperature.

Future work will determine if the limit of mechanical stability is reduced in the presence of ethane, as well as how selective are these films for the adsorption capacity of certain problematic light gases.