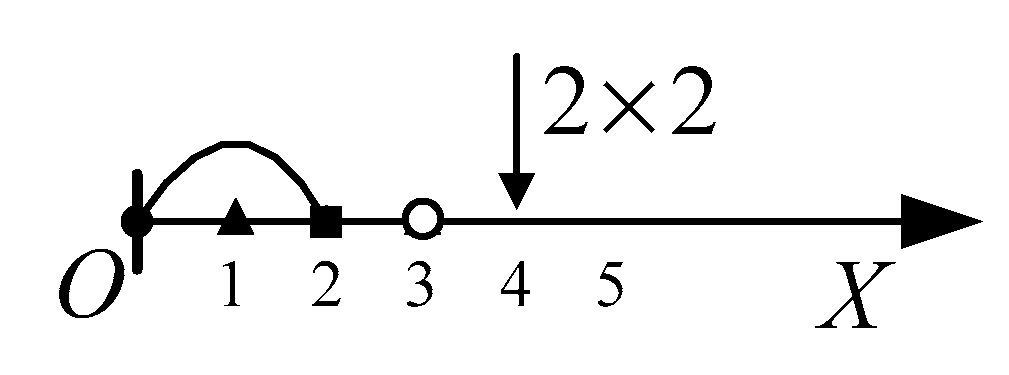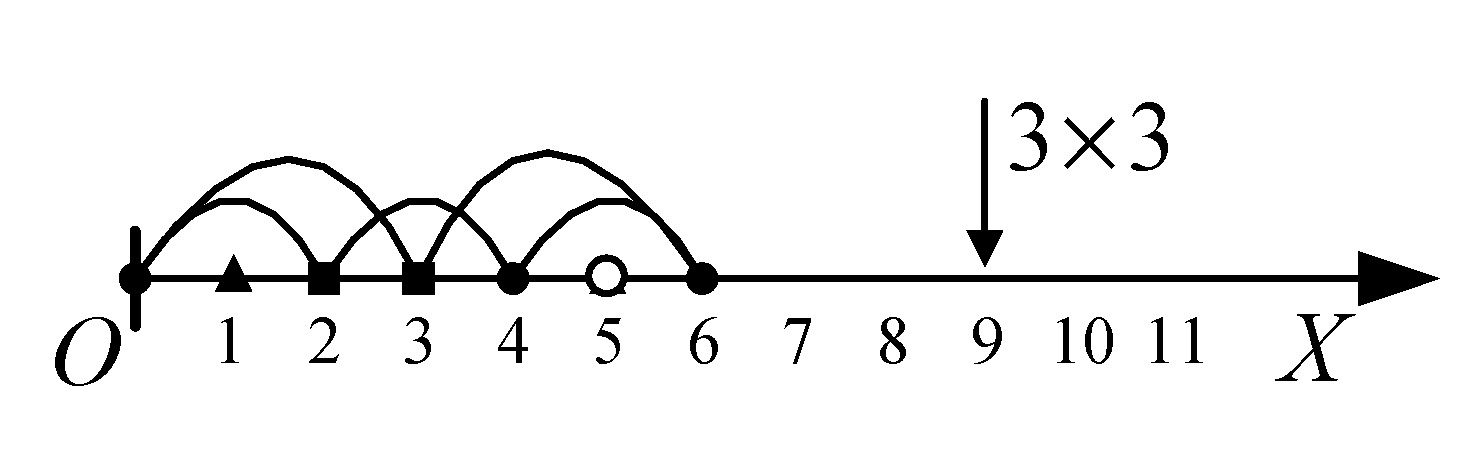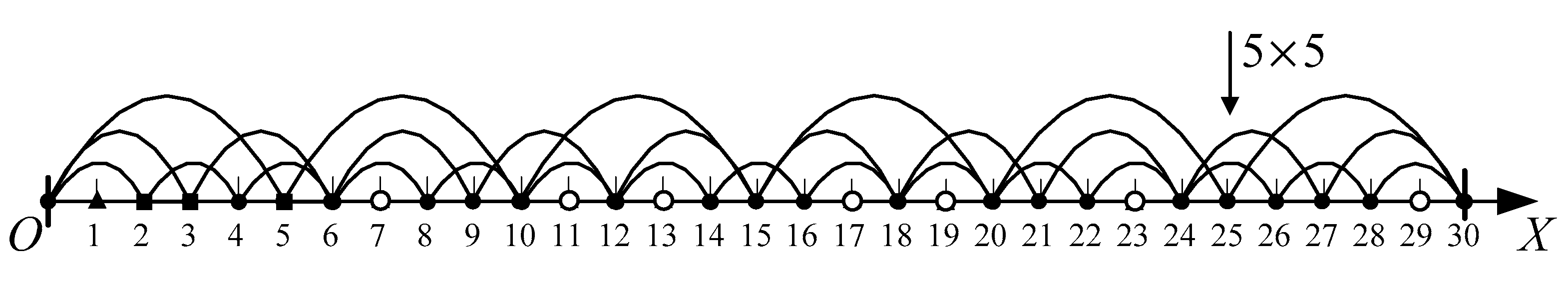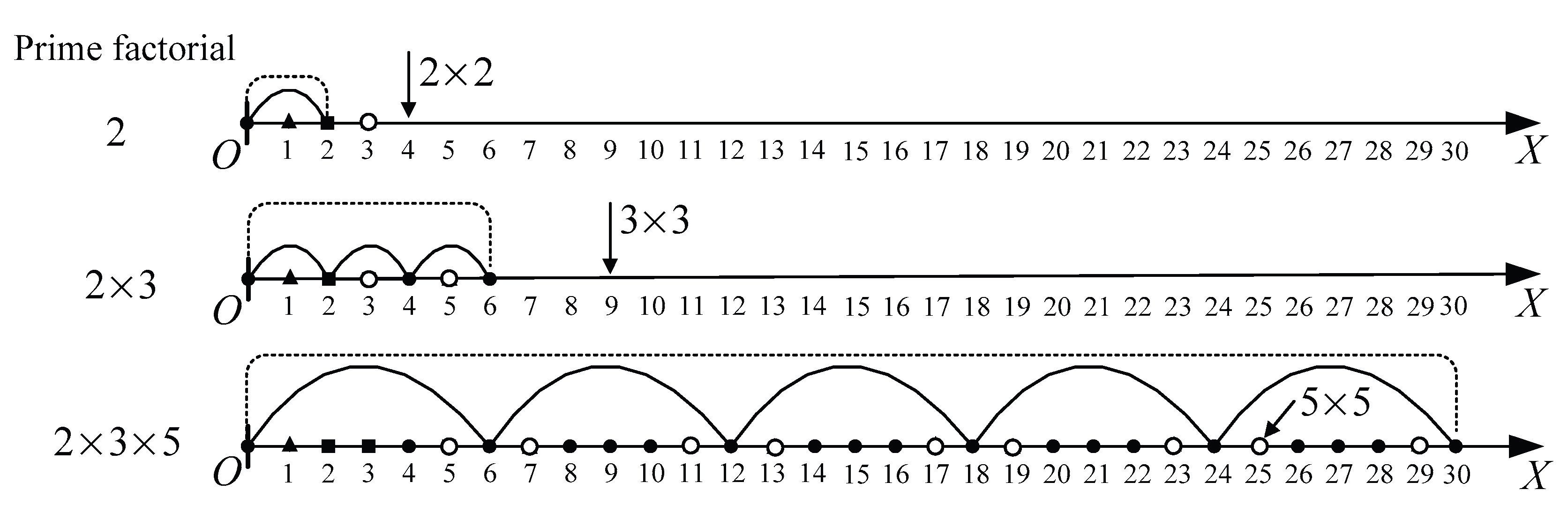The Number of Prime Numbers and Twin Prime Numbers Is Infinite

1. Introduction

The infinity of prime numbers is the starting point of the study of prime numbers. As early as over 2000 years ago, Euclid used the method of proof by contradiction to prove that the number of prime numbers is infinite [1]. In recent history Euler has conducted pioneering research on prime numbers, proposed the Euler product formula, which is another method of proving the infinity of prime numbers.

The proof of infinity of prime numbers and the analysis of prime numbers are complementary. For example, it is only meaningful to continue searching for new prime numbers when it is determined that the number of prime numbers is infinite, and the famous Eratosthenes sieve method is proposed because it can not only sieve for prime numbers, but also tell us that as long as the sieving range is expanded, prime numbers will always appear [2,3]. In fact, the introduction of every new method for proving the infinity of prime numbers will bring progress to prime number analysis, and it is also an unavoidable problem in prime number analysis.

The Euler product formula is the foundation of modern prime number research. The Euler product formula not only reveals the relationship between prime numbers and harmonic series, but also reveals the reasons for the infinity of prime numbers. Therefore, many theories are based on this relationship [4,5]. For example, the famous Riemann conjecture solves the problem of prime number distribution by introducing complex functions into it.

Along with the problem of infinity of prime numbers, people have also observed that twin prime numbers seem to be infinite. Obviously, this is very natural because twin prime numbers are generated along with the generation of prime numbers. Prime numbers are infinite, and twin prime numbers must also be infinite. Furthermore, it can be further inferred that if there is a certain distance between any two adjacent prime numbers, other prime pairs with the same distance can be found. That is to say, the number of adjacent prime numbers with the same distance is also infinite.

This paper proposes a new representation method for prime numbers to reveal the process of generating prime numbers, thereby proving that the number of prime numbers and twin prime numbers are infinite.

2. Definition and Representation of Prime Numbers

2.1. Prime and Composite Numbers

Definition 1: A positive integer greater than 1 that can only be divided by 1 or itself is called a prime number.

Definition 2: A positive integer is called a composite number if it can be divided not only by 1 or itself, but also by other numbers.

Definition 3: The property of whether a positive integer is prime number is called primality.

Definition 4: If the difference between two prime numbers is equal to 2, then these two prime numbers are called a pair of twin prime numbers.

It can be seen that any composite number can be decomposed into the product of several prime numbers, that is, a composite number is obtained by combining several prime factors through product from the definition.

The number 1 is quite special, as it is neither a prime nor a composite number, so there is:

Definition 5: number 1 is a special number.

2.2. Span-Arc Representation of Prime Number

The span-arc graphical method in graph theory can be used to represent prime numbers [6].

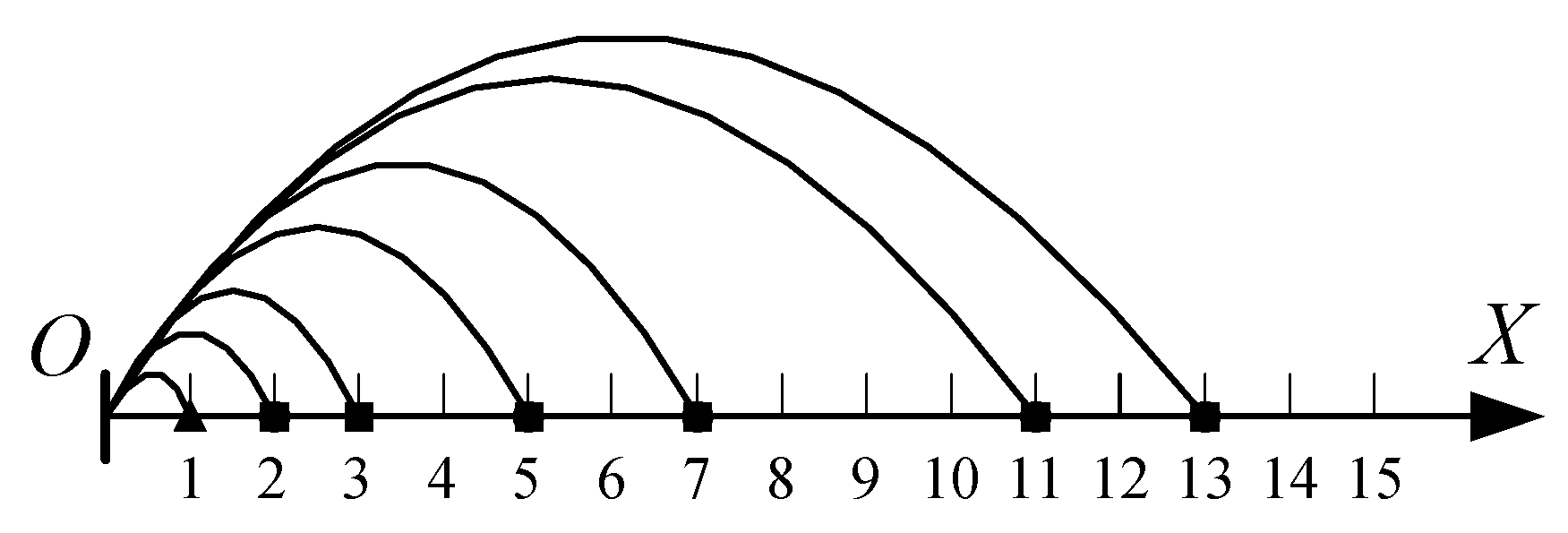
Definition 6: A point on the coordinate axis representing a prime number is called a prime point, and the span-arc connecting the origin of the prime coordinate system to the prime point is called the generating span-arc of that prime number.

Definition 7: Copying the generating span-arc of a prime number and placing them in a prime coordinate system in a tail to tail manner, resulting in countless span-arcs. These span-arcs are called the control span-arcs of prime numbers, and their endpoints are called control points (excluding the points at the endpoint of the generating span-arc).

Prime number generating span-arcs and control span-arcs can be collectively referred to as prime number span-arcs.

Definition 8: The coordinate axis using generating span-arcs and controls span-arcs is called the prime span-arc coordinate axis, abbreviated as the prime coordinate axis.

Figure 1 is a typical prime coordinate axis, representing the generating span-arcs of prime numbers 2, 3, 4, 7, 11, and 13 using span-arcs.

As shown in Figure 2, a prime number has only one generating span-arc, represented by a solid line, but has countless controlling span-arcs, represented by dashed lines.

Obviously, the numbers corresponding to control points are multiples of prime numbers, and they can all be divisible by that prime number, so they are composite points. The generating and control span-arcs of a prime number are connected, so one endpoint on the generating span arc coincides with the endpoint of another control span arc. This point is called a prime point, not a control point.

Assuming that prime numbers are generated one by one.

Definition 9: In the process of generating prime numbers, points are called undetermined points which are temporarily uncertain whether they are prime numbers or composite numbers.

Obviously, the undetermined point is not the control point for all generated prime numbers at present.

On the prime coordinate axis, there are four types of points: prime points, composite points, undetermined points, and special points. Composite points are represented by a solid circle ●, prime points are represented by a square point ■, and undetermined points are represented by a hollow circle ○. As a special point, 1 is represented by a triangle ▲ or a hollow circle ○. When drawing a prime span-arc coordinate axis, points that do not need to be represented by any symbol may be one of the four types of points, that is, composite points, prime points, special points, or undetermined points. These points are not specifically stated at the moment, so they are not marked.

2.3. Waveform Representation of Prime Numbers

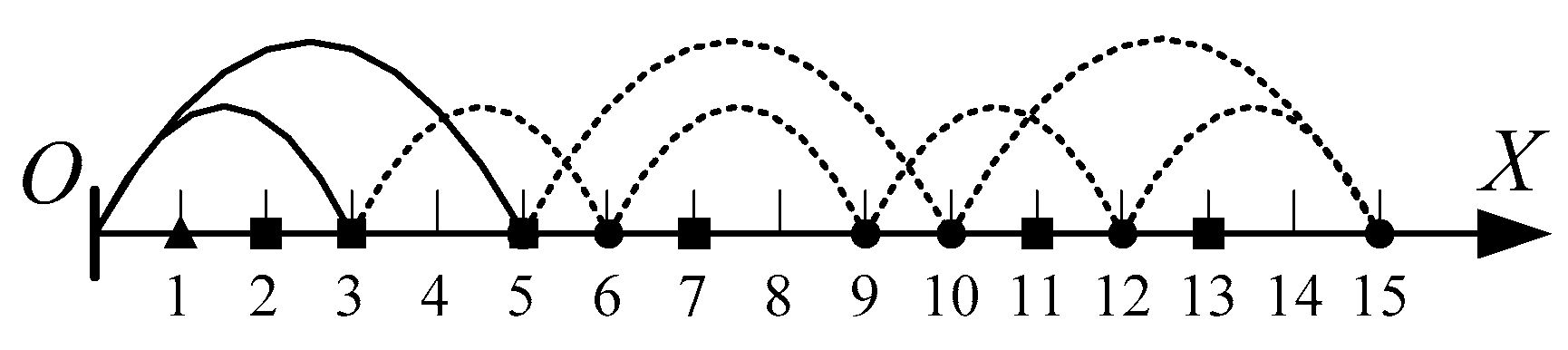
If the generating span-arcs and control span-arcs are alternately placed up and down, a waveform representation as shown in Figure 3 is obtained.

So a prime number and its multiples can be understood as the intersection point of the wave from the origin of the prime number with the coordinate axis. The wavelength of the wave is twice that of the prime number, and the amplitude of the wave at any point is the remainder of the point on the coordinate axis divided by the prime number.

Multiple prime numbers can be represented by stacking multiple waveform graphs.

3. Generation of Prime Numbers

3.1. The Generation Process of Prime Numbers

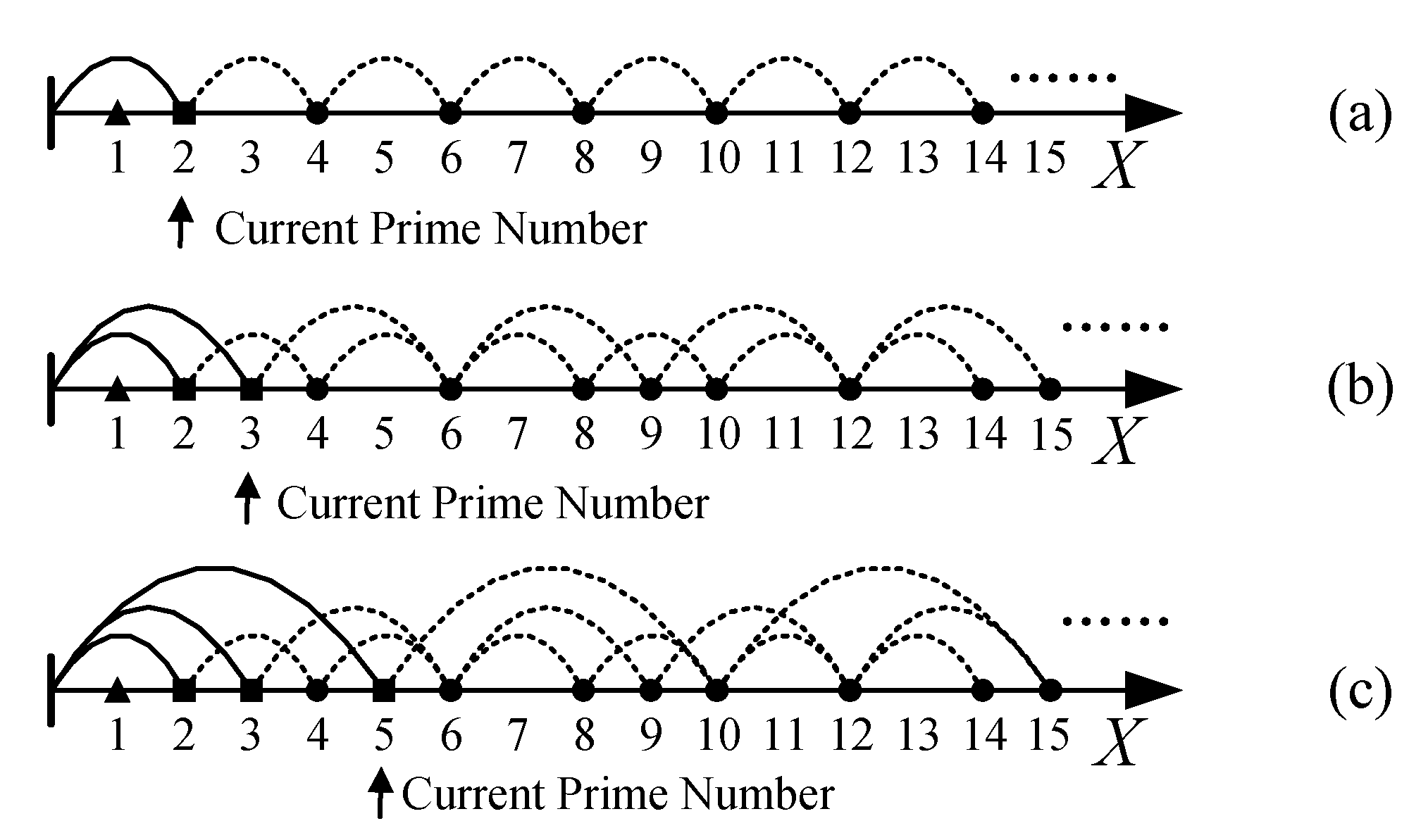
Assuming that all prime numbers on the prime coordinate system are dynamically generated, that is, in the initial state, there are only positive integer points on the prime coordinate system, and there are no prime numbers or their span-arcs. Then, by moving point by point along the positive direction of the coordinate axis, each prime number is determined one by one, and the prime number generating span-arcs and their control span-arcs are given for each prime number, thereby determining all prime numbers in the entire prime coordinate system.

Definition 10: The generation of prime numbers is a dynamic addition process. When moving point by point along the coordinate axis from point 2 in the positive direction, if the current point is not the control point of a prime number, it is defined as a prime point and added to the current set of prime numbers. Otherwise, it is defined as a composite point.

Obviously, this definition is consistent with Definition 1 and Definition 2.

The dynamic generation process of prime numbers is represented by the prime number span-arc method shown in Figure 4.

As shown in Figure 4 (a), since the number 1 cannot be defined as a prime number, move to the first non control point: number 2, define number 2 as the first prime number, and generate the generating span-arc of prime number 2 and its all control span-arcs.

Continue moving to the right along the coordinate axis and find the first non control point 3 in the first control span arc of prime number 2, as shown in Figure 4 (b). Define the number 3 as the second prime number. Then, make the generating and control span arcs for prime number 3.

Continue moving to the right along the coordinate axis to obtain non control point 5, define it as a prime number, and make the generating and control span-arcs of the prime number 5, as shown in Figure 4 (c).

By continuously moving to the right using the same method, all prime numbers can be obtained one by one.

3.2. Hierarchical Generation of Prime Numbers

Because prime numbers are dynamically generated, the hierarchy of prime numbers can be determined based on the order in which they are formed.

It can be seen from the span-arc of prime numbers that number 1 is the basis for constructing any number, but 1 is not distinguishable, so number 1 cannot be defined as a prime number.

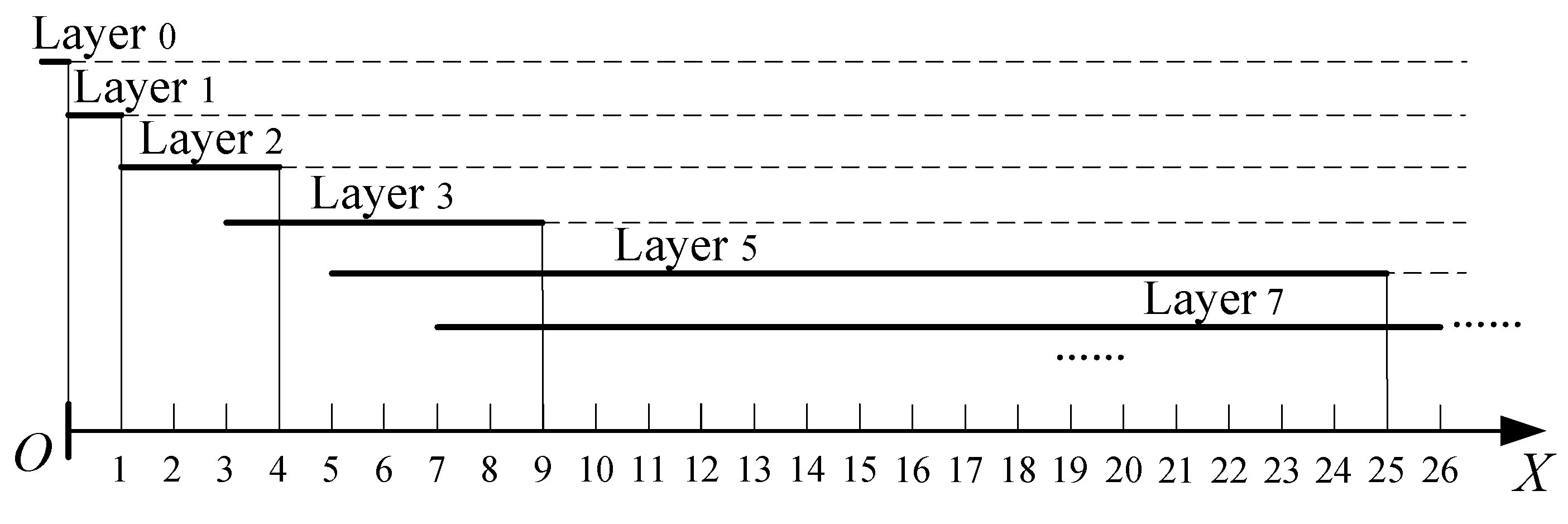
Definition 11: The interval $[p,p^2)$ where the current prime number p(p>2) is located is called the prime control layer, abbreviated as the control layer or current layer. The interval $[p^2,\infty )$ it affects is called the prime influence layer, abbreviated as the influence layer.

As shown in Figure 5, the thick solid line represents the control layer of the prime number, while the dashed line represents the influence layer of the prime number.

The specific hierarchical division of prime numbers is as follows:

The 0th layer is a special layer that is the top layer of all layers. It does not contain any numbers.

The 1th layer has no prime numbers. Its control layer interval is [0,1), and the influence layer interval is $[1,\infty )$.

The 2th layer has two prime numbers: 2 and 3. Its control layer interval is $[1，4)$, and the influence layer interval is $[4,\infty )$. The 2th layer is relatively special because 2 is the only even prime number, so the endpoint of the right interval of the control layer is an even square point.

The 1th layer control interval can also be [1,1], and the 2th layer control interval can also be $[2,4)$, which can have the same definition as the subsequent control layer intervals.

The interval of the 3th control layer is $[3，9)$, and the interval of the influence layer is $[9,\infty )$.

Any prime number $p$is in the p-th layer, with a control layer interval $[p,p^2)$ and an influence layer interval $[p^2,\infty )$.

Here, the value of the prime number $p$ is in the p-th layer, and the number of layers is not continuous, but defined according to the prime number.

Theorem 1: In an interval $[p,p^2)$, every endpoint of control span-arc of a prime number $p$ coincides with the endpoint of a prime number’s control span-arc in interval $[2,p)$.

Proof: Because the control span-arc endpoints of any prime number $p$ can be used to represent with $kp$, obviously $k<p$ within the interval $[p,p^2)$, $k$ can only be one or more combinations of prime numbers in an interval $[2,p]$, and this point coincides with the control span-arc endpoints of these prime numbers .■

Theorem 2: In the process of dynamically determining prime number $p$, the primality of other positive integers in the current prime layer $[p,p^2)$ is determined, while the primality of the positive integers in its influencing layer $(p^2,\infty )$ is undetermined.

Proof: In the proof of Theorem 1, it is known that for a point in the control layer $[p,p^2]$, if it is a control point of a prime number in an interval $[2,p]$, then it is determined to be a composite point. If it is not a control point of all prime numbers in an interval $[2,p]$, then it is a prime point, so its prime is determined. However, for a point in the influence layer $[p^2,\infty )$, even if it is not a control point of all prime numbers in an interval $[2,p]$, it may still be a multiple of a determined prime point in an interval $[p,p^2]$, so its primality cannot be determined.■

The following theorem can be obtained from Theorem 1 and Theorem 2.

Theorem 3: If a number cannot be exactly divided by all prime numbers within its square root, then the number is a prime number.

According to Theorem 3, a commonly used algorithm for determining prime numbers can be obtained, which is the Eratosthenes sieve method.

3.3. Prime Factorial Segment

Definition 12: If all prime numbers are arranged in an ascending order, the product $p_1{p}_2\dots p_k$ of prime numbers $p_1,p_2,\dots ,p_k$ is called prime $p_k$ factorial, denoted as $p_k!$, and the interval equal to the prime $p_k!$ factorial value is called the prime $p_k!$ factorial segment.

When generating any prime number, if the prime coordinate axis is segmented according to the size of the prime $p_k!$ factorial segments starting from the origin, it is known that the prime span-arc shape of these factorial segments is exactly the same because $p_1{p}_2\dots p_k$ are the least common multiple of the prime number $p_1,p_2,\dots ,p_k$. That is, every $p_1{p}_2\dots p_k$ interval, their prime span-arc shape is repeated.

For example, the span-arc structures of factorial nodes of prime numbers 2, 3, and 5 are shown in Figure 6, Figure 7 and Figure 8. If all the span-arc graphs of prime numbers are continued to be drawn, the span-arc structures of the following parts are completely similar to these factorial segments.

3.4. The Copy and Sieve Process of Prime Factorial Segments

In the process of generating prime numbers, for each newly generated prime number $p_{k+1}$, a new prime $p_{k+1}$ factorial segment is formed. It is an extension of the previous prime $p_k$ factorial segment, extending from the span-arc structure of the prime $p_k$ factorial segment to the prime $p_{k+1}$ factorial segment structure. The extension process is shown in Figure 9, where the span-arc structures of prime numbers 2 and 3 are not drawn during the extension of prime number 5 factorial segment, and only the type of point is given. The range within the dashed line is the current prime factorial segment.

Definition 13: If the current added prime number is $p_1,p_2,\dots ,p_k$, the operation of copying $p_{k+1}-1$ copies from the current prime factorial span-arcs and their endpoint types, and sequentially connecting them is called copying of the prime factorial segment, the copied segment to be is called the first segment, the segment copied from the first segment is called the continuation segment, and the operation of marking the point types in the current copied and connected prime $p_{k+1}$ factorial segment is called sieve.

Figure 9 only shows the copying operation and does not represent the sieve operation.

In the process of expanding prime factorial segment, if a copy operation is performed, the undetermined points (Including special point 1) in the first segment will still appear in the form of undetermined points in the continuation segment. If the undetermined points in the first segment are determined to be prime points, they will become composite points in the continuation segment and continue to maintain the composite point type in the subsequent expansion process.

The copying purpose is to construct the span-arc of the current prime number $p_{k+1}$, forming a complete prime $p_{k+1}$ factorial segment, while the purpose of sieve is to remove those newly added composite points. The sieve process is divided into two steps.

The first step is to identify the points $p_1,p_2,\dots ,p_k$ at the first prime position in each copied segment as composite points, because the copied block satisfies a common multiple relationship, so these points at prime positions naturally become composite points.

The second step starts from the point $p_{k+1}^2$ in the first segment, and marks the corresponding points as composite points every $2p_{k+1}$ position in the prime $p_{k+1}$factorial segment. The use of identification here of $2p_{k+1}$ is because even points have already been marked and do not need to be marked again.

3.5. Twin Prime Number Egg

Definition 14: In the process of expanding prime factorial segment, if two undetermined points differ by 2, they are called twin prime number egg.

Twin prime number egg only has the basic conditions to become twin prime number and may not ultimately become twin prime number.

Definition 15: The process of generating twin prime number eggs during the expansion of prime factorial segments is called the incubation of twin prime number eggs.

There are no twin prime numbers in the factorial segment of prime number 2. In the factorial segment of prime number 3, there is the first twin prime number pair 3, 5. In the factorial segment of prime number 5, there are twin prime number pairs added, including 5 and 7, 11 and 13, 17 and 19. 23, and 25, which are also twin prime number eggs. However, since 25 becomes a composite number, it does not form a twin prime number. If we observe the generation position of twin prime numbers, we can see that they are twin prime number eggs before transforming into prime numbers, so the generation of prime numbers is closely related to their position in the prime factorial segment.

From the expansion process of prime factorial segment, it can be seen that there are two ways to conceive twin prime number eggs: replication and splicing. If a twin prime number egg appears in the middle of the first prime factorial segment, due to the overall replication of the span-arc structure, a twin prime number egg will be automatically bred at the corresponding position of the subsequent segment. This type of twin prime number egg is called replication. When two factorial segments are spliced, the junction of the point at the tail of the previous segment and the point at the head of the following segment also forms twin prime number eggs. This type of twin prime number eggs breeding method is called concatenation. For example, the only pair of twin prime numbers in a prime number 3 factorial segment is spliced, and all newly added twin prime numbers in a prime number 5 factorial segment are also spliced. The twin prime number eggs in prime numbers 7 and higher factorial segments are not only generated by concatenation, but also by replication.

Due to the $p_{k+1}-1$ duplications of the twin prime number eggs in the previous prime number $p_k$ factorial during replication, $p_{k+1}-1$ pair of twin prime number eggs will be formed during splicing. Therefore, as the prime factorial segment expands, the number of twin prime number eggs produced by replication is much greater than that produced by splicing.

4. Infinity of Prime Numbers and Twin Prime Numbers

Theorem 4: The number of prime numbers and twin prime numbers is infinite.

Proof: The process of generating prime numbers is also a process of copying and sieving the factorial segments of prime numbers. The copying process expands the undetermined points in the first segment by $p_{k+1}-1$times, greatly increasing the likelihood of new prime numbers and twin prime number pairs appearing. However, due to the existence of a sieving process, if all undetermined points are filtered out during the sieving process, new prime and twin prime numbers will no longer be generated. Therefore, it needs to be proven that the sieving process cannot filter out all undetermined points.

When using prime number $p_{k+1}$ to filter the continuation sections of prime number $p_k$ factorial segments, it is known that the number of $p_{k+1}$ position in the continuation segment cannot be exactly divided by $p_{k+1}$, so these undetermined points cannot be filtered out. Furthermore, for points $m{p}_1{p}_2\dots p_k+x$,（$0\le m<p_{k+1}$） at the same position on the prime factorial segment (including the first segment and the continuation segment), if $x$ cannot be exactly divided by $p_1,p_2,\dots ,p_k$, then it is a undetermined point. Obviously, only one of these points can be exactly divided by $p_{k+1}$, and the other points will not be filtered out, so there are always undetermined points that cannot be filtered out. Because any extension or sieving of the factorial segment of prime numbers will not filter out all undetermined points, there are always unfiltered undetermined points confirmed as prime numbers, so prime numbers are infinite.

From the process of generating twin prime number eggs, it can be seen that there are replication and splicing operations in the process of expanding from prime number $p_k$ factorial segments to prime number $p_{k+1}$ factorial segments. replication operations will increase the number of twin prime number eggs by $p_{k+1}-1$ times in the prime number $p_k$ factorial segment, and splicing operations will add $p_{k+1}-1$ twin prime number eggs. Similarly, if an undetermined point is filtered out in a prime factorial segment, so the undetermined points at the same position in another prime factorial segment will definitely not be filtered out. When the number of undetermined points increase to 2, the maximum number of sieved out undetermined points is 2, which is relatively small. Therefore, the sieving operation cannot filter out all twin prime number eggs. To put it another way, even if all replicated twin prime number eggs are filtered out, new twin prime pairs of eggs may always be generated during splicing, so twin prime number eggs will always exist, twin prime number eggs are always possible to transform into twin prime pairs, and the number of twin prime pairs is also infinite. ■

As the factorial segment of prime number $p_{k+1}$ expands, the sieving interval $[p_{k+1}^2,p_1{p}_2\dots p_k{p}_{k+1}]$ becomes extremely large, and there may be cases where there are no twin prime numbers in a larger interval, but this does not affect the conclusion that prime numbers and twin prime numbers are infinite.

From Theorem 4, it can be inferred that if there are adjacent undetermined points with arbitrary distance during the expansion process of a prime factorial segment, the number of adjacent prime pairs with the same distance must also be infinite.

As the prime number $p_{k+1}$ increases, from the perspective of prime factorial, the number of prime numbers is not decreasing, but increasing.

5. Conclusion

Using span-arcs to represent prime numbers and their relationships can fully utilize the advantages of graphs in analyzing and solving problems. Therefore, this method can transform Euclidean prime product used to prove that prime numbers are infinite into prime factorials with periodic characteristics, and transform the special point 1 it uses into a more general undetermined point. This not only proves that the number of prime numbers is infinite, but also can be proven that the pair number of twin prime numbers is infinite, and it can even be proven that the number of adjacent prime numbers with any specific distance is infinite.