Goldbach's Conjecture Proof of its Interaction with the Riemann Hypothesis and the Golden Spiral via Inner Number Digit Summation (INDS)

1. Introduction

Goldbach's conjecture states that every even composite number can be expressed as the sum of two prime numbers—a possibility that has been examined repeatedly, yet no comprehensive mathematical proof has been established. [1] Goldbach's conjecture depends on the logical relationship between prime numbers and even composite numbers. Although at first glance the outcome of its proof may seem unrelated to other phenomena, the fundamental structure of numerical logical relationships underpins the interpretation of many phenomena in physics.[2] This article investigates the essential importance of this conjecture based on the inherent properties of numbers and the grouping of prime and non-prime numbers according to their internal digit sums (INDS).[3,4] Grouping the prime numbers into six groups based on their INDS provides a simpler approach to proving Goldbach's conjecture. Analyzing even composite numbers in terms of modulo 9 can help identify the regions where the contributing prime number pairs are located. Consequently, various methods emerge for finding pairs of prime numbers that align with these prime number groups. This, in turn, establishes a logical connection between the internal digit sum of an even composite number and that of prime numbers, thereby making the proof of Goldbach's conjecture feasible. Moreover, the logical relationship between the internal digit sum of prime numbers and logarithmic spirals creates an overlap that links Goldbach's conjecture with the Riemann hypothesis and the zeta function. This study reveals the reason behind natural symmetries and their association with the groups of prime numbers, even composite numbers, and the Riemann hypothesis in nature [4,5,6,7].

2. Goldbach's Conjecture

Every even integer greater than two is the sum of two prime numbers. (2.1)

$$2n=P_{\upsilon }+P_{\mu }nϵz$$

2.1

A: INDS:

Identifying prime numbers through the sum of their internal digits is also possible.

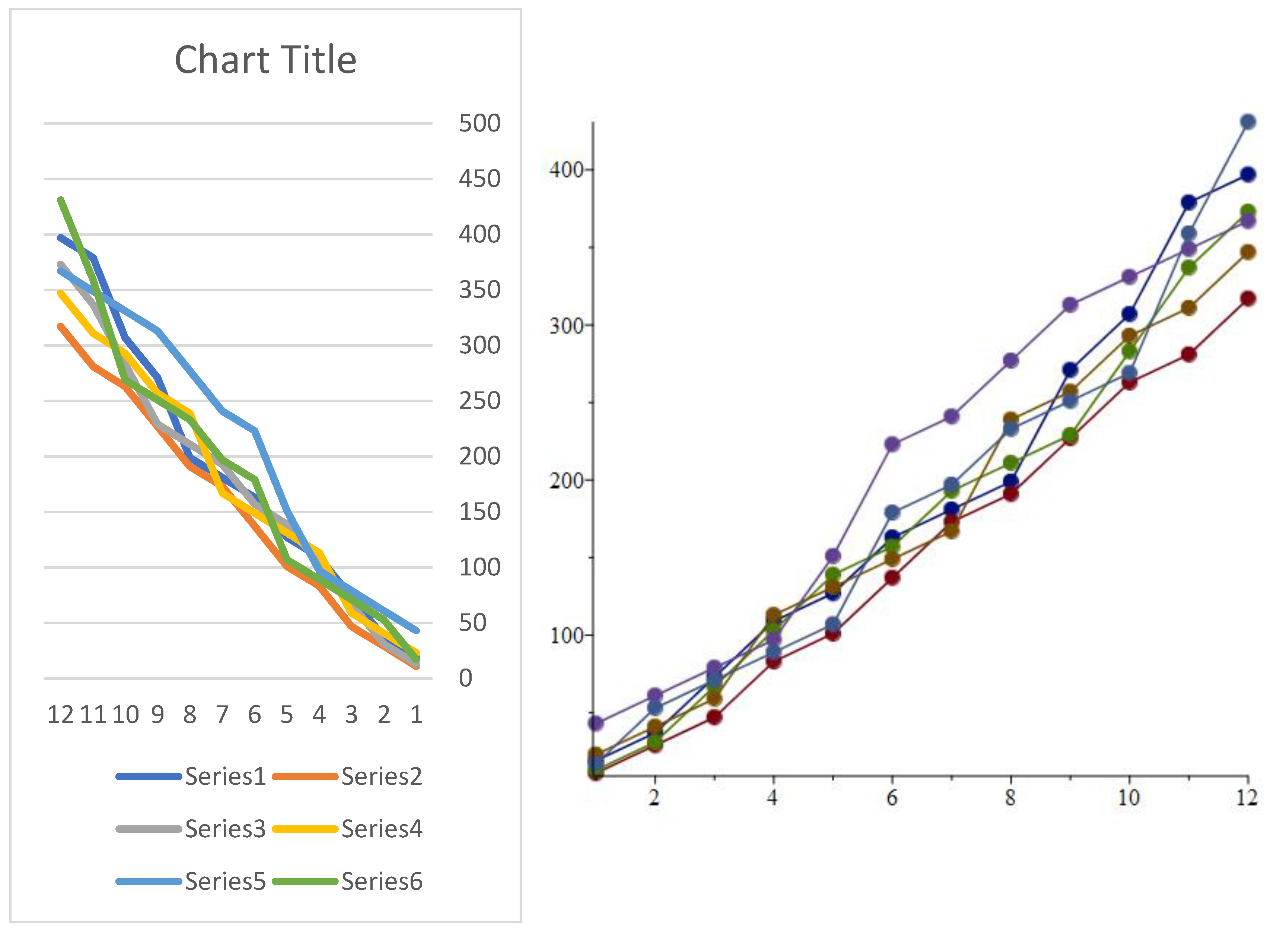
First statement: Based on the internal digit sum of multi-digit numbers, prime numbers are categorized into six groups. Table 1. Table 2. Figure 1. (2.2)

$$\alpha \beta \gamma \dots \eta \to \alpha +\beta +\gamma +\dots +\eta$$

2.2

First conjecture: Except for the number 3, no prime number falls into groups 3, 6, and 9. For example, the internal digit sum of the number 1859668549875 ends in the number 9, and this number is not a prime number. And also, the internal digit sum of the number 10000000000037 ends in the number 2, and this prime number belongs to group 2 and is indeed a prime number. (2.3)

$$1859668549875\to \mathrm{INDS}=81\mathrm{INDS}=8+1=9\notin \mathrm{P}$$

$$10000000000037\to \mathrm{INDS}=11\mathrm{INDS}=1+1=2\in \mathrm{P}$$

2.3

Second assumption: Accordingly, any multi-digit number whose digit sum equals 3, 6, or 9 is not a prime number.

Note: Some numbers containing zeros, whose internal digit sum ends in a number belonging to the six groups, are not prime. For instance, 300041 appears to belong to group eight, but the count of zeros in a six-digit number and the oddness of zeros indicate that this number is composite. (2.4)

$$300041\to \mathrm{INDS}=8\notin \mathrm{P}$$

$$40367\to \mathrm{INDS}=2\in \mathrm{P}$$

2.4

For instance, consider the following numbers:

1009 - Zero in the second digit.

10301 - Zeros in the third and fourth digits.

20011 - Zero in the second digit.

70001 - Zero in the second digit.

300007 - Zeros in the second and third digits.

1000033 - Zeros in the second, third, and fourth digits.

The first number is a four-digit number, and considering the presence of a zero in the second digit, due to the existence of two zeros in this number, it belongs to group one and is a prime number.

The second number is a six-digit number, and the presence of two zeros does not affect its primality. This number belongs to group five.

The third number belongs to group four, and considering the presence of two zeros in a five-digit number, this number is also a prime number.

The fourth number belongs to group eight, and according to the previous rule, it is a prime number.

The fifth number belongs to group one, and considering that it is a six-digit number and an odd number, this number is also prime.

And the sixth number belongs to group seven. It also contains four zeros and is a seven-digit prime number.

Statement: 

The number of zeros in a number, the total number of its digits, and whether the number is even or odd establish a direct relationship with the groups, which distinguishes prime numbers from composite numbers.

For instance, a six-digit number that contains two zeros and has an internal digit sum that is an even number is not a prime number.

Lemma: 

Considering the three proposed conditions, two of these conditions may also suffice for a number

Table 3. Algorithm for Checking Composite Evens Containing Zeros.

Table 3. Algorithm for Checking Composite Evens Containing Zeros.

3. Result:

A:

Based on this research, it is possible to prove Goldbach's conjecture using the sum of internal digits. Every number possesses properties that are directly related to the sum of its internal digits, its parity (whether it is even or odd), and its magnitude or order.

Statement: The subtraction of the number formed by the sum of the digits of a multi-digit number from the number itself is divisible by nine. (3.1)

$$\alpha \beta \gamma \dots \eta \to \alpha +\beta +\gamma +\dots +\eta =\Lambda \Rightarrow \alpha \beta \gamma \dots \eta -\Lambda =9\lambda$$

3.1

Statement: The number obtained by summing the digits of a multi-digit number, after multiplication and subtraction of the internal digits sum from the resulting number, is a prime number. (3.2)

$$\alpha \beta \gamma \dots \eta \to \alpha +\beta +\gamma +\dots +\eta =\Lambda \Rightarrow \alpha \beta \gamma \dots \eta -\Lambda =9\lambda$$

$$9\lambda =\varrho \dots \rho \Rightarrow \varrho +\dots +\rho =\varphi \Rightarrow 9\lambda -\varphi =P_{\upsilon }$$

3.2

3.2

Lemma 1. 

By subtracting the number obtained from the sum of the internal digits from the final number obtained from the initial multiplication, we divide the result by 9 and 3. We add the two obtained numbers together. If the sum of the internal digits of the obtained number is divisible by the number of digits, we add the number with minus 1. One of the prime numbers obtained by adding two prime numbers is obtained. (3.3)

$$\alpha \beta \gamma \dots \eta \to \alpha +\beta +\gamma +\dots +\eta =\Lambda \mathsf{\Lambda }\left(\alpha \beta \gamma \dots \eta \right)=\varrho \dots \rho =\varphi ⟹{\displaystyle \frac{\varphi }{9}}=P_{\upsilon }$$

$${\displaystyle \frac{\varphi }{3}}=P_{\mu }\Rightarrow P_{\upsilon }+P_{\mu }=\tau \tau -1=P_a$$

$$P_a+P_b=\alpha \beta \gamma \dots \eta$$

3.3

Note: Each number belongs to a group, and therefore the specified condition applies only to a particular group.

Second Lemma 

: After adding the digits inside and subtracting the first step and dividing the final number by 9 and 3 and the sum of the two numbers obtained, we subtract the sum of the three numbers 3, 6 and 9 from the resulting number. And we add the final number to the number 1. The result of the second case is the sum of the first two numbers. (3.4)

$$\alpha \beta \gamma \dots \eta \to \alpha +\beta +\gamma +\dots +\eta =\Lambda \mathsf{\Lambda }\left(\alpha \beta \gamma \dots \eta \right)=\varrho \dots \rho =\varphi ⟹{\displaystyle \frac{\varphi }{9}}=P_{\upsilon }$$

$${\displaystyle \frac{\varphi }{3}}=P_{\mu }\Rightarrow P_{\upsilon }+P_{\mu }=\tau \tau -\left(3+6+9\right)=\acute{\tau }\acute{\tau }+1=\acute{P_a}$$

$$\acute{P_a}+\acute{P_b}=\alpha \beta \gamma \dots \eta$$

3.4

3.4

Statement: 

Accordingly, every composite number has two sums of prime numbers, which is used in decoding binary numbers. (3.5)

$$\acute{P_a}+\acute{P_b}=1$$

$$P_a+P_b=0$$

3.5

Note: Each number belongs to a group, and therefore the specified condition applies only to a particular group.

The Pythagorean theorem holds true for prime numbers in non-Euclidean geometry with different dimensions.

Considering the various groups of numbers, there are different methods that can decompose a composite number into two prime numbers. For instance, the sum of the digits within the number (Inner Number Digit Sum=INDS)230 is 5. This number emerges through successive steps. (3.6)

$$230+5=235235-IDNS\left(235\right)=234{\displaystyle \frac{234}{9}}=2626+5=31230-31=199$$

3.6

3.6

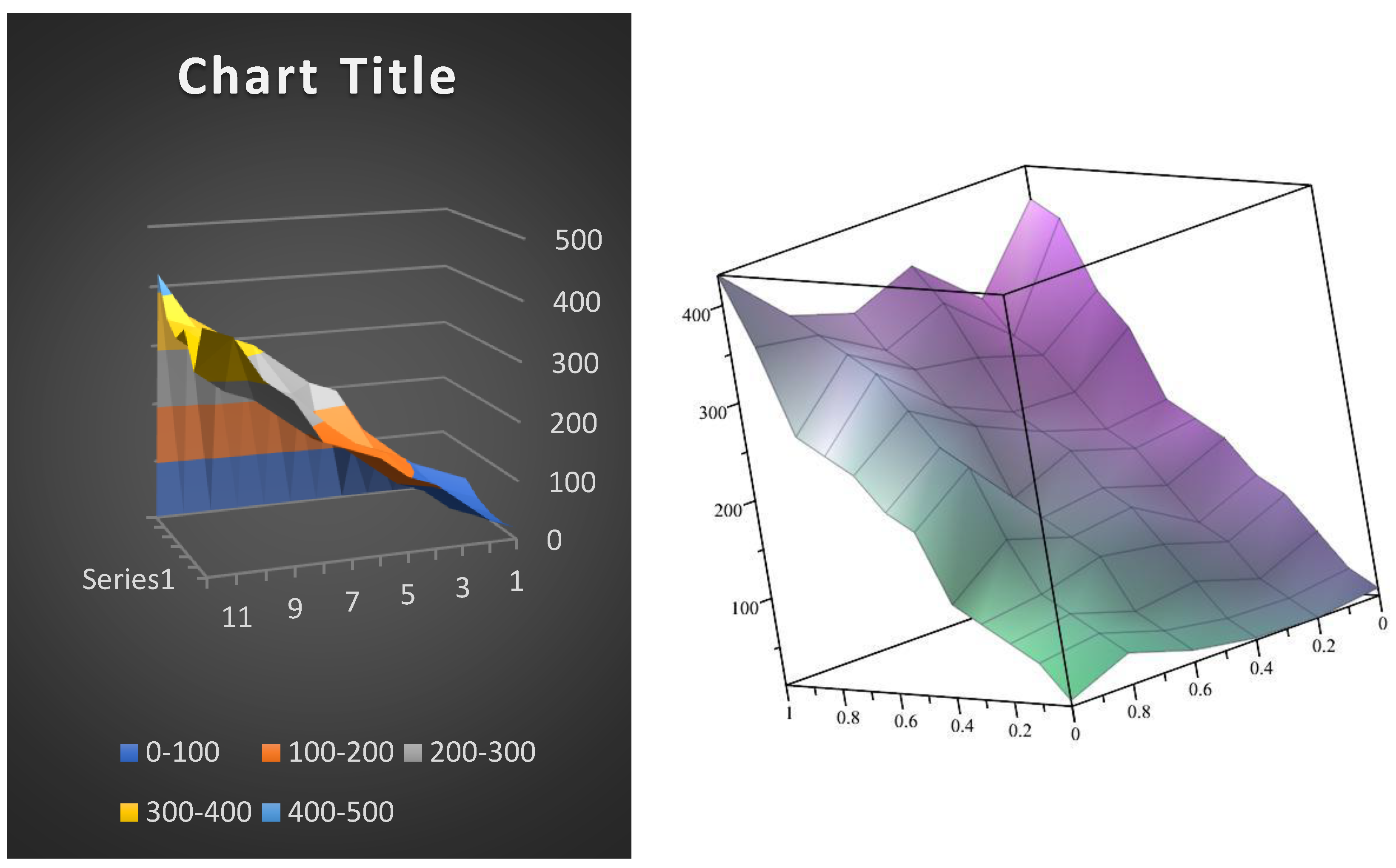
Given the existence of various groups of prime and composite numbers, there are numerous methods to decompose a composite number based on the divisibility of composite numbers. The reason for this lies in the relationships between numbers in a non-Euclidean space. (3.7) Figure 2

$$\tan \left(30\right)\times 2n~P_{1}24\tan \left(28.44292862437\right)=1324-13=11$$

3.7

B:Proof:

Statement: Based on the definitions of groups for prime numbers in complex space, the groups can be associated with trigonometric ratios dependent on logarithmic spirals in complex space with natural numbers. (3.8)

$$\begin{gathered} \left(\sqrt{0}+1i\right)\left(\sqrt{0}-1i\right) \\ \left(\sqrt{1}+1i\right)\left(\sqrt{1}-1i\right) \\ \left(\sqrt{2}+1i\right)\left(\sqrt{2}-1i\right) \\ \left(\sqrt{1}+2i\right)\left(\sqrt{1}-2i\right) \\ \left(\sqrt{3}+2i\right)\left(\sqrt{3}-2i\right) \\ \left(\sqrt{2}+3i\right)\left(\sqrt{2}-3i\right) \\ \left(\sqrt{1}+4i\right)\left(\sqrt{1}-4i\right) \\ \left(\sqrt{3}+4i\right)\left(\sqrt{3}-4i\right) \\ \left(\sqrt{2}+\left(\left(\sqrt{2}+1i\right)\left(\sqrt{2}-1i\right)\right)i\right)\left(\sqrt{2}-\left(\left(\sqrt{2}+1i\right)\left(\sqrt{2}-1i\right)\right)i\right) \\ \left(2\sqrt{1}+\left(\left(\sqrt{2}+1i\right)\left(\sqrt{2}-1i\right)\right)i\right)\left(2\sqrt{1}-\left(\left(\sqrt{2}+1i\right)\left(\sqrt{2}-1i\right)\right)i\right) \\ \left(2\sqrt{2}+\left(\left(\sqrt{2}+1i\right)\left(\sqrt{2}-1i\right)\right)i\right)\left(2\sqrt{2}-\left(\left(\sqrt{2}+1i\right)\left(\sqrt{2}-1i\right)\right)i\right) \\ \left(3\sqrt{2}+\left(\left(\sqrt{0}+1i\right)\left(\sqrt{0}-1i\right)\right)i\right)\left(3\sqrt{2}-\left(\left(\sqrt{0}+1i\right)\left(\sqrt{0}-1i\right)\right)i\right) \end{gathered}$$

3.8

Statement: The inner digits sum of a composite number is equal to the inner digits sum of its constituent prime numbers. (3.9)

$$IDNS\left(2n\right)=IDNS\left(P_{\mu }\right)+IDNS\left(P_{\upsilon }\right)$$

3.9

Lemma: 

Based on the constituent groups of prime numbers, an even composite number can be rewritten in several ways as a sum of prime numbers. (3.10)

$$IDNS\left(2n\right)=IDNS\left(P_{\mu }\right)+IDNS\left(P_{\upsilon }\right)\mu ,\upsilon =1,2,3,4,5,6$$

3.10

3.10

Based on this, an algorithm(Table 4) can be created to identify pairs of prime numbers whose sums are associated with a given even composite number. Here's how it would proceed:

• Calculate the internal digit sum (INDS) of the even composite number: This step determines the numeric target by summing the digits of the composite number.
• Generate all prime numbers less than the composite number: Create a list of primes smaller than the given number to consider possible pairs.
• Iterate through prime pairs: Evaluate every pair of primes to find combinations where the sum of their INDS matches the INDS of the composite number.
• Group and validate: Ensure the identified pairs meet additional constraints, like group membership based on modular arithmetic or other specified rules.

Table 4. Algorithm for Finding Prime Number Pairs Forming an Even Composite Number.

Table 4. Algorithm for Finding Prime Number Pairs Forming an Even Composite Number.

For example, the number 24 is decomposed into several pairs of sums of prime numbers. (3.11)

$$\begin{gathered} 1,2,3,4,6,8,12,24\Rightarrow INDS\left(24\right)=6 \\ INDS\left(23)+INDS(1\right)=INDS\left(24\right)\Rightarrow G_5+G_1 \\ INDS\left(11)+INDS(13\right)=INDS\left(24\right)\Rightarrow G_2+G_4 \end{gathered}$$

$${\left(INDS\left(17)+INDS(7\right)\right)}_2=INDS\left(24\right)\Rightarrow G_8+G_7\to \left(INDS\left(15\right)\right)=6{\left(INDS\left(19)+INDS(5\right)\right)}_2=INDS\left(24\right)\Rightarrow G_1+G_5\to \left(INDS\left(15\right)\right)=6$$

3.11

statement 

: The inner digit sum of composite numbers has a direct relationship with the number of pairs of prime number sums and the divisibility of the composite number. For example, the number 24 can be obtained by the sum of six pairs of prime numbers. Divisibility does not include the number itself or the number one. (3.12)

$$INDS\left(2n\right)\propto mINDS\left(m\right)\propto INDS\left(P_{\mu }+P_{\upsilon }\right)\upsilon ,\mu \propto m$$

3.12

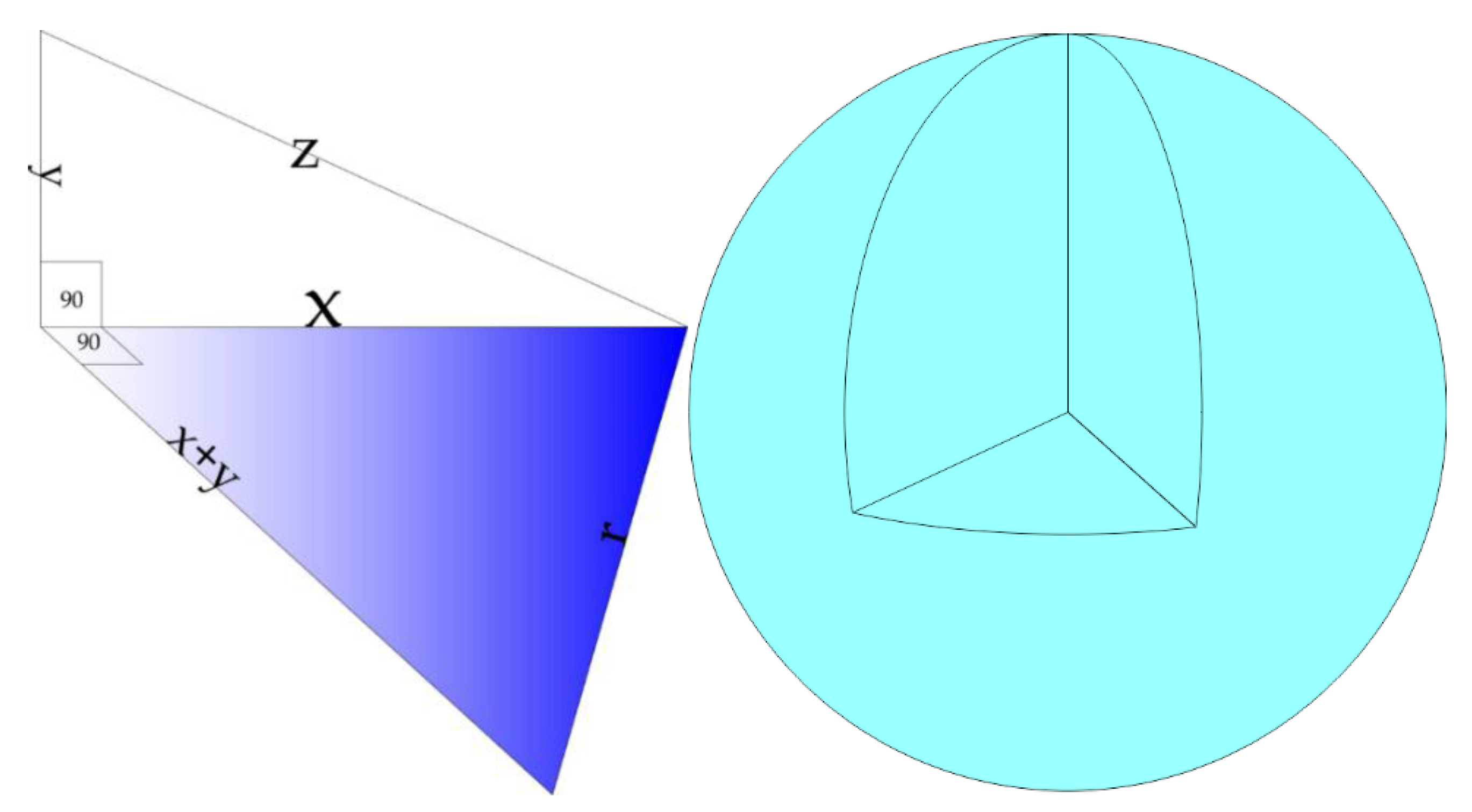
The critical strip of the zeros of the Riemann zeta function is the golden aperture that rotates on another axis. Based on this, the groups of prime numbers classified according to trigonometric ratios and Goldbach's conjecture are differentiated from one another. Furthermore, with the constant ratio of the chord to the sides—reminiscent of a lighthouse—the centers of the groups shift according to the growth of the golden spiral. Accordingly, the internal aggregation among the numbers provides the angle and causes an overlap in the properties across the different groups. Figure 3

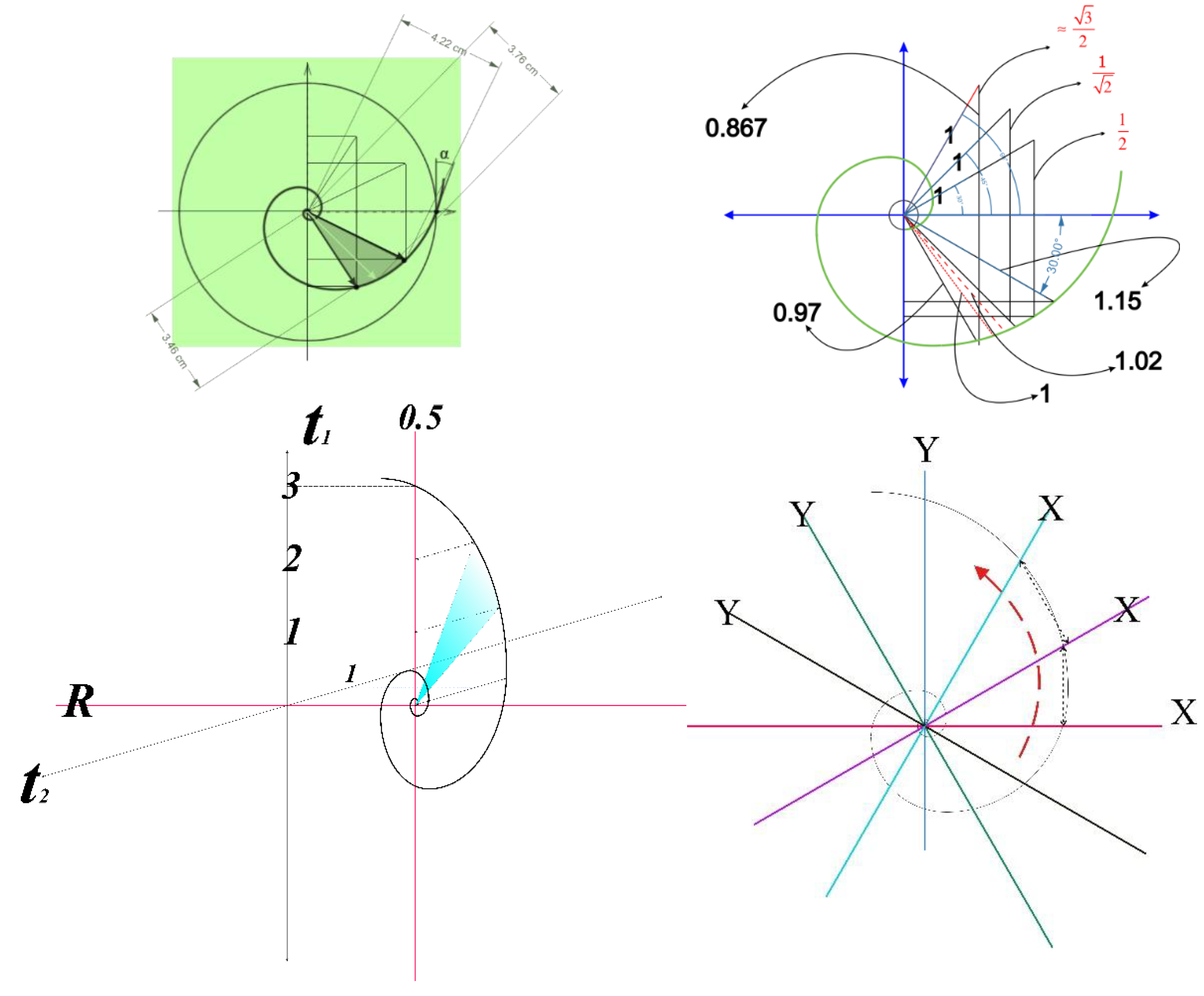
The connection between the Riemann zeta function in the critical strip is achievable through the Fibonacci spiral linked to prime groups. The growth rate of the Fibonacci spiral and the rotation of the coordinate system attached to the spiral preserve the properties of prime number groups within the framework of Möbius space. Based on the Riemann Hypothesis, the logarithmic spiral, and the ratios between numbers in three dimensions—real and imaginary—the connection between groups, the Riemann Hypothesis, and the golden spiral in the six-dimensional space of numbers becomes evident.

$$\begin{gathered} s=\left(0.5+i\left(G_{\upsilon }\right)\right) \\ \zeta \left(s\right)={\displaystyle \prod }_{p\in \mathbb{P}}{\displaystyle \frac{1}{1-p^{-s}}}={\displaystyle \frac{1}{1-2^{-s}}}⟹{\displaystyle \frac{1}{1-3^{-s}}}⟹{\displaystyle \frac{1}{1-5^{-s}}}⟹{\displaystyle \frac{1}{1-7^{-s}}}⟹⟹⟹ \\ \zeta \left(s^{*}\right)={\displaystyle \prod }_{p\in \mathbb{P}}{\displaystyle \frac{1}{1-p^{-s}}}={\displaystyle \frac{1}{1-2^{-s}}}⟹{\displaystyle \frac{1}{1-3^{-s}}}⟹{\displaystyle \frac{1}{1-5^{-s}}}⟹{\displaystyle \frac{1}{1-7^{-s}}}⟹⟹⟹ \\ \sin (co{s}^{-1}\left({\displaystyle \frac{x}{r}}\right))=\sqrt{1-{\displaystyle \frac{x^2}{r^2}}}\Rightarrow si{n}^2\left(\theta \right)=1-{\displaystyle \frac{x^2}{r^2}}\Rightarrow \sec (si{n}^{-1}({\log }_r\left({\displaystyle \frac{z}{y}}\right)))={\displaystyle \frac{1}{\sqrt{1-\frac{{\left(\ln \left(\frac{z}{y}\right)\right)}^2}{{\left(\ln (\left(r\right)\right)}^2}}}} \\ s=q+it\Rightarrow 2^s=2^q{.2}^{it}{2}^{it}=e^{it\left(\ln \left(2\right)\right)} \\ se{c}^2\left(\vartheta \right)={\displaystyle \frac{1}{1-\frac{x^2}{r^2}}} \\ {\displaystyle \frac{x^2}{r^2}}={\displaystyle \frac{1}{2^q}}\left(\cosh \left(\mathrm{it}(\ln \left(2)\right)\right)-\mathrm{isinh}\left(it\left(\ln \left(2\right)\right)\right)\right) \\ \zeta \left(s\right)={\displaystyle \prod }_{p\in \mathbb{P}}{\displaystyle \frac{1}{1-P_{\mu }^{-\left(0.5+G_{\mu }I\right)}}}.{\displaystyle \frac{1}{1-P_{\upsilon }^{-\left(0.5+G_{\upsilon }I\right)}}}\zeta \left(s^{*}\right)={\displaystyle \prod }_{p\in \mathbb{P}}{\displaystyle \frac{1}{1-P_{\mu }^{-\left(0.5-G_{\mu }I\right)}}}.{\displaystyle \frac{1}{1-P_{\upsilon }^{-\left(0.5-G_{\upsilon }I\right)}}} \end{gathered}$$

3.13

$$\begin{gathered} \zeta {\zeta }^{*}=si{n}^2\left(\theta \right) \\ {P}_{\mu }=\alpha \beta \gamma \dots \eta \Rightarrow \alpha +\beta +\gamma +\dots +\eta =\lambda \Rightarrow \left({\displaystyle \frac{1}{2^{\alpha }}}+{\displaystyle \frac{1}{2^{\beta }}}+{\displaystyle \frac{1}{2^{\gamma }}}+\dots +{\displaystyle \frac{1}{2^{\eta }}}\right)=\chi \Rightarrow co{s}^{-1}\left(\chi \right)=\theta \sin \left(\theta \right)=\xi \\ Arcsec\left(2^3{2}^1\right)=Arcsec\left(2^4\right)INDS\left(31\right)=4 \end{gathered}$$

Based on the definition of sine squared for Goldbach's Conjecture, sin^2(θ) represents the complex space and expresses the ratio related to the values of two prime numbers, in connection with the golden spiral and Taylor expansion at the point 0.5.(3.14)

$$\zeta {\zeta }^{*}=si{n}^2\left(\theta \right)⟹P_{\mu }+P_{\upsilon }⟹90\pm i{\varphi }_{G_{\mu +\upsilon }}$$

3.14

Goldbach's conjecture also establishes the fundamental basis for the connection between Möbius space and the wave function. The overlap between the Fourier series and the wave function depends on the Taylor expansion in Möbius space. (3.15)

$$\begin{gathered} \left|\mathsf{\Psi }=b_1\left|{\tilde{\psi }}_1+b_2\left|{\tilde{\psi }}_2+\dots +b_n\left|{\tilde{\psi }}_n\right.\right.\right.\right. \\ \left|\tilde{\psi }={\alpha }_1\left|A_1+{\alpha }_2\left|A_2+{\alpha }_3\left|A_3+{\alpha }_4\left|A_4+\right.\right.\right.\right.\right.{\alpha }_5\left|A_5+{\alpha }_6\left|A_6\right.\right. \\ {b}_{\mu }=x_{\mu }+ti,X_{\mu }=\left(x_1,x_2,x_3,x_4,x_5,x_6\right)\Rightarrow b_{\mu }{b}_{\mu }*=\left({\displaystyle \frac{1}{3}}\right) \\ w={\displaystyle \frac{az+P_{\mu }}{cz+P_{\upsilon }}}\Rightarrow {\displaystyle \frac{\left(INDS\left(P_{\mu }\right)\right)\left(INDS\left(2n\right)\right)+P_{\mu }}{\left(INDS\left(P_{\upsilon }\right)\right)\left(INDS\left(2n\right)\right)+P_{\upsilon }}}\Rightarrow \left[\left(INDS\left(P_{\upsilon }\right)\right)\left(INDS\left(2n\right)\right)+P_{\upsilon }\right]=\rho \\ =\epsilon \left[\left(INDS\left(P_{\mu }\right)\right)\left(INDS\left(2n\right)\right)+P_{\mu }\right]=\epsilon \Rightarrow 2n=\epsilon +\left(\epsilon -\rho \right) \end{gathered}$$

3.15

The ratio w represents the tangent of the angle θ in maintaining the rotation of the coordinate system based on the golden spiral and preserving the properties of the group. (3.16)

$$\tan \left(\theta \right)=w$$

3.16

In an expanding six-dimensional space, this ratio has a pair that is represented by the angle φ. Based on this, the prime number pairs that contribute to the sum of an even composite number can be represented using the six-dimensional and repetitive states of the wave function. (3.17) Figure 4

$${\cos }^2\left(\theta \right)+{\cos }^2\left(\varphi \right),si{n}^2\theta si{n}^2\varphi$$

3.17

$$g_{\mu \nu }=\left[\begin{array}{cccccc}co{s}^2\theta co{s}^2\varphi & 0& 0& 0& 0& 0\\ 0& co{s}^2\theta & 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& si{n}^2\theta & 0\\ 0& 0& 0& 0& 0& si{n}^2\theta si{n}^2\varphi \end{array}\right]$$

$$2{\sin }^2\left(\theta \right)+{\sin }^2\left(\varphi \right)+2{\cos }^2\left(\theta \right)+{\cos }^2\left(\varphi \right)$$

3.18

Typically, this space, dependent on geometric ratios and the properties of numbers within groups, forms the foundation of fundamental constants. (3.19)

$$\left({\displaystyle \frac{{\left(\frac{1}{2\pi }\right)}^3+{\left(\frac{1}{2}\right)}^6{\pi }^3\left(\frac{1}{6}\right){\pi }^3\left(\frac{\left(\frac{3\pi -6}{2\pi }\right)}{360}\right){\phi }^3}{c}}\right)\cong 6.6765834\times {10}^{-11}\cong G$$

3.19

$${\left({\displaystyle \frac{{\left(\frac{1}{2\pi }\right)}^3+{\left(\frac{1}{2}\right)}^6{\pi }^3{e}^{\tan \left(\frac{180}{\pi }\right)}}{c^2}}\right)}^2=6.5693903027\times {10}^{-34}\cong h$$

The Irregulara nature of sets of symmetrycal is based on the golden ratio and fractals. However, within the essence of symmetries, natural irregularities exist. Most of these irregularities are related to the relationships between numbers in groups associated with the sum of their inner digits (INDS) Figure 5

$$\alpha \beta \gamma \dots \eta \to \alpha +\beta +\gamma +\dots +\eta =\mathsf{\Lambda }\Rightarrow \alpha \beta \gamma \dots \eta -\mathsf{\Lambda }=9\lambda$$

4. Discussion

This study examines Goldbach’s conjecture from a different perspective, in which the grouping of numbers based on their internal digit sum (INDS) transforms Goldbach’s conjecture into a tool for proving and interpreting other mathematical problems. The intrinsic properties of numbers, when combined with mathematical frameworks, are the source for describing natural physical phenomena. Each group of numbers possesses its own unique characteristics, and multi-digit numbers tend to affiliate with a specific group based on their INDS. The separation between prime and composite numbers forms the basis for the exploration of Goldbach’s conjecture in this study. Moreover, the INDS of the participating prime numbers in the structure of an even composite number is identical to the INDS of the composite number; this phenomenon underpins the proof of Goldbach’s conjecture. The proof establishes the connection between the intrinsic properties of various numbers—especially prime numbers—and the Riemann hypothesis, as well as the logarithmic spiral, by means of the six-fold grouping of primes and trigonometric ratios. The profound relationship of the golden spiral at the differentiable point on the critical strip of the Riemann zeta function reveals the link between the Taylor expansion and the Fourier series with the wave function and Möbius space, thereby demonstrating the importance of a geometric proof of Goldbach’s conjecture. Additionally, the manifestation of irregular symmetries in nature indicates the presence of inherent inhomogeneities in natural ratios and intensities over time. In summary, this research introduces a practical tool for examining a unified six-dimensional theory through a geometric proof of Goldbach’s conjecture and presents a systematic framework for exploring other mathematical and physical phenomena. The interrelation of properties among numbers in different groups reflects an approach that uncovers the latent information in nature—information that intertwines the fabric of space-time and energy. On this basis, a meticulous examination of this perspective by other researchers is a recommended next step.