Submitted:
02 October 2025
Posted:
03 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Formulation of the Problem
3. Approximate Solutions
3.1. Finite Parameter Space
3.2. Infinite Parameter Space
4. Bayesian Input Signal Design in Quasi-Linear Control Systems
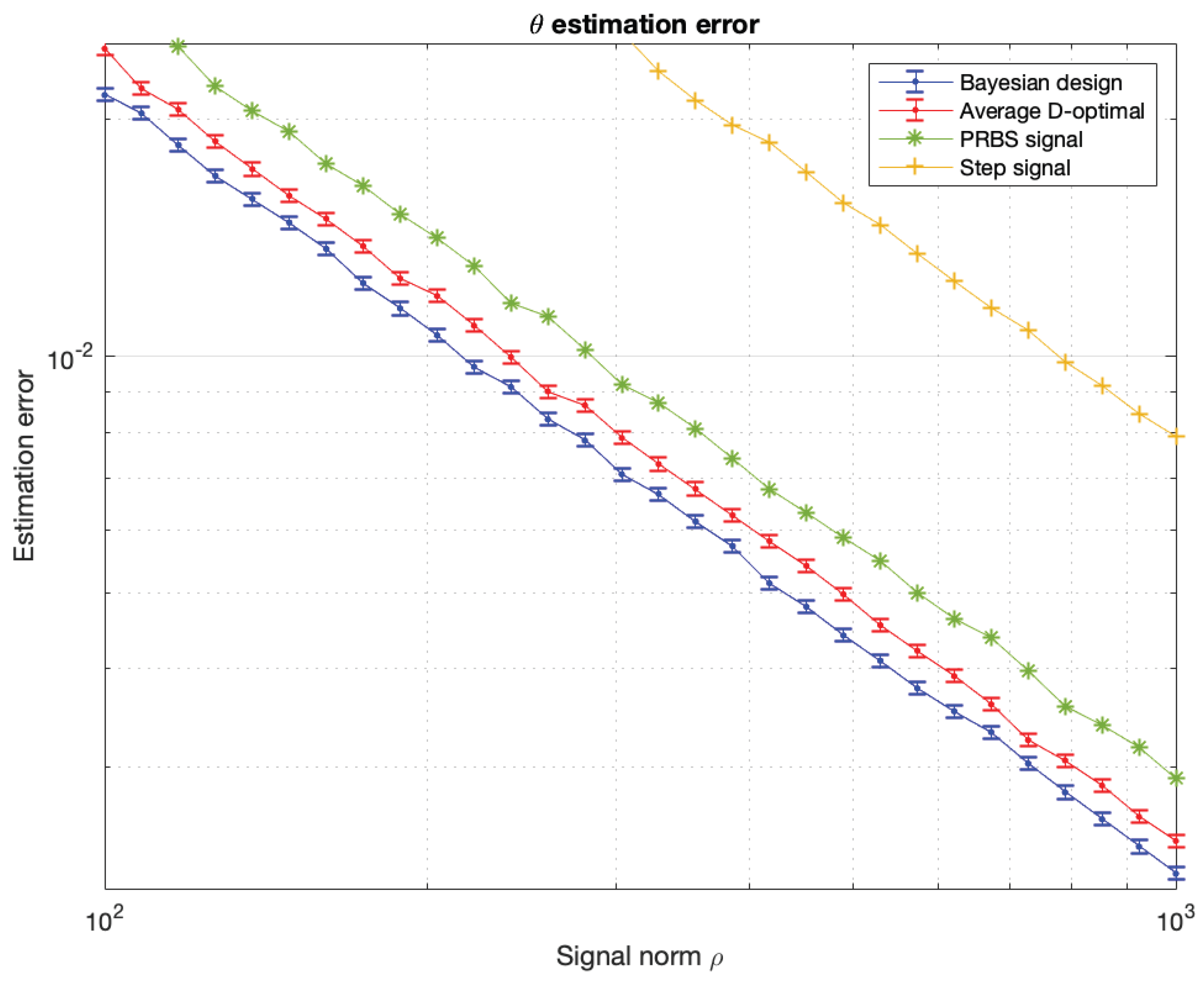
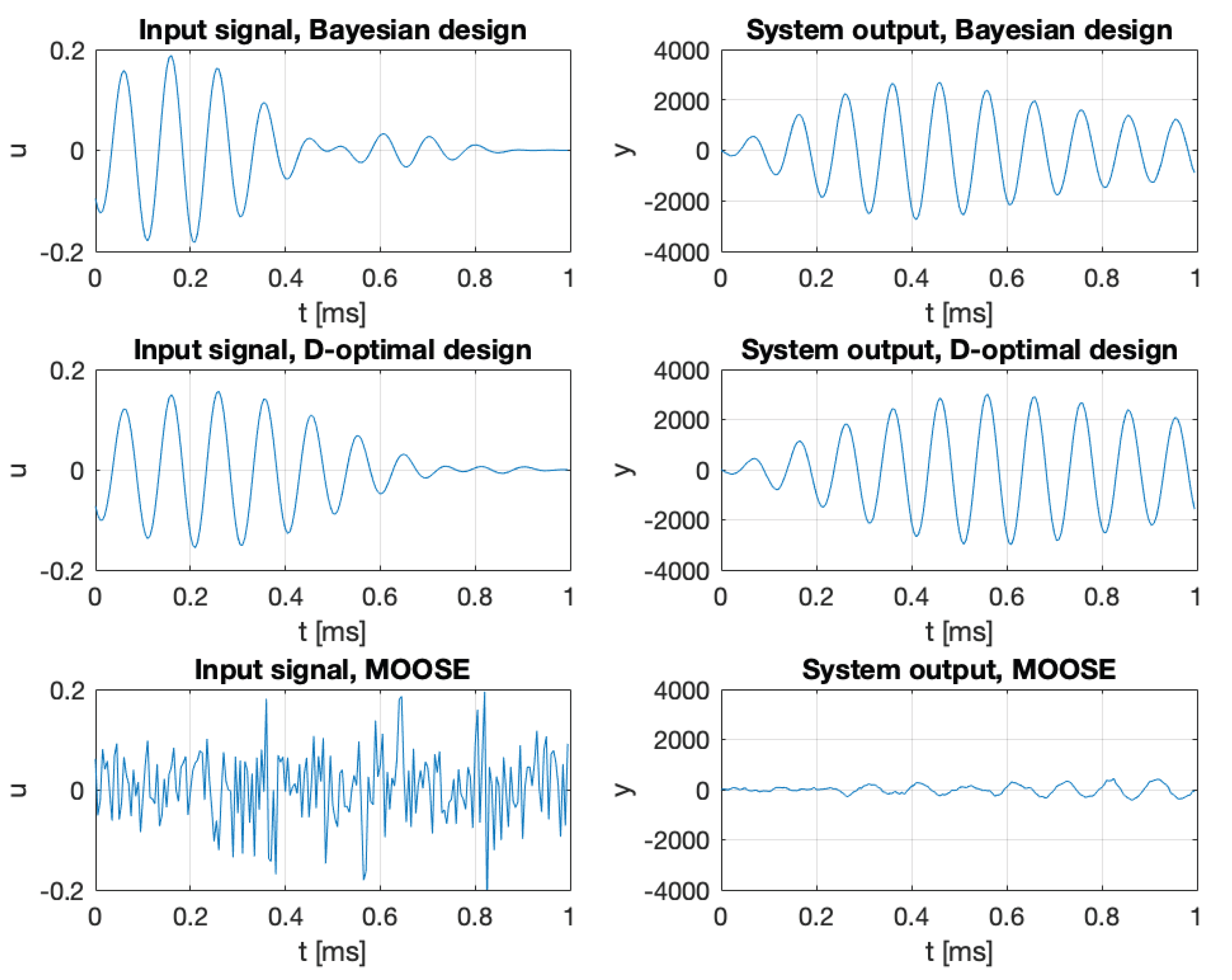
5. Comparison with Classical Methods of Input Signal Design
6. Examples of Input Signal Design
6.1. Elementary Example
6.2. Example with a Non-Gaussian Prior Distribution
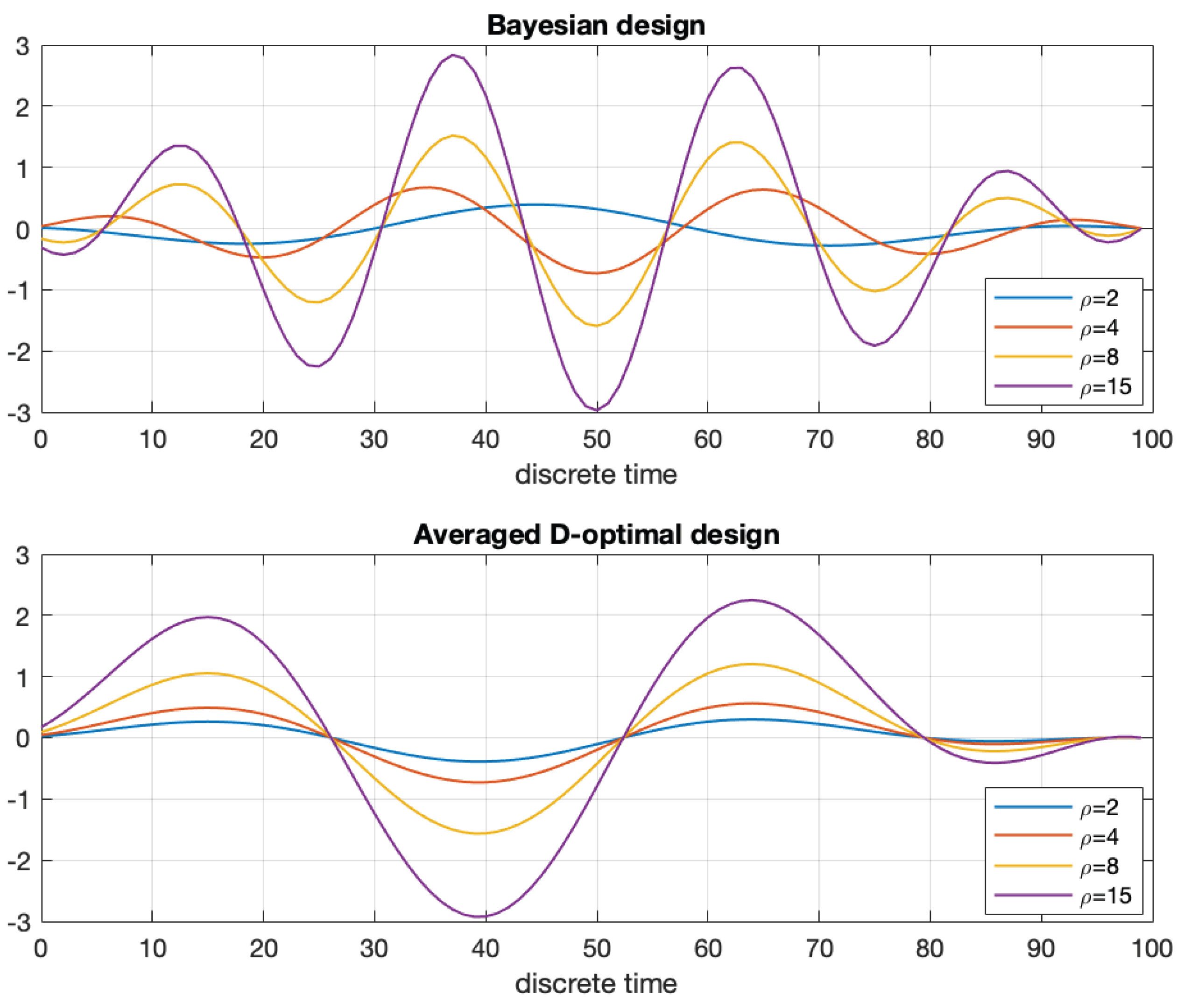
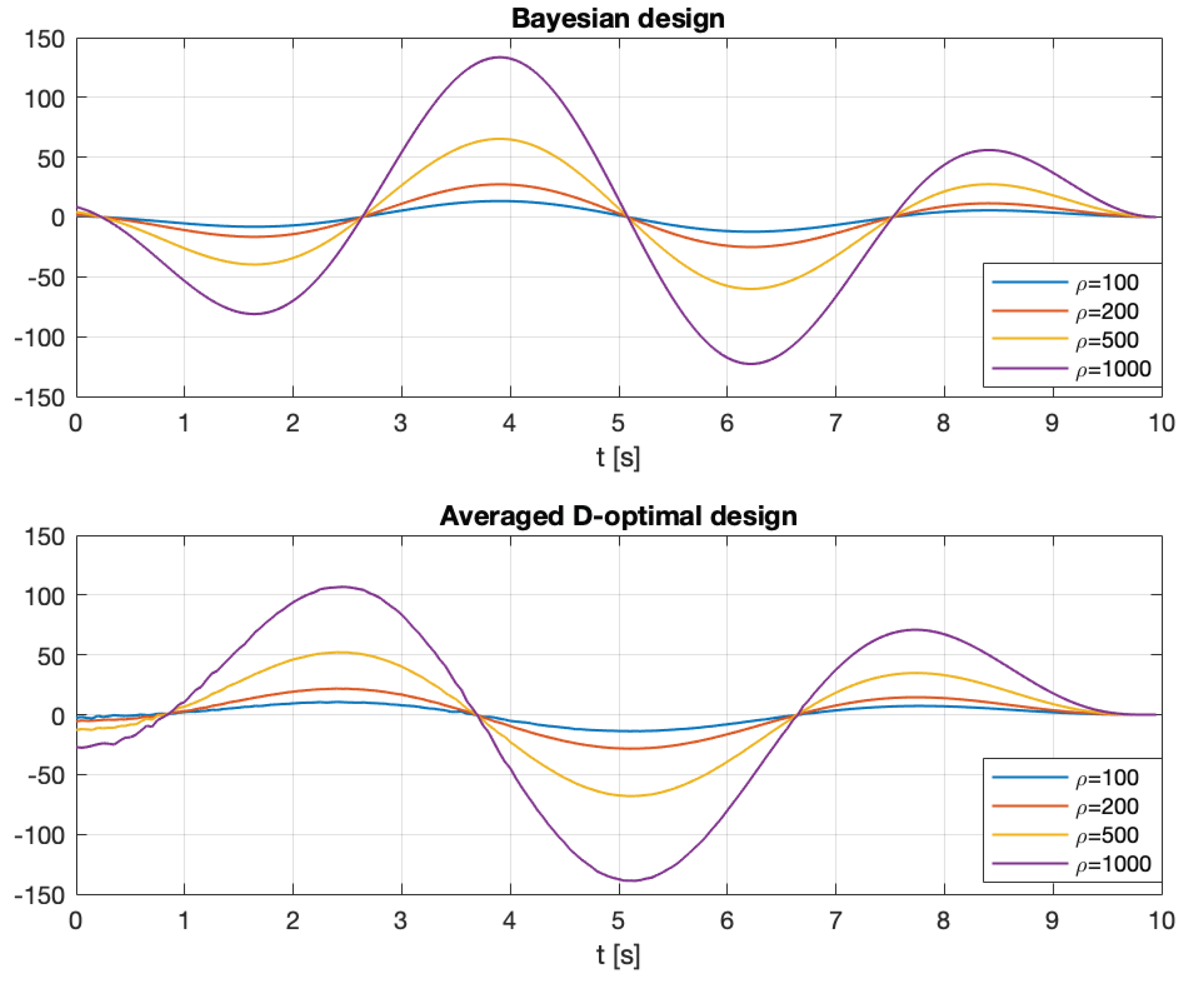
6.3. Optimal Input Design for Atomic Sensor Model
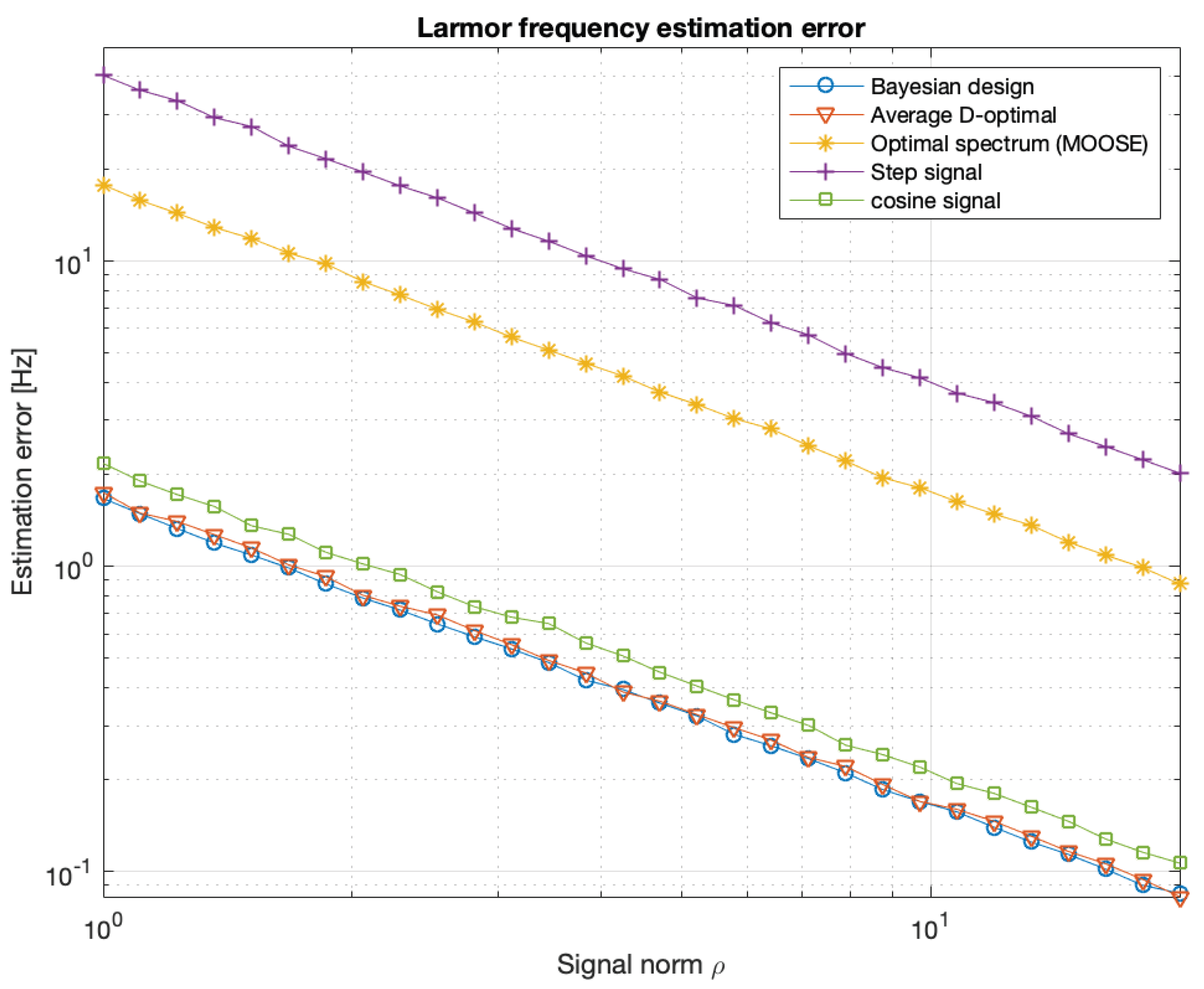
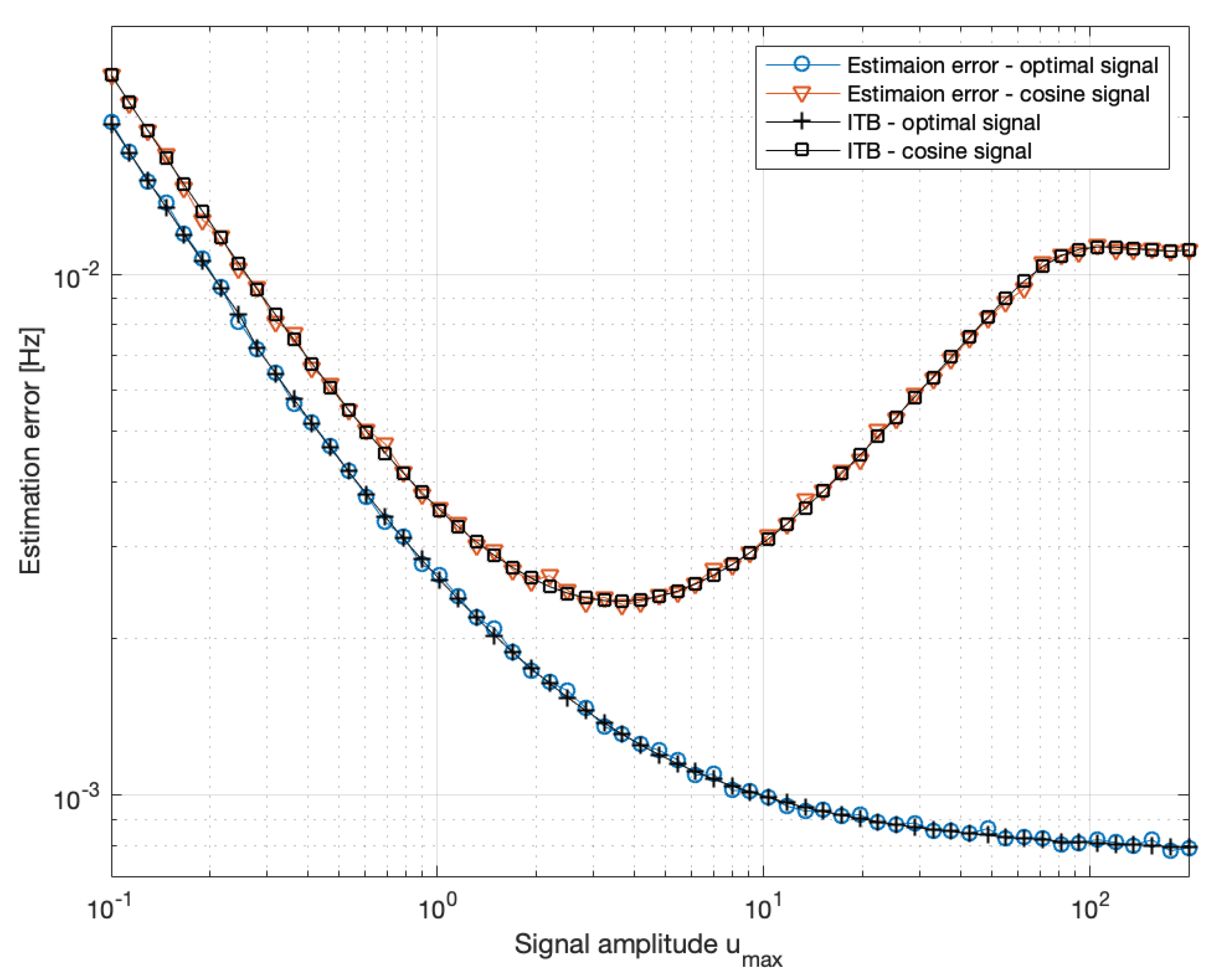
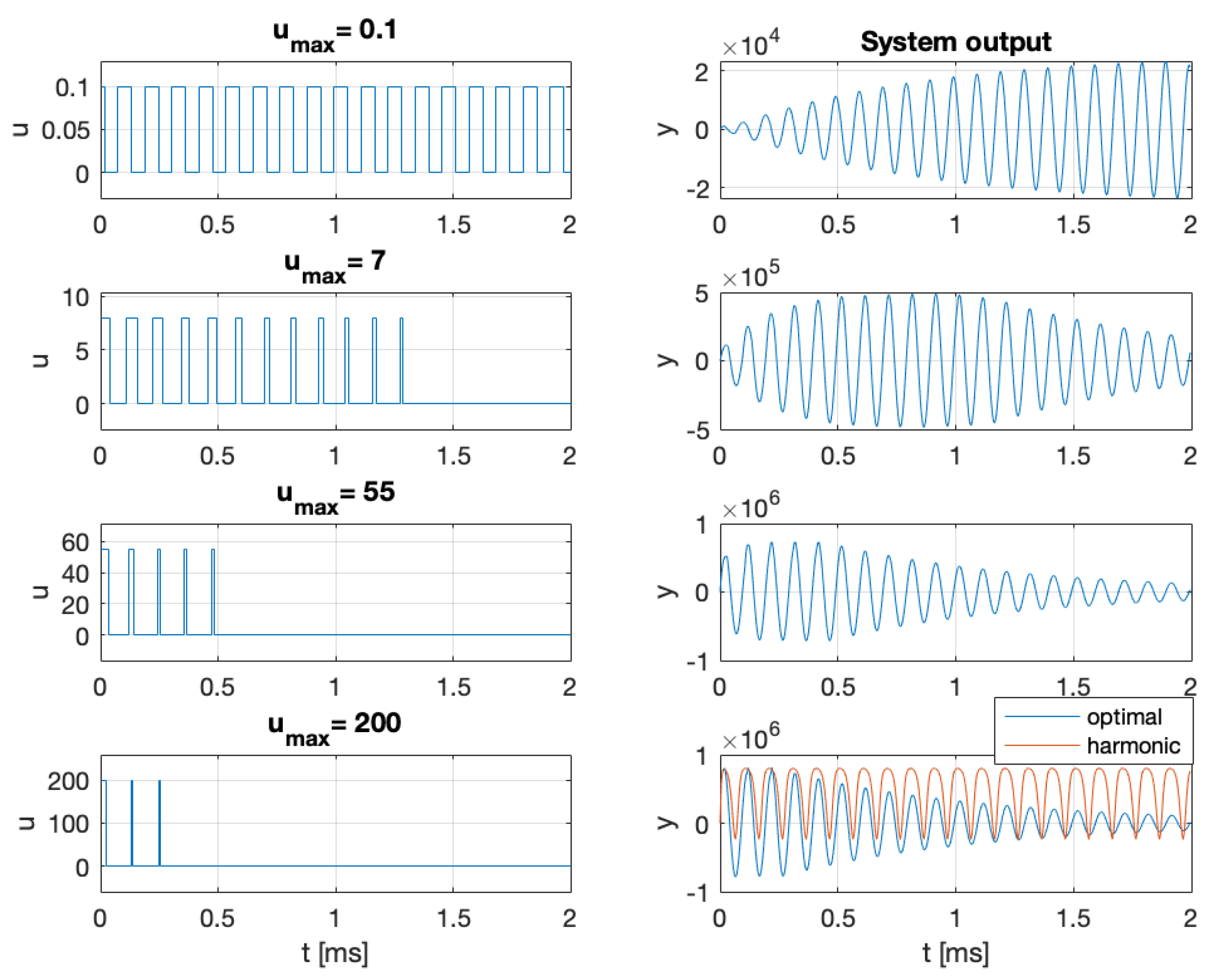
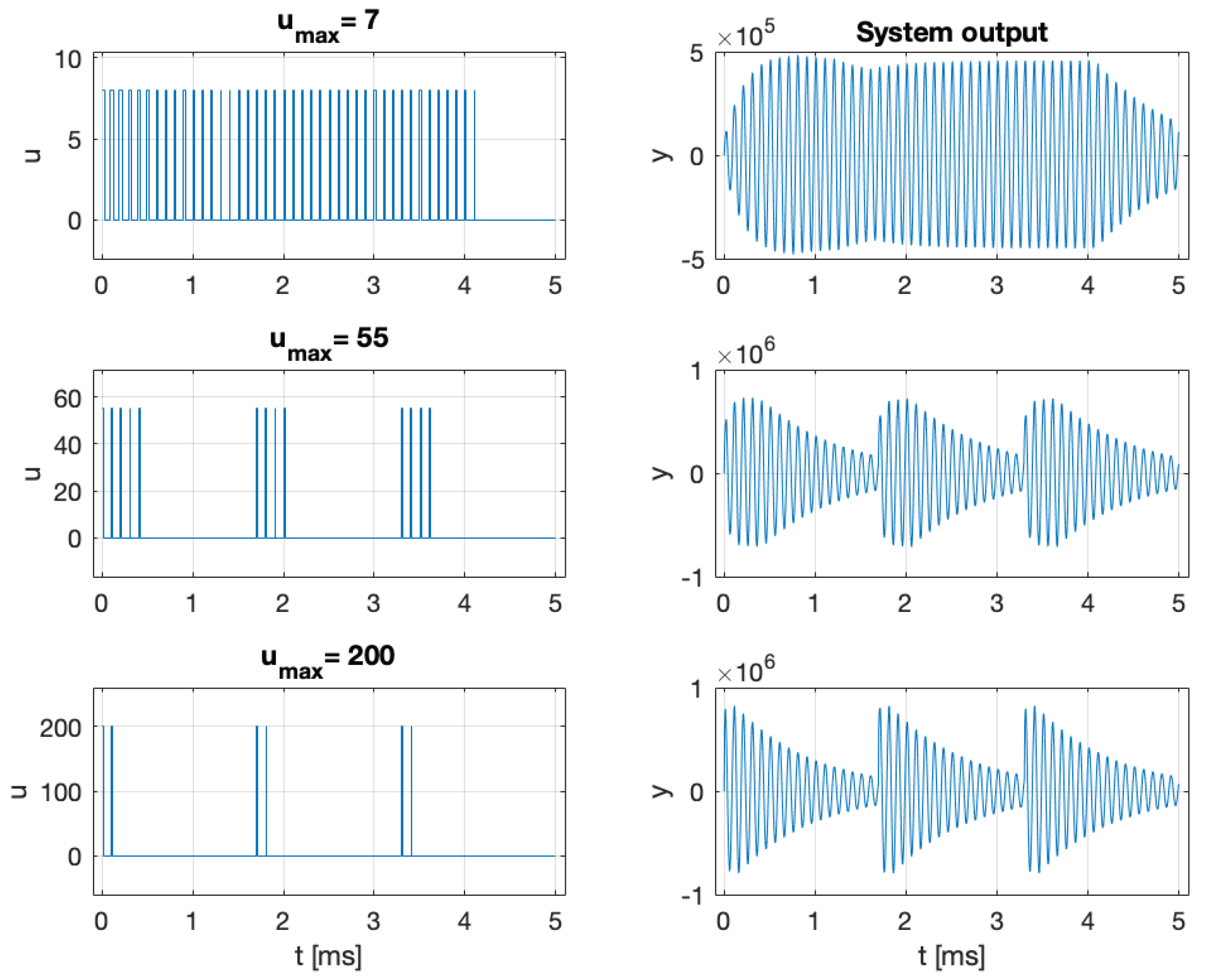
6.4. Bayesian Input Signal Design for Pump Laser in Optically Pumped Magnetometer
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
Appendix A. Proofs
Appendix B. An example of the gap between ITB and BCRB
Appendix C. Discretization of linear SDE
References
- Goodwin, G.C.; Payne, R.L. Dynamic System Identification: Experiment Design and Data Analysis; Academic Press: New York, 1977.
- Ljung, L. System Identification: Theory for the User, second ed.; Prentice Hall PTR, 1999.
- Söderström, T.; Stoica, P. System Identification; Prentice-Hall international series in systems and control engineering, Prentice-Hall, 1989.
- Pronzato, L. Optimal experimental design and some related control problems. Automatica 2008, 44, 303–325. https://doi.org/10.1016/j.automatica.2007.05.016.
- Huan, X.; Jagalur, J.; Marzouk, Y. Optimal experimental design: Formulations and computations. Acta Numerica 2024, 33, 715–840. https://doi.org/10.1017/S0962492924000023.
- Rainforth, T.; Foster, A.; Ivanova, D.R.; Bickford Smith, F. Modern Bayesian Experimental Design. Statistical Science 2024, 39, 100–114. https://doi.org/10.1214/23-STS915.
- Fedorov, V.V.; Hackl, P. Model-oriented design of experiments; Vol. 125, Springer, 1997.
- Lindley, D.V. On a Measure of the Information Provided by an Experiment. The Annals of Mathematical Statistics 1956, 27, 986–1005.
- Arimoto, S.; Kimura, H. Optimum input test signals for system identification - An information-theoretical approach. International Journal of Systems Science 1971, 1, 279–290. https://doi.org/10.1080/00207727108910011.
- Chaloner, K.; Verdinelli, I. Bayesian Experimental Design: A Review. Statistical Science 1995, 10, 273–304.
- Ryan, E.; Drovandi, C.; McGree, J.; Pettitt, A. A Review of Modern Computational Algorithms for Bayesian Optimal Design. International Statistical Review 2015, 84.
- Kolchinsky, A.; Tracey, B.D. Estimating Mixture Entropy with Pairwise Distances. Entropy 2017, 19. https://doi.org/10.3390/e19070361.
- Kolchinsky, A.; Tracey, B.D. Estimating Mixture Entropy with Pairwise Distances. arXiv preprint arXiv:1706.02419 2017. v4, 22 August 2018.
- Altafini, C.; Ticozzi, F. Modeling and Control of Quantum Systems: An Introduction. IEEE Transactions on Automatic Control 2012, 57, 1898–1917. https://doi.org/10.1109/TAC.2012.2184120.
- Dong, D.; Petersen, I.R. Quantum control theory and applications: A survey. IET Control Theory & Applications 2010, 4, 2651–2671. https://doi.org/10.1049/iet-cta.2009.0508.
- Friedly, J.C. Dynamic Behavior of Processes; Prentice-Hall International Series in the Physical and Chemical Engineering Sciences, Prentice-Hall: Englewood Cliffs, NJ, 1972; p. 590.
- Lorenz, S.; Diederichs, E.; Telgmann, R.; Schütte, C. Discrimination of Dynamical System Models for Biological and Chemical Processes. Journal of Computational Chemistry 2007, 28, 1384–1399. https://doi.org/10.1002/jcc.20585.
- Bania, P. Bayesian Input Design for Linear Dynamical Model Discrimination. Entropy 2019, 21, 351. https://doi.org/10.3390/e21040351.
- Bania, P.; Baranowski, J. Field Kalman Filter and its approximation. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), 2016, pp. 2875–2880. https://doi.org/10.1109/CDC.2016.7798697.
- Bania, P. Example for equivalence of dual and information based optimal control. International Journal of Control 2018. https://doi.org/10.1080/00207179.2018.1436775.
- Baranowski, J.; Bania, P.; Prasad, I.; Cong, T. Bayesian fault detection and isolation using Field Kalman Filter. EURASIP Journal on Advances in Signal Processing 2017, 2017. https://doi.org/10.1186/s13634-017-0502-0.
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2 ed.; John Wiley & Sons, Inc.: Hoboken, New Jersey, 2006.
- Lee, K.Y. New Information Inequalities with Applications to Statistics. Phd thesis, University of California, Berkeley, 2022. EECS Department, UC Berkeley Technical Report.
- Van Trees, H.L. Detection, Estimation and Modulation Theory; Vol. I, Wiley, 1968.
- Efroimovich, S.Y. Information Contained in a Sequence of Observations. Problemy Peredachi Informatsii 1979, 15, 24–39.
- Van Trees, H.L.; Bell, K.L., Eds. Bayesian Bounds for Parameter Estimation and Nonlinear Filtering/Tracking; Wiley-IEEE Press: Hoboken, NJ, 2007.
- Jakowluk, W. Optimal Input Signal Design in Control Systems Identification; Oficyna Wydawnicza Politechniki Białostockiej: Białystok, Poland, 2024. Available at: https://pb.edu.pl/oficyna-wydawnicza/wp-content/uploads/sites/4/2024/06/Optimal-input-signal-design-in-control-systems-identification.pdf.
- Jiménez-Martínez, R.; Kołodyński, J.; Troullinou, C.; Lucivero, V.G.; Kong, J.; Mitchell, M.W. Signal Tracking Beyond the Time Resolution of an Atomic Sensor by Kalman Filtering. Phys. Rev. Lett. 2018, 120, 040503. https://doi.org/10.1103/PhysRevLett.120.040503.
- Troullinou, C.; Shah, V.; Lucivero, V.G.; Mitchell, M.W. Squeezed-Light Enhancement and Backaction Evasion in a High-Sensitivity Optically Pumped Magnetometer. Phys. Rev. Lett. 2021, 127, 193601. https://doi.org/10.1103/PhysRevLett.127.193601.
- Bobrovsky, B. Z.; Mayer–Wolf, E.; Zakai, M. Some Classes of Global Cramér–Rao Bounds. The Annals of Statistics 1987, 15, 1421–1438. https://doi.org/10.1214/aos/1176350602.
- Jeong, M.; Dytso, A.; Cardone, M. A Comprehensive Study on Ziv-Zakai Lower Bounds on the MMSE. IEEE Transactions on Information Theory 2025, 71, 3214–3236. https://doi.org/10.1109/TIT.2025.3541987.
- Huber, M.F.; Bailey, T.; Durrant-Whyte, H.; Hanebeck, U.D. On entropy approximation for Gaussian mixture random vectors. In Proceedings of the 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, 2008, pp. 181–188. https://doi.org/10.1109/MFI.2008.4648062.
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research and Financial Engineering, Springer: New York, NY, 2006. https://doi.org/10.1007/978-0-387-40065-5.
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration, 2nd ed.; Academic Press: Orlando, FL, 1984.
- Stroud, A.H. Approximate Calculation of Multiple Integrals; Prentice Hall: Englewood Cliffs, NJ, 1971.
- Smolyak, S.A. Quadrature and interpolation formulas for tensor products of certain classes of functions. Soviet Mathematics Doklady 1963, 4, 240–243.
- Jansson, H. Experiment Design with Applications in Identification for Control; Royal Institute of Technology (KTH), 2004.
- Annergren, M.; Larsson, C.A. MOOSE2—A toolbox for least-costly application-oriented input design. SoftwareX 2016, 5, 96–100. https://doi.org/10.1016/j.softx.2016.05.003.
- Fabricant, A.; Novikova, I.; Bison, G. How to build a magnetometer with thermal atomic vapor: A tutorial. New Journal of Physics 2023, 25, 025001. https://doi.org/10.1088/1367-2630/acb840.
- Budker, D.; Jackson Kimball, D.F., Eds. Optical Magnetometry; Cambridge University Press, 2013. https://doi.org/10.1017/CBO9780511846380.
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. https://doi.org/10.1103/PhysRevLett.103.210401.
- Shen, H.Z.; Shang, C.; Zhou, Y.H.; Yi, X.X. Unconventional single-photon blockade in non-Markovian systems. Phys. Rev. A 2018, 98, 023856. https://doi.org/10.1103/PhysRevA.98.023856.
- Magrini, L.; Rosenzweig, P.; Bach, C.; Deutschmann-Olek, A.; Hofer, S.G.; Hong, S.; Kiesel, N.; Kugi, A.; Aspelmeyer, M. Real-time optimal quantum control of mechanical motion at room temperature. Nature 2021, 595, 373–377. https://doi.org/10.1038/s41586-021-03602-3.
- Amorós-Binefa, J.; Kołodyński, J. Noisy Atomic Magnetometry with Kalman Filtering and Measurement-Based Feedback. PRX Quantum 2025, 6, 030331. https://doi.org/10.1103/k7nk-lrwd.
- Särkkä, S. Bayesian Filtering and Smoothing; Vol. 3, Institute of Mathematical Statistics Textbooks, Cambridge University Press, 2013. https://doi.org/10.1017/CBO9781139344203.

| Parameter | Abbreviation | Typical value |
|---|---|---|
| Number of atoms | ||
| Spin number | F | 1 |
| Larmor frequencies | kHz | |
| Parameter | 600 Hz | |
| Parameter | 550 Hz | |
| Typical relaxation time | 0.87 ms | |
| Typical relaxation rate | 1149 Hz | |
| Pumping rate | P | 0-200 kHz |
| Measurement noise level | ||
| Sampling time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





