Submitted:
12 September 2025
Posted:
15 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Asymptotic Perturbation Bounds
2.1. Asymptotic Bounds for the Perturbation Parameters
2.2. Asymptotic Componentwise Eigenvector Bounds
2.3. Eigenvalue Sensitivity
2.4. Sensitivity of One Dimensional Invariant Subspaces
3. Probabilistic Asymptotic Bounds
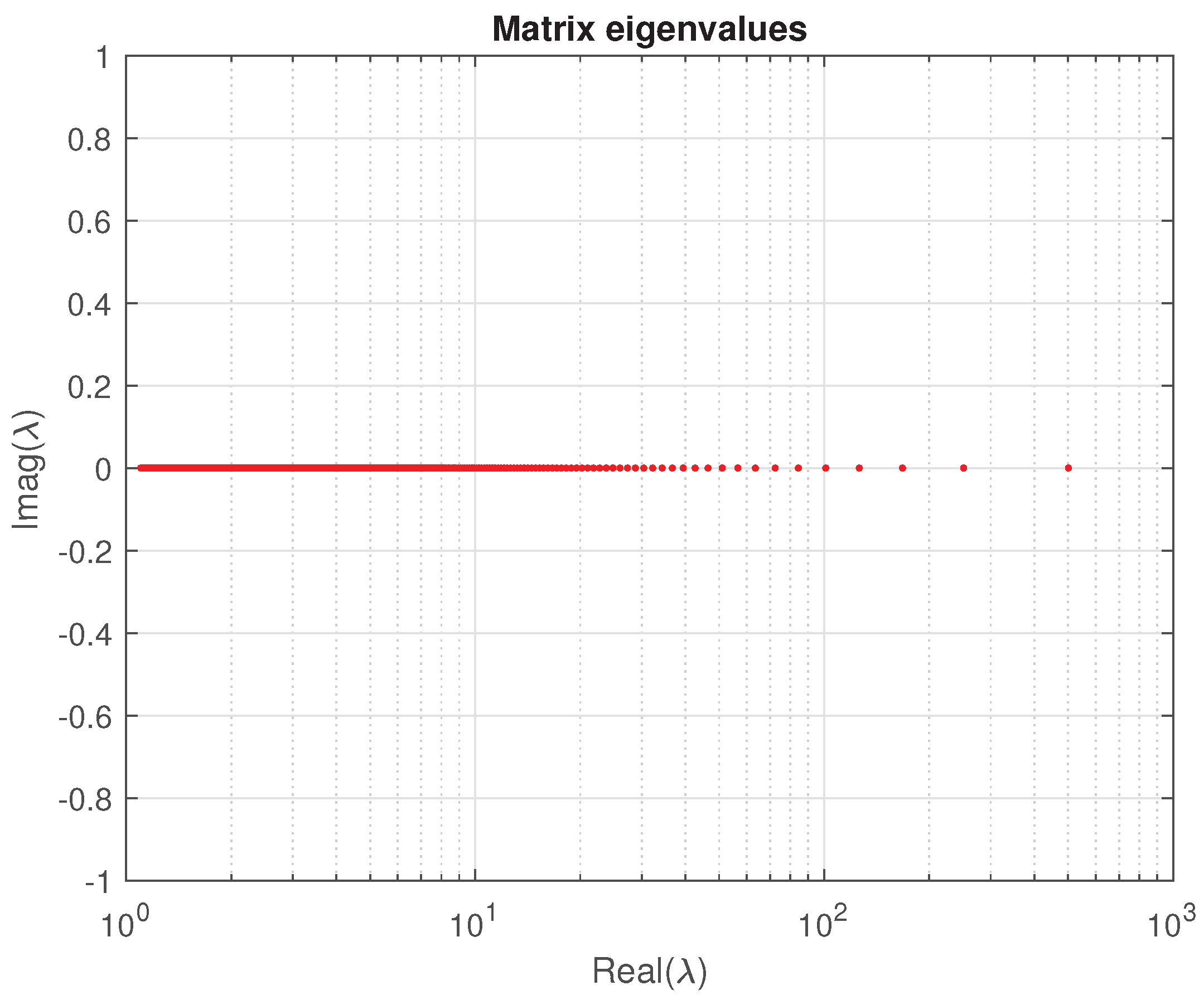
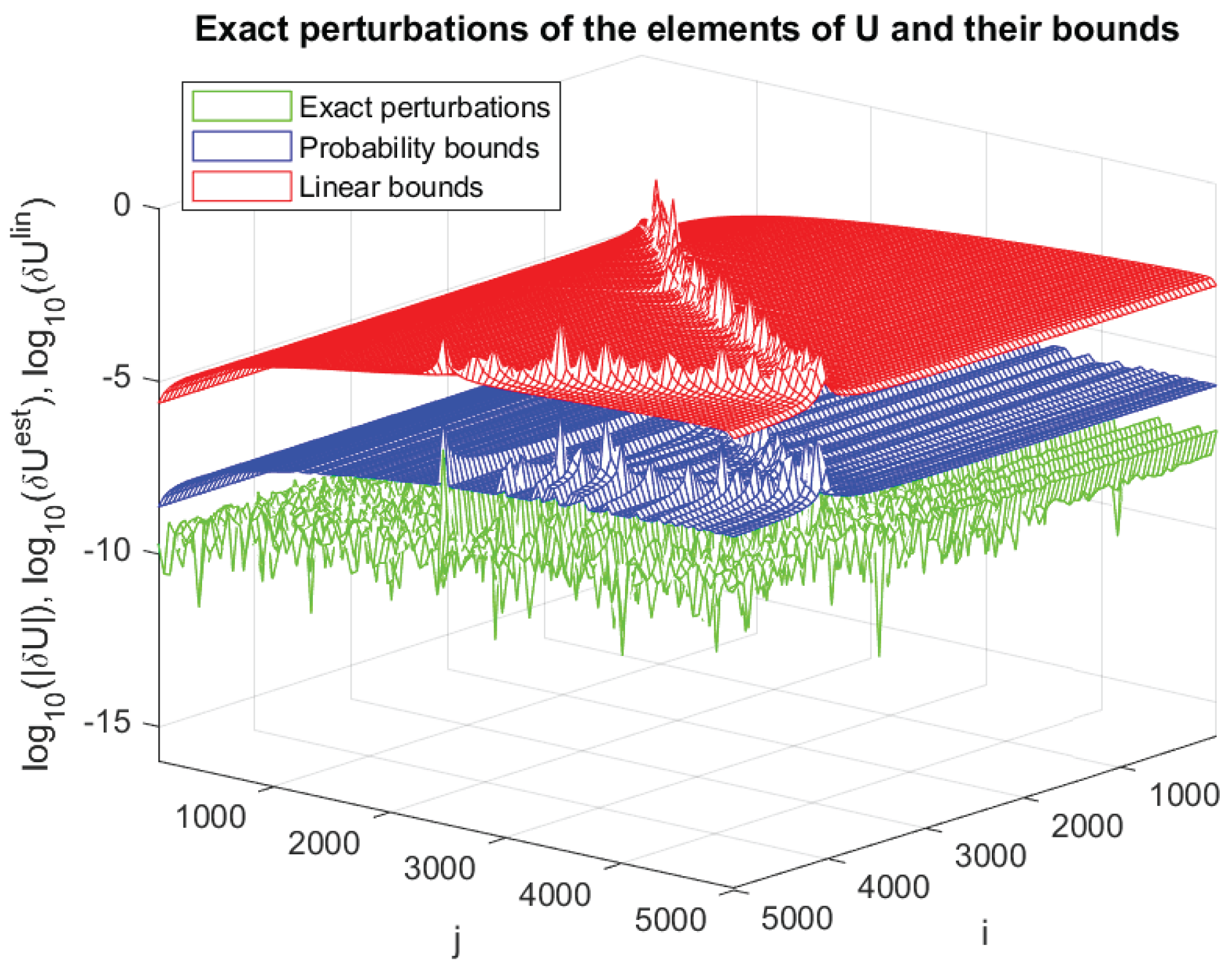
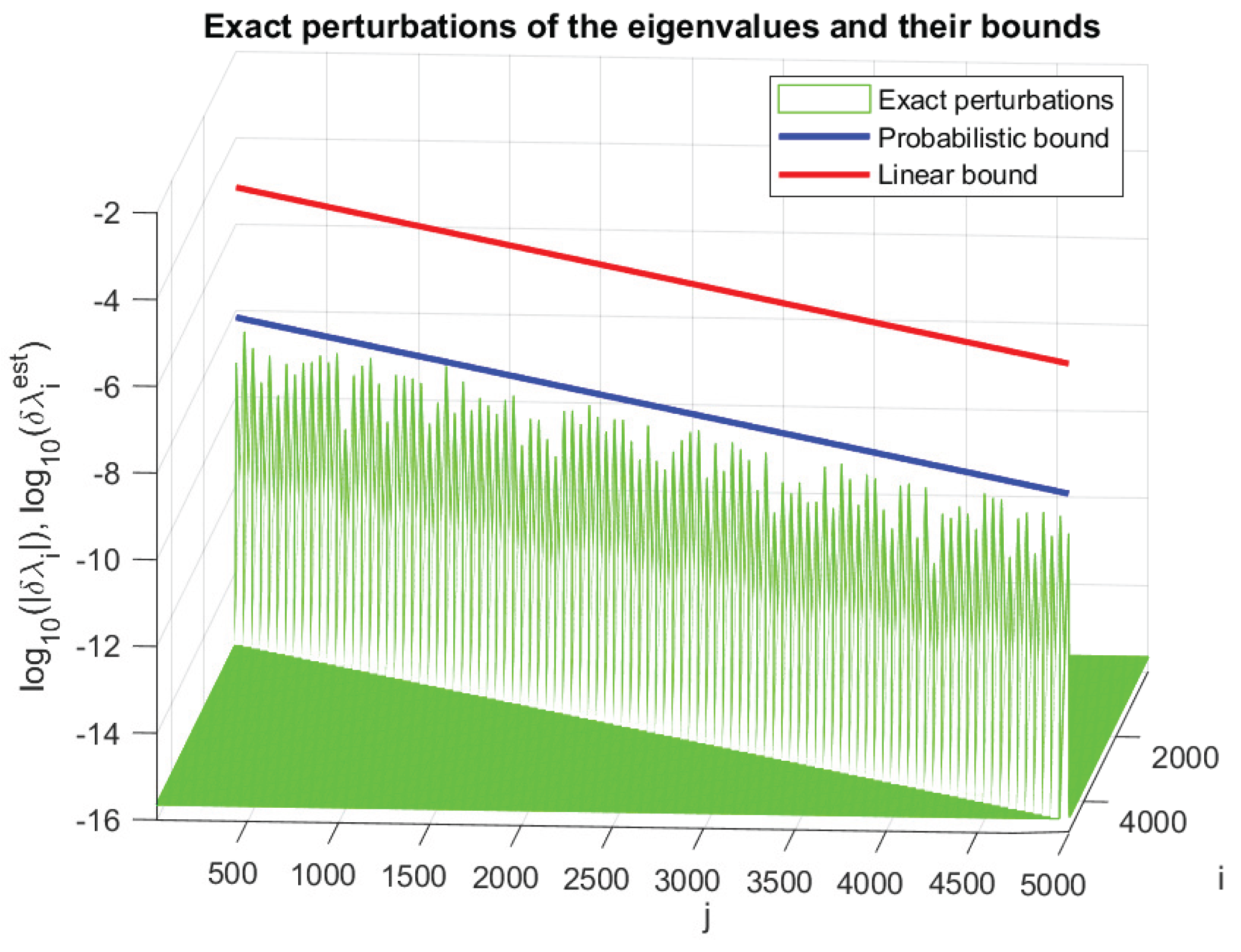
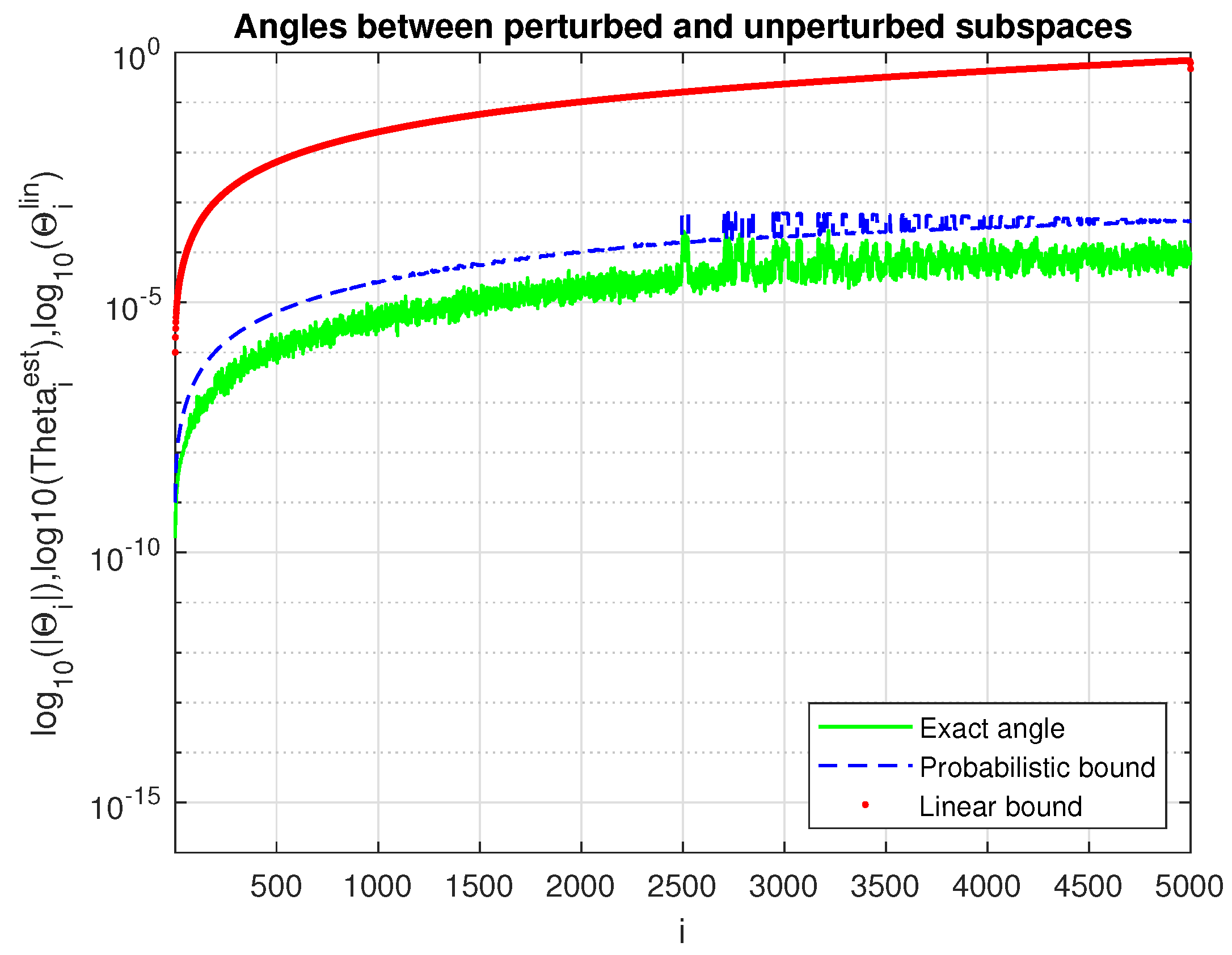
4. Numerical Experiments
5. Conclusions
6. Notation
| , | the set of complex numbers; |
| , | the space of complex matrices; |
| , | a matrix with entries ; |
| , | the jth column of A; |
| , | the ith row of an matrix A; |
| , | the jth column of an matrix A; |
| , | the strictly lower triangular part of A; |
| , | the matrix of absolute values of the elements of A; |
| , | the Hermitian transposed of A; |
| , | the zero matrix; |
| , | the unit matrix; |
| , | the perturbation of A; |
| , | the spectral norm of A; |
| , | the Frobenius norm of A; |
| , | equal by definition; |
| ⪯, | relation of partial order. If , then means |
| ; | |
| , | the subspace spanned by the columns of X; |
| , | the orthogonal complement of U, ; |
| ❒, | the end of a proof. |
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- V. Angelova and P. Petkov, Componentwise perturbation analysis of the Singular Value Decomposition of a matrix, Applied Sciences, 14 (2024), 1417. [CrossRef]
- J. Barlow and I. Slapničar, Optimal perturbation bounds for the Hermitian eigenvalue problem, Lin. Alg. Appl., 309 (2000), pp. 19–43. [CrossRef]
- Z. Bai and J. Demmel and A. Mckenney, On computing condition numbers for the nonsymmetric eigenproblem, ACM Trans. Math. Software, 19 (1993), 202–223. [CrossRef]
- R. Bhatia, Perturbation Bounds for Matrix Eigenvalues, Society of Industrial and Applied Mathematics, Philadelphia, PA, 2007. 8987; -3. [CrossRef]
- A. Björck and G. Golub, Numerical methods for computing angles between linear subspaces, Math. Comp., 27 (1973), pp. 579–594. [CrossRef]
- M. Carlsson, Spectral perturbation theory of Hermitian matrices, in: Bridging Eigenvalue Theory and Practice – Applications in Modern Engineering, B. Carpentieri, ed., IntechOpen, London, 2025. 8363; -9. [CrossRef]
- F. Chatelin, Eigenvalues of Matrices, Society of Industrial and Applied Mathematics, Philadelphia, PA, 2012. ISBN 978-1-611972-45-0. [CrossRef]
- C. Davis and W. M. Kahan, The Rotation of Eigenvectors by a Perturbation. III, SIAM J. Numer. Anal., 7 (1970), pp. 46. [CrossRef]
- G. H. Golub and C. F. Van Loan, Matrix Computations, The Johns Hopkins University Press, Baltimore, MD, fourth ed., 2013. ISBN 978-1-4214-0794-4.
- A. Greenbaum and R.-C. Li and M.L. Overton, First-order perturbation theory for eigenvalues and eigenvectors, SIAM Review, 62 (2020), pp. 463–482. [CrossRef]
- I.C.F. Ipsen, An overview of relative sin(Θ) theorems for invariant subspaces of complex matrices. J. Comp. Appl. Math., 123 (2000), pp. 131–153. [CrossRef]
- T. Kato, Perturbation Theory for Linear Operators, Springer-Verlag, Berlin, second ed., 1995. ISBN 978-0-540-58661-6.
- M. Konstantinov and P. Petkov, Perturbation Methods in Matrix Analysis and Control, NOVA Science Publishers, Inc., New York, 2020. https://novapublishers.com/shop/perturbation-methods-in-matrix-analysis-and-control.
- R. Li, Matrix perturbation theory, in Handbook of Linear Algebra, L. Hogben, ed., Discrete Math. Appl., CRC Press, Boca Raton, FL, second ed., 2014, pp. (21–1)–(21–20).
- <sc>R.-C. Li, Y. R.-C. Li, Y. Nakatsukasa, N. Truhar and W.-g. Wang, Perturbation of multiple eigenvalues of Hermitian matrices, Linear Algebra Appl., 437 (2012), pp. 202–213. [CrossRef]
- R. Mathias, Quadratic residual bounds for the Hermitian eigenvalue problem, SIAM J. Matrix Anal. Appl., 19 (1998), pp. 541–550. [CrossRef]
- The MathWorks, Inc., MATLAB Version 9.9.0.1538559 (R2020b), Natick, MA, 2020. https://www.mathworks.com.
- Y. Nakatsukasa, Sharp error bounds for Ritz vectors and approximate singular vectors, Math. Comput., 89 (2018), pp. 1843–-1866. [CrossRef]
- A. Papoulis, Probability, Random Variables and Stochastic Processes, McGraw Hill, Inc., New York, 3rd edition, 1991. ISBN 0-07-048477-5.
- B.N. Parlett, The Symmetric Eigenvalue Problem, Society of Industrial and Applied Mathematics, Philadelphia, PA, 1998. [CrossRef]
- P. Petkov, Componentwise perturbation analysis of the Schur decomposition of a matrix, SIAM J. Matrix Anal. Appl., 42 (2021), pp. 108–133. [CrossRef]
- P. Petkov, Componentwise perturbation analysis of the QR decomposition of a matrix, Mathematics, 10 (2022). [CrossRef]
- P. Petkov, Probabilistic perturbation bounds of matrix decompositions, Numer. Linear Algebra Appl., 31(2024), pp. 1–40. [CrossRef]
- P. Petkov, Probabilistic perturbation bounds for invariant, deflating and singular subspaces, Axioms, 13(2024), 597. [CrossRef]
- G.W. Stewart, Error and perturbation bounds for subspaces associated with certain eigenvalue problems, SIAM Review, 15 (1973), pp. 727–764. [CrossRef]
- G. Stewart, Matrix Algorithms; Vol. II: Eigensystems, SIAM: Philadelphia, PA, 2001; ISBN 0-89871-503-2. [Google Scholar]
- G. W. Stewart and J.-G. Sun, Matrix Perturbation Theory, Academic Press, New York, 1990. ISBN 978-0126702309.
- J.-g. Sun, Perturbation expansions for invariant subspaces, Linear Algebra Appl., 153 (1991), pp. 85–97. [CrossRef]
- J.-g. Sun, Stability and Accuracy. Perturbation Analysis of Algebraic Eigenproblems. Technical Report, Department of Computing Science, Umeå University, Umeå, Sweden, 1998, pp. 1–210.
- K. Veselić and I. Slapničar, Floating-point perturbations of Hermitian matrices, Linear Algebra Appl., 195 (1993), pp. 81–116. [CrossRef]
- J. Wilkinson, The Algebraic Eigenvalue Problem. Clarendon Press, Oxford, UK, 1965. ISBN 978-0-19-853418-1.
- G. Zhang and H. Li and Y. Wei, Componentwise perturbation analysis for the generalized Schur decomposition, Calcolo, 59 (2022). [CrossRef]
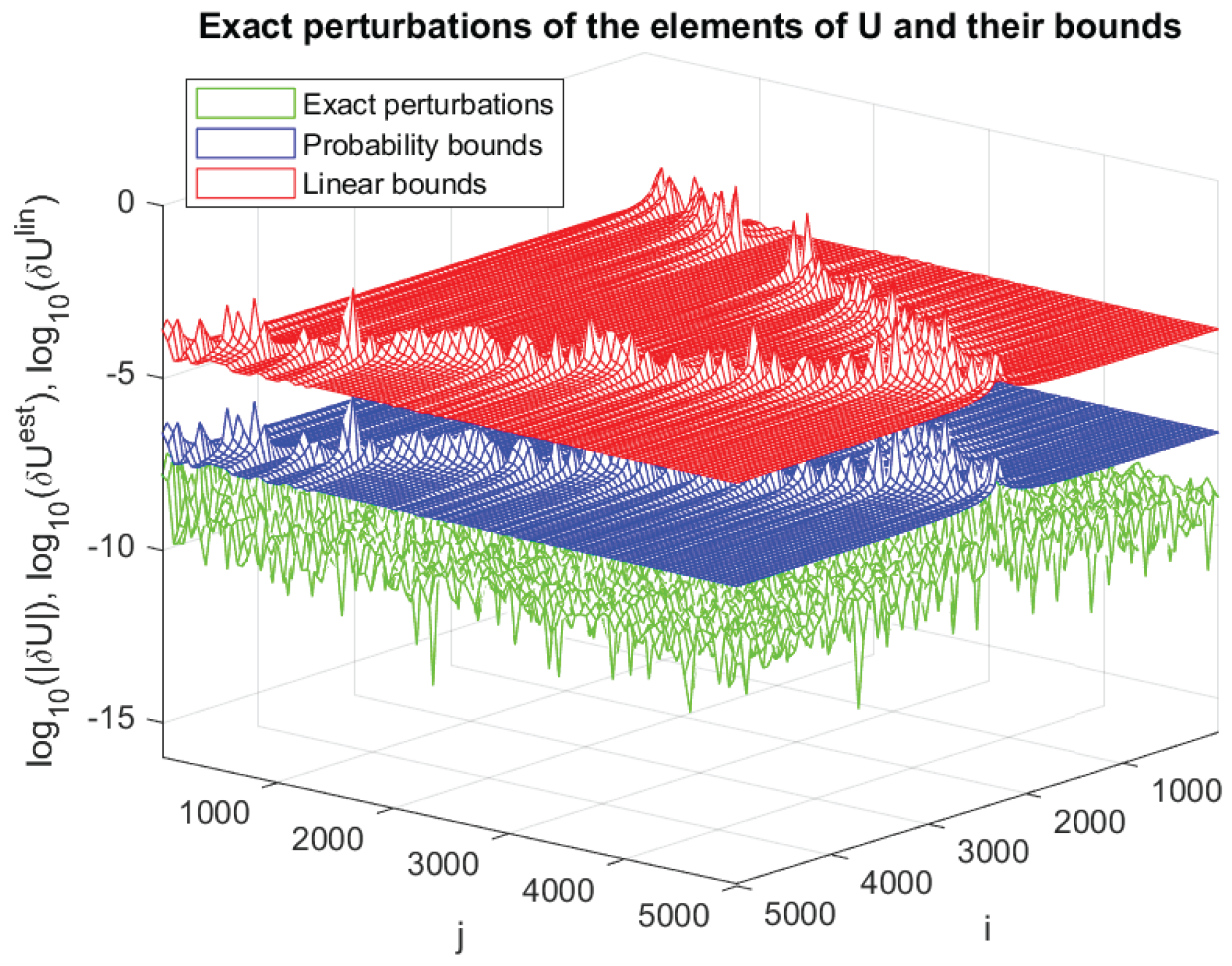
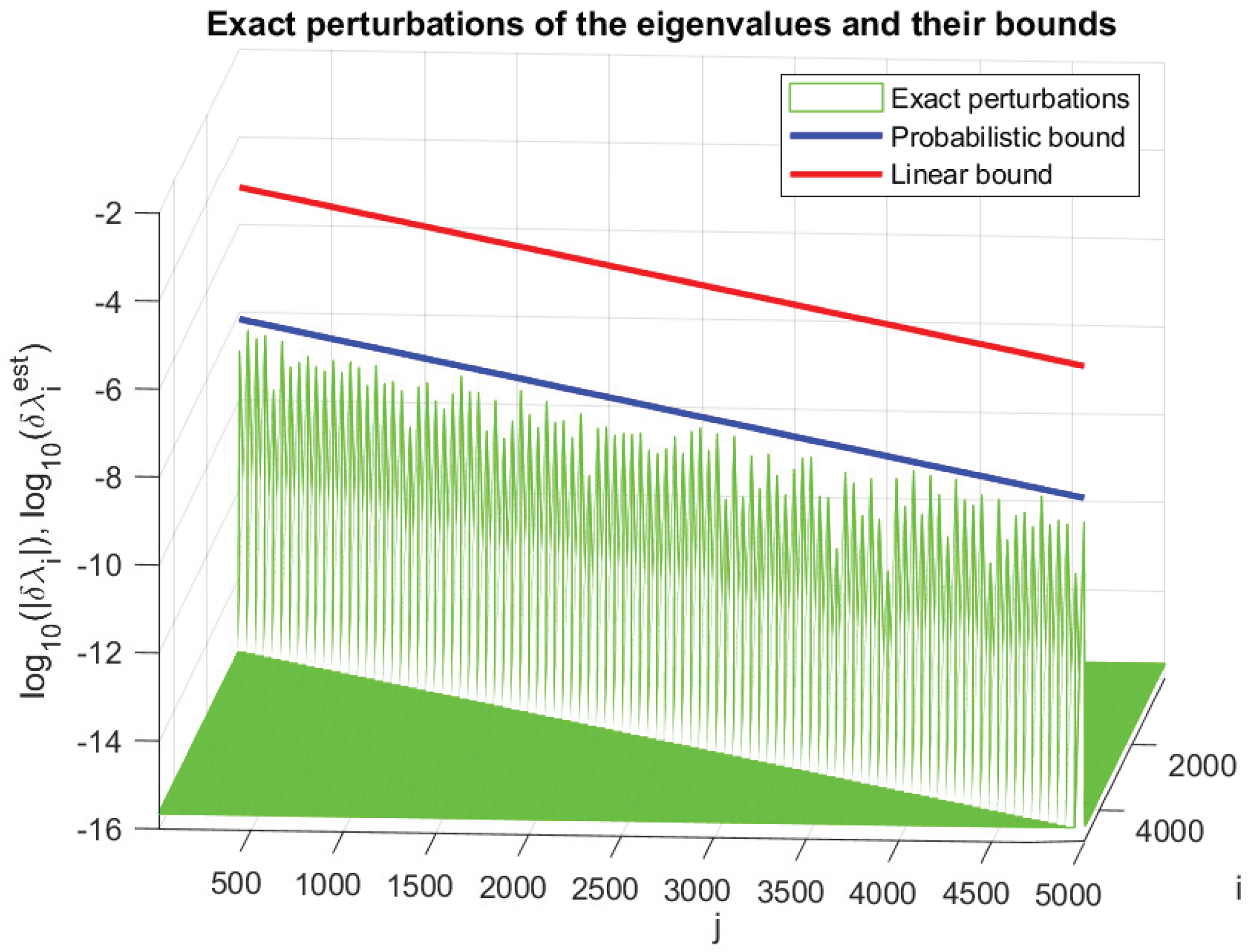
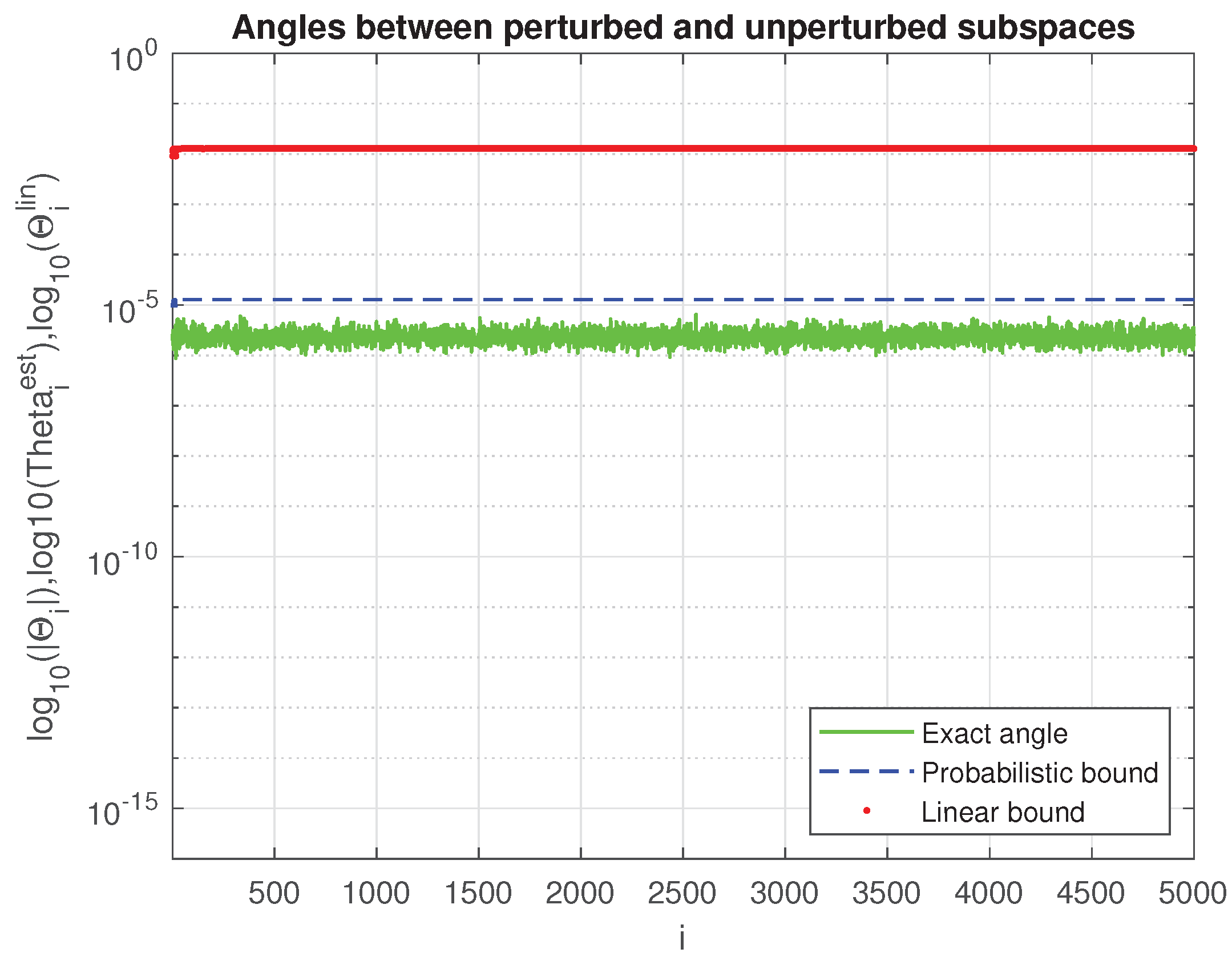
| j | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





