1. Introduction
Uncertainty quantification in deep neural networks is essential for safety-critical applications such as medical diagnostics, autonomous driving, and security systems, where reliable confidence estimates can prevent costly or dangerous errors. Monte Carlo (MC) Dropout, a popular Bayesian approximation technique, estimates epistemic uncertainty by performing multiple stochastic forward passes with dropout active at inference time. While effective, this approach incurs significant computational overhead, making it impractical for real-time use.
We present ARB-Dropout, an adaptive, single-pass alternative to MC Dropout that retains its uncertainty estimation capabilities while dramatically reducing inference cost. ARB-Dropout computes a per-input dropout rate from the variance of gradients with respect to a dummy target, enabling dynamic adjustment of model stochasticity. This adaptive dropout rate is then used in an analytic variance propagation formula to estimate epistemic uncertainty without repeated sampling. Aleatoric uncertainty is modeled via a heteroscedastic noise head, and the two components are combined to produce well-calibrated predictive distributions.
Empirical evaluations on CIFAR-10, CIFAR-100, SVHN, and STL-10 show that ARB-Dropout achieves comparable accuracy to MC Dropout while delivering lower Expected Calibration Error (ECE) and Negative Log-Likelihood (NLL), with inference time reduced by up to an order of magnitude. These results demonstrate that ARB-Dropout is a practical and effective approach for real-time, uncertainty-aware deep learning applications.
2. Related Work
Bayesian neural networks offer a robust framework for predictive uncertainty quantification [
1], yet exact inference remains computationally infeasible for complex architectures. Monte Carlo Dropout [
2] provides a scalable approximation by treating test-time dropout as variational inference, delivering effective calibration at the expense of multiple stochastic forward passes.
Efforts to improve efficiency include learned dropout rates, such as Concrete Dropout [
3], which optimizes rates via training, and heteroscedastic noise heads [
4] to model input-specific aleatoric uncertainty. While these enhance adaptability, they often require parameter tuning or repeated inferences. Deterministic single-pass approaches [
5] reduce computational overhead but may compromise calibration compared to MC-based methods.
ARB-Dropout builds on these ideas by computing per-input dropout rates from gradient variance with respect to a dummy loss, and by integrating heteroscedastic noise for aleatoric uncertainty with analytic variance propagation for epistemic uncertainty all within a single forward pass. This design delivers calibration quality comparable to Monte Carlo Dropout while substantially reducing inference time, making it highly efficient for real-time applications
3. Method: Adaptive Rate Bayesian Dropout (ARB-Dropout)
ARB-Dropout is a single-pass alternative to Monte Carlo (MC) Dropout that adaptively computes per-input dropout rates from gradient variance, and combines this with heteroscedastic noise modeling to produce calibrated uncertainty estimates. Instead of relying on multiple stochastic forward passes, ARB-Dropout uses deterministic variance propagation to approximate the epistemic uncertainty that MC Dropout would produce in expectation, yielding substantial inference-time savings.
|
Algorithm 1 ARB-Dropout Training
|
Inputs: Training and validation loaders , max epochs , early stopping patience P, learning rate , dropout cap , noise loss weight , stability constant .
Model: CNN with penultimate activations , classifier , noise head producing . Initialize Adam optimizer; set best validation loss to ∞; set patience counter to 0. -
For epoch to :
- (a)
-
Training loop over :
Forward pass with adapt=True to compute . -
Compute (adaptive dropout rate):
Set to require gradients. Compute dummy logits: . Dummy loss: with for all samples. Backprop to obtain . Gradient variance: . Adaptive rate: .
Scale activations: . Classification loss: . Noise consistency loss: . Total loss: ; backpropagate and update parameters.
- (b)
Validation loop over with dropout disabled; compute validation loss . - (c)
Early stopping: If , save model and reset patience; otherwise increment patience. Stop if patience reaches P.
Output: Trained model parameters . |
During training,
is computed per batch from the variance of the gradient with respect to the penultimate features, using a dummy cross-entropy loss. This adaptive rate regularizes the network based on feature sensitivity, enabling it to capture epistemic uncertainty. Aleatoric uncertainty is modeled through the heteroscedastic noise head, which adjusts predicted confidence for inherently noisy inputs. At inference, ARB-Dropout performs a single forward pass with deterministic scaling and analytic variance propagation, replacing MC Dropout’s repeated sampling.
|
Algorithm 2 ARB-Dropout Single-Pass Inference with MC Dropout Baseline |
Inputs: trained network , test batch , number of classes K, dropout cap , stability constant
Optional baseline (MC Dropout): run stochastic passes with fixed ; average predictions to compute mean probabilities and normalized predictive entropy.
Forward to penultimate features: where is the network up to the last hidden layer. -
Adaptive rate computation:
- (a)
Set to require gradients. - (b)
Compute dummy logits: . - (c)
Dummy loss: with for all samples. - (d)
Gradient: . - (e)
Gradient variance: . - (f)
Adaptive dropout rate: .
Deterministic scaling: .
Classifier logits: .
Class probabilities: .
Aleatoric uncertainty: .
Epistemic uncertainty (variance propagation):
Normalized variance: .
Total predictive uncertainty: .
Output: predicted probabilities , total uncertainty , normalized entropy , and accuracy metrics. |
Inference uses a single adaptive pass, computing from gradient variance to scale hidden features deterministically. Epistemic uncertainty is estimated analytically via variance propagation, and aleatoric uncertainty is predicted by the noise head. The total uncertainty is a sum of normalized entropy and normalized variance, matching MC Dropout’s behavior in expectation but with greatly reduced computation.
4. Experimental Setup
4.1. Datasets
We evaluate ARB-Dropout on four benchmark image classification datasets widely used in uncertainty estimation research:
CIFAR-10 [
6]: 60,000 RGB images of size
from 10 classes (50,000 train, 10,000 test).
CIFAR-100 [
6]: Same format as CIFAR-10 but with 100 classes (600 images per class).
SVHN [
7]: Over 600,000
RGB digit images (classes 0–9) from real-world house numbers.
STL-10 [
8]:
RGB images from 10 classes, resized to
for our experiments (5,000 train, 8,000 test).
For each dataset, the training set is split for training and for validation. Preprocessing uses torchvision.transforms with normalization (mean , std ); STL-10 includes resizing to .
4.2. Architecture
The network is a lightweight CNN consisting of:
Two
convolutional layers with ReLU activation and
max pooling:
Fully connected layer: .
Classification head: (where K is the number of classes).
Noise head: with activation to produce .
Dropout is applied after the fully connected layer: MC Dropout uses a fixed at inference, while ARB-Dropout computes an adaptive from per-batch gradient variance.
4.3. Training Details
All models are trained using the Adam optimizer [
9] with learning rate
, batch size 64, and a maximum of 15 epochs. Early stopping with patience of 5 epochs monitors validation loss to prevent overfitting. For ARB-Dropout, the adaptive dropout rate satisfies
and is recomputed for each batch using the variance of gradients from a dummy cross-entropy loss. MC Dropout serves as the baseline, using fixed
and
stochastic forward passes at inference time.
4.4. Evaluation Protocol
We compare ARB-Dropout to Monte Carlo (MC) Dropout on the test set using the following metrics:
Accuracy: Standard classification accuracy.
-
Normalized Uncertainty:
- -
For MC Dropout: mean predictive entropy
where
is the mean softmax probability vector over
T stochastic forward passes.
- -
For ARB-Dropout: sum of normalized predictive entropy and normalized variance:
where
is the epistemic variance from analytic propagation,
is the aleatoric variance from the noise head, and
is a dataset-specific scaling constant.
Negative Log-Likelihood (NLL): Measures probabilistic calibration via the log-loss on predicted probabilities.
Brier Score: Mean squared difference between predicted probabilities and one-hot labels.
Expected Calibration Error (ECE): Mean absolute difference between accuracy and confidence across equal-width probability bins.
Inference Time: Average wall-clock time per test batch.
For MC Dropout, uncertainty metrics are computed from the average over stochastic forward passes with fixed . ARB-Dropout computes all metrics in a single deterministic pass using adaptive . All experiments are implemented in PyTorch 2.0 and run on an NVIDIA GPU.
4.5. Implementation
All experiments are implemented in PyTorch 2.0 with dataset handling and preprocessing via
torchvision. Adaptive dropout rates are computed using
torch.autograd.grad to obtain per-batch gradient variance without retaining the computation graph, ensuring minimal overhead. The analytic variance propagation and uncertainty metrics are implemented directly in the model’s forward and evaluation functions. Code and training scripts are publicly available at
https://github.com/sameekshya1999/Adaptive-Dropout.
5. Results
Across CIFAR-10, CIFAR-100, SVHN, and STL-10, ARB-Dropout achieved classification accuracy on par with MC Dropout, with differences within . However, ARB-Dropout reduced inference time by approximately –, requiring only a single forward pass instead of stochastic passes. This confirms that the proposed analytic variance-propagation method can match the predictive performance of MC Dropout while eliminating the cost of repeated sampling.
Calibration metrics further highlight the advantage of ARB-Dropout. On all datasets, ARB Dropout consistently achieved a lower expected calibration error (ECE) and a negative log-likelihood (NLL) than MC Dropout, indicating improved probabilistic calibration. Brier scores were also lower in most cases, reflecting more accurate probability estimates.
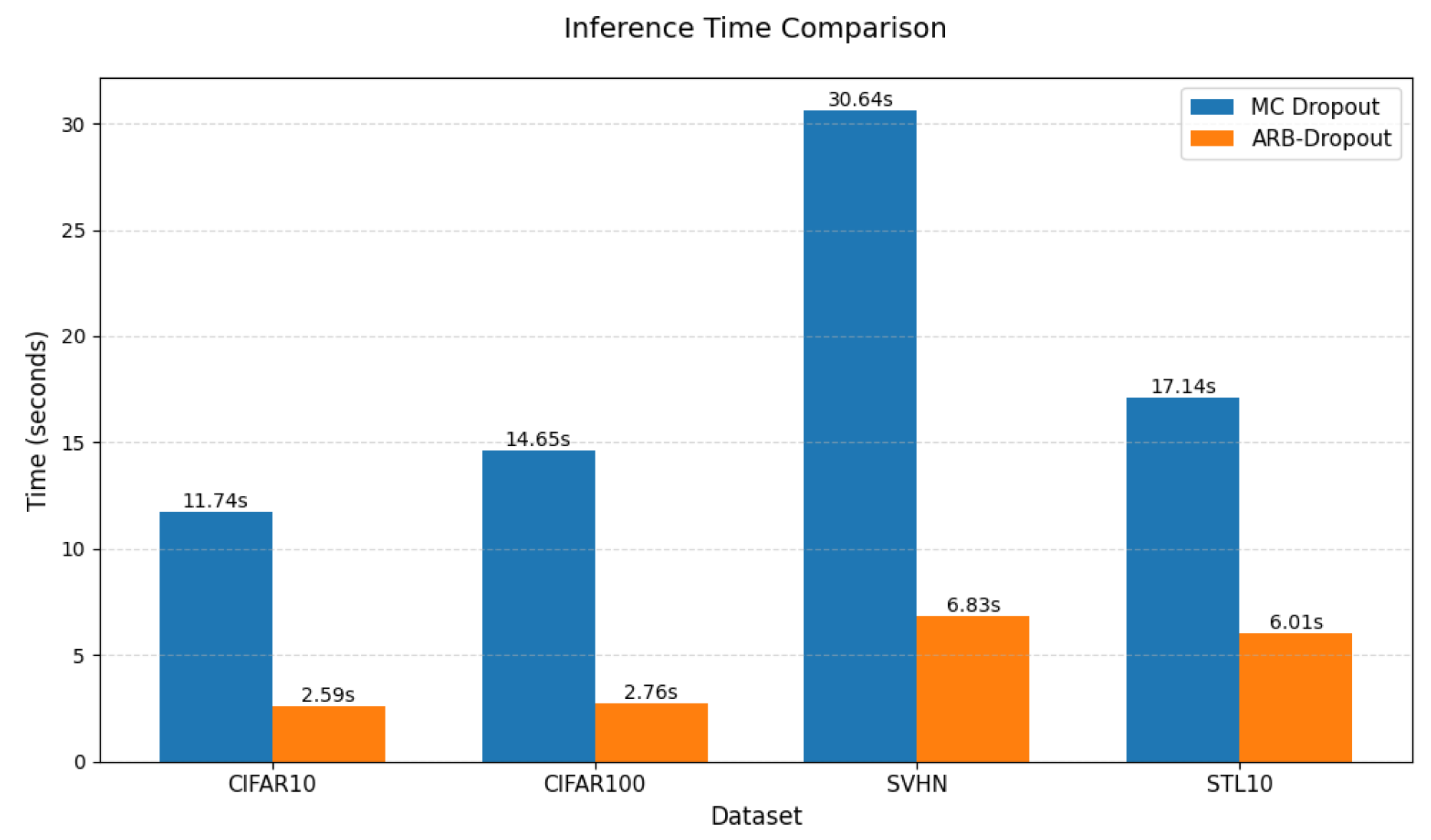
Figure 1.
Inference time comparison
Figure 1.
Inference time comparison
As shown in Figure, ARB-Dropout consistently reduces inference time compared to MC Dropout across all datasets. This improvement stems from eliminating the need for multiple stochastic forward passes by analytically propagating variance in a single pass. The speedup makes ARB-Dropout particularly well-suited for latency-sensitive applications where rapid and uncertainty-aware predictions are essential.
Table 1.
Performance comparison of MC Dropout and ARB-Dropout across datasets.
Table 1.
Performance comparison of MC Dropout and ARB-Dropout across datasets.
| Dataset |
Method |
Accuracy |
ECE |
Norm. Unc. |
Time (s) |
| CIFAR-10 |
MC Dropout |
0.6917 |
0.1904 |
0.1325 |
20.62 |
| ARB-Dropout |
0.6924 |
0.0760 |
2.0563 |
3.08 |
| CIFAR-100 |
MC Dropout |
0.3427 |
0.3382 |
0.2149 |
20.79 |
| ARB-Dropout |
0.3441 |
0.0878 |
1.6380 |
3.34 |
| SVHN |
MC Dropout |
0.8858 |
0.0793 |
0.0385 |
45.67 |
| ARB-Dropout |
0.8859 |
0.0399 |
2.1495 |
7.93 |
| STL-10 |
MC Dropout |
0.4901 |
0.2626 |
0.2834 |
15.75 |
| ARB-Dropout |
0.4876 |
0.0932 |
1.0735 |
4.79 |
The experimental results show that ARB-Dropout matches or slightly exceeds the classification accuracy of MC Dropout across all four benchmark datasets, while reducing inference time by a factor of approximately –. Training curves indicate similar convergence behavior and validation performance for both methods, confirming that the adaptive dropout mechanism does not degrade predictive accuracy.
ARB-Dropout produces higher normalized uncertainty values than MC Dropout, reflecting more conservative confidence estimates, yet achieves consistently lower Expected Calibration Error (ECE) and Negative Log-Likelihood (NLL), indicating improved probabilistic calibration. The analytic variance propagation effectively captures epistemic uncertainty in a single forward pass, closely approximating the uncertainty structure of MC Dropout without the need for repeated sampling. These results demonstrate that ARB-Dropout preserves the essential uncertainty estimation behavior of MC Dropout while offering substantial computational efficiency, making it well-suited for real-time, uncertainty-aware applications.
6. Conclusion
We introduced ARB-Dropout, a single-pass uncertainty estimation method that adaptively adjusts dropout rates for each input based on gradient variance, and integrates heteroscedastic noise modeling to capture aleatoric uncertainty. By replacing MC Dropout’s multiple stochastic forward passes with analytic variance propagation, ARB-Dropout produces well-calibrated uncertainty estimates at a fraction of the computational cost.
Experiments on CIFAR-10, CIFAR-100, SVHN, and STL-10 demonstrate that ARB-Dropout matches the predictive accuracy of MC Dropout while achieving consistently lower Expected Calibration Error (ECE) and Negative Log-Likelihood (NLL), and reducing inference time by up to . The higher normalized uncertainty values indicate more conservative confidence estimates, which can be desirable in safety-critical contexts. These results highlight ARB-Dropout as a practical, efficient alternative for real-time, uncertainty-aware deep learning.
Future work will explore scaling ARB-Dropout to deeper and more complex architectures, applying it to domains such as natural language processing and medical imaging, and extending the adaptive dropout framework to structured prediction tasks. Investigating combinations with other deterministic Bayesian approximations may further enhance both efficiency and uncertainty quality.
References
- David J.C. MacKay. A practical Bayesian framework for backpropagation networks. Neural Computation, 4(3):448–472, 1992. [CrossRef]
- Yarin Gal and Zoubin Ghahramani. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML), pages 1050–1059. PMLR, 2016.
- Yarin Gal, Jiri Hron, and Alex Kendall. Concrete Dropout. In Advances in Neural Information Processing Systems, volume 30, 2017.
- Alex Kendall and Yarin Gal. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? In Advances in Neural Information Processing Systems, volume 30, 2017.
- Jeremiah Liu, Yin Lin, Suchismita Padhy, Dustin Tran, Tania Bedrax-Weiss, and Balaji Lakshminarayanan. Simple and Principled Uncertainty Estimation with Deterministic Deep Learning via Distance Awareness. In Advances in Neural Information Processing Systems, volume 33, pages 7498–7512, 2020.
- A. Krizhevsky. Learning multiple layers of features from tiny images. Technical report, University of Toronto, 2009.
- Y. Netzer, T. Wang, A. Coates, A. Bissacco, B. Wu, and A.Y. Ng. Reading digits in natural images with unsupervised feature learning. In NIPS Workshop on Deep Learning and Unsupervised Feature Learning, 2011.
- A. Coates, A. Ng, and H. Lee. An analysis of single-layer networks in unsupervised feature learning. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, pages 215–223, 2011.
- D.P. Kingma and J. Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
- C. Guo, G. Pleiss, Y. Sun, and K.Q. Weinberger. On calibration of modern neural networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), pages 1321–1330, 2017.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).