Coupling Molecular and Cellular Dynamics in a Large‐Scale Monte Carlo Simulation

1. Introduction

The dynamics of cellular structure emerge from intricate molecular interactions that drive fundamental biological processes essential for life. Coordinated networks of protein–protein interactions, membrane dynamics, and signaling cascades enable cells to respond, adapt, and function within their environment [1]. These interactions underlie the structural plasticity required for processes such as cell division, locomotion, secretion and uptake, protein recycling, membrane fusion, cytoskeletal reorganization, organelle trafficking, and more.

A particularly striking example of a highly dynamic cell structure is the immune synapse (IS) formed between T cells and antigen-presenting cells (APCs) [2].

As central orchestrators of adaptive immunity, T cells must rapidly decide whether to mount responses against foreign antigens while maintaining tolerance to self. These decisions require extraordinary specificity and sensitivity, leading to outcomes such as proliferation, differentiation, cytokine secretion, or cytotoxicity. Dysregulated signaling can result in autoimmunity or graft rejection, whereas insufficient signaling may cause anergy. How T cells integrate multiple molecular cues at the IS into accurate and reliable immune decisions remains a central question in immunology.

The IS exemplifies how molecular interactions generate dynamic cellular organization. Engagement of T cell receptors (TCRs) with peptide–MHC complexes initiates the formation of supramolecular activation clusters (SMACs), with TCR–CD3 complexes concentrating centrally (cSMAC) and integrins such as LFA-1 forming a surrounding peripheral ring (pSMAC)[3,4]. This “bull’s-eye” pattern, supported by actin cytoskeletal remodelling [5], stabilizes the T cell–APC interface. Synapse formation proceeds rapidly, reaching maximal organization within ~30 minutes, and is subject to temporal regulation that shapes the ensuing immune response.

Within the IS, molecular interactions are tightly coupled to the physical topography and dynamics of the interface. Receptor–ligand binding and adhesion molecules such as integrins [6,7] drive assembly, while surface architecture reciprocally regulates molecular distribution: protrusions enrich certain molecules [8], whereas bulky proteins may be excluded from close contacts [9]. Reaction–diffusion processes and motor-driven transport further refine the spatiotemporal organization of proteins, giving rise to the rich and dynamic patterning observed at the IS [3].

Since the underlying mechanisms of IS formation and T cell activation are under intensive study, simulations have been developed to complement experiments and shed light on the mechanisms that affect molecular patterning and IS formation [10,11,12]. More recently, we have shown that detailed microscopy images of the immune synapse can provide starting conditions and constraints for quantitatively predictive simulations of molecular organization at the IS [13]. 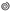Still, previous computational modeling and simulations could capture only relatively small segments of the IS (~1m²), with a limited number of molecular species (<10) and copy numbers (typically, <100K). Monte-Carlo driven simulations of significantly larger scale, such as MCell3 [14] and MCell4 [15], have been developed and can potentially serve for broader, and more detailed description of the IS. Still, these simulations have not been designed so far to dynamically modify the simulated surfaces in response to molecular interactions. Thus, such simulations cannot readily capture the complex dynamics of signaling and cell reorganization that occur at the immune synapse and enable T cell decision-making.

Here, we introduced physical forces into MCell4 [15] to enable large-scale simulation of the IS. Specifically, we provide a demonstration of the feedback between the binding of freely-diffusion receptors and ligands on the surface of interacting cells with their target cells or surfaces. Molecular interactions reinforce the tight interface, while bringing the interacting surfaces close to each other facilitates additional receptor-ligand interactions. We expect that the various types of forces that we have introduced into the large-scale MCell4 simulations will become a valuable tool for enhanced simulations, and thus better understanding, of immune synapses as well as additional dynamic cellular systems. Furthermore, this tool will provide a framework to add physical forces for ever increasing complexity of cellular simulations of various cell types, such as neurons, myocytes, epidermal cells, and others.

2. Results

2.1. Our Approach for Large-Scale Monte-Carlo Simulations with Added Forces

MCell4 is a relatively new implementation to MCell in C++ that provides a Python API [15]. It also enables custom biochemical reaction modeling through native support for BioNetGen (BNGL) [16] species, reactions, and the rate constants associated with the given reactions. Further, it allows parallelization and easier extensibility. Using MCell4 in conjunction with the Blender add-on ‘CellBlender’ for visualization, one can produce highly detailed simulations with elaborated meshes containing millions of nodes and edges. Moreover, highly realistic meshes can be generated with AI support, purchased online, or captured by microscopy, to be used in simulations.

Together with the MCell4 and CellBlender basis, we aimed to integrate multiple force types, including elastic forces of cell membrane stretching, the kinetic forces that are exerted by molecules impinging on segments of the membrane, thermal fluctuations, and inner or external pressure. The goal of this integration was to simulate dynamics of complex cell processes, focusing on T cell spreading on an activating surface as an outstanding example. The required forces for such a simulation were first created and tested separately through simple configurations. Each force adds to the complexity of object dynamics that can be encapsulated in a single simulation.

2.2. Integration of Multiple Force Types into MCell4

The first force introduced was kinetic molecular interactions between a planar rigid membrane with freely diffusing and non-interacting particles, such as atoms of an ideal gas (Figure 1A). This can be viewed as a simplified model of a piston relying on particle collisions. The particles were free to move in the top and bottom compartments of the piston chamber (Figure 1A). All particles were given a mass. Next, various numbers of particles were released in each compartment, ranging from 100 to 100,000. The number of released particles could be essentially much larger, yet run-times increase proportionally to this number. The piston membrane in the middle of the chamber was not given a mass for simplicity.

In theory, the piston membrane can be assumed to move in the manner of a 1-dimensional random walk when both the top and bottom particles are of equal mass and count. Using this knowledge, we recorded the resulting z-axis movement of the piston membrane for various masses and particles counts.

First, as a sanity check, the particles on the top compartment were given significantly more mass than bottom particles, i.e. massive particles were placed on top. After one collision the piston membrane immediately dropped to the bottom of the piston and remained there, as desired. Next, we released an equal number of particles with equal mass in each compartment. This configuration resulted in the expected one-dimensional random walk of the piston membrane (Figure 1B). There appears to be a random and miniscule amount of movement on the order of nanometers caused by the kinetic forces of the impinging particles. The calculated mean squared displacement (MSD) of the simulation was 8.44x10^-23 m² compared to the predicted MSD of 1.64x10^-22 m². During the simulation, we also recorded the energies of the system prior and after each iteration. The subtracted energy serves to calculate the probability of accepting or rejecting movements in each step using the Metropolis criterion (see Methods).

Next, bottom molecules were given additional mass. As can be seen, the desired general outcome was obtained of moving the piston membrane up via drift (Figure 1C). Here, the calculated MSD was 7.75x10^-22 m² which is compared to the predicted MSD of 1.64x10^-22 m². When the top compartment had enough particles with larger mass, the opposite effect was obtained as desired (Figure 1D).

Having incorporated the interactions of particles with a mesh to MCell, we next added elastic stretching forces to the simulation. Such stretching forces also enable the membrane to fluctuate, given some ambient temperature. The energy calculated was due to the extent a face was stretched relative to a predefined relaxed position. Movement was again subjected to the Metropolis criterion for changes in the position of membrane nodes.

The elastic forces were tested by stretching a single point on a flat flexible membrane, which undergoes thermal fluctuations (Figure 2A, left image). Upon release of the stretching force, the spike height dropped (Figure 2A, middle and right images). The peak membrane height dropped over time in nearly a linear fashion (Figure 2B), likely due to thermal dampening of its motion

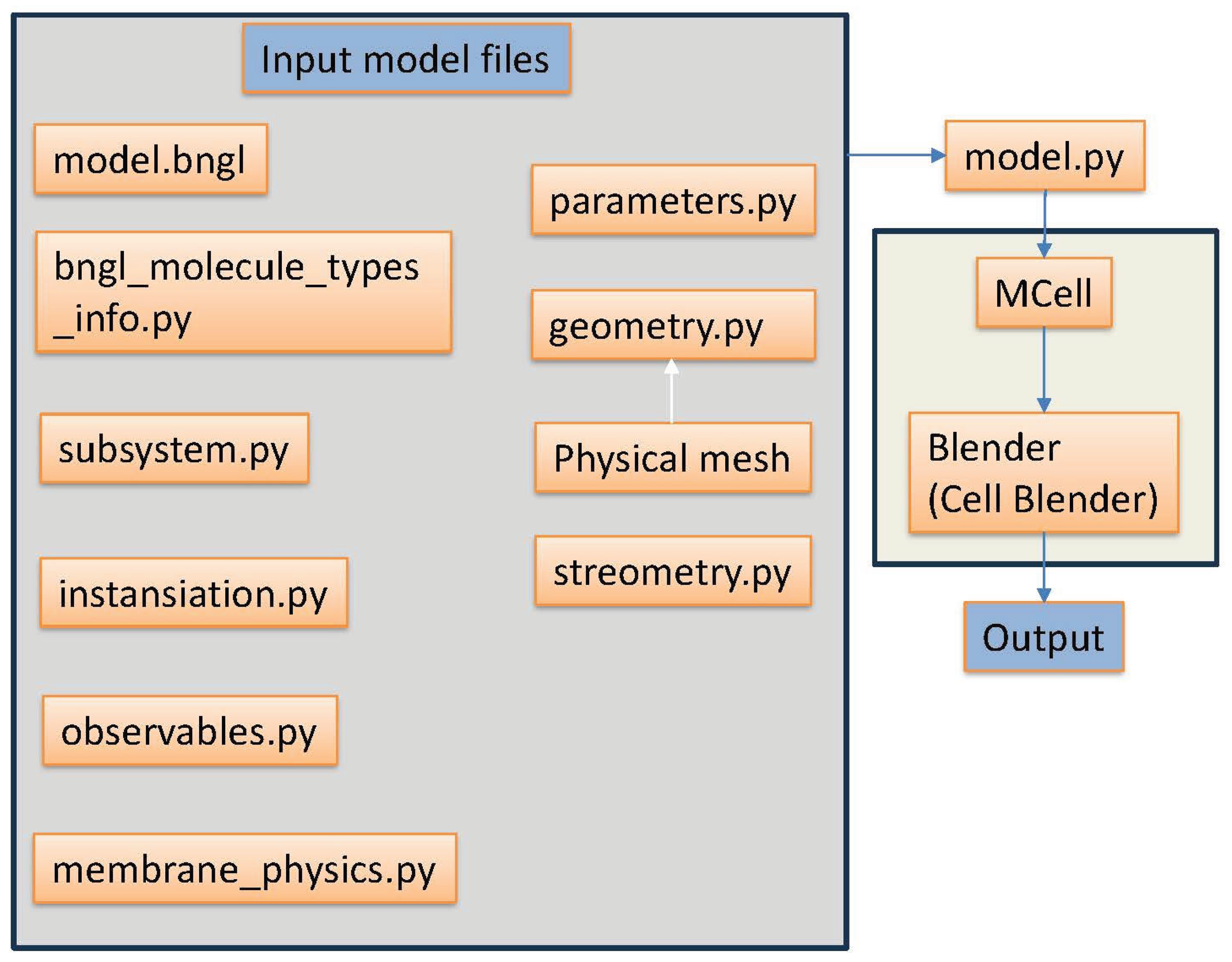
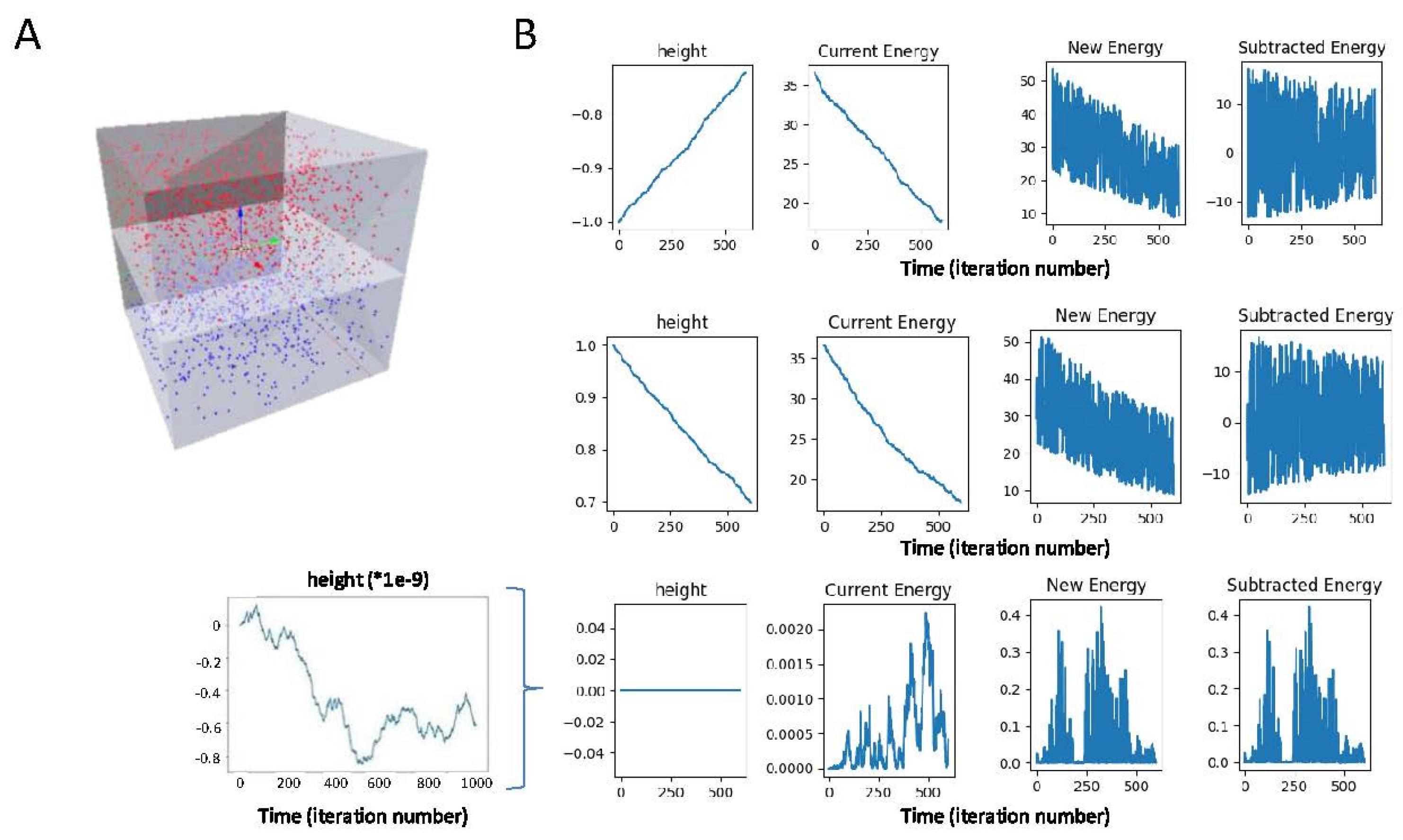
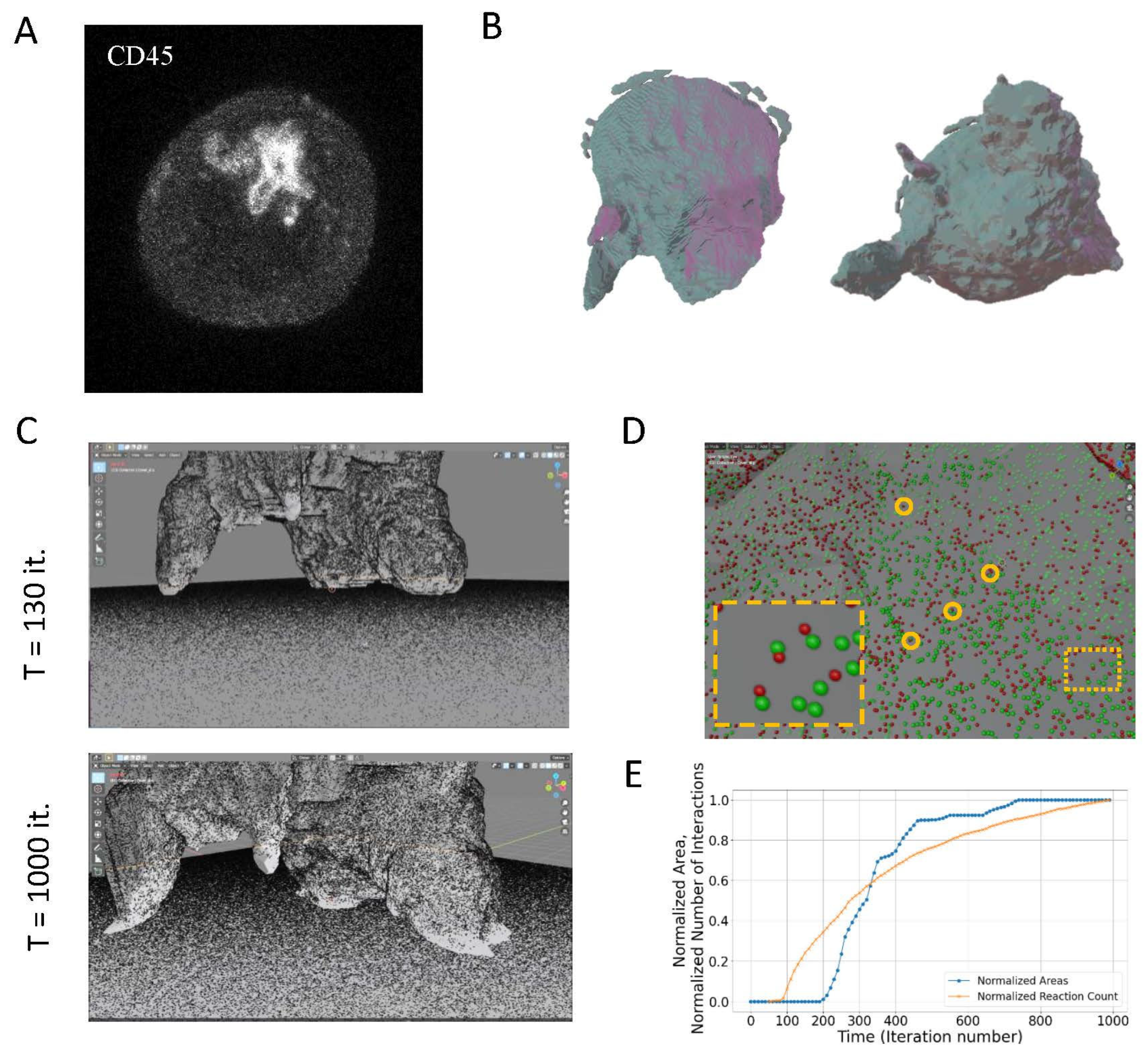
2.3. Simulations of Interacting Cells

We next used MCell4 with its integration of forces to model the dynamic interface between cells, such as the immune synapse that forms between a T cell and an APC. Previously, we have captured such interactions using fluorescence confocal microscopy (Figure 2C) [17]. In this example, the T cell and the antigen presenting cell are each labeled with a different stain, adhere to opposing surfaces, and brought into contact under the microscope [17] (see Methods). This imaging approach allows for high-resolution imaging of the cells’ interaction its resultant interface – i.e. the immune synapse.

In a fairly simple realization, each cell was first modeled as an approximated sphere (i.e. icoshpere), with membrane ruffles. The cells' model included surface molecules that diffuse and interact. There were 10⁴ and 10⁵ surface molecules, including T cell antigen receptor (TCR) molecules on the surface of one sphere and peptide-MHC (pMHC) molecules on the surface of the second sphere. In the simulation, the two spheres were brought into close contact as an initial condition. Upon encounter, one sphere was able to plastically deform the surface of the other sphere, forming a tight and dynamic contact.

To approach a more physiological appearance, we applied a uniform force (through an increase in internal pressure) that drove one cell to contact the other more closely, showing induced spreading, aside from merely plastic deformation. The geometric configuration then comes to a steady state to allow for receptor-ligand interactions to dominate the cell-to-cell interaction.

2.4. T Cell Spreading: Towards Realistic Simulation of the Immune Synapse

Next, we aimed to simulate an even more realistic configuration of an experiment involving a T cell spreading on an activating coverslip [18]. We follow a similar imaging approach as for the previous example, only now letting the cell interact with the coverslip and its resultant spreading. The experiment involves the adherence of the T cell to an upper surface. Next, the surface and cells are placed upside down onto a glass bottom surface coated with an activating antibody (typically, anti-CD3e). Here, we aimed to capture the initial contacts between the T cell and the activating surface. Thus, the upper surface was separated from the bottom coverslip with beads with a 20 mm diameter (47148-10, Carposcular), which is larger than the cells size (typically, 12-15 mm). The cells were fixed, labeled using anti-CD45 Alexa647 (BioLegend, 304056), and fluorescently imaged using an Abberior confocal microscope equipped with high (x100) magnification objective (see Methods). The cells show enrichment of membrane structures at the lower side of the cell (Figure 3A, maximal intensity projection). For incorporation into MCell4, we converted the cell image into a 3D mesh. Faces with a typical length smaller than 1 mm were smoothed out. This rendering shows pronounced membrane protrusions, including microvilli and lamellipodia, directed toward the bottom surface (Figure 3B; side and bottom views).

Next, we established a physical model of cell spreading, following Wahl et al. [19]. In this model, polymerized actin pushes normally on the face of the plasma membrane. The polymerized actin undergoes inward motion due to myosin forces; thus, the actin mesh undergoes a treadmilling motion. The membrane tension balances the actin mesh force on the membrane, resulting in its fluctuating motion. Only upon contact with the activating surface, surface molecules on the cell membrane (namely receptors and integrins) can specifically bind their molecular partners (cognate pMHCs and integrins, respectively) embedded on the surface of the coverslip. These interactions create effective friction forces that lead to extension of the cell contacts with that surface and its eventual spreading.

In our simulation, we included up to 250K surfaces molecules on the cell surfaces, and an identical number of binding molecules on the activating surface. For simplicity, we simulated the actin forces implicitly, yet membrane tension and molecular interactions were simulated explicitly. We then let the simulation run for 1000 iterations, allowing the cell to be brought into contact with the surface, while its surface molecules could diffuse and interact with that surface. During the simulation, we routinely captured the location of the surface node coordinates, the diffusing molecules and their interaction with the surface molecules.

We show the time evolution of the cell spreading on the coverslip (Figure 3C; Movie M1). As expected, the number of contacts and the spreading area grew monotonically over time (Figure 3D, E). Still, the relation between the growth of these parameters was non-trivial and showed earlier rise in molecular interactions (Figure 3E, orange curve), yet faster growth in contact area (blue curve).

Taken together, we demonstrate how the iterative coupling of molecular interactions with cell membrane can lead to the emergent process of T cell spreading on functional surfaces; all within a realistic configuration defined by microscopy.

3. Discussion

Over the past two decades, high and super resolution microscopy has been used to image TCR-dependent signaling complexes in single molecule detail in fixed and live T cells [20,21,22]. Thus, we and others have recognized multiple mechanisms that are critical for robust TCR triggering [23]. Such mechanisms include receptor clustering [21,24], conformational changes of receptor chains [25,26,27], dynamic formation of signaling complexes [20], cooperativity in triggering within clusters [28,29], physical segregation of glycoprotein-phosphatases [9,13,30], effects of cell topography [30,31], and more. A major effort in the field is to integrate such mechanisms, thus accounting for the unique properties of T cell recognition – i.e. their sensitivity, selectivity and speed [32]. Still, current computational modeling and simulations cannot capture the complex dynamics of signaling and cell reorganization that occur at the immune synapse and enable T cell decision-making. Similarly, other complex and dynamic cellular processes that involve molecular interactions cannot be readily simulated and require state-of-the-art modeling approaches and computational power (e.g. [33,34,35,36]).

Here, we integrated physical forces into MCell4. Our forces include the interaction of molecules with membrane meshes as well as membrane stretching, thermal fluctuations and pressure. Such forces enable elaborate dynamic simulations that encapsulate the chemistry and physics of cell-to-cell interactions. In our case, we simulated such interactions leading to the physiological outcome of T cell spreading on an activating surface. For that, we had to incorporate the variety of these added forces into MCell4. Arguably, our model is a small and limited biological encapsulation of cell signaling demonstrated in MCell4. Moreover, full scale simulation of the immune synapse is clearly more complex, as it involves interactions of many more molecules.

Future effort could integrate additional molecular species on the surface (co-receptors, glycoproteins, etc.), subcellular entities (e.g. nucleus, cytoskeleton, vesicles, actin filaments) and intracellular molecules (e.g. for signaling). Additional future forces may include object twisting and bending [37].

Our simulations were conducted primarily on a desktop PC. There exists a computational limit without using a significantly large cluster or a supercomputer. On a PC computer containing an Intel i7 processor, Nividia Geforce GTX 1650, and 32 GBs of RAM, we get runtimes ranging from minutes to days, depending on the number of interacting molecules (Table 1) and nodes, with their associated algorithms and interactions.

Simulations can also be done with clusters or supercomputers with much more computing power than any computer equivalent to the one discussed above. For instance, the Abacus Summit cosmological N-body simulation suite simulated a total 6x10¹³ particles [38] using a supercomputer. There are approximately 2x10¹⁰ water molecules in an E. coli bacterium and 10⁹ lipid molecules in the cell membrane of a small eukaryotic cell [1] adding to a total of approximately 2.1x10¹⁰ particles that must be simulated in this mixed cell. This puts simulation of an entire eukaryotic cell close to the limit of some of the best supercomputers today.

Our integrated simulation framework can simulate multiple other intercellular and intracellular interactions, beyond the shown examples. Such examples may include vesicles transporting material within and across the cell, cellular signaling networks, passive and active transport in various cell types, etc. This is in part due to Blender allowing the user to create realistic models of high triangulation density. We conclude that our approach provides a versatile foundation for simulating a variety of dynamic cell systems and processes.

4. Methods

The Python interface used allows for a high degree of flexibility. Full control of the geometry is allowed throughout the simulation (Figure S1). Definition of various reactions uses the new BioNetGen library added to MCell4. Parallelization is defined by determining the 3D partition size in Python. This allows for further optimization of runtimes in the simulation.

Installation of the simulation, instructions, and examples can be found in the following link: jchaiken12/3D_cell_simulation: GitHub repository for research paper Towards large scale 3D modelling and simulation of the immune synapse (https://github.com/jchaiken12/3D_cell_simulation)

4.1. Detailed Molecular Simulation

Requirements. For ease of use, employing a standard PC with an i7 processor, a GPU, and at least 16GBs of RAM are advisable. The physics is coded in python version 3.9. The user should follow the directions on MCell’s website on how to download MCell4 given their operating system. The structure of the simulation is depicted in Figure 4 and is explained in detail below.

Simulation Setup. Each simulation requires multiple input files (Figure 4). The geometry.py defines the Euclidean positions of the nodes along with their edges. This must be a triangulated mesh. The physical mesh is the triangulated mesh created in Blender to be exported with a custom export function to create the geometry file. The stereometry.py file contains some useful geometric functions used to create the simulation. The membrane_physics.py contains energy and elastic displacement calculations used in the model.py file. The parameters.py file defines the number of iterations, pairing distance, time step, and random seed of the simulation to be run. The model.bngl file defines the reactions and their associated reaction rates. The bngl_molecule_types_info.py file defines if the molecules are 3D or 2D surface molecules and their given diffusion speeds. Next the instantiation.py file defines the initial release location and adds the molecules and geometries to the simulation. The observables.py handles the export of the visualization data. The subsystem.py file loads in the model.bngl file with its reaction and rate along with additional information such as diffusion constants for loaded elementary molecule types.

Figure 4. A schematic overview of the simulation. Files and outputs are produced sequentially by order of the arrows.

Figure 4. A schematic overview of the simulation. Files and outputs are produced sequentially by order of the arrows.

First the simulation is run by calling the main execution file named model.py in the terminal. This file uses all the files above to be woven together to produce a physical simulation of a cell of the user’s choice. A k-d tree is used to determine distances of static molecules distributed on the coverslip to molecules diffusing on the cell. Once the simulation is finished, the user references the newly created visualization data and runs Blender with the CellBlender add-on again in the terminal. This produced the desired simulation to be visualized in Blender. This process is repeated for any simulation that the user creates.

Input. Input parameters include parameters that describe the physical properties of the interacting cells and of the molecules that interact within and across the interfaces. The cell meshes are made by the user on Blender and extracted to create a custom cell to cell interaction.

Simulation Main Run File. As stated above, the model.py file is the main run file. This contains the energetics of the simulation explained in more detail in a later section. The surface molecule interactions are defined within MCell4. Briefly, in our simulation we assume specific Hamiltonians of a quasi-equilibrium system and with mean-field approximations. The simulation simplifies noncrucial elements in the cell-to-cell interaction considering only their general effects. Such entities include lipids on the membranes and water molecules which are not specifically described in the simulation. In contrast, protein molecules of interest are simulated. The simulation algorithms are done using Monte-Carlo simulations using Metropolis criterion to determine the probability between possible configurations.

Outputs. The energies of each region of the cell are calculated along position of each specific region that is maintained and updated each iteration. The surface proteins’ positions are also recorded each iteration. Visualization output is made available using CellBlender after the main run file finishes running by a command on the terminal, referencing the newly created data. This ultimately produces a movie in CellBlender.

Monte Carlo Simulations

Simulation Energetics. In the simulations we used the Hamiltonian H = H_int + H_el, to calculate the energetics of the overall interactions between the T cell membrane and the APC membrane or the activating surface. A bending component, H_bend, could be added in the future, as detailed below. The interaction part, H_int, is defined as:

$$H_{int}={\sum }_i^n{\displaystyle \frac{1}{2}}{m}_i{v}_i^2$$

(1)

where each particle is represented as i. The movements were made by changes in the momentum, P_int, incurred by each particle collision with the membrane. The momentum is defined as:

$$P_{int}={\sum }_i^n{m}_i{v}_i$$

(2)

The elastic part of the Hamiltonian, H_el, is defined as [37]:

$$H_{el}={\sum }_i^n{\displaystyle \frac{\kappa }{2a_i^2}}{(∆a_i)}^2$$

(3)

where $\kappa ={\kappa }_1·{\kappa }_2/({\kappa }_1+{\kappa }_2)$, is the general effective bending rigidity of two membranes. In this case, the bending rigidity is effectively $\kappa \approx {\kappa }_1$, since ${\kappa }_2\gg {\kappa }_1$ and is simulated at different values. The area, $a_i$, is defined for each face. The new area is determined by attempting another move and calculating the new area after the potential move is made.

In the current implementation of the forces, we have not incorporated bending energies. In the future, the bending part of the Hamiltonian, H_bend, could be defined as [37]:

$$H_{bend}=2{{\kappa }_{\mathrm{b}}\mathrm{M}}_2$$

(4)

This is the Helfrich bending energy [39], assuming our model is minimal i.e., not a bilayer couple model, area-difference elasticity model or a spontaneous curvature model. This assumption is valid given our membrane in the simulation does not have two layers. κ_b is the bending elastic constant.

The moment M₂ is defined as:

$$H_{el}={\sum }_i^{N_{\nu }}{{\displaystyle \frac{1}{4}}{a}_i\left[{\left({\nabla }_s^{2}x\right)}_i\right]}^2$$

(5)

where a_i is the area of triangles around node i, N_v is the total number of nodes, x is the surface coordinate and ${\nabla }_s^2$ is the discrete Laplace-Beltrami operator. Lastly, the membrane would move proportionally to the energy related to the pressure. The displacement was determined by setting an initial volume of the cell and assuming pressure remained constant. The displacement due to pressure is defined as follows:

$$D_P=c{\displaystyle \frac{{(∆V)}^2}{V_{int}}}$$

(6)

where c is the displacement constant.

Simulations Dynamics. The simulation propagates in time by iterations of 1 μs. In every iteration all molecules and nodes of the mesh attempt to move. The nodes of the mesh have the following rules for movement:

1. The node is not outside movement space and not crossing another mesh.

2. The probability of the move according to the Metropolis criterion is:

$$P(oldstate\to newstate)=\{\begin{array}{cc}1& \Delta E<0\\ \mathrm{e}\mathrm{x}\mathrm{p}(-\Delta E)& \Delta E>0\end{array}$$

(7)

4.2. Sample Preparation and Confocal Microscopy

For imaging cell-cell conjugates (Figure 3B), we employed our previously published approach [17]. Briefly, we let Jurkat J76 (CD8+) and T2 hybridoma cells (both, a kind gift from the Acuto lab at Oxford) interact. Twenty-four hours prior imaging, the T2 cells were loaded with NY-ESO-1 peptides, thus serving as APCs. Each cell type adhered to a different surface: the bottom of an 8 well ibidi #1.5 coverslip and a small glass that fit into the well. Adherence to the glass surfaces was promoted by their coating with non-stimulatory antibodies (aCD45 and αCD11a; BD Pharmingen, PMG555480 and 555378, respectively). The cells were brought into contact as the small glass was placed (upside down) on the bottom glass of the well. The upper surface was separated from the bottom coverslip with beads with a 20 mm diameter (47148-10, Carposcular), which is larger than the cells size (typically, 12-15 mm). For imaging, the plasma membrane of the cells was stained for αCD45 and Alexa647 (BioLegend, 304056) and the PM of the T2 cells was stained using DPEE-Atto565. Prior imaging, the cells were fixed by 2.4% Paraformaldehyde (PFA) for 30min in 37°C and washed with PBS.

For imaging cell protrusions (Figure 3C,D), the cells were attached to an upper coverslip, which was placed on the bottom of a well without any cells. The same beads were used for spacing the two surfaces. The upper glass was placed into an ibidi well. The cells were fixed and labeled with an aCD45 antibody (as above).

Single and two-color fluorescent confocal microscopy using an Abberior STED/confocal microscope (Expert line; Abberior Instruments, Göttingen, Germany), mounted on a TiE Nikon microscope and operated by the Imspector software (v0.13.11885; Abberior Instruments, Göttingen, Germany). The microscope was equipped with a high magnification (x100, 1.49 NA) oil immersion objective (CFI SR HP Apochromat TIRF, Nikon Instruments). Samples were excited with either a 2mW 561nm pulsed laser (60ps) or with a 2mW 640nm pulsed laser (60ps) at 10%. The pinhole was set to 1 Airy unit. Three-dimensional imaging used a piezo stage to scan the area with 1μm axial resolution.