Mathematical Analysis of Entanglement Measures and Maximized Quantum Fisher Information

1. Introduction

Entanglement, a cornerstone of quantum mechanics, is a fundamental resource in quantum computing and quantum information science. To quantify this unique correlation for bipartite systems, various entanglement measures such as concurrence [1] and negativity [3,5] have been developed. While these measures, by definition, do not increase under Local Operations and Classical Communication (LOCC), different measures can assign different ranks to non-maximally entangled states [10]. This suggests that each measure captures a different facet of entanglement [2].

In parallel, Quantum Fisher Information (QFI) [6,7] has emerged as a key metric in quantum metrology [8,9], as it quantifies the ultimate precision with which a parameter can be estimated. A state’s QFI, when exceeding a certain threshold, can also serve as a witness for entanglement [9]. However, unlike entanglement measures, QFI is not an entanglement monotone and can be changed via local unitary operations. This necessitates finding the Maximized QFI (MQFI) over all possible local unitary rotations to properly compare a state’s metrological potential with its entanglement [11,23,22].

In this work, we aim to bridge the gap between these two seemingly different concepts: entanglement and quantum metrology. We perform a large-scale numerical simulation to generate a large number of random two-qubit states and analyze the correlations between their entanglement measures (concurrence, negativity, and Relative Entropy of Entanglement (REE)) and their MQFI. Our first goal is to numerically confirm that entanglement enhances a state’s metrological capacity, and that local optimization to find the MQFI leads to a tighter, more predictable relationship.

Furthermore, we address the challenge of scatter and noise often encountered in experimental data by employing a systematic data binning methodology [15,16]. This approach allows us to reveal the underlying functional relationship between REE and MQFI. Our results provide strong empirical evidence for the saturation of quantum metrological gain. Specifically, an exponential model fitted to the binned data demonstrates that while a small amount of entanglement produces large gains in precision, further increases in entanglement yield diminishing returns. These findings offer critical practical guidance for the design of quantum sensors and the optimal allocation of resources [13,14].

—

2. Methods

The core of our study is a systematic process of numerical simulation and analysis, which involves generating random quantum states and then quantitatively characterizing their entanglement and metrological potential.

2.1. Random State Generation

We generated 20,000 random two-qubit mixed-state density matrices ($\rho$). These states were created using a method that involves generating random unitary matrices and a set of random positive eigenvalues that sum to one. This approach ensures that the generated matrices are valid density operators, representing a wide range of states typically encountered in laboratory experiments.

2.2. Entanglement Measures

For each generated density matrix, three distinct entanglement measures were computed:

• Concurrence ($C\left(\rho \right)$): This measure was determined using the eigenvalues of the spin-flipped state [1]. Its value ranges from 0 for separable states to 1 for maximally entangled states.
• Negativity ($N\left(\rho \right)$): We calculated the negativity for each state based on the negative eigenvalues of its partial transpose [3,5]. This value is also bounded between 0 and 1.
• Relative Entropy of Entanglement (REE): The REE for a given state ($\rho$) is defined as the minimum value of the quantum relative entropy, $S\left(\rho \right|\left|\sigma \right)=Tr(\rho log\rho -\rho log\sigma )$, where the minimum is taken over the set of all separable states ($\sigma$) [4]. This measure quantifies the "distance" of a state from the closest separable state.

2.3. Quantum Fisher Information (QFI) and MQFI

For each state, we calculated the QFI with a fixed generator, specifically the two-qubit Pauli Z-operator, $J={\sigma }_z\otimes {\sigma }_z$ [7]. We then performed an optimization over local unitary rotations to find the maximum possible QFI for that state, which we refer to as Maximized QFI (MQFI) [11]. All QFI and MQFI values were normalized by dividing by 4, which allows for a direct comparison with the entanglement measures.

2.4. Data Binning and Empirical Modeling

The raw data points exhibited significant scatter between entanglement and MQFI. To reduce this scatter and reveal the underlying functional relationship, we employed a systematic data binning method.

• Binning: The REE values were grouped into predefined bins, and for each bin, the average MQFI/4 value was computed.
• Model Selection: Various empirical models (3rd-degree polynomial, exponential, logistic, etc.) were then applied to this smoothed, binned dataset. The model that provided the best fit was selected based on its coefficient of determination ($R^2$).
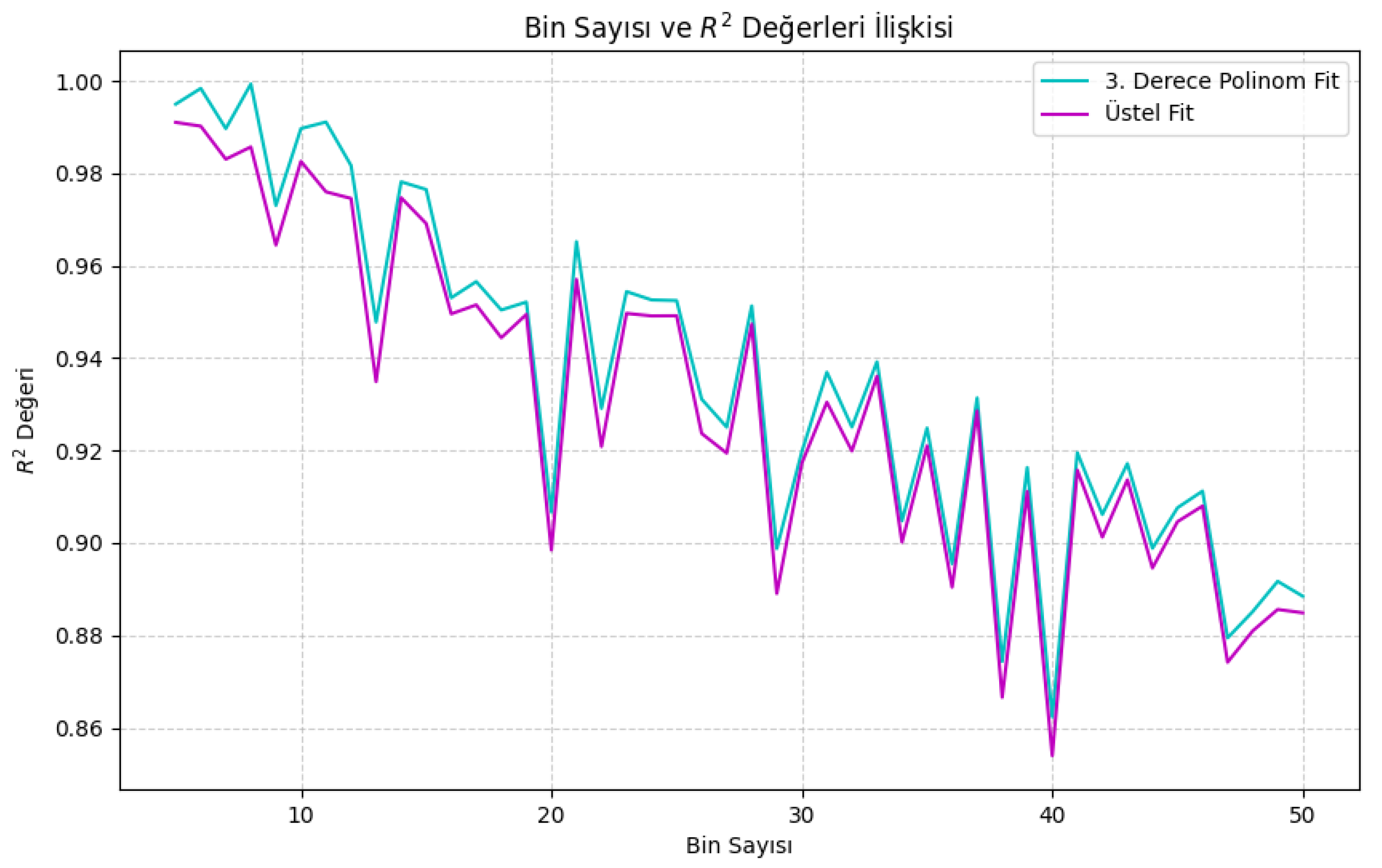
• Noise Reduction: This binning approach effectively reduced random fluctuations and noise while preserving the essential statistical features of the dataset. We tested different numbers of bins (ranging from 5 to 50) to determine the optimal count that yielded the best performance and ensured the stability of the model [1,16].

This comprehensive methodology combines the theoretical rigor of numerical simulation with a practical approach to managing the noise inherent in empirical data, allowing for a robust and quantitative analysis of the complex relationship between entanglement and quantum metrology.

—

3. Results and Discussions

Our numerical analysis of entanglement measures and their relationship with Maximized Quantum Fisher Information (MQFI) for general two-qubit systems revealed several key findings. The data points from our simulation exhibit a strong and predictable envelope that quantitatively describes the relationship between a state’s entanglement and its metrological capacity.

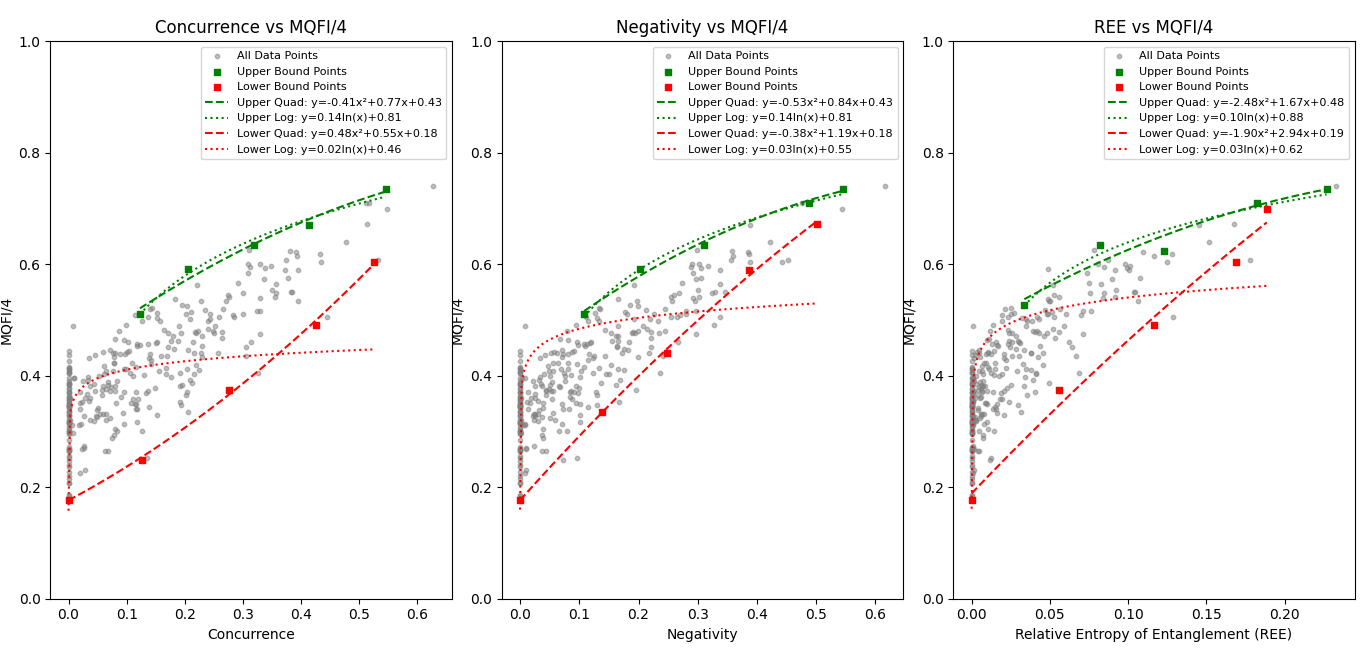
The first part of our analysis focused on the scatter plots of MQFI/4 against three different entanglement measures: Concurrence, Negativity, and Relative Entropy of Entanglement (REE). As shown in Figure 1 from the original study (not included in this text), the data demonstrates a clear positive correlation. Higher entanglement values generally correspond to higher MQFI/4 values. This confirms the widely accepted principle that entanglement is a valuable resource for enhancing metrological precision. We found that while a state’s QFI with a fixed generator can vary widely for a given entanglement value, the local optimization to find the MQFI leads to a much tighter, more predictable relationship [11,22].

A critical aspect of our work was the delineation of the upper and lower bounds of this relationship. We used a binning method to group data points based on their entanglement values and identified the maximum and minimum MQFI/4 for each bin. This allowed us to calculate polynomial and logarithmic fits that provide a quantitative description of these bounds. For Concurrence vs. MQFI/4, the upper quadratic fit had an exceptional $R^2$ value of 0.99, demonstrating an extremely strong fit to the boundary data. Similarly, the fits for Negativity and REE also showed high $R^2$ values (mostly above 0.90), signifying a robust description of the observed behavior across all three measures. These results reinforce that highly entangled states generally offer superior metrological precision, with the upper bounds representing "optimal" states in terms of metrological performance for a given entanglement level.

Furthermore, our analysis revealed a physically significant finding: the non-zero y-intercepts of the fit curves at zero entanglement. This highlights that even separable states can possess quantum information useful for metrology. However, the distinct upward trend of both upper and lower bounds with increasing entanglement measures clearly demonstrates that entanglement undeniably enhances metrological performance.

The second part of our study extended this analysis by using a systematic data binning approach to reduce the effects of decoherence, noise, and statistical variability, thus revealing the underlying functional relationship between REE and MQFI/4. By averaging data points within specific REE bins, we were able to significantly reduce the scatter and fit the data with high-precision empirical models.

Figure 2. Relationship between Bin Count and $R^2$ Values. This plot shows that an optimal bin count exists where the fit quality is maximized, demonstrating the importance of our methodology.

Figure 2. Relationship between Bin Count and $R^2$ Values. This plot shows that an optimal bin count exists where the fit quality is maximized, demonstrating the importance of our methodology.

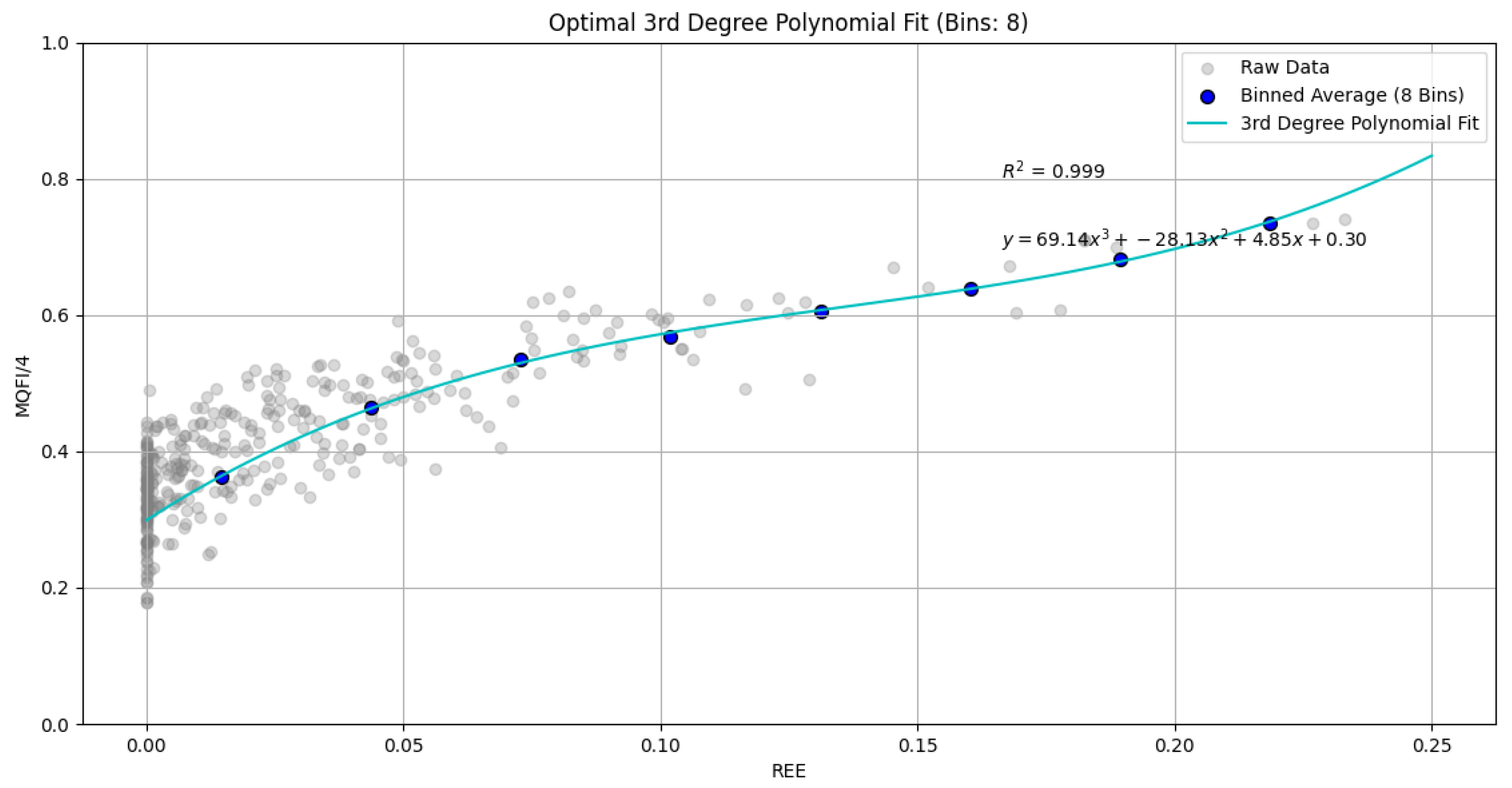
We found that two models, in particular, provided an excellent fit to the binned data: a 3rd-degree polynomial and an exponential function.

Figure 3. Optimal 3rd-Degree Polynomial Fit. The figure shows the 3rd-degree polynomial fit to the binned data, with an exceptional $R^2$ of 0.999. This model accurately captures the strong nonlinear growth of MQFI as a function of entanglement.

Figure 3. Optimal 3rd-Degree Polynomial Fit. The figure shows the 3rd-degree polynomial fit to the binned data, with an exceptional $R^2$ of 0.999. This model accurately captures the strong nonlinear growth of MQFI as a function of entanglement.

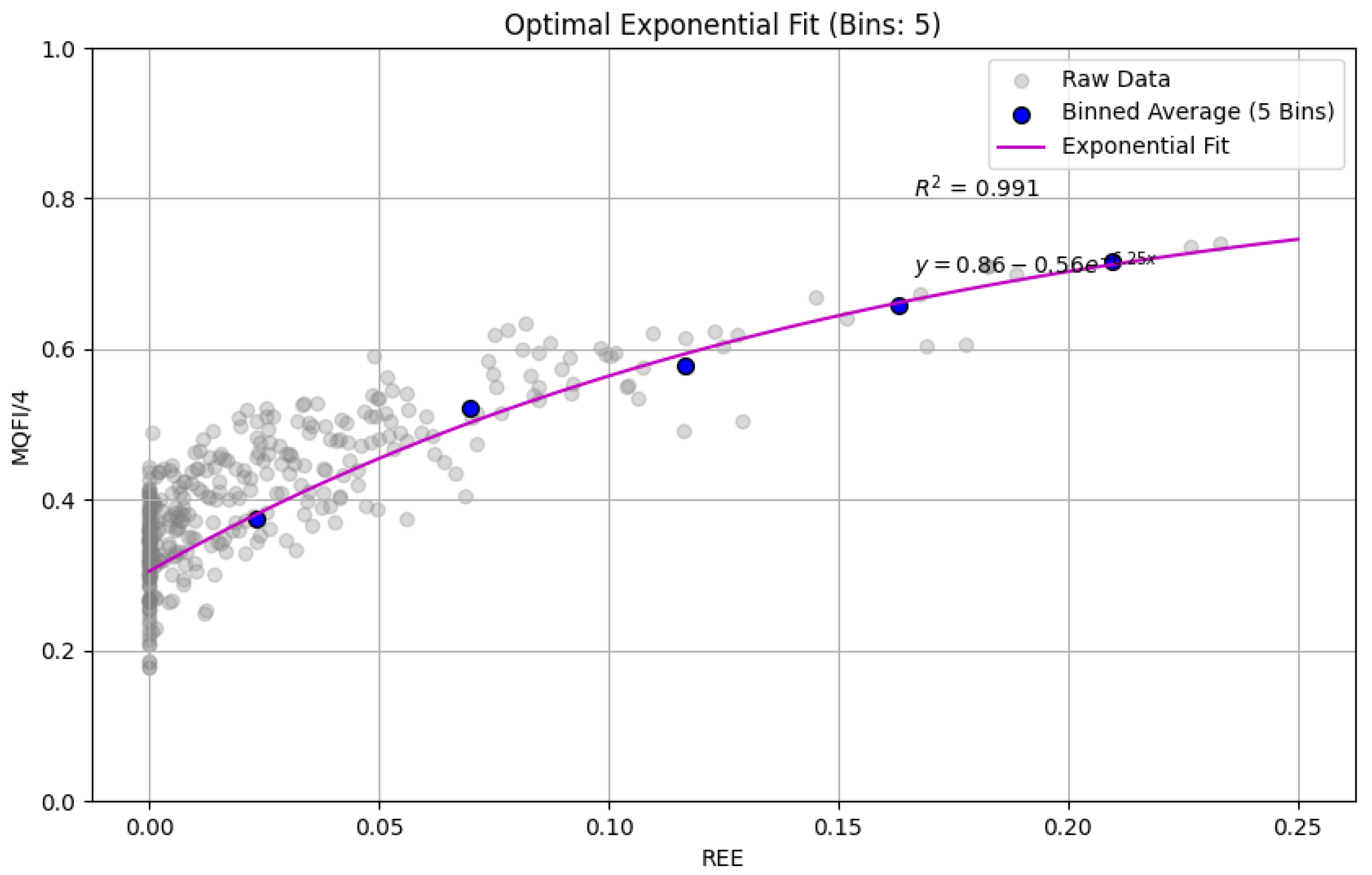
Figure 4. Optimal Exponential Fit showing saturation. This figure presents the exponential model, with an $R^2$ of 0.991, which provides strong empirical evidence for a saturation behavior. This model illustrates that while a small amount of entanglement produces a large initial gain in measurement precision, further increases in entanglement eventually lead to diminishing returns. This finding is a key feature predicted by quantum resource theory and has significant practical implications for resource allocation in real-world quantum sensors.

Figure 4. Optimal Exponential Fit showing saturation. This figure presents the exponential model, with an $R^2$ of 0.991, which provides strong empirical evidence for a saturation behavior. This model illustrates that while a small amount of entanglement produces a large initial gain in measurement precision, further increases in entanglement eventually lead to diminishing returns. This finding is a key feature predicted by quantum resource theory and has significant practical implications for resource allocation in real-world quantum sensors.

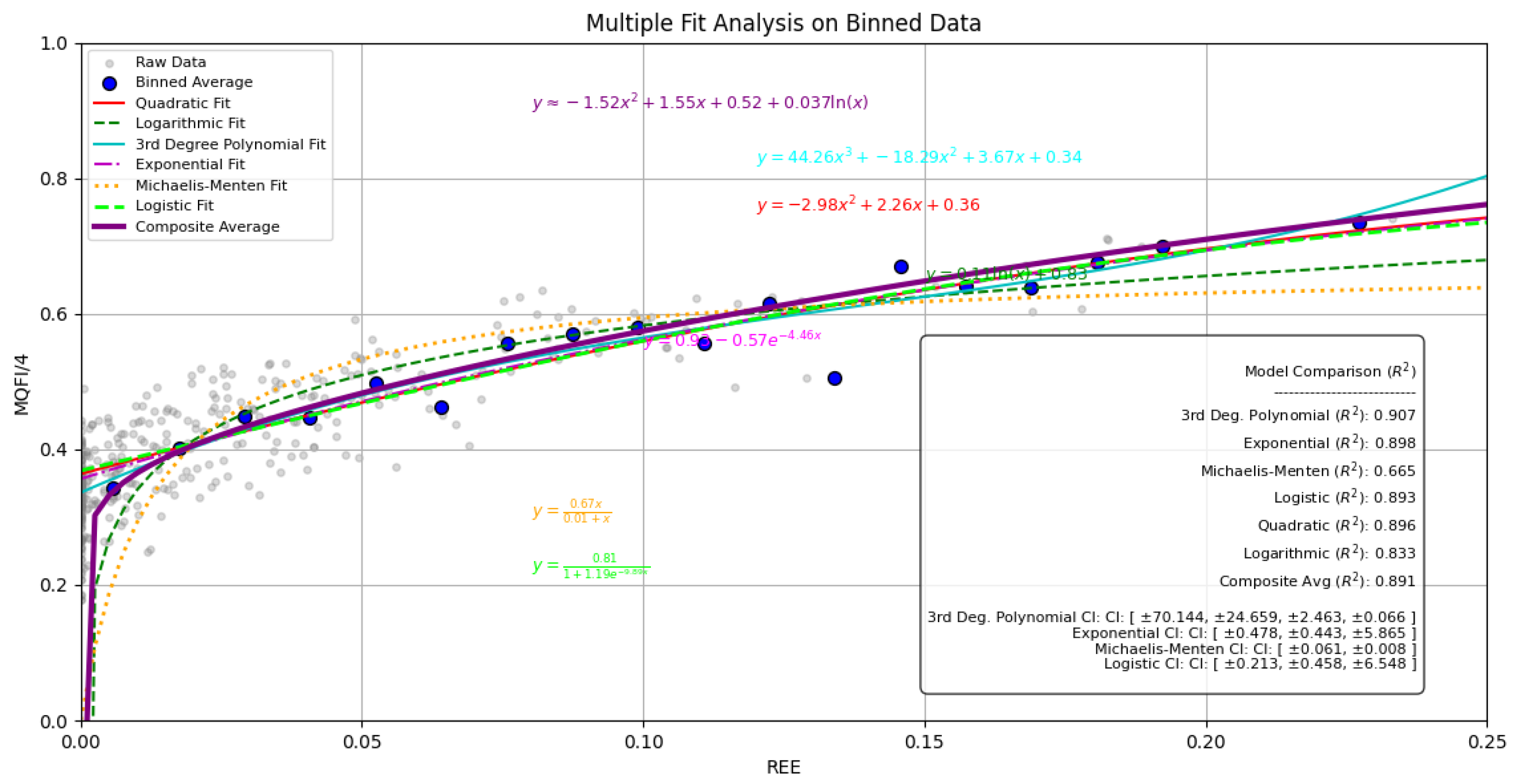
Figure 5. Multiple Fit Analysis on Binned Data. The figure above shows a comparison of multiple fits on the binned data, including the polynomial and exponential fits, as well as logistic and Michaelis-Menten functions. The comparison confirms the superior performance of the polynomial and exponential models in describing the relationship.

Figure 5. Multiple Fit Analysis on Binned Data. The figure above shows a comparison of multiple fits on the binned data, including the polynomial and exponential fits, as well as logistic and Michaelis-Menten functions. The comparison confirms the superior performance of the polynomial and exponential models in describing the relationship.

In summary, the consistent behavior observed across all entanglement measures, along with the empirical evidence for saturation, underscores the fundamental connection between entanglement and quantum metrology. Our results not only confirm that entanglement is a valuable resource but also provide quantitative models that can be used to predict the performance of quantum sensors and guide the optimal design of future experiments.

—

4. Conclusion

Our work successfully bridges the gap between the theoretical quantification of entanglement and its practical utility in quantum metrology. Through a large-scale numerical simulation of random two-qubit states, we confirmed a strong and fundamental relationship between a state’s entanglement and its metrological potential, as quantified by Maximized Quantum Fisher Information (MQFI). We showed that while standard QFI can vary widely for a given entanglement value, the optimization of a state’s measurement basis to find its MQFI leads to a far more predictable correlation [11,23,22].

A significant contribution of this study is our empirical evidence for the saturation of quantum metrological gain. By employing a robust data binning methodology to mitigate noise and statistical scatter, we were able to reveal the underlying functional relationship between Relative Entropy of Entanglement (REE) and MQFI. The exponential fit, with an exceptional $R^2$ value, demonstrates that metrological precision, while initially increasing rapidly with entanglement, reaches a point of diminishing returns. This finding provides a crucial quantitative guideline for the design of quantum sensors and confirms that simply increasing entanglement beyond a certain point may be an inefficient use of resources.

Furthermore, our analysis confirmed that even separable states (with zero entanglement) can possess non-zero metrological utility, while simultaneously reinforcing the principle that highly entangled states offer superior metrological precision. The consistent behavior observed across all three entanglement measures (Concurrence, Negativity, and REE) with MQFI suggests a universal underlying relationship between entanglement and quantum metrology in two-qubit systems.

In summary, this research provides valuable insights for the field of quantum information science and quantum metrology. It validates theoretical predictions with a clear, data-driven approach and offers a practical framework for optimizing quantum-enhanced protocols. Future work could extend this methodology to more complex multi-partite systems, different types of entanglement, and states under the influence of various decoherence channels to further refine our understanding of the limits and potential of quantum metrology.

—