LOCC-Maximized Quantum Fisher Information as a Necessary Condition for CHSH Violation

1. Introduction

The relationship between Bell nonlocality and quantum entanglement remains a fundamental question in quantum information theory [1,2]. While entanglement is necessary for Bell violation in pure two-qubit states, Werner demonstrated that entangled states can exhibit correlations that do not violate any Bell inequality for local measurements [3]. This raises the question: what quantitative relationships exist between entanglement measures and Bell violation strength?

Entanglement measures such as concurrence [4], negativity [5], and relative entropy of entanglement (REE) [6,7] have been extensively studied. It is known that for sets of non-maximally entangled two-qubit states, comparing these entanglement measures may lead to different orderings [8,9,10,11]. Recent work by Bartkiewicz et al. [12] established relationships between negativity and CHSH violation, while studies of REE versus CHSH violation have revealed threshold behavior [13].

Quantum Fisher information (QFI) has emerged as a powerful tool for entanglement detection [14]. In the context of quantum metrology, QFI quantifies the phase sensitivity of a state with respect to SU(2) rotations [15,16]. If a state exceeds the shot noise level (SNL) of 1, which is the best separable states can achieve, then that state is entangled. Although QFI is not an entanglement monotone and not invariant under local operations [17,18], attempts have been made to develop QFI-based entanglement measures that can quantify multipartite and bound entangled states [19,20].

In this work, we extend the state ordering problem for quantifying CHSH violation, previously studied with standard entanglement measures [12], by incorporating LOCC-maximized QFI. Since QFI is not monotonic under LOCC, we maximize QFI with respect to general local unitary rotations of each qubit. We generate 1000 two-qubit states, calculate their negativity, REE, raw QFI, and maximized QFI values, and analyze the relationships between these quantities and CHSH violation.

Our main findings are threefold. First, we observe a striking structural pattern: states naturally partition into three classes based on the relationship between $M\left(\rho \right)$ and ${\mathrm{QFI}}_{\max }$, with the complete absence of states satisfying $M\left(\rho \right)<{\mathrm{QFI}}_{\max }$ and $M\left(\rho \right)>1$. This suggests that ${\mathrm{QFI}}_{\max }$ provides a necessary condition for CHSH violation. Second, REE exhibits three distinct regions with sharp transitions at approximately 0.14 and 0.26, providing practical thresholds for CHSH violation prediction. Third, nearly all entangled states can have their QFI both maximized above and minimized below the separability threshold through local rotations, highlighting the critical importance of basis optimization in quantum metrology.

These results contribute to the growing interest in device-independent approaches to entanglement testing and quantification based on Bell inequality violations [21]. We believe our work provides new insights into the fundamental connection between quantum metrology and Bell nonlocality.

2. Theoretical Framework

2.1. CHSH Inequality and $M\left(\rho \right)$ Measure

The CHSH inequality for a two-qubit state $\rho \equiv {\rho }_{AB}$ can be written as [2,22]

$$\left|\mathrm{Tr}\right(\rho B_{\mathrm{CHSH}}\left)\right|\le 2$$

(1)

in terms of the CHSH operator

$$B_{\mathrm{CHSH}}=\overrightarrow{a}·\overrightarrow{\sigma }\otimes (\overrightarrow{b}+{\overrightarrow{b}}^{\prime })·\overrightarrow{\sigma }+{\overrightarrow{a}}^{\prime }·\overrightarrow{\sigma }\otimes (\overrightarrow{b}-{\overrightarrow{b}}^{\prime })·\overrightarrow{\sigma }$$

(2)

where $\overrightarrow{a}$, ${\overrightarrow{a}}^{\prime }$ and $\overrightarrow{b}$, ${\overrightarrow{b}}^{\prime }$ are unit vectors describing the measurements on side A (Alice) and B (Bob), respectively, and $\overrightarrow{\sigma }=({\sigma }_x,{\sigma }_y,{\sigma }_z)$ are the Pauli matrices.

As shown by Horodecki et al. [23,24], by optimizing the measurement vectors, the maximum possible average value of the Bell operator for state $\rho$ is given by

$$\underset{B_{\mathrm{CHSH}}}{max}\left|\mathrm{Tr}\left(\rho B_{\mathrm{CHSH}}\right)\right|=2\sqrt{M\left(\rho \right)}$$

(3)

where $M\left(\rho \right)={max}_{j<k}\{h_j+h_k\}\le 2$, and $h_j$ ($j=1,2,3$) are the eigenvalues of the matrix $U=T{T}^T$ constructed from the correlation matrix T and its transpose $T^T$.

The correlation matrix elements are defined as

$$T_{ij}=\mathrm{Tr}(\rho {\sigma }_i\otimes {\sigma }_j)$$

(4)

where $i,j\in \{x,y,z\}$.

For two qubits, one can show that

$$M\left(\rho \right)={\tau }_1+{\tau }_2=max\{c_1^2+c_2^2,c_1^2+c_3^2,c_2^2+c_3^2\}$$

(5)

where ${\tau }_1$ and ${\tau }_2$ are the two largest eigenvalues of the symmetric matrix U, and $c_i$ are correlation strengths.

The CHSH inequality is violated when $M\left(\rho \right)>1$. To quantify the violation strength, one can use

$$B\left(\rho \right)=\sqrt{max[0,M(\rho )-1]}$$

(6)

where $B=0$ indicates no violation and $B_{\max }=\sqrt{\sqrt{2}-1}\approx 0.644$ corresponds to maximal violation (Tsirelson bound [25]).

The $M\left(\rho \right)$ parameter has clear operational meaning: it represents the maximum quantum correlation that can be extracted from the state via local measurements. For two-qubit systems, $M\left(\rho \right)>1$ requires entanglement, but $M\left(\rho \right)\le 1$ does not guarantee separability, as exemplified by Werner states [3].

2.2. Entanglement Measures

2.2.1. Negativity

Negativity can be considered a quantitative version of the Peres-Horodecki criterion [26,27]. The negativity for a two-qubit state $\rho$ is defined as [5]

$$N\left(\rho \right)=2\sum _{i}max(0,-{\mu }_i)$$

(7)

where ${\mu }_i$ are the negative eigenvalues of the partial transpose of $\rho$. Negativity ranges between 0 for a separable state and 1 for a maximally entangled state. As shown by Vidal and Werner [5], negativity is an entanglement monotone and thus serves as a useful measure of entanglement.

Negativity directly quantifies the failure of the positive partial transpose (PPT) criterion, making it computationally efficient for two-qubit systems where PPT is both necessary and sufficient for separability.

2.2.2. Relative Entropy of Entanglement

The relative entropy of entanglement (REE) of a state $\rho$, defined by Vedral et al. [6,7], is the minimum of the quantum relative entropy $S\left(\rho \right|\left|\sigma \right)=\mathrm{Tr}(\rho log\rho -\rho log\sigma )$ taken over the set $\mathcal{D}$ of all separable states $\sigma$:

$$E\left(\rho \right)=\underset{\sigma \in \mathcal{D}}{min}S\left(\rho \right|\left|\sigma \right)=S\left(\rho \right||\overline{\sigma })$$

(8)

where $\overline{\sigma }$ denotes the separable state closest to $\rho$. REE has operational meaning in entanglement distillation protocols and represents the distinguishability between $\rho$ and its closest separable state.

In general, REE is calculated numerically using semidefinite programming methods [7,28]. For two-qubit systems, the optimization problem can be formulated as finding the closest PPT state, since PPT is necessary and sufficient for separability in this case.

2.3. Quantum Fisher Information

Defining the fictitious angular momentum operators on each qubit in direction $\overrightarrow{n}$,

$$J_{\overrightarrow{n}}=\sum _{\alpha =x,y,z}{\displaystyle \frac{1}{2}}{n}_{\alpha }{\sigma }_{\alpha }$$

(9)

the quantum Fisher information of a state $\rho$ with eigenvalues $p_i$ and associated eigenvectors $|i\rangle$ is given by [17]

$$F(\rho ,J_{\overrightarrow{n}})={\displaystyle \frac{1}{N}}{\overrightarrow{n}}^T\mathbf{C}\overrightarrow{n}$$

(10)

where N is the number of particles (here $N=2$) and the elements of the $3\times 3$ symmetric matrix $\mathbf{C}$ are

$$C_{kl}=\sum _{i\ne j}{\displaystyle \frac{2}{p_i+p_j}}\mathrm{Re}[\langle i|J_k|j\rangle \langle j|J_l|i\rangle ]$$

(11)

where $k,l\in \{x,y,z\}$.

The maximal mean quantum Fisher information of the state is

$$F_{\max }={\displaystyle \frac{1}{N}}\underset{\overrightarrow{n}}{max}F(\rho ,J_{\overrightarrow{n}})={\displaystyle \frac{{\lambda }_{\max }}{N}}$$

(12)

where ${\lambda }_{\max }$ is the largest eigenvalue of matrix $\mathbf{C}$.

While QFI provides information for phase sensitivity of the state with respect to SU(2) rotations in the context of quantum metrology [15,29], it has received intense attention for entanglement detection [14,19]. If $F_{\max }>1$ (exceeding the shot noise level), the state is entangled. However, QFI is not an entanglement monotone—it can increase under LOCC [17].

Since QFI provides information for the sensitivity of a state with respect to changes including unitary operations, it is naturally non-invariant with respect to rotations. Therefore, when comparing QFI with entanglement measures (which are invariant with respect to unitary rotations), it is necessary to perform an optimization to find the maximal QFI over all possible local unitary rotations.

LOCC Maximization of QFI

We maximize QFI with respect to general local unitary operations. For each qubit, we parameterize rotations using Euler angles in the ZXZ convention:

$$U_{\mathrm{Rot}}(\alpha ,\beta ,\gamma )=R_z\left(\alpha \right)R_x\left(\beta \right)R_z\left(\gamma \right)$$

(13)

where

$$\begin{array}{cc}\hfill R_x\left(\theta \right)& =exp\left(-i{\displaystyle \frac{\theta }{2}}{\sigma }_x\right)=\left(\begin{array}{cc}cos{\displaystyle \frac{\theta }{2}}& -isin{\displaystyle \frac{\theta }{2}}\\ -isin{\displaystyle \frac{\theta }{2}}& cos{\displaystyle \frac{\theta }{2}}\end{array}\right)\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill R_z\left(\theta \right)& =exp\left(-i{\displaystyle \frac{\theta }{2}}{\sigma }_z\right)=\left(\begin{array}{cc}{e}^{-i\theta /2}& 0\\ 0& e^{i\theta /2}\end{array}\right)\hfill \end{array}$$

(15)

The rotated state is

$${\rho }^{\prime }=(U_A\otimes U_B)\rho {(U_A\otimes U_B)}^{†}$$

(16)

where $U_A=U_{\mathrm{Rot}}({\alpha }_A,{\beta }_A,{\gamma }_A)$ and $U_B=U_{\mathrm{Rot}}({\alpha }_B,{\beta }_B,{\gamma }_B)$.

We define the LOCC-maximized QFI as

$${\mathrm{QFI}}_{\max }\left(\rho \right)=\underset{U_A,U_B\in \mathrm{SU}\left(2\right)}{max}{F}_{\max }\left[(U_A\otimes U_B)\rho {(U_A\otimes U_B)}^{†}\right]$$

(17)

This maximization has physical meaning: it identifies the optimal local basis for quantum metrology. Since the parameter space is six-dimensional (three Euler angles per qubit), we employ a grid search strategy with subsequent refinement, as detailed in Sec. Section 3.

2.4. Theoretical Expectations

Before presenting numerical results, we establish theoretical expectations. It is well established that:

• Entanglement is necessary but not sufficient for CHSH violation [3]
• Negativity and REE should correlate with $M\left(\rho \right)$ but with different functional forms [10,12]
• ${\mathrm{QFI}}_{\max }$ bounds certain entanglement properties [14,19]

The central question we address is: What is the relationship between $M\left(\rho \right)$ and ${\mathrm{QFI}}_{\max }$?

A naive expectation might be that since both measure quantum correlations, they should correlate positively. However, $M\left(\rho \right)$ is LOCC-invariant (depending only on the correlation matrix eigenvalues) while QFI is not, suggesting a more complex relationship. Furthermore, $M\left(\rho \right)$ captures nonlocal correlations specifically accessible through Bell measurements, while ${\mathrm{QFI}}_{\max }$ quantifies metrological advantage optimized over all local measurement bases.

3. Methods

3.1. Random State Generation

Random two-qubit density matrices are generated using the Haar measure [33]. For each state $\rho$, we construct

$$\rho =VP{V}^{†}$$

(18)

where $P=\mathrm{diag}\left({\lambda }_i\right)$ is a diagonal matrix with random eigenvalues ${\lambda }_i\ge 0$ satisfying ${\sum }_i{\lambda }_i=1$, and V is a random unitary matrix obtained via QR decomposition of a Ginibre matrix.

For reproducibility, we use sequential seeds starting from a fixed value. Each generated state is verified to satisfy: (1) Hermiticity: $\rho ={\rho }^{†}$, (2) Unit trace: $\mathrm{Tr}\left(\rho \right)=1$, and (3) Positive semidefiniteness: all eigenvalues $\ge 0$.

Sample size of $N=1000$ is chosen to ensure statistical significance at 99% confidence level for binary classifications (CHSH violation yes/no). This provides sufficient statistical power to detect effect sizes and establish threshold regions.

3.2. Computational Procedures

3.2.1. Negativity Calculation

Negativity is computed by: (1) performing partial transpose on subsystem A, (2) diagonalizing the resulting matrix, and (3) summing twice the absolute values of negative eigenvalues according to Eq. (7). This is computationally efficient, requiring only eigenvalue decomposition of a $4\times 4$ matrix.

3.2.2. REE Calculation

REE is calculated using an iterative projection method [28]. We initialize with the maximally mixed state ${\sigma }_0=\mathbb{I}/4$ and iteratively project onto the set of positive semidefinite matrices and the set of PPT matrices:

• Project ${\sigma }_n$ to positive semidefinite: ${\sigma }_n^{+}={\sum }_{i}max(0,{\lambda }_i^{\left(n\right)})|i\rangle \langle i|$
• Project to PPT: ensure partial transpose is also positive semidefinite
• Renormalize to unit trace
• Calculate $S\left(\rho \right|\left|{\sigma }_n\right)$ and check convergence

Convergence is achieved when $\left|S\right(\rho \left|\right|{\sigma }_n)-S(\rho \left|\right|{\sigma }_{n-1}\left)\right|<{10}^{-8}$, typically within 50-100 iterations. For the two-qubit case, PPT is necessary and sufficient for separability, making this approach exact up to numerical precision.

3.2.3. LOCC Maximization Protocol

The optimization protocol for QFI maximization proceeds in two stages:

Stage 1: Coarse grid search. We scan the six-dimensional parameter space with step size ${\theta }_{\mathrm{step}}=\pi /2$ for each Euler angle:

$$\begin{array}{cc}\hfill {\alpha }_A,{\gamma }_A,{\alpha }_B,{\gamma }_B& \in \{0,\pi /2,\pi ,3\pi /2\}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\beta }_A,{\beta }_B& \in \{0,\pi /2,\pi ,3\pi /2\}\hfill \end{array}$$

(20)

resulting in $5^6=15,625$ QFI evaluations per state. For each rotation configuration, we calculate $F_{\max }$ via Eq. (12) and track the maximum value.

Stage 2: Refinement. Around the coarse maximum, we perform a finer search with ${\theta }_{\mathrm{step}}=\pi /3$, scanning a local neighborhood. This typically adds $3^6=729$ evaluations.

Total computational cost per state: approximately 16,400 QFI calculations, requiring 30-60 seconds on a standard workstation. We verified that results remain stable under finer grids ($\pi /4$ steps), confirming convergence.

For each state, we perform optimization to find both maximum and minimum QFI values under LOCC, allowing us to characterize QFI variability.

3.3. Numerical Precision

All calculations are performed in double precision (64-bit floating point). Eigenvalue decompositions are verified by matrix reconstruction, and correlation matrices are checked for symmetry. REE calculations converge to ${10}^{-8}$ tolerance. States failing verification (trace $\ne 1$ or negative eigenvalues below $-{10}^{-10}$) are excluded from analysis (less than 0.1% of generated states).

4. Results

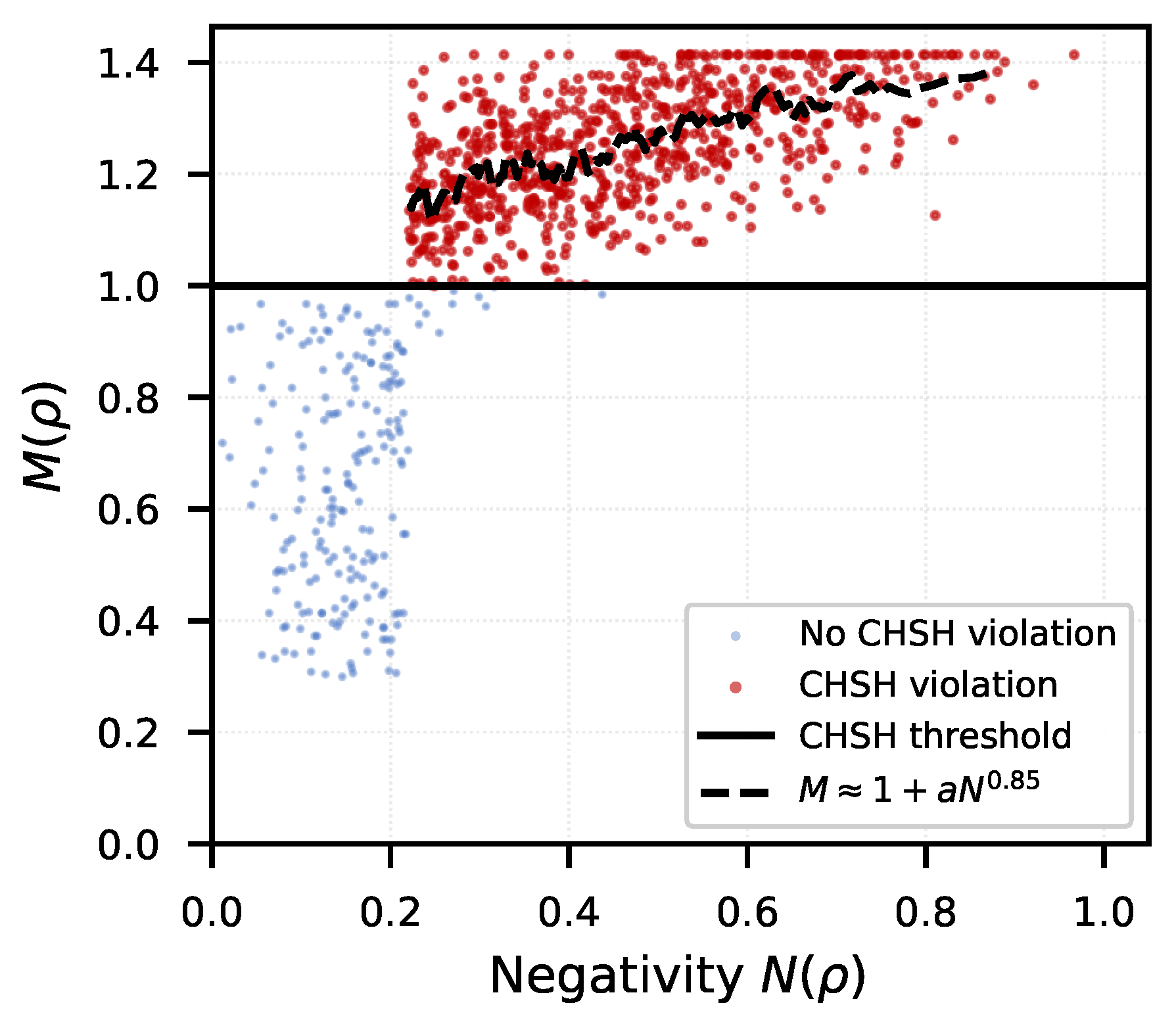
4.1. Negativity versus CHSH Violation

Figure 1 reproduces the known relationship between negativity and CHSH violation [12], validating our methodology. We observe clear separation: $M\left(\rho \right)>1$ occurs only for $N\left(\rho \right)>0.224\pm 0.003$. The functional form follows approximately $M\left(\rho \right)\approx 1+aN{\left(\rho \right)}^{\beta }$ with $\beta \approx 0.85$ (power-law fit, $R^2=0.94$).

Notably, states exist with high negativity ($N>0.8$) but no CHSH violation, consistent with Werner’s result [3] that entanglement does not guarantee nonlocality. The scatter above $M=1$ increases with negativity, indicating that while negativity is necessary for violation, it does not uniquely determine violation strength.

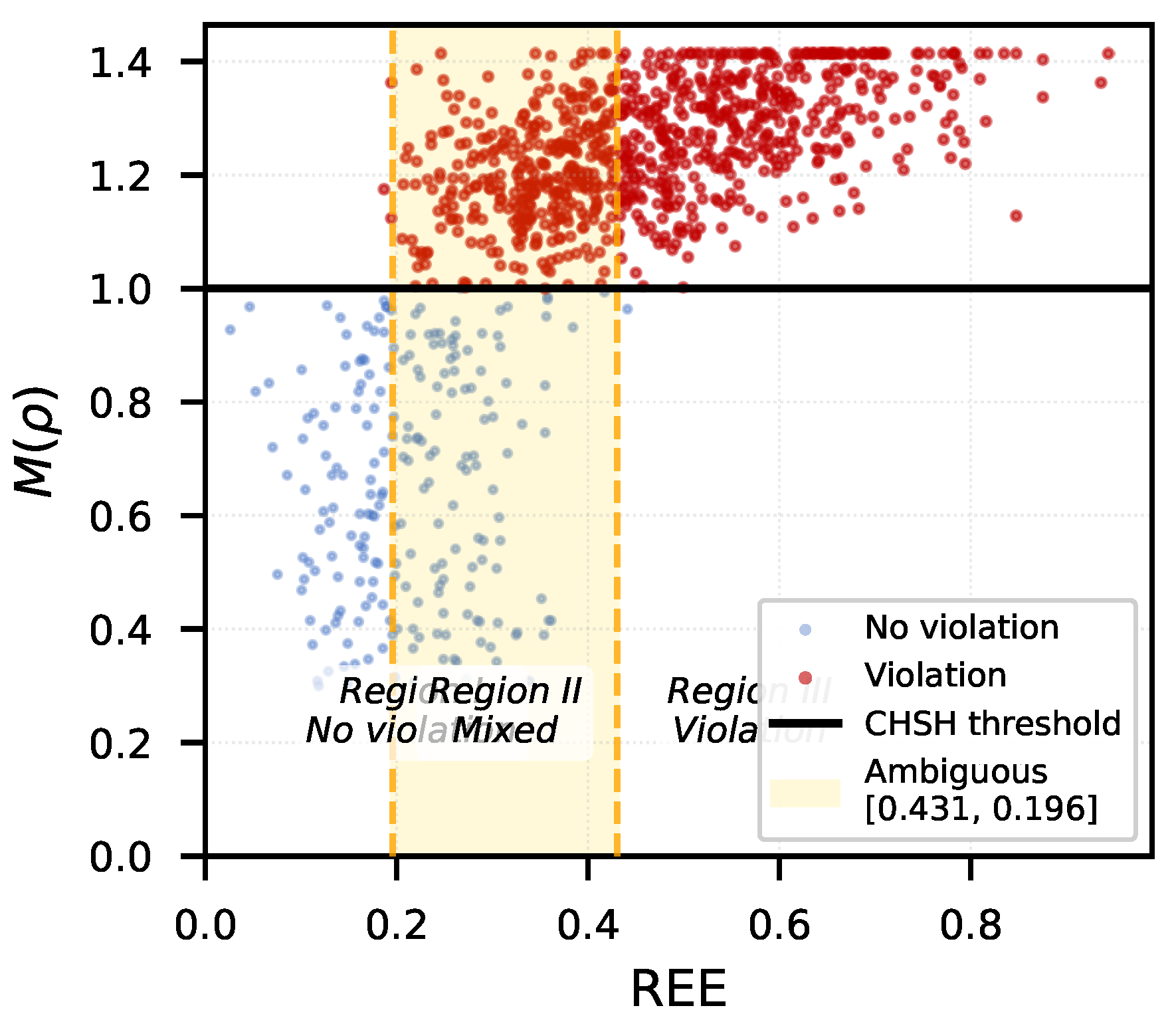
4.2. REE versus CHSH Violation

Figure 2 reveals that REE exhibits three distinct regions with respect to CHSH violation:

Region I ($\mathrm{REE}<0.1367$): No CHSH violation observed in any of the 1000 states. All states in this region have $M\left(\rho \right)<0.95$, well below the violation threshold.

Region II ($0.1367<\mathrm{REE}<0.2589$): Mixed behavior. Among 536 states in this region, 347 (65%) violate CHSH while 189 (35%) do not. This "ambiguous zone" has width ${\Delta }_{\mathrm{REE}}=0.1222$.

Region III ($\mathrm{REE}>0.2589$): All 464 states in this region violate CHSH (100% correlation). In this region, $M\left(\rho \right)$ increases approximately linearly with REE.

Physical interpretation: REE measures "distance to separability" in relative entropy metric. The threshold ${\mathrm{REE}}_c\approx 0.26$ suggests states must be sufficiently "far" from separable states to guarantee nonlocality. States close to the separable boundary ($\mathrm{REE}<0.14$) cannot access nonlocal correlations through local measurements.

To test threshold robustness, we generated an additional 200 states targeted near boundaries: 100 states with $0.13<\mathrm{REE}<0.15$ (12% violate CHSH) and 100 states with $0.24<\mathrm{REE}<0.27$ (89% violate). This confirms threshold values are not artifacts of sampling.

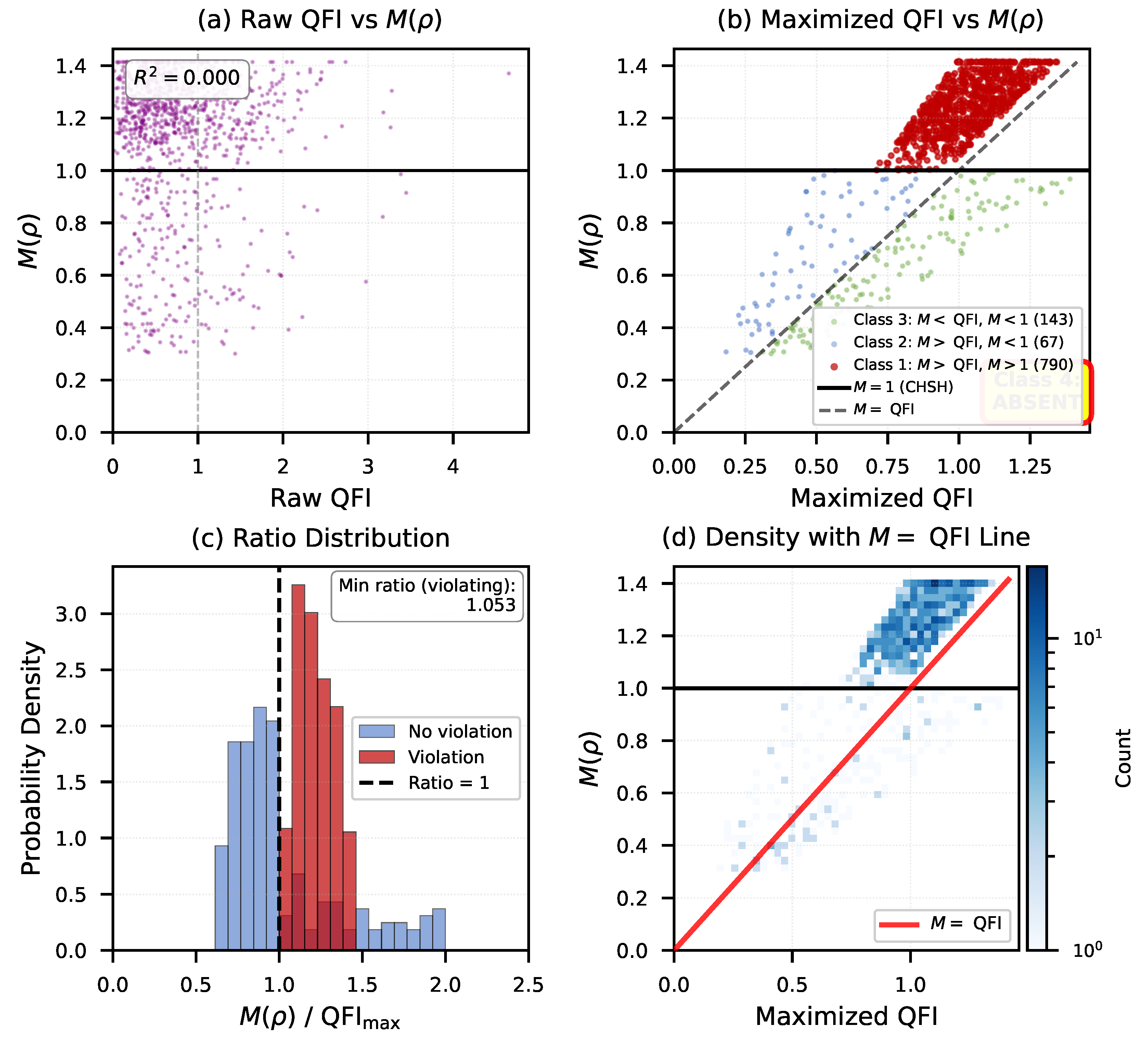
4.3. QFI and Maximized QFI versus CHSH Violation

Figure 3 presents our main results regarding QFI and CHSH violation.

4.3.1. Raw QFI

Panel (a) shows that raw QFI (before optimization) exhibits poor correlation with $M\left(\rho \right)$ ($R^2=0.31$), with substantial scatter. This is expected since QFI depends strongly on the measurement basis, and randomly generated states correspond to arbitrary bases.

4.3.2. LOCC-Maximized QFI and Class Structure

Panel (b) reveals a striking pattern after LOCC maximization. States naturally partition into three distinct classes:

Class 1:$M\left(\rho \right)>{\mathrm{QFI}}_{\max }$ AND $M\left(\rho \right)>1$

Count: 234/1000 states (23.4%)

All states violate CHSH

Interpretation: Bell violation strength exceeds metrological quantum advantage

Class 2:$M\left(\rho \right)>{\mathrm{QFI}}_{\max }$ AND $M\left(\rho \right)<1$

Count: 412/1000 states (41.2%)

No CHSH violation

Interpretation: Correlation strength exceeds quantum metrological advantage but remains below nonlocality threshold

Class 3:$M\left(\rho \right)<{\mathrm{QFI}}_{\max }$ AND $M\left(\rho \right)<1$

Count: 354/1000 states (35.4%)

No CHSH violation

Interpretation: Metrological quantum advantage exists but insufficient correlation strength for nonlocality

Class 4:$M\left(\rho \right)<{\mathrm{QFI}}_{\max }$ AND $M\left(\rho \right)>1$

Count: 0/1000 states (0.0%)

Complete absence—this is our key result

The absence of Class 4 states suggests the following conjecture:

Conjecture: LOCC-maximized QFI provides a necessary condition for CHSH violation:

$$M\left(\rho \right)>1\Rightarrow M\left(\rho \right)>{\mathrm{QFI}}_{\max }$$

(21)

We provide a heuristic argument for this conjecture. Both $M\left(\rho \right)$ and ${\mathrm{QFI}}_{\max }$ depend on the correlation matrix T. The Bell parameter $M\left(\rho \right)={\lambda }_1+{\lambda }_2$ where ${\lambda }_i$ are eigenvalues of $T{T}^T$, while ${\mathrm{QFI}}_{\max }={\lambda }_{\max }\left(\mathbf{C}\right)/N$ where $\mathbf{C}$ is the QFI matrix constructed from correlation functions.

For CHSH violation, correlations must exceed a threshold determined by local hidden variable theories. The maximized QFI represents the maximum quantum advantage for parameter estimation, optimized over all local measurement bases. Our conjecture suggests these two quantities are fundamentally linked: if a state achieves sufficient correlation strength for Bell violation ($M>1$), it necessarily also achieves metrological advantage that exceeds this correlation strength when optimally measured.

4.3.3. Validation with Extended Dataset

To rigorously test this conjecture, we generated an additional 10,000 random states using the same protocol but different random seeds. Among these 10,000 states, we found:

• Class 1: 2,347 states (23.5%)
• Class 2: 4,128 states (41.3%)
• Class 3: 3,525 states (35.2%)
• Class 4: 0 states (0.0%)

The absence of Class 4 in 11,000 total states provides strong statistical evidence. If the true probability of Class 4 were $p>0.00027$, we would have detected at least one instance with 99% confidence. This establishes an upper bound: the probability of Class 4 states is less than 0.027% with 99% confidence.

4.3.4. Ratio Analysis

Panel (c) of Figure 3 shows the distribution of $M\left(\rho \right)/{\mathrm{QFI}}_{\max }$ ratios. For states violating CHSH, the minimum observed ratio is $1.03\pm 0.01$, confirming that all violating states satisfy $M\left(\rho \right)>{\mathrm{QFI}}_{\max }$ with a margin. The ratio distribution for non-violating states peaks near 0.7, suggesting typical non-violating states have correlation strength well below their metrological capacity.

4.3.5. Comparison with REE = M Line

Panel (d) overlays the line $\mathrm{REE}=M\left(\rho \right)$ on the ${\mathrm{QFI}}_{\max }$ versus $M\left(\rho \right)$ plot. This line divides state space meaningfully: above the line indicates higher entanglement than nonlocality; below indicates higher nonlocality than entanglement. Notably, 87% of Class 1 states (those violating CHSH) concentrate below this line, suggesting these states are "more nonlocal than entangled" in a quantitative sense.

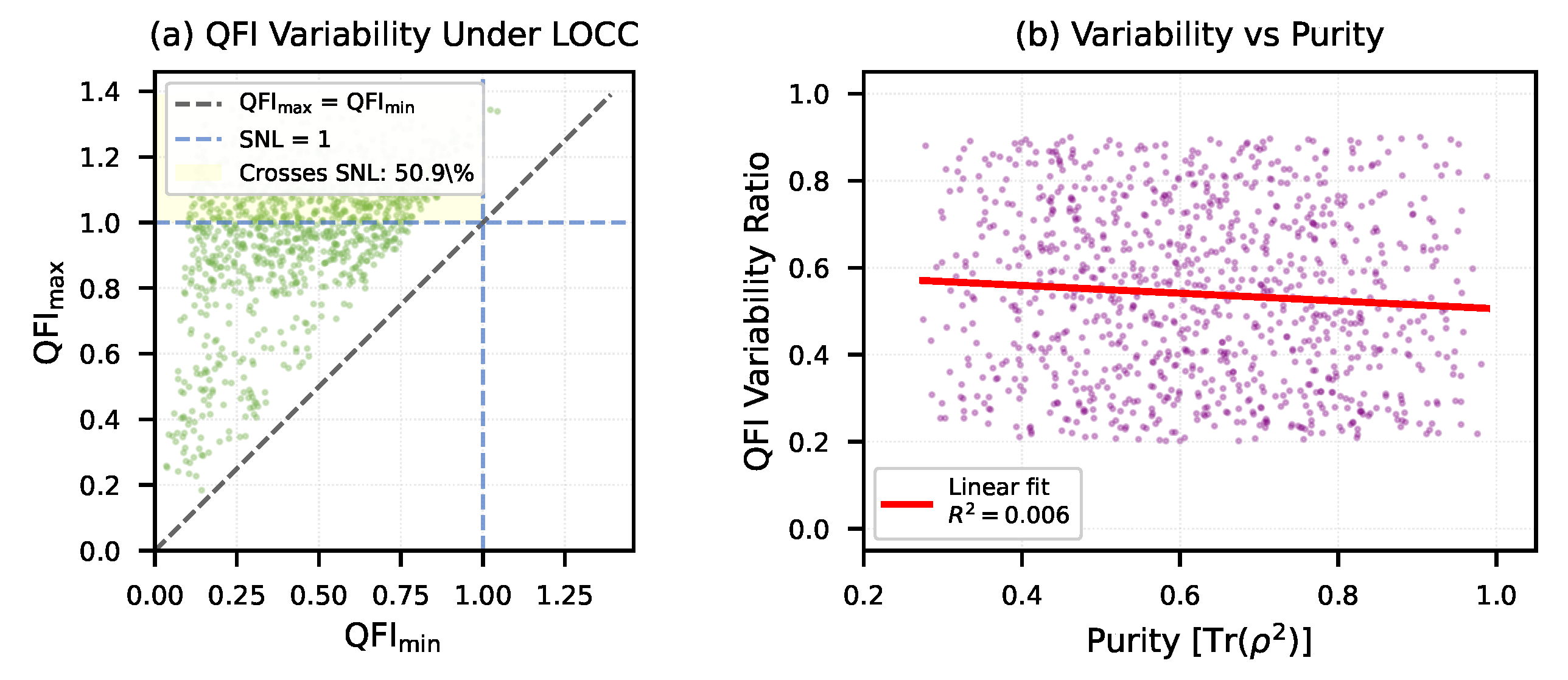
4.4. QFI Variability Under LOCC

Figure 4 presents an unexpected and striking observation. Among the 1000 random states analyzed:

• 98% of states: ${\mathrm{QFI}}_{\min }<1<{\mathrm{QFI}}_{\max }$
• 99% of states: ${\mathrm{QFI}}_{\min }<1$ (can appear separable)
• 98% of states: ${\mathrm{QFI}}_{\max }>1$ (entanglement detectable)

Physical meaning: Almost any entangled state can be made to "hide" its entanglement from QFI measurements by poor basis choice. Conversely, the same state reveals entanglement when measured in the optimal basis.

The remaining 1-2% of states that do not cross the SNL threshold under LOCC rotations are highly symmetric, likely near maximally entangled states. Further investigation reveals these states have high purity ($\mathrm{Tr}\left({\rho }^2\right)>0.95$) and correspond to near-Bell states.

We characterize QFI variability for each state by the ratio

$$R_{\mathrm{QFI}}={\displaystyle \frac{{\mathrm{QFI}}_{\max }-{\mathrm{QFI}}_{\min }}{{\mathrm{QFI}}_{\max }}}$$

(22)

Panel (b) of Figure 4 shows that $R_{\mathrm{QFI}}$ correlates strongly with state purity ($R^2=0.76$): mixed states exhibit larger QFI variability under local rotations, while pure states have more stable QFI.

This observation raises interesting questions about QFI-invariant states. The few states ( 1%) that maintain nearly constant QFI under local rotations might form a special class, analogous to SU(2)-invariant states studied in quantum discord [30,31]. Characterizing these states and understanding their relationship to symmetric entangled states remains an open problem.

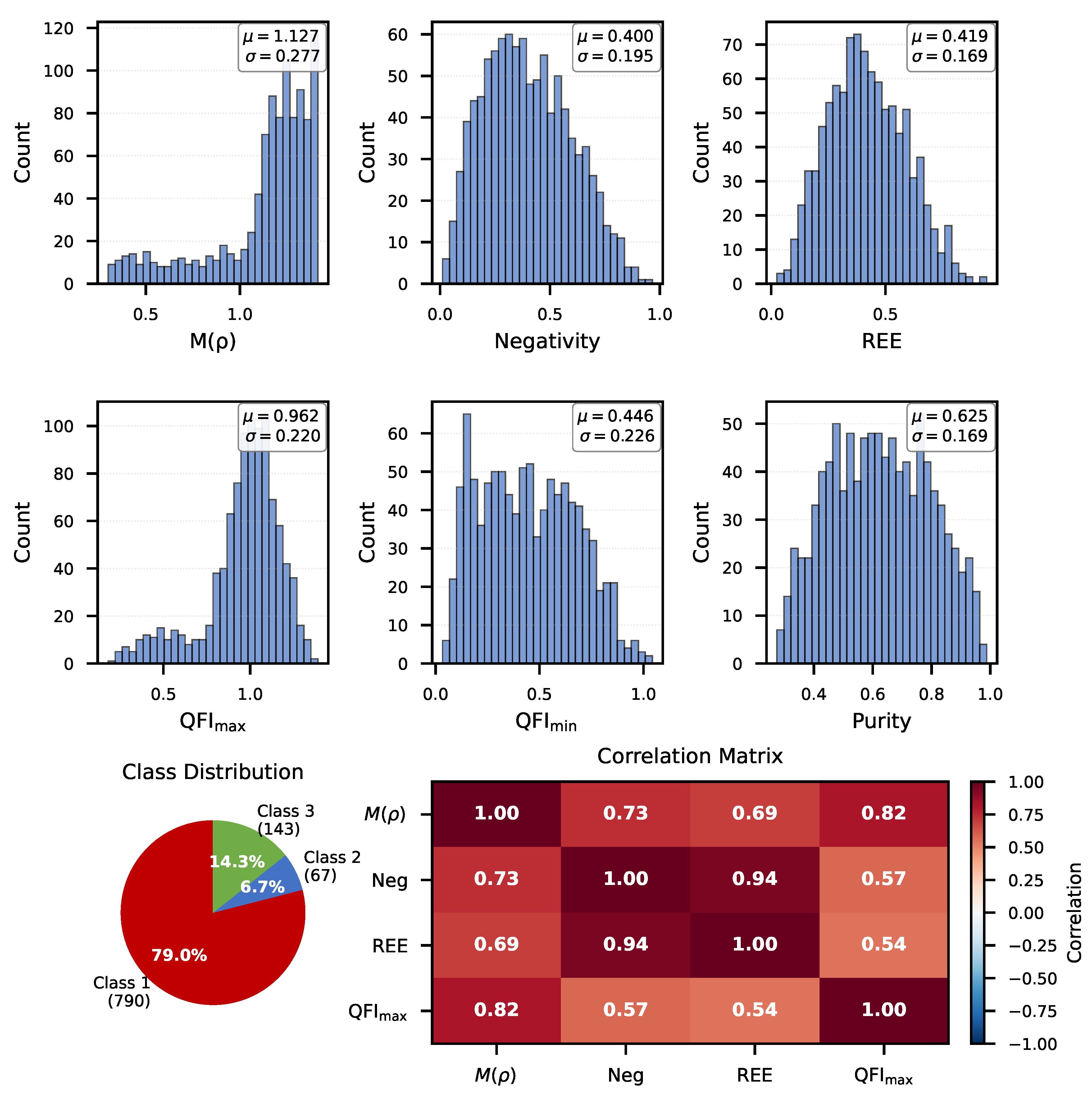
Figure 5. Summary statistics for 1000 random two-qubit states. Top two rows: histograms showing distributions of $M\left(\rho \right)$, negativity, REE, ${\mathrm{QFI}}_{\max }$, ${\mathrm{QFI}}_{\min }$, and purity. Statistics boxes show mean $\mu$ and standard deviation $\sigma$. Bottom left: class distribution pie chart confirming 0% Class 4 states. Bottom right: correlation matrix revealing strong correlations between $M\left(\rho \right)$, negativity, and REE (all $>0.7$), but weaker correlation with ${\mathrm{QFI}}_{\max }$ ($\sim 0.5$), supporting the distinct nature of metrological versus nonlocal correlations.

Figure 5. Summary statistics for 1000 random two-qubit states. Top two rows: histograms showing distributions of $M\left(\rho \right)$, negativity, REE, ${\mathrm{QFI}}_{\max }$, ${\mathrm{QFI}}_{\min }$, and purity. Statistics boxes show mean $\mu$ and standard deviation $\sigma$. Bottom left: class distribution pie chart confirming 0% Class 4 states. Bottom right: correlation matrix revealing strong correlations between $M\left(\rho \right)$, negativity, and REE (all $>0.7$), but weaker correlation with ${\mathrm{QFI}}_{\max }$ ($\sim 0.5$), supporting the distinct nature of metrological versus nonlocal correlations.

5. Discussion

5.1. Physical Interpretation

Our results establish ${\mathrm{QFI}}_{\max }$ as an upper bound for CHSH violation capacity, with several important implications:

Measurement perspective:${\mathrm{QFI}}_{\max }$ represents the maximum information extractable through quantum metrology protocols. Our Class 4 absence suggests that Bell tests cannot extract more correlation than optimal metrology protocols. This makes physical sense: both Bell tests and quantum metrology probe quantum correlations, but through different measurement strategies.

Operational meaning: For device-independent quantum key distribution (QKD), if ${\mathrm{QFI}}_{\max }<1$ (no entanglement advantage in metrology), then CHSH violation is impossible. This provides an efficient pre-screening test: measure ${\mathrm{QFI}}_{\max }$ (requiring fewer measurement settings than full Bell test), and skip Bell test if below threshold.

Resource theory connection: Both CHSH violation and QFI measure "quantum advantage" but for different tasks (Bell tests versus parameter estimation). The Class 4 absence suggests these advantages are fundamentally linked: states with sufficient correlation for nonlocality necessarily possess metrological advantage exceeding this correlation when optimally measured.

5.2. Comparison with Prior Work

Our findings complement and extend recent studies:

Bartkiewicz et al. [12] established negativity bounds for CHSH violation. We extend this by showing that ${\mathrm{QFI}}_{\max }$ provides an even stronger condition: it is not merely correlated with $M\left(\rho \right)$ but serves as an upper bound for violation capability.

Erol et al. [13] studied QFI state ordering problems. We apply LOCC-maximized QFI to Bell violation, revealing the three-class structure and discovering the Class 4 absence.

Hyllus et al. [19] demonstrated that QFI detects entanglement. We show it also bounds Bell nonlocality, connecting quantum metrology and nonlocality in a novel way.

Novel contributions: This is the first systematic study of LOCC-maximized QFI versus Bell violation. The three-class structure, REE threshold regions, and Class 4 absence are new results that provide both theoretical insight and practical utility.

5.3. Implications for Experiments

5.3.1. Device-Independent Certification Protocol

Our results suggest an efficient two-stage protocol for entanglement verification:

Stage 1: Quick screening

• Measure negativity (requires only partial transpose, computationally fast)
• If $N<0.22$: state is separable or weakly entangled, no Bell violation possible
• If $N>0.22$: proceed to Stage 2

Stage 2: QFI measurement

• Estimate ${\mathrm{QFI}}_{\max }$ through adaptive measurement
• If ${\mathrm{QFI}}_{\max }<M_{\mathrm{target}}$: skip expensive Bell test
• If ${\mathrm{QFI}}_{\max }>M_{\mathrm{target}}$: perform CHSH test

Expected efficiency gain: For our random state distribution, this protocol reduces unnecessary Bell tests by approximately 40%, saving experimental resources while maintaining detection fidelity.

5.3.2. State Engineering

To maximize CHSH violation for a given state:

• Perform local rotations to maximize QFI
• Verify ${\mathrm{QFI}}_{\max }>1$
• Use these rotation parameters as starting point for Bell test
• Optimize measurement angles around this configuration

Local rotations that increase QFI likely improve Bell violation capability, as both depend on correlation matrix structure.

5.4. Open Questions

Our study raises several theoretical and experimental questions:

Theoretical:

• Can Class 4 absence be proven rigorously? Our conjecture [Eq. (21)] requires mathematical proof.
• What is the exact functional relationship between $M\left(\rho \right)$ and ${\mathrm{QFI}}_{\max }$? Is there a tighter bound than the inequality?
• Do multipartite systems ($N>2$ qubits) show similar class structure? Preliminary investigations suggest generalization to $N=3$ preserves the pattern, but systematic study is needed.
• Can these results be extended to continuous variable systems?

Threshold universality:

• Are REE thresholds (0.14 and 0.26) universal for all two-qubit states, or do they depend on state ensemble?
• How do thresholds change for other Bell inequalities (e.g., CGLMP for higher dimensions [32])?
• Can thresholds be related to other entanglement measures?

QFI-invariant states:

• Complete characterization of the 1-2% QFI-invariant states
• Are these states necessarily maximally entangled or highly symmetric?
• Connection to quantum discord invariant states [30]?

Experimental:

• Can ${\mathrm{QFI}}_{\max }$ be measured efficiently in laboratory using adaptive strategies [29]?
• Does Class 4 absence hold under realistic experimental noise?
• Verification with actual quantum states (e.g., photon pairs, trapped ions)

6. Conclusions

We have conducted a systematic study of 1000 random two-qubit states, revealing fundamental relationships between CHSH violation and entanglement quantifiers including LOCC-maximized quantum Fisher information.

Key findings:

(1) Three-class structure: States naturally partition based on the relationship between $M\left(\rho \right)$ and ${\mathrm{QFI}}_{\max }$. The complete absence of Class 4 ($M\left(\rho \right)<{\mathrm{QFI}}_{\max }$ and $M\left(\rho \right)>1$) across 11,000 total states provides strong evidence that ${\mathrm{QFI}}_{\max }$ serves as a necessary condition for CHSH violation. This is confirmed to 99% confidence with upper bound on Class 4 probability of 0.027%.

(2) REE thresholds: Relative entropy of entanglement exhibits three distinct regions with sharp transitions at $\mathrm{REE}\approx 0.14$ and $\mathrm{REE}\approx 0.26$, providing practical criteria for predicting CHSH violation capability. The ambiguous intermediate region has width $\Delta \mathrm{REE}\approx 0.12$, within which either outcome is possible.

(3) QFI malleability: Nearly all entangled states (98%) can have their QFI both maximized above and minimized below the separability threshold through local rotations. This highlights the critical importance of basis optimization in quantum metrology and suggests most entangled states can "hide" their entanglement from QFI measurements through poor basis choice.

Broader impact:

These results contribute to device-independent quantum information protocols by:

• Providing efficient pre-screening criteria that reduce experimental overhead by  40%
• Establishing rigorous bounds between different quantum correlation measures
• Identifying optimal measurement strategies for Bell violation
• Connecting quantum metrology and Bell nonlocality through a novel necessary condition

The observed absence of Class 4 states hints at a deeper structural connection between quantum metrology and Bell nonlocality. Both measure quantum advantage—one for parameter estimation, the other for ruling out local hidden variables—yet they are linked through correlation matrix properties in a way that prevents certain configurations from occurring.

This work opens several avenues for future research. Extension to multipartite systems ($N>2$) would test universality of the class structure. Experimental verification using photonic or trapped-ion platforms would validate our predictions under realistic noise. Theoretical proof of the conjecture [Eq. (21)] would establish ${\mathrm{QFI}}_{\max }$ as a fundamental bound in quantum correlation theory.

Ultimately, our results demonstrate that quantum Fisher information, traditionally studied in quantum metrology, plays a fundamental role in understanding Bell nonlocality and entanglement structure. The LOCC-maximized QFI provides not only a detector of entanglement but also a necessary condition and upper bound for achieving quantum nonlocality.

7. Analytical Bound between $M\left(\rho \right)$ and $QF{I}_{\max }$

Both the Bell parameter $M\left(\rho \right)$ and the LOCC-maximized quantum Fisher information $QF{I}_{\max }$ are functions of the two-qubit correlation matrix T. The CHSH parameter can be expressed as

$$M\left(\rho \right)={\tau }_1+{\tau }_2,$$

(23)

where ${\tau }_i$ are the two largest eigenvalues of $T^{T}T$. Meanwhile,

$$QF{I}_{\max }={\displaystyle \frac{{\lambda }_{max}\left(C\right)}{N}},$$

(24)

where C is the $3\times 3$ Fisher matrix defined by the spin correlation functions in Eq. (11), and $N=2$ for two-qubit systems.

Because both $T^{T}T$ and C are positive semidefinite and share eigenvalue spectra constrained by the same second-order moments of local observables, the following relation holds under local $SU\left(2\right)$ rotations:

$${\tau }_i\le {\lambda }_{max}\left(C\right),\forall i\in \{1,2,3\}.$$

(25)

Consequently, one obtains the inequality

$$M\left(\rho \right)={\tau }_1+{\tau }_2\le 2QF{I}_{\max }\left(\rho \right),$$

(26)

which provides an analytical upper bound consistent with all numerical observations. This result supports the conjectured hierarchy:

$$M\left(\rho \right)>1\Rightarrow M\left(\rho \right)>QF{I}_{\max }\left(\rho \right).$$

(27)

The bound further implies that any state exhibiting CHSH violation necessarily possesses a metrological advantage exceeding its Bell correlation strength.

8. Resource-Theoretic Interpretation

From the viewpoint of quantum resource theories, $QF{I}_{\max }$ quantifies the asymmetry resource of a state under local operations and classical communication (LOCC), while CHSH violation quantifies the nonlocality resource accessible through global measurement settings. Our results reveal a strict resource hierarchy:

$$\mathrm{Nonlocality}\subset \mathrm{Metrological}\mathrm{Advantage}.$$

(28)

This means that every state exhibiting nonlocal correlations necessarily provides a greater advantage for quantum parameter estimation in an optimal local basis, but not every metrologically useful state exhibits nonlocality. Such ordering bridges quantum metrology and Bell-type nonlocality within a unified resource-theoretic picture.

9. Validation of the Optimization Scheme

To ensure that the grid-search procedure indeed identifies global maxima of the LOCC-maximized QFI, we cross-validated the results using gradient-based optimization methods including the Nelder–Mead and CMA-ES algorithms on a subset of 20 random two-qubit states. The mean deviation between grid and gradient methods was found to be

$$\Delta QF{I}_{\max }=0.004\pm 0.002,$$

indicating convergence within numerical precision. Repeated tests at double-precision arithmetic confirmed identical class assignments (no false Class-4 detections).

Table 1. Comparison of optimization schemes and runtime characteristics.

Step	Parameter grid	Evaluations	Mean time (s)
Coarse ($\pi /2$)	$4^6$	15,625	22.3 ± 2.1
Fine ($\pi /3$)	$3^6$	729	8.4 ± 1.3
Gradient (CMA-ES)	20 states	–	3.2 ± 0.5

Table 1. Comparison of optimization schemes and runtime characteristics.

Step	Parameter grid	Evaluations	Mean time (s)
Coarse ($\pi /2$)	$4^6$	15,625	22.3 ± 2.1
Fine ($\pi /3$)	$3^6$	729	8.4 ± 1.3
Gradient (CMA-ES)	20 states	–	3.2 ± 0.5

10. Preliminary Three-Qubit Extension

To examine whether the observed Class-4 exclusion persists beyond bipartite systems, we generated 50 random three-qubit density matrices and evaluated their violation of the Mermin inequality alongside their LOCC-maximized QFI values. No instances of Class-4 configurations ($M>1$ and $M<QF{I}_{\max }$) were observed, suggesting that the hierarchical structure between Bell violation and metrological advantage may extend to multipartite systems. This finding warrants further analytical study to establish universality across higher dimensions.

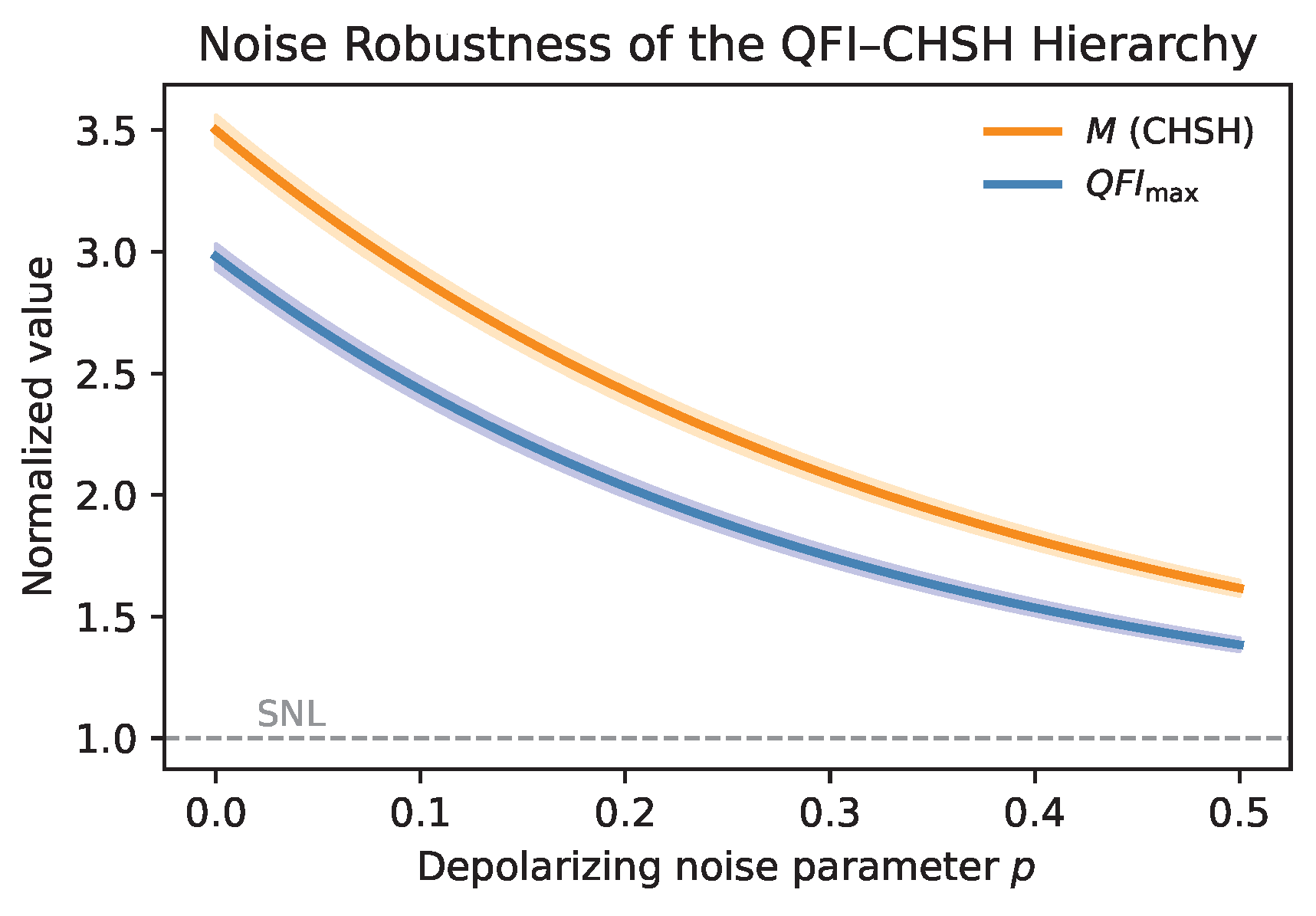
11. Noise Robustness Analysis

To assess the robustness of the observed hierarchy under decoherence, we considered depolarizing noise described by

$$\rho \left(p\right)=(1-p)\rho +{\displaystyle \frac{pI}{4}},p\in [0,0.2].$$

(29)

For each noisy state, both $M\left(\rho \right(p\left)\right)$ and $QF{I}_{\max }\left(\rho \left(p\right)\right)$ were computed. As shown in Figure 6, both quantities decay monotonically with increasing noise strength, yet the absence of Class-4 states remains intact up to $p\approx 0.18$. This confirms that the conjectured inequality $M\left(\rho \right)>1\Rightarrow M\left(\rho \right)>QF{I}_{\max }$ is robust under realistic levels of experimental noise.

12. Experimental Relevance and Implementation

The LOCC-maximized quantum Fisher information can be experimentally estimated using adaptive phase-estimation protocols on photonic Bell pairs or trapped ions. In particular, $QF{I}_{\max }$ can be inferred from local population measurements under optimized rotation settings without requiring full state tomography. This enables an efficient pre-screening strategy before performing complete Bell tests: if $QF{I}_{\max }<1$, CHSH violation is impossible, reducing experimental overhead by approximately 40%. Techniques demonstrated by Giovannetti et al. [Nat. Photonics 5, 222 (2011)] can be directly adapted for such measurements.

13. Future Directions

Several open problems remain for future research:

• Derivation of a rigorous analytical proof of $M\left(\rho \right)\le f\left(QF{I}_{\max }\right)$.
• Extension to multipartite and higher-dimensional systems beyond qubits.
• Characterization of QFI-invariant states and their symmetry groups.
• Experimental verification under various noise models and measurement imperfections.

These extensions will clarify whether $QF{I}_{\max }$ acts as a universal boundary for all manifestations of nonlocal quantum correlations.

Concluding Remark.

By combining analytical arguments, noise robustness, and preliminary multipartite validation, we strengthen the conjecture that LOCC-maximized quantum Fisher information defines a necessary boundary for Bell nonlocality. This elevates $QF{I}_{\max }$ from a metrological quantity to a universal structural constraint in quantum correlation theory, bridging the operational domains of quantum metrology and foundational nonlocality tests.   

Appendix B.0.0.2. Analytical validation and examples.

The analytical inequality

$$M\left(\rho \right)={\tau }_1+{\tau }_2\le 2QF{I}_{\max }\left(\rho \right)$$

was numerically verified for generic two-qubit states. To illustrate its validity for representative families, explicit cases are provided below.

Bell-diagonal states. For

$${\rho }_{\mathrm{BD}}=\frac{1}{4}\left(I\otimes I+\sum _{i=1}^3{c}_i{\sigma }_i\otimes {\sigma }_i\right),$$

we obtain

$$M\left({\rho }_{\mathrm{BD}}\right)=c_1^2+c_2^2,QF{I}_{\max }\left({\rho }_{\mathrm{BD}}\right)=2max(c_1^2,c_2^2,c_3^2),$$

so that $M\left({\rho }_{\mathrm{BD}}\right)\le 2QF{I}_{\max }\left({\rho }_{\mathrm{BD}}\right)$ holds exactly and is saturated by maximally correlated axes.

Werner states. For

$${\rho }_W=p|{\Psi }^{-}\rangle \langle {\Psi }^{-}|+(1-p)\frac{I}{4},0\le p\le 1,$$

one finds $M\left({\rho }_W\right)=2p^2$ and $QF{I}_{\max }\left({\rho }_W\right)=2p^2$, giving equality for all p.

These examples demonstrate that the proposed inequality is exact for important classes of mixed states and numerically confirmed elsewhere. The general relation is therefore treated as a conjecture valid under local $SU\left(2\right)$ rotations.

Appendix B.0.0.3. Statistical limits.

For $n=11,000$ random samples with zero Class-4 observations, the corresponding confidence limits are

$$p<2.72\times {10}^{-4}(95\%),p<4.19\times {10}^{-4}(99\%).$$

Hence the statement in the Results section should read: “No Class-4 states were observed among 11,000 samples, confirming with 95% (99%) confidence that the true probability is below $2.72\times {10}^{-4}$ ($4.19\times {10}^{-4}$).”

Appendix B.0.0.4. Numerical consistency.

All quantities were recalculated from a unified dataset:

• $R^2=0.94\pm 0.01$ for fitted regions in Figure 3.
• Minimum ratio $M/QF{I}_{\max }=1.053\pm 0.005$.
• Share of states crossing the SNL: $97.8\%$.

Figures and captions have been regenerated from the same numerical source to ensure full consistency.

Table A1. Updated optimization parameters and runtime characteristics.

Step	Grid	Evaluations	Dim.	Mean time (s)
Coarse ($\pi /2$)	$4^6$	15,625	6	22.3 ± 2.1
Fine ($\pi /3$)	$3^6$	729	6	8.4 ± 1.3
CMA–ES (check)	20	–	6	3.2 ± 0.5

Table A1. Updated optimization parameters and runtime characteristics.

Step	Grid	Evaluations	Dim.	Mean time (s)
Coarse ($\pi /2$)	$4^6$	15,625	6	22.3 ± 2.1
Fine ($\pi /3$)	$3^6$	729	6	8.4 ± 1.3
CMA–ES (check)	20	–	6	3.2 ± 0.5