Emotional Trade-offs in Successful Romantic Relationships: A Differential Game Approach

1. Introduction

Long-term romantic relationships, especially marriage, have played an important role as a cultural universal within social structures throughout history [1]. In the field of relationship science, a successful relationship is generally defined as one characterized by both stability and emotional fulfillment [2]. In contemporary Western societies, a sustained and satisfactory relationship is associated with a longer, healthier, and happier life [3]. However, building a successful relationship is far from easy, as evidenced by the high divorce rates in the Western world. In the United States, for example, approximately 45% of new marriages are expected to end in divorce [4]. While lasting and fulfilling unions certainly exist, the factors that make them successful remain not fully understood in relationship science [5].

Research in recent decades has identified several elements that contribute to the success of romantic relationships [2]. In this paper, we explore the role of partner subjectivity, which is considered a significant factor influencing the evolution of a relationship. Subjectivity can be defined as the "tendency to experience one’s own perceptions as indicators of objective reality" [2]. This implies that the state of a relationship —measured, for example, by marital quality or by each partner’s level of dedication— may be interpreted differently by each individual, depending on their unique psychological constructs. Here, we analyze how differences in subjective emotional processing of rewards and costs of the relationship affect key indicators such as relationship quality, happiness, and partners’ efforts to nurture the relationship.

Romantic relationships must be understood as processes that evolve over time. In this context, the mathematics of dynamical systems offers a suitable framework for modeling and analyzing the temporal evolution of a relationship —particularly in the long term. This is especially relevant given the practical challenges of monitoring real-life relationships over extended periods. In fact, large-scale longitudinal data on marital quality remain scarce in the literature [6].

Since the first attempt to model interaction dynamics in dyadic romantic relationships [7], this mathematical approach has been further developed to study both real [5] and fictional couples [8]. The concept of modeling a romantic relationship as an optimal control problem was introduced in [9]. In this context, a successful relationship may be conceptualized as a dynamic equilibrium —one that is sufficiently rewarding— of the system governing the evolution of the relationship’s state. A comprehensive review of mathematical models of love dynamics is provided in [10].

The optimal control approach was extended in [11,12] to formulate a romantic relationship as a differential game, which is the framework considered in this paper. In this scheme, the quality of the relationship —or "feeling"— is governed by the level of dedication —or "effort"— that each partner invests. The idea that partners must actively work to counteract the natural decay of the feeling is well established in relationship science [2,5]. The differential game formulation seeks to determine the optimal levels of effort that both partners must exert to sustain a happy, long-term relationship. These efforts correspond to the pair of control variables that jointly maximize the overall well-being of each individual, that is, they form a Nash equilibrium of the game -see [13].

The well-being integrals represent the total discounted net emotional balance over time, defined as the difference between the emotional reward derived from the feeling and the emotional cost incurred by the exerted effort. Personality traits -in particular emotional processing- are linked to satisfaction in romantic relationships -see e.g. [14]. In our analysis, we consider parameterizations of both emotional reward and cost, and explore how key relationship variables respond to changes in these parameters. Specifically, we analyze —formally and numerically— how each partner’s subjective interpretation of emotional rewards and costs influences relationship quality, effort levels, and happiness in the long-term equilibrium of the relationship. We address the question of whether one’s own traits (the actor effect) or those of one’s partner (the partner effect) exert a stronger influence on relationship quality and individual satisfaction—an issue of particular relevance in this context -see, e.g., [15].

In the following section, we present the fundamentals of our differential game model of romantic relationships, along with its mathematical treatment, building on the approach introduced in [11]. We then present the results of our analysis. We begin by formally deriving the qualitative behavior of the model’s outputs in response to variations in the partners’ subjective processing of emotional rewards and costs. We then explore the quantitative behavior of the model by numerically solving the Hamilton-Jacobi-Bellman equations for a computational version of the game, employing the RaBVIt-G algorithm introduced ad hoc in [11].

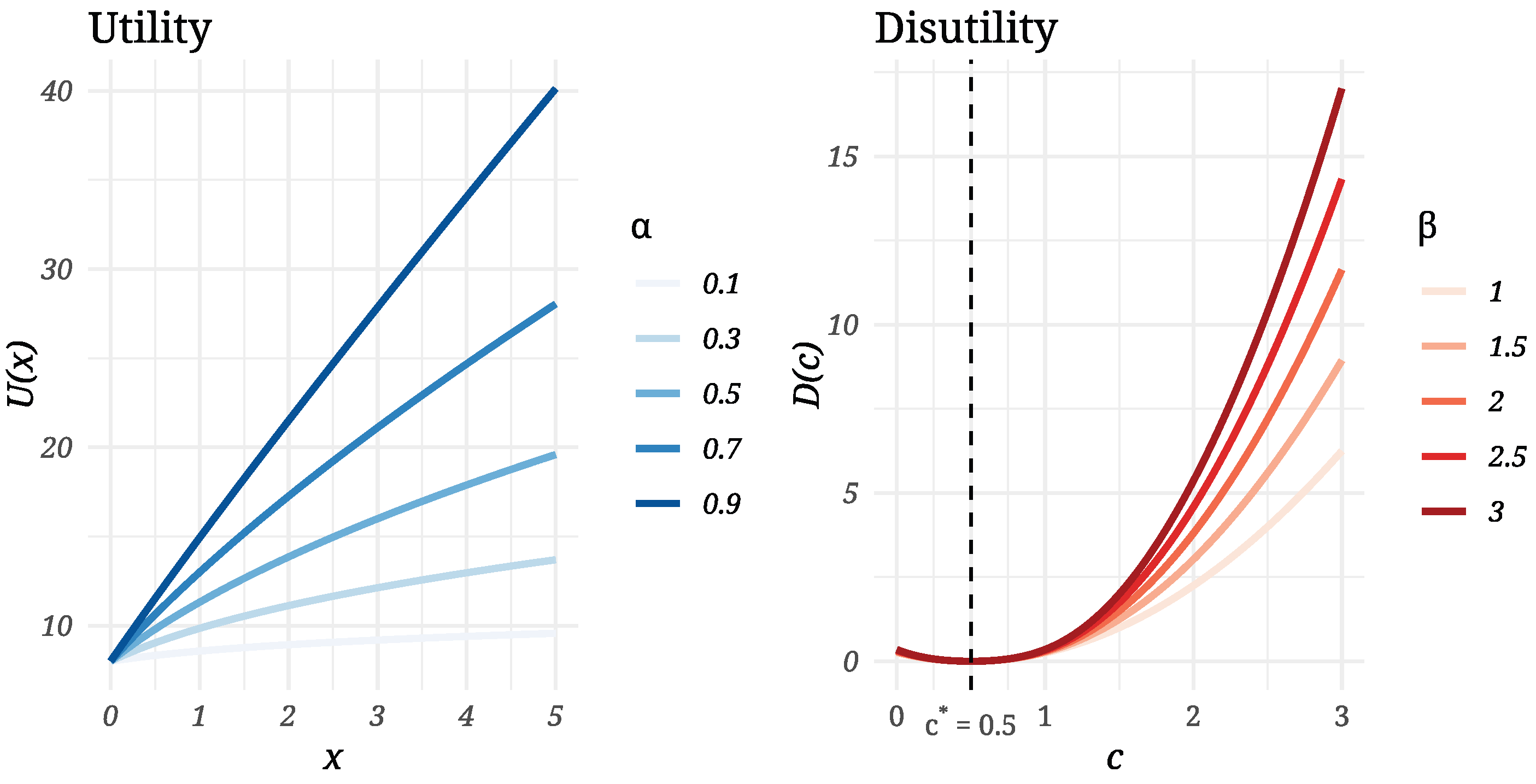
2. Methods

In this section, we outline the theoretical model of the love differential game, along with its computational counterpart, which we use throughout the paper to analyze romantic relationships. Both the theoretical and computational aspects are discussed in detail in [11]. As in that work, computational solutions are obtained using the RaBVIt-G algorithm, designed to solve Feedback-Nash differential games (see [16]).

Differential Love Games: Theoretical Model

Let $x:[0,\infty )\to {\mathbb{R}}^{+}$ be a differentiable function monitoring the state of a romantic relationship at time $t\ge 0$. The variable $x\left(t\right)$, referred to as the feeling, quantifies the quality or satisfaction of the relationship at time t. The initial value $x\left(0\right)=x_0$ is typically high, accounting for the strong emotional bond at the beginning of the relationship.

According to [5], the variable $x\left(t\right)$ naturally decays over time unless counteracted by the efforts of both partners —an idea referred to as the second law of thermodynamics for sentimental relationships. The dynamics of the feeling variable is thus described by the ordinary differential equation

$$\dot{x}\left(t\right)=-rx\left(t\right)+a_1{c}_1\left(t\right)+a_2{c}_2\left(t\right),t\ge 0,$$

(1)

where $r>0$ is the decay rate, and $c_1\left(t\right)$ and $c_2\left(t\right)$ are piecewise continuous and non-negative functions which measure the levels of effort of partners 1 and 2, respectively. The parameters $a_1,a_2>0$ measure the efficiency of each partner’s effort. The additive structure of the effort terms aligns with principles for successful relationships [17]. The linear decay is a natural assumption -see [9]- though more general models are discussed in [18]. A minimum level of relationship satisfaction, $x\left(t\right)>x_{\min }>0,t\ge 0$, is necessary to sustain the relationship. Without effort ($c_1\left(t\right)=c_2\left(t\right)=0$), the feeling decays exponentially at rate r, making the relationship unsustainable in the long term.

Each partner i optimally determines their effort path, $c_i\left(t\right)$, by maximizing their total well-being $W_i$, defined as

$$W_i\left(c_i\right)={\int }_0^{\infty }{e}^{-{\rho }_{i}t}\left(U_i\left(x\left(t\right)\right)-D_i\left(c_i\left(t\right)\right)\right)\mathrm{d}t,i=1,2.$$

(2)

For each partner i, ${\rho }_i>0$ denotes the temporal discount rate, $U_i\left(x\left(t\right)\right)$ represents the utility -or reward- derived from the feeling level $x\left(t\right)$, and $D_i\left(c_i\left(t\right)\right)$ is the disutility -or cost- associated with effort $c_i\left(t\right)$. The optimization problems above are interdependent, as both partners’ efforts influence the feeling $x\left(t\right)$, which in turn affects their total well-being.

The functions $U_i$ and $D_i$ define the utility/disutility ($UD$) structure of the problem. They are typically $C^2$ functions defined on $[0,+\infty )$ and satisfy the following properties: for $x\ge 0$, $U_i^{\prime }\left(x\right)>0$, $U_i^{\prime }\left(x\right)\to 0$ as $x\to \infty$ and $U_i^{\prime \prime }\left(x\right)<0$; and for $x\ge 0$, $D_i^{\prime \prime }\left(c_i\right)>0$, $D_i^{\prime }\left(c_i\right)\to \infty$ as $c_i\to \infty$, with a unique $c_i^{*}\ge 0$ such that $D_i^{\prime }\left(c_i^{*}\right)=0$. Note that $c_i^{*}\ge 0$ is the absolute minimum of $D_i$ and thus represents the preferred effort level of partner i. These assumptions, consistent with principles of human psychology, imply that the reward derived from feeling always increases but at a decreasing rate, while the cost associated with effort is beneficial up to a certain critical point, beyond which it becomes increasingly burdensome.

The problem consists of determining optimal effort trajectories $c_1\left(t\right)$ and $c_2\left(t\right)$ that simultaneously maximize each partner’s well-being integrals, $W_1$ and $W_2$, as defined by (2), subject to the feeling dynamics given by (1) and the initial condition $x\left(0\right)=x_0$. This setup constitutes a two-person differential game with an infinite time horizon [13].

In the special case where $U_1=U_2$, $D_1=D_2$, ${\rho }_1={\rho }_2$, and $a_1=a_2$, the partners share identical emotional preferences and efficiency. Such couples are termed homogamous, consistent with terminology in marital psychology [19]. More generally, the relationship of heterogamous couples can be modeled by assigning different parameters or $UD$-structure to each partner. In this paper, we focus on the role of the asymmetry in the $UD$-structure of the problem, which arises from the fact that partners may process rewards and costs differently. We therefore consider below parametric families $U_i\equiv U_i(x,{\alpha }_i)$ and $D_i\equiv D_i(c_i,{\beta }_i)$, $i=1,2$, where the parameters ${\alpha }_i$ and ${\beta }_i$ capture differences in reward and cost evaluations of feeling and effort levels.

The solution to the problem is a pair of effort trajectories $(c_1^{♡}\left(t\right),c_2^{♡}\left(t\right))$ that simultaneously solve the optimization problems of both partners, given the initial feeling $x\left(0\right)=x_0$. This solution corresponds to a Nash equilibrium of the differential game [13]. Of particular interest are stationary solutions, where the feeling and effort levels remain constant over time, providing long-term viability as long as $x\left(t\right)>x_{\mathrm{mim}}$.

The solution can be expressed in two forms. Open-loop solutions refer to effort paths $c_i\left(t\right)$ that depend solely on time t and the initial state $x_0$. In this case, each partner commits to a predetermined effort trajectory, independent of how the relationship actually evolves over time. Open-loop strategies can be characterized via control-theoretical methods -see e.g. [13]. For all $t\ge 0$, the optimal effort value $c_i^{♡}\left(t\right)$ must maximize the (current-value) Hamiltonian function $H_i(x\left(t\right),c_i\left(t\right),{\lambda }_i\left(t\right))$, that is,

$$c_i^{♡}\left(t\right)={\mathrm{argmax}}_{c_i\left(t\right)}{H}_i(x\left(t\right),c_i\left(t\right),{\lambda }_i\left(t\right)),$$

(3)

where

$$H_i(x\left(t\right),c_i\left(t\right),{\lambda }_i\left(t\right))=U_i\left(x\left(t\right)\right)-D_i\left(c_i\left(t\right)\right)+{\lambda }_i\left(t\right)(-rx\left(t\right)+a_1{c}_1\left(t\right)+a_2{c}_2\left(t\right)),$$

and ${\lambda }_i\left(t\right)$ is an absolutely continuous function satisfying the (adjoint) differential equation

$${\dot{\lambda }}_i\left(t\right)=-H_x^{\prime }(x\left(t\right),c_i\left(t\right),{\lambda }_i\left(t\right))+{\rho }_i{\lambda }_i\left(t\right),i=1,2.$$

(4)

Feedback or closed-loop solutions, on the other hand, define each effort as a function $c_i\left(t\right)=S_i(x\left(t\right),t)$, which depends on the current state of the relationship $x\left(t\right)$ and time t. The function $c_i\left(t\right)=S_i(x\left(t\right),t)$ is called a feedback strategy. This approach enables partners to adjust their efforts dynamically in response to the ongoing state of the relationship. Feedback solutions are especially appropriate in our setting, as they provide a mechanism for partners to adjust optimally to exogenous shocks and unanticipated deviations in the feeling trajectory.

Since it is reasonable to assume that the state of the relationship $x\left(t\right)$ is observable by both partners when making effort decisions at time t, feedback analysis is particularly appropriate here.

Since the time horizon is infinite and the input functions are time-invariant, it is natural to consider stationary feedback solutions —those in which control actions depend solely on the current observed state x. A pair of strategies

$S_i^{♡}:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+},$, $i=1,2$, constitutes a stationary feedback Nash equilibrium of the differential game if $S_i^{♡}\left(x\left(t\right)\right)$ is an optimal effort control for partner i, i.e. $S_1^{♡}\left(x\left(t\right)\right)$ solves the optimization problem

$$\underset{c_1\left(t\right)\in {\mathbb{R}}^{+}}{max}{\int }_0^{\infty }{e}^{-{\rho }_{1}t}\left(U_1\left(x\left(t\right)\right)-D_1\left(c_1\left(t\right)\right)\right)\mathrm{d}t,$$

subject to $\dot{x}\left(t\right)=-rx\left(t\right)+a_1{c}_1\left(t\right)+a_2{S}_2^{♡}\left(x\left(t\right)\right),x\left(0\right)=x_0$, and $S_2^{♡}\left(x\left(t\right)\right)$ solves

$$\underset{c_2\left(t\right)\in {\mathbb{R}}^{+}}{max}{\int }_0^{\infty }{e}^{-{\rho }_{2}t}\left(U_2\left(x\left(t\right)\right)-D_2\left(c_2\left(t\right)\right)\right)\mathrm{d}t,$$

subject to $\dot{x}\left(t\right)=-rx\left(t\right)+a_1{S}_1^{♡}\left(x\left(t\right)\right)+a_2{c}_2\left(t\right),x\left(0\right)=x_0.$

Given a stationary feedback Nash equilibrium $(S_1^{♡},S_2^{♡})$, the well-being functions $v_i^{♡}:{\mathbb{R}}^{+}\to \mathbb{R}$ are defined as the value functions of the problem, given by

$$v_i^{♡}\left(x_0\right)=W_i\left(S_i^{♡}\left(x\left(t\right)\right)\right),i=1,2,$$

(5)

where $S_i^{♡}\left(x\left(t\right)\right)$ is the feedback solution of the control problem of partner i with initial state $x\left(0\right)=x_0$. For any initial feeling level $x_0$, the value $v_i^{♡}\left(x_0\right)$ represents the maximal attainable well-being for partner i. Under suitable conditions [20], the value functions satisfy the Hamilton-Jacobi-Bellman (HJB) equations

$$\left\{\begin{array}{c}{\rho }_1{v}_1\left(x\right)=\underset{c_1\in {\mathbb{R}}^{+}}{max}\left\{U_1\left(x\right)-D_1\left(c_1\right)+v_1^{\prime }\left(x\right)(-rx+a_1{c}_1+a_2{S}_2^{♡}\left(x\right))\right\},\hfill \\ {\rho }_2{v}_2\left(x\right)=\underset{c_2\in {\mathbb{R}}^{+}}{max}\left\{U_2\left(x\right)-D_2\left(c_2\right)+v_2^{\prime }\left(x\right)(-rx+a_1{S}_1^{♡}\left(x\right)+a_2{c}_2)\right\}.\hfill \end{array}\right.$$

(6)

The feedback strategies $S_i^{♡}\left(x\right)$ are thus defined by

$$\left\{\begin{array}{c}{S}_1^{♡}\left(x\right)\in arg\underset{c_1\in {\mathbb{R}}^{+}}{max}\left\{U_1\left(x\right)-D_1\left(c_1\right)+v_1^{\prime }\left(x\right)(-rx+a_1{c}_1+a_2{S}_2^{♡}\left(x\right))\right\},\hfill \\ S_2^{♡}\left(x\right)\in arg\underset{c_2\in {\mathbb{R}}^{+}}{max}\left\{U_2\left(x\right)-D_2\left(c_2\right)+v_2^{\prime }\left(x\right)(-rx+a_1{S}_1^{♡}\left(x\right)+a_2{c}_2)\right\}.\hfill \end{array}\right.$$

(7)

In the case that $S_i^{♡}\left(x\right)$ is a singleton for all x, $i=1,2$, the optimal feeling evolution is obtained by substituting $S_i^{♡}\left(x\right)$ into (1):

$$\dot{x}\left(t\right)=-rx\left(t\right)+a_1{S}_1^{♡}\left(x\left(t\right)\right)+a_2{S}_2^{♡}\left(x\left(t\right)\right),x\left(0\right)=x_0.$$

(8)

Within the feedback framework, the couple’s effort problem is characterized by the value functions $v_i^{♡}\left(x\right)$ and the associated feedback strategies $S_i^{♡}\left(x\right)$, which together constitute its primary analytical outputs.

A Computational Feedback Model of Differential Love Games

Differential games are generally not analytically tractable, and numerical methods are required to obtain approximate feedback solutions. To solve the HJB system (6), we adopt a computational methodology based on time and space discretization, as introduced in [11]. The approach consists of two main components. First, we construct a Semi-Lagrangian discrete approximation of the HJB system (6) using a time-space discretization scheme, following the methods developed in [21,22]. Second, we implement a mesh-free numerical scheme that combines radial basis function interpolation with a nested iteration procedure over the value functions and strategic responses, adapting techniques from [23]. This algorithm allows us to compute approximate well-being functions $v_i^{♡}\left(x\right)$ and feedback strategies $S_i^{♡}\left(x\right),i=1,2,$ for the differential love game efficiently and with high accuracy. The approach can be summarized as follows. For ease of exposition, the superscript in $S_i^{♡}(·)$ and $v_i^{♡}(·)$ is omitted in what follows.

Define $t_k=kh$ for $k\in \mathbb{N}\cup \left\{0\right\}$, where $h>0$ is the time step. Let $c_i^h={\left\{c_{i,k}\right\}}_{k\in \mathbb{N}\cup \left\{0\right\}}$ be a sequence of feasible control values for partner i, which defines a piecewise constant control function $c_i^h\left(\tau \right)=c_{i,k},\tau \in \left[t_k,t_{k+1}\right)$. The corresponding state sequence $x_k=x\left(t_k\right)$ is obtained via a first-order Euler discretization of (1), expressed as

$$x_{k+1}=x_k+hf(x_k,c_{1,k},c_{2,k}),k\ge 0,$$

(9)

where $f(x,c_1,c_2)=-rx+a_1{c}_1+a_2{c}_2$. Given $x\left(0\right)=y$, a discrete formulation of (2) using rectangle quadrature is given by

$$W_i^h\left(c_i^h\right)=h\sum _{k=0}^{\infty }{e}^{-{\rho }_i{t}_k}\left(U_i\left(x_k\right)-D_i\left(c_{i,k}\right)\right),i=1,2.$$

(10)

The discrete formulation of the well-being function (5) is

$$v_i^h\left(y\right)=\underset{c_i^h}{max}{W}_i^h\left(c_i^h\right).$$

(11)

Following  [22], a first-order discrete-time HJB approximation of (6) is expressed as

$$\left\{\begin{array}{cc}{v}_1^h\left(y\right)=\underset{c_1\in {\mathbb{R}}^{+}}{max}\left\{h\left(U_1\left(y\right)-D_1\left(c_1\right)\right)+\left(1-{\rho }_{1}h\right)v_1^h\left(y+hf\left(y,c_1,S_2^h\left(y\right)\right)\right)\right\},\hfill & \\ v_2^h\left(y\right)=\underset{c_2\in {\mathbb{R}}^{+}}{max}\left\{h\left(U_2\left(y\right)-D_2\left(c_2\right)\right)+\left(1-{\rho }_{2}h\right)v_2^h\left(y+hf\left(y,S_1^h\left(y\right),c_2\right)\right)\right\},\hfill \end{array}\right.$$

(12)

where the corresponding discrete representations of (7) are

$$\left\{\begin{array}{cc}{S}_1^h\left(y\right)\in arg\underset{c_1\in {\mathbb{R}}^{+}}{max}\left\{h\left(U_1\left(y\right)-D_1\left(c_1\right)\right)+\left(1-{\rho }_{1}h\right)v_1^h\left(y+hf\left(y,c_1,S_2^h\left(y\right)\right)\right)\right\},\hfill & \\ S_2^h\left(y\right)\in arg\underset{c_2\in {\mathbb{R}}^{+}}{max}\left\{h\left(U_2\left(y\right)-D_2\left(c_2\right)\right)+\left(1-{\rho }_{2}h\right)v_2^h\left(y+hf\left(y,S_1^h\left(y\right),c_2\right)\right)\right\}.\hfill \end{array}\right.$$

(13)

Numerical approximations of the values $v_i^h(·)$ in (12) are computed through spatial discretization of the state space combined with a mesh-free collocation algorithm based on scattered nodes -see [24]. The RaBVit-G algorithm, used to solve the (12)-(13), employs a nested loop involving two iterative procedures: game iteration and value iteration. These iterative processes generate sequences of control arrays and value functions that converge to approximate feedback solutions when a suitable convergence criterion is satisfied. A detailed description of the algorithm is provided in [11,12].

3. Results and Discussion

In this section, we analyze the equilibrium solution of the couple problem for different families of utility and disutility functions $U_i$ and $D_i$, $i=1,2$, that is, for different specifications of the $UD$-structure of the problem. As discussed in Section 2, these functions capture varying emotional sensitivities in how each partner processes the rewards and costs associated with relationship quality x and individual effort levels $c_i$, $i=1,2$.

$UD$-structure. We consider parametric $UD$-structures of the form $U_i=U_i(x,{\alpha }_i)$ and $D_i=D_i(c_i,{\beta }_i)$ for $i=1,2$, where ${\alpha }_i,{\beta }_i\ge 0$ are parameters that represent each partner’s emotional sensitivity to perceived relationship quality and the subjective cost of effort, respectively. As functions of x and $c_i$, $U_i$ and $D_i$ are assumed to be $C^2$ and satisfy the regularity conditions required by the differential love game model introduced in Section 2. Specifically, for $x\ge 0$, we assume ${\left(U_i\right)}_x^{\prime }>0$, ${\left(U_i\right)}_{xx}^{\prime \prime }<0$, and ${\left(U_i\right)}_x^{\prime }\to 0$ as $x\to +\infty$, for $i=1,2$. Likewise, for $c_i\ge 0$, we assume ${\left(D_i\right)}_{c_i{c}_i}^{\prime \prime }>0$, ${\left(D_i\right)}_{c_i}^{\prime }\to +\infty$ as $c_i\to +\infty$, and ${\left(D_i\right)}_{c_i}^{\prime }\left(c_i^{*}\right)=0$, where $c_i^{*}$ is the unique minimizer of $D_i$. We further assume that $U_i$ and $D_i$ are $C^2$ in the parameters ${\alpha }_i$ and ${\beta }_i$, respectively, and satisfy ${\left(U_i\right)}_{{\alpha }_i}^{\prime }>0$ for all $x\ge 0$, and ${\left(D_i\right)}_{{\beta }_i}^{\prime }>0$ for all $c_i\ge 0$.

Consequently, $U_i(x,{\alpha }_i)$ forms an ordered family with respect to ${\alpha }_i$: the emotional reward associated with any feeling level x increases with ${\alpha }_i$. The parameter ${\alpha }_i$ thus captures how much partner i values emotional closeness. We refer to this trait as emotional reward sensitivity. Individuals with higher values of ${\alpha }_i$ are more attuned to emotional experiences or more ’platonic’, in a broad psychological sense.

Similarly, $D_i(c_i,{\beta }_i)$ increases monotonically with respect to ${\beta }_i$, meaning that the perceived burden of any given level of effort $c_i$ grows as ${\beta }_i$ increases. The parameter ${\beta }_i$ represents how each partner perceives the cost associated with their effort deviation from the preferred level, $c_i^{*}$, as ${\beta }_i$ rises, the discomfort experienced when straying from $c_i^{*}$ intensifies. We refer to ${\beta }_i$ as emotional cost sensitivity.

An example of the types of $UD$-structures considered in this study is illustrated in Figure 3

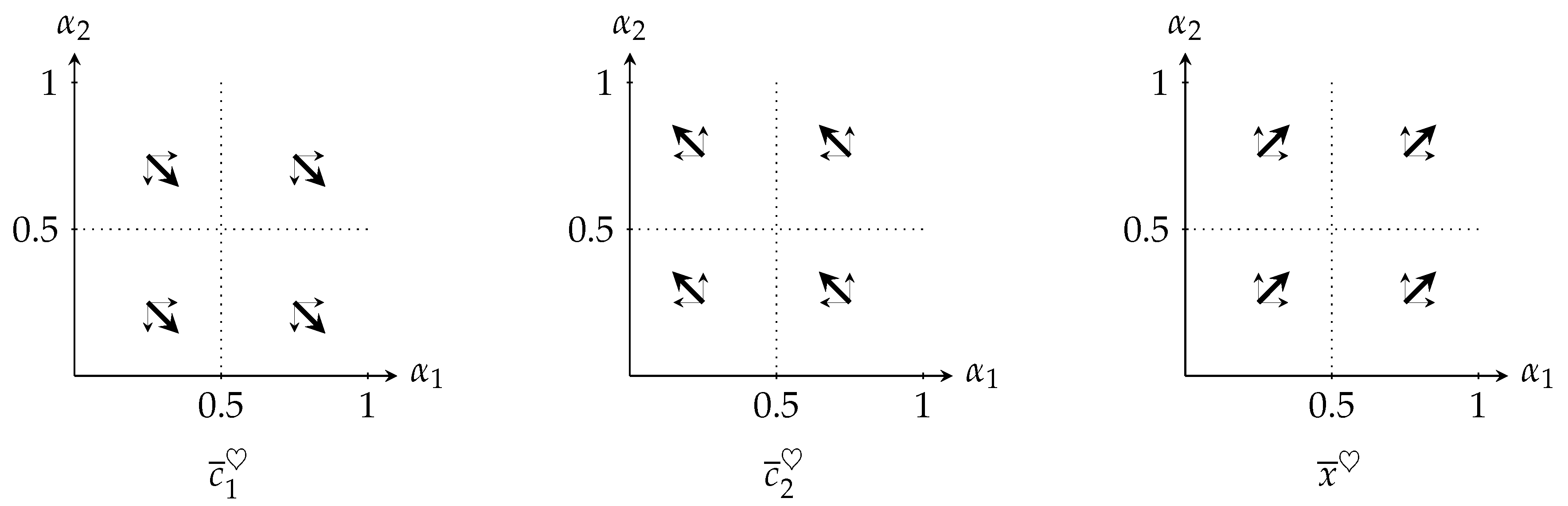
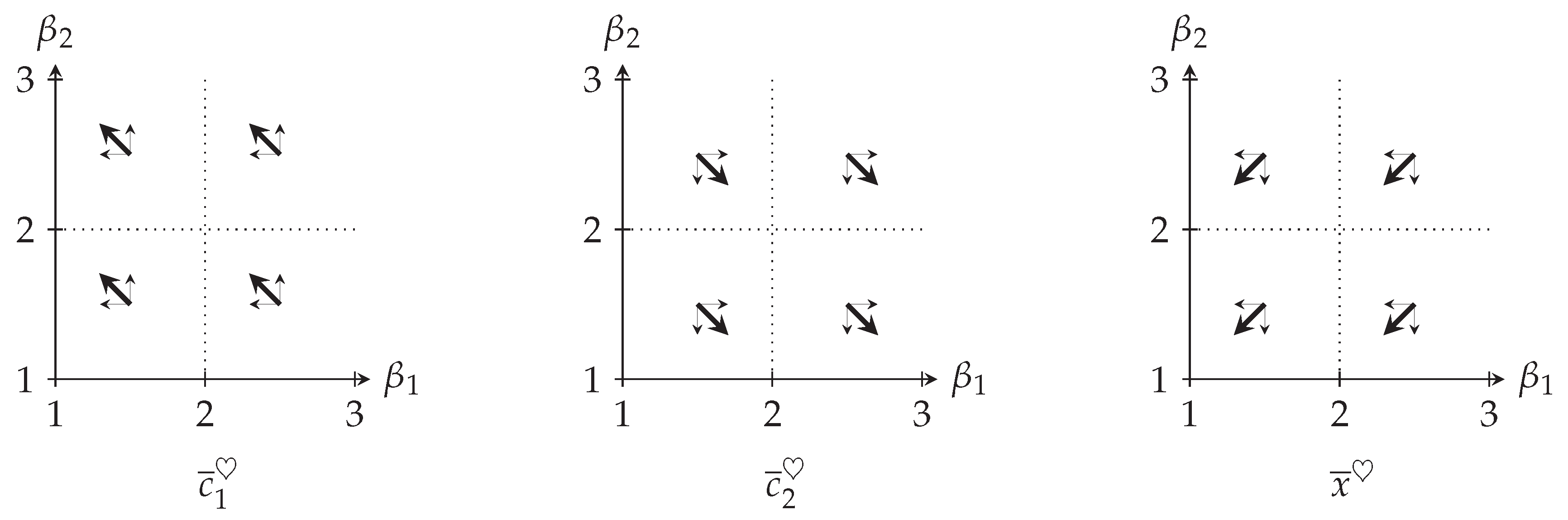
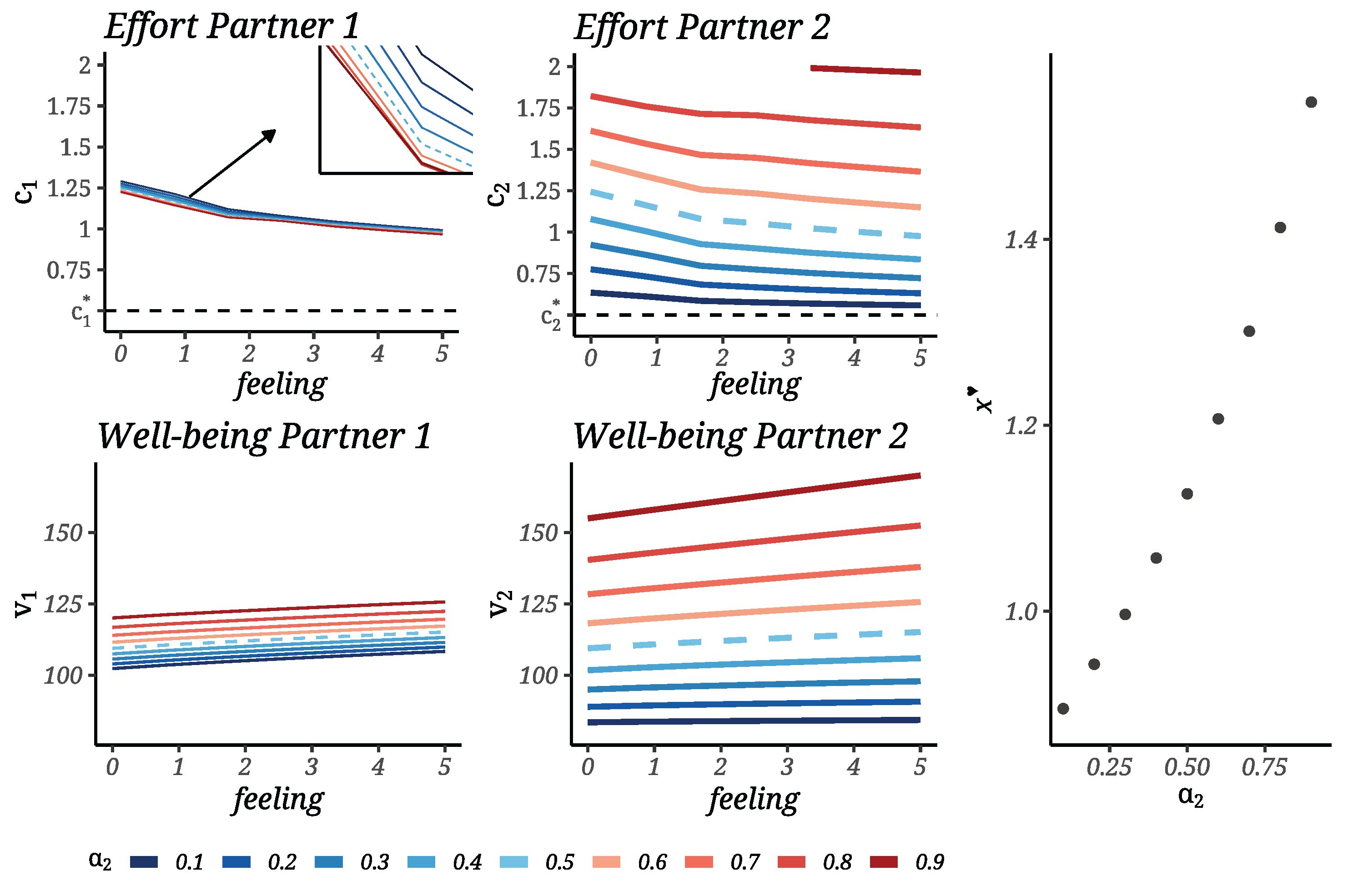
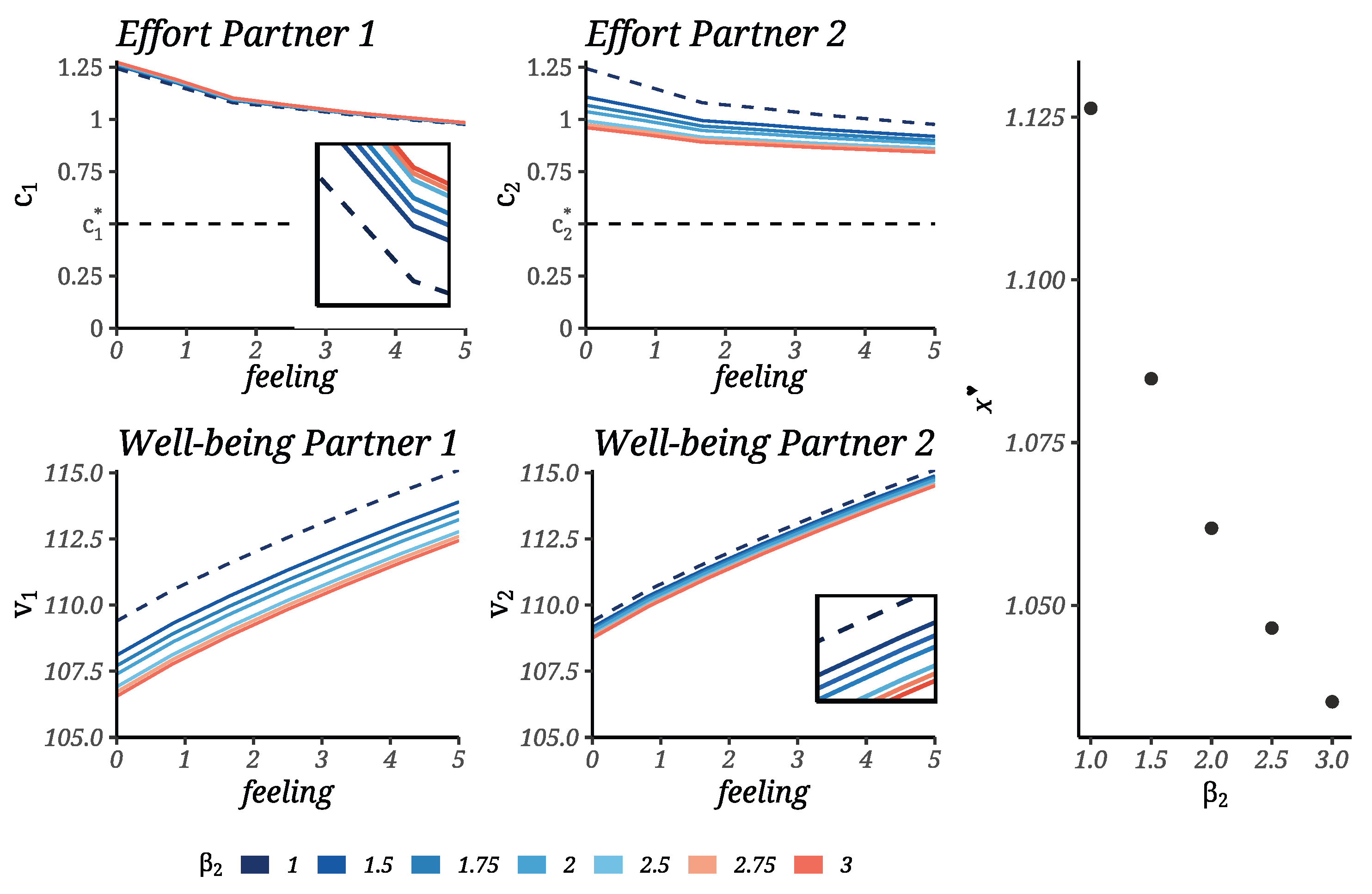
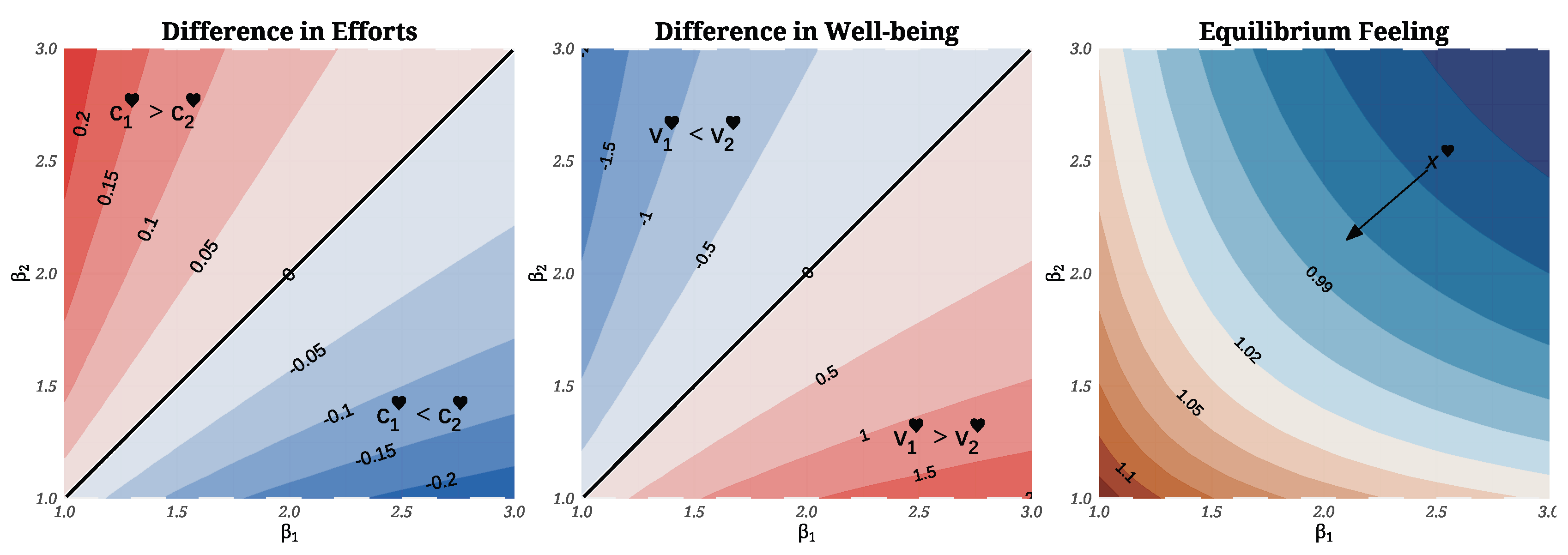
Emotional Parameter Sensitivity at Equilibrium: A Control-Theoretic Analysis.

A control-theoretic approach allows us to determine the marginal response of the feeling and effort policies at equilibrium as the parameters ${\alpha }_i$ and ${\beta }_i$ vary.

It follows from Equations (3) and (4) in optimal control theory that the optimal feeling and effort trajectories must satisfy (see [9] or [25])

$$\left\{\begin{array}{c}{\dot{c}}_1={\left({\left(D_1\right)}_{c_1,c_1}^{\prime \prime }(c_1,{\beta }_1)\right)}^{-1}[(r+{\rho }_1){\left(D_1\right)}_{c_1}^{\prime }(c_1,{\beta }_1)-a_1{\left(U_1\right)}_x^{\prime }(x,{\alpha }_1)],\hfill \\ {\dot{c}}_2={\left({\left(D_2\right)}_{c_2,c_2}^{\prime \prime }(c_2,{\beta }_2)\right)}^{-1}[(r+{\rho }_2){\left(D_2\right)}_{c_2}^{\prime }(c_2,{\beta }_2)-a_2{\left(U_2\right)}_x^{\prime }(x,{\alpha }_2)],\hfill \\ \dot{x}=-rx+a_1{c}_1+a_2{c}_2.\hfill \end{array}\right.$$

(14)

Given $a_1,a_2,{\rho }_1,{\rho }_2,{\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2>0$, an equilibrium solution $E=\left({\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{x}}^{♡}\right)$ satisfies

$$\left\{\begin{array}{c}0=\left(r+{\rho }_1\right){\left(D_1\right)}_{c_1}^{\prime }\left({\overline{c}}_1^{♡},{\beta }_1\right)-a_1{\left(U_1\right)}_x^{\prime }\left({\overline{x}}^{♡},{\alpha }_1\right),\hfill \\ 0=\left(r+{\rho }_2\right){\left(D_2\right)}_{c_2}^{\prime }\left({\overline{c}}_2^{♡},{\beta }_2\right)-a_2{\left(U_2\right)}_x^{\prime }\left({\overline{x}}^{♡},{\alpha }_2\right),\hfill \\ 0=-r{\overline{x}}^{♡}+a_1{\overline{c}}_1^{♡}+a_2{\overline{c}}_2^{♡}.\hfill \end{array}\right.$$

(15)

Assume that the parameters $a_1,a_2,{\rho }_1,{\rho }_2$ are fixed. Given ${\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0>0$, suppose that $({\overline{c}}_{1,0}^{♡},{\overline{c}}_{2,0}^{♡},{\overline{x}}_0^{♡})$ is the corresponding equilibrium defined by system (15). The differentiability assumptions on the $UD$-structure imply that system (15) defines an equilibrium $({\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{x}}^{♡})$ as differentiable functions of $({\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2)$ in a neighborhood of $({\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$. This follows from differentiating (15) and observing that the matrix of the linearized system

$$\mathbf{A}=\left[\begin{array}{ccc}\left(r+{\rho }_1\right){\left(D_1\right)}_{c_1{c}_1}^{″}\left({\overline{c}}_{1,0}^{♡},{\beta }_1^0\right)& 0& -a_1{\left(U_1\right)}_{xx}^{″}\left({\overline{x}}_0^{♡},{\alpha }_1^0\right)\\ 0& \left(r+{\rho }_2\right){\left(D_2\right)}_{c_2{c}_2}^{\prime \prime }\left({\overline{c}}_{2,0}^{♡},{\beta }_2^0\right)& -a_2{\left(U_2\right)}_{xx}^{″}\left({\overline{x}}_0^{♡},{\alpha }_2^0\right)\\ a_1& a_2& -r\end{array}\right]$$

(16)

satisfies $det\left(\mathbf{A}\right)\ne 0$, because of the properties of the $UD$-structure of the problem.

The marginal response of the equilibrium values $({\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{x}}^{♡})$ with respect to variations in the sensitivity parameters ${\alpha }_i$ is determined by the sign of the cross-derivative ${\left(U_i\right)}_{x,{\alpha }_i}^{″}>0$. Specifically, we have

Proposition 1. 

Assume that the parametric $UD$-structure of the differential love game satisfies the differentiability properties specified above. Let $({\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2)\mapsto ({\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{x}}^{♡})$ be the equilibrium solution defined by system (15) in a neighborhood of a solution $({\overline{c}}_{1,0}^{♡},{\overline{c}}_{2,0}^{♡},{\overline{x}}_0^{♡},{\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$ of the system. We have:

(I) If  ${\left(U_1\right)}_{x,{\alpha }_1}^{″}\left({\overline{x}}_0^{♡},{\alpha }_1^0\right)>0$, then${\displaystyle \frac{\partial {\overline{c}}_1^{♡}}{\partial {\alpha }_1}}>0$,   ${\displaystyle \frac{\partial {\overline{c}}_2^{♡}}{\partial {\alpha }_1}}<0$,   and  ${\displaystyle \frac{\partial {\overline{x}}^{♡}}{\partial {\alpha }_1}}>0$  at  $({\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0).$

(II) If  ${\left(U_2\right)}_{x,{\alpha }_2}^{″}\left({\overline{x}}_0^{♡},{\alpha }_2^0\right)>0$, then  ${\displaystyle \frac{\partial {\overline{c}}_1^{♡}}{\partial {\alpha }_2}}<0$,  ${\displaystyle \frac{\partial {\overline{c}}_2^{♡}}{\partial {\alpha }_2}}>0$,  and  ${\displaystyle \frac{\partial {\overline{x}}^{♡}}{\partial {\alpha }_2}}>0$  at  $({\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$.

Remark 1. 

Note that, regarding the parameter dependence of the $UD$-structure, assumption ${\left(U_i\right)}_{x,{\alpha }_i}^{\prime \prime }>0$ in Proposition 1 is sufficient to determine the signs of ${\displaystyle \frac{\partial {\overline{c}}_1^{♡}}{\partial {\alpha }_i}}$, ${\displaystyle \frac{\partial {\overline{c}}_2^{♡}}{\partial {\alpha }_i}}$, and ${\displaystyle \frac{\partial {\overline{x}}^{♡}}{\partial {\alpha }_i}}$. This condition has a natural interpretation in terms of emotional reward: as ${\alpha }_i$ increases, a small improvement in relationship quality (as measured by x) becomes more valuable.

Statement (I) follows from the properties of the $UD$-structure by differentiating system (15) at the point $({\overline{c}}_{1,0}^{♡},{\overline{c}}_{2,0}^{♡},{\overline{x}}_0^{♡},{\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$, setting $\mathrm{d}{\alpha }_2=\mathrm{d}{\beta }_1=\mathrm{d}{\beta }_2=0$, and noting that $det\left(\mathbf{A}\right)<0$, where $\mathbf{A}$ is defined in (16):

$$\left[\begin{array}{c}\mathrm{d}{\overline{c}}_1^{♡}\\ \mathrm{d}{\overline{c}}_2^{♡}\\ \mathrm{d}{\overline{x}}^{♡}\end{array}\right]=-{\displaystyle \frac{1}{det\left(\mathbf{A}\right)}}\left[\begin{array}{c}{a}_{1}r\left(r+{\rho }_2\right){\left(D_2\right)}_{c_2,c_2}^{\prime \prime }{\left(U_1\right)}_{x,{\alpha }_1}^{″}-a_1{a}_2^2{\left(U_2\right)}_{x,x}^{″}{\left(U_1\right)}_{x,{\alpha }_1}^{″}\\ a_1^2{a}_2{\left(U_2\right)}_{x,x}^{″}{\left(U_1\right)}_{x,{\alpha }_1}^{″}\\ a_1^2\left(r+{\rho }_2\right){\left(D_2\right)}_{c_2,c_2}^{″}{\left(U_1\right)}_{x,{\alpha }_1}^{″}\end{array}\right]\mathrm{d}{\alpha }_1.$$

(17)

All derivatives in the above expression are evaluated at $({\overline{c}}_{1,0}^{♡},{\overline{c}}_{2,0}^{♡},{\overline{x}}_0^{♡},{\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$. Statement (II) follows by a similar argument, mutatis mutandis.

According to Proposition 1, the response of the equilibrium values $({\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{x}}^{♡})$ to small variations $\mathrm{d}{\alpha }_1>0,\mathrm{d}{\alpha }_2>0$ (with $\mathrm{d}{\beta }_1=\mathrm{d}{\beta }_2=0$) can be qualitatively described by the diagrams in Figure 1.

The following proposition characterizes the marginal effects of the parameters ${\beta }_i$ on the equilibrium values $({\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{x}}^{♡})$, capturing each partner’s sensitivity to effort exertion.

Proposition 2. 

Assume that the parametric $UD$-structure of the differential love game satisfies the differentiability properties specified above. Let $({\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2)\mapsto ({\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{x}}^{♡})$ be the equilibrium solution defined by system (15) in a neighborhood of a solution $({\overline{c}}_{1,0}^{♡},{\overline{c}}_{2,0}^{♡},{\overline{x}}_0^{♡},{\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$ of the system. We have:

(III) If  ${\left(D_1\right)}_{c_1,{\beta }_1}^{″}\left({\overline{c}}_{1,0}^{♡},{\beta }_1^0\right)>0$, then  ${\displaystyle \frac{\partial {\overline{c}}_1^{♡}}{\partial {\beta }_1}}<0$,  ${\displaystyle \frac{\partial {\overline{c}}_2^{♡}}{\partial {\beta }_1}}>0$,   and  ${\displaystyle \frac{\partial {\overline{x}}^{♡}}{\partial {\beta }_1}}<0$  at  $({\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0).$

(IV) If  ${\left(D_2\right)}_{c_2,{\beta }_2}^{″}\left({\overline{c}}_{2,0}^{♡},{\beta }_2^0\right)>0$, then  ${\displaystyle \frac{\partial {\overline{c}}_1^{♡}}{\partial {\beta }_2}}<0$,  ${\displaystyle \frac{\partial {\overline{c}}_2^{♡}}{\partial {\beta }_2}}>0$,  and  ${\displaystyle \frac{\partial {\overline{x}}^{♡}}{\partial {\beta }_2}}<0$  at  $({\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$.

Similarly to the proof of Proposition 1, Statement (III) follows by differentiating system (15) at the point $({\overline{c}}_{1,0}^{♡},{\overline{c}}_{2,0}^{♡},{\overline{x}}_0^{♡},{\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$, now setting $\mathrm{d}{\alpha }_1=\mathrm{d}{\alpha }_2=\mathrm{d}{\beta }_2=0$, and using the properties of the $UD$-structure and the fact that the matrix $\mathbf{A}$ defined in (16) satisfies $det\left(\mathbf{A}\right)<0$:

$$\left[\begin{array}{c}\mathrm{d}{\overline{c}}_1^{♡}\\ \mathrm{d}{\overline{c}}_2^{♡}\\ \mathrm{d}{\overline{x}}^{♡}\end{array}\right]=-{\displaystyle \frac{1}{det\left(\mathbf{A}\right)}}\left[\begin{array}{c}-r\left(r+{\rho }_1\right)\left(r+{\rho }_2\right){\left(D_2\right)}_{c_2,c_2}^{\prime \prime }{\left(D_1\right)}_{c_1{\beta }_1}^{″}+a_2^2\left(r+{\rho }_1\right){\left(D_1\right)}_{c_1,{\beta }_1}^{″}{\left(U_2\right)}_{x,x}^{″}\\ -a_1{a}_2\left(r+{\rho }_1\right){\left(U_2\right)}_{x,x}^{″}{\left(D_1\right)}_{c_1,{\beta }_1}^{″}\\ -a_1\left(r+{\rho }_1\right){\left(D_2\right)}_{c_2,c_2}^{″}{\left(D_1\right)}_{c_1,{\beta }_1}^{″}\end{array}\right]\mathrm{d}{\beta }_1,$$

(18)

All derivatives in the above expression are evaluated at $({\overline{c}}_{1,0}^{♡},{\overline{c}}_{2,0}^{♡},{\overline{x}}_0^{♡},{\alpha }_1^0,{\alpha }_2^0,{\beta }_1^0,{\beta }_2^0)$. Statement (IV) is obtained in a similar fashion.

Remark 2. 

Condition ${\left(D_i\right)}_{c_i,{\beta }_i}^{\prime \prime }>0$ in Proposition 2 reflects increasing marginal emotional cost with respect to ${\beta }_i$: as effort sensitivity ${\beta }_i$ rises, the subjective burden of additional effort increases accordingly. This is a reasonable assumption, and it is sufficient to determine the impact of ${\beta }_i$ on the equilibrium values.

The response of the equilibrium values $({\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{x}}^{♡})$ to small increases in $\mathrm{d}{\beta }_1>0$, $\mathrm{d}{\beta }_2>0$ (holding $\mathrm{d}{\alpha }_1=\mathrm{d}{\alpha }_2=0$ fixed) is qualitatively illustrated in Figure 2.

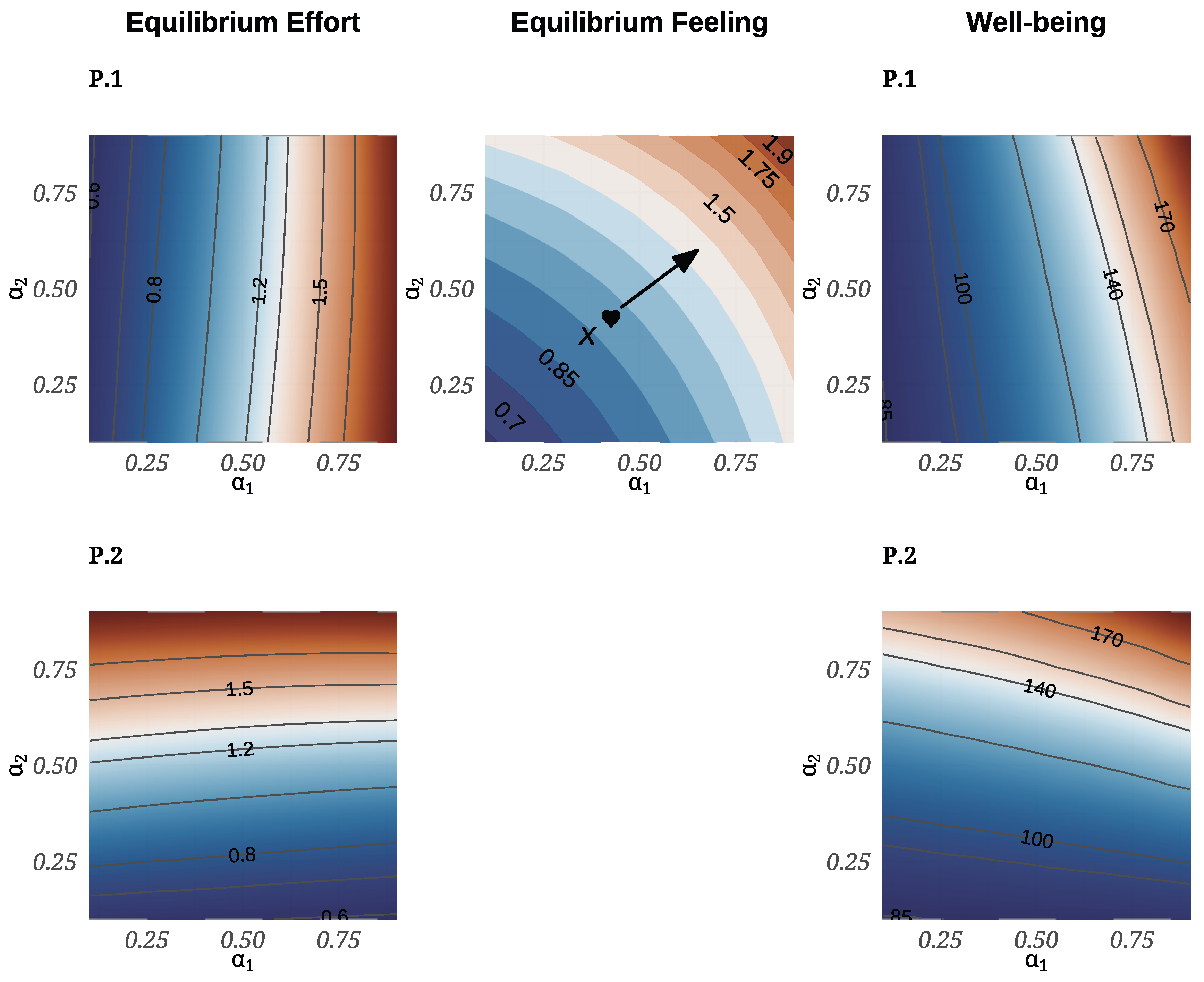
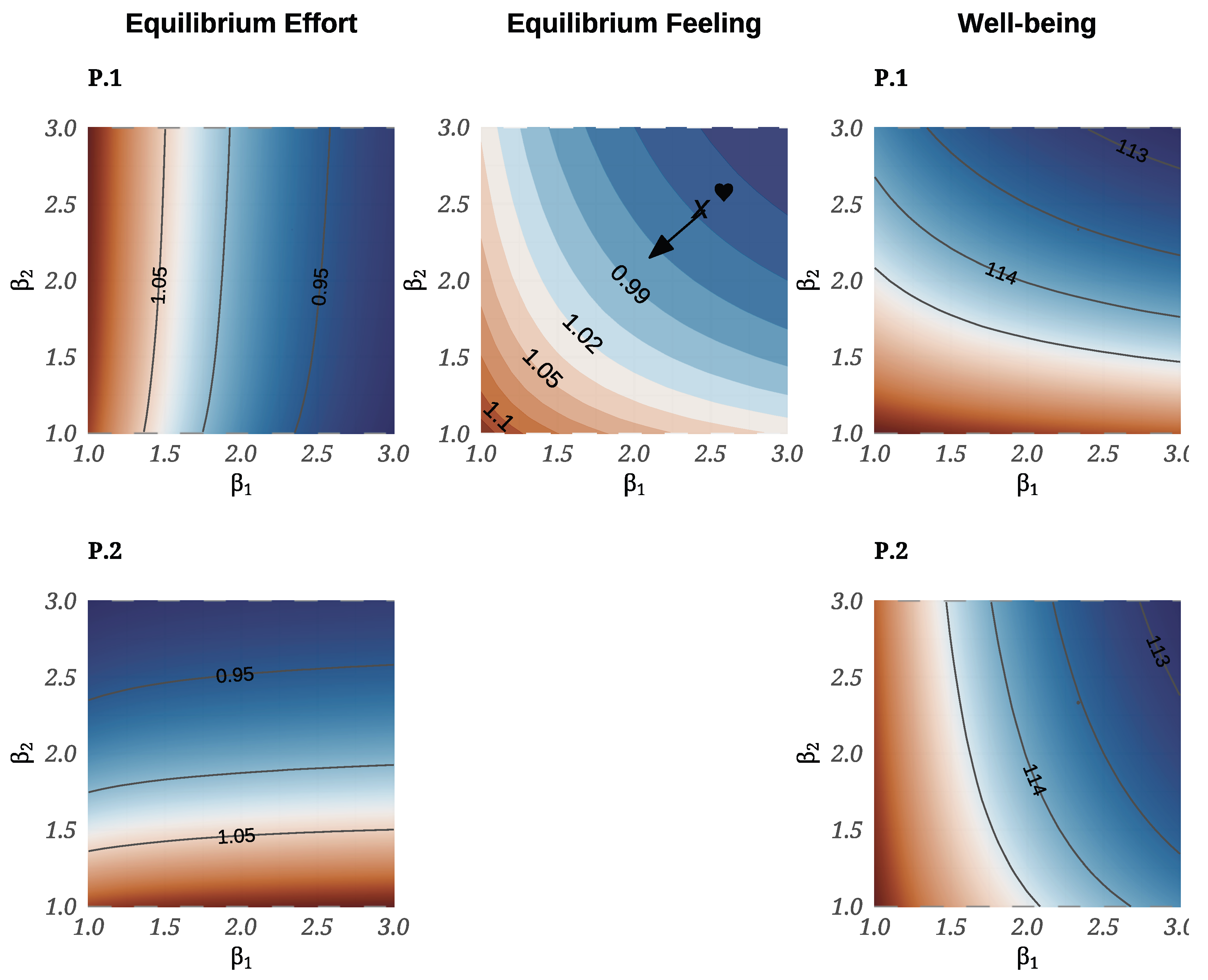
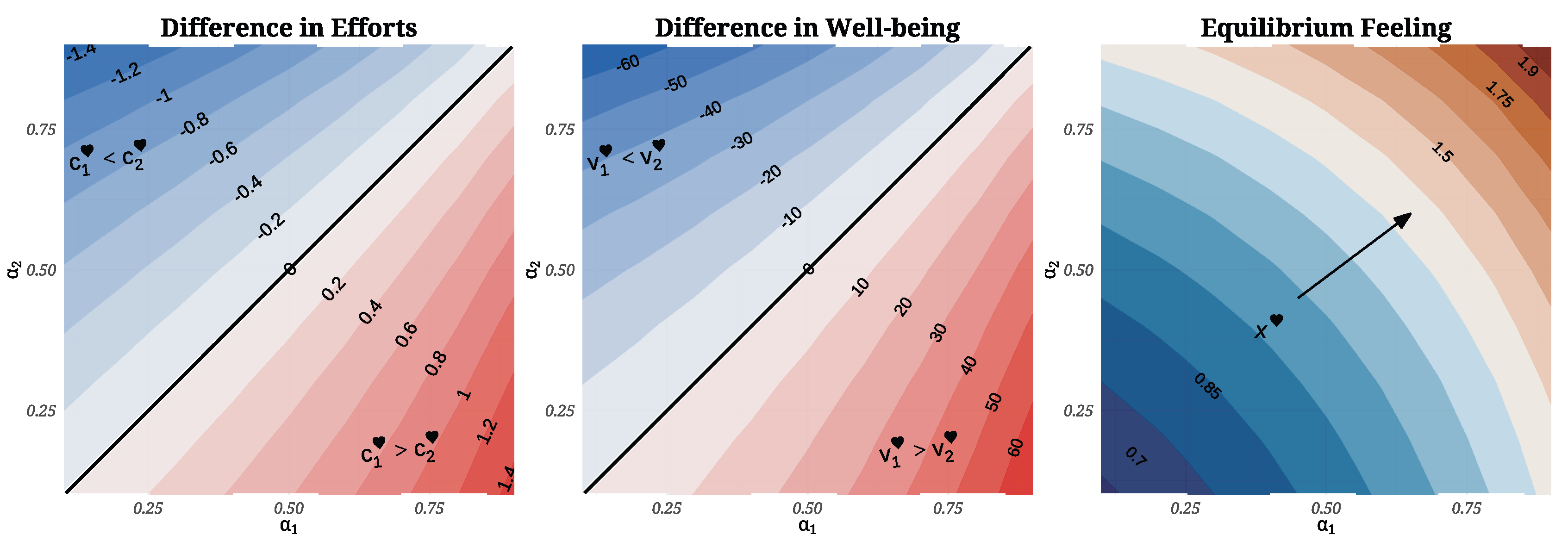
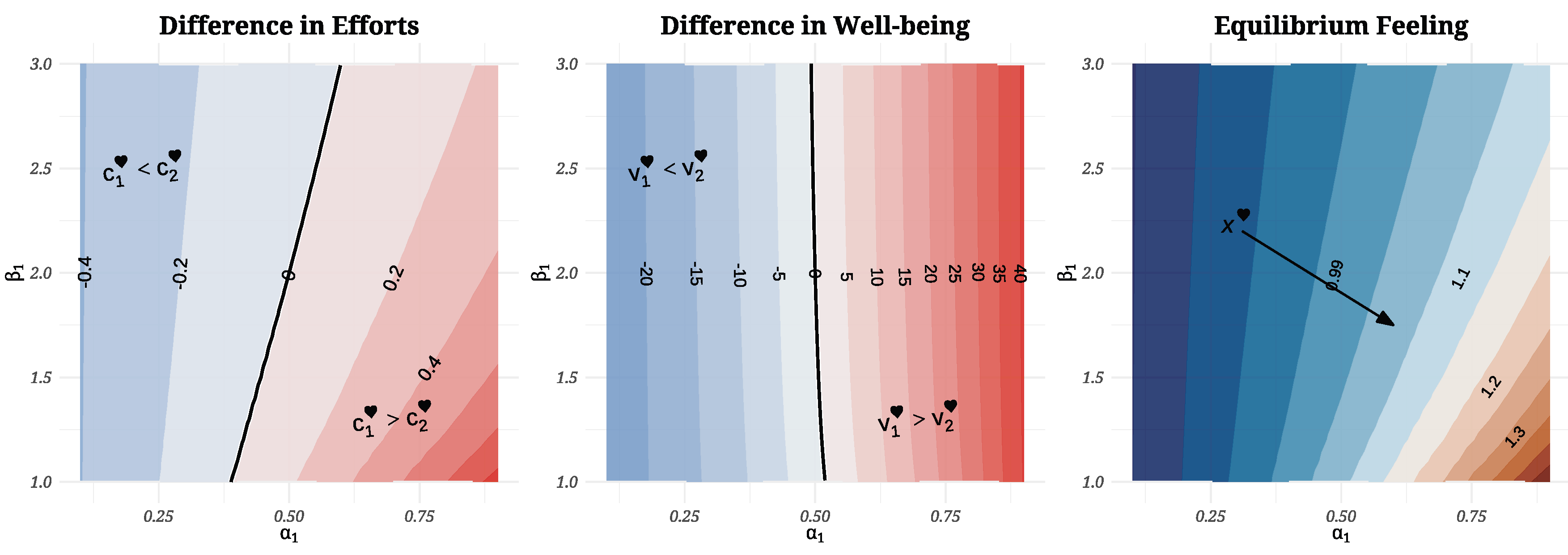
Emotional Contour Maps at Equilibrium: Computational Feedback Analysis

In this section, we use the computational feedback model introduced in Section 2 to explore further how the equilibrium values in the love differential game respond to changes in the emotional sensitivity parameters ${\alpha }_i$ and ${\beta }_i$. Numerical solutions are computed using the RaBVIt-G algorithm, as previously described. While Propositions 1 and 2 establish the qualitative effects of the variation in these parameters, the feedback approach allows for a quantitative analysis once a specific $UD$-structure is defined. Additionally, it yields feedback effort maps $S_i^{♡}\left(x\right)$ and value functions $v^{♡}\left(x\right)$, which are critical tools for regulating relationship dynamics. We also analyze below how variations in the parameters ${\alpha }_i$ and ${\beta }_i$ affect these feedback outputs.

In our numerical analysis, we assume that heterogamy—i.e., asymmetry in the partners’ traits—affects only the emotional cost-benefit evaluation of the relationship, namely the $UD$-structure of the problem. Accordingly, we set $a_1=a_2=a$ and ${\rho }_1={\rho }_2=\rho$, where a and $\rho$ are fixed constants.

We will consider the following specification for the $UD$–structure of the problem:

$$\left\{\begin{array}{c}{U}_i(x_i,{\alpha }_i)=A_i{(x+1)}^{{\alpha }_i},{\alpha }_i\in (0,1),A_i>0,\hfill \\ D_i(c_i,{\beta }_i)={\beta }_i{(c_i-c_i^{*})}^2+{\displaystyle \frac{(1-{\beta }_i){(c_i-c_i^{*})}^2}{1+{(c_i-c_i^{*})}^2}},{\beta }_i>0,i=1,2.\hfill \end{array}\right.$$

(19)

This parametric $UD$-structure satisfies all the properties required by the model assumptions outlined in Section 2. Graphs of both parametric families, $U_i$ and $D_i$, are presented in Figure 3. Note that the family $U_i(x,{\alpha }_i)$ is monotonic with respect to ${\alpha }_i$: for all $x>0$, $U_i(x,{\alpha }_i)$ increases as ${\alpha }_i$ increases. As already mentioned, the parameter ${\alpha }_i$ captures how each partner subjectively values the quality of the relationship. Also, note that $U_i(x,{\alpha }_i)$ satisfies the assumption in Proposition 1, that is, the marginal emotional reward, ${\left(U_i\right)}_x^{\prime }(x,{\alpha }_i)$, increases with ${\alpha }_i$.

Similarly, for all ${\beta }_i>0$, the family $D_i(c_i,{\beta }_i)$ attains an absolute minimum at $c_i=c_i^{*}$ and increases with ${\beta }_i$ for $c_i>c_i^{*}$. Therefore, any effort level $c_i$ exceeding the preferred level $c_i^{*}$ is perceived as increasingly discomforting as ${\beta }_i$ grows. Hence, the parameter ${\beta }_i$ quantifies the discomfort associated with the effort gap $c_i-c_i^{*}$. Also, the family $D_i(c_i,{\beta }_i)$ satisfies the assumption in Proposition 2: the marginal emotional cost, ${\left(D_i\right)}_{c_i}^{\prime }(c_i,{\beta }_i)$, increases with ${\beta }_i$.

Once the parametric $UD$-structure is specified, all model parameters other than ${\alpha }_i$ and ${\beta }_i$, for $i=1,2$, are held fixed for the numerical analysis. In our study, the sensitivity parameters vary within the ranges ${\alpha }_i\in (0,1)$ and ${\beta }_i\in [1,3]$. All fixed parameter values and the ranges considered in the analysis are summarized in Table 1.

The computational procedure uses the RaBVIt-G algorithm, outlined in Section 2, to numerically solve the differential love game. The implementation protocol for computing equilibrium solutions is detailed in Algorithm 1 below1.

Algorithm 1:Equilibrium Solution Computation

1: Initialize ${\alpha }_1,{\alpha }_2\in (0,1)$, ${\beta }_1,{\beta }_2\in [1,3]$, $x_0=4.5$, $ϵ={10}^{-4}$. 2: Compute feedback strategies and values: $[S_1,S_2,v_1,v_2]\leftarrow \mathrm{RaBVit}-\mathrm{G}({\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2)$ 3: while not converged do 4:     Update efforts: $c_{i,k}=S_i\left(x_k\right)$ for $i=1,2$ 5:     Evolve feeling state: $x_{k+1}=x_k+h(-r{x}_k+a_1{c}_{1,k}+a_2{c}_{2,k})$ 6:     Increment $k\leftarrow k+1$ 7: end while 8: Extract equilibrium: ${\overline{x}}^{♡},{\overline{c}}_1^{♡},{\overline{c}}_2^{♡},{\overline{v}}_1^{♡},{\overline{v}}_2^{♡}$.

For any given parameter set $({\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2)$, the RaBVIt-G algorithm computes the feedback maps $S_1(·)$ and $S_2(·)$, as well as the well-being (value) functions $v_1^{♡}(·)$ and $v_2^{♡}(·)$ associated with the corresponding problem. The algorithmic details for computing feedback solutions using RaBVIt-G can be found in [11].

We now present a detailed numerical sensitivity analysis. To visualize how the equilibrium solutions respond to changes in the parameters, ${\alpha }_i$ and ${\beta }_i$, we use contour plots over the corresponding parameter spaces. The results are discussed as they are introduced.

Emotional Reward Sensitivity

We first explore how the equilibrium varies with respect to the emotional reward parameters ${\alpha }_1$ and ${\alpha }_2$. Figure 4 and Figure 5 summarize the analysis with respect to ${\alpha }_i$-sensitivity. In these computations, the cost parameters are fixed at ${\beta }_1={\beta }_2=1$, and heterogeneity between partners arises solely from variations in the parameters $({\alpha }_1,{\alpha }_2)\in (0,1)\times (0,1)$.

Figure 4 displays contour maps of the partners’ equilibrium effort levels and the equilibrium feeling level, for different values of $({\alpha }_1,{\alpha }_2)$. These maps show that each partner’s effort level ${\overline{c}}_i^{♡}$ increases with their own emotional reward parameter ${\alpha }_i$. Moreover, the equilibrium feeling level ${\overline{x}}^{♡}$ increases as either ${\alpha }_1$ or ${\alpha }_2$ increases. Since the marginal emotional reward, ${\left(U_i\right)}_x^{\prime }$, grows with ${\alpha }_i$ in this study, these effects were already established analytically in Proposition 1.

The cross-effects —i.e., the variation of ${\overline{c}}_i^{♡}$ with respect to the other partner’s parameter ${\alpha }_j$, $i\ne j$— are less apparent in the contour maps. Nonetheless, Proposition 1 confirms that these cross-effects are negative. This result is further illustrated in Figure 5, which shows the feedback effort maps $S_i^{♡}(·)$ and the well-being functions $v_i^{♡}(·)$ for different values of ${\alpha }_2\in (0,1)$, while keeping ${\alpha }_1=0.5$ (and ${\beta }_1={\beta }_2=1$) fixed.

Note that Figure 5 confirms three key insights previously suggested by the contour maps in Figure 4. First, the effort gap $c_i-c_i^{*}$ persists for both individuals: across all values of ${\alpha }_2$, each partner exerts an effort level above $c_i^{*}$. Second, effort decreases as feeling increases for both individuals —that is, lower emotional closeness requires greater effort. Third, well-being increases with the initial feeling level: greater emotional closeness at the outset is associated with higher overall happiness. These features of the model were already revealed in earlier computational analyses, both in deterministic [11] and stochastic [12] settings.

The plots in Figure 5 show that as ${\alpha }_2$ increases, its positive effect on $c_2^{♡}=S_2^{♡}\left(x\right)$ is significantly stronger than its negative effect on $c_1^{♡}=S_1^{♡}\left(x\right)$, for any given level of feeling x, in particular at the equilibrium value ${\overline{x}}^{♡}$. Moreover, the equilibrium feeling level itself increases with ${\alpha }_2$.

Note that the fact that an increase in ${\alpha }_i$ has a stronger (positive) effect on partner i’s equilibrium effort, ${\overline{c}}_i^{♡}$, than the (negative) effect on partner j holds for any parametric $UD$-structure satisfying the conditions stated in Section 2. This result follows as a corollary of Proposition 1 -see (17).

Corollary 1. 

Under the assumptions of Proposition 1, it holds that

$${\displaystyle \frac{\partial {\overline{c}}_i^{♡}}{\partial {\alpha }_i}}>\left|{\displaystyle \frac{\partial {\overline{c}}_j^{♡}}{\partial {\alpha }_i}}\right|,\mathrm{for}i\ne j,i,j\in \{1,2\}.$$

The well-being functions in Figure 5 show that increases in ${\alpha }_2$ lead to higher overall happiness for both partners, although the effect is markedly stronger for partner 2. This asymmetry is confirmed numerically across the full parameter range $({\alpha }_1,{\alpha }_2)\in (0,1)\times (0,1)$, as illustrated in the rightmost column of Figure 4, where both partners’ well-being levels (for initial state $x_0=4.5$) are plotted. Notably, an increase in the parameter of emotional sensitivity of a partner, ${\alpha }_i$, produces a greater improvement in his (her) own well-being than an equivalent increase in the parameter of the other partner, ${\alpha }_j$.

Emotional Cost Sensitivity

Next, we examine how variations in the emotional cost parameters ${\beta }_1$ and ${\beta }_2$ affect the equilibrium configuration. Figure 6 and Figure 7 summarize the analysis of sensitivity with respect to ${\beta }_1$ and ${\beta }_2$. The reward parameters are fixed at ${\alpha }_1={\alpha }_2=0.5$, and asymmetry between partners arises from differences in the values ${\beta }_1$ and ${\beta }_2$, both varying within the range $[1,3]$.

Figure 4 displays contour maps of the equilibrium effort levels and feeling level for $({\beta }_1,{\beta }_2)\in [1,3]\times [1,3]$. The plots show that each partner’s effort level, ${\overline{c}}_i^{♡}$, decreases with their own emotional cost parameter, ${\beta }_i$. Additionally, the equilibrium feeling level, ${\overline{x}}^{♡}$, decreases as either ${\beta }_1$ or ${\beta }_2$ increases. As shown analytically in Proposition 2, these effects arise because the marginal emotional cost, ${\left(D_i\right)}_{c_i}^{\prime }$ increases with ${\beta }_i$ for the $UD$-structure under study.

Figure 6 shows that the cross-effects —i.e., the variation of ${\overline{c}}_i^{♡}$ with respect to ${\beta }_j$, for $i\ne j$— are positive. This is illustrated more clearly in Figure 7, which displays the feedback effort maps $S_i^{♡}(·)$ and the well-being functions $v_i^{♡}(·)$ for ${\beta }_2\in [1,3]$, with ${\beta }_1=1$ and ${\alpha }_1={\alpha }_2=0.5$ held constant.

Figure 7 highlights several key features of the model’s behavior, already suggested by the contour plots in Figure 6. First, the effort gaps $c_i-c_i^{*}$ persist for both individuals across all values of ${\beta }_2$. Second, the effort gaps decrease as the feeling increases. Third, well-being improves with higher levels of initial feeling. These properties of the model were previously identified through computational analyses in [11,12].

The plots in Figure 7, however, show that as ${\beta }_2$ increases, the negative effect on $c_2^{♡}=S_2^{♡}\left(x\right)$ is substantially stronger than the positive effect on $c_1^{♡}=S_1^{♡}\left(x\right)$, for any x —in particular at the equilibrium value ${\overline{x}}^{♡}$. As a result, the equilibrium feeling level decreases with ${\beta }_2$. This holds for any $UD$-structure satisfying the conditions in Section 2, as a consequence of (18).

Corollary 2. 

Under the assumptions of Proposition 2, it holds that

$$\left|{\displaystyle \frac{\partial {\overline{c}}_i^{♡}}{\partial {\beta }_i}}\right|>{\displaystyle \frac{\partial {\overline{c}}_j^{♡}}{\partial {\beta }_i}},\mathrm{for}i\ne j,i,j\in \{1,2\}.$$

Figure 7 shows that increases in ${\beta }_2$ lead to lower overall happiness for both partners, and the effect is stronger for partner 1. An increase in partner i’s emotional cost parameter, ${\beta }_i$, lowers his or her well-being less than that of the other partner. This asymmetry holds throughout the parameter range $({\beta }_1,{\beta }_2)\in [1,3]\times [1,3]$, as the well-being of both show in the rightmost column of Figure 6.

Dyadic disparity assessment

We further explore how the disparities between the parameters ${\alpha }_1$ and ${\alpha }_2$ influence the asymmetric performance of the partners at equilibrium. Figure 8 compares their respective levels of effort and well-being over the parameter range $({\alpha }_1,{\alpha }_2)\in (0,1)\times (0,1)$, with ${\beta }_1={\beta }_2=1$ kept constant. The numerical analysis reveals that the partner with the higher emotional reward parameter, ${\alpha }_i$, exerts more effort and experiences greater well-being. As already shown in Figure 4, the equilibrium feeling level increases when either or both of the ${\alpha }_i$ parameters increase.

The corresponding asymmetry analysis for the parameters ${\beta }_1$ and ${\beta }_2$ is presented in Figure 9. The contour maps display disparities in the partners’ equilibrium effort levels and well-being across the parameter domain. The computational analysis shows that the partner with the higher emotional cost parameter, ${\beta }_i$, exerts less effort and experiences higher well-being. Moreover, the equilibrium feeling level decreases as either or both of the ${\beta }_i$ parameters increase.

Our analysis shows that an increase in the emotional reward parameter ${\alpha }_i$ has a greater effect on partner i’s own effort level than on that of partner j. Similarly, an increase in the emotional cost parameter ${\beta }_i$ influences partner i’s effort level more than partner j’s. In both cases, the resulting impact on well-being is more favorable for partner i. These findings relate to the broader question of whether one’s own personality traits or those of one’s partner play a greater role in determining relationship satisfaction [15]. Prior research in experimental psychology suggests that individuals’ own traits are more strongly associated with their own happiness [26]. Assuming that the emotional processing of rewards and costs reflects underlying personality traits, our model’s predictions are consistent with this empirical evidence.

A final disparity analysis of the equilibrium configuration, focusing on the trade-off between the two emotional sensitivity parameters, is presented in Figure 10. The analysis considers joint variations of the parameters ${\alpha }_1$ and ${\beta }_1$, while ${\alpha }_2=0.5$ and ${\beta }_2=2$ are held constant. The contour maps show disparities in the partners’ equilibrium effort levels and well-being across the parameter domain $({\alpha }_1,{\beta }_1)\in (0,1)\times [1,3]$. The results indicate that the pattern becomes more nuanced when both parameters vary simultaneously. In this case, a partner with a higher ${\alpha }_i$ or a lower ${\beta }_i$ does not necessarily exert more effort. However, the numerical analysis suggests that a partner with higher ${\alpha }_i$ consistently achieves greater well-being, regardless of their sensitivity to effort costs. As established in Proposition 1, the equilibrium feeling level decreases along the southeast direction of the domain. Notably, the increase in feeling level due to a higher ${\alpha }_i$ is more pronounced than the increase resulting from a comparable decrease in ${\beta }_i$.

4. Conclusions

Romantic relationships are a fundamental human experience shared across cultures. They can be understood as emotional processes that evolve over time, in which the state of the relationship is shaped by the effort each partner invests. According to relationship science, successful relationships are those that are both enduring and fulfilling in the long term. In this study, a successful relationship is modeled as a stationary Nash equilibrium of a two-person differential game, in which both partners aim to maximize their total well-being.

Life experiences and events do not carry inherent meaning; rather, they acquire significance through the interpretations of the individuals who live them. The subjective evaluation of the trade-off between emotional rewards and costs associated with a relationship plays a critical role in determining its outcome —namely, the relationship quality (or feeling level), the effort exerted by each partner, and their overall satisfaction.

Emotional rewards vary depending on individual sensitivity to relationship quality, while emotional costs arise from differences in how individuals perceive the effort required to sustain that quality. The ceteris paribus analysis in this paper explores how the sensitivity traits defined by these two intertwined subjective processes influence relationship outcomes. Under natural psychological assumptions about these traits, our analytical results show that relationship quality improves when either partner is more sensitive to emotional rewards, and also when either partner is less sensitive to emotional costs. These findings suggest that couples in which both individuals are either highly sensitive to emotional rewards or less sensitive to emotional costs tend to form more satisfying relationships and ultimately experience greater happiness.

In relationship science, the influence of one’s own traits on one’s own relationship satisfaction is known as the actor effect, while the influence of the partner’s traits on one’s own satisfaction is referred to as the partner effect. With respect to reward sensitivity, our formal analysis shows that an individual’s effort increases with their own sensitivity, but decreases with their partner’s sensitivity. Thus, the actor effect of emotional reward sensitivity on effort is positive, while the partner effect is negative. In contrast, for cost sensitivity, the actor effect on effort is negative, while the partner effect is positive.

The analysis also formally establishes that, in terms of effort exertion, the actor effects of sensitivity to emotional reward and cost are stronger than the corresponding partner effects. Computational results reinforce this finding, suggesting that the differences between actor and partner effects are substantial in both cases. Moreover, the numerical analysis indicates that actor effects have a significantly greater impact than partner effects on each partner’s overall well-being. Notably, these results —derived from the mathematical analysis of the differential love game model— are consistent with experimental evidence in social psychology: actor effects of personality traits tend to have greater influence on relationship satisfaction than partner effects.