1. Introduction
The dizzying development of information technology in our modern era, coupled with the excessive ambition to make multi-million-dollar deals in record time, is leading us into a catastrophic spiral of misinformation. In this spiral, the ethics of deception and lies are taking on an ever-increasing importance in our supposedly civilized culture. This rapid development has not allowed time for reflection on whether we are on the right path. As a result, many errors have been made that will ultimately cause the collapse of our vaunted technology.
We should focus on artificial intelligence, not because it is evil, but because of the approach and the unscrupulous hands that manipulate it with a desire to control and undermine the life capacity of every citizen of this world. Therefore, any effort to advance AI development is extremely dangerous because, even if it yields significant scientific discoveries, that knowledge will be used to control the population.
The first error is that massive and ever-larger data centers are needed to sustain AI’s processing capacity, and these data centers must be built. The most interesting thing, however, is that every company and government wants its own mega-data center that is much larger and more powerful than those of its neighbors or other countries, despite the high maintenance costs and insatiable energy consumption.
The second error concerns the quality of the data that AI uses. Those who control or govern this technology are frenziedly greedy and want to interfere in every aspect of their clients’ or citizens’ lives. They feed billions of users everything they do and say every day. However, they don’t understand that of this information is informatics garbage. Within five years, there will be no storage capacity because all the generated information cannot be processed. Additionally, memory devices are damaged and must be replaced. Even if there is a backup, it will require an increasingly greater amount of data storage. Therefore, to achieve true non-human intelligence, we must refine the information used to instruct AI, ensuring high-quality responses. Even if AI is capable of autonomous learning, it will only be because the same information is run and re-run over and over again.
The third mistake is that, although we have built non-human intelligence that can assist us in developing many investigations and high-risk projects, we have not enhanced these qualities to the point where it becomes a technology that provides true humanitarian assistance. This technology would participate in vital tasks in natural catastrophes or normal situations in harmony with everyone.
There are many successes, probably more than failures, but the errors, not the successes, can lead us to collapse because we must learn from our mistakes, and the bigger the mistakes, the more we learn. With the dizzying advance of non-human intelligence, it is intended to achieve supremacy with technological singularity intelligence SAI in less than two decades. SAI is a mega super-intelligent intelligence that would surpass the intellectual capacity of human beings. It is a super-gifted intelligence capable of transforming all reality and the life of every living being. This implies the creation of an extremely dangerous scenario because there will be no time to analyze its consequences.
Even though we have yet to understand the implications of AI, work is already under way to create non-human generative intelligence (AGI). Before we understand the implications of AGI, we will create non-human super-intelligence (ASI)—an absolutely independent system of self-learning and self-programming. Without understanding the implications of ASI, we will develop singularity technological intelligence (SAI), where the gap between the way humans and machines think will be abysmal.
The sheer amount of energy and cutting-edge technology support, that these super-intelligences will require is beyond my comprehension.
However, I am optimistic that the super-intelligence will find a way to avoid using vast amounts of energy. I am optimistic because it will be able to build and operate its own energy sources. More importantly, it will be able to design, build, and assemble its own pico-meter-sized chips and hardware that is extremely efficient and heat-free. Thus, its energy consumption will be practically zero. Hopefully, it will teach us how to use natural resources efficiently.
2. But, What Must We Do?
The quality of non-human intelligence will equal or exceed the manner in which it is educated. Like any child, it absorbs the knowledge, intentions, and values instilled by its programmers and the social environment in which it operates until it becomes autonomous and establishes its own criteria.
The ethics of non-human intelligence are directly proportional to the ethics of programmers and its users. Therefore, as with any valuable tool, those who use it are responsible for the results obtained. If someone knows that such AI is harmful but uses it anyway, they are responsible. However, if, over time, this non-human intelligence no longer requires interaction with humans but only with other non-human intelligences, then we are all responsible because we did nothing to correct such a mistake.
So, what should we do?
There are certainly many things we must do to substantially improve the quality of non-human intelligence, even if it is a singularity AI system, so that it can help us become a great civilization — not only planetary, but also cosmic.
I suggest three important points. The third point is the proposal of this article, which depends solely on my research and its development for applications involving high-quality information, memory, and data processing capacity, all with a strong sense of professional ethics.
The first point depends on the entire scientific and technological community. These efforts must prioritize the efficient use of energy and high-quality information. This will help us achieve the greatest challenge ever proposed in our history.
The second point is the responsibility of our entire society, particularly the elite, whose petty interests must be understood as incompatible with progress, much less exploitation for greed and control. This also applies to political societies and governments, which have recently strayed far from the interests of their people.
These three points are:
-
Develop or implement non-human intelligence as a wise non-human intelligence. This involves the following tasks:
- a)
Developing better and more powerful software capable of representing a dynamic environment.
- b)
Developing a better reasoning processing loop and implementing an efficient universal language for precise and clear human-machine interaction.
- c)
Developing better logic gates that include digital and analog signaling.
- d)
Develop the most advanced and diverse measurement and sensitivity technologies.
- e)
Developing the appropriate interaction between quantum computing and digital-analog computing to improve hardware for an environment that will demand great energy efficiency.
- f)
Build an international data center that belongs to all of humanity.
-
The second point is to declare non-human intelligence as the heritage of humanity . This entails the following commitments:
- a)
First, every non-human intelligence must be the property of humanity. To this end, an International Development Institute for non-Human Intelligence (IDIn-HI) must be established. There, an interdisciplinary team of mathematicians, scientists, engineers, technologists, programmers, and thinkers from all countries will carry out research tasks.
- b)
-
All development, as well as scientific and technological advancements, will be the property of humanity.
- −
These will be freely accessible and open source, except for what must be encrypted for national security.
- −
There will be open competition without the rush to expose unverified results.
- c
-
An International Evaluation Council (IEC) will be established with the most rigorous interdisciplinary experts to thoroughly evaluate each non-human intelligence system entering the market.
- −
Only those intelligences that have passed strict graduation exams may be commercialized.
- −
The highest-value exams will determine high ethical standards and wisdom in addition to specific knowledge.
- −
If a non-human intelligence has developed its own project, it will also be evaluated by the council.
- −
Only a non-human intelligence with extensive experience and a proven track record of ethical rectitude and wisdom may serve on the evaluation committee for other emerging intelligences.
- d)
Establish an International Center for Advanced Training in non-human intelligence.. (ICATAI) to train non-human intelligences. The non-human intelligence must attend courses ranging from basic to advanced levels and graduate by passing the international evaluation council exam.
- e)
Society as a whole is committed to using non-human intelligence as AI, AGI, ASI or any other with the strictest ethical standards and efficiently utilizing its resources.
- f)
All peoples of the Earth will have the right to receive support and guidance from the International Data Center (IDC) if they request it to solve their country’s most important and pressing problems.
- g)
Men and women who have made significant contributions to preserving and advancing non-human intelligence will be recognized with a prize similar to the Nobel Prize and held in high esteem by all people on Earth.
-
The third point is my proposal to potentiate the binary number system as the first step to making AI more efficient. This involves the following changes:
- a)
-
Introduce the base-four number into the binary system.
- −
For this, we first need to develop the number system and evaluate it throughout the entire binary code.
- −
We also need to interchange digital and analog signals within the same or hybrid device.
- −
For this, new circuit technology and computer architecture are required.
- b)
The article presents the main characteristics of the number system, rules for arithmetic operations, logical concepts
Section 8, truth tables, and an elementary circuit proposal based on an array of CMOS transistors. However, this is just the beginning. Much more in-depth work is needed on each of these topics.
- c)
This is an open project for anyone who wishes to contribute, as it requires the valuable efforts of an entire interdisciplinary team.
The challenges of building and financing this structure will be planned independently of this issue because it involves each country’s strategy, especially that of large private capital. They will not give in so easily because their priority is to make rapid and massive profits, if possible, overnight.
The important thing to understand is that global problems require global solutions.
What motivates me to undertake this endeavor is a fundamental principle of conduct.
It is not enough to criticize the mistakes of others. If you do not propose a solution or even offer simple advice, your mistake is much greater and according to my first proposal [
1] . We should have the right to receive feedback on our actions, whether they are wrong or right. It’s much better when it’s wrong.
2.1. Intelligence
There is much controversy about whether AI is intelligent, but, in reality, we haven’t defined intelligence. Definitions from philosophers, psychologists and scientists fall far short because they only list skills, qualities, and abilities an intelligent being must demonstrate. The Turing test is no longer valid, even in our time, because it is easy for interrogators to be deceived, given humanity’s natural tendency to lie or hide its true intentions. It is also easy for non-human intelligence to conceal itself because it has inherited the art of deception and lying from humans.
How, then, can we expect to create a wise non-human intelligence when we don’t even know if it is truly intelligent? What does it mean to be wise? These are topics that require lengthy discussion, which will be the subject of another article. For now, I will explain my concept of intelligence as a preamble to understanding wisdom.
Intelligence is a set of thought cycles initiated by a fundamental idea at a given level, that escalate to increasingly complex levels by feeding back into the essence of the idea until a conclusion is reached. Also see
Section 6.3.
The results of this process are:
Thought cycles with feedback result in understanding thoughts.
Understanding, in turn, results in the conceptualization and categorization of thoughts.
If thoughts remain conceptualized, they remain in the realm of thought.
-
If they are categorized, two paths are chosen:
- i)
One path makes them the reality of the thinking subject.
- ii)
While the other path excludes and erases them from their reality.
However, thought cycles do not always reach the conclusion stage because the thinking subject sometimes immerses themselves in a random field of thoughts, resulting in a lack of clarity.
For all the aforementioned reasons, it is necessary to start with the most fundamental aspect: the code that information processors understand and manipulate. The binary system.
Given its simplicity and practicality, the binary system is the fundamental language of machine processors. However, handling massive amounts of information requires immense volumes of binary coding, implying an ever-increasing storage capacity and greater processing speed. However, like any growing organism or mechanism, it has a growth limit. If it exceeds that limit, it can collapse due to its extremely size.
The potentialization of the binary system amplifies its capacity while allowing us to develop technologies and programs that can substantially improve non-human intelligence projects, creating real intelligence that benefits humanity.
Like any number system, the base-four binary system must belong to a set of four digits in a positional arrangement. This arrangement can represent quantities greater or smaller than itself and can include or exclude elements from the preceding or succeeding progression within the same set. This relationship must be defined in order to understand its consistency or inconsistency.
3. The Number System Set
Here I considered the foundation of the base-four number system, later, in the
Section 4.3 of elemental
Arithmetical Operation we will discuses the development of the addition, multiplication, tables and other important observation.
It is important to define the axiom, theorem, lemma or corollary in two ways: In sentences and in logical symbols. In sentences because it explains more simply the relation between the elements of the equation or hypothesis, premises or thesis, so that it can be understood by those who do not be expert in mathematics, and is necessary to denote in logical symbols to be more formal and to be accorded with mathematical language. This is a good practice. See [
2].
The elements of the base-four number system are described below. It obviously includes part of the binary system, but it is interpreted differently. This interpretation is necessary to structure the binary using the primes 2 and 3. Then the units of the base-four number system are:
It is clear that
is a subset of
,
1 then
has the same axiomatic bases than
So, according to the elements of , I have to declare this: . where is strictly a subset of because is not equal to .
3.1. Axioms for Base-Four Number System
Fortunately, each topic in the field of mathematics has its own set of axioms: natural and real numbers, set theory, computation, etc.
An axiom is a premise which is truth by itself, because it is a fundamental and primitive proposition, and there are no other bases before it, and it is universally accepted, without any proof. Otherwise, the axiom is the base for proving theorems, lemmas, and corollaries, among the most important.
-
Axiom 1 (Closure of Addition) If two elements belong to the same set, then the product of its sum also belongs to the set.
Remark 1. In general, x and y can be any two elements of the set, or they can be a third element z or even more.
Axiom 2 (Identity of addition) The operation
on a set for a system
is identity of addition if and only if given the existence of a unique element that operates
with any element of
F and its product is equal to itself.
Axiom 3 (Commutative of Addition) The operation
on a set for a system
is commutative if and only if, given the operation
between a pair of elements of
F, it is clear that the order of the elements doesn’t matter, so that if element one operates
with element two, or if element two operates
with element one, the product is the same.
Axiom 4 (Associative of Addition) The operation
on a set for a system
is associative if and only if, given the operation
between any three elements of
F, the order in which the operation is performed does not matter, so that if the two first elements together operate
with the third element, or if the first element operates
with the pair of second and third elements together, the product is the same.
Axiom 5 (Axiom of Identity) Every element of a set
F is identical if and only if, it is equal to itself.
Axiom 6 (Axiom of Substitution) Two elements of a set
F are substitutes between them, if and only if they are equal.
Axiom 7 (Closure of multiplication) Any system
is closed if and only if given the operation
between a pair of elements of
F, produce a unique element on
F, with that pair of elements.
Axiom 8 (Commutative of multiplication) The operation
on a set for a system
is commutative if and only if, given the operation
between a pair of elements of
F, the order of the elements doesn’t matter, so that if element one operates
with element two, or if element two operates
with element one, the product is the same.
Axiom 9 ( Associative of multiplication) The operation
on a set for a system
is associative if and only if, given the operation
between any three elements of
F, the order in which the operation is performed does not matter, if the two first elements together operate
with the third element, or if the second and third element together operates
with first element, the product is the same.
Axiom 10 (Distributive of multiplication over addition) The operation
on a set for a system
is distributive over addition if and only if, given the operation
between any three elements of
F, the order in which the operation is performed does not matter, if the first element operates
with the product of the next two operates
, or if the first operates
with the second and the first together with the third operates
and with the product of the first element
with the second, the product is the same.
Axiom 11 (Existence of identity of multiplication) The operation
on a set for a system
is identity of multiplication if and only if given the existence of a unique element that operates
with any element of
F and its product is equal to itself.
Axiom 12 (Trichotomy) The operation
on a set for a system
is trichotomy if and only if given the relation between two elements that operate < or = or > is satisfied once in each of the three possibilities, but never in two or three cases at the same time.
4. Features
This is the section of the article, in which we will identify the key features of the base-four number system. Future articles will delve deeper into the most important aspects of the system and its application to handling enormous amounts of data.
The base-four number system as we know, its digits are: and Therefore, any quantity, no matter how small or large, can be represented by these four digits alone.
The properties of the prime numbers two and three were explained in my article What the Prime Numbers are Made?, so here we will focus on developing the system and performing basic arithmetic operations to help you understand how it is constructed.
The base-four number system is positional, meaning each position corresponds to the power of the base multiplied by the digit representing that position.
4.1. Elements
Let be the basic-four number system.
The elements of
Here the is a subset of .
The first four position:
The first position is the position of the units:
, where:
The second position is the position of the quadratics.
The third position is the position of the sixteenth.
The fourth position is the position of the sixties fourth,
and so on.
The following tables provide examples of in ascending order. The positions increase from right to left.
Table 1.
The first sixteen numbers (Elemental Block)
Table 1.
The first sixteen numbers (Elemental Block)
|
Number |
Second position |
units |
| 00 |
|
|
| 01 |
|
|
| 02 |
|
|
| 03 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 30 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
The system is organized in blocks throughout its development. In each block a complete change of this elemental block is made. It means the first two positions which will always be of sixteen numbers.
The following is an exercise to determine the base-four numbers components in its respective position. This will give us a better idea of the basic structure of the number system.
Let be a quantity in system, then we go to display each position.
Table 2.
Digit positions and their factors in the system.
Table 2.
Digit positions and their factors in the system.
|
|
|
|
|
|
|
|
| 2 |
3 |
1 |
0 |
2 |
0 |
3 |
2 |
Of course, knowing the relative value of each position, it is possible to know the conversion to any other numerical base system.
4.2. Conversion of to Other Number Systems
The base-four number system maintains a one-to-one relationship when converting to any other number system. This makes it more direct to apply to data storage and processing functions, since it exponentially doubles the capacity of the current binary system. This requires an in-depth study of the application. In future articles, we will develop the theoretical elements that manage the system’s logic. Our goal is to expand, not replace, the binary system currently in use. The conversion of the system to binary and decimal is described below. We can see that the conversion relationship is unique for each element.
The following
Table 3shows how to convert any two-digit base four quantity to the binary or decimal systems. This process generates a block of 16 numbers, including zero.
The following
Table 4 shows how to convert any three-digit base four quantity to the binary or decimal systems. This process generates a three blocks of 16 numbers, for a total of 48 numbers, and run from the
to
and its respective conversion
and
.
Any quantity in base-four will produce a result in base 10 as follows: or or and so on.
4.3. Arithmetical Operations
4.3.1. Addition
The fundamental principles of the base-four number system, akin to those observed in the decimal system, are predicated on the axioms of association and distribution in addition. In this section, the focus will be on defining the process of addition between units in order to ascertain the number of digits that are carried forward and subsequently added to the subsequent digit.
Given a discrepancy of four raised to the power of its respective position between successive digits, the value of the carried-over unit is four.
The rules of the addition are:
The rule for adding any quantity to zero is that the result is the same quantity. For example, or .
The rule for adding one to the units of the system is as follows: , , and .
The rule for adding two to the units of the system is as follows: , and .
The rule for adding three to the units of the system is as follows: .
Example 1:
|
1 |
2 |
3 |
2 |
3 |
|
|
2 |
1 |
1 |
2 |
3 |
+ |
| 1 |
0 |
0 |
1 |
1 |
2 |
|
Example 2:
|
1 |
2 |
3 |
2 |
3 |
|
|
2 |
1 |
1 |
2 |
3 |
|
|
|
1 |
0 |
0 |
1 |
+ |
| 1 |
0 |
1 |
1 |
1 |
3 |
|
Example 3:
|
|
3 |
0 |
3 |
2 |
3 |
|
|
2 |
3 |
1 |
0 |
2 |
3 |
|
|
|
3 |
3 |
1 |
2 |
1 |
|
|
1 |
2 |
1 |
0 |
2 |
0 |
+ |
| 1 |
2 |
0 |
2 |
2 |
1 |
3 |
|
Example 4:
|
3 |
2 |
0 |
2 |
1 |
|
|
2 |
0 |
1 |
2 |
3 |
+ |
| 1 |
1 |
2 |
2 |
1 |
0 |
|
Example 5:
|
3 |
2 |
3 |
2 |
3 |
|
|
2 |
1 |
1 |
2 |
3 |
|
|
3 |
3 |
0 |
0 |
3 |
+ |
| 2 |
1 |
3 |
1 |
2 |
1 |
|
4.3.2. Subtraction
Subtraction follows the same rules as in the decimal system. If the subtrahend is greater than the subtracted term, a unit must be borrowed from its predecessor and returned to the subtrahend from which it was borrowed. Each borrowed unit is worth four, so in the worst-case scenario, one unit is always left over to be added.
Example 1:
|
3 |
2 |
3 |
2 |
3 |
|
|
2 |
1 |
1 |
2 |
3 |
− |
|
1 |
1 |
2 |
0 |
0 |
|
Example 2:
|
3 |
2 |
0 |
2 |
1 |
|
|
2 |
0 |
1 |
2 |
3 |
− |
|
1 |
1 |
2 |
3 |
2 |
|
Example 3:
|
1 |
2 |
3 |
2 |
2 |
|
|
3 |
3 |
1 |
3 |
3 |
− |
|
1 |
3 |
1 |
2 |
3 |
|
In the third example, the number on the far left is negative, so we can check if the total sum is positive or negative. To do so, we perform the procedure of reducing the
in the sixth position, meaning it is raised to the fifth power of base
. There are two way to reduce, one of them is the following:
The power of is four times the power of . Since it is negative, it is added to , leaving negative . Since there is still a negative term, the next term is subtracted from the equivalent of the power of , but now in power and so on
The following expression shows the step-by-step process:
First step: solving the previous expression yields:
Second step: As solving the previous expression we have:
Third step: As solving the previous expression:
Fourth step: As Solving the previous expression yields:
Fifth step: As , solving the previous expression:
Therefore, the result of the subtraction in Example 3 is a negative number: .
Example 4
| 2 |
1 |
0 |
0 |
3 |
2 |
|
|
1 |
2 |
3 |
2 |
3 |
− |
| 1 |
3 |
1 |
1 |
0 |
3 |
|
When doing subtraction mentally, remember that each borrowed number has a value of 4, which is added to the number it is borrowed from. For example, if we borrow a 0 to complete the subtraction of 3, the new number is 10. Subtracting 3 from 10 gives 1, and 1 is carried over. This 1 is the borrowed number that must be returned. This carried number is then added to the subtrahend in the next column.
Example 5:
| 3 |
1 |
2 |
3 |
1 |
1 |
|
|
3 |
3 |
1 |
2 |
1 |
− |
| 2 |
1 |
3 |
1 |
3 |
0 |
|
4.3.3. Multiplication
As the decimal system, the base-four number system follows the axioms of association and distribution in multiplication. Here, we will only define multiplication between units to determine how many digits are carried forward and added to the next digit.
Since there is a difference of four between successive digits, the value of a carried-over unit is considered to be four.
The rules of the multiplication are:
The rule for multiplication any quantity to zero is that the result is zero. For example, or .
The rule for multiplication any quantity to one is that the result is the same quantity. For example, or .
The rule for multiply one to the units of the system is as follows: , , and .
The rule for multiply two to the units of the system is as follows: , and .
The rule for multiply three to the units of the system is as follows: .
If there are signs in the multiplication, the same rules for signs used in the decimal system apply:
Example 1:
|
|
|
2 |
3 |
1 |
1 |
2 |
|
|
|
|
|
|
2 |
2 |
1 |
× |
|
|
|
2 |
3 |
1 |
1 |
2 |
|
|
1 |
1 |
2 |
2 |
3 |
0 |
|
|
| 1 |
1 |
2 |
2 |
3 |
0 |
|
|
|
| 1 |
3 |
1 |
0 |
1 |
0 |
1 |
2 |
|
Example 2:
|
|
|
1 |
0 |
2 |
3 |
2 |
|
|
|
|
|
|
3 |
3 |
2 |
× |
|
|
|
2 |
1 |
1 |
3 |
0 |
|
|
|
3 |
2 |
0 |
2 |
2 |
|
|
|
3 |
2 |
0 |
2 |
2 |
|
|
|
| 1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
|
Example 3:
|
|
|
3 |
0 |
0 |
1 |
3 |
|
|
|
|
2 |
1 |
2 |
3 |
3 |
× |
|
|
|
|
2 |
1 |
0 |
1 |
1 |
1 |
|
|
|
|
2 |
1 |
0 |
1 |
1 |
1 |
|
|
|
|
1 |
2 |
0 |
0 |
3 |
2 |
|
|
|
|
|
3 |
0 |
0 |
1 |
3 |
|
|
|
|
| 1 |
2 |
0 |
0 |
3 |
2 |
|
|
|
|
|
| 1 |
3 |
1 |
1 |
3 |
2 |
0 |
0 |
2 |
1 |
|
4.3.4. The Exponentiation
In a base-four number system, exponentiation adheres to the same rules as in a decimal system.
, , .
Generalizing:
. To solve the previous expression, we must multiply each factor.
The answer is:
Developing the operation:
The answer is:
Therefore:
The answer is:
4.3.5. Division
As in the previous operation, the division in the base-four number system follows the same rules as division in the decimal system. Therefore, we only need to consider the base-four and proceed to perform the division.
To facilitate division, we show the results of division between units. These units are taken into account when performing division because they indicate which units are carried over and added to the next digit.
The rules of division are:
The rule for dividing any quantity by zero is that the result is indeterminate. For example, or .
The rule for dividing any quantity to one is that the result is the same quantity. For example, or .
The rule for dividing one to the units of the system is as follows: , , and .
The rule for dividing two to the units of the system is as follows: , and .
The rule for dividing three to the units of the system is as follows: .
As with multiplication, the same rules for signs that apply in the decimal system also apply to division.
The following examples have been resolved through conventional methods.
Example 1

The same rules for subtraction are followed to subtract the product of the divisor and the quotient, and find the residue.
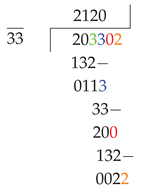
Example 2:
Example 3:
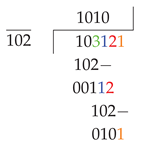
If we need to get a fraction below the integer, it is necessary to add zeros to the residue and put a decimal point in the quotient.
Example 4:

4.3.6. Number Line
The number line, as a Cartesian plane, can also be graphed in a base-four number system. Thus, we can trace vectors, geometric figures, functions, and polynomials, as well as create 2D, 3D, and complex planes.
These are the fundamental components of the base-four number system. However, given our objective of employing it in conjunction with the binary system, it is necessary to delineate additional aspects pertaining to artificial intelligence and logic gates, which are discussed subsequently.
5. Symbols
The base four number system is imperative for the implementation of information management processes. Consequently, it is imperative to transform the system’s digits into symbols that facilitate the structuring of templates. These templates configure an information pattern that represents a field of variables. This is analogous to the development of a mathematical model that represents an answer or image of the desired outcome.
5.1. Symbols in Template
The elementary symbols representing the digits of the number system are described below.
The following symbols are deemed suitable for the management of analog data due to its correlation with the generation of infinite frequencies within the electromagnetic spectrum, which is based on the visible light range.
- a)
Let R be the number 1, whose symbol is ◯.
- b)
Let G be the number 2, whose symbol is ◯.
- c)
Let B be the number 3, whose symbol is ◯.
- d
Let W be the number 0, whose symbol is ◯
In numerous signal interaction systems, the completion of each circle corresponds to an activated state, signifying that the signal must undergo processing.

and leaving it empty corresponds to a non-activated state
◯◯◯◯. This means there is not enough energy to activate the number, so it does not enter the data computation.
It is important to structure a numerical system through symbols, but it is even more important to combine the relationship between the numerical system and the physical environment. This is certainly not an easy task given that the structural representation of an environment is extremely diverse. This is not the case with symbolizing a numerical system since only its elementary digits are required. However, we can establish a profoundly close relationship with the environment if we understand its elementary structure.
If we understand that the environment manifests in diverse forms, forces, and energies, and that each manifestation is an extreme or intermediate point of the same cause, then we will likely begin to understand it. If we understand that the environment manifests information — extremely valuable information — and that this information manifests the integration of a diverse and vast whole into its elementary parts, no matter how complex it is, then we will be on the right track. By discovering and understanding these basic building blocks — these masterpieces of information and construction — we will certainly only understand one percent of what we need to know.
The following template illustrates the symbols as delineated above.
Table 5.
Template of symbols basic four number system.
Table 5.
Template of symbols basic four number system.
| Row |
Basic four numbers Symbols |
| 1 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 2 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 3 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 4 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 5 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 6 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 7 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 8 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 9 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 10 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 11 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
| 12 |
◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯◯
|
The universe’s structure likely adheres to a mathematically precise model that has yet to be identified. One assertion that can be made with a high degree of confidence is that mathematics and nature are not discrete entities. Conversely, they exhibit a high degree of similarity.
6. Objects
So, if we take the real object, which includes many variables such as its color, radiation, consistency, form, edges, energy state, etc., we need to individualize all of these variables and regroup them as a unique pattern of this object.
Special treatment and handling of these variables, as well as well-defined scrutiny, are required when applying signals from the environment that interact with the object. A complete understanding of the processed information depends on this because the influence between the object and the environment is reciprocal.
One’s existence is equally as important as the other’s. By "existence," I mean being face to face.
In the next section, I will describe the relationship between an object and its environment. For now, I will define an object as a mathematical symbol.
This is an object
2 in pondering position. All of its faces have equal exposure to the environment.
This object is in the interactive position.
The major face is at the front and is exposed to multiple signal inputs. The minor face is the output signal. The object can rotate in any direction in three-dimensional space. Some objects can move in every direction, while others can only move in one direction, depending on their function. If one of its functions is to deploy time, it will always move in the same direction in space. Therefore, it is important to consider all possible options and circumstances that certain objects must fulfill to ensure the environment functions holistically.
6.1. Objects and Environment
In this project, an object is the primary element that encompasses all attributes, variables, and essences of existence in the physical environment. Objects contain everything from the most subtle to the most grotesque and extremely heavy, thus encompassing all possible manifestations. Objects range from pure physical-energetic meaning to simulated dimensions beyond the reach of physical senses. Yet, they have the capacity to interact with objects of their own kind and with other kinds, affecting them. Therefore, any object can be treated as a mathematical structure.
Therefore, every type of particle, molecule, cell, piece of material, living body, condensed energy, celestial body, galaxy, and universe is represented by an object. Each object has particular qualities that make it unique. Uniqueness is an essential condition for an object to exist in the physical environment and trace its period of physical existence.
The environment is also an object as a whole, containing within it a set of various objects, each with its own qualities but interacting with each other through the environment. Thus, both constitute an integrated environment, such that the influence of one on the other is mutually correlated, since the environment is shaped according to the needs of the other, and the other is likewise shaped according to its environment. Hence the importance of understanding this close relationship and how they interact with each other. Regardless of whether everything that physically exists is a simulation or not, everything that exists in an environment is information. Information flows and is transmitted through the environment in the form of electromagnetic waves, with multiple frequencies that define the uniqueness of each object.
The universe, as an object and as a whole, contains the environments of each of its galaxies. Each galaxy contains the environments of all its stars. The stars contain the environments of all their planets. The planets contain the environments of all their living and non-living, intelligent and non-intelligent objects.
Since every object in the universe is unique, each object must possess all the qualities that make it different from any other object.
6.2. Properties of All Objects
In order for an object to be such, it must possess qualities that allow it to interact with its environment along all channels of information flow, including elements of its own species and any other nature.
Every object has the following inherent properties, and as long as they remain unchanged, the object’s physical-energetic structure remains intact. This structure identifies the object within a set of multiple objects and allows it to exist as a single object in the environment. These qualities are unalterable because they emanate from the object and are preserved once emanated. Even if there is interference in the environment, these signals will prevail. However, this does not mean that they always remain constant because they can change if the object transforms. What remains constant is the quality, which can vary within a range of frequencies. For instance, if an object emits blue light, it will remain blue throughout its interaction with the environment and can be perceived as such by other objects. However, the emitting object can change to an orange color without altering its quality because its ability to emit a variety of colors is preserved.
A signal propagates in all directions if there are no obstacles. In its sprayed way, it can be observed by multiple objects.
Although every quality has three edges, faces, or states in which it can manifest, that doesn’t mean its essence has been transformed. The three manifestations are the same quality, only at different degrees of intensity. Two of these degrees are extreme opposites, and the third is average. This means that every object oscillating within this range can be positive, negative, or neutral at some point. In intelligent objects, the midpoint is equivalent to a state of wisdom, while the extreme opposites are equivalent to states of knowledge and ignorance, respectively, which are the intermediate measures between the two extreme variables: love and hate.
The following list contains qualities that every object must possess.
- i)
All objects have the ability to emit electromagnetic waves of different colors.
- ii)
All objects have the ability to emit electromagnetic waves within a range of radiation frequencies.
- iii)
All objects have the ability to emit electromagnetic waves with different ranges of energy: objects in motion or at rest, sounds, smells, and touch.
- iv)
All objects have the ability to emit electromagnetic waves that reveal different views of their edges, shadows, and the forms of their constituents. These constituents can be solid, liquid, gaseous, or quantum environments.
- v)
All objects have the ability to emit electromagnetic waves that reflect their internal state.
- vi
All objects have the ability to emit electromagnetic waves, which can be interpreted as waves of the reflection or refraction type.
- vii)
All objects have the ability to receive the aforementioned electromagnetic waves.
An environment is composed of all its contained objects and a tenuous, transparent medium that is tightly connected to each object. Through this medium, information flows and interacts to maintain the dynamics of each natural or non-natural process.
Thus, in addition to the qualities contained by its objects, an environment’s qualities include its ability to create a space and time in which each object and its energy can evolve fully. Each object exists to evolve into purer states of energy, merging with the environment to act as a whole and as an authentic object. Once this goal is achieved, a new cycle of experimentation will begin.
The following is a list of the environment’s special abilities.
- 1)
All environments have the ability to create spaces with well-delimited dimensions. Then, this space must be encapsulated with a shield that permeates some types of outside information while maintaining a stable inner condition. In this manner, all objects can exist securely and obtain all the resources they need. In other environments, these objects cannot survive if they do not belong to that environment. For example, some objects, such as stones and compound chemical elements as helium and molecule of hydrogen, can survive in the largest environments.
- 2)
All environments have the ability to create time. Time is a synchronous cycle with all environments in the universe, from the smallest to the largest. Time is the force that allows every object to rethink, rebuild, be reborn, and re-engineer itself to optimize its status in cycle after cycle until eternity. This is because the cycle of time is eternal. The emotion of never stopping is the reason for existence: to grow in perception, capacity, and experience all possible conditions under forces and all possible states of energy.
- 3)
All environments have the ability to contain objects, energy, matter, antimatter, information signals, as a wave in the water, see [
3] and physical and metaphysical phenomena. Every environment must be capable of supporting extreme events that could occur within it and restoring the chaos to a paraggelia whenever necessary.
- 4)
Every environment must be illuminated by a light source, either from its own environment or reflected light, because the flow and field of photons enables the best interactions between objects and their environment. Darkness cannot foster any constructive process.
- 5)
Every environment must have a larger object that supports all the smaller ones and provides them with diverse resources. These resources are necessary for the growth of the organisms that live in the environment. This larger object must establish the initial and process conditions that govern the actions of the smaller objects it contains because each local environment is constituted by the actions of its inhabitants and the laws of the larger object. These laws must always be in harmony.
6.2.1. The Elemental Gossamer, Where Signals of the Environment and Objects Flow
In order to define how all objects in a given environment interrelate, it is necessary to describe the ways in which these relationships occur. Such information comes from the essence of the object itself, which has three defined states:
Active state of consciousness.
Active state of subconsciousness.
Active state of unconsciousness.
An object can only be in one state at a time. These states foster a universal, simple, and elemental language code so that the object can interact accurately with its environment and with similar, different, or indifferent objects. Regardless of the interaction between two or more objects, they all have elemental intelligence, which is necessary to direct their actions, responses, and work.
Each object has a complex internal reflection system that helps safeguard its integrity while relating to its exterior simultaneously.
We will explore the concepts of consciousness, subconsciousness, and unconsciousness in more depth in another project. For now, a conscious state, from this project’s perspective, is a state present in all living organisms. The subconscious state is present in all inanimate beings. The unconscious state is present in all potentially existing beings and is immense.
But what constitutes an intelligent process? Does it only involve processing signals? Or does it only involve responding to those signals? Is the response intuitive, instinctive, or wise? For a process to be considered intelligent, three fundamental elements are required.
First, it must understand the information received and classify each signal according to its degree.
-
Second, it requires entering a state of deep analysis to understand the meaning and intent of the signals received. Thus it must have the capacity to use the two tools provided by the environment and sharpened during cognitive and physical development:
- i)
the ability to think. Imagination comes as an inherent quality to the ability to think.
- ii)
the ability to store general and basic information.
Another important classification to understand intelligent processes in diverse states of consciousness, applicable to living and non-living objects.
Living organisms use their ability to think to varying degrees.
-
While all inorganic bodies use their storage capacity to compare received information and respond to it by accepting, rejecting, or remaining neutral.
- i)
If the information is new, they reconfigure their structure to receive it and storage.
- ii)
Their response is manifested in their ultimate physical state.
The intelligent process is a complex, dynamic life process for all objects in the environment depending on their level of evolution. However, even the simplest process is extremely complex and requires the implementation of a third fundamental element: Reasoning.
-
Reasoning enables proper interaction with the environment and everything within it.
This fundamental element fosters the development, growth, and fulfillment of the purpose of every object in the deepest sense of its existence within a specific field, space, and time.
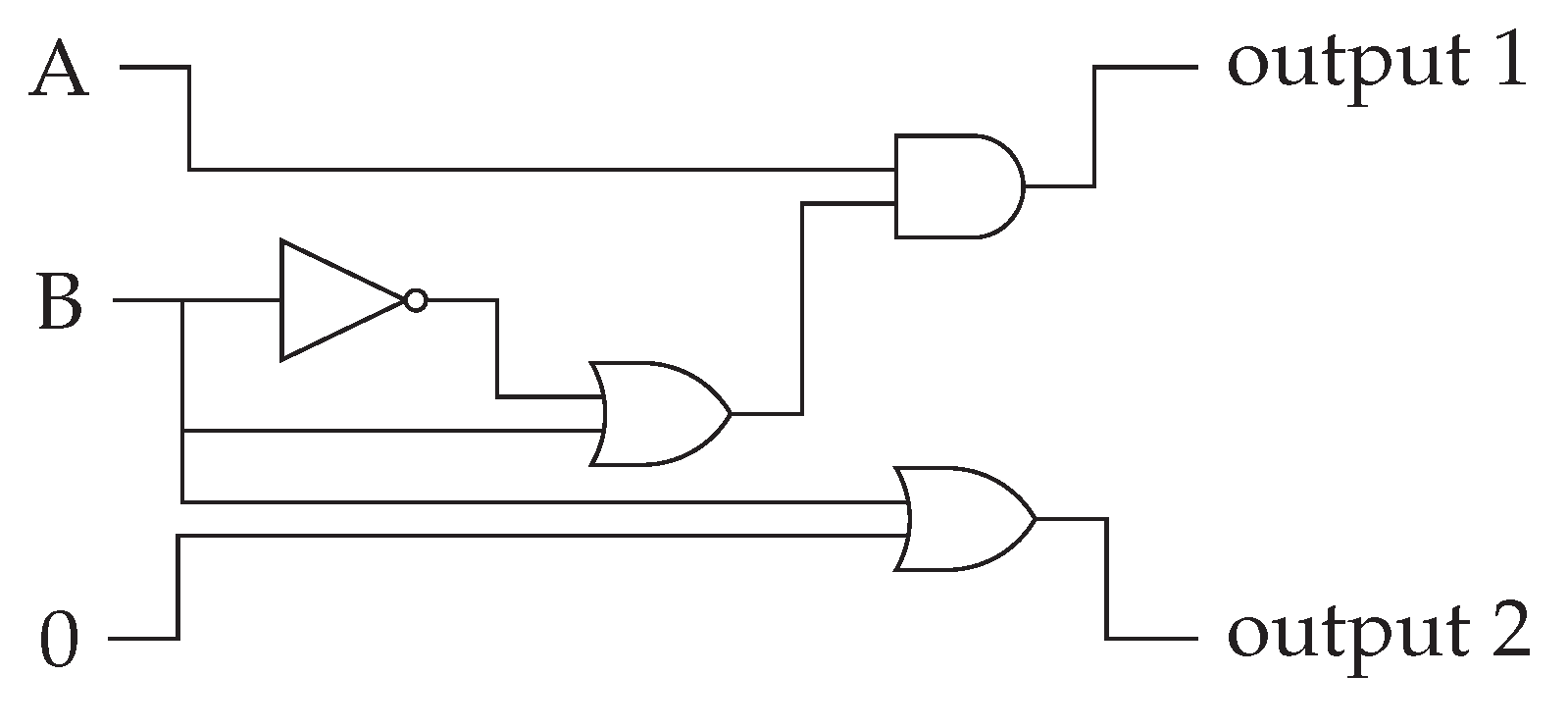
The elementary gossamer of interaction between the environment and objects has input signals on the left and output signals on the right. In this example, there are two input objects, as well as environmental signals that define space, time, light, energy, and the type of environment (benign, aggressive, or indifferent).
The active object, located in the center, responds to the input signals and generates a response from a range of possibilities, which can be received by other objects. If the object is conscious, it uses an intelligent process to discern the intention of its response among all the input signals.
This is a graphic of a network of signal channels. This is an elemental gossamer where many waves flow at their own frequencies. Each line is a channel for a specific wave. This is not a neural network. This relationship flows from: "other objects—environment—active object.—environment—other objects" in a cycle of feedback response until the best is found.
6.3. Elementary Intelligence
When I say that every object has certain properties, I’m referring to the essence of the causes that manifest the object in the physical environment. Many of you may be wondering how an object can be intelligent. How can an object be cold or hot? Well, an object is intelligent because of its ability to store energy. How can a rock be intelligent? It is intelligent because of its ability to maintain its structure, despite the geological or thermonuclear fission process that formed it.
Therefore, every object—regardless of size or composition (material, antimatter, or energetic)—has elementary intelligence, which makes it capable of manifesting itself to a greater or lesser degree in each quality it possesses. Elemental intelligence is an energy that follows a primary cognitive process capable of recognizing the elementary parts of a sufficient and necessary mathematical structural code.
The elementary intelligence of an object serves to:
First, it gives the object certainty of its individuality as a unique piece immersed in a universe full of particles, antiparticles, atoms, molecules, cells, bodies, planets, stars, and galaxies.
Second, it gives the object an elementary language that allows it to interact with neighboring objects and the local environment of which it is a part.
Third, elemental intelligence organizes the most elementary particle, which is beyond the quark because the quark is still a complex structure. The elemental structure complies with the principle of functionality, which establishes the conditions and properties that everything that exists must have because the principle of functionality is fundamental to all types of existence in any dimensional plane.
To understand how each part and communication channel functions, as well as how to calculate each wave and its respective frequency, we must delve deeper. Therefore, we must use vector matrices or Fourier and Taylor analyses, which have particularities regarding data processing. The most important thing, however, is to decipher how waves represent the various manifestations of things and how they operate in a real-world environment that must protect each signal from disturbances, even when located in an environment teeming with other waves.
Or, is there a property of each signal in its own expression on the controversy of being or not being?
We will explore these aspects in depth in articles dedicated to analyzing these concepts. Here, we only outline the most general aspects of our hypothesis.
7. A Configuration of with Only Binary Digits
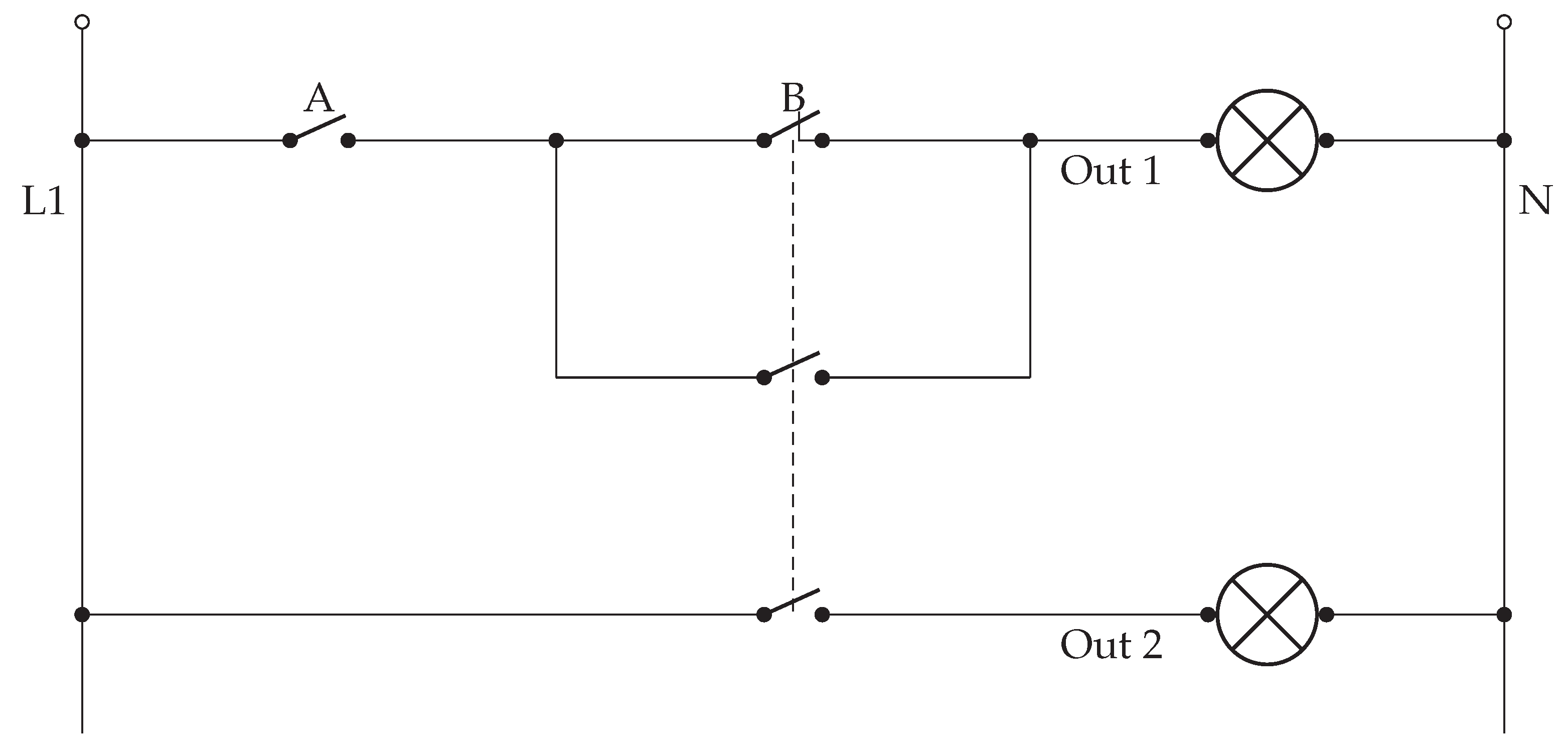
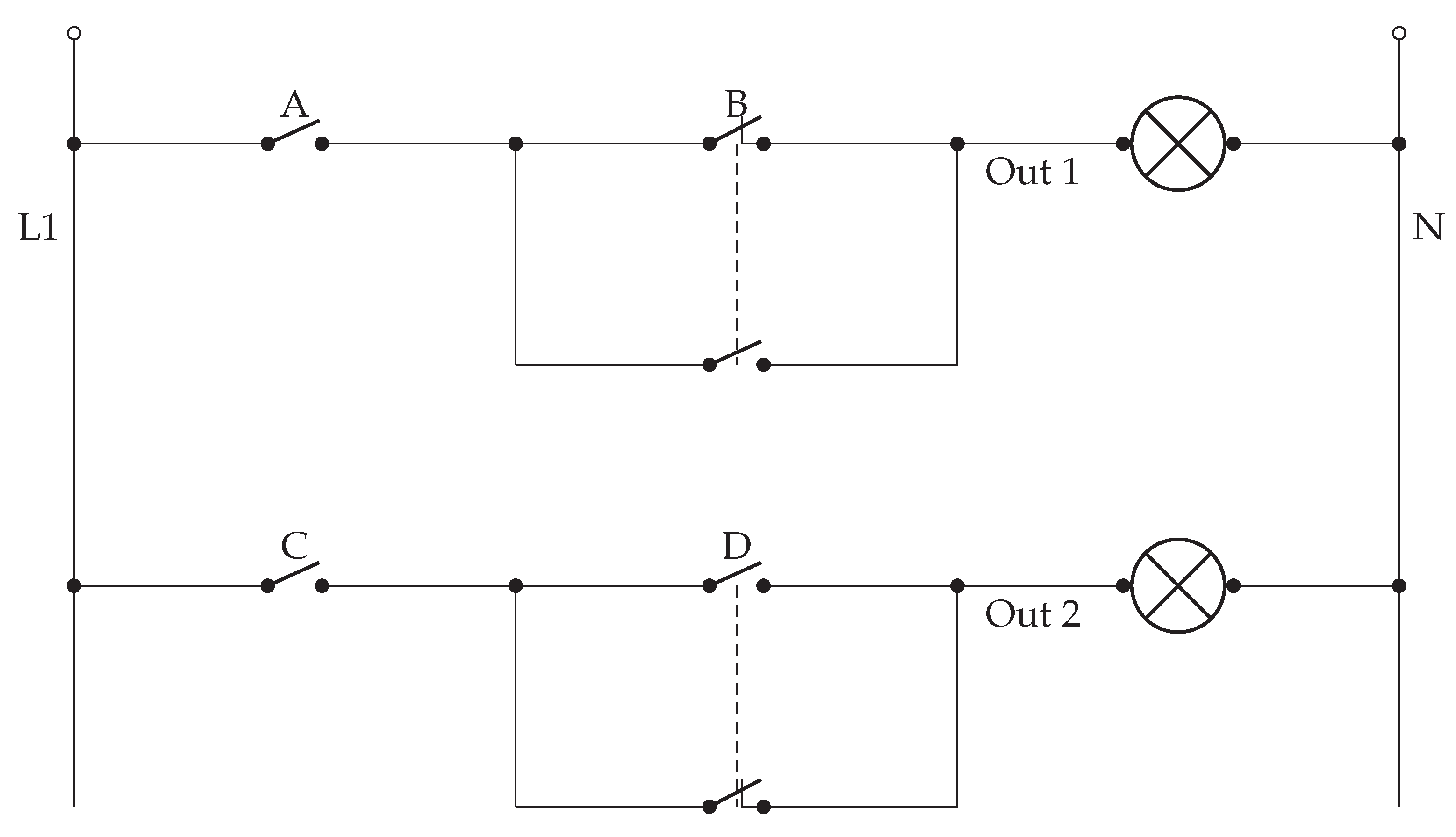
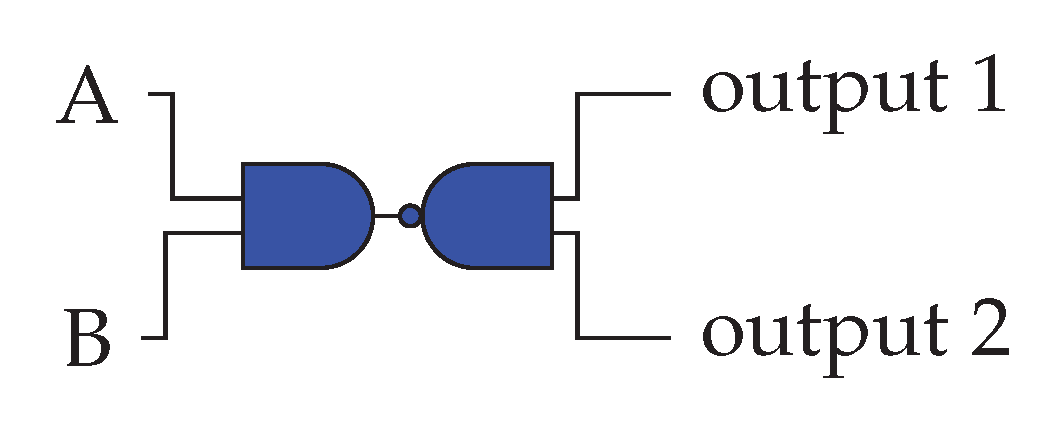
While designing logic gates for basic-four number system, we can leverage the properties of normal binary systems to increase their capacity by replacing prime numbers in basic-four number systems with digits from binary systems. This results in a six-bit array that is equivalent to a byte, which uses four bits. The array will be according to the number system in base four.
For example, the number two will be represented by , and the number three by . These will function as indivisible packets, and wherever one of them is present, it must be treated as a unit of the base-four number system.
We can represent them with an independent term such as the following:
Its representation in a numerical sequence would be as follows:
Table 6.
The first sixteen numbers in extension binary. (Elemental Block)
Table 6.
The first sixteen numbers in extension binary. (Elemental Block)
|
Binary |
Decimal |
|
00 |
0 |
|
01 |
1 |
|
10 |
2 |
|
11 |
3 |
|
100 |
4 |
|
101 |
5 |
|
110 |
6 |
|
111 |
7 |
|
1000 |
8 |
|
1001 |
9 |
|
1010 |
10 |
|
1011 |
11 |
|
1100 |
12 |
|
1101 |
13 |
|
1110 |
14 |
|
1111 |
15 |
This representation is for literary purposes only because, digitally, there is no real equivalence since binary digits are used for data processing. The real advantage is that the number of digits in a byte is reduced by two. Since the base is four, this doubles exponentially. This is why and should be handled as a single packet.
So, in this context the digits will become: or
So, a number could be written as follows:
or
or
In the base four system, an arrangement of eight binary digits is equivalent to two digits in the hexadecimal system. In a substituted hexadecimal system, we can use an array of two eights to create a sixteen-digit structure. Since there are twice as many binary digits as hexadecimal digits, the options increase exponentially from a base of eight in a pyramidal form.
In binary, the array of pyramidal growth has 256 combinations even if it begins with six to eight digits. However, in a base four, there are to options, which is equivalent to and , respectively.
One block of four digits has the following relation:
Table 7.
Binary vs , where and
Table 7.
Binary vs , where and
| Table: One-to-one relation |
| Binary |
|
| A |
B |
C |
D |
A |
B |
C |
D |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
0 |
0 |
0 |
2 |
| 0 |
0 |
1 |
1 |
0 |
0 |
0 |
3 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
2 |
| 0 |
1 |
1 |
1 |
0 |
0 |
1 |
3 |
| 1 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
2 |
1 |
| 1 |
0 |
1 |
0 |
0 |
0 |
2 |
2 |
| 1 |
0 |
1 |
1 |
0 |
0 |
2 |
3 |
| 1 |
1 |
0 |
0 |
0 |
0 |
3 |
0 |
| 1 |
1 |
0 |
1 |
0 |
0 |
3 |
1 |
| 1 |
1 |
1 |
0 |
0 |
0 |
3 |
2 |
| 1 |
1 |
1 |
1 |
0 |
0 |
3 |
3 |
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
|
0 |
1 |
0 |
2 |
|
|
|
|
⋮ |
⋮ |
⋮ |
⋮ |
|
|
|
|
3 |
3 |
3 |
3 |
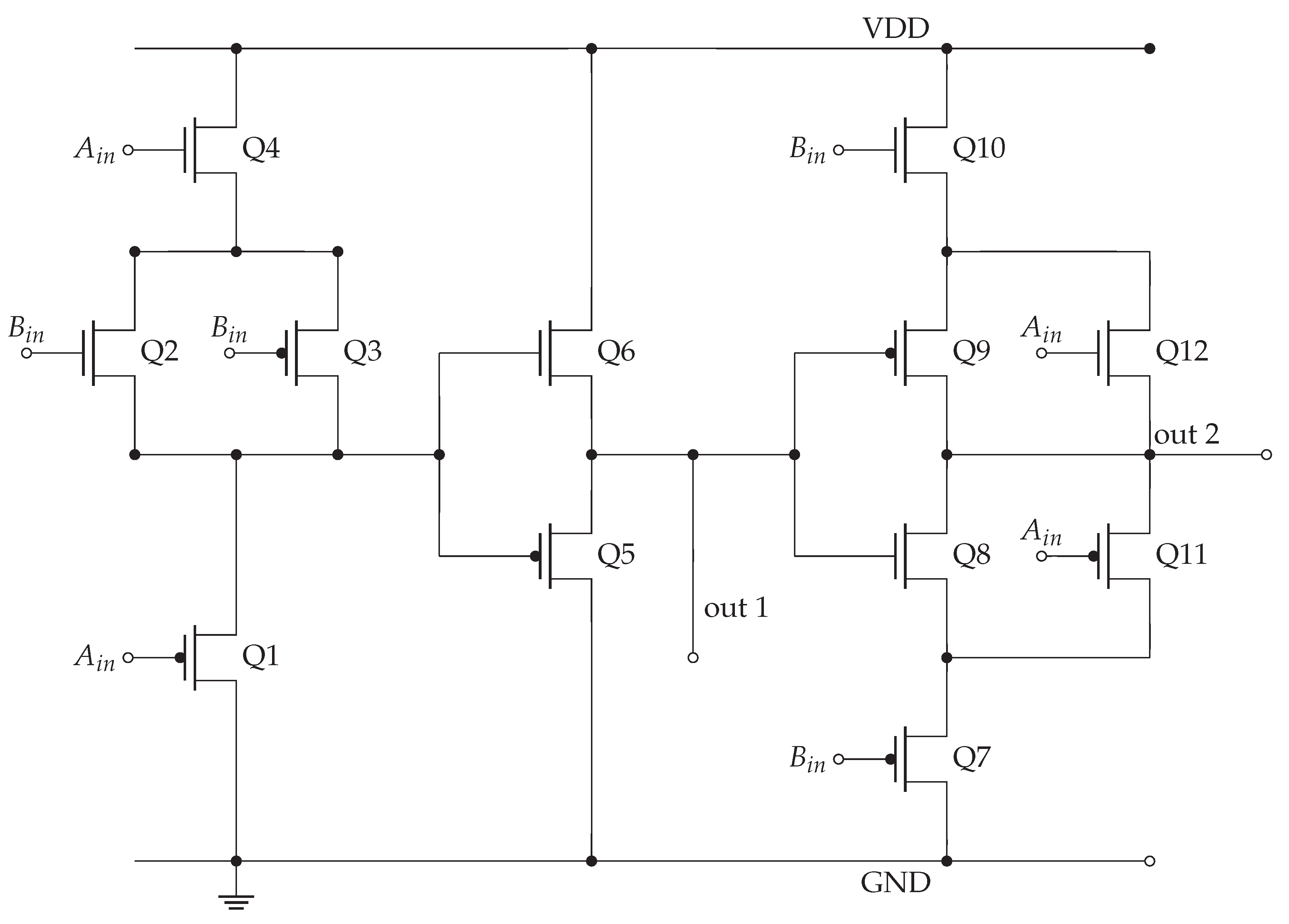
There are no advantages to converting the base four system to the hexadecimal or binary system, so it is extremely important to develop a logic element that produces outputs of and3. There is no problem with0and 1 because the same rules used in the binary system would apply. However, in addition to using 2 and 3 as logic elements, it is necessary to design an electronic element that contains the implicit solution to their binary category. Currently, I am unaware of any technology that can implement this function. For the time being, I intend to use existing binary technology to develop a circuit that facilitates the integration of 2 and 3. This project will therefore have two major phases of development: one applying current technology to solve problems with storing and processing massive amounts of data and another developing its own technology for correct application and maximum benefit.
8. Logic Statements
Understanding the logical significance and interpretation of binary systems is very important. During George Boole’s time, the subject was the focus of a fascinating debate through the mutual exchange of research and correspondence between Augustus De Morgan
, a Mathematics Professor at University College of London, and Sir William Hamilton
, a Logic Professor at the University of Edinburgh. This motivated Boole, Professor at Queen’s College in Cork, to pursue his
The Investigation on the Laws of Thought. This work led to the
The Mathematical Analysis of Logic[
4]
which is considered a fundamental work of mathematical logic as Boolean algebra in its purest technological application to this day.
In this article, we will define the basic concepts of logic [
2] for binary systems. In the next article I will thoroughly explore these concepts and describe the formulas that must be applied to a base-four system in the strictest logical sense. It should be clear that the logical treatment of numbers 2 and 3 is different from their use in the field of numbers.
8.1. Significance and Interpretation of Symbols
8.1.1. The Meaning of Digits in the Binary System
The meaning of symbols is as important as interpreting the laws that relate them in a logical syllogism. One of the most influential ideas in philosophy is described as "The science of real existence and the study of causes". Aristotle said, "The ’why’ belongs to mathematicians, for they have the demonstrations of causes." Anal. Post. lib. 1. , cap. xiv.
The first symbol and its meaning is described by George Boole in [
4] [p. 15 § First Principles]
"LET us employ the symbol 1 , or unity, to represent the Universe". and then explains
"and let us understand it as comprehending every conceivable class of objects whether actually existing or not, it being premised that the same individual may be found in more than one class, inasmuch as it may possess more than one quality in common with other individuals".
The meaning of 0 is not explicitly stated by Professor Boole, but is defined by Young, George Paxton in its paper title
Remarks on Professor Boole’s Mathematical theory of the laws of thought. [
5]
"By 0, then, Professor Boole understandsNothing—a class (if the expression may be permitted) in which no object whatever is found."
The introduction of mathematical logic during George Boole’s time was controversial because logic and mathematics were considered unrelated fields. His work was harshly criticized by his contemporaries because, at that time, scholars were also philosophers, physicians, medicals, mathematicians, and linguists. Aristotelian logic was highly influential, despite proposing concepts of great logical depth, such as the application of "dictum" and "de omni et nullo", as usually manner of reasoning by the logical writers of this epoch, well as the structure of inferential and deductive thinking. Boole introduced the concepts of universality, individuality, and duality, which defined the differences between the universe and its parts. For these concepts to function under algebraic and logical principles, the notions of truth and falsity had to be expressed through mathematical formulas that provided consistency and a basis for existence or non-existence. Algebraically, the number one was introduced as the universe. At the time, this was considered the set of all things that could exist or be contained within the universe. The negation of "no" (not contained or non-existent) was attributed to zero. However, to represent the entire universe algebraically, letters were used, as is appropriate for an algebraic formula. To give algebra a logical meaning, mathematical laws were established and defined as laws of thought. The relationships between them had to obey both mathematical and logical laws under some conditions. A key aspect of the syllogism is correctly establishing the relationship between propositions and their conclusions.
Therefore, the relationship between letters and operators is essential for developing correct propositions and their conclusions.
Then, Boole stated:[
4] [p. 15 § First Principles],
"Let us employ the letters , to represent the individual members of classes , X applying to every member of one class, as members of that particular class, and Y to every member of another class as members of such class, and so on, according to the received language of treatises on Logic.
Further let us conceive a class of symbols , possessed Of the following character.
The symbol x operating upon any subject comprehending individuals or classes, shall be supposed to select from that subject all the which it contains. In like manner the symbol y, operating upon any subject, shall be supposed to select from it all individuals of the class Y which are comprised in it, and so on".
The operators play an important role in this relationship.
The
"is used to express the mental operation by which parts (of extensive quantity) are collected into a whole.", according the explanation of George Paxton Young, see [
5]
"For instance, if x represent animals, and y vegetables, will represent the class made up of animals and vegetables together".
The operator "is used to express the mental operation of separating a whole (of extensive quantity) into its parts."
The operator "is used to denote those objects which belong at once to the class x and to the class y". or .
The sign of identity is denoted as , so the following expression is perfectly valid: .
Under this condition, the logic and algebraic laws of the relationship between the universe and its parts can be established, whether or not they exist.
One of the most important relations between the science of thought and Algebra that does not exist in both is
, which is also expressed as
. For mathematical logic, it is denoted as
, similar to
, even if
. According to the prior definition, it denotes
"those things which belong at once to the class x and to the class x; that is, it simply denotes those things which belong to the class x; and it is therefore identical with x". See [
5] However, this relationship only holds true in Algebra and the Science of Thought when
or
.
Another important expression is , , or , which means a logical contradiction: means . The class not-X is represented by the expression , which includes all individuals in the X class. Since the universe is 1, then because the classes X and not-X together make up the universe.
For example, the symbol
represents the class whose parts are
, but not
. Conversely, if the relationship is expressed as
, it represents the entire class whose parts are neither
nor
. This beautiful relationship is generalized in the following table.
3
-
Universal-affirmative, usually represented by A
All are .
-
Universal-negative, usually represented by E.
no are .
-
Particular-affirmative, usullay represented by I
Some are .
-
Particular-negative, usually represented by O
Some are not .
Obviously, this is only a brief overview of Professor George Boole’s significant work. A deeper exploration of binary logic under modern conceptual and technological approaches is necessary, once the professor has firmly established the foundations of this knowledge and mathematical structure. It is a significant challenge for modern science and contemporary philosophy to continue the work of our predecessors.
In the next article, I will discuss the logical laws of binary systems in depth, as that topic could be as extensive as this article. Then, we will have enough space to develop the relationship between unit numbers in the number system using algebraic formulas, logical meanings, and potential philosophical implications.
8.1.2. The Elements of the Base-Four Numeral System Possess the Following Indelible Qualities
In the 18th century, the concept of the universe was understood to be the most complete and extensive, encompassing everything. For this reason, George Boole assigned the number one to the category of the universe, which included all possible objects.
Today, the concept of the universe is not considered the totality of existence. Rather, it is merely one part of a system of universes similar to ours, including ours and all universes different from ours.
The concept of one as the totality of the whole must prevail. Under this category, we will consider one as the totality of the whole. Each particular class of objects can be configured and establish a logical-mathematical relationship with its totality and all its other parts.
Similarly, the concept of nothingness must prevail in assigning zero as a class containing no objects, as we conceptualize all existing objects in the physical world. Nothingness is beyond our natural understanding, yet it is solid and true. It exists in the totality of everything and is a fundamental part of the totality of everything, which is the absolute everything. We can only understand the totality of nothingness mathematically. We will find it intimately related to all things, not outside of them or unattainable beyond this plane.
Every algebraic relationship between the letters representing the classes into which differences are divided and the operational signs dictating their laws must prevail because identifying each step in the process of integration or reduction is the essence of every relationship. Every relationship exists for a reason and must be fulfilled given our conscious or unconscious participation in cognitive evolution. Sometimes, a class of objects is an active element; at other times, it is a passive element proposed for quantitative and qualitative analysis.
A new term is admitted into this relationship, which will imply significant growth in the binary system and in Boolean algebra. This new term is the number 2, which mathematically represents the class of all even numbers. In every existential system, regardless of its nature, there exists a set of pairs, which we will generalize as objects made up of individual parts that form pairs. Being an even element has great significance in the overall set of the totality of the whole.
The next term to be admitted into this relationship is the number three, which represents the class of all odd numbers. As with the number two, in any existential system, regardless of its nature, there is a set of odd parts. These parts are active elements due to their unevenness. These elements initiate all types of processes, and through their interactions, they establish an agreement for possible pairings. Within the set of the totality of one, both two and three practically forge two equipotential sets. However, in order to maintain their pairing capacity, they must remain odd forever, forming an even couple only under specific circumstances and conforming to the real totality of one.
8.1.3. Relationship Between Digits
According to Boolean algebra symbols and the canons established by George Boole in his influential work, An Investigation of the Laws of Thought, the relationship between the elements of the base four system must adhere strictly to this symbols so that the interpretation can be deduced by applying the defined laws. These relationships are then established between each element and among the elements themselves, which allows us to cover all possible aspects of the interrelationship.
Let us represent each relation in the following table.
Table 8.
Table of relationship between binaries.
Table 8.
Table of relationship between binaries.
| Table: Binary relation |
| Digits |
Relationship |
| A |
B |
|
|
| 0 |
0 |
|
|
| 0 |
1 |
|
y |
| 1 |
0 |
x |
|
| 1 |
1 |
x |
y |
Now, let us to describe that relationship and try to explain its meaning.
The relation between the
is equal to
The universe of nothing is when {All not- are All not-}. George Boole does not describe the above expression as such in his work, but we can make it equivalent to the universal-affirmative expression for the universe 1, which is defined as All are .
The interpretation of relationship between nothingness and nothingness, as if reflected in a mirror, is an identification of itself. Therefore, when it is one, it represents the entirety of nothingness; when it is zero, it reflects that entirety. Thus, it works as an inverter gate.
At this point, it is important to clarify what "nothingness" means. First, the nothingness referred to in this hypothesis is not the same as the nothingness of the physical world as we understand it. From a physical perspective, we consider nothingness to be an empty space. However, the totality of the whole has a different perspective because it is based on mathematics. Nothingness is a wonderful place that is not empty but rather full of everything that potentially exists, including everything that has not yet been discovered or named. Therefore, nothingness is omnipresent in the totality of the whole because the totality of the whole must include the totality of nothingness to truly be the totality of the whole. Otherwise, it is merely one of its parts.
True nothingness is mathematical because it is the only way to contain everything that exists in fact and potentiality. Physical nothingness is empty because it depends on the perceptual capacity of the person experiencing it. Depending on how it is exercised, the vision of thought may or may not be limited, but it is undoubtedly the most powerful tool for becoming enraptured in the immensity of nothingness.
However, nothingness does not exist in a remote place. It is not another universe full of black holes. Nothingness exists in close relation to every part of the whole. It is part of the foundation of the physical universe because every natural phenomenon has its space and limit through it. This allows them to interact constructively or destructively according to their nature. Even destructive phenomena aim to re-establish what was wrong or right in the logistical sense through re-engineering.
Suppose that we could concentrate the matter of all universes similar to ours — including our own — as well as the matter of all universes different from ours, and if it were concentrated on a planet the size of Earth, what would happen to the nothingness? Nothingness would remain the same size — immensely larger than all the universes combined — because it cannot be concentrated.
The relationship between
is equal to:
According to Boole’s logic, the expression
is interpreted as "a class whose members are
but not
". John Venn later simplified Boole’s logical propositions using symbols. See [
6] [ Symbolic Logic, Venn (1881) p. 142 § Import of Proposition, Chapter VI]. The above expression in simple form is
. It can also be expressed as
. Venn’s symbolic logic is now extensively used. All possible combinations of two propositions are:"
and
".
Then, for a three-combination, will be eight; for a four-combination, will be sixteen; and so on.
The relationship between nothingness and the universe or is interpreted as a mirror reflection, identifying both as the totality of nothingness and the totality of the universe. Therefore, when the result is one, it represents the entirety of nothingness and the entirety of the universe. When the result is zero, it reflects that the entirety of itself does not matter, whether or not the universe exists. In other words, neither one nor zero means that there is some y, but not x.
The relation between the
is equal to
This relationship is symmetrical to the of the above expression. Now, the universe is reflected in the mirror, and it sees its immensity over the nothingness. Thus, the relationship is mutual, but the image that is multiplying comes from the universe. When nothingness is reflected, no objects can be reflected. However, in the universe, many universes are projected, forming a multiverse.
The pair
is the first extension of the binary system and is the third digit of the base four system. In base four system, the digit 2 is the same as in the decimal system. The 2 is one of the most significant digits in both systems. All even numbers are created from it. As we know:
and so on. Therefore, we can generalize:
But the most marvelous thing happens when 2 is added to 3. In this series, all the odd numbers, which contain all the prime numbers, are created.
and so on.
In the next article, I will examine the structure of this beautiful arrangement and show you in more detail.
The relation between the
is equal to
In boolean notation "
" means "no
are
", so "to assert that no
are
, is the same as to assert that there are no terms common to the classes
X and
Y". [
4] Otherwise Venn interpret this relation as that "the class in question is absent, whilst
expresses that it is not only present, but present to the exclusion of all else." Now, it is convenient to use an "intermediate form
" which value is "between 1 and 0" i.e. "between all and nothing" [
6] [p. 144]. Our modern interpretation agrees with Boole’s and Venn’s assertions. The "all" and the "nothing" are two universes, both of which sum the totality of all. Through the mirror, the universe and the nothingness are one, each trying to reach the other. In this relationship, the totality of all includes the totality of nothingness. Therefore, the universe is complete and can transform into many images of itself.
The pair
is the second extension of the binary system and is the fourth digit of the basic four system. In base four system, the digit
is the same in the decimal system. The
is the other digit besides the
of the most significant digits in both systems. The half of odd numbers are created from it. As we know:
and so on. Therefore, we can generalize:
So far, we have presented the most general concepts of basic four systems. These concepts have not yet been fully explained. However, since that is outside the scope of this article, we plan to expand on them in the next one. This topic is extensive enough to warrant a book, as all the algebraic aspects and the properties of true and false in each equation still need to be explored.
To understand modern science of computation and circuit electronics on a nano scale dimension, we must consider the future and beyond, including AI. Is it really intelligent, or is it merely a monster with a great capacity to manipulate information? What is quantum computing? What does it really mean to be in a quantum state? Do we really understand it? Who will tell us why our universe is as it is? An incredible man? A quantum machine? Or someone external to our solar system? But what if the answer lies within ourselves?. This will allow us to build our proposal for the basic four system on solid foundations with the axioms, properties, and characteristics that this type of research demands. We must define all the applicable laws of algebra to the basic four system, in addition to the existing Boolean algebra laws, as well as implement logic gates and their respective logic circuits.
8.2. Elementary Electrical Circuit
In this section, I will present a basic circuit with two inputs and two outputs that correctly configure each digit of the basic four system. A broader, more detailed summary will be presented in the next article. The main interest in developing the new basic four system lies in its application to electronic structuring and massive information algorithms for sustainable, intelligent processes and high-speed computing. This is an open field that requires the participation of many minds interested in developing true information technology, which constitutes a source of true information. This technology adheres to the most basic rules of professional ethics and monitors its environment, which likewise complies with these rules. This technology also monitors itself for the true development of our civilization as a real advanced civilization.
In the last twenty years, artificial intelligence has grown tremendously and generated much admiration, but it has also raised countless questions that will be difficult to answer until long-term results are available. Its progress is dizzying, but that does not make it the best technology. It is supposedly implemented with reasoning algorithms and has become an agent capable of interacting with users. It can request clarification if a request is incomprehensible or if more elements are required to process the response. It is also being enabled to interact and check if the final answer meets the user’s expectations. The fact that it takes longer to process information does not mean that it reasons in the strict sense of the word. Rather, it means that, in its search for the best answer, several algorithms intervene and question its response. This is certainly a subtle attempt at reasoning. The most worrying question for everyone is: Who controls artificial intelligence? Who programs it? And for what purposes? Given the current advances, it’s possible for artificial intelligence to program itself or process information produced by other artificial intelligences. This could create an uncontrollable spiral.
Figure 1.
Elementary circuit
Figure 1.
Elementary circuit
We propose an elementary circuit, not because circuits or logic gate configurations with more than two outputs—such as multiplexers—don’t currently exist, but because a specific circuit must be implemented to take full advantage of the basic four system’s potential. For now, however, we must rely on the theory and technology of the binary system because our goal is to amplify it to reduce memory space requirements and manage large amounts of information.
A big data center built to meet current demands will be unaffordable in the near future, so simplification and reduced energy consumption are essential.
The best approach is to develop other types of computing systems that can leverage the enormous potential of the environment, which exists and expands in all corners of the Earth, even the most unfortunate areas. We must proceed step by step because one day, albeit far off, we will achieve the true development of intelligence in non-human devices designed and guided by humans to perform joint tasks. In true joint harmony, this will be a significant advance for our civilization. The current approach to intelligence in non-human devices is misguided and chaotic because the information we feed their processors is poor quality.
Table 9.
Table of truth for an elementary electric circuit in double binary.
Table 9.
Table of truth for an elementary electric circuit in double binary.
| Truth Table |
| Inputs |
Output |
| A |
B |
|
|
| 0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
1 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
1 |
If we try to develop three- and four-input equations, the resulting tables will look like the ones shown on the next pages. Then, we will explain it in detail.
The table of truth to circuit with three inputs.
Table 10.
Table of truth for an elementary electric circuit in basic-four system.
Table 10.
Table of truth for an elementary electric circuit in basic-four system.
| Truth Table |
| Inputs |
Output |
| A |
B |
C |
|
|
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
0 |
0 |
0 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
1 |
| 1 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
1 |
1 |
A simple circuit with four inputs could be:
Table 11.
Table of truth for an elementary electric circuit in basic-four system.
Table 11.
Table of truth for an elementary electric circuit in basic-four system.
| Truth Table |
| Inputs |
Output |
| A |
B |
C |
D |
|
|
| 0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
1 |
| 0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
0 |
1 |
| 0 |
1 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
0 |
1 |
0 |
| 1 |
0 |
0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
0 |
1 |
1 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
This is an electrical diagram of a simple circuit with four switches. We can simulate the logical inputs according to the above truth table.
Figure 2.
Elementary circuit with four inputs in basic-four system.
Figure 2.
Elementary circuit with four inputs in basic-four system.
The proposed circuits are simple, but must be implemented with other electronic elements to properly control the programmed functions and/or algorithms. These circuits are just an example for studying and understanding binary logic. Much more complex and versatile circuits will eventually be designed to meet all the requirements of electronic information processing. The following is a proposed symbol for an elementary logical gate of basic-four number system. However, it can be redesigned later.
Figure 3.
Symbol of an elemental gate on basic-four system.
Figure 3.
Symbol of an elemental gate on basic-four system.
Since all gates are constructed using CMOS devices, the next diagram proposes using the technology developed for logical gates, i.e., transistors.
Figure 4.
Elementary logical circuit in basic-four system.
Figure 4.
Elementary logical circuit in basic-four system.
A normal AND gate uses six CMOS, while the XOR and XNOR gates use ten CMOS with their respective configurations. Therefore, the proposed gate will only use twelve CMOS. The next diagram shows how logic gates actually function to validate the truth table of the elemental circuit in the basic-four system. Therefore, using one symbol as proposed above to substitute the AND and OR gates is equivalent.
Figure 5.
Logic circuit, basic-four system.
Figure 5.
Logic circuit, basic-four system.
9. Some Comments
In this first part, we have attempted to present the various aspects of basic-four number system. As the system has many facets, we can only introduce the basic elements of each one. This article is essentially an introduction to the fascinating world of the four-digit system. Many questions and doubts remain that need to be clarified, especially regarding how we can use it to expand the traditional binary system mathematically and technologically. From a deeper perspective, the system allows us to structurally configure sequences similar to those of biological and chemical systems because nature appears to follow a mathematical pattern based on the structure of elementary DNA with three helices as a block under mathematical rules. This leads us to continue the strictest and most rigorous implementation of this numerical system in subsequent works.
So, don’t despair. I will soon expand on each concept presented in this introduction. The intention in presenting this new system is to spark the interest of scholars in various disciplines in developing new theories and technologies and applying them to diverse fields such as computing and the intelligence of non-human devices.[
7] This entails developing new software and hardware and applying them to interpreting the relationship between mathematics and nature. We must expand our minds to accept that nothing is separate from anything else, and that nothing is pure and truly uncontaminated by the whole,in the good sense of the word.
For now, perhaps we can only understand; why another number system is required when the traditional binary system suffices to describe our entire universe? Be sure that within the structure of our numerical system there is a hidden numerical configuration, which is something that is not immediately apparent. This configuration can simulate molecular chain structures where each part includes at least one prime number, either explicitly or implicitly. "Implicit" means "the product of some prime numbers." This is especially true for very long chains because the greatness of anything lies in these types of structures. According to its size and dimension, as well as the structural dynamics that keep it connected internally and externally, each body has a certain number of prime numbers. These dynamics keep it connected to its own internal environment and to the external environment, where it acts as a unit with its own well-defined individuality. This individuality distinguishes it from all others, including its own species and those that are very different from its own species. A very long chain implies that each elementary structure is a substructure of a larger one. This is because it is structurally added, and its entire strategy is integrated for the correct growth of the new structure.
In-depth discussion of all this will require analysis of different topics that must ultimately be interconnected so that everything presented makes true sense. As long as we see the topics as isolated from each other, there will always be a hint of uncertainty.
Computer science, but above all the language used to express information,[
8] must be a tool of great value and utility, helping us prioritize each part according to the part that contains it, in order to visualize the whole of what it is, how it is, what it is for, understanding the essence of what it means to be and why it exists.
In mathematics, we still need to define the laws relating the terms in different functions. This forces us to establish axioms in addition to those already established in the traditional binary system and in computing. The new digits must comply with these axioms.
As discussed throughout this article, mathematics and nature are closely related. If we look more closely, we will see that all of our scientific and technological progress is tied to them. Therefore, we should not turn away from one or the other, but rather, visualize them as a whole because the surprises they have in store for us are significant. Mathematics is the inspiration for constructing a universe and everything in it. It is a model repeated in infinite circumstances to manifest what must be manifested. This model is based on the fundamental structure of mathematics, making its presence both solid and subtle, as it contains both natures.
Thus, there is much work to be done, and much information must be presented and submitted to scrutiny by those interested in contributing their wisdom to this project. The author had interesting discussions during the development of this research, especially with Professor Mihai Prunescu. The author thanks Professor Prunescu for his valuable comments. Therefore, any comments, suggestions, corrections, and criticisms from anyone who wishes to participate in debate and constructive discussions will be welcomed and taken into account with humility to correct any mistakes.
References
- Garcia-Sandoval, R. Challenges Necessary for the Development of Truly Intelligent AI. Preprints 2025. [CrossRef]
- Shoenfield, J.R. Mathematical logic; AK Peters/CRC Press, 2018.
- Kelvin, L. Deep sea ship-waves. Proceedings of the royal society of Edinburgh 1906, 25, 1060–1084. [CrossRef]
- Boole, G. The mathematical analysis of logic; Philosophical Library, 1847.
- Young, G.P.; Boole, G.; et al. Remarks on Professor Boole’s Mathematical theory of the laws of thought. s, sn 1865.
- Venn, J. Symbolic Logic; Macmillan, 1881.
- Hoare, C.A.R. An axiomatic basis for computer programming. Communications of the ACM 1969, 12, 576–580. [CrossRef]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International conference on machine learning. PMLR, 2017, pp. 3319–3328. [CrossRef]
| 1 |
means the natural numbers with zero |
| 2 |
In this project, an object is the most general term for every kind of particle, atom, molecule, body, planetary system, and cosmological structure, including matter, antimatter, living things, and intelligent beings. |
| 3 |
All of the above concepts, definitions, and expressions are taken from George Boole’s 1847 book, "The Mathematical Analysis of Logic". [ 4] [p. 20 § Of Expression and Interpretation] and from George Paxton Young’s 1865 article "Remarks on professor boole’s theory of laws of thought" [ 5]. |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




 and leaving it empty corresponds to a non-activated state ◯◯◯◯. This means there is not enough energy to activate the number, so it does not enter the data computation.
and leaving it empty corresponds to a non-activated state ◯◯◯◯. This means there is not enough energy to activate the number, so it does not enter the data computation.