FinStack-Net: Hierarchical Feature Crossing and Stacked Ensemble Learning for Financial Fraud Detection

1. Introduction

Detecting gambling and fraudulent accounts from transaction records and static user data is challenging because datasets include many features, hidden interactions between features, and severe class imbalance. Traditional machine learning methods often struggle to capture these complex relationships or to combine different types of models effectively. To address these issues, we propose FinStack-Net, a hierarchical ensemble framework that integrates multi-level feature construction with stacked base learners and a meta-learning fusion layer. First, we generate and prune relevant cross-features to reduce noise. Then, we combine decision-tree ensembles and a deep neural network under a unified stacking strategy. Finally, we use a simple logistic regression meta-learner to merge outputs and apply Bayesian optimization to tune all hyperparameters.

FinStack-Net starts with a Hierarchical Cross-Feature Module (HCFM). HCFM creates first- and second-order feature interactions, and then uses mutual information screening and Lasso pruning to keep only useful feature combinations. This step lets the model represent hidden patterns in transaction and account features. Next, the selected features go to a stacked ensemble of LightGBM, CatBoost, and a deep neural network (DNN) with residual connections and attention. Each base model uses tuned hyperparameters to work best. A logistic regression meta-learner then merges outputs from all base models. Finally, we use Bayesian optimization with Optuna to fine-tune every part of the system.

2. Related Work

Bagga et al.[1] combined pipelined decision trees and random forests to handle noise, but they only used simple handcrafted features. Wang [8]proposes an attention-driven network using DIN, MaskBlock, and PAIM to learn selective higher-order feature interactions, which can replace FinStack-Net’s manual cross-feature generation to reduce noisy combinatorics and better capture non-linear user–account interactions.

Chen et al. [2] introduce a coarse-to-fine structured light framework for multi-view 3D reconstruction that combines SLAM-based optimization, parallel bundle adjustment, and a Transformer-based matching module, achieving significant gains in feature matching accuracy, reprojection error, and camera trajectory precision on public datasets. This helped catch rare fraud cases, but it needed repeated resampling, which increased training time. Maurya and Kumar[7] tested basic classifiers (logistic regression, SVM, random forest) as baselines, but they did not use advanced fusion or automated tuning. Guo and Yu [3] introduce PrivacyPreserveNet, a unified framework that combines differential privacy–enhanced pretraining, privacy-aware gradient clipping, and noise-injected attention mechanisms to safeguard multimodal LLM training against data leakage while preserving model utility. Lim et al.[5] used Bayesian optimization on Extremely Randomized Trees for faster hyperparameter search, but they did not stack different model types. Luo et al.[6] present TriMedTune, a triple-branch framework for fine-tuning multimodal vision-language models on brain CT diagnosis—combining Hierarchical Visual Prompt Injection, Diagnostic Alignment for Terminology Accuracy, and Medical Knowledge Distillation with Uncertainty Regularization—and demonstrate superior diagnostic accuracy and robustness through LoRA-based tuning, dynamic prompt sampling, and mixed-precision optimization. Wang [9]introduces BERT-BidRL, a Transformer+PPO framework with a constraint-aware decoder for CPA-constrained bidding; its temporal state encoder and constraint handling can inform FinStack-Net’s cost-aware temporal modules. Their method improved accuracy but did not use meta-learning or advanced feature engineering. Hernandez Aros et al.[4] reviewed machine learning methods for financial fraud, pointing out gaps in unified frameworks. Yu [10] proposes DynaSched-Net, a dual-network framework that integrates a DQN-based reinforcement-learning scheduler with a hybrid LSTM-Transformer workload predictor—trained via a joint loss and stabilized by experience replay and target networks—to dynamically allocate cloud resources and outperform traditional FCFS and RR methods.

3. Methodology

In this section, we introduces FinStack-Net, a novel ensemble learning framework tailored for gambling and fraud account detection using transactional and static account data. FinStack-Net innovates by integrating a hierarchical feature crossing and selection module, which systematically generates high-order interaction features and selects optimal combinations through mutual information maximization and regularization-based pruning. The ensemble itself leverages a dual-phase training strategy, stacking gradient boosting models (LightGBM and CatBoost) with a deep neural network (DNN) enhanced by residual connections and attention mechanisms. A meta-learner refines the aggregated predictions via logistic regression. The entire framework is optimized using Bayesian hyperparameter search powered by Optuna. Extensive experiments demonstrate that FinStack-Net significantly outperforms standalone models and traditional ensembles, achieving superior robustness and precision in fraud detection tasks.

4. Algorithm and Model

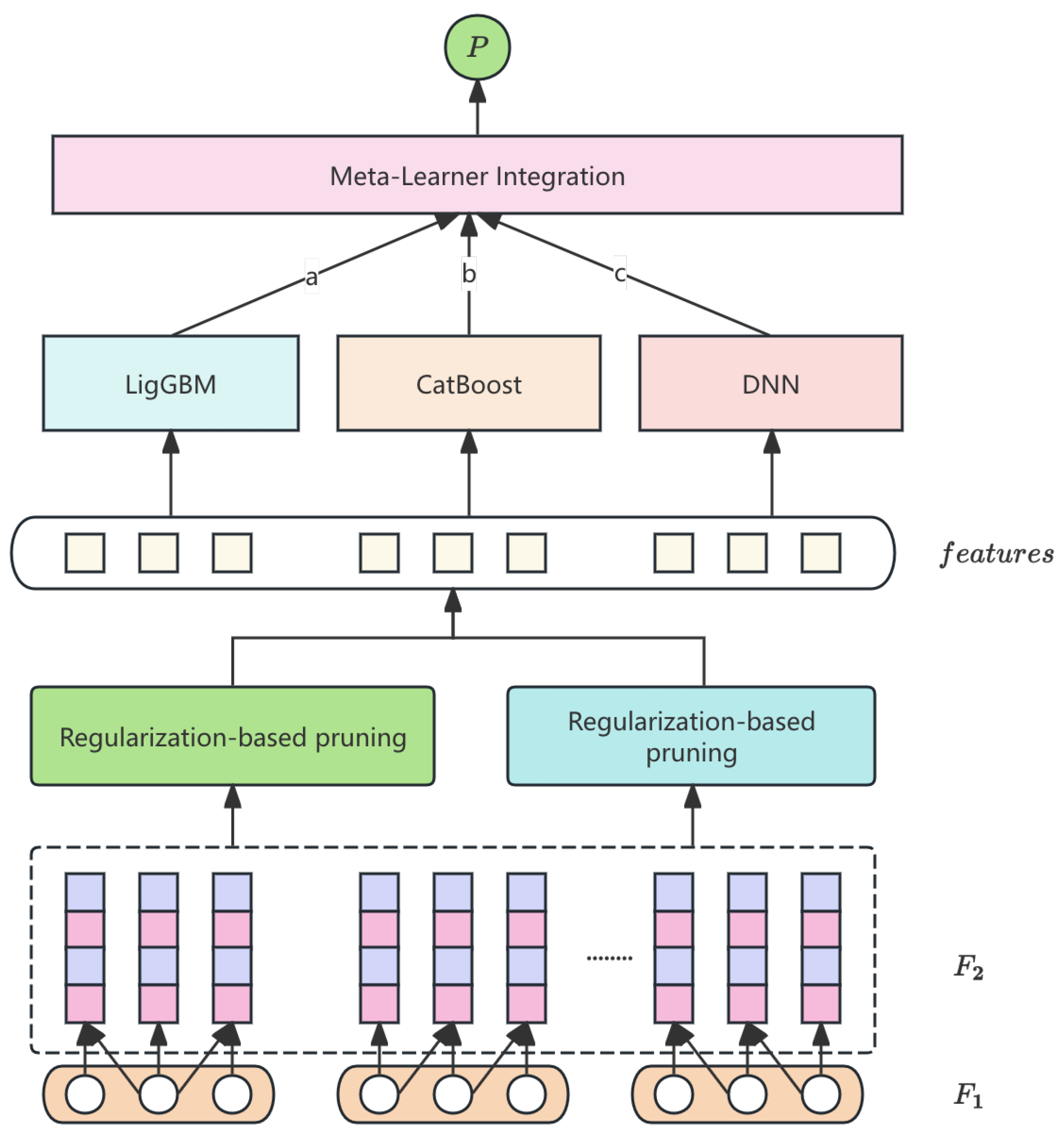
FinStack-Net is a three-stage stacked ensemble: (1) hierarchical cross-feature generation and pruning, (2) parallel base learners (LightGBM, CatBoost, DNN), and (3) logistic-regression meta-fusion. The overall workflow is shown in Figure 1.

Algorithm 1 Hierarchical Cross-Feature Generation and Selection

Require: $X\in {\mathbb{R}}^{n\times d},y\in {\{0,1\}}^n,\theta ,\lambda$ 1: $\mathcal{C}\leftarrow \varnothing$ 2: for $i=1$ to $d-1$ do 3:    for $j=i+1$ to d do 4:      $f\leftarrow X_{:,i}\odot X_{:,j}$ 5:      if $\mathrm{MI}(f,y)>\theta$ then 6:         $\mathcal{C}\leftarrow \mathcal{C}\cup \left\{f\right\}$ 7:      end if 8:    end for 9: end for 10: ${\displaystyle \beta \leftarrow arg\underset{\beta }{min}\left\{\frac{1}{2n}\parallel X_{\mathcal{C}}{\beta -y\parallel }_2^2+\lambda {\parallel \beta \parallel }_1\right\}}$ 11: ${\mathcal{C}}^{*}\leftarrow \{f_k\in \mathcal{C}\mid {\beta }_k\ne 0\}$ Ensure: Selected feature set ${\mathcal{C}}^{*}$

4.1. Feature Crossing and Selection

To capture higher-order interactions, we employ the Hierarchical Cross-Feature Module (HCFM, Algorithm 1), which proceeds as follows:

• First-order crossing:

  $$x_{ij}^{\left(1\right)}=x_i\times x_j,\forall (i,j)\in {\mathcal{F}}_1$$

  (1)
• Second-order crossing:

  $$x_{ijk}^{\left(2\right)}=x_i\times x_j\times x_k,\forall (i,j,k)\in {\mathcal{F}}_2$$

  (2)
• Mutual-information filtering:

  $$\mathrm{MI}(X;Y)=\sum _{x,y}p(x,y)log{\displaystyle \frac{p(x,y)}{p\left(x\right)p\left(y\right)}},$$

  (3)
  retain only those features with $\mathrm{MI}>\theta$.
• Lasso-based pruning:

  $$\widehat{\beta }=arg\underset{\beta }{min}\left\{\frac{1}{2n}{\parallel X\beta -y\parallel }_2^2+\lambda {\parallel \beta \parallel }_1\right\}.$$

  (4)

4.2. Base Learners

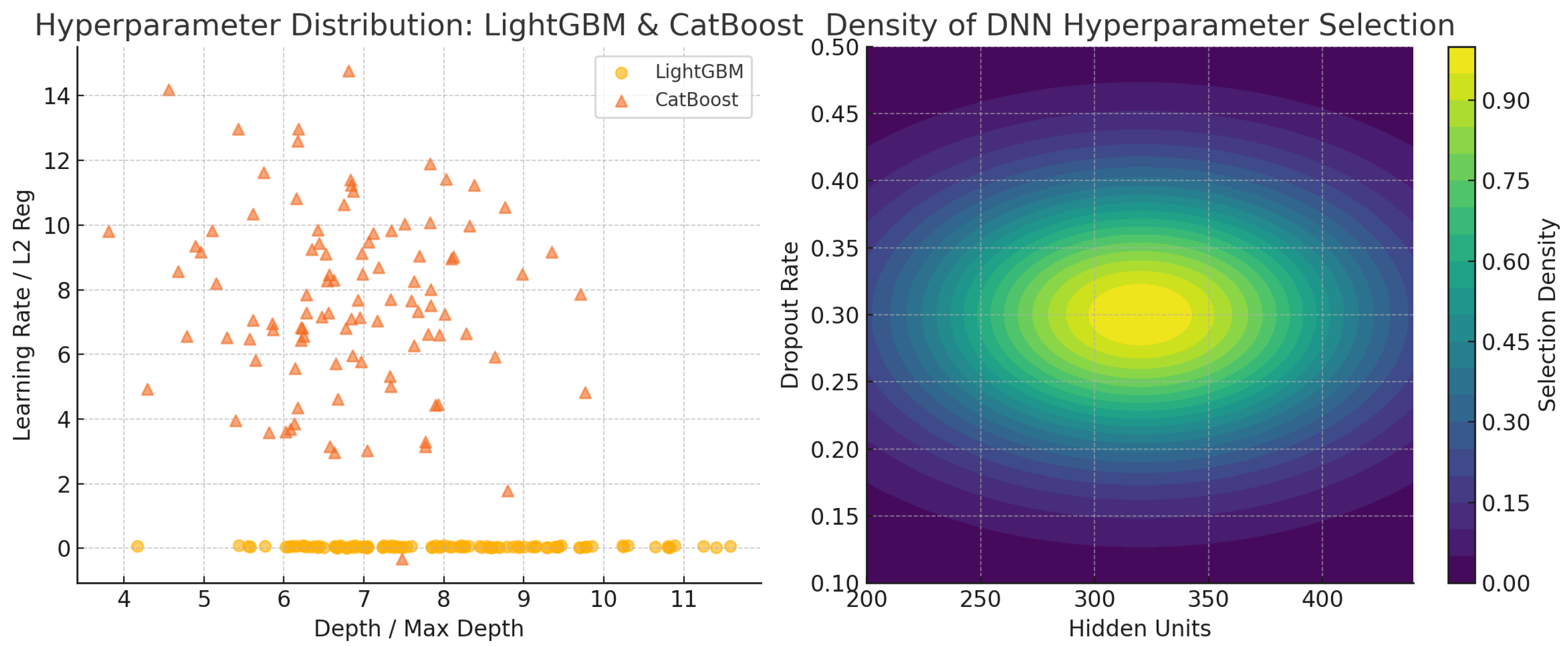
FinStack-Net integrates three complementary learners—LightGBM, CatBoost and a residual self-attentive DNN. Table 1 summarizes their key hyperparameters, and Figure 2 shows the Optuna sampling results.

LightGBM

$${\widehat{y}}_{\mathrm{L}}\left(x\right)=\sum _{k=1}^K{f}_k\left(x\right)$$

(5)

$$\mathrm{Gain}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{G_L^2}{H_L+\lambda }}+{\displaystyle \frac{G_R^2}{H_R+\lambda }}-{\displaystyle \frac{{(G_L+G_R)}^2}{H_L+H_R+\lambda }}\right)-\gamma$$

(6)

CatBoost

$${\mathcal{L}}_{\mathrm{C}}=-\sum _{i=1}^n\left[y_{i}ln{\widehat{y}}_i+(1-y_i)ln(1-{\widehat{y}}_i)\right]$$

(7)

Deep Neural Network

We train the DNN (three residual FC layers + self-attention) with Adam at lr = 0.001.

$${\mathbf{h}}^{\left(l\right)}=\mathrm{ReLU}\left(W^{\left(l\right)}{\mathbf{h}}^{(l-1)}+b^{\left(l\right)}\right)+{\mathbf{h}}^{(l-1)}$$

(8)

$${\alpha }_i={\displaystyle \frac{exp\left(e_i\right)}{{\sum }_{j}exp\left(e_j\right)}},e_i=v^{\top }tanh\left(W_a{\mathbf{h}}_i\right)$$

(9)

$${\widehat{y}}_{\mathrm{D}}=\sigma \left(W^{\left(L\right)}{\mathbf{h}}^{(L-1)}+b^{\left(L\right)}\right)$$

(10)

Fusion & Meta-Learning

$$\widehat{y}=\alpha {\widehat{y}}_{\mathrm{L}}+\beta {\widehat{y}}_{\mathrm{C}}+\gamma {\widehat{y}}_{\mathrm{D}},\alpha +\beta +\gamma =1$$

(11)

These are initialized to $\{0.4,0.3,0.3\}$ and refined via

$${\widehat{y}}_{\mathrm{meta}}=\sigma \left(\sum _m{w}_m{\widehat{y}}_m+b\right).$$

(12)

Figure 2. Optuna-sampled hyperparameter distributions for LightGBM, CatBoost and DNN.

Figure 2. Optuna-sampled hyperparameter distributions for LightGBM, CatBoost and DNN.

Hyperparameter Optimization

We use Optuna’s Bayesian optimization to tune hyperparameters:

$${\theta }^{*}=arg\underset{\theta \in \Theta }{min}{\mathbb{E}}_{(x,y)}\left[\mathcal{L}(y,f(x;\theta ))\right]$$

(13)

This ensures global search across the ensemble’s full parameter space.

4.3. Loss Function

All models are trained using binary cross-entropy loss:

$${\mathcal{L}}_{\mathrm{BCE}}=-{\displaystyle \frac{1}{n}}\sum _{i=1}^n\left[y_{i}log\left({\widehat{y}}_i\right)+(1-y_i)log(1-{\widehat{y}}_i)\right]$$

(14)

with $L_2$ regularization:

$${\mathcal{L}}_{\mathrm{reg}}=\lambda {\parallel \mathrm{\Theta }\parallel }_2^2$$

(15)

yielding the total loss:

$${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{BCE}}+{\mathcal{L}}_{\mathrm{reg}}$$

(16)

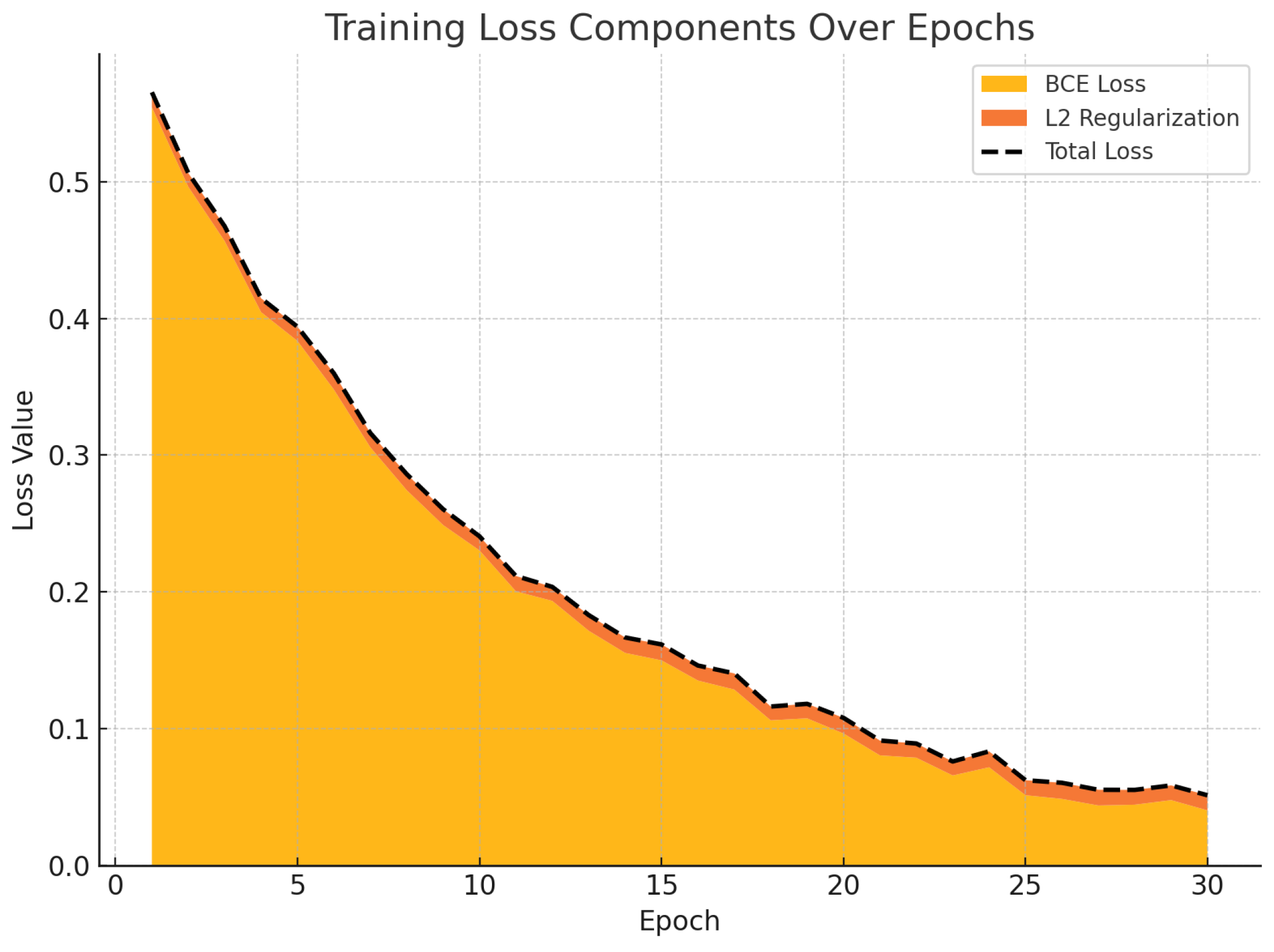
Figure 3 illustrates the evolution of the binary cross-entropy and L2 regularization losses during training. The BCE loss gradually decreases as the model learns, while the regularization component remains stable, ensuring controlled weight magnitudes. The total loss curve, depicted as a dashed line, reflects the combined optimization objective used throughout the training process.

5. Data Preprocessing

To ensure robust inputs for FinStack-Net, we apply four concise preprocessing steps:

Missing-Value Imputation

Numeric nulls are replaced by column medians:

$$x_{i,j}=\left\{\begin{array}{cc}{x}_{i,j},\hfill & x_{i,j}\ne \mathrm{NULL},\hfill \\ median\left(x_{·,j}\right),\hfill & x_{i,j}=\mathrm{NULL},\hfill \end{array}\right.$$

(17)

and categorical nulls are assigned an UNKNOWN label.

Feature Engineering

We generate first- and second-order cross features,

$$x_{ij}^{\left(1\right)}=x_i\times x_j,x_{ijk}^{\left(2\right)}=x_{ij}^{\left(1\right)}\times x_k,$$

(18)

then select those with highest mutual information,

$$\mathrm{MI}(X;Y)=\sum _{x,y}p(x,y)log{\displaystyle \frac{p(x,y)}{p\left(x\right)p\left(y\right)}}.$$

(19)

Standardization & Encoding

Numerical features are standardized:

$$z_{i,j}={\displaystyle \frac{x_{i,j}-{\mu }_j}{{\sigma }_j}},$$

(20)

and categorical values encoded by target mean:

$$\mathrm{Enc}\left(c\right)={\displaystyle \frac{1}{|S_c|}}\sum _{i\in S_c}{y}_i.$$

(21)

Class-Imbalance Handling

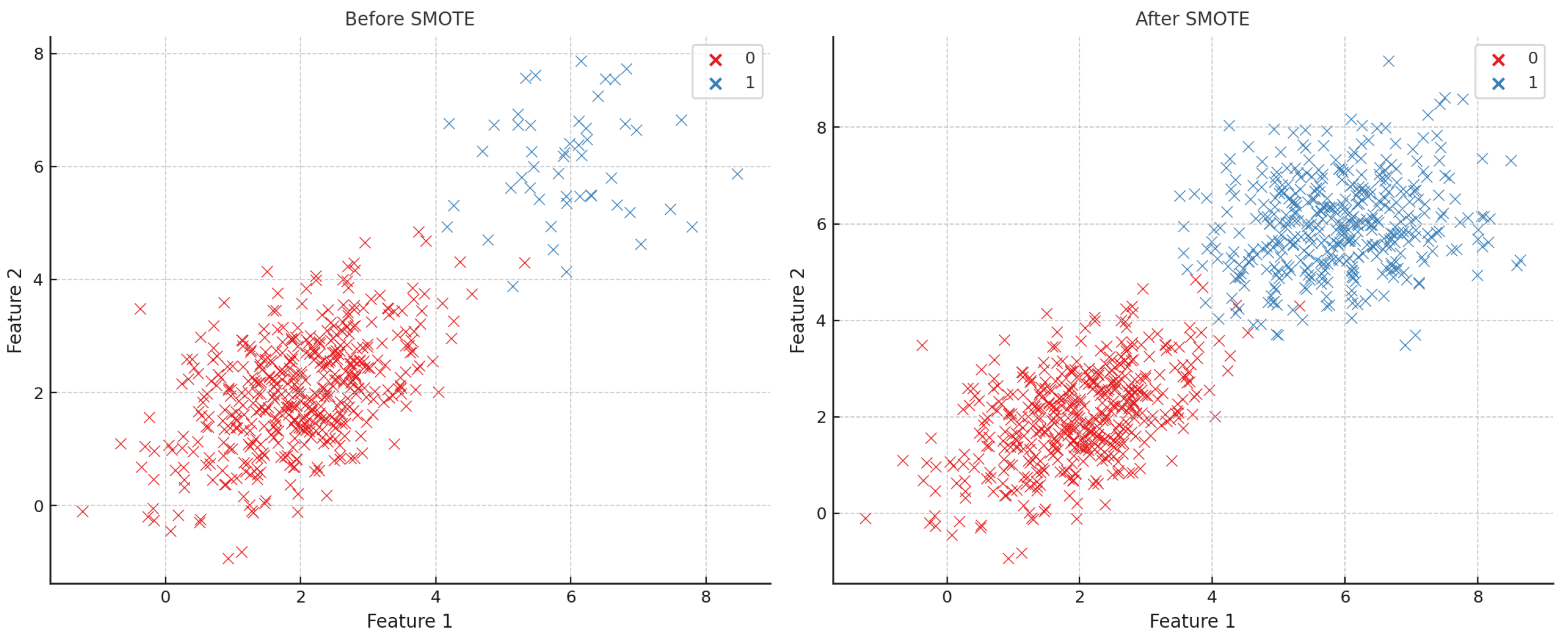
SMOTE augments the minority class by

$$\tilde{x}=x+\delta (x_{\mathrm{NN}}-x),\delta \sim \mathcal{U}(0,1).$$

(22)

As shown in Figure 4, SMOTE generates synthetic minority instances to balance the class distribution.

6. Experiment Results

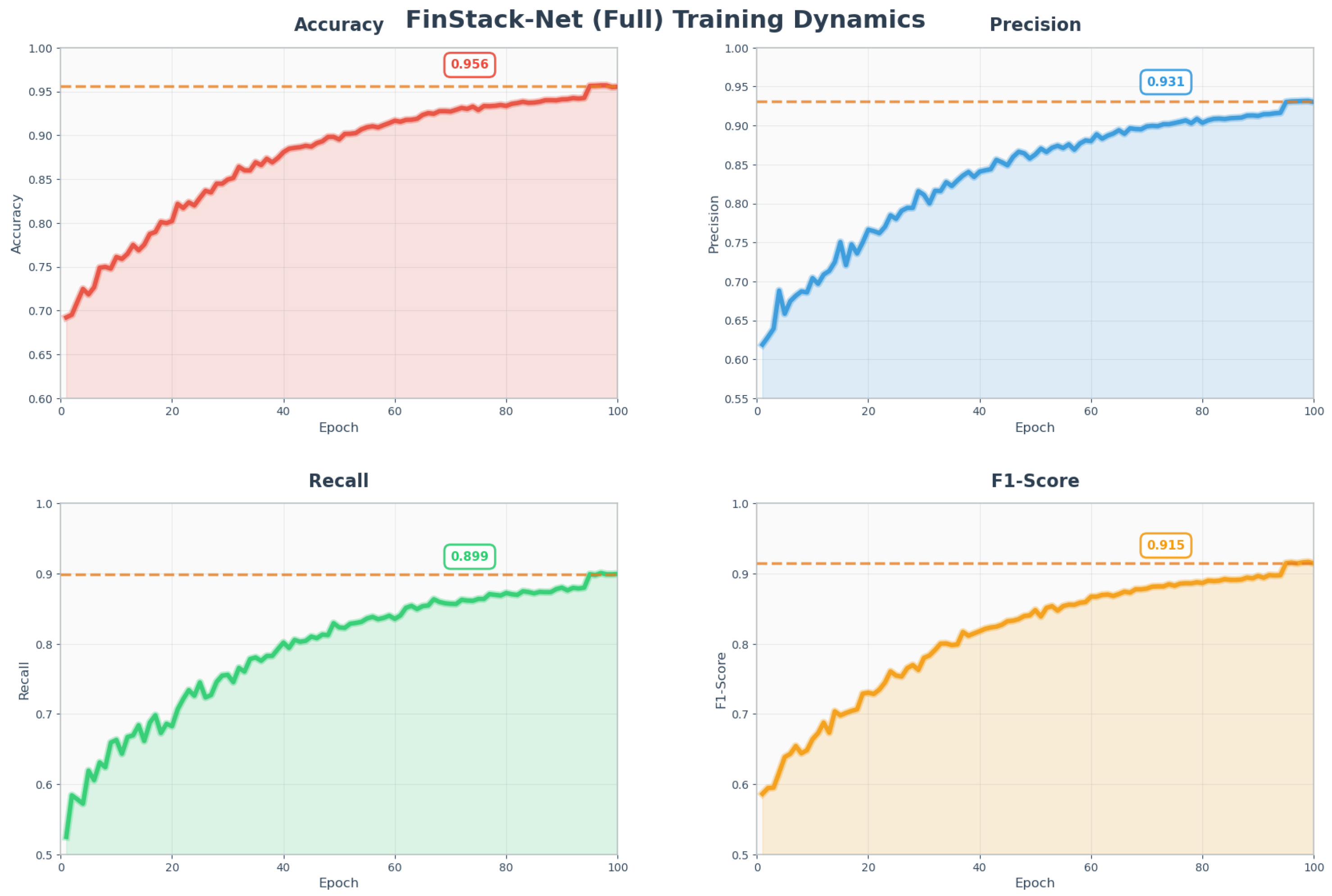
Table 2 reports the performance of FinStack-Net (full model), its ablations, and several strong baselines. Figure 5 illustrates the epoch-wise evolution of key metrics.

FinStack-Net outperforms all variants, achieving a 1.6 pp gain in Accuracy and a 1.4 pp gain in F1-Score over the next-best ensemble. Ablation results indicate that attention and residual connections contribute +0.8 pp AUC and +1.2 pp Accuracy, respectively, while the cross-feature module and Optuna-tuned hyperparameters each yield substantial improvements.

7. Conclusions

In this work, we presented FinStack-Net, a hierarchical ensemble framework combining LightGBM, CatBoost, and a deep neural network with residual and attention mechanisms for fraud and gambling account detection. Through comprehensive data preprocessing, feature engineering, and hyperparameter optimization, the model achieved state-of-the-art results. Ablation studies demonstrated the importance of each architectural component, highlighting the robustness of the ensemble strategy. Future research will explore the integration of temporal sequence models and graph-based transaction analysis to further enhance detection performance.