Submitted:
26 August 2025
Posted:
23 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Steady State Solutions
3. Conditions of Turing Instability
4. Linearization of Reaction System
5. Linearization of Reaction-Diffusion System (RDS)
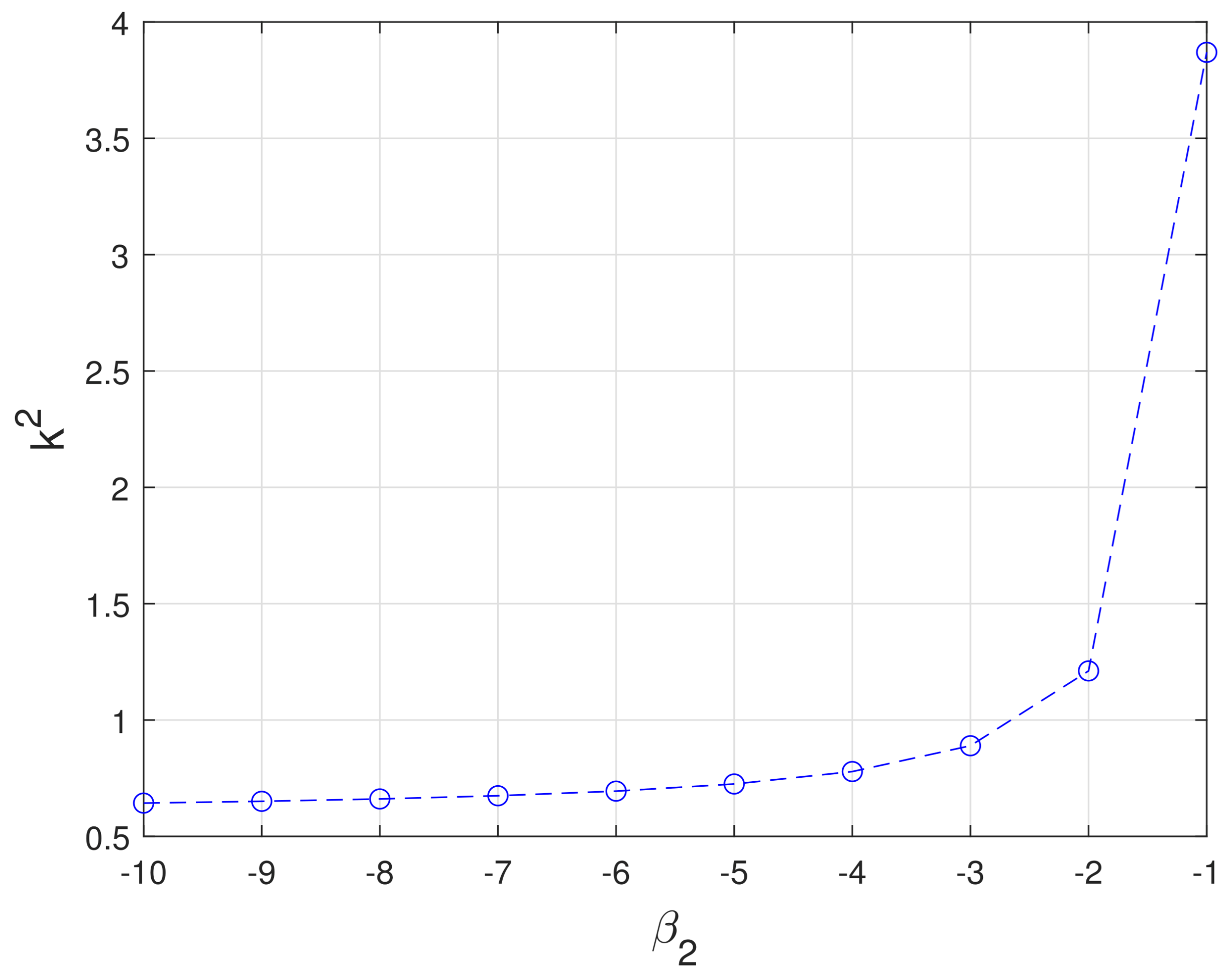
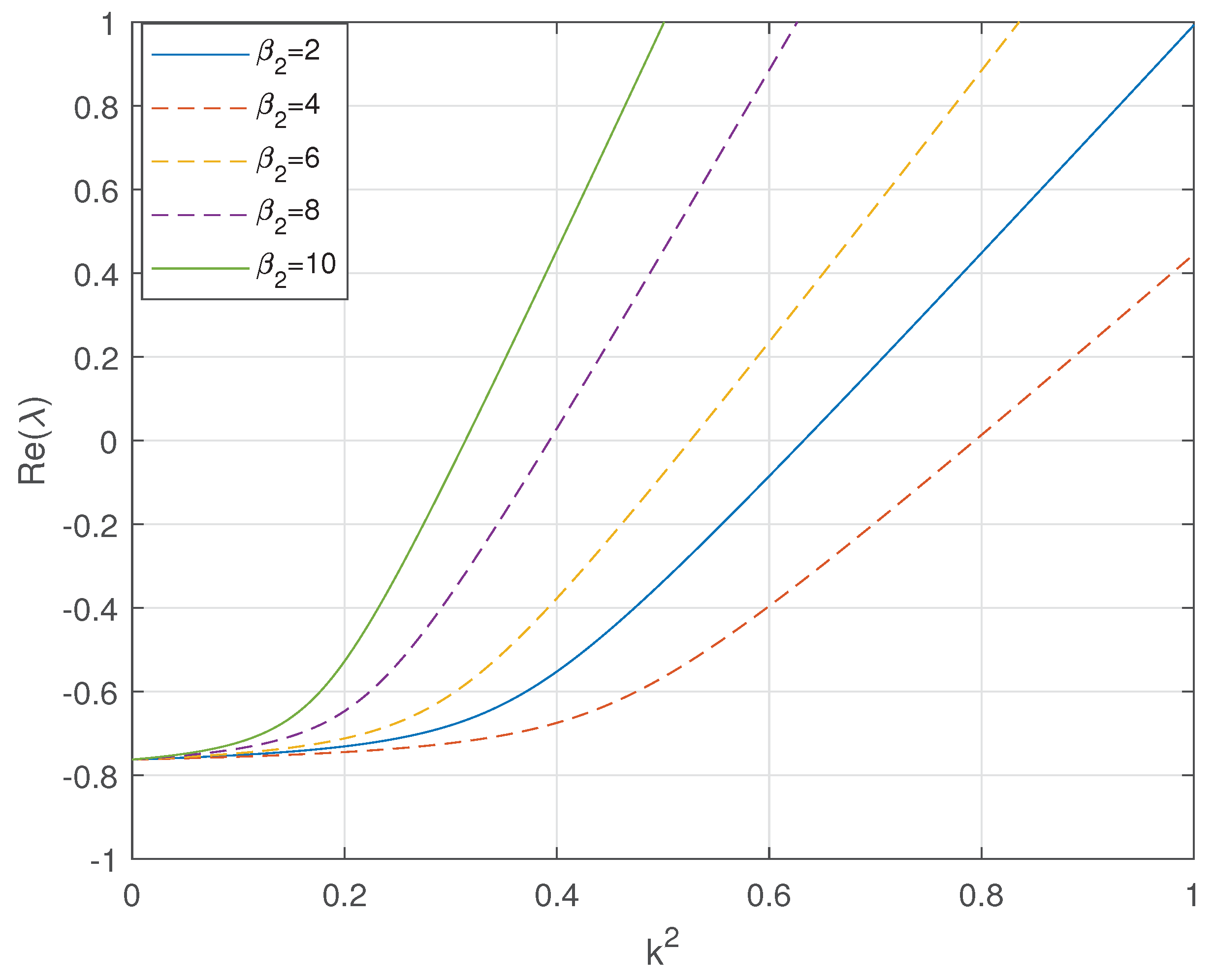
5.1. Turing Bifurcation Threshold
6. Pattern Formations for RDS (1) and (2) in Two Dimensions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Y. Almirantis, S. Papageorgiou, Cross–diffusion effects on chemical and biological pattern formation, J. Theor. Biol. 151 (1991) 289–311. [CrossRef]
- Murray JD. Parameter space for Turing instability in reaction-diffusion mechanisms: a comparison of models. J Theor Biol 1982;98:143–63. [CrossRef]
- V.K. Vanag, I.R. Epstein, Cross–diffusion and pattern formation in reaction-diffusion system, Phys. Chem. Phys. 11 (2009) 897–912. [CrossRef]
- Turing AM. The Chemical Basis of Morphogenesis: Philosophical Transactions of the Royal Society of London. Ser. B, Biol. Sci., vol. 237, 1952. [CrossRef]
- Y. Peng, T. Zhang, Stability and Hopf bifurcation analysis of a gene expression model with diffusion and time delay, Abstr. Appl. Anal. 2014 (2014) 1. [CrossRef]
- A. Okubo, Diffusion and Ecological Problems: Mathematical Models, Biomathematics, Springer–Verlag, Berlin, Heidelberg, 1980. [CrossRef]
- L.A. Segel, J.L. Jackson, Dissipative structure: an explanation and an ecological example, J. Theor. Biol. 37 (1972) 545–559. [CrossRef]
- Maxime Breden, Christian Kuehn, Cinzia Soresina. On the influence of cross-diffusion in pattern formation. Journal of Computational Dynamics, (2021), 8 (2), pp.213. [CrossRef]
- T. Zhang, Y. Xing, H. Zang, M. Han, Spatiotemporal dynamics of a reaction-diffusion system for a predator-prey model with hyperbolic mortality, Nonlinear Dyn. 78 (2014) 265–277. [CrossRef]
- Page KM, Maini PK, Monk NAM. Complex pattern formation in reaction-diffusion systems with spatially varying parameters. Phys D Nonlinear Phenom 2005;202:95–115. [CrossRef]
- Nanako Shigesada, Kohkichi Kawasaki, and Ei Teramoto. Spatial segregation of interacting species. Journal of Theoretical Biology, 79(1):83–99, 1979. [CrossRef]
- Dunbar SR. Traveling wave solutions of diffusive Lotka-Volterra equations: a heteroclinic connection in R4. Trans Am Math Soc 1984:557–94. [CrossRef]
- Woolley, T. E., Krause, A. L., & Gaffney, E. A. (2021). Bespoke Turing systems. Bulletin of Mathematical Biology, 83, 1-32. [CrossRef]
- Cross M, Greenside H. Pattern formation and dynamics in nonequilibrium systems. Cambridge University Press; 2009. [CrossRef]
- Rasheed SM. Pattern Formation for a New Model of Reaction-Diffusion System. 2018 Int. Conf. Adv. Sci. Eng., IEEE; 2018, p. 99–104.
- Turing AM. The chemical basis of morphogenesis. Bull Math Biol 1990;52:153–97. [CrossRef]
- Li, S., & Ling, L. (2020). Complex pattern formations by spatial varying parameters. Advances in Applied Mathematics and Mechanics, 12(6), 1327–1352. [CrossRef]
- F. Brauer. On the populations of Competing Species. Mathematical Biosciences, vol. 19, (1974), 299-306. [CrossRef]
- K. Gopalsamy. Exchange of Equilibria in Two Species Lotka-Voltera Competition Models. J. Austral. Math. Soc., vol. 24, (1982), 160–170. [CrossRef]
- J.F. AL-Omari, S. A. Gourley. Stability And Travelling Fronts In Lotka-Voltera Competition Models With Stage Structure. J. Appl. Math, vol. 63, (2003), 2063–2086. [CrossRef]
- S. A. Gourley. Two-Species Competition With High Dispersal: The Winning Strategy. Mathematical Biosciences And Engineering, vol.2, No.2 (2005), 345-362. [CrossRef]
- V. Volpert, S.Petrovskii. Reaction-diffusion waves in biology. Physics of Life Reviews, vol.6, (2009), 267-310. [CrossRef]
- Y. Hosono. Travelling Waves For A Diffusive Lotka-Volterra Competition Model I: Singular Perturbations. Discrete And Continous Dynamical Systems-Series B, vol. 3, (2003), 97-95. [CrossRef]
- Z. Li. Asymptotic Behaviour of Travelling Wavefronts of Lotka-Volterra Competitive System. Int. Journal of Math. Analysis, vol. 2, (2008), 1295–1300.
- Rasheed, Shaker M., and J. Billingham. A Reaction-Diffusion Model for Inter-Species Competition and Intra-Species Cooperation. Mathematical Modelling of Natural Phenomena 8.3 (2013): 154-181. [CrossRef]
- Krebs, C.J., 1994. Ecology—The Experimental Analysis of Distribution and Abundance, 4th ed. Harper Collins College Publishers, New York, p. 801.
- Lotka, A.J., 1925. Elements of Physiological Biology. Dover Publications, New York, 1956.
- Volterra, V., 1926. Fluctuation in the abundance of a species considered mathematically. Nature 118, 558–560. [CrossRef]
- Breden, M., Kuehn, C., Soresina, C. (2019). On the influence of cross-diffusion in pattern formation. arXiv preprint arXiv:1910.03436. [CrossRef]
- Kazuo Kishimoto and Hans F. Weinberger. The spatial homogeneity of stable equilibria of some reaction-diffusion systems on convex domains. Journal of Differential Equations, 58:15–21, 1985. [CrossRef]
- J.D. Murray. Mathematical Biology I: An introduction. Springer-Verlag, New York, 2002.
- K. Gopalsamy. Exchange of Equilibria in Two Species Lotka-Voltera Competition Models. J. Austral. Math. Soc., vol. 24, (1982), 160–170. [CrossRef]
- N. Britton. Reaction-Diffusion Equations And Their Applications To Biology. Academic Press INC. (London) LTD, 1986. [CrossRef]
- Y. Hosono. Travelling Waves For A Diffusive Lotka-Volterra Competition Model I: Singular Perturbations. Discrete And Continous Dynamical Systems-Series B, vol. 3, (2003), 97-95. [CrossRef]
- Turing Instability in the Solid State: Void Lattices in Irradiated Metals Phys. Rev. Lett. 124, (2020),167-401. [CrossRef]
- F.A. dos S. Silva, R.L. Viana, S.R. Lopes, Pattern formation and Turing instability in an activator-inhibitor system with power-law coupling, Physica A 419 (2015) 487–497. [CrossRef]
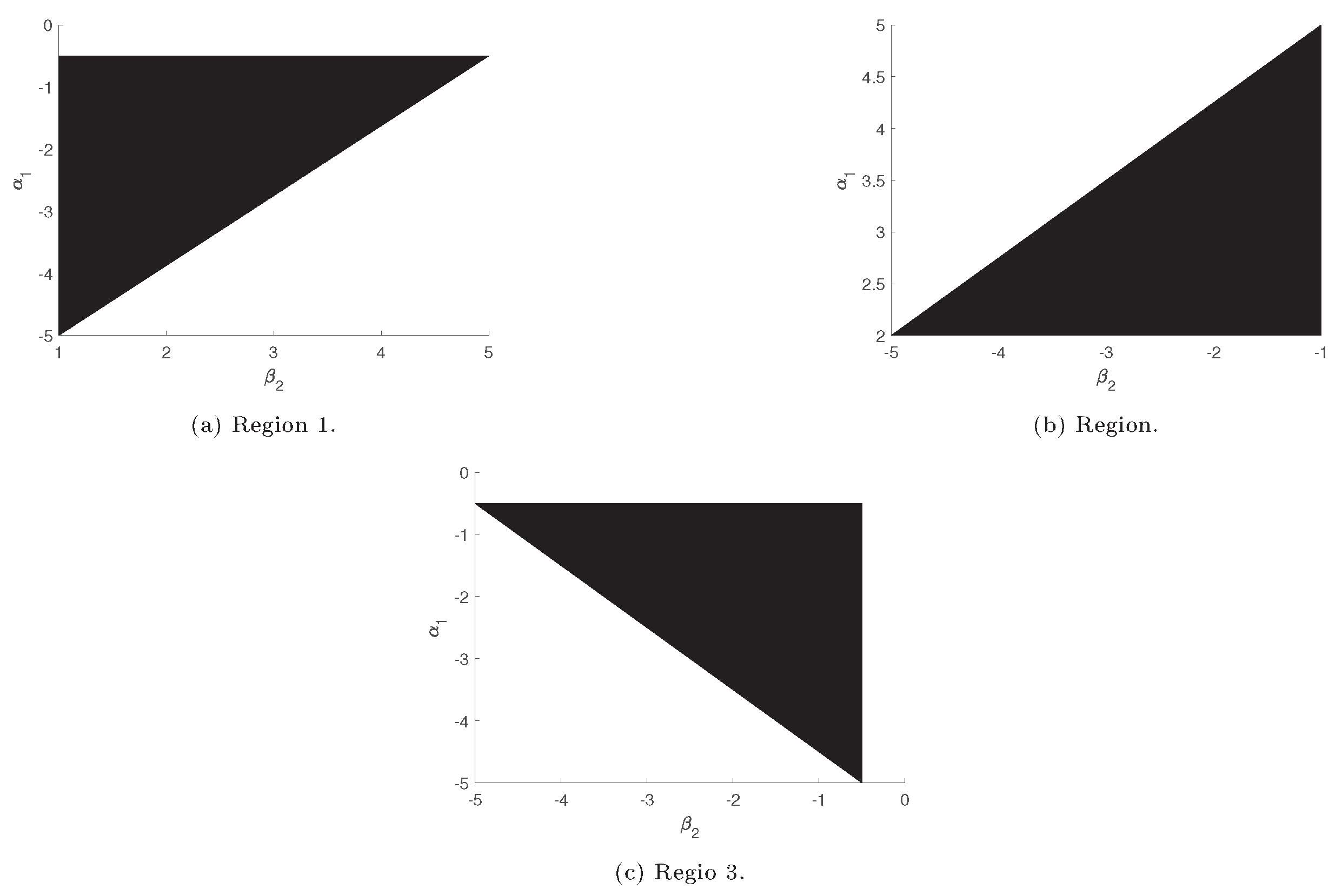


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



