Limit Theorem for Kernel Estimate of the Conditional Hazard Function with Weakly Dependent Functional Data

1. Introduction

Recent advances in computational technology and data acquisition systems have made it possible to store and process massive datasets that vary over time, including curves and images. These types of observations are commonly referred to as functional data. Effectively analyzing and modeling such data presents both a challenge and an opportunity for statisticians, leading to the development of powerful statistical tools—chief among them, nonparametric estimation methods.

Pioneering contributions by Bosq and Lecoutre [1], Ferraty and Vieu [2], Ferraty, Mas, and Vieu [3], and Laksaci and Mechab [4] have laid the foundation for nonparametric estimation in the functional data context. Their works have significantly influenced the theoretical aspect and practical implementation of kernel method, making them key references in the domain of nonparametric functional statistics.

Numerous researchers have addressed the study of nonparametric models from both theoretical and practical perspectives. For instance, in the context of kernel estimation, Ferraty and Vieu [5], and Ferraty, Goia, and Vieu [6] investigated regression operators for functional data. Laksaci and Mechab [7] explored the asymptotic behavior of regression functions under weak dependence, Azzi et al. [8] present the function modal regression for functional data, while Hyndman and Yao [9] proposed estimation techniques and symmetry tests for conditional density functions. Daoudi et al. [10] show conditional density estimation under weak dependence and Censorship phenomena. Other notable contributions include those of Attaoui, Laksaci, and Ould Said [11], as well as Xu [12] and Abdelhak et al. [13], who studied single-index models, Daoudi and Mechab [14], who focused on estimating the conditional distribution function under quasi-association assumptions.

These contributions, centered around kernel-based methods for conditional models, have led to significant insights into the asymptotic properties of estimators related to prediction, conditional distribution functions, and their derivatives, particularly the conditional density function. Furthermore, Bulinski and Suquet [15] examined random fields with both positive and negative dependence structures, Bouaker et al. [16] examine the consistency of the kernel estimator for conditional density in high dimensional statistics, and Newman [17] investigated asymptotic independence and limit theorems in similar settings.

Regarding the hazard function, several works have addressed its estimation in dependent contexts. Ferraty, Rabhi, and Vieu [18], Laksaci and Mechab [19], and Gagui and Chouaf [20] obtained the asymptotic normality results in the case of $\alpha$-mixing conditions. Belguerna et al. [21] further analyzed the MSE of the conditional hazard function estimator.

The concept of quasi-association for real-valued stochastic processes, presented in [22] as a particular form of weak dependence, was later extended by Bulinski and Suquet [23]. Further contributions were made by Kallabis and Neumann [24], who derived exponential inequalities under weak dependence conditions.

More recently, a number of studies have investigated nonparametric models involving quasi-associated random variables. Bassoudi et al. [25] evaluate the asymptotic characteristics of the conditional hazard estimator derived from the local linear technique for ergodic data. Attaoui [26], Tabti and Ait Saidi [27], and Douge [28] have contributed to this direction.

Furthermore, recent research has increasingly focused on the asymptotic analysis of conditional functional models under weak dependence structures, particularly quasi-association. Daoudi, Mechab, and Chikr Elmezouar [29], as well as Daoudi et al. [30], have investigated asymptotic properties of estimators of conditional hazard functions in single-index models for quasi-associated data. Similarly, Bouzebda, Laksaci, and Mohammedi [31] studied the single-index regression model, while Rassoul et al. [32] examined the mean squared error of the conditional hazard rate, highlighting its asymptotic behavior under weak dependence assumptions. Daoudi et al. [35] demonstrate asymptotic results of a conditional risk function estimate for associated data case in high-dimensional statistics.

In the same context, additional contributions have strengthened the theoretical foundation of kernel-based nonparametric estimators. For instance, the asymptotic normality and consistency of the conditional density and hazard function estimators have been addressed under quasi-associated and weakly dependent functional data settings [33]. High-dimensional statistics and complex dependence frameworks have also been tackled, including the asymptotic behavior of regression estimator under quasi-associated functional censored time series [35] and [36]. These works confirm the growing interest in developing robust asymptotic results for conditional models in dependent functional data, offering theoretical tools that support their practical implementation.

This study examines the asymptotic characteristics of the conditional hazard function estimator for functional data under quasi-associated phenomena, with the aim of establishing its asymptotic properties. We begin by introducing the functional model along with all necessary notation and mathematical tools. As a first result, we establish the almost complete consistency. Then, we derive its asymptotic normality by employing various analytical techniques and decomposition strategies. All theoretical developments are supported with rigorous proofs.

To validate the theoretical findings, we conduct a numerical study demonstrating the asymptotic normal approximation of the proposed estimator. In this context, we generate three datasets of different sizes to examine the impact of key parameters such as sample size and bandwidth on estimator performance. Graphical comparisons between theoretical and empirical results are provided to illustrate the estimator’s effectiveness and assess the quality of the estimation.

This paper is structured as follows. In Section 2, we present the quasi-associated sequence, outline the model construction, and present the estimator. Section 3 states the necessary assumptions and develops the results concerning almost complete convergence and asymptotic normality of the estimator. Section 4 provides a comprehensive numerical study supporting the theoretical findings and offering asymptotic confidence bounds. Finally, the detailed proofs of our main results are given in Appendices Appendix A and Appendix B.

2. The Model

Let $Z_i={(S_i,T_i)}_{1\le i\le n}$, be an $\mathcal{H}\times \mathbb{R}$-valued measurable and strictly stationary stochastic process defined on a probability space $(\Omega ,\mathcal{A},\mathbb{P})$, where $(\mathcal{H},d)$ denotes a semi metric space, where $\mathcal{H}$ is a normed $\Vert .\Vert$ Hilbert space, provided with an inner product $<.,.>$. The semi metric noted d defined by $d(s,s^{\prime })=\Vert s-s^{\prime }\Vert ,\forall s,s^{\prime }\in \mathcal{H}$. We consider a fixed point s in $\mathcal{H}$, ${\mathcal{N}}_s$ a fixed neighborhood of s and $\mathcal{S}$ be a fixed compact subset of $\mathbb{R}$. We assume the existence of a regular version of the conditional probability distribution of the random variable T given S. Furthermore, for all $s\in N_s$, we suppose that the conditional distribution function of T given $S=s$ denoted by $G^s(·)$ is three times continuously differentiable. We denote its corresponding conditional density function by $g^s(·)$.

In this paper, we investigate the kernel estimation of the conditional hazard function of T given $S=s$, denoted ${\lambda }^s\left(t\right)$, for all $t\in \mathbb{R}$ such that $G^s\left(t\right)<1$, is given by:

$${\lambda }^s\left(t\right)={\displaystyle \frac{g^s\left(t\right)}{1-G^s\left(t\right)}}.$$

In our functional context, the kernel estimate of this function is given by:

$$\begin{array}{c}\hfill {\widehat{\lambda }}^s\left(t\right)={\displaystyle \frac{{\widehat{g}}^s\left(t\right)}{1-{\widehat{G}}^s\left(t\right)}},\forall t\in \mathbb{R}.\end{array}$$

(1)

where ${\widehat{G}}^s(·)$ is the conditional distribution functional estimator, given by:

$$\begin{array}{c}\hfill {\widehat{G}}^{·}\left(t\right)={\displaystyle \frac{{\sum }_{i=1}^{n}K\left({\theta }_K^{-1}d\left(·,S_i\right)\right)H\left({\theta }_H^{-1}\left(t-T_i\right)\right)}{{\sum }_{i=1}^{n}K\left({\theta }_K^{-1}d\left(·,S_i\right)\right)}},\forall t\in \mathbb{R}\end{array}$$

(2)

and ${\widehat{g}}^s(·)$ is the conditional density functional estimator, given by:

$$\begin{array}{c}\hfill {\widehat{g}}^{·}\left(t\right)={\displaystyle \frac{{\sum }_{i=1}^{n}K\left({\theta }_K^{-1}d\left(·,S_i\right)\right)H^{\prime }\left({\theta }_H^{-1}\left(t-T_i\right)\right)}{{\sum }_{i=1}^{n}K\left({\theta }_K^{-1}d\left(·,S_i\right)\right)}},\forall t\in \mathbb{R}\end{array}$$

(3)

with K denote a kernel function, H be a given differentiable distribution function with derivative $H^{\prime }$. The quantities ${\theta }_K={\theta }_{K,n}$ and ${\theta }_H={\theta }_{H,n}$ represent sequences of positive bandwidth parameters. Under this framework, the estimator ${\widehat{\lambda }}^s\left(t\right)$ can be expressed as:

$${\widehat{\lambda }}^s\left(t\right)={\displaystyle \frac{{\widehat{g}}_N^s\left(t\right)}{{\widehat{G}}_D^s-{\widehat{G}}_N^s\left(t\right)}}.$$

(4)

where

$$\begin{array}{cc}\hfill {\widehat{G}}_D^{·}& ={\displaystyle \frac{1}{n\mathbb{E}\left[K_1(·)\right]}}\sum _{i=1}^n{K}_i(·)\hfill \\ \hfill {\widehat{G}}_N^{·}\left(t\right)& ={\displaystyle \frac{1}{n\mathbb{E}\left[K_1(·)\right]}}\sum _{i=1}^n{K}_i(·)H_i\left(t\right)\hfill \\ \hfill {\widehat{g}}_N^{·}\left(t\right)& ={\displaystyle \frac{1}{n{h}_H\mathbb{E}\left[K_1(·)\right]}}\sum _{i=1}^n{K}_i(·)H_i^{\prime }\left(t\right)\hfill \end{array}$$

(5)

with notational convenience:

$$K_i(·)=K\left({\theta }_K^{-1}d\left(·,S_i\right)\right),\mathrm{and}{H}_i\left(t\right)=H\left({\theta }_H^{-1}\left(t-T_i\right)\right).$$

Our primary objective is to establish both the consistency and the asymptotic normality of the estimator (4) under suitable hypothesis, where the sequence of variables ${\left(S_n\right)}_{n\in \mathbb{N}}$ verify the quasi-association as defined by Bulinski and Suquet [18].

Definition 1.

Given $I_1$ and $I_2$ subsets of $\mathbb{N}$ where $I_1\cap I_2=\varphi$, for all lipschitzian $f_1$ and $f_2$ functions, we consider ${\left(S_n\right)}_{n\in \mathbb{N}}$ as a sequence of quasi associated random vector if :

$$\begin{array}{c}\hfill Cov\left(f_1\left(S_{\tau },\tau \in I_1\right),f_2\left(S_{\kappa },\kappa \in I_2\right)\right)\le Lip\left(f_1\right)Lip\left(f_2\right)\sum _{\tau \in I_1}\sum _{\kappa \in I_2}\sum _{u=1}^d\sum _{u=1}^d\left|Cov\left(S_{\tau }^u,S_{\kappa }^u\right)\right|\end{array}$$

$$Lip\left(f_1\right)=\underset{s\ne t}{sup}{\displaystyle \frac{|f_1\left(s\right)-f_1\left(t\right)|}{\parallel s-t\parallel }},\mathrm{with}∥\left(s_1,\dots ,s_n\right)∥=\left|s_1\right|+\dots +\left|s_n\right|.$$

$S_{\tau }^u$ represent the $u^{th}$ component of $S_{\tau }$, defined as $S_{\tau }^u:=<S_{\tau },e^u>$, where $\left(e^u,s\ge 1\right)$ is an orthonormal basis.

3. Main Results

3.1. Assumptions

In the sequel, when no confusion will likely to arise, we will denote by $\alpha$ and ${\alpha }^{\prime }$ strictly positive constants, and by ${\chi }_u$ the covariance coefficient defined as:

$$\begin{array}{c}\hfill {\chi }_u=su{p}_{v\ge u}\sum _{\mid i-j\mid \ge v}{\chi }_{i,j}\end{array}$$

Where

$$\begin{array}{c}\hfill {\chi }_{i,j}=\sum _{u>1}\sum _{i>1}\mid Cov(S_i^u,S_j^u)\mid +\sum _{u>1}\mid Cov(S_i^u,T_j)\mid +\sum _{i>1}\mid Cov(T_i,S_j^u)\mid +\mid Cov(T_i,T_j)\mid .\end{array}$$

For $\rho >0$, let $B(s,\rho ):=\{s^{\prime }\in \mathcal{H}/d(s,s^{\prime })<\rho \}$ be a small ball, shis center and $\rho$ his radius.

To achieve the desired goal, we begin by stating the following required assumptions.

($H_1$)

$\mathbb{P}(S\in B(s,{\theta }_K))={\varphi }_s\left({\theta }_K\right)>0$, and ${\varphi }_s(·)$ is a differentiable at 0. Moreover, $\exists {\beta }_s(·)$ such that

$${\displaystyle \forall u\in [-1,1],\underset{{\theta }_K\to 0}{lim}\frac{{\varphi }_s\left(u{\theta }_K\right)}{{\varphi }_s\left({\theta }_K\right)}={\beta }_s\left(u\right).}$$

($H_2$)

Assume that the Hölder continuity condition is hold for both functions $G^s\left(t\right)$ and $g^s\left(t\right)$.

$$\begin{array}{cc}\hfill \left|G^{s_1}\left(t_1\right)-G^{s_2}\left(t_2\right)\right|& \le \alpha \left(d^{{\gamma }_1}(s_1,s_2)+{|t_1-t_2|}^{{\gamma }_2}\right)\hfill \\ \hfill \left|g^{s_1}\left(t_1\right)-g^{s_2}\left(t_2\right)\right|& \le {\alpha }^{\prime }\left(d^{{\gamma }_1}(s_1,s_2)+{|t_1-t_2|}^{{\gamma }_2}\right)\hfill \end{array}$$

for all $(s_1,s_2)\in {\mathcal{N}}_s^2$ and $(t_1,t_2)\in {\mathcal{S}}^2$, with constants ${\gamma }_1>0$, ${\gamma }_2>0$, and $\mathcal{S}$ be a subset of $\mathbb{R}$ ($\mathcal{S}$ compact).

($H_3$)

H is an even and bounded function, with a bounded and Lipschitz continuous derivative $H^{\prime }$, satisfying:

$$\int H^{\prime }\left(z\right)dz=1,\int {\left|z\right|}^{{\gamma }_2}{H}^{\prime }\left(z\right)dz<\infty and\int {\left(H^{\prime }\left(z\right)\right)}^{2}dz<\infty .$$

($H_4$)

For a differentiable, Lipschitz continuous and bounded kernel K, $\exists \alpha$ and ${\alpha }^{\prime }$ such:

$$\begin{array}{c}\hfill \alpha {\mathbb{I}}_{[0,1]}(.)<K(.)<{\alpha }^{\prime }{\mathbb{I}}_{[0,1]}(.)\end{array}$$

${\mathbb{I}}_{[0,1]}(.)$ : is the indicator function on $[0,1]$, $K^{\prime }(.)$ is derivative of $K(.)$ with:

$$-\infty <\alpha <K^{\prime }\left(z\right)<{\alpha }^{\prime }<0\mathrm{for}0\le z\le 1$$

.

($H_5$)

The random pairs $(S_{\kappa },T_{\kappa }),\kappa \in \mathbb{N}$ is a quasi-associated sequence with covariance coefficient ${\chi }_u$, $u\in \mathbb{N}$ satisfying :

$$\begin{array}{c}\hfill \exists a>0,\exists \alpha >0,\mathrm{such}\mathrm{that}{\chi }_u\le \alpha e^{-au}.\end{array}$$

($H_6$)

$$\begin{array}{cc}\hfill {\displaystyle 0<\underset{i\ne j}{sup}\mathbb{P}\left[(S_i,S_j)\in B(s,{\theta }_K)\times B(s,{\theta }_K)\right]}& =\underset{i\ne j}{max}\left\{\mathbb{P}\left(d\left(s,S_i\right)<{\theta }_K\right),\mathbb{P}\left(d\left(s,S_j\right)<{\theta }_K\right)\right\}\hfill \\ \hfill & =O\left({\varphi }_s^2\left({\theta }_K\right)\right).\hfill \end{array}$$

($H_7$)

The bandwidths ${\theta }_K$ and ${\theta }_H$ satisfy :

i-

${lim}_{n\to \infty }{\displaystyle \frac{1}{n{\theta }_H{\varphi }_s\left({\theta }_K\right)}}=0$, ${lim}_{n\to \infty }{\displaystyle \frac{{log}^{5}n}{n{\theta }_H{\varphi }_s\left({\theta }_K\right)}}=0.$

ii-

${lim}_{n\to \infty }n{\theta }_H^5{\varphi }_s\left({\theta }_K\right)=0$ and ${lim}_{n\to \infty }n{\theta }_H^2{\theta }_K{\varphi }_s\left({\theta }_K\right)=0$.

iii-

${lim}_{n\to \infty }\left({\theta }_H^2+{\theta }_K\right)\sqrt{n{\varphi }_s\left({\theta }_K\right)}=0$

($H_8$)

For $m\in \{0,2\}$, the functions ${\Phi }_l(·)=\mathbb{E}\left[{\displaystyle \frac{{\partial }^m{g}^S\left(t\right)}{\partial t^m}}-{\displaystyle \frac{{\partial }^m{g}^s\left(t\right)}{\partial t^m}}\mid d(s,S)=·\right]$ and

$\Psi (·)=\mathbb{E}\left[{\displaystyle \frac{{\partial }^m{G}^S\left(t\right)}{\partial t^m}}-{\displaystyle \frac{{\partial }^m{G}^s\left(t\right)}{\partial t^m}}\mid d(s,S)=·\right]$ are derivable at 0.

3.2. Comments on the Assumptions

($H_1$) This assumption specifies conditions governing the probability that S lies within a neighborhood of s, along with the consistence behavior of the corresponding probability ratio as the neighborhood size approaches zero. These conditions are essential for applying local convergence theorems. ($H_2$) The Hölder continuity assumption imposed on the conditional distribution and their derivatives represents a standard regularity condition in the literature. ($H_3$), ($H_4$), and ($H_7$) are technical, ensuring the convergence of the convolution kernel, and enabling the use of Taylor expansions. ($H_5$) This quasi-association assumption on the data is interesting, as it covers a more general framework than classical independence. ($H_6$) This assumption characterizes the asymptotic behavior of the joint distribution. ($H_8$) This last assumption concerns the control of the joint probability of two S variables in a neighborhood of s, which helps control the covariance terms in the asymptotic developments. Such assumptions are typical in the setting of nonparametric estimation when dealing with functional covariate.

3.3. Main Results

3.3.1. The Almost Consistency

Our goal is to derive the almost complete convergence (a.co.) of ${\widehat{\lambda }}^s\left(t\right)$ to ${\lambda }^s\left(t\right)$, and this result is formalized in the following theorem.

Theorem 1.

Under the conditions ($H_1$)-($H_8$), we have

$$\begin{array}{c}\hfill \widehat{{\lambda }^s}\left(t\right)-{\lambda }^s\left(t\right)=O\left({\theta }_H^2+{\theta }_K\right)+O_{\mathrm{a}.\mathrm{co}.}\left(\sqrt{{\displaystyle \frac{logn}{n{\theta }_H{\varphi }_s\left({\theta }_K\right)}}}\right)\mathrm{as}n\to \infty \end{array}$$

Proof 

(Proof of theorem 1). needed this decomposition:

$$\begin{array}{cc}\hfill \widehat{{\lambda }^s}\left(t\right)-{\lambda }^s\left(t\right)& ={\displaystyle \frac{{\widehat{g}}_N^s\left(t\right)}{{\widehat{G}}_D^s-{\widehat{G}}_N^s\left(t\right)}}-{\displaystyle \frac{g^s\left(t\right)}{1-G^s\left(t\right)}}\hfill \\ \hfill & ={\displaystyle \frac{1}{{\widehat{G}}_D^s-{\widehat{G}}_N^s\left(t\right)}}\left({\widehat{g}}_N^s\left(t\right)-\mathbb{E}\left[{\widehat{g}}_N^s\left(t\right)\right]\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\widehat{G}}_D^s-{\widehat{G}}_N^s\left(t\right)}}\left\{{\lambda }^s\left(t\right)\left(\mathbb{E}\left[{\widehat{G}}_N^s\left(t\right)\right]-G^u\left(v\right)\right)+\left(\mathbb{E}\left[{\widehat{g}}_N^s\left(t\right)\right]-g^s\left(t\right)\right)\right\}\hfill \\ \hfill & +{\displaystyle \frac{{\lambda }^s\left(t\right)}{{\widehat{G}}_D^s-{\widehat{G}}_N^s\left(t\right)}}\left\{1-\mathbb{E}\left({\widehat{G}}_N^s\left(t\right)\right)-\left({\widehat{G}}_D^s-{\widehat{G}}_N^s\left(t\right)\right)\right\}\hfill \end{array}$$

(6)

And the following subsequent results.

Lemma 1.Under the assumptions ($H_1$), ($H_4$)-($H_7$), and for any fixed t, we have

$$\left|{\widehat{g}}_N^s\left(t\right)-\mathbb{E}\left({\widehat{g}}_N^s\left(t\right)\right)\right|=O_{\mathrm{a}.\mathrm{co}.}\left(\sqrt{{\displaystyle \frac{logn}{n{\theta }_H{\varphi }_s\left({\theta }_K\right)}}}\right)\mathrm{as}n\to \infty .$$

Lemma 2.Assuming that the conditions ($H_1$)-($H_8$) hold, then for $n\to \infty$, we infer:

$$\mathbb{E}\left({\widehat{G}}_N^s\left(t\right)\right)-G^s\left(t\right)=N_B^G(s,t)+o\left({\theta }_H^2\right)+o\left({\theta }_K\right)$$

$$\mathbb{E}\left({\widehat{g}}_N^s\left(t\right)\right)-g^s\left(t\right)=N_B^g(s,t)+o\left({\theta }_H^2\right)+o\left({\theta }_K\right)$$

where

$$\begin{array}{cc}\hfill N_B^G(s,t)=& {\displaystyle \frac{{\theta }_H^2}{2}}\int v^2{H}^{\prime }\left(v\right)dv\left({\displaystyle \frac{{\partial }^2{G}^s\left(t\right)}{\partial t^2}}+{\theta }_K{\Psi }_2^{\prime }\left(0\right){\displaystyle \frac{{\omega }_0}{{\omega }_1}}\right)\hfill \\ \hfill N_B^g(s,t)=& {\displaystyle \frac{{\theta }_H^2}{2}}\int v^2{H}^{\prime }\left(v\right)dv\left({\displaystyle \frac{{\partial }^2{g}^s\left(t\right)}{\partial t^2}}+{\theta }_K{\Phi }_2^{\prime }\left(0\right){\displaystyle \frac{{\omega }_0}{{\omega }_1}}\right)\hfill \\ \hfill {\omega }_0=& K\left(1\right)-{\int }_0^1{\left(uK\left(u\right)\right)}^{\prime }{\beta }_s\left(u\right)du\hfill \\ \hfill {\omega }_{\tau }=& K^{\tau }\left(1\right)-{\int }_0^1{\left(K^{\tau }\right)}^{\prime }\left(u\right){\beta }_s\left(u\right)du\mathrm{for}\tau =1,2\hfill \end{array}$$

Corollary 1. Making use the assumptions ($H_1$)-($H_8$), we get:

$$\begin{array}{cc}\hfill Var\left({\widehat{G}}_D^s\right)& ={\displaystyle \frac{1}{n}}\left[{\displaystyle \frac{K^2\left(1\right)-{\int }_0^1{\left(K^{\prime }\left(u\right)\right)}^2{\beta }_s\left(u\right)du}{{\varphi }_s\left({\theta }_K\right){\left(K\left(1\right)-{\int }_0^1{K}^{\prime }\left(u\right){\beta }_s\left(u\right)du\right)}^2}}-1\right]+o\left({\displaystyle \frac{1}{n{\varphi }_s\left({\theta }_K\right)}}\right)\hfill \\ \hfill Var\left[{\widehat{G}}_N^s\left(t\right)\right]& ={\displaystyle \frac{G^s\left(t\right)}{n{\varphi }_s\left({\theta }_K\right)}}\int H^{\prime 2}\left(v\right)dv\left({\displaystyle \frac{\left(K^2\left(1\right)-{\int }_0^1{\left(K^2\left(u\right)\right)}^{\prime }{\beta }_s\left(u\right)du\right)}{{\left(K\left(1\right)-{\int }_0^1{K}^{\prime }\left(u\right){\beta }_s\left(u\right)du\right)}^2}}\right)+o\left({\displaystyle \frac{1}{n{\varphi }_s\left({\theta }_K\right)}}\right)\hfill \\ \hfill Cov\left({\widehat{G}}_D^s,{\widehat{G}}_N^s\left(t\right)\right)& ={\displaystyle \frac{G^s\left(t\right)\left(K^2\left(1\right)-{\int }_0^1{\left(K^2\right)}^{\prime }\left(u\right){\beta }_s\left(u\right)du\right)}{n{\varphi }_s\left({\theta }_K\right){\left(K\left(1\right)-{\int }_0^1{K}^{\prime }\left(u\right){\beta }_s\left(u\right)du\right)}^2}}-{\displaystyle \frac{G^s\left(t\right)}{n}}+o\left({\displaystyle \frac{1}{n{\varphi }_s\left({\theta }_K\right)}}\right)\hfill \end{array}$$

Lemma 3. Under the assumptions of Theorem 1

$${\widehat{G}}_D^s-{\widehat{G}}_N^s\left(t\right)⟶1-G^s\left(t\right),\mathrm{in}\mathrm{probability}.$$

And

$$\sqrt{{\displaystyle \frac{n{\theta }_H{\varphi }_s\left({\theta }_K\right)}{{\sigma }_{\widehat{\lambda }}^2}}}\left[1-\mathbb{E}\left({\widehat{G}}_N^s\left(t\right)\right)-\left({\widehat{G}}_D^s-{\widehat{G}}_N^s\left(t\right)\right)\right]=O_{\mathrm{p}}\left(1\right)$$

with

$${\sigma }_{\widehat{\lambda }}^2={\displaystyle \frac{{\omega }_2{\lambda }^s\left(t\right)}{{\omega }_1^2\left(1-G^s\left(t\right)\right)}}\int {\left(H^{\prime }\left(u\right)\right)}^{2}du.$$

□

3.3.2. Asymptotic Normality

Theorem 2.

Under ($H_1$)-($H_7$), we infer:

$$\sqrt{n{\theta }_H{\varphi }_s\left({\theta }_K\right)}\left({\widehat{\lambda }}^s\left(t\right)-{\lambda }^s\left(t\right)\right)\stackrel{\mathcal{D}}{\to }\mathcal{N}\left(0,{\sigma }_{\widehat{\lambda }}^2\right),\forall s\in \mathcal{A};n\to \infty$$

where

$$\begin{array}{cc}\hfill \mathcal{A}=& \left\{s\in \mathcal{H},g^s\left(t\right)\left(1-G^s\left(t\right)\right)\ne 0\right\}.\hfill \end{array}$$

and ${\sigma }_{\widehat{\lambda }}^2$ is defined in Lemma 3.

Proof of Theorem 2.

Needed the decomposition (6), the results shown in above Lemmas (2 and 3) and the following subsequent result (Lemma 4):

Lemma 4. Assuming that ($H_1$)-($H_7$) hold, then

$$\sqrt{n{\theta }_H{\varphi }_s\left({\theta }_K\right)}\left({\widehat{g}}_N^s\left(t\right)-\mathbb{E}\left({\widehat{g}}_N^s\left(t\right)\right)\right)\stackrel{\mathcal{D}}{\to }\mathcal{N}\left(0,{\sigma }_g^2\right)$$

with

$${\sigma }_g^2={\displaystyle \frac{{\omega }_2{g}^s\left(t\right)}{{\omega }_1^2}}\int {\left(H^{\prime }\left(u\right)\right)}^{2}du$$

The rigorous proof and demonstrations of the intermediate results (Lemmas 1,2,3 and 4), and Corollary □

4. Application and Numerical Study

4.1. Confidence Bounds

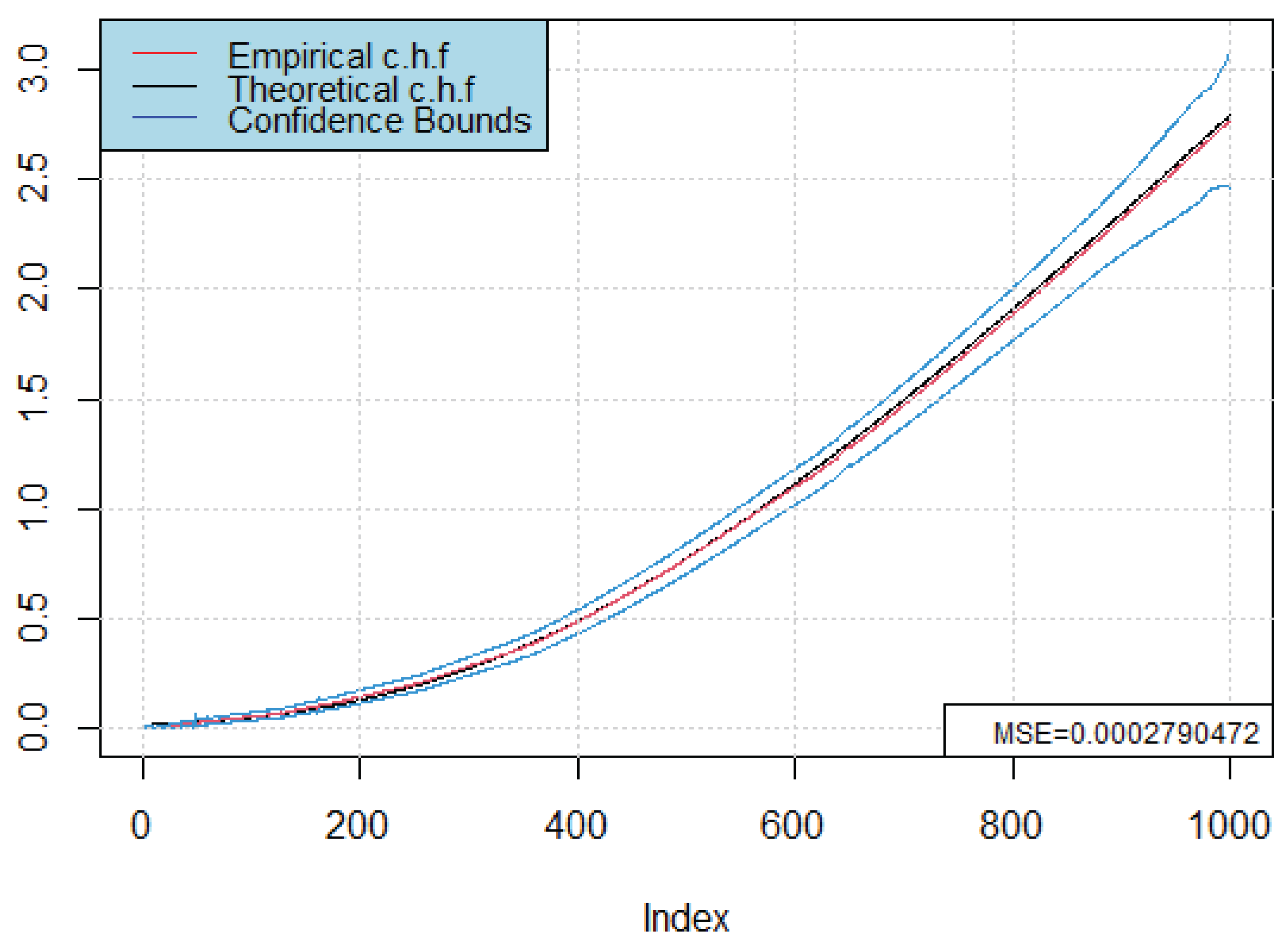
Constructing reliable confidence bounds is a key aspect of statistical analysis, as they characterize the variability and reliability of model estimators. Proper interpretation of these bounds enables more informed and robust conclusions about the underlying estimator. In the context of survival and hazard function estimation, confidence bounds are particularly valuable since they provide a quantitative assessment of the uncertainty surrounding the estimated conditional hazard function, thereby guiding both theoretical analysis and practical decision-making. Moreover, confidence bounds serve as a diagnostic tool: narrow bounds suggest stable and precise estimators, while wider bounds highlight regions where the estimator is less reliable due to limited data or high variability.

As an application of the result established in Theorem 2, we construct confidence bounds for ${\lambda }^s\left(t\right)$ at the confidence level $1-\alpha$. To this end, we must first estimate the unknown components of the asymptotic variance as follows: these include the conditional density, the conditional survival function, and kernel-based quantities that appear in the variance expression. Consistent estimation of these components is essential, since any bias or misspecification would directly affect the coverage probability of the resulting bounds. Once these quantities are estimated, the asymptotic normality result in Theorem 2 allows us to approximate the distribution of the estimator and derive pointwise confidence intervals for ${\lambda }^s\left(t\right)$ across the range of t. This methodology not only validates the theoretical properties of the proposed estimator but also ensures its applicability in empirical studies where inference on the conditional hazard function is required.

$${\widehat{\omega }}_q=:{\displaystyle \frac{1}{n{\widehat{\varphi }}_s\left({\theta }_K\right)}}\sum _{\tau =1}^n{K}_{\tau }^q,q=1,2;$$

$${\widehat{\varphi }}_s\left({\theta }_K\right)={\displaystyle \frac{\#\left\{\tau :\left|d\left(S_{\tau },s\right)\right|\le {\theta }_K\right\}}{n}}$$

where $\#\left(A\right)$ represents the cardinality of the set A. Also, ${\sigma }_{\widehat{\lambda }}^2$ is estimated by:

$$\widehat{{\sigma }_{\widehat{\lambda }}^2}=:{\displaystyle \frac{\widehat{{\omega }_2}{\widehat{\lambda }}^s\left(t\right)}{{\widehat{\omega }}_1^2}}\int {\left(H^{\prime }\left(u\right)\right)}^{2}du.$$

(7)

Corollary 2.

When the assumptions of Theorem 2 hold, we set:

$$\sqrt{n{\theta }_H{\widehat{\varphi }}_s\left({\theta }_K\right)}\left({\widehat{\lambda }}^s\left(t\right)-{\lambda }^s\left(t\right)\right)\stackrel{d}{⟶}N\left(0,\widehat{{\sigma }_{\widehat{\lambda }}^2}\right),n\to \infty .$$

(8)

Moreover, the confidence bounds will be,

$$\left[{\widehat{\lambda }}^s\left(t\right)-Z_{1-{\displaystyle \frac{\alpha }{2}}}{\left({\displaystyle \frac{\widehat{{\sigma }_{\widehat{\lambda }}^2}}{n{\theta }_H{\widehat{\varphi }}_s\left({\theta }_K\right)}}\right)}^{1/2},{\widehat{\lambda }}^s\left(t\right)+Z_{1-{\displaystyle \frac{\alpha }{2}}}{\left({\displaystyle \frac{\widehat{{\sigma }_{\widehat{\lambda }}^2}}{n{\theta }_H{\widehat{\varphi }}_s\left({\theta }_K\right)}}\right)}^{1/2}\right]$$

where $Z_{1-{\displaystyle \frac{\alpha }{2}}}$ is the quartile $1-{\displaystyle \frac{\alpha }{2}}$ of $\mathcal{N}(0,1)$.

4.2. Numerical Study

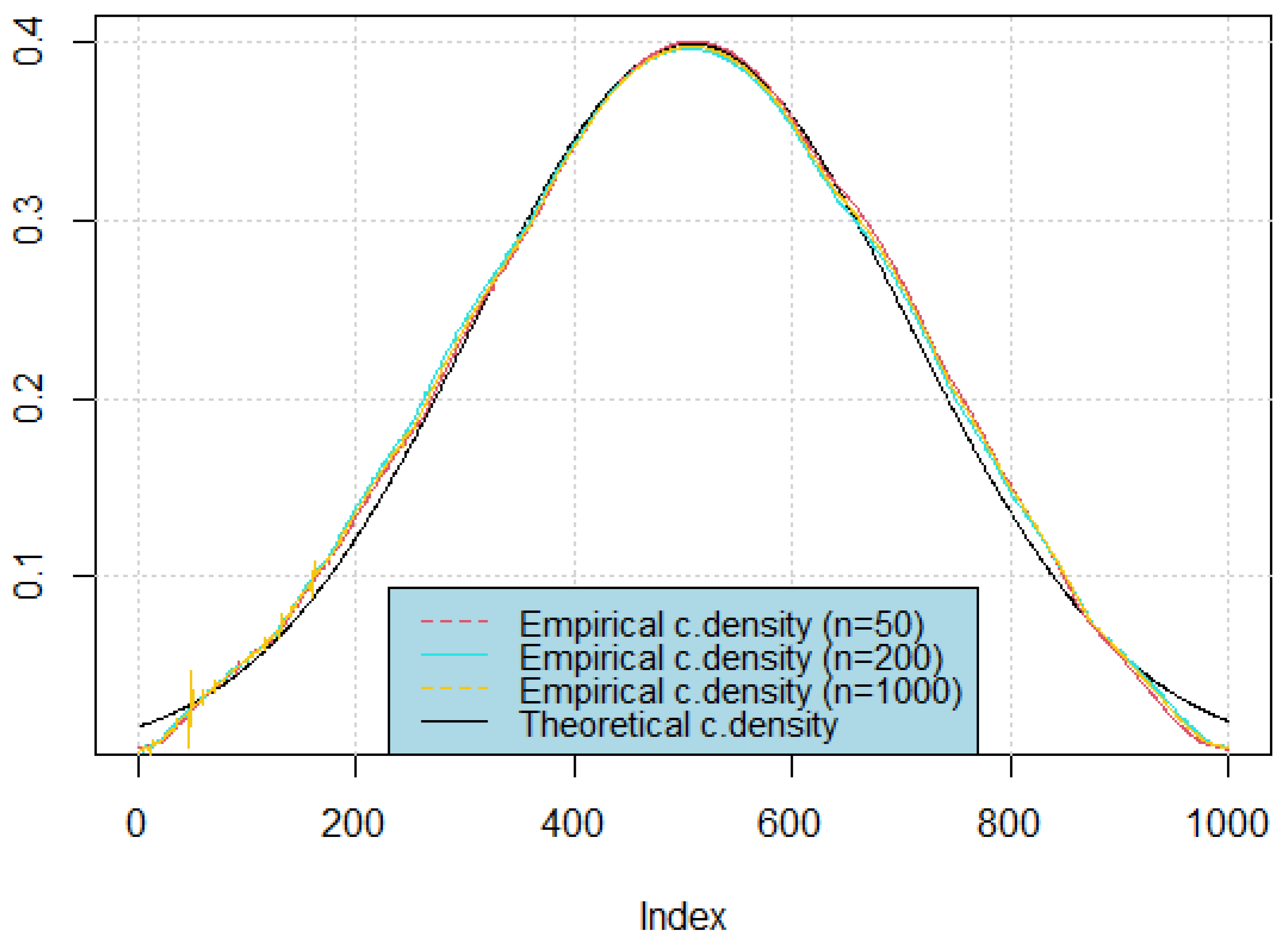
In this part, we conduct a numerical study using R software to illustrate and validate the theoretical results through graphical representations. The aim of this simulation is to assess the finite-sample performance of the proposed estimator and to highlight the extent to which the asymptotic properties established in the theoretical framework are reflected in practice. By generating controlled data under specific dependence structures and censoring mechanisms, we are able to visualize the behavior of the conditional density and hazard estimators, compare them with their theoretical counterparts, and evaluate their accuracy across different sample sizes. This numerical experiment also provides insights into the rate of convergence, the influence of the smoothing parameters, and the robustness of the estimator under varying conditions.

This simulation is based on the following points: we describe the data-generating process and the dependence structure imposed, specify the choice of kernel functions and bandwidths, outline the implementation of the random censoring mechanism, and finally present the graphical outputs and error metrics that allow for a systematic comparison between theoretical and empirical curves. The numerical results obtained will not only complement the theoretical findings but also serve as practical evidence of the efficiency and reliability of the proposed estimation methodology.

• Definite our model by choosing functional covariate as :

  $$S_{\kappa }\left(u\right)=cos\left(W_{\kappa }u\right)+sin\left(W_{\kappa }+u\right)+0.7\left(W_{\kappa }u\right),u\in [0,+\pi ]\mathrm{for}\kappa =1,\dots ,n$$
  The process $\left(W_{\kappa }\right)$ satisfies a specific dependence structure,namely a quasi-associated sequence, which is generated as a non-strong mixing auto-regressive process of order 1. This process is constructed by setting the auto-regressive coefficient $\rho =0.1$ and modeling the innovation term as a binomial distribution $Binom(10,0.25)$ [18]. We use 100 discretization points of u to obtain the curves $S_{\kappa }$ shown below in Figure 1, Figure 2 and Figure 3, corresponding to different sample sizes.
  For the real variable is defined as $T=m\left(S\right)+ϵ$. Where m is the nonlinear regression operator,

  $$m\left(S\right)={\displaystyle \frac{1}{5}}\times exp\left\{2-{\displaystyle \frac{1}{{\left({\int }_0^{\pi }{S}^{\prime }\left(u\right)du\right)}^2}}\right\}$$
  Where $ϵ$ is standard normal distribution. Its clear that the explicit form of the conditional density given by:

  $$g^s\left(t\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\mathrm{e}}^{-{\displaystyle \frac{1}{2}}{\left(t-m\left(s\right)\right)}^2}$$
  . In the next, we select the distance in $\mathcal{H}$ as:

  $$d\left(s_1,s_2\right)={\left({\int }_0^{\pi }{\left(s_1^{\prime }\left(u\right)-s_2^{\prime }\left(u\right)\right)}^{2}du\right)}^{1/2}\forall s_1,s_2\in \mathcal{H}$$
  Also

  $$K\left(s\right)={\displaystyle \frac{15}{16}}{\left(1-s^2\right)}^2,s\in [-1,1];H\left(s\right)={\int }_{-\infty }^{s}K\left(u\right)du$$
  .
• A bandwidth Selection Algorithm: The smoothness of the estimators (2) and (3) is controlled by the smoothing parameter ${\theta }_K$ and the regularity of the cumulative distribution function (CDF). Therefore, choosing these parameters plays a critical role in the computational process. An optimal selection leads to effective estimation with a small mean squared error (MSE), which, for the conditional hazard function, is given by:

  $$MSE\left(\widehat{\lambda }\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left({\widehat{\lambda }}^s\left(t_i\right)-{\lambda }^s\left(t_i\right)\right)}^2.$$
  Let $H(.)$ be a distribution function on $\mathbb{R}$ and $H_{\theta }\left(s\right)=H(s/\theta )$. Note that as $\theta \to 0$.

  $$\mathbb{E}\left\{H_{\theta }\left(t-T_i\right)\mid S_i=s\right\}=G^s\left(t\right)+O\left({\theta }^2\right).$$
  This indicates that $G^s\left(t\right)$ can be interpreted as a regression of $H_{\lambda }\left(t-T_i\right)$ on $S_i$, Consequently, we adapt this regression framework to our estimation problem. By combining this approach with the normal reference rule [7], we derive an effective algorithm for selecting the bandwidth parameters.

  i-

  Compute the bandwidth ${\theta }_H$ using the normal reference rule.

  ii-

  Given ${\theta }_H$, use cross-validation (as proposed by [1]) to determine the optimal value of ${\theta }_K$ (using the function fregre.np.cv in the package fda.usc) for our calculation of ${\theta }_K$.

• Calculate the estimates of both the conditional distribution and the conditional density functions, and compare these estimates with their theoretical counterparts on the same graphs.(Figure 4 and Figure 5).
  It is apparent that our estimations exhibit high accuracy when optimal bandwidths are selected. To assess the performance of each model more rigorously, we compute the mean squared error, as shown in Table 1.
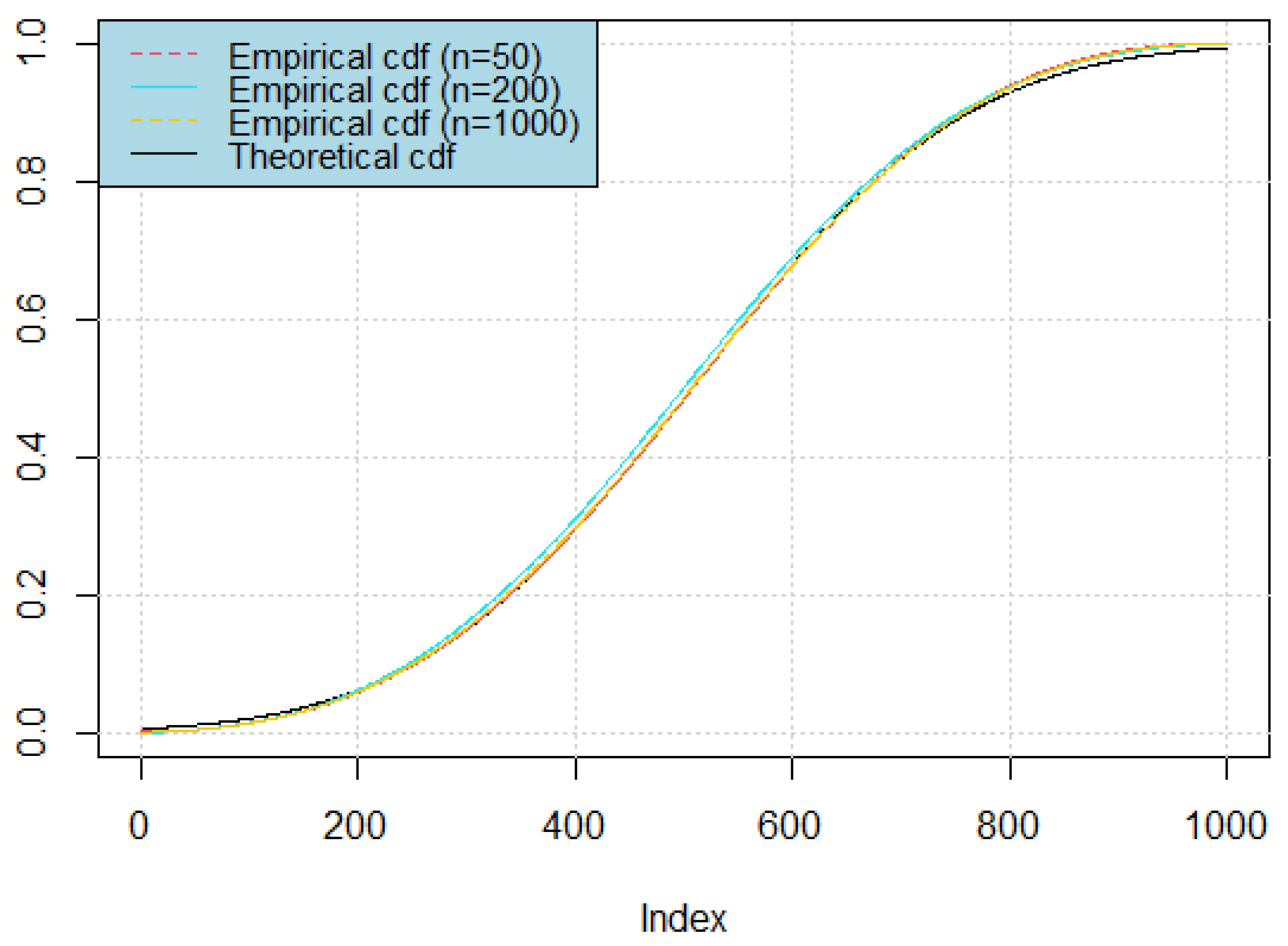
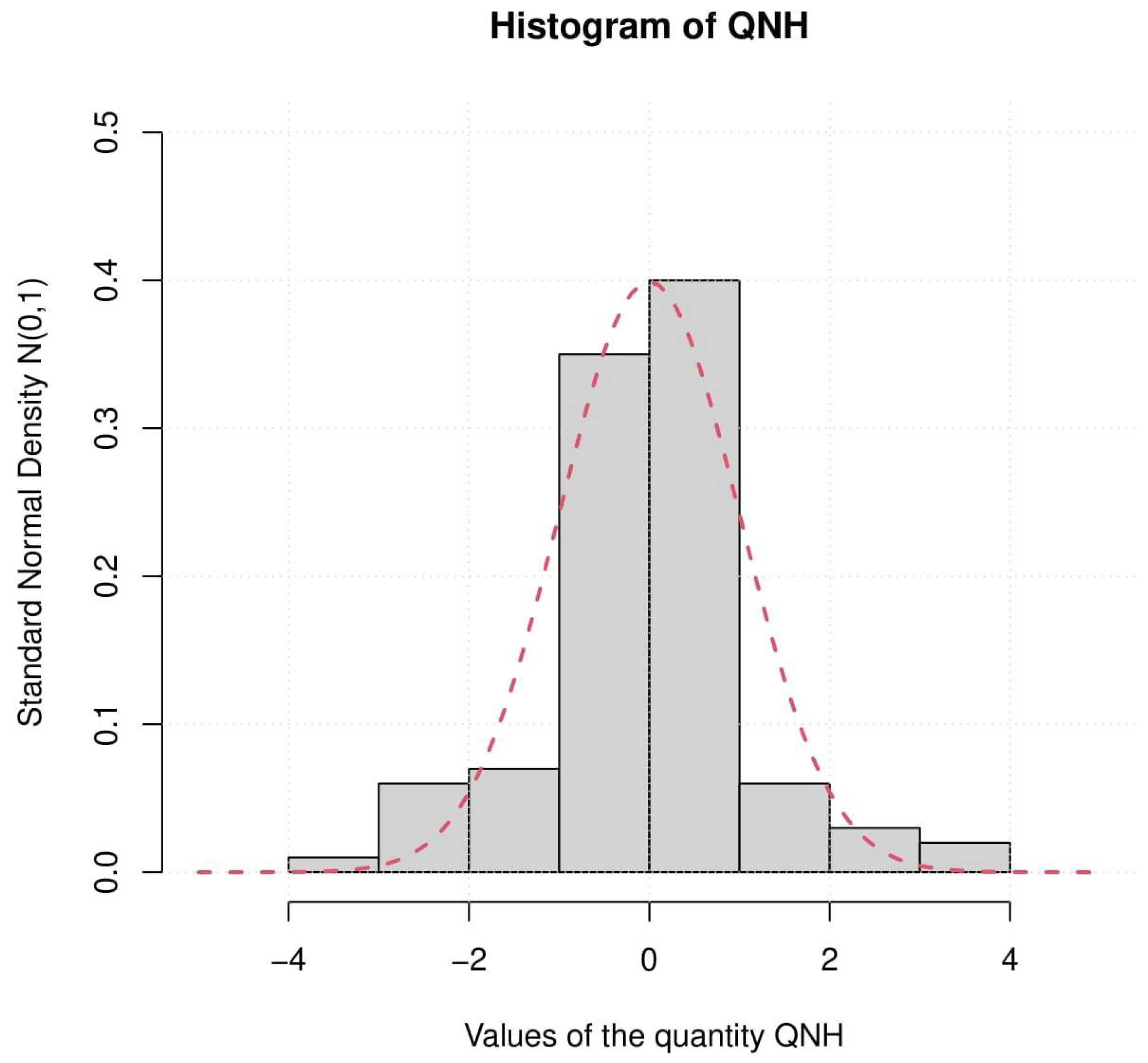
  For the next step in achieving the desired objective and firmly establishing the normal approximation of ${\widehat{\lambda }}^s\left(t\right)$ with high effectiveness, we selected the sample that produced an estimate with the smallest MSE (sample size $n=1000$), and followed the subsequent steps:
  • We compute the conditional hazard function estimator using (1), the asymptotic variance $\widehat{{\sigma }_{\widehat{\lambda }}^2}$ defined in (7), and the empirical estimate ${\widehat{\varphi }}_s\left({\theta }_K\right)$.
  • Under the condition:

    $$\underset{n\to \infty }{lim}\sqrt{n{\theta }_H{\varphi }_s\left({\theta }_K\right)}{N}_B^{\lambda }(s,t)=0,$$

    we can ignore the bias term $N_B^{\lambda }(s,t)$ and compute the quantity referred to in (8), namely QNH, as:

    $$\sqrt{{\displaystyle \frac{n{\theta }_H{\widehat{\varphi }}_s\left({\theta }_K\right)}{\widehat{{\sigma }_{\widehat{\lambda }}^2}}}}\left({\widehat{\lambda }}^s\left(t\right)-{\lambda }^s\left(t\right)\right).$$
  • Plot a histogram of QNH and compare it with the standard normal density. (Figure 6).
  • Finally building a confidence bounds (see Figure 7).

5. Conclusion and Some Perspectives

Due to the complexity of the conditional hazard function estimate ${\widehat{\lambda }}^s\left(t\right)$ by the kernel approach, we began by decomposing the estimator into three parts, as shown in (6). The first part corresponds to the numerator of the density function estimator, denoted ${\widehat{g}}_N^s\left(t\right)$, which is considered the dominant component influencing the estimator’s properties. We showed that the denominator of the corresponding term converges in probability to $1-G^s\left(t\right)$. The remaining two parts account for the bias in both the conditional distribution and density function estimators, arising from ${\widehat{C}}_N^s\left(t\right)$ and ${\widehat{g}}_N^s\left(t\right)$.

From a practical perspective, we conducted a simulation study to validate the theoretical findings. Despite the inherent challenges in selecting and tuning parameters such as bandwidths, the proposed estimator demonstrated strong performance, achieving a low mean squared error.

These results are promising and contribute to the growing body of research in this field. However, further investigation is needed to assess the robustness of the method in diverse real-world settings and to explore potential extensions that could improve its applicability and generalizability.

A potential direction for future work is to examine the sensitivity of the estimator to kernel choice and bandwidth selection procedures. Exploring data-driven or adaptive bandwidth strategies may enhance finite-sample performance. Additionally, investigating the behavior of the estimator in high-dimensional or complex data settings could broaden its practical utility.

This study enhances both the theoretical and empirical comprehension of the asymptotic characteristics of the proposed estimator, laying the foundation for future developments and applications in areas where estimating conditional functional parameters is essential.