Submitted:
20 August 2025
Posted:
22 August 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
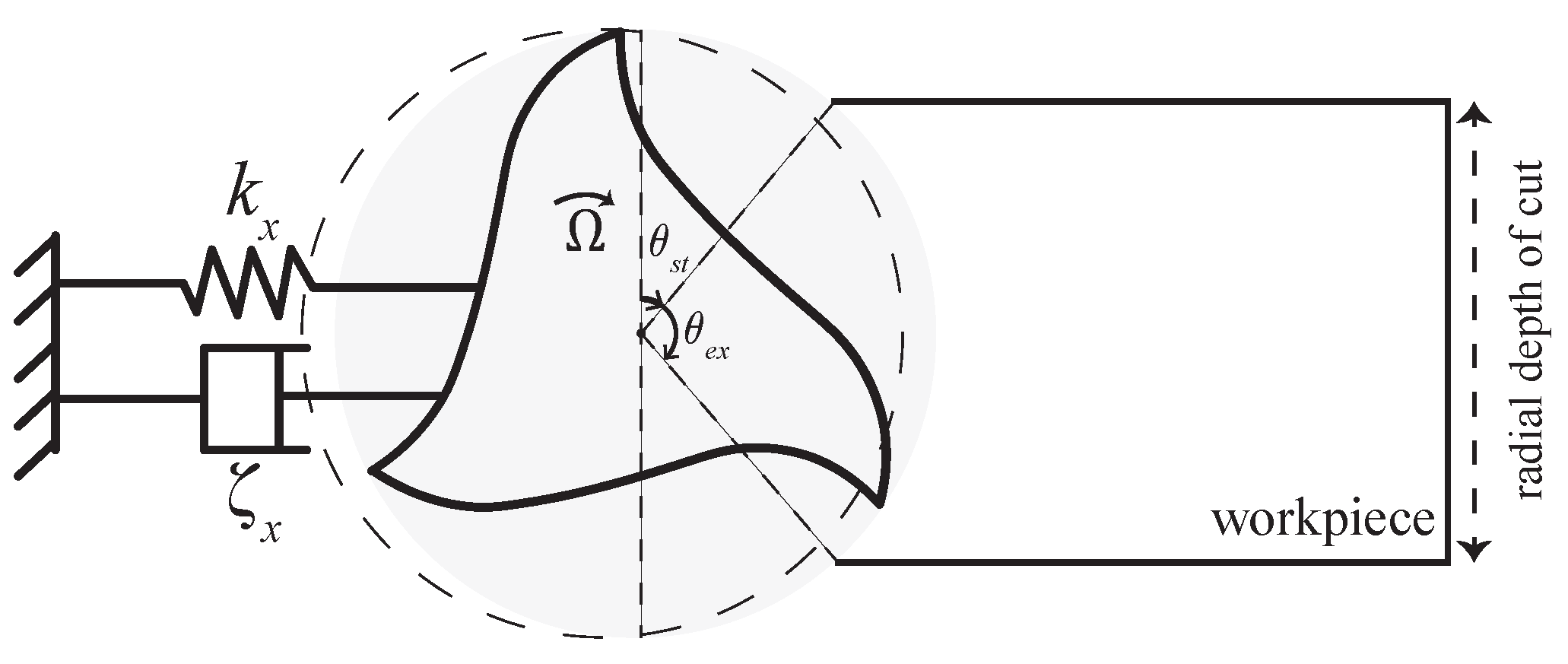
2. Milling Dynamics
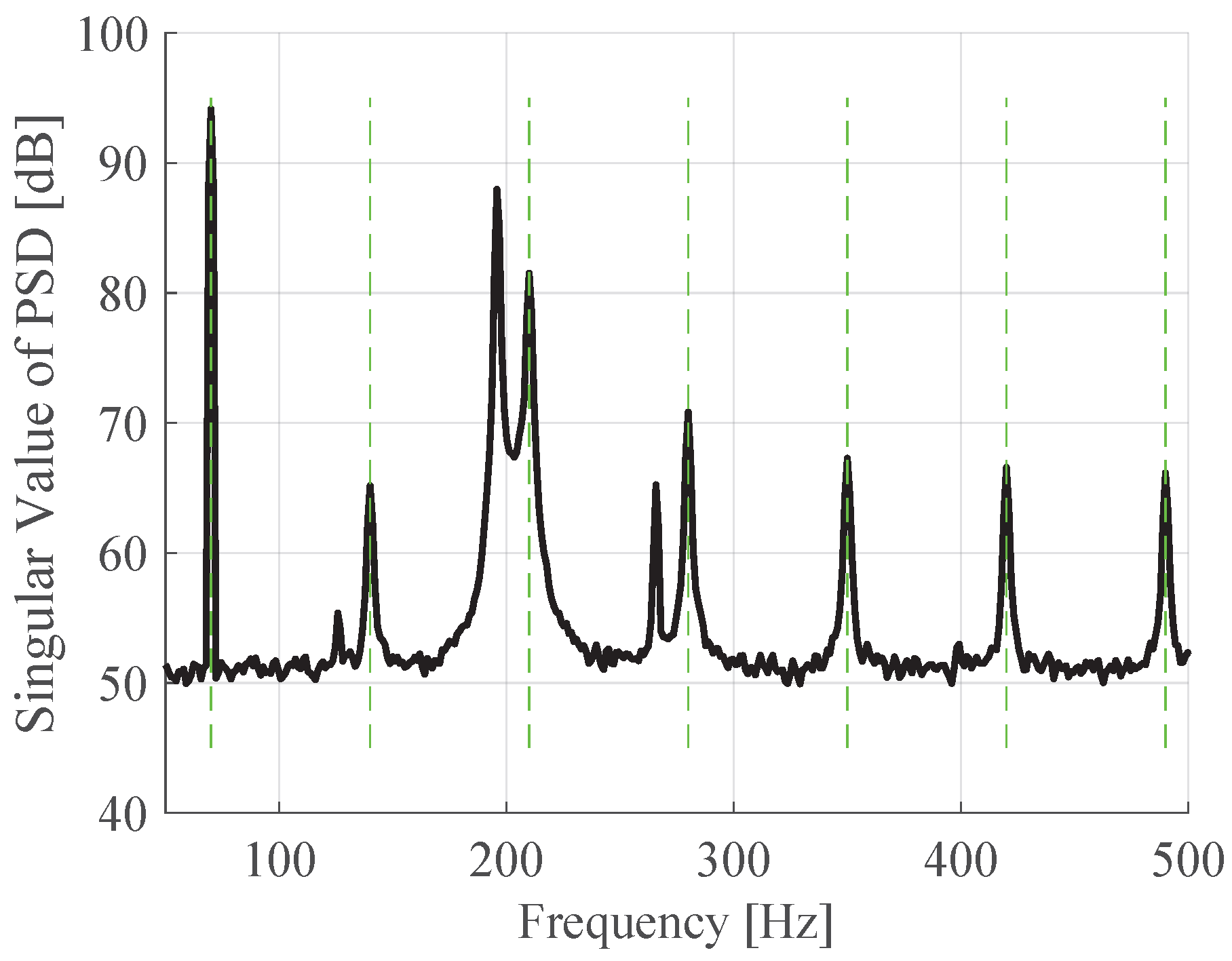
2.1. Operational Modal Analysis
2.2. Model Updating
3. Results
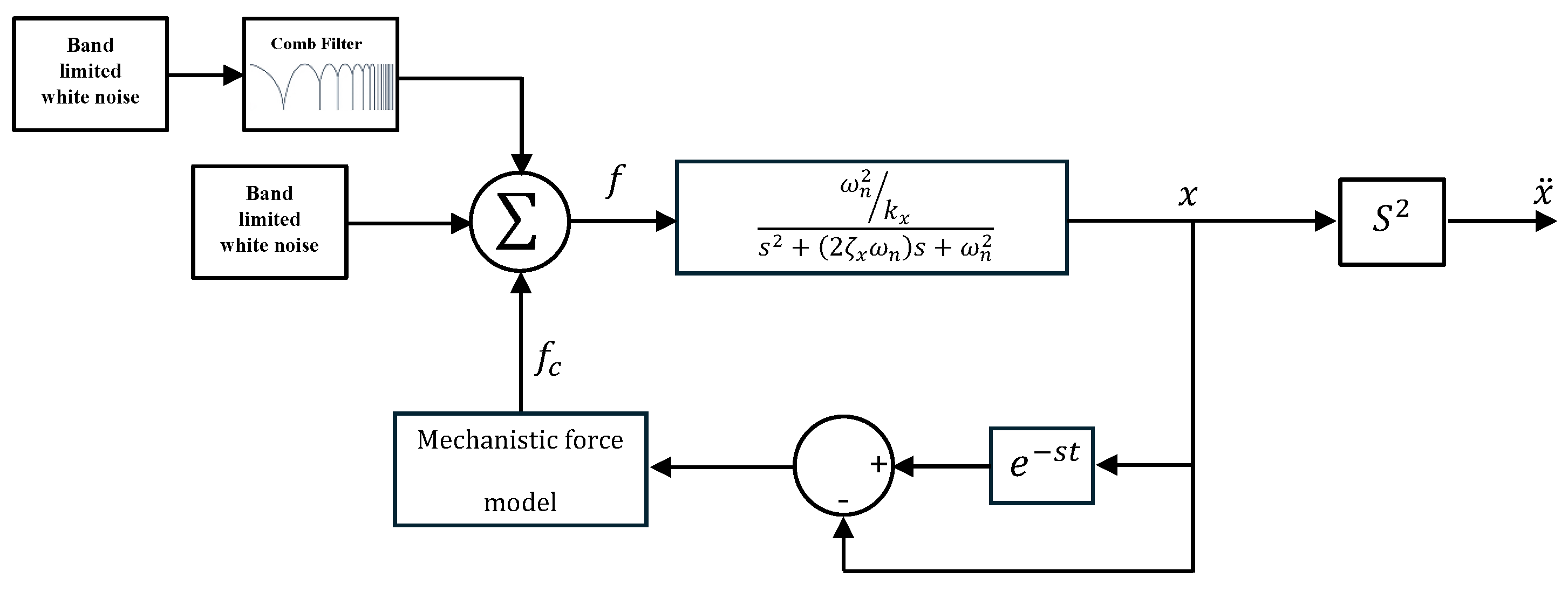
3.1. Numerical Simulation
3.2. Experimental Case Study
4. Conclusions
Acknowledgments
References
- Tobias, S.A. Machine Tool Vibration; Blackie and Sons Ltd., 1965.
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Annals 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. International Journal of Machine Tools and Manufacture 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Altintas, Y.; Stepan, G.; Budak, E.; Schmitz, T.; Kilic, Z.M. Chatter Stability of Machining Operations. Journal of Manufacturing Science and Engineering 2020, 142, 110801. [Google Scholar] [CrossRef]
- Iglesias, A.; Taner Tunç, L.; Özsahin, O.; Franco, O.; Munoa, J.; Budak, E. Alternative experimental methods for machine tool dynamics identification: A review. Mechanical Systems and Signal Processing 2022, 170, 108837. [Google Scholar] [CrossRef]
- Suzuki, N.; Kurata, Y.; Kato, T.; Hino, R.; Shamoto, E. Identification of transfer function by inverse analysis of self-excited chatter vibration in milling operations. Precision Engineering 2012, 36, 568–575. [Google Scholar] [CrossRef]
- Özşahin, O.; Budak, E.; Özgüven, H. In-process tool point FRF identification under operational conditions using inverse stability solution. International Journal of Machine Tools and Manufacture 2015, 89, 64–73. [Google Scholar] [CrossRef]
- Grossi, N.; Sallese, L.; Scippa, A.; Campatelli, G. Improved experimental-analytical approach to compute speed-varying tool-tip FRF. Precision Engineering 2017, 48, 114–122. [Google Scholar] [CrossRef]
- Postel, M.; Özsahin, O.; Altintas, Y. High speed tooltip FRF predictions of arbitrary tool-holder combinations based on operational spindle identification. International Journal of Machine Tools and Manufacture 2018, 129, 48–60. [Google Scholar] [CrossRef]
- Eynian, M. In-process identification of modal parameters using dimensionless relationships in milling chatter. International Journal of Machine Tools and Manufacture 2019, 143, 49–62. [Google Scholar] [CrossRef]
- Karandikar, J.; Traverso, M.; Abbas, A.; Schmitz, T. Bayesian Inference for Milling Stability Using a Random Walk Approach. Journal of Manufacturing Science and Engineering 2014, 136, 031015. [Google Scholar] [CrossRef]
- Karandikar, J.; Honeycutt, A.; Schmitz, T.; Smith, S. Stability boundary and optimal operating parameter identification in milling using Bayesian learning. Journal of Manufacturing Processes 2020, 56, 1252–1262. [Google Scholar] [CrossRef]
- Rahimi, M.H.; Huynh, H.N.; Altintas, Y. On-line chatter detection in milling with hybrid machine learning and physics-based model. CIRP Journal of Manufacturing Science and Technology 2021, 35, 25–40. [Google Scholar] [CrossRef]
- Postel, M.; Bugdayci, B.; Wegener, K. Ensemble transfer learning for refining stability predictions in milling using experimental stability states. The International Journal of Advanced Manufacturing Technology 2020, 107, 4123–4139. [Google Scholar] [CrossRef]
- Wiederkehr, P.; Finkeldey, F.; Siebrecht, T. Reduction of experimental efforts for predicting milling stability affected by concept drift using transfer learning on multiple machine tools. CIRP Annals 2024, 73, 301–304. [Google Scholar] [CrossRef]
- Minis, I.E.; Magrab, E.B.; Pandelidis, I.O. Improved Methods for the Prediction of Chatter in Turning, Part 1: Determination of Structural Response Parameters. Journal of Engineering for Industry 1990, 112, 12–20. [Google Scholar] [CrossRef]
- Özşahin, O.; Budak, E.; Özgüven, H. Investigating Dynamics of Machine Tool Spindles under Operational Conditions. Advanced Materials Research 2011, 223, 610–621. [Google Scholar] [CrossRef]
- Brincker, R. Introduction to Operational Modal Analysis; John Wiley & Sons, 2015.
- Kim, S.; Ahmadi, K. Estimation of vibration stability in turning using operational modal analysis. Mechanical Systems and Signal Processing 2019, 130, 315–332. [Google Scholar] [CrossRef]
- Ebrahimi-Tirtashi, A.; Ahmadi, K. Automated Operational Modal Analysis of Self-Excited Vibrations in Turning. Mechanical Systems and Signal Processing 2025, 233, 112705. [Google Scholar] [CrossRef]
- Zorlu, A.; Ahmadi, K.; Ebrahimi-Tirtashi, A. Operational Modal Analysis of Self-Excited Vibrations in Milling Considering Periodic Dynamics. Journal of Manufacturing Science and Engineering 2025, 147, 021010. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating Models and Their Uncertainties. I: Bayesian Statistical Framework. Journal of Engineering Mechanics 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Beck, J.L. Bayesian system identification based on probability logic. Structural Control and Health Monitoring 2010, 17, 825–847. [Google Scholar] [CrossRef]
- Goller, B.; Beck, J.; Schueller, G. Evidence-based identification of weighting factors in Bayesian model updating using modal data. Journal of Engineering Mechanics 2012, 138, 430–440. [Google Scholar] [CrossRef]
- Ahmadi, K. Bayesian updating of modal parameters for modeling chatter in turning. CIRP Journal of Manufacturing Science and Technology 2022, 38, 724–736. [Google Scholar] [CrossRef]
- Insperger, T.; Mann, B.; Stépán, G.; Bayly, P. Stability of up-milling and down-milling, part 1: alternative analytical methods. International Journal of Machine Tools and Manufacture 2003, 43, 25–34. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Updated semi-discretization method for periodic delay-differential equations with discrete delay. International Journal for Numerical Methods in Engineering 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Annals 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Allen, M.S.; Sracic, M.W.; Chauhan, S.; Hansen, M.H. Output-only modal analysis of linear time-periodic systems with application to wind turbine simulation data. Mechanical Systems and Signal Processing 2011, 25, 1174–1191. [Google Scholar] [CrossRef]
- Bamieh, B.; Pearson, J.B.; Francis, B.A.; Tannenbaum, A. A lifting technique for linear periodic systems with applications to sampled-data control. Systems & Control Letters 1991, 17, 79–88. [Google Scholar] [CrossRef]
- Chib, S.; Jeliazkov, I. Marginal Likelihood From the Metropolis–Hastings Output. Journal of the American Statistical Association 2001, 96, 270–281. [Google Scholar] [CrossRef]
- Friel, N.; Pettitt, A.N. Marginal Likelihood Estimation via Power Posteriors. Journal of the Royal Statistical Society Series B: Statistical Methodology 2008, 70, 589–607. [Google Scholar] [CrossRef]
- Betz, W.; Papaioannou, I.; Straub, D. Transitional Markov Chain Monte Carlo: Observations and Improvements. Journal of Engineering Mechanics 2016, 142, 04016016. [Google Scholar] [CrossRef]
- Ching, J.; Chen, Y.C. Transitional Markov Chain Monte Carlo Method for Bayesian Model Updating, Model Class Selection, and Model Averaging. Journal of Engineering Mechanics 2007, 133, 816–832. [Google Scholar] [CrossRef]
- Ramussen, C.E. Gaussian Processes in Machine Learning. In in Summer school on machine learning; Lecture Notes in Computer Science, 2003; pp. 63–71.
- Insperger, T.; Stépán, G.; Bayly, P.; Mann, B. Multiple chatter frequencies in milling processes. Journal of Sound and Vibration 2003, 262, 333–345. [Google Scholar] [CrossRef]
- Budak, E.; Altintas¸, Y.; Armarego, E.J.A. Prediction of Milling Force Coefficients From Orthogonal Cutting Data. Journal of Manufacturing Science and Engineering 1996, 118, 216–224. [Google Scholar] [CrossRef]
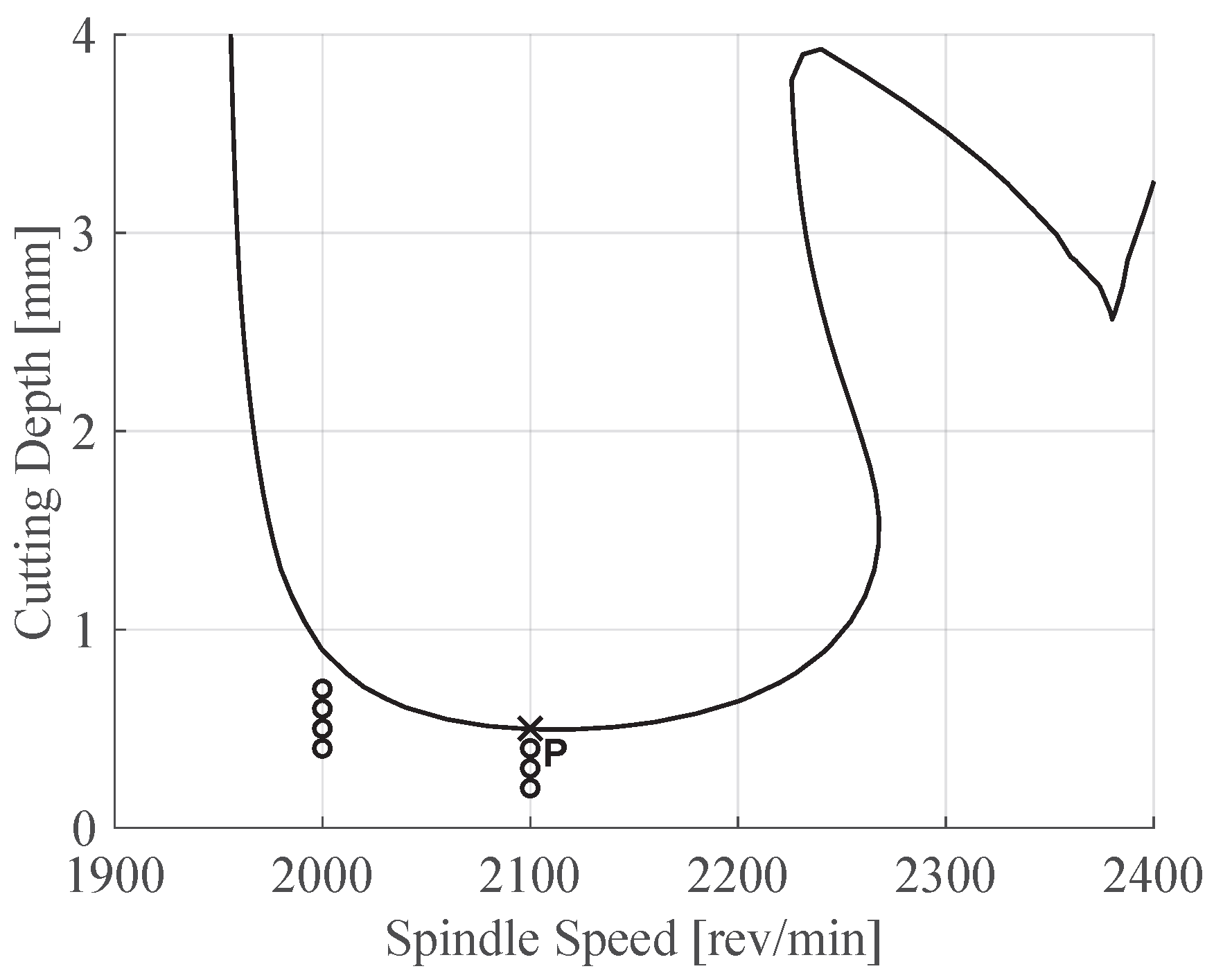
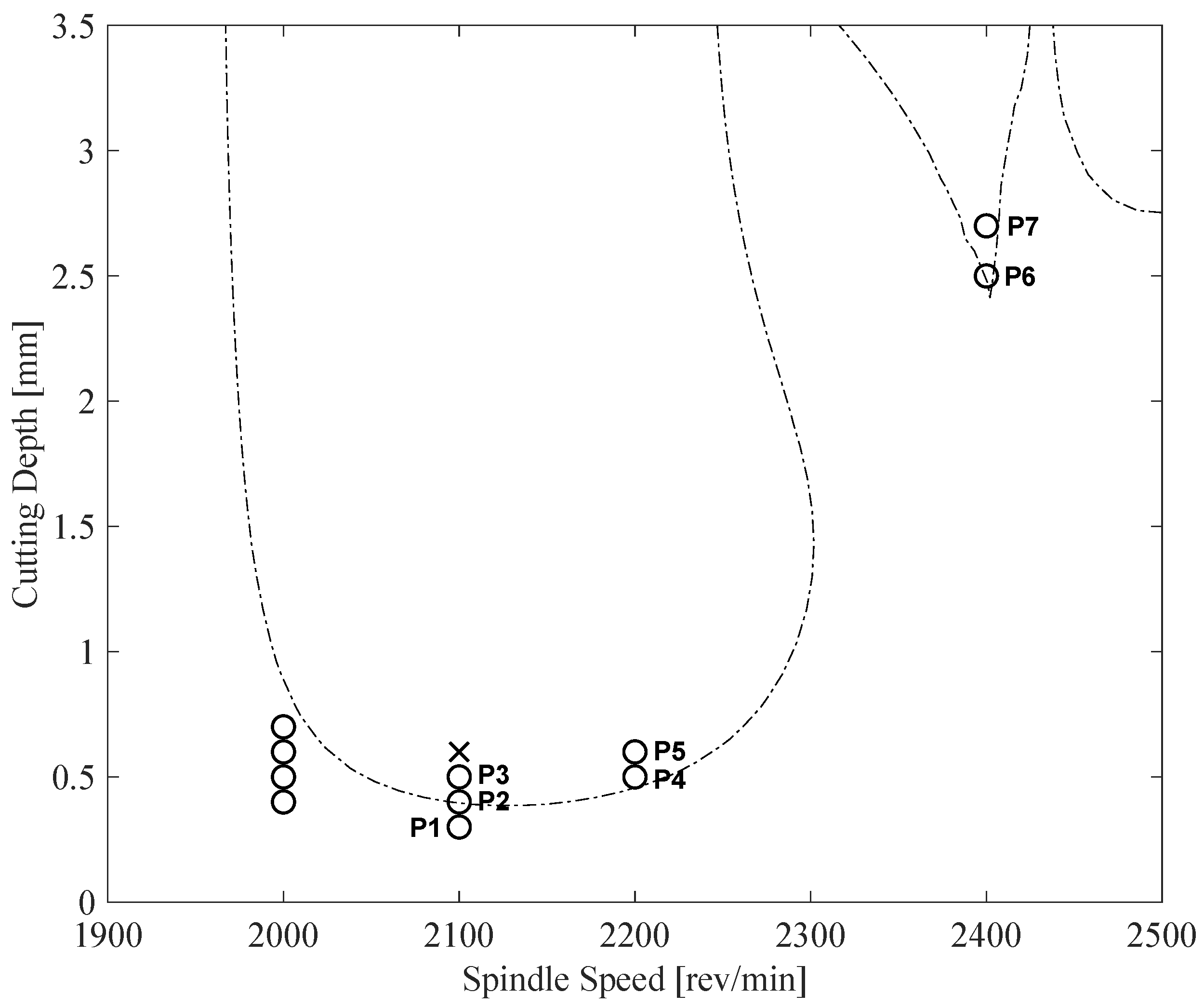
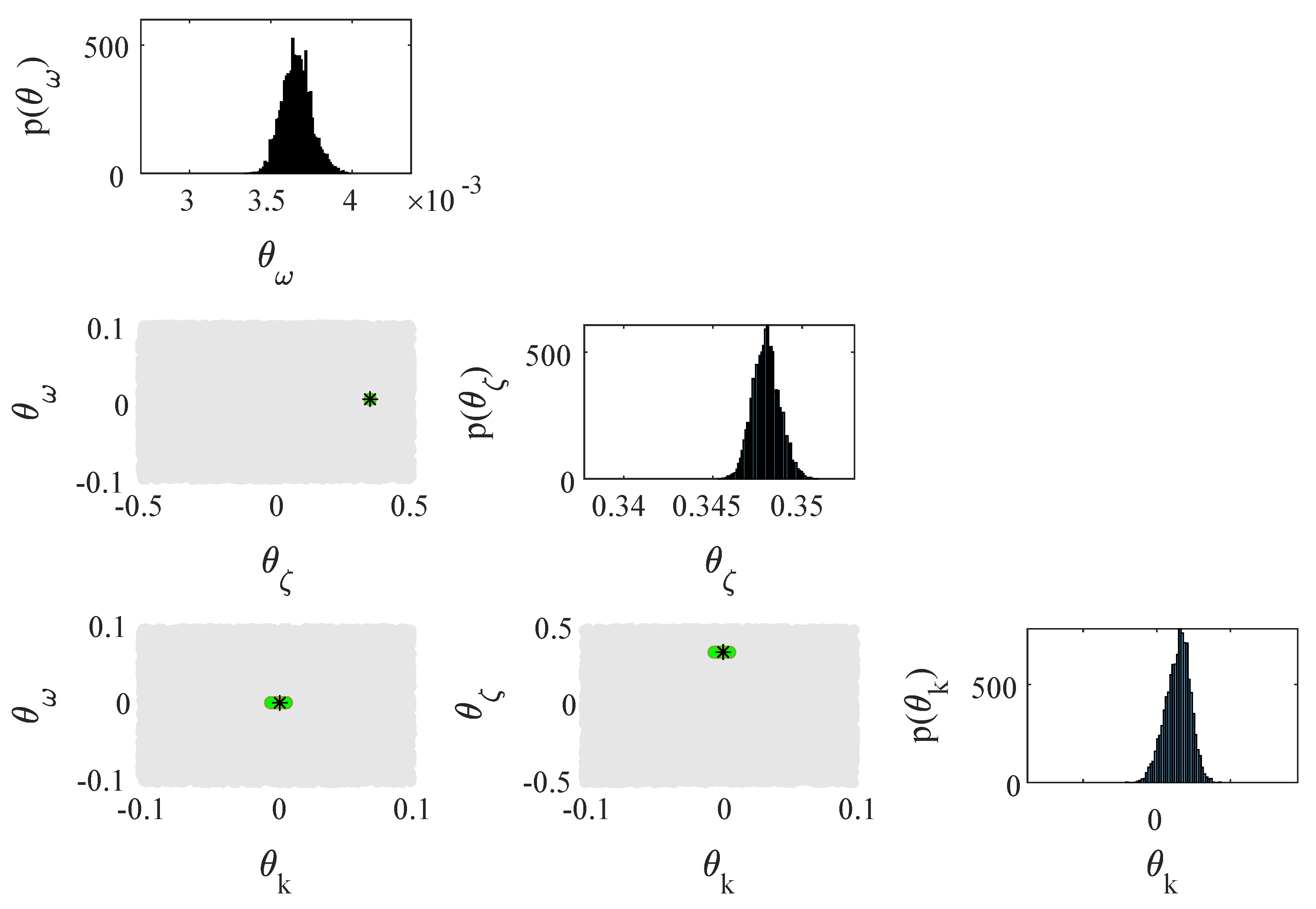
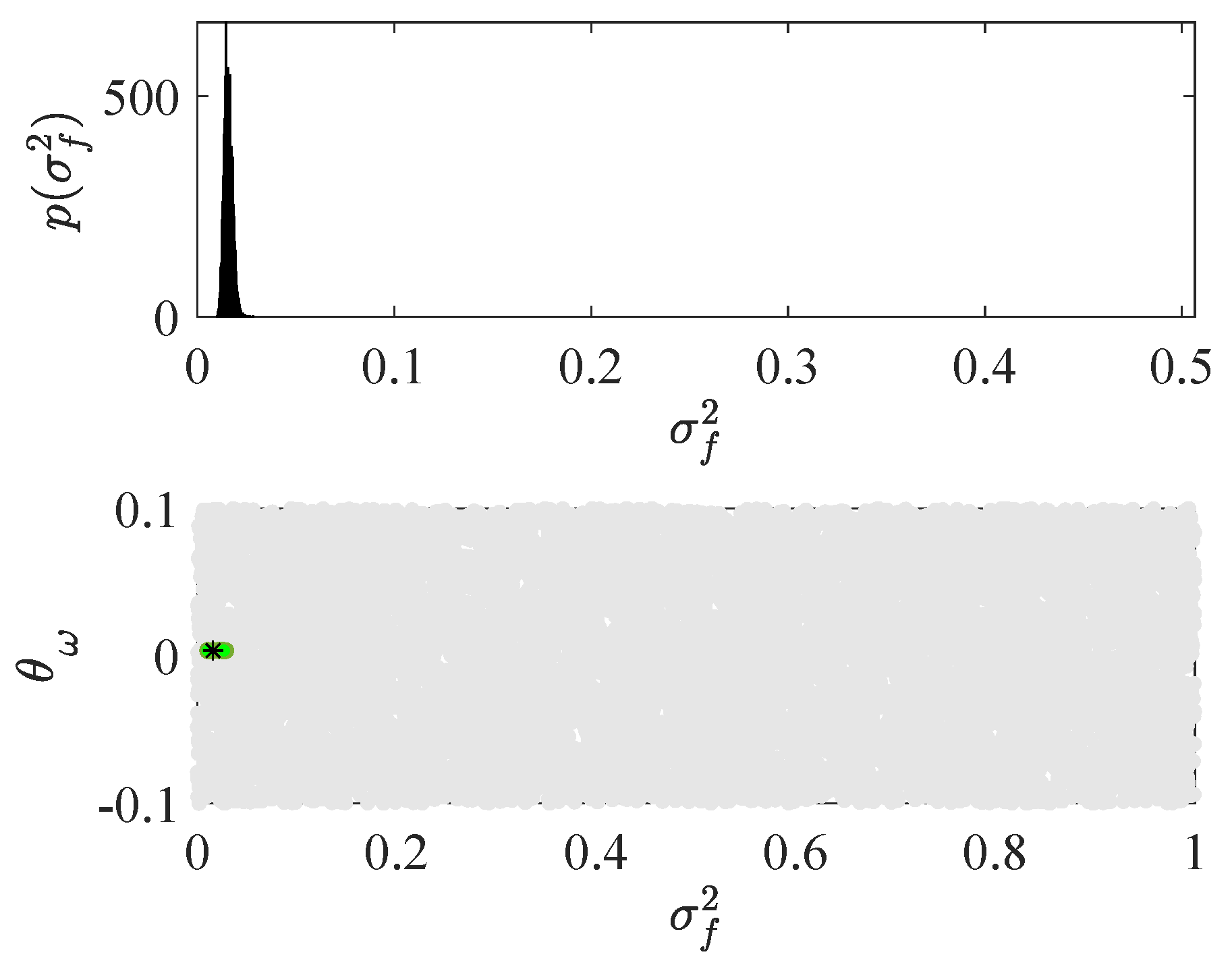
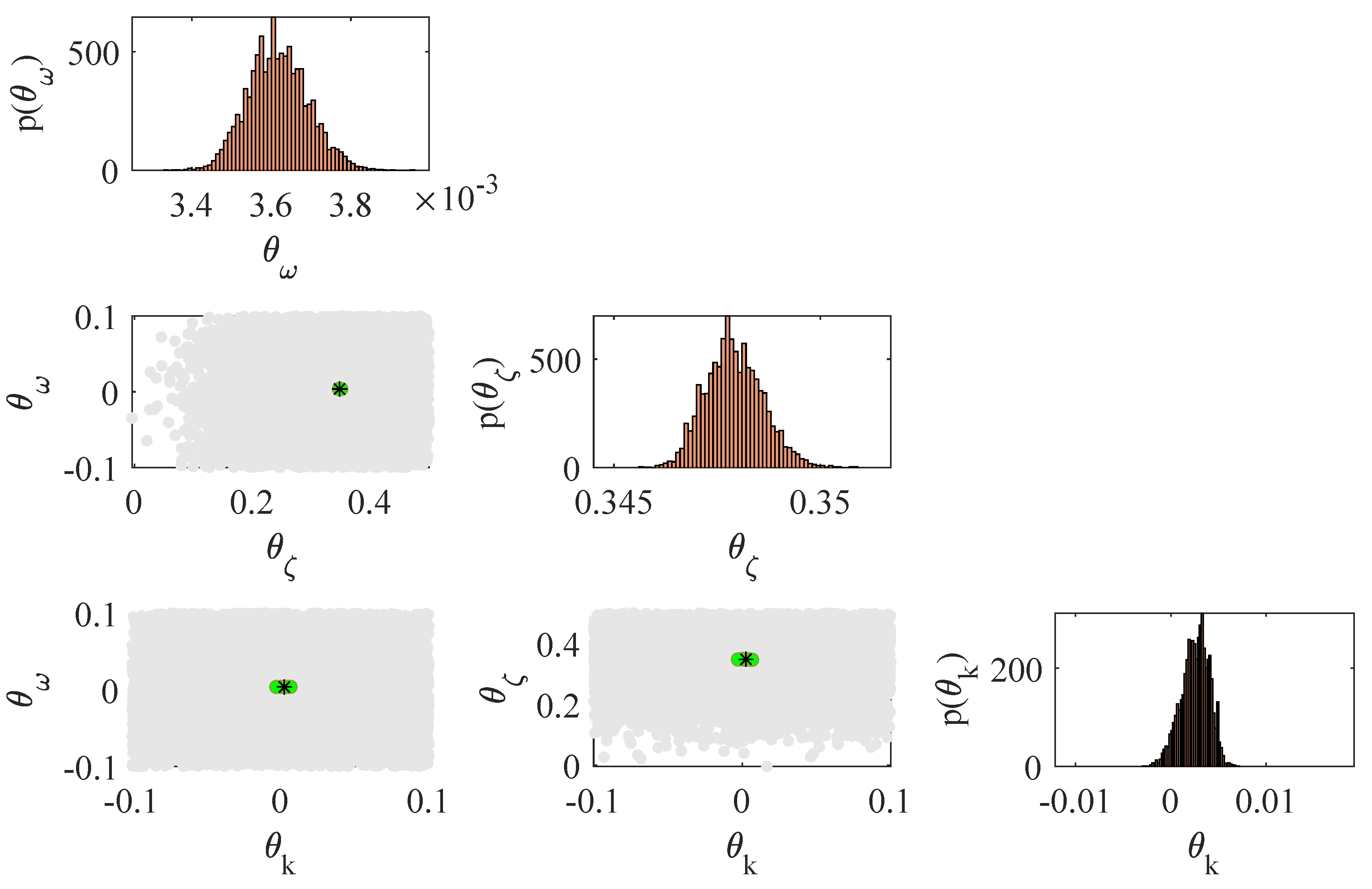
 : Initial SLD using parameters obtained by impact hammer test before starting the milling operations. ,
: Initial SLD using parameters obtained by impact hammer test before starting the milling operations. ,  : updated SLD using mean of posterior ,
: updated SLD using mean of posterior ,  : SLD using parameters obtained by impact hammer test after operations [21], circles and crosses are experimentally determined stable and unstable points, respectively. P1-P7 are the stable points used in model updating.
: SLD using parameters obtained by impact hammer test after operations [21], circles and crosses are experimentally determined stable and unstable points, respectively. P1-P7 are the stable points used in model updating.
 : Initial SLD using parameters obtained by impact hammer test before starting the milling operations. ,
: Initial SLD using parameters obtained by impact hammer test before starting the milling operations. ,  : updated SLD using mean of posterior ,
: updated SLD using mean of posterior ,  : SLD using parameters obtained by impact hammer test after operations [21], circles and crosses are experimentally determined stable and unstable points, respectively. P1-P7 are the stable points used in model updating.
: SLD using parameters obtained by impact hammer test after operations [21], circles and crosses are experimentally determined stable and unstable points, respectively. P1-P7 are the stable points used in model updating.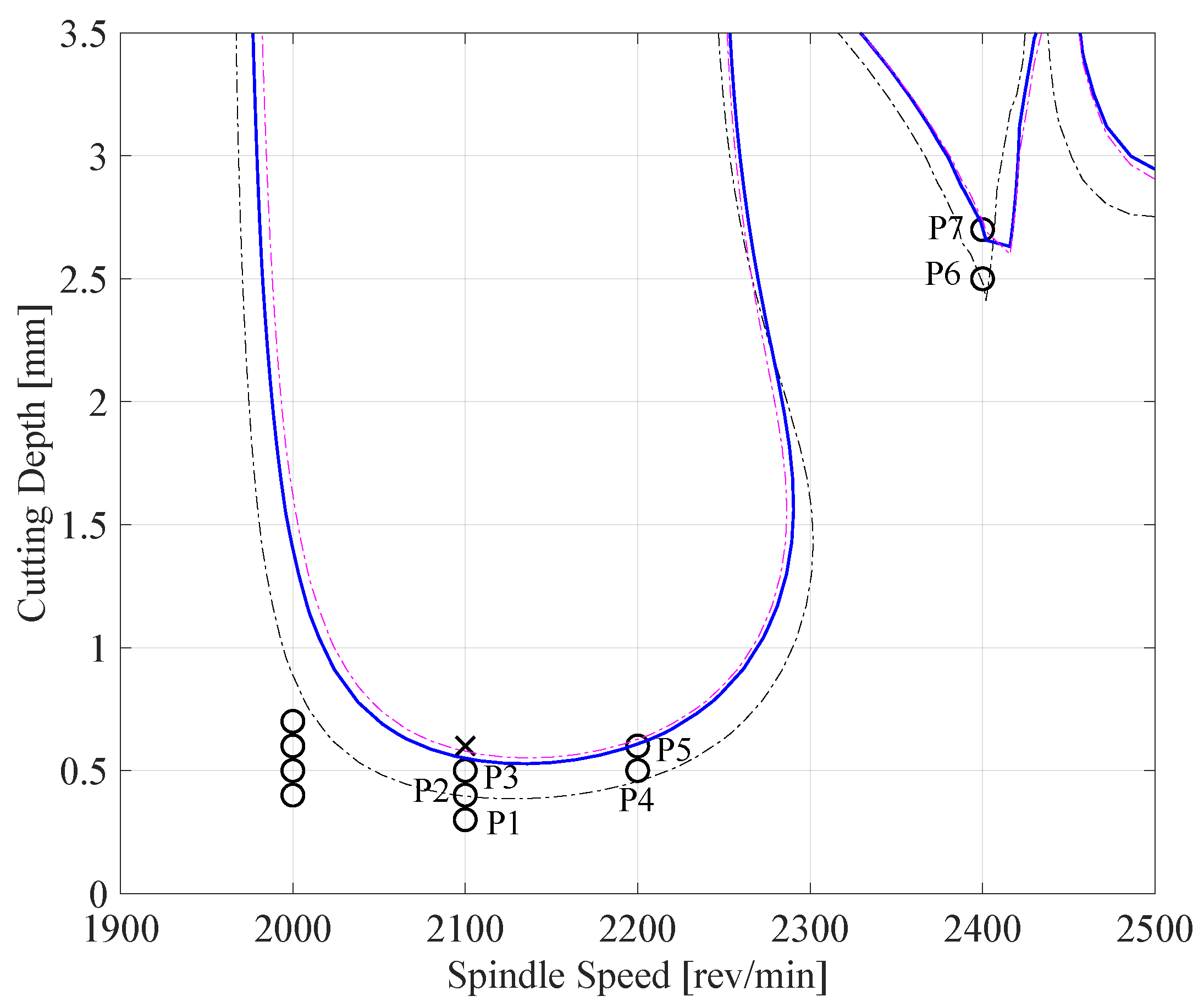
| p | spindle speed [rev/min] |
cutting depth [mm] |
[Hz] |
|
|---|---|---|---|---|
| 1 | 2000 | 0.4 | ||
| 2 | 2000 | 0.5 | ||
| 3 | 2000 | 0.6 | ||
| 4 | 2000 | 0.7 | ||
| 5 | 2000 | 0.8 | ||
| 6 | 2100 | 0.3 | ||
| 7 | 2100 | 0.4 |
| p | spindle speed [rev/min] |
cutting depth [mm] |
[Hz] |
|
|---|---|---|---|---|
| 1 | 2100 | 0.3 | ||
| 2 | 2100 | 0.4 | ||
| 3 | 2100 | 0.5 | ||
| 4 | 2200 | 0.5 | ||
| 5 | 2200 | 0.6 | ||
| 6 | 2400 | 2.5 | ||
| 7 | 2400 | 2.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





