Bucket Attention: Fixed-Size Space for Any Length of Context

1. Introduction

In recent years, attention mechanisms [1] have played a key role in natural language processing, driving the rapid advancement of large language models (LLMs) such as BERT [2], GPT [3] and DeepSeek-R1 [4]. As the powerful capabilities of the attention mechanism [1] have been recognized, transformers have gradually replaced convolutional neural networks. Hypernetworks [5] is also a perspective for viewing the relationship between networks and different inputs. Studies indicate that attention mechanisms can be viewed as hypernetworks [6,7,8], where inputs are context. Therefore, context is crucial for LLMs, as it provides conditions and extensive information that profoundly influence the outputs.

Many tasks [9] require handling extremely long contexts, which often exceed standard context-length limits. It typically requires a large amount of space and takes a significant amount of time. To alleviate the challenges, a variety of methods have been proposed. Sparse attention [10,11,12] computes only a portion of attention scores, effectively reducing memory usage and improving the computation speed by limiting the interaction scope or density of each element. Essentially, it is very similar to the approach of pruning the KV cache [13,14]. A straightforward approach is to compute local attention based on the position of each element [15,16,17]. Furthermore, Locality-Sensitive Hashing (LSH) [18,19] is a powerful tool to compute the correlation between elements. The other approach employs hierarchical structures to capture contextual information at different levels, gradually integrating long-distance dependencies, and thus reducing spatial and temporal costs [20,21,22]. Another approach leverages a sleep mechanism [23] to compress the context into network parameters, but is unable to handle dynamic long-context tasks.

However, these methods have not completely resolved the issue. To better address this challenge, we propose an innovative attention mechanism that utilizes fixed-size storage, enabling the attention mechanism to effectively manage contexts of any length. Key contributions of this paper include the following:

• Through analyzing the attention mechanism, we propose a novel perspective: sequential inputs do not need to be organized in order within attention mechanisms.
• We introduce a novel approach to organizing context of LLMs that is capable of handling any length of context using a fixed size space, i.e. bucket attention.
• We propose a method to convert a pre-trained model based on traditional attention into that of bucket attention.
• We propose a method to train a model with bucket attention from scratch.

2. Analysis

LLMs generally employ next token prediction and unidirectional attention. Therefore, throughout this paper, attention specifically refers to unidirectional attention.

2.1. Attention is Unordered

First, it is important to recognize that the attention mechanism is inherently unordered, which is why position encoding becomes essential. The organization of natural language is sequential, but fundamentally, this orderliness is linked only to position encoding, not to the attention mechanism itself. A notable fact is that we can completely rearrange the order of elements within the KV cache. Thus, we can modify the organization of the KV cache, enabling it to be structured as any efficient data structure rather than just a sequence. Numerous studies [20,21,22] have organized the context into hierarchical structures. However, merely rearranging the order of the context is insufficient to fit an arbitrarily long context into a fixed space. To accomplish this, it is crucial to compress or trim the context while minimizing information loss. Information theory tells us that it is impossible to compress a random sequence into a very small space. However, natural language is not a random sequence, which contains a great deal of redundancy, allowing large portions of text to be summarized effectively.

2.2. Finite-Dimensional Context

We assume that the concepts in the world are finite, and consequently, the logical relationships between them are also finite. Therefore, the state of context should reside in a finite-dimensional space. This gives us hope that context can be described using this finite-dimensional space, rather than relying on a potentially infinite sequence. It is challenging to enumerate keywords and key relationships, but models learn the language structure, extract essential contextual information, and summarize it into key concepts. We can interpret it as a state, yet unlike the abstract states within Recurrent Neural Network (RNN), this state is fundamentally a form of attention.

Based on the above assumptions and analysis, we present a conceptual attention mechanism within a finite-dimensional space. The relationship between the novel attention mechanism and the traditional attention mechanism is similar to that between the Lebesgue integration and the Riemann integration. We partition the context into a fixed number of intervals by keys, aggregating values within each interval, thereby constructing attention that uses a fixed space.

We use equations to provide a more precise description of our approach. The formula for calculating attention is as follows.

$$A_i=\mathrm{softmax}\left({\displaystyle \frac{Q_i{K}_{0\dots i}^{\top }}{\sqrt{d_k}}}\right)V_{0\dots i}\triangleq \mathrm{softmax}\left({\displaystyle \frac{Q_i{[K_0\dots K_i]}^{\top }}{\sqrt{d_k}}}\right)[V_0\dots V_i],$$

(1)

where $K_{0\dots i}$ and $V_{0\dots i}$ are keys and values of the tokens from 0-th to i-th. We partition the space of keys into N groups (buckets) and we have the following.

$$A_i=\mathrm{softmax}\left({\displaystyle \frac{Q_i{[K_{G_0}\dots K_{G_{N-1}}]}^{\top }}{\sqrt{d_k}}}\right)[V_{G_0}\dots V_{G_{N-1}}],$$

(2)

where $G_0\dots G_{N-1}$ are groups of keys and each group includes multiple elements. We need to approximately convert each group containing multiple elements into a single element. Since we group them by keys, we first select a representative element ${\overrightarrow{K}}_t$ from each group $G_t$, where ${\overrightarrow{K}}_t$ is a unit vector indicating direction. Assume $K_j$ belongs to the $t\left(j\right)$-th group (bucket) $G_{t\left(j\right)}$, $K_j\doteq {\alpha }_j{\overrightarrow{K}}_{t\left(j\right)}$.

$$\begin{array}{cc}\hfill A_i& =\mathrm{softmax}\left({\displaystyle \frac{Q_i{[{\alpha }_0{\overrightarrow{K}}_{t\left(0\right)}\dots {\alpha }_i{\overrightarrow{K}}_{t\left(i\right)}]}^{\top }}{\sqrt{d_k}}}\right)[V_0\dots V_i]\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & =\mathrm{softmax}\left({\displaystyle \frac{Q_i{[{\beta }_0{\overrightarrow{K}}_0\dots {\beta }_{N-1}{\overrightarrow{K}}_{N-1}]}^{\top }}{\sqrt{d_k}}}\right)[{\overline{V}}_0\dots {\overline{V}}_{N-1}],\hfill \end{array}$$

(4)

where ${\beta }_t$ is derived by weighting ${\alpha }_j$ from the same group and ${\overline{V}}_t$ is derived by weighting $V_j$ from the same group.

$$\mathrm{i}.\mathrm{e}.\left\{\begin{array}{c}{\beta }_t=log\left(\sum _{j\in G_t}{e}^{{\alpha }_j}\right)\hfill \\ {\gamma }_j=e^{{\alpha }_j/\sqrt{d_k}}/e^{{\beta }_t/\sqrt{d_k}}\hfill \\ {\overline{V}}_t=\sum _{j\in G_t}{\gamma }_j{V}_j\hfill \end{array}\right..$$

(5)

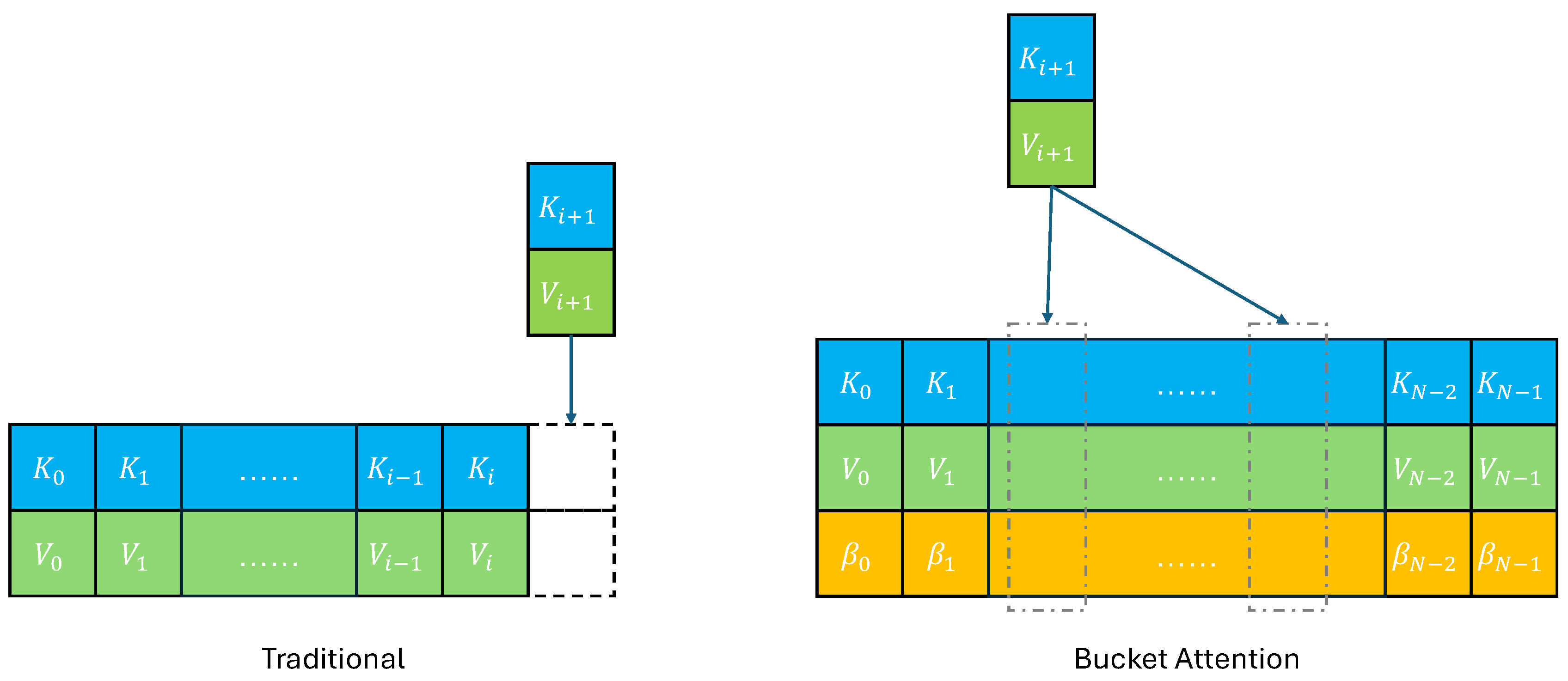
Therefore, by employing a grouping method, we can compress an arbitrarily long context into fixed-length N buckets.

3. Bucket Attention

3.1. Training-free Approach

Building on the above analysis, we can intuitively develop an inference-time scaling algorithm that requires no training and efficiently stores arbitrarily long contexts using only a fixed space during inference. Analyzing the formula above, during inference we need to update the bucket cache of ${\overrightarrow{K}}_t$, ${\overline{V}}_t$ and ${\beta }_t$. Compared to typical inference with the KV cache, we will need to store an additional variable ${\beta }_t$. The detail is shown in Algorithm 1.

Algorithm 1 Single Bucket: Calculate $A_i$ and Maintain State

Input: $K_i,Q_i,V_i$ and prefilled $\overrightarrow{K},\overline{V},\beta$ $t\leftarrow$ the bucket index of $K_i$ ${\alpha }_i\leftarrow$ the projected length of $K_i$ ${\beta }_t^{\prime }\leftarrow log(e^{{\beta }_t}+e^{{\alpha }_i})$ ${\overline{V}}_t\leftarrow (e^{{\beta }_t/\sqrt{d_k}}{\overline{V}}_t+e^{{\alpha }_i/\sqrt{d_k}}{V}_i)/e^{{\beta }_t^{\prime }/\sqrt{d_k}}$ ${\beta }_t\leftarrow {\beta }_t^{\prime }$ $A_i\leftarrow \mathrm{softmax}\left({\displaystyle \frac{Q_i{[{\beta }_0{\overrightarrow{K}}_0\dots {\beta }_{N-1}{\overrightarrow{K}}_{N-1}]}^{\top }}{\sqrt{d_k}}}\right)[{\overline{V}}_0\dots {\overline{V}}_{N-1}]$ return  $A_i$

Furthermore, we can extend each layer of attention to span multiple buckets rather than being confined to just one. In practice, this is also essential. Note that in high-dimensional spaces, any two randomly chosen vectors are almost orthogonal. This provides a theoretical foundation for the fact that the representative elements of any two buckets are nearly orthogonal. Thus, we can avoid performing Schmidt orthogonalization on them. Consequently, a vector can be decomposed into multiple buckets by projection, which could be dense or sparse according to its principal components. The detail is shown in Algorithm 2 and Figure 1. To improve computational efficiency, we use sparse bucket attention, which limits the number of buckets involved each time, that is, $|T_i|\ll N$.

We may need to consider different application scenarios to decide whether to use bucket attention. Essentially, this approach is a variant and enhancement of the KV cache, allowing flexible switching between traditional KV cache and bucket attention.

Algorithm 2 Multiple Buckets: Calculate $A_i$ and Maintain State

Input: $K_i,Q_i,V_i$ and prefilled $\overrightarrow{K},\overline{V},\beta$ $T_i\leftarrow$ { t ∣ the bucket indices of $K_i$ } ${\left\{{\alpha }_t^i\right\}}_t\leftarrow$ the projected length of $K_i$ for each t in $T_i$ do    ${\beta }_t^{\prime }\leftarrow log(e^{{\beta }_t}+e^{{\alpha }_t^i})$    ${\overline{V}}_t\leftarrow (e^{{\beta }_t/\sqrt{d_k}}{\overline{V}}_t+e^{{\alpha }_t^i/\sqrt{d_k}}{V}_i)/e^{{\beta }_t^{\prime }/\sqrt{d_k}}$    ${\beta }_t\leftarrow {\beta }_t^{\prime }$ end for $A_i\leftarrow \mathrm{softmax}\left({\displaystyle \frac{Q_i{[{\beta }_0{\overrightarrow{K}}_0\dots {\beta }_{N-1}{\overrightarrow{K}}_{N-1}]}^{\top }}{\sqrt{d_k}}}\right)[{\overline{V}}_0\dots {\overline{V}}_{N-1}]$ return  $A_i$

3.2. Partitioning of Buckets

Partitioning buckets is an intriguing issue to investigate. The simplest method is to divide the space uniformly, but this does not capture the distribution of the data. A more effective approach is to sample and partition based on data density, utilizing algorithms similar to K-Nearest Neighbors (KNN) [24].

An important issue to consider is the selection of the total number of buckets N and the number of principal components $|T_i|$. As the number of buckets increases, the algorithm becomes more similar to traditional attention. Therefore, the fundamental principle is to utilize as much memory as possible. Furthermore, N of each attention layer could be independently selected. Although it is common practice to keep the parameters consistent across layers, they can also be varied empirically. Another selection method involves estimating the intrinsic dimensionality of the corpus through error analysis.

3.3. Training From Scratch

If we train a model from scratch instead of converting a pre-trained model, we can simplify the process further. We can allow the model to learn the buckets implicitly, similar to learning an embedding, rather than explicitly partitioning them. We call this method implicitly bucket attention, where the neural network outputs the decomposition coefficients of keys and queries in the bucket space instead of directly outputting values. This approach has the advantage of embedding the bucket partitions within the model parameters while reducing computational effort. Moreover, we can directly employ dense bucket attention without incurring any additional computational cost.

We describe the computation method of implicit bucket attention using equations.

$$\begin{array}{cc}\hfill & Q_i{K}_{0\dots i}^{\top }={\mathsf{\theta }}^i{\mathsf{\alpha }}^{\top }\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \mathrm{where}& \left\{\begin{array}{cc}{K}_j\hfill & =[{\mathsf{\alpha }}_0^j{\overrightarrow{K}}_{t\left(0\right)}\dots {\alpha }_{N-1}^j{\overrightarrow{K}}_{N-1}]\triangleq {\mathsf{\alpha }}^j\hfill \\ K_{0\dots i}=\left[\begin{array}{c}{\alpha }^0\\ ⋮\\ {\mathsf{\alpha }}^i\end{array}\right]\hfill & =[{\alpha }_0{\overrightarrow{K}}_{t\left(0\right)}\dots {\alpha }_{N-1}{\overrightarrow{K}}_{N-1}]\triangleq \mathsf{\alpha }\hfill \\ Q_i\hfill & =[{\theta }_0^i{\overrightarrow{K}}_{t\left(0\right)}\dots {\theta }_{N-1}^i{\overrightarrow{K}}_{N-1}]\triangleq {\mathsf{\theta }}^i\hfill \end{array}\right.,\hfill \end{array}$$

(7)

where $\mathsf{\alpha }$ and $\mathsf{\theta }$ are outputs of the networks. The form of the above equation resembles multi-head latent attention (MLA) [25], where the buckets can be viewed as a type of latent space. Note that $\mathsf{\alpha }$ remains a sequence and we need to accumulate $\mathsf{\alpha }$ to obtain $\mathsf{\beta }$ to represent the state.

$$\begin{array}{c}\hfill Q_i{K}_{0\dots i}^{\top }={\mathsf{\theta }}^i{{\mathsf{\beta }}^i}^{\top }={\mathsf{\theta }}^i{[{\mathsf{\beta }}_0^i\dots {\mathsf{\beta }}_{N-1}^i]}^{\top },\end{array}$$

(8)

where

$$\begin{array}{c}\hfill {\mathsf{\beta }}_t^i=log\left(\sum _{j=0}^i{e}^{{\alpha }_t^j}\right).\end{array}$$

(9)

The computation method for the value is the same as that in the training-free approach and will be omitted here.

4. Implementation

4.1. Training-Free Approach

The implementation details that need to be considered consist of two parts: one involves the partitioning of buckets, and the other pertains to the bucket attention. We utilize KNN to partition the buckets. We implement bucket attention according to Equations 5, during which we only need to maintain a fixed-size cache of ${\overrightarrow{K}}_t$, ${\overline{V}}_t$ and ${\beta }_t$.

4.2. Training From Scratch

Based on the formulas and analysis in Section 3.3, compared to the traditional implementation of attention mechanisms, we only need to redefine an additive operation for features. Then, we can replace individual elements with the exponential cumulative sum of these elements. The exponential cumulative sum is defined in Equations 5 and 9.

5. Conclusions

In conclusion, our analysis of attention mechanisms has led to a groundbreaking insight that sequential inputs within these mechanisms do not need to adhere to a strict order. We have successfully introduced bucket attention, a novel approach that organizes context within large language models (LLMs) and adeptly manages contexts of varying lengths using fixed-size spaces. Additionally, we have developed techniques to transform pre-trained models based on traditional attention into the bucket attention paradigm, accompanied by methodologies for training models with bucket attention from the ground up. These advances provide practical solutions to significantly enhance the efficiency and scalability of LLMs, paving the way for more robust and adaptable models in the future.