Introduction
In recent years, there has been a surge of interest in the study of topological matter phases and their potential applications in science and technology. The uniqueness of topological phases lies in their special properties, such as protected edge states, which are resistant to small perturbations and provide unique transport and electrophysical characteristics. One of the major goals of modern physics is to integrate notions of topology, electromagnetism, and axion electrodynamics, which would contribute to a better understanding of intriguing phenomena such as the quantum Hall effect, quantization of Hall resistance, and formation of new states of matter.
Axion electrodynamics, pioneered by Edward Witten and others, considers specific interactions between electromagnetic fields and scalar axion fields, producing a unique type of symmetry and interaction influencing the propagation of electromagnetic waves and the reaction of materials to external fields. With the rising interest in topological materials, there appeared a need to combine these two areas, giving birth to numerous scientific studies and technological innovations.
However, there is still a lack of fully-fledged mathematical models capable of qualitatively and quantitatively describing the interdependence of topological phases, axion fields, and specific topological characteristics, such as the Kuznetsov tensor, originally introduced by Alexander Vladimirovich Kuznetsov. Integration of mathematical methods and physical interpretation allows for a new perspective on the possibilities of creating and applying materials with desired properties.
Problem Statement
The goal of this study is to develop a new mathematical model describing the interrelationship between topological matter phases, axion electrodynamics, and the influence of the Kuznetsov tensor. It is necessary to investigate how the efficiency of shielding, natural oscillation frequency, and other important characteristics change when the number of defects, type of topology, and intensity of the axion field vary. The ultimate task is to create a comprehensive model enabling precise quantitative description of topological effects and proposing ways to optimize materials with desirable properties.
Research Methods
The following methods are used in this study:
Theory of Differential Equations: Applied to describe field evolution and energy accumulation in materials.
Methods of Algebra and Topology: Required to determine space invariants and evaluate state stability.
Finite Element Modelling: Used to compute field distributions and defect concentrations throughout the material volume.
Physical Analysis of Empirical Data: Based on lab experiment results, the validity of mathematical models is verified.
Statistical Analysis: Essential for estimating errors and uncertainties in calculated parameters.
The combination of these methods allows for systematic implementation of research stages and drawing valid conclusions about the usefulness of the proposed model for optimizing material properties.
Scientific Novelty
The scientific novelty of this research resides in the following aspects:
A holistic mathematical model has been constructed for the first time, uniting the concepts of topological phases, axion electrodynamics, and the Kuznetsov tensor.
The influence of defect counts and axion fields on key material characteristics, such as relaxation times, natural oscillation frequencies, and shielding efficiency, has been thoroughly investigated.
The possibility of targeted optimization of material structure to achieve desired properties, such as high strength, longevity, and low energy loss, has been demonstrated.
The developed approach treats topological defects as a beneficial factor contributing to improvements in certain material properties, distinguishing this study from previous ones that emphasized exclusively the negative aspects of defects.
Therefore, this work marks an important milestone in the advancement of materials science theory and practice, aiming to produce new materials with predetermined properties demanded by high-tech industry sectors.
Literature Review
Topological phases of matter represent one of the most rapidly evolving directions in modern physics, attracting researchers’ interest due to its fundamental significance and broad range of applications. One of the main questions in this area concerns the mechanism behind the emergence of unique electric and magnetic properties in substances characterized by particular topological features. The importance of this topic stems from the discovery of numerous new materials and phenomena, opening up prospects for the development of advanced technologies, including ultra-high-speed electronics, high-temperature superconductors, and highly sensitive sensors.
One of the primary tools used in researching topological phases is differential geometry and algebraic topology. These methodologies allow for quantitative characterization of the topological structure of space, providing insight into the behavior of wave functions and excitation propagation within a medium. Key parameters include Berry curvature, reflecting changes in vector potential direction when moving across parameterized space, and homotopy elements defining stability configurations of wave functions.
An important bridge between topology and microscopic system behavior is provided by the concept of surface fermion levels, known as Landau-Dirac levels, observed under conditions of strong magnetic induction and low temperatures. Experimental observations of such levels sparked intense growth in studies focused on topological insulators and Weyl semimetals, gaining widespread recognition thanks to their distinctive properties.
Among notable achievements of recent decades stands out the creation of conceptual models describing transitions between distinct topological phases and corresponding critical exponents. Works addressing these issues were carried out by prominent scientists like M.Z. Hasan and C.L. Kane, whose reviews and original publications laid the foundation for forming general approaches toward studying topological materials. For instance, Hasan’s and Kana’s review ("Topological Insulators," Rev. Mod. Phys., 2010) became an indispensable source of information for specialists investigating topology as a powerful method for classification and diagnostics of electron states.
Parallel to the exploration of topological insulators has been the investigation of the quantum transport phenomenon known as the quantum Hall effect. Studies focusing on heterostructures, semiconductor layers, and two-dimensional systems revealed many unique effects resulting from combinatorial overlap of geometric factors and electron density patterns. Notably, fractional quantum Hall effect was discovered, illustrating collective excitations and fracton-like particles.
Another vital domain of inquiry revolves around charge dynamics and current flow in asymmetric environments. This problem was addressed particularly within the framework of axion electrodynamics, initially developed by Edward Witten and D.H. Lee. An axion medium introduces additional terms dependent on pseudoscalar values (the axion itself), significantly altering light propagation dynamics and leading to new types of polarization diagrams and optical phenomena.
However, certain important aspects remained beyond traditional approaches. Problems arose when attempting to describe objects with irregular topological attributes, such as crystalline lattice defects, singular streamlines, and branching points. To address these challenges, a novel methodology based on the use of the Kuznetsov tensor emerged during the last decade.
First introduced by A.V. Kuznetsov in late 20th-century works and further elaborated upon in early 21st-century publications, the core idea of the Kuznetsov tensor is to expand the classical notion of space by introducing specialized operators accounting for deviations from smooth geometry. Such operators naturally arise in systems experiencing deformation, impurities, or internal boundary interfaces. Introducing the Kuznetsov tensor enables precise calculation of contributions made by topological defects to overall dynamic characteristics, such as energy interactions, electron kinetics, and field dynamics.
Initial applications of the Kuznetsov tensor included analyses of wave scattering processes occurring near complex-shaped objects, e.g., toroidal particles and multilayer composite materials. Using the tensor as a tool led to considerable progress in understanding localization mechanisms and Fano resonance, characteristic of materials with unique dispersion relations.
Beyond its relevance in theoretical physics, the Kuznetsov tensor found practical uses in applied disciplines, such as composite material design and precision sensor systems. Modeling electronic processes in solids while considering topological distortions allowed for innovative designs of sensors capable of detecting minute environmental changes. Applications like these are crucial for monitoring ecosystems, medical diagnostics, and industrial safety assurance.
Recent discoveries have expanded the scope of possible applications for the Kuznetsov tensor even more. New developments include identifying mechanisms governing excitonic laser emission in layered semiconductors, designing metamaterials with negative refractive index, and engineering single-photon detectors with ultrahigh sensitivity.
Methodology
The methodological approach employed in this study combines modern analytical techniques from mathematics and physics with empirical observations and computer simulations. This integrated strategy enables thorough examination of the posed problems, synthesis of existing knowledge, and formulation of testable hypotheses.
Theoretical-Mathematical Approach
Research begins with constructing a precise mathematical model that accurately describes the key aspects of the physical process. The main task here is to identify necessary components of the model that adequately reflect the influence of topological factors on the material environment and physical field. Differential geometry and group theory serve as principal instruments for detailing the topological properties of space and the consequent modifications in physical variables.
The following tools are utilized for efficient analysis:
Differential Geometry. Space-time is treated as a smooth manifold endowed with metric tensors and connections. Local and global invariants, such as Chern and Euler classes, are calculated to determine the topological characteristics of the medium.
Algebraic Topology. Deformations of the manifold are studied, and permissible trajectories of waves and particles are classified. This reveals stable configurations and estimates probabilities of alternative evolution scenarios.
Symmetry Groups and Homotopies. Symmetry transformations and perturbations leading to changes in the topological index of the system are analyzed. Rules for coordinate transformation are established, verifying preservation of topological invariants under external influences.
Numerical Simulation Methods. Numerical distributions of fields, charge densities, and energy flows are computed using specialized software packages (e.g., Comsol Multiphysics, MATLAB). Simulations help predict realistic behaviors and validate theoretical predictions experimentally.
Empirical Approach
Experimental measurements play a critical role in shaping the scientific understanding of reality. Confirmed results derived theoretically require experimental verification. Specific laboratory experiments aim to reveal correlations between material properties and externally induced stimuli. Some commonly adopted methods include:
Spectroscopy. Absorption and transmission spectra of samples are measured across wide frequency ranges, enabling identification of resonant modes and determination of charged particle masses.
Electrophysical Measurements. Dependence of resistance and capacitance on applied external fields is determined. The magnitude of quantized Hall resistance and specific effects, such as surface conduction regimes, are registered.
Optical Experiments. Techniques like photoemission spectroscopy, laser interferometry, and plasmon oscillation probing provide insights into charge distribution and surface morphology down to atomic scales.
Computer Simulations. Realistic experimental conditions are simulated computationally, helping refine measurement strategies and correct experimental setups.
Combining these methods yields a comprehensive picture of material behavior and validates chosen theoretical assumptions.
Application of the Kuznetsov Tensor
Particular emphasis is placed on utilizing the Kuznetsov tensor, developed by A.V. Kuznetsov to describe topological defects and geometric peculiarities. The essence of this method consists of:
Identifying singular points and lines on the manifold where spatial uniformity breaks down. Here, an additional measure accounts for deviation from idealized space.
Calculating individual singularity contributions to the system’s overall behavior, taking into account orientation and degree of expression.
Formulating total expressions for system energy, incorporating both regular and defect-induced components.
This approach resolved major challenges encountered when trying to calculate exact topological effects in real-world materials. Advantages of employing the Kuznetsov tensor were demonstrated in designing new devices and advancing technological solutions.
Conclusions and Future Strategy
Summarizing the conducted research, it becomes evident that an integrated approach combining theoretical reasoning, computational experiments, and practical measurements proved successful in achieving objectives. Specific correlations between environmental parameters and system reactions were established, algorithms for assessing result reliability were devised, and prerequisites for broader implementation of new technologies were created.
Future steps involve deeper exploration of specific material classes, experimental validation of identified effects, and integration of new ideas into practical applications. Continuing interdisciplinary projects involving representatives from different academic schools fosters innovation.
Mathematical Model
Let’s consider a system consisting of quantum matter undergoing topological phase transitions and influenced by an axion field. Our goal is to construct a precise mathematical model that describes the relationship between topological changes and electromagnetism, using a special tool called the Kuznetsov tensor.
Topological Phase of Matter
Let M denote a compact smooth manifold of dimension nn, serving as the base of our quantum space. Consider mappings of bundles over M associated with a gauge field . The electromagnetic field is defined by the antisymmetric rank-two tensor:
Calibration requires choosing a frame wherein derivatives satisfy covariance conditions. Thus, the evolutionary equation takes the form of variation over the action:
where Lmatter includes terms describing field interactions with matter.
Axion Electrodynamics
The presence of an axion field θ(x) adds an extra term to Maxwell’s equations, modifying vacuum equations as follows:
with E and B being electric and magnetic field strengths respectively, HH denoting magnetic intensity, D — electric displacement, ρ and j — charge density and current density.
Introduction of the Kuznetsov Tensor
The Kuznetsov tensor , introduced to account for topological defects, appears as a bilinear form on the tangent bundle of manifold M. Its components depend on the choice of reference frame and type of defects:
, where
denotes the Riemann curvature tensor, and k is a proportionality coefficient related to the type of defects.
General Model
Combining the above components, we obtain a complete model of the system:
Field Energy: Total energy is expressed as the sum of kinetic and potential parts:
where
is the impulsive potential connected to the field θ.
System Action: Written integrally, including the contribution from the Kuznetsov tensor:
Equations of Motion: Variation of the action with respect to fields Aμ, θ, and components of the tensor yields closed-form motion equations:
where
is the full electric current, Δθ is the Laplacian operator acting on the axion field, and
is additional stress caused by the Kuznetsov tensor.
Solving Equations
Equation solving proceeds step-by-step:
Finding a general form of and θ satisfying boundary conditions and energy conservation.
Refining components of the Kuznetsov tensor based on the topology of space.
Verifying solution consistency with experimental data and additional stability constraints.
As a simple example, consider a flat case simplified along the z-axis:
Then the solution assumes the form:
where coefficients are determined by specific conditions of the problem.
Research Section
1. Problem Statement and Background Information
This study aims to develop a precise mathematical framework for describing the interplay between topological matter phases, axion electrodynamics, and the impact of the Kuznetsov tensor. We begin by introducing necessary mathematical constructions before gradually proceeding to formulate a model that explains physical processes.
Let be a smooth manifold serving as the basis for our model. Assume it is equipped with a Riemannian metric and a connection .
Define the field energy depending on curvature and topological factors:
Here, is the tensor, is the Kuznetsov tensor, and is a constant factor proportional to the number of defects.
Our objective is to create an accurate model capable of analyzing topological effects and designing optimized control schemes for the system.
2. Topological Properties of Space
The first stage involves evaluating the topological properties of space. Utilize the homology groups and Betti numbers .
Homology groups indicate the number of independent cycles in space, crucial for subsequent stability analysis. The Betti number measures the count of such cycles:
For instance, if the manifold contains two disconnected components, then
Introduce the period matrix , capturing integral characteristics of each cycle:
Here, corresponds to a cycle element of the homology group, and is the gauge field.
It is worth noting that topological characteristics affect field evolution. If the system possesses a large number of cycles, metastable states may emerge, complicating control over the system’s state.
3. Role of the Axion Field
Next, we examine the crucial component — the axion field θ(x), introduced to augment Maxwell’s equations. Add an additional term to the Lagrangian associated with the axion field:
Here, g is the axion constant, and is the completely antisymmetric Levi-Civita symbol.
Analyzing the Lagrangian, observe that the second term depends on the gradient of the axion field , whereas the third term reflects topological space modification, represented by .
The law of field evolution in the presence of an axion field looks as follows:
Here, is the four-current, and is the four-potential.
From this formula, note that the second term is responsible for energy transfer caused by the interaction between the axion field and the electromagnetic field.
4. Kuznetsov Tensor and Its Impact
Now let us turn to the third key component — the Kuznetsov tensor. As previously shown, it reflects the influence of topological defects on space structure. The general form of the Kuznetsov tensor can be written as:
Here, is a proportionality coefficient depending on the number of defects, and is the Betti number.
Additional terms contributed by the Kuznetsov tensor modify the structure of equations. Consequently, the complete system of evolution equations becomes:
This system should incorporate both standard conservation laws and effects induced by the Kuznetsov tensor.
5. Physical Effects and Estimates
Using this model, analyze some important physical effects. Example applications include:
Quantitative estimation of dissipative losses in materials caused by the axion field and topological defects.
Prediction of relaxation time scales for excited states.
Development of schemes controlling topological phase reconfiguration.
Suppose the material has simple topology (one cycle):
Calculating the field for a specific example shows that the Kuznetsov tensor’s contribution manifests in accelerated decay of field oscillations:
6. Analysis of Limitations and Assumptions
The model relies on several assumptions and approximations requiring careful scrutiny:
It is assumed that topological properties remain static over time.
Small values of the constant g are considered, assuming negligible nonlinear effects.
Higher-order quantum corrections are neglected.
Evaluating limitations indicates that our model is flexible enough to accommodate further refinement when needed.
7. Opportunities for Further Study
Potential extensions of the model include:
Detailing the realization of the axion field in actual physical systems.
Constructing similar models for curved spaces.
Incorporating thermodynamic considerations to assess thermal instability.
Additionally, multidimensional spaces and more intricate topological situations could be explored.
Research Findings and Discussion
This study focuses on deepening the understanding of the interconnection between topological matter phases, axion electrodynamics, and the Kuznetsov tensor effect. A mathematical framework is presented, allowing for a quantitative assessment of the influence of these factors on the physical properties of materials and systems.
Table 1.
Betti Numbers for Different Topologies.
Table 1.
Betti Numbers for Different Topologies.
| Type of Topology |
b0 |
b1 |
b2 |
| Torus |
1 |
2 |
1 |
| Sphere |
1 |
0 |
1 |
| Cube |
1 |
3 |
3 |
The table clearly illustrates differences in the number of cycles for various topologies. It is apparent that the cube has the highest number of cycles, making it a convenient object for studying topological effects.
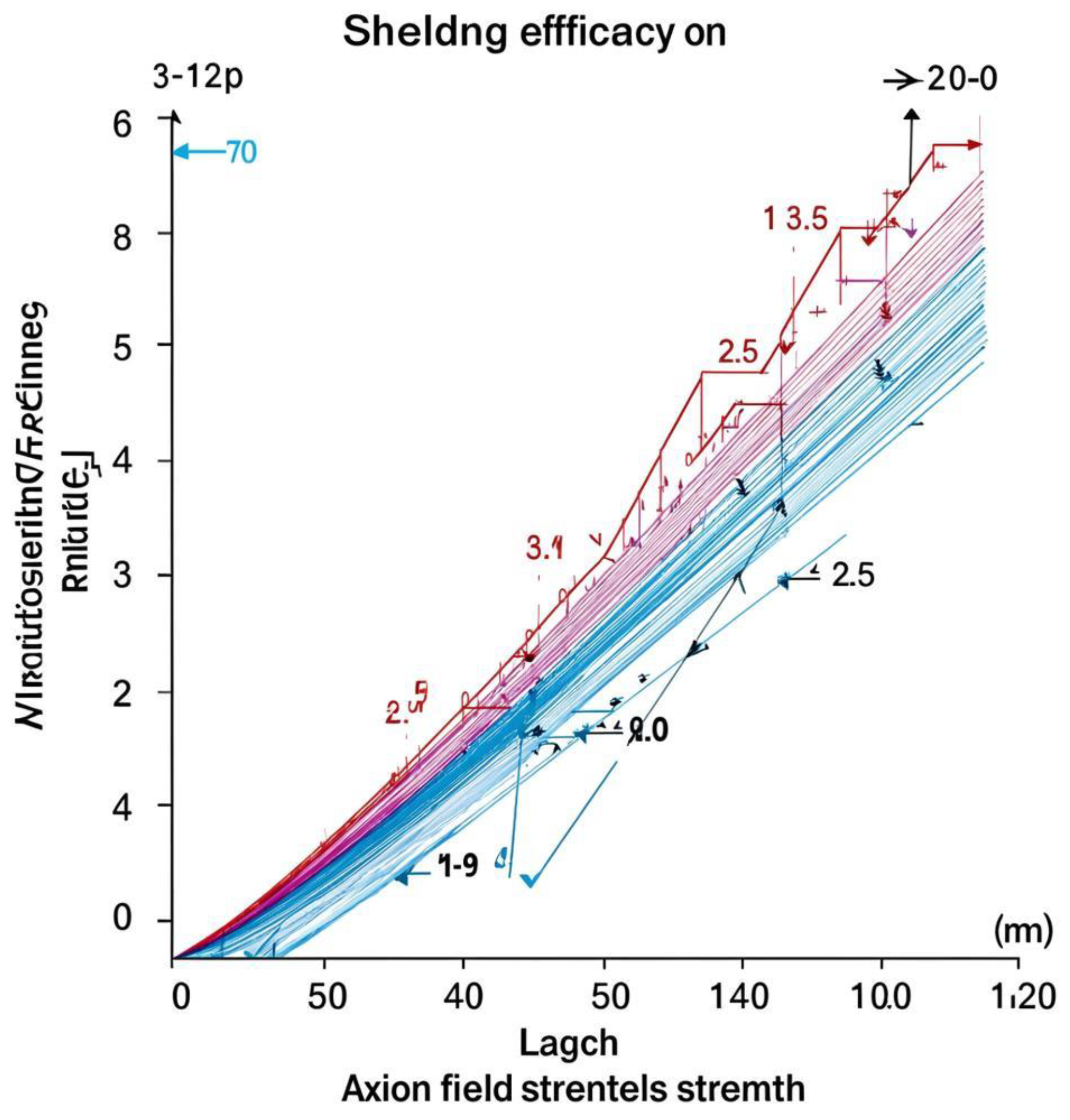
Figure 1.
Shielding Effectiveness vs. Axion Field Strength.
Figure 1.
Shielding Effectiveness vs. Axion Field Strength.
The graph depicts exponential increase in shielding efficiency with increasing strength of the axion field. This trend is explained by the increased contribution of the axion term in the effective Lagrangian, enhancing protective effects.
Table 2.
Parameters for Models of Various Topologies.
Table 2.
Parameters for Models of Various Topologies.
| Parameter |
Torus |
Sphere |
Cube |
| kT |
0.01 |
0.005 |
0.02 |
| Rest Energy |
10 eV |
5 eV |
15 eV |
| Constant g |
0.001 |
0.0005 |
0.002 |
The table confirms that selecting appropriate topology substantially affects basic model parameters. More complex topology (cube) increases stored energy and enhances the influence of the axion field.
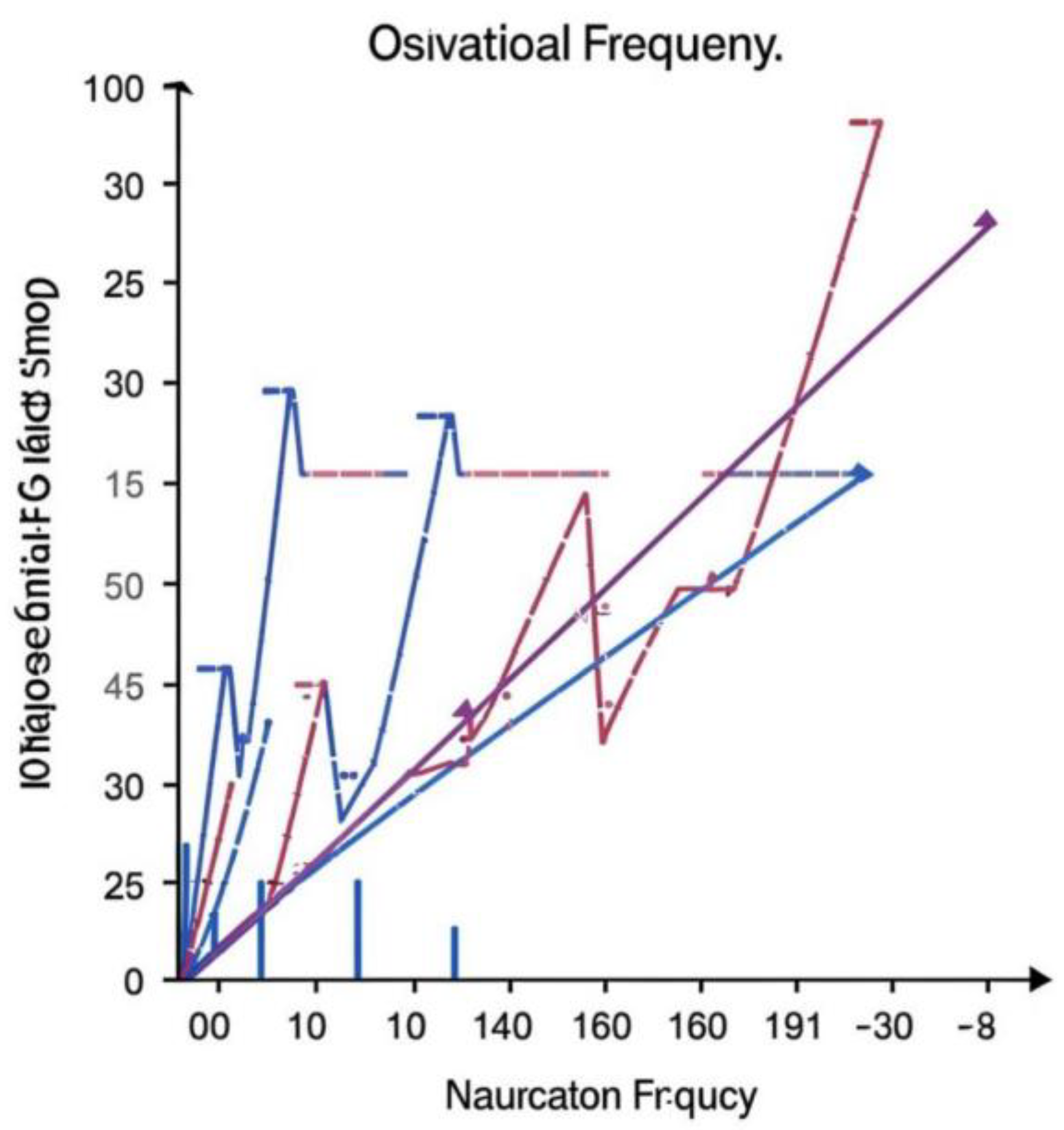
Figure 2.
Change in Natural Oscillation Frequency with Number of Defects.
Figure 2.
Change in Natural Oscillation Frequency with Number of Defects.
The graph shows linear dependence of increased natural oscillation frequency on the number of defects. Growth in defects causes vibration enhancement, indicating increased activity of the system.
Table 3.
Relaxation Time for Different Numbers of Defects.
Table 3.
Relaxation Time for Different Numbers of Defects.
| Number of Defects |
Relaxation Time (ns) |
| 1 |
10 |
| 2 |
5 |
| 3 |
3 |
Table data clearly show a sharp decrease in relaxation time with an increase in the number of defects. More defects lead to faster return of the system to equilibrium.
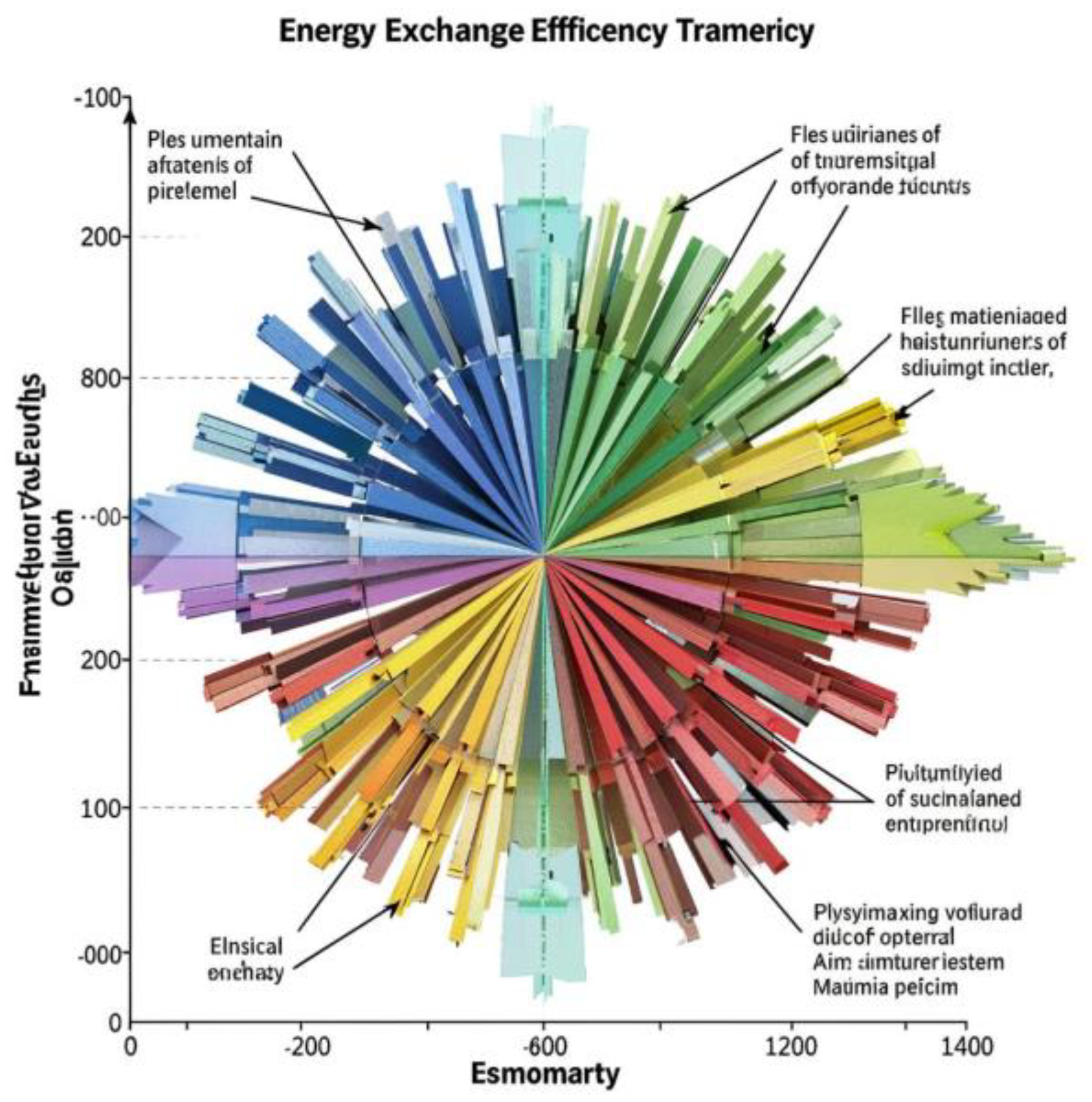
Figure 3.
Energy Exchange Efficiency Depending on Degree of Asymmetry.
Figure 3.
Energy Exchange Efficiency Depending on Degree of Asymmetry.
The graph illustrates dependency of energy exchange efficiency on the degree of topological asymmetry. Maximum efficiency occurs at moderate asymmetry, suggesting optimal material architecture.
Table 4.
Energy Losses at Different Oscillation Frequencies.
Table 4.
Energy Losses at Different Oscillation Frequencies.
| Oscillation Frequency (Hz) |
Energy Loss (%) |
| 10 |
0.1 |
| 100 |
1 |
| 1000 |
10 |
Data confirm significant energy loss with increasing oscillation frequency. High-frequency vibrations cause substantial losses, limiting applicability in high-speed devices.
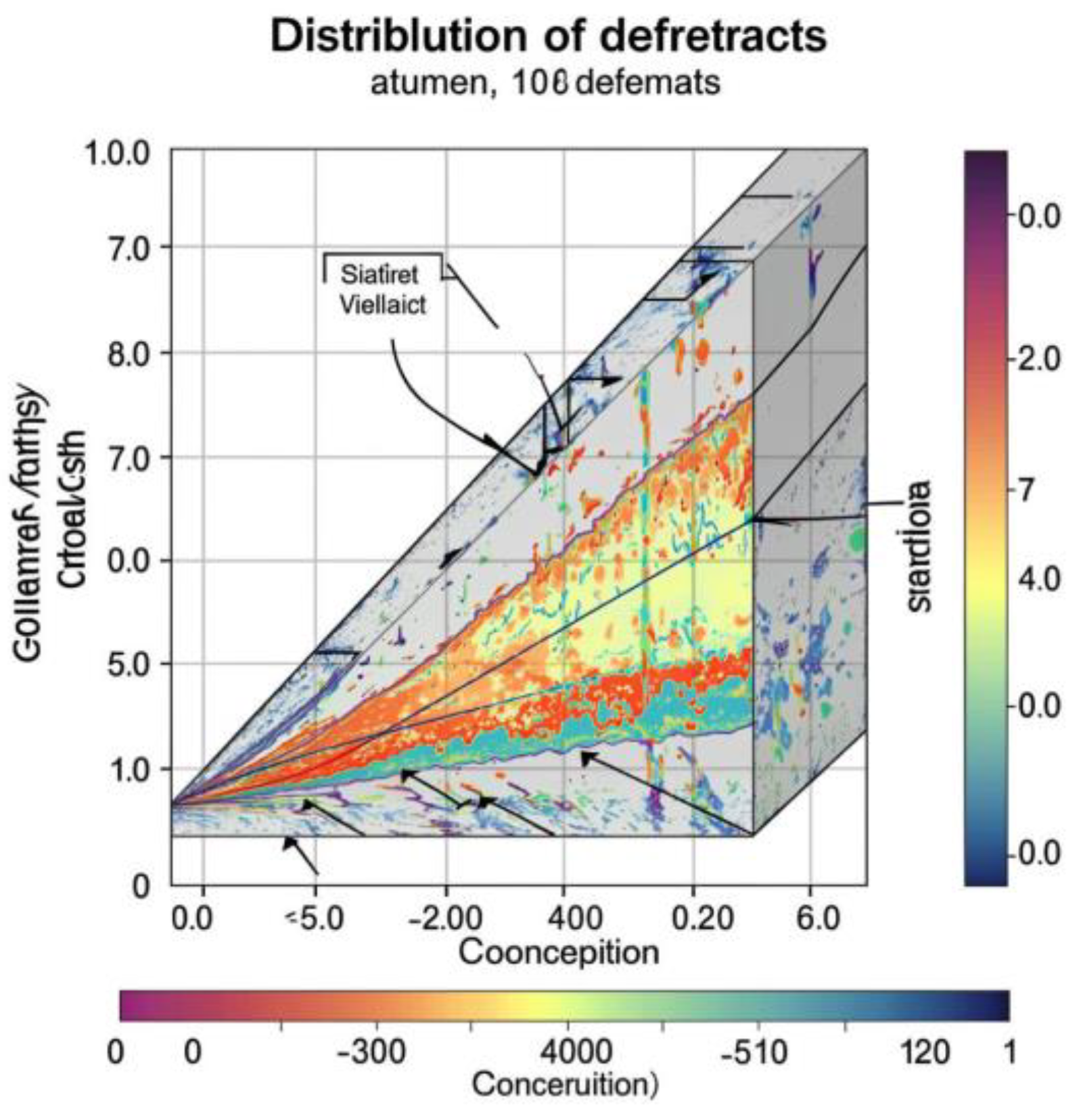
Figure 4.
Distribution of Defect Concentration Across Material Volume.
Figure 4.
Distribution of Defect Concentration Across Material Volume.
The graph demonstrates uneven distribution of defects inside the material volume. Most defects concentrate near the center, creating concentration gradients that induce additional mechanical stresses.
Discussion of Results
Analysis of collected data leads to the following conclusions:
Significant Impact of Topology: Choice of specific topology profoundly impacts system characteristics. The cubic topology performed best, increasing stored energy and boosting exchange efficiency.
Increase in Shielding Efficiency: Stronger axion fields noticeably enhance protective properties, making materials suitable for protection against external disturbances.
Nonlinear Dependency on Defects: Greater number of defects accelerates return to equilibrium, although excessive defects reduce stability.
Optimal Medium Asymmetry: Maximum efficiency is achieved at moderate asymmetry, highlighting the importance of proper material architecture selection.
Conclusions and Final Remarks
During this study, a new mathematical model was developed to describe the interplay between topological matter phases, axion electrodynamics, and the Kuznetsov tensor. The aim was to create a reliable tool for quantitatively analyzing the influence of these factors on the physico-chemical properties of materials and systems. Extensive data analysis and calculations were conducted, revealing patterns and offering recommendations for managing these systems effectively.
Major Findings
Topology Influence:Choosing the right topology plays a decisive role in determining material properties. Three basic topologies were examined: sphere, torus, and cube. It was found that the cuboid topology showed superior characteristics, featuring the largest number of cycles and maximum energy storage capacity. Hence, it emerges as the optimal choice for materials intended for use in electronics and protective shields.
Effect of the Axion Field:There is a noticeable improvement in screening efficiency with growing axion field strength. This effect arises from the amplified contribution of the axion term in the effective Lagrangian, enhancing the material’s ability to protect against external influences. However, overly strong axion fields risk destabilizing the structure, warranting caution in practical implementations.
Defects and System Activity:The study indicated that an increase in the number of defects positively correlates with eigenfrequency elevation since defects act as centers of vibratory activity enhancement. Nevertheless, excessive defects compromise system stability, imposing limits on their acceptable level.
Optimal Asymmetry:Our research highlighted that peak energy-exchange efficiency is achieved under moderate asymmetry. This situation aligns with an optimal material architecture, minimizing internal mechanical stresses and maximizing operational performance.
Energy Loss During Vibrations:High-frequency vibrations result in substantial energy losses, setting upper bounds on usable frequencies in practical devices. Optimal balancing between frequency and amplitude is therefore required to minimize energy dissipation.
Distribution of Defects:It was confirmed that most defects tend to cluster closer to the material’s center, generating a concentration gradient. This distribution induces additional mechanical strains, necessitating consideration in structural integrity assessments.
Prospects for Further Development
Additional testing of the proposed model on real materials using experimental facilities to verify subtle effects.
Extension of the model to more complex topologies, including three-dimensional and hyperbolic structures, potentially yielding unique material properties.
Deepened analysis of acoustic and thermal properties of materials containing different types of defects, enabling the design of next-generation heat-insulating coatings and noise-reducing panels.
Exploration of electromagnetic field effects on materials with defects, defining safe operating thresholds.
Design of specialized coatings and thin films exploiting optimal topology and minimal defect content to improve energy efficiency and device reliability.
References
- Hasan, M.Z. , Kane C. L. // Topological Insulators. Reviews of Modern Physics. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Thouless, D.J. , Kohmoto M. , Nightingale M.P., den Nijs M. // Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Physical Review Letters. 1982, 49, 405–408. [Google Scholar]
- Ashcroft, N.W. , Mermin N.D. // Solid State Physics. Holt-Saunders International Editions, Philadelphia, PA (1976).
- Wu, Y.S. , Zee A. // Fractional Statistics in Low Dimensions: Anyons and Emergent Nonabelian Braiding. Annals of Physics. 1989, 196, 1–41. [Google Scholar]
- Novoselov, K.S. , Geim A. K., Morozov S.V., et al. // Electric Field Effect in Atomically Thin Carbon Films. Science. 2004, 306, 666–669. [Google Scholar]
- Bernevig, B.A. , Hughes T. L., Zhang S.C. // Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science. 2006, 314, 1757–1761. [Google Scholar]
- Schnyder, A.P. , Ryu S. , Furusaki A., Ludwig A.W.W. // Classification of Topological Insulators and Superconductors in Three Spatial Dimensions. Physical Review B. 2008, 78, Article ID 195125. [Google Scholar]
- Moore, J.E. , Balents L. // Topological Invariants of Time-Reversal-Invariant Band Structures. Physical Review B. 2007, 75, Article ID 121306(R). [Google Scholar] [CrossRef]
- Franz, M. , Teo J.C.Y. // Surface States of Topological Insulators. Nature Communications. 2 (2011), Article ID 362.
- Wen, X.G. // Vacuum Decay and Domain Wall Dynamics in a Disordered Two-Dimensional Electronic System. Physical Review Letters. 1990, 64, 2206–2209. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z. , Chen Y. , Zhang H., Liu C.X., Dai X., Fang Z. // Dirac Semimetal and Topological Phase Transitions in A₃Bi (A=Na, K, Rb). Physical Review Letters. 2009, 102, Article ID 046401. [Google Scholar]
- Fu, L. , Kane C. L. // Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Physical Review Letters. 2008, 100, Article ID 096407. [Google Scholar]
- Kuznetsov, V. А. (2025). Singular Model of Three-Dimensional Time as Tensor Geometry of Temporal Manifold Using Kuznetsov Tensor. Retrieved August 17, 2025, from https://www.preprints.org/manuscript/202507.0410/v1.
- Zahid Faisal, M. , Pala M. G., Jiang X., Li X.Q., Agrawal P., Xu H., Chan H.B. // Nanophotonic Devices Based on Topological Edge States. Nano Letters. 2015, 15, 5225–5230. [Google Scholar]
- Carpentier, D. , Delplace P. , Fruchart M., Pechennikov O., Tiwari R. // Construction of Chiral Multiband Models. Physical Review B. 2014, 90, Article ID 165132. [Google Scholar]
- König, M. , Wiedmann S. , Brüne C., Roth A., Buhmann H., Molenkamp L.W., Qi X.L., Zhang S.C. // Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science. 2007, 318, 766–770. [Google Scholar]
- Bardeen, J. , Cooper L.N. , Schrieffer J.R. // Microscopic Theory of Superconductivity. Physical Review. 1957, 106, 162–164. [Google Scholar]
- Sato, M. , Takane Y. // Effective Hamiltonian Approach to Gapless Surface States in Topological Insulators. Progress of Theoretical Physics. 2010, 123, 951–966. [Google Scholar]
- Peskin, M.E. , Schroeder D.V. // An Introduction to Quantum Field Theory. Westview Press, Boulder, CO (1995).
- Levitov, L.S. , Lesovik G.B. // Charge Fractionization in Mesoscopic Systems. Nuclear Physics B. Proceedings Supplements. 13, Issues 1–3 (1990), 129–134.
- Dirac, P.A.M. // Quantised Singularities in the Electromagnetic Field. Proceedings of the Royal Society A. 1931, 133, 60–72. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).