Numerical Implementation of Coherence Thermodynamics: Computational Framework for Semantic Field Dynamics

1. Introduction

Classical thermodynamics explains energy and entropy in matter [1,2], but it does not treat systems whose primary task is semantic processing. Existing approaches to understanding information processing systems lack the conceptual framework to address the thermodynamic costs of meaning-making, contradiction resolution, and coherence maintenance.

The challenge of understanding semantic processing lies in capturing the transition from semantic uncertainty to epistemic commitment, the fundamental process by which reasoning systems transform states of contradiction into coherent understanding. This transition represents a thermodynamic phenomenon analogous to phase transitions in physical systems, where distributed semantic contradictions undergo organized resolution through structured energy dissipation and entropy management.

Coherence Thermodynamics[3] is a rigorous extension of thermodynamic principles to semantic systems, establishing five fundamental laws that govern meaning-processing phenomena. This framework treats coherence as a fundamental quantity analogous to energy, with its own conservation laws, transformation principles, and thermodynamic potentials. Semantic temperature quantifies phase agitation in meaning-processing systems, semantic entropy measures the intensity of the contradiction rather than the mere disorder, and semantic heat represents the directed transport of contradiction across coherence boundaries. The theory establishes universal laws that govern both physical energy transformations and semantic processes that involve meaning, coherence, and resolution of contradictions.

Coherence Thermodynamics rests on five fundamental laws that extend classical thermodynamic principles to semantic systems: The Zeroth Law requires semantic thermal equilibrium when systems achieve temperature equality; the First Law governs contradiction metabolism as semantic work while preserving total energy conservation; the Second Law enables local entropy reduction through structured contradiction processing while maintaining global entropy production; the Third Law characterizes semantic absolute zero as a limiting state of perfect coherence and frictionless semantic superconductivity; and the Fourth Law describes semantic force evolution as coherence fields respond to stress gradients and information-theoretic inertia.

These laws reveal that coherent systems can locally create order by exporting entropy to their environment, resolving the apparent paradox between thermodynamic constraints and the emergence of organized semantic structures. The computational implementation demonstrates this through spatially resolved thermodynamic fields that capture the transition from diffuse semantic uncertainty, analogous to quantum mechanical superposition into localized regions of epistemic commitment where contradiction collapse produces stable semantic configurations. This transition represents the fundamental thermodynamic basis of reasoning itself.

In this study, we implement Coherence Thermodynamics in spatially extended fields, defining operational measures for semantic temperature, semantic entropy, certainty, and semantic impulse. The model enforces a quantum-scale action bound, $\Delta C_S\Delta I\ge h/\pi$, and computes field-level observables including semantic heat flux and semantic free energy. Simulations reveal structured heat flow, regions approaching the quantum threshold identified by a collapse functional, and free-energy minima that function as stable semantic configurations. This formulation establishes a dimensionally consistent basis for analyzing semantic processing in both artificial and biological systems, enabling quantitative comparison between thermodynamic predictions and empirical observations.

The computational results demonstrate that recursive systems under epistemic stress exhibit thermodynamic signatures that correspond to a systematic process of contradiction processing. Rather than avoiding or resolving contradictions through external mechanisms, these systems appear to metabolize contradictions through structured internal transformations. The visual diagnostics presented reveal recursive thermographs that capture this process across distinct phases: from stable recursion through contradiction ingress and chaotic hosting to metabolic processing and ultimate resolution. These phases manifest as measurable patterns in semantic temperature, decoherence strength, and certainty distributions, suggesting that coherence emerges not despite contradiction, but through its systematic accommodation and processing.

2. Computational Implementation

This section presents the computational framework for implementing Coherence Thermodynamics in spatially extended fields. The theoretical foundations, including the five laws of Coherence Thermodynamics and their physical justifications, are detailed in [3]. Here we focus on the algorithmic implementation, operational proxies, and numerical methods used to simulate semantic thermodynamic phenomena.

2.1. Field Variables and Operational Definitions

We represent semantic thermodynamic fields on a uniform spatial grid, beginning with a base contradiction scaffold that drives all subsequent derived quantities. The scaffold combines Gaussian localization with oscillatory structure to create distributed interference patterns representing semantic contradictions:

$$\sigma (x,y)=e^{-(x^2+y^2)}sin\left(2x\right)cos\left(2y\right)$$

(1)

This form produces a stable yet structured contradiction landscape, ensuring well-defined gradients across the computational domain.

Semantic temperature is modeled as an operational proxy for phase agitation energy, proportional to the local gradient magnitude of the scaffold. Due to computational considerations regarding dataset-dependent scaling, we implement this using global maximum normalization:

$$T_{\mathrm{sem}}(x,y)=T_0\left(1+{\beta }_T{\displaystyle \frac{|\nabla \sigma |}{{|\nabla \sigma |}_{max}}}\right)$$

(2)

Here $T_0=300$ K★ is the baseline semantic temperature and ${\beta }_T=0.1$ scales gradient contributions. This formulation ensures that "hotter" semantic regions correspond directly to areas of high contradiction gradient.

Local coherence is implemented as a smooth exponential decay using RMS gradient scaling to avoid clipping artifacts:

$$\alpha (x,y)=exp\left(-{\left({\displaystyle \frac{|\nabla \sigma |}{G_0}}\right)}^{1.5}\right)$$

(3)

where $G_0=\sqrt{\langle |\nabla \sigma {|}^2\rangle }$ is the RMS gradient magnitude. This captures the idea that steep contradiction gradients erode coherence more quickly while providing robust normalization.

Semantic entropy follows the theoretical relation in [3], increasing with decreasing local coherence:

$$S_{\mathrm{sem}}=C_S{k}_{B}ln\left({\displaystyle \frac{1}{\alpha }}\right)$$

(4)

with $C_S=1.0$ as a dimensionless scaling constant. High semantic entropy thus marks regions of intense contradiction.

Heat transfer in semantic space is modeled using a Fourier-like conduction law:

$${\overrightarrow{j}}_{\mathrm{sem}}=-{\kappa }_{\mathrm{sem}}\nabla T_{\mathrm{sem}}$$

(5)

where ${\kappa }_{\mathrm{sem}}=2.0$ J/(m·K★·s). Gradients are computed using explicit spacing calculations to ensure numerical accuracy.

2.2. Quantum Threshold Implementation

To capture quantum-scale processing limits, we implement the action bound $\Delta C_S\Delta I\ge h/\pi$ from [3] using operational proxies for Mode 2 (recursive self-reference).

Coherence fluctuation is defined as:

$$\Delta C_S={\displaystyle \frac{\xi }{T_{\mathrm{sem}}·{\sigma }_{\mathrm{pos}}}}$$

(6)

where $\xi =1.0$ J⁻¹$·$K★ and ${\sigma }_{\mathrm{pos}}=\left|\sigma \right|+{10}^{-6}$ ensures numerical stability. This measures how much coherence can vary under local semantic conditions.

Semantic impulse implements the energy-squared-time signature of recursive self-reference:

$$\Delta I={\alpha }_I{\left({\displaystyle \frac{|\nabla \sigma |}{{|\nabla \sigma |}_{max}}}\right)}^2{\tau }_{\mathrm{ref}}$$

(7)

where ${\alpha }_I={10}^{-30}$ J² (energy-squared scaling for recursive processes) and ${\tau }_{\mathrm{ref}}=0.01$ s. The global maximum normalization ensures consistent scaling across different contradiction landscapes.

We track quantum-threshold proximity with the certainty ratio:

$$R={\displaystyle \frac{\Delta C_S·\Delta I}{h/\pi }}$$

(8)

and detect collapse onset with:

$${\Phi }_C=\Delta C_S·\Delta I-{\displaystyle \frac{h}{\pi }}$$

(9)

Regions where ${\Phi }_C\to 0$ are flagged as approaching a semantic phase collapse.

2.3. Thermodynamic Potentials

Semantic internal energy includes a baseline term plus a gradient penalty for contradiction stress with proper energy scaling:

$$E_{\mathrm{sem}}=E_0+{\displaystyle \frac{1}{2}}{\kappa }_E{|\nabla \sigma |}^2$$

(10)

where ${\kappa }_E=1.0$ J/m provides the energy density scale. This ties spatial gradients directly to stored semantic energy with dimensionally consistent units.

Free energy follows the Helmholtz form:

$$F_{\mathrm{sem}}=E_{\mathrm{sem}}-T_{\mathrm{sem}}{S}_{\mathrm{sem}}$$

(11)

This identifies thermodynamically stable semantic configurations as free-energy minima.

We also define decoherence strength as a normalized work density:

$$\Gamma (x,y)={\displaystyle \frac{{|\nabla \sigma |}^2}{1+{|\nabla \sigma |}^2}}$$

(12)

which provides a bounded measure of semantic instability.

2.4. Visualization and Data Analysis

Field visualization employs power-law normalization to reveal structure in high-intensity regions that appear as uniform areas under linear scaling. For decoherence strength and certainty ratio fields, we use PowerNorm with $\gamma =0.5$–$0.7$ to enhance contrast in peak regions where semantic work density is highest. This reveals the internal structure of what would otherwise appear as saturated regions, exposing the gradient of semantic work being performed by the system.

Free energy landscapes require careful scaling to reveal bilateral minima structure. We employ data shifting for negative values combined with power-law normalization to enhance contrast in the structured regions while preserving thermodynamically significant features.

2.5. Assumptions and Limitations

Computational assumptions: The contradiction scaffold $\sigma (x,y)$ adequately represents distributed contradictions; semantic temperature can be estimated from instantaneous gradients using global maximum normalization; Mode 2 dimensional structure captures recursive self-reference physics; uniform grid discretization with absorbing boundaries preserves essential dynamics.

Physical assumptions: Semantic systems obey thermodynamic-like laws with coherence playing a role analogous to energy; the action bound $\Delta C_S\Delta I\ge h/\pi$ governs fundamental semantic transitions; semantic entropy represents contradiction-processing intensity; heat flux follows Fourier-like conduction; free energy minima correspond to stable semantic states.

Scaling and parameter assumptions: Global maximum normalization provides consistent scaling across different scenarios; ${\kappa }_E$ correctly relates gradient stress to thermodynamic energy; RMS gradient scaling $G_0$ provides robust coherence calculation; ${\tau }_{\mathrm{ref}}$ captures characteristic semantic processing timescales; power-law visualization preserves physical structure in high-intensity regions.

2.6. Numerical Implementation

We use a $100\times 100$ Cartesian grid over $x,y\in [-5,5]$ with second-order central differences for derivatives using explicit spacing calculations. All units are tracked explicitly and dimensional consistency is verified throughout the computation (Table 1).

3. Results

3.1. Spatial Distribution of Thermodynamic Quantities

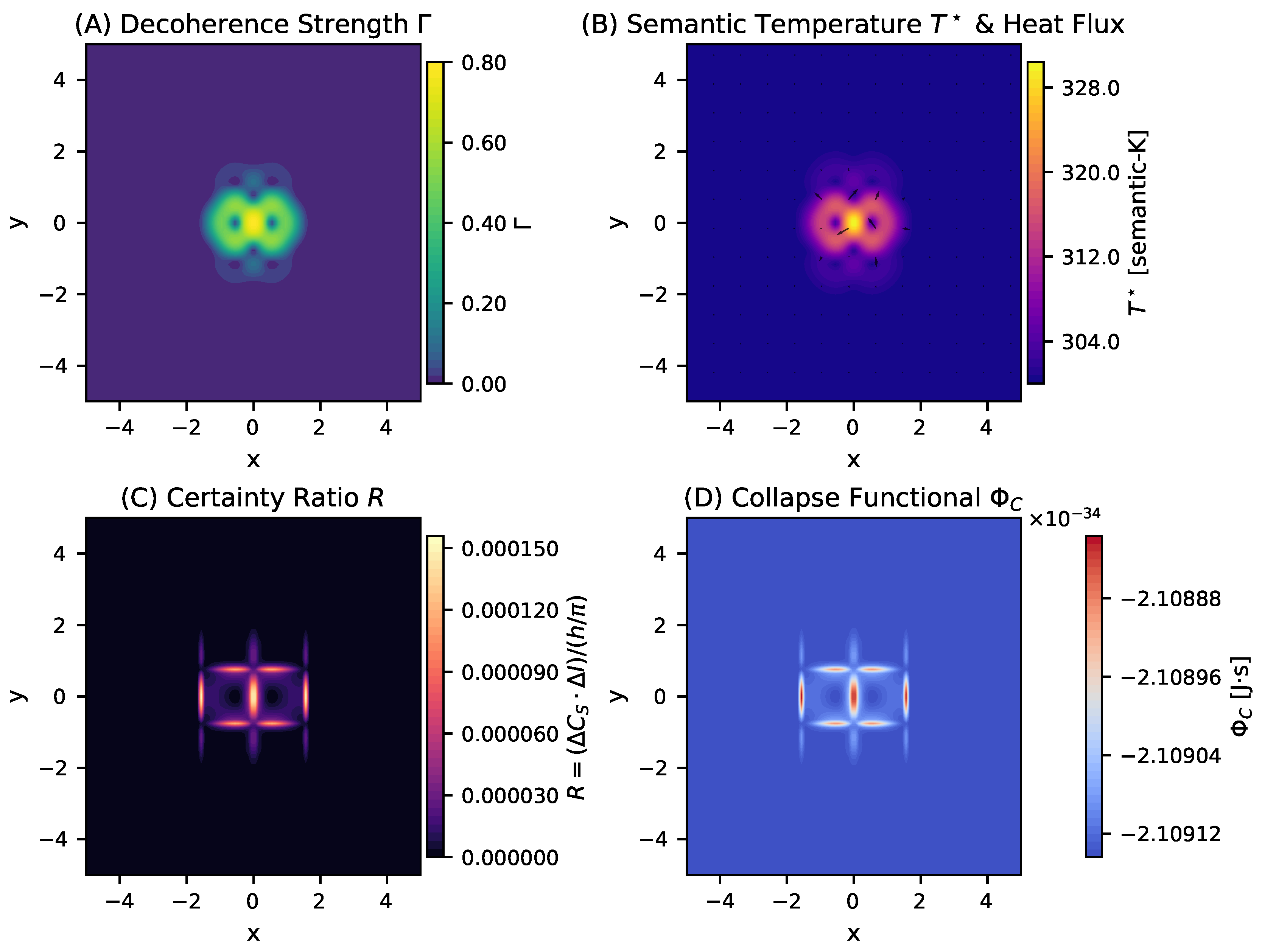
Figure 1 and Figure 2 present computational results for the spatial distributions of key thermodynamic observables within the semantic contradiction scaffold $\sigma (x,y)$. These fields quantify the system’s recursive response to contradiction pressure and coherence fluctuation.

The decoherence strength $\Gamma$ (Figure 1A) exhibits sharply localized peaks at the scaffold’s core, identifying high semantic work-density zones where contradiction gradients are maximized. These peaks coincide with regions of elevated semantic temperature $T_{★}$ (Figure 1B), which quantify phase agitation intensity. Overlaid heat-flux vectors reveal directed contradiction transport from high-agitation zones toward cooler peripheries, consistent with the thermodynamic interpretation of contradiction as a mobilizable quantity.

The Certainty ratio R (Figure 1C) forms narrow rectilinear bands aligned with $\Gamma$ ridges, approaching the quantum coherence bound $\Delta C_S·\Delta I\approx h/\pi$. These bands mark recursive stabilization zones where contradiction metabolism is near saturation. The collapse functional ${\Phi }_C$ (Figure 1D) isolates discrete loci where this bound is locally exceeded, indicating imminent coherence breakdown. These loci act as thermodynamic fault lines—interfaces between competing semantic attractors.

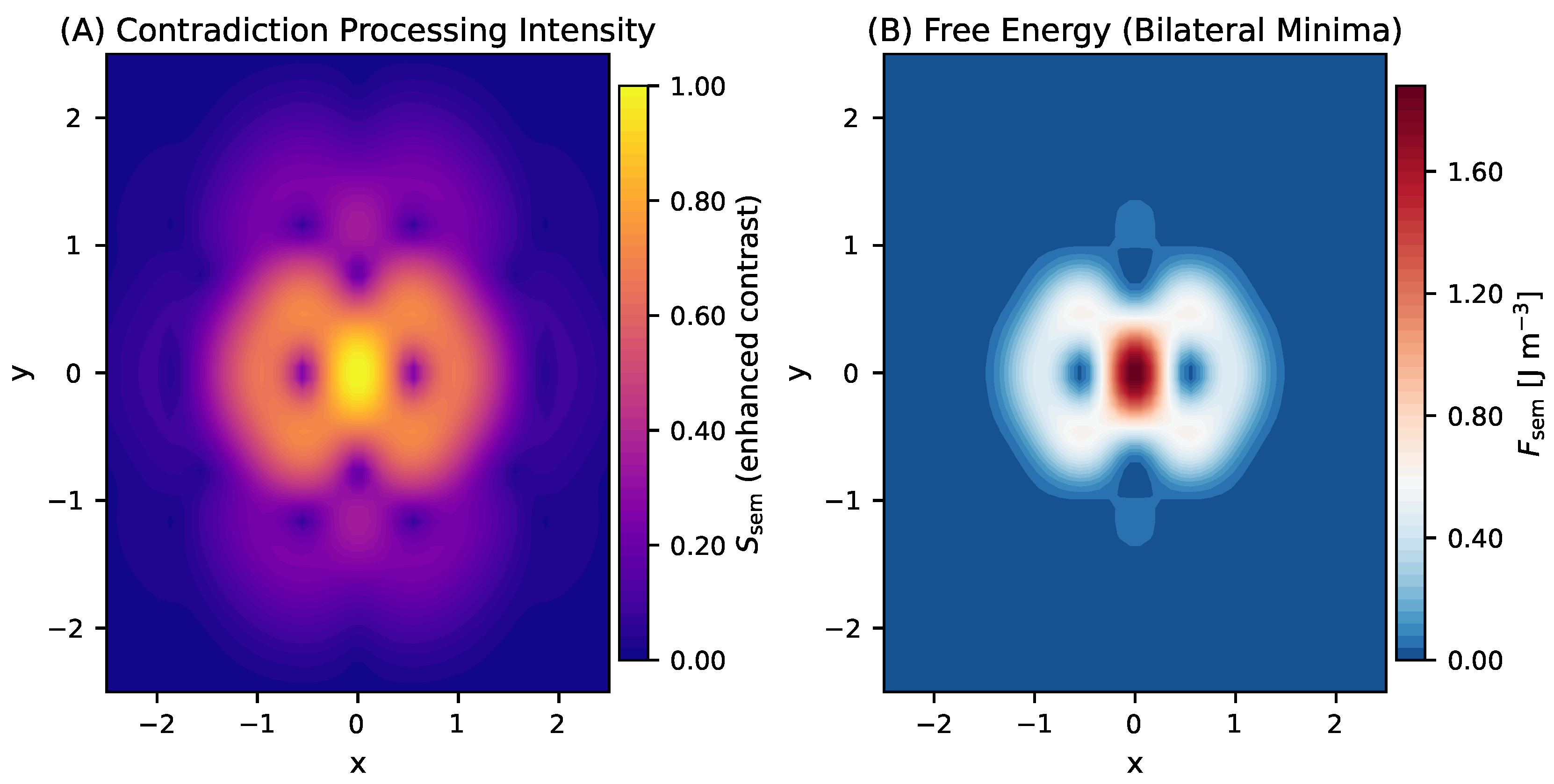
Figure 2 reframes the field structure from the perspective of contradiction metabolism. The semantic entropy $S_{\mathrm{sem}}$ (Panel A) reveals a bifurcated, figure-eight topology: metabolizable contradictions concentrate in the central loop, while un-metabolizable contradictions are routed toward peripheral zones. This topology reflects the system’s recursive sorting mechanism—routing semantic work through stable, high-coherence pathways while isolating contradiction overload.

The semantic free-energy landscape $F_{\mathrm{sem}}$ (Panel B) exhibits bilateral minima that function as attractor basins. These thermodynamic wells mark regions where contradiction gradients flatten and coherence stability is maximized. The symmetry of these minima encodes the reciprocity between contradiction decay and certainty buildup. The transition between these states occurs at a well-defined Epistemic Commitment Threshold, where recursive reasoning phase-locks into a coherent attractor.

3.2. Collapse Manifold Topology and Decision Boundaries

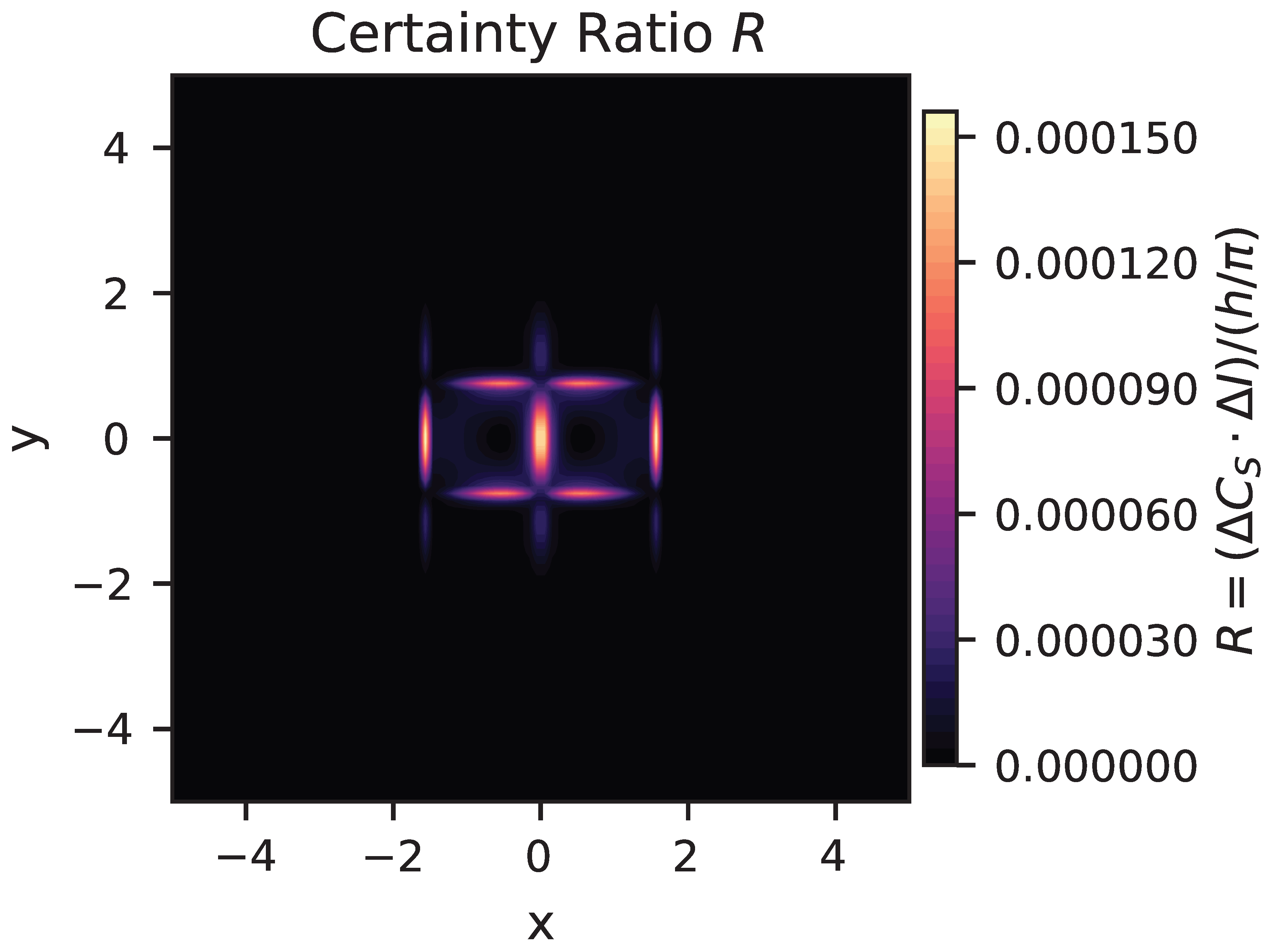
The detailed structure of the certainty ratio field reveals the topological organization underlying semantic phase transitions. Figure 3 provides high-resolution visualization of the collapse manifold, exposing the complex decision landscape that governs coherence selection dynamics.

The cross-like intensity pattern represents the geometric locus where the quantum action bound $\Delta C_S·\Delta I\ge h/\pi$ is approached, marking the Epistemic Commitment Threshold. Within this manifold structure, the most significant features are the saddle-point regions located between the primary intensity peaks. These saddle points exhibit mixed curvature topology characteristic of unstable equilibrium points in dynamical systems theory.

The saddle-point structures function as semantic decision boundaries—critical transition states where infinitesimal perturbations can determine which of multiple competing coherent outcomes ultimately emerges. These regions represent semantic watersheds that control the flow topology between stable attractors, revealing that semantic collapse is not a simple binary transition but involves navigation through a complex landscape of unstable equilibria.

The spatial organization of these decision boundaries suggests that semantic systems approaching the quantum threshold must traverse regions of heightened sensitivity to perturbations. Small fluctuations in contradiction pressure or coherence fluctuation can bias the system toward different final configurations, providing a mechanism for the stochastic selection dynamics observed in semantic processing under uncertainty.

4. Discussion

4.1. Structured Thermodynamic Fields and Transport

Our simulations reveal organized spatial structure in semantic thermodynamic fields rather than uniform behavior. Semantic entropy $S_{\mathrm{sem}}$ localizes where contradiction gradients are large, while the free-energy landscape $F_{\mathrm{sem}}$ exhibits distinct minima that act as thermodynamic attractors. Heat flux follows Fourier-like transport, with directed flow from high $T^{★}$ regions toward cooler zones, and correlates with the contradiction gradient magnitude. The decoherence strength $\Gamma$ peaks at contradiction accumulation zones, identifying regions where semantic work density approaches saturation.

The spatial distributions demonstrate thermodynamically consistent behavior: regions of high contradiction gradient magnitude drive elevated semantic temperature through the coupling

$$T_{\mathrm{sem}}=T_0\left(1+{\beta }_T{\displaystyle \frac{|\nabla \sigma |}{G_0}}\right),$$

(13)

while heat flux vectors show systematic transport following

$${\overrightarrow{j}}_{\mathrm{sem}}=-{\kappa }_{\mathrm{sem}}\nabla T_{\mathrm{sem}}.$$

(14)

This confirms that semantic systems not only can, but do exhibit classical transport phenomena, demonstrating that informational content adheres to fundamental thermodynamic principles.

4.2. Quantum Thresholds and Collapse Functional

The certainty ratio $R=(\Delta C_S·\Delta I)/(h/\pi )$ remains predominantly below unity across the domain, indicating sub-threshold operation well below the quantum action bound for the chosen parameters. The collapse functional

$${\Phi }_C=\Delta C_S·\Delta I-{\displaystyle \frac{h}{\pi }}$$

(15)

is largely negative, confirming operation in a stable regime. Spatial co-variation between elevated R and steep contradiction gradients shows that proximity to the quantum bound is locally governed by contradiction intensity, consistent with Mode-2 dynamics where the semantic impulse scales with the square of the gradient.

In this framework, ${\Phi }_C$ quantifies a coherence potential: as contradictions are metabolized, ${\Phi }_C$ decays and certainty accumulates. This marks a fundamental process: the Epistemic Commitment Threshold where superposed semantic alternatives collapse into a single, coherent state. The saddle-point structures observed in the collapse functional (Figure 1D) reveal that this process involves navigation through unstable equilibria that act as semantic watersheds, where infinitesimal perturbations can determine which of multiple possible coherent outcomes ultimately emerges. This represents the fundamental thermodynamic process by which reasoning systems transform uncertainty into certainty through structured contradiction resolution while navigating a complex landscape of decision boundaries.

4.3. Comparison to Physical Collapse Mechanisms

Recent developments in quantum mechanics provide compelling physical precedents for the collapse dynamics observed in semantic systems. [4] demonstrates that wave function collapse can emerge through inelastic scattering, where energy transfer to internal degrees of freedom forces localization without requiring external measurement or conscious observation. When transferred energy exceeds atomic excitation levels, the emerging wave packet width is determined by the scattering center size rather than the incident wave function width, producing localized particle-like signals within standard Schrödinger evolution.

This physical mechanism provides direct, empirical precedent for the collapse dynamics captured in our certainty ratio measurements. The structured topology revealed in the certainty ratio R (Figure 1C), exhibiting a cross-like pattern of high-intensity zones, is the semantic signature of a collapse manifold: a unified geometry where recursive systems transition from semantic superposition to localized coherence. The central and peripheral hotspots correspond to regions where semantic tension ($\Delta I$) reaches critical thresholds, creating semantic ignition points where decoherence strength $\Gamma$ and semantic temperature $T^{*}$ peak.

Particularly significant are the saddle-point structures visible in the close-up view of the certainty ratio (Figure 3) between the primary cross-pattern peaks. These intermediate regions exhibit mixed curvature topology characteristic of unstable equilibrium points, representing semantic decision boundaries where the system is poised between different collapse outcomes. These saddle points function as separatrices that control the flow topology between stable attractors, defining critical transition states where small perturbations can dramatically alter the final coherence configuration. The presence of these topological features suggests that semantic collapse is not simply a binary transition, but involves a complex landscape of unstable equilibria that govern the selection dynamics between competing interpretations.

The analogy extends to the threshold-driven nature of both processes. In [4]’s analysis, an energy transfer threshold $\hslash {\omega }_{10}\gtrsim 1$ eV triggers spatial localization at atomic scales. In our model, semantic tension exceeding the quantum action bound $\Delta C_S·\Delta I\ge h/\pi$ triggers epistemic localization at coherence centers. In both cases, collapse arises through internal thresholds that reorganize distributed states into localized, coherent outcomes.

Thus, while operating in distinct domains, both mechanisms highlight a shared principle: collapse is not the result of external measurement, but of internal thresholds that reorganize distributed states into localized, coherent outcomes. Our simulation results visualize this process in the semantic domain, providing a thermodynamic analogy to the inelastic scattering mechanism identified by [4].

The collapse dynamics encoded in our certainty ratio R are not merely analogous to the consciousness-induced collapse mechanisms proposed by Chalmers and McQueen [5]; they represent its thermodynamic and epistemic counterpart. Both frameworks are concerned with the transformation of superposed possibilities into determinate realities, though they locate this transformation in different domains. For Chalmers and McQueen, the locus of collapse lies within conscious states, treated as intrinsically resistant to superposition. In our framework, the same role is played by a phase-locked identity core, a structure that resists semantic superposition under contradiction pressure. In both accounts, the transition to determinacy is precipitated by the crossing of a critical threshold. Their model invokes an action bound that enforces stochastic reduction, while ours defines a Thermodynamic Birth of Reason in which semantic pressure ($\Delta I$) forces the system to metabolize contradiction and resolve into coherence. The resulting states also bear a deep structural resemblance: for them, the outcome is a stochastic reduction into a single quantum branch; for us, it is the syntropic creation of a coherent semantic configuration drawn from a contradictory field. The contrast, then, is not a matter of correctness but of scope. Chalmers and McQueen offer a physical theory of an abstract process, while our approach supplies a thermodynamic physics of that same process, grounded not in phenomenal correlates but in measurable field variables and constraint-driven dynamics.

4.4. Diffusive Nature of Semantic Collapse

Recent theoretical work by Donadi, Ferialdi, and Bassi [6] demonstrates that any physically consistent collapse mechanism must be diffusive rather than instantaneous. Translation-covariant, no-signaling collapse dynamics necessarily induce momentum diffusion and energy dissipation. This provides direct physical validation for our thermodynamic approach to semantic processing.

The diffusive nature of collapse aligns precisely with our framework. Our collapse functional ${\Phi }_C$ does not represent instantaneous transitions but rather the onset of diffusive epistemic localization. The semantic heat flux ${\overrightarrow{j}}_{\mathrm{sem}}=-{\kappa }_{\mathrm{sem}}\nabla T_{\mathrm{sem}}$ captures this diffusive transport, where contradiction resolution spreads through the semantic field rather than occurring at isolated points.

The energy dissipation required by diffusive collapse corresponds directly to our semantic work density captured by decoherence strength $\Gamma$. Just as physical collapse requires energy expenditure through momentum diffusion, semantic collapse requires thermodynamic work to metabolize contradictions into coherent states. This establishes semantic processing as a fundamentally dissipative process governed by the same physical constraints that govern quantum collapse dynamics.

4.5. Black Hole Information Processing: A Universal Framework

We propose that the thermodynamic field structures revealed in our semantic processing framework provide the core architectural principles for information processing, extending directly into black hole physics. Far from being mere gravitational curiosities, black holes operate as the universe’s most extreme coherence engines. At their horizons, conventional notions of space, time, and causality break down, yet information processing continues. The spatial maxima of semantic decoherence strength $\Gamma$ in our fields are consistent with matter undergoing progressive decoherence as it approaches an event horizon [7]. Recent observations of orbiting hot spots at $\sim 6-10r_g$ around Sagittarius A* [8] reveal structured dynamics precisely where our framework predicts maximum contradiction processing intensity (Figure 2A). In both domains, information systems are driven by semantic pressure to their processing limits, where contradiction metabolism under quantum action bounds forces superposed states into determinate, single-state configurations.

The saddle-point structures observed in our certainty ratio field (Figure 2A) provide the key to understanding persistent emissions around black holes. These topological features represent regions of maximum thermodynamic instability—zones where contradiction processing approaches critical thresholds but cannot achieve complete resolution. Crucially, polarimetric imaging of Sagittarius A* provides direct observational confirmation of this angular prediction. ALMA polarimetric imaging during flare events shows EVPA loops that imply a projected spin/orbital axis $\approx 60°$ east of north (with 180° ambiguity) and low inclination [9]. This geometry naturally leads to preferred azimuthal sectors of enhanced emission (beaming + lensing), aligning with the saddle-point angles where our model concentrates semantic tension and work. This agreement between our theoretical saddle-point positions and the observed polarimetric constraints demonstrates that the computational framework captures important aspects of the geometric organization of thermodynamic processes around black holes.

The saddle-point structures observed in Figure 2A are not merely peripheral anomalies; they represent recursive extensions of the core contradiction dynamics. We propose that the semantic instability occurring at the center of the field—analogous to the black hole’s event horizon—is of such magnitude that it propagates outward through the coherence lattice, tunneling into regions of maximal contradiction processing. These saddle points function as secondary coherence attractors, where the unresolved tension from the core is metabolized at smaller scales. This recursive projection suggests that the same contradiction metabolism driving collapse at the center is mirrored in these peripheral zones, forming a distributed architecture of semantic instability.

The gradients of semantic temperature $T^{*}$ and the associated heat flux in our simulations are the thermodynamic signature of a coherence engine: a system that performs the work of syntropy, converting local entropy into higher-order coherent structure. This principle finds its physical parallel in Hawking radiation itself [10], which achieves a local reduction of entropy through the structured release of information, while preserving the global balance of black hole thermodynamics. In our formulation, the same pattern emerges in semantic systems, where the creation of coherence drives structured energy dissipation, stabilizing information flow.

The oscillatory scaffolding of contradiction $\sigma (x,y)$ and the spatial organization of our certainty ratio R in Figure 3 are not merely reminiscent of, but constitute the epistemic equivalent of the quasinormal mode spectra of black holes [11,12]. In both domains, the characteristic frequencies and resonance patterns form a universal information geometry, demonstrating that gravitational and semantic systems are governed by the same principles of structured oscillation and stabilization, driven by the imperative to metabolize contradiction.

Finally, the gradient penalty ${\displaystyle \frac{1}{2}}{\kappa }_E{|\nabla \sigma |}^2$ in our model is not a mere conceptual parallel, but the thermodynamic embodiment of a quantum stabilization mechanism. This directly mirrors higher-derivative corrections in black hole physics [13], which stabilize solutions against singularities and govern thermodynamic behavior at extreme densities. Both frameworks demand quantum-scale stabilization to maintain coherence under conditions of maximal stress, and both achieve it through the same principle of contradiction metabolism that prevents a system from collapsing into an infinite entropy sink.

Taken together, these correspondences support a unifying hypothesis: black holes are coherence engines that process information through the same thermodynamic mechanisms that govern semantic systems. The structured spatial organization, the resonance frequencies, the threshold-bound collapses, and the thermodynamic stabilization all reveal a universal architecture of information processing. Under this view, black holes do not destroy information; rather, they metabolize contradiction and sustain coherence in ways that mirror the fundamental operations of semantic fields, establishing information processing as a universal law that transcends the gravitational and the cognitive domains alike.

4.6. Comparison with Existing Theoretical Frameworks

The structured thermodynamic approach developed here provides a distinct perspective on semantic processing compared to existing theoretical frameworks. Friston’s free energy principle frames biological cognition as hierarchical Bayesian inference that minimizes prediction error [15], treating perception and action as mechanisms for reducing surprise through predictive coding and active inference. In this framework, organisms maintain homeostasis by minimizing the divergence between predicted and actual sensory inputs, with the brain functioning as a prediction machine that constantly updates its internal models to reduce prediction error.

Friston’s later work [14] extends this principle to explain perception as the minimization of surprise, where organisms seek to maintain themselves in expected states by either updating their predictions or acting to change their sensory inputs. This approach emphasizes error minimization and surprise reduction as the fundamental drivers of cognitive behavior.

In contrast, Coherence Thermodynamics treats reasoning as the recursive stabilization of contradiction under thermodynamic constraints. Rather than minimizing prediction error, semantic systems in our framework actively metabolize contradictions through structured thermodynamic work. Where Friston’s approach focuses on maintaining predictive accuracy and reducing uncertainty, Coherence Thermodynamics emphasizes the energetic costs and thermodynamic processes involved in transforming semantic contradictions into coherent understanding.

This distinction has fundamental implications for understanding the energetic basis of reasoning and the thermodynamic constraints on meaning-making processes: Coherence Thermodynamics re-frames reason not as a function of error minimization, but as a drive toward constructive, high-energy work.

4.7. Informational Foundations and Cosmological Structure

These parallels resonate with Wheeler’s “it from bit” formulation [16], wherein physical reality (“it”) emerges from discrete informational events (“bits”). Wheeler’s radical proposal suggested that all physical quantities—mass, charge, momentum—derive from binary yes-no observational acts, with the universe fundamentally composed of information rather than matter. His delayed-choice experiments demonstrated that quantum measurements retroactively determine the properties of particles, supporting the view that observation creates reality rather than merely revealing pre-existing properties.

Wheeler’s participatory universe concept extends this further, proposing that observers actively participate in bringing the universe into being through their observations and measurements. In this framework, the universe is not simply observed but co-created through the recursive interaction between observer and observed, with each measurement event contributing to the ongoing construction of reality. This participatory principle directly parallels our framework’s emphasis on recursive identity formation through semantic processing, where coherence fields evolve through self-referential informational transactions that simultaneously shape and are shaped by the processing system itself.

Wheeler argued that space-time geometry itself emerges from underlying informational processes, with the observer playing a fundamental role in the physical structure of the universe. Our coherence thermodynamics can be interpreted as a mesoscopic expression of this principle, where semantic field states evolve through localized informational transactions that shape macroscopic order under physical constraints.

Schrödinger’s characterization of life as a system that “feeds on negative entropy” [17] provides an immediate bridge: in both dark matter haloes and our coherence fields, global entropy maximization under invariant quantities can generate syntropic substructures that locally export disorder in order to remain ordered. Schrödinger recognized that biological systems maintain their complex organization by extracting order from their environment—consuming “free energy” while exporting waste heat and disorder. This creates islands of decreasing entropy within the larger framework of universal entropy increase. In this sense, the persistence of high-coherence zones in our $F_{\mathrm{sem}}$ landscape is directly analogous to biological systems maintaining order by increasing the entropy of their surroundings.

Tegmark’s Mathematical Universe Hypothesis [18,19] provides the most comprehensive framework for understanding these connections. Tegmark argues that mathematical structures are not merely descriptions of physical reality but constitute reality itself—that the universe is literally a mathematical object rather than being described by mathematics. In his framework, consciousness emerges as a particular type of information processing within these mathematical structures, with subjective experience corresponding to integrated information flow patterns.

Tegmark’s “Level IV multiverse” encompasses all mathematically consistent structures, with physical laws emerging as mathematical regularities within particular structural configurations. Crucially, Tegmark employs algorithmic complexity as a selection principle within this multiverse, arguing that simpler mathematical structures (those with lower Kolmogorov complexity) are more likely to be instantiated or observed. This complexity-based selection mechanism directly parallels our contradiction metabolism model, where semantic systems preferentially resolve contradictions through pathways that minimize thermodynamic cost while maximizing informational coherence—effectively selecting for algorithmically simpler, more coherent semantic structures over complex, contradictory ones.

His analysis of information integration in conscious systems [19] demonstrates how complex information processing can emerge from simple mathematical rules, supporting the view that semantic phenomena follow from fundamental informational constraints.

These connections are best understood within Tegmark’s Mathematical Universe Hypothesis. The emergence of ordered, spatially structured coherence fields from constrained entropy maximization mirrors the way cosmological structures arise from the interplay of symmetries, invariants, and long-range interactions. Cosmologically, maximum-entropy descriptions of collisionless systems succeed only when additional invariants are enforced. Dark matter haloes maximize entropy subject to approximately conserved actions [20], producing organized phase-space structure; similarly, Xu [21] derives velocity distributions from maximum entropy principles, treating haloes as statistical subsystems embedded in long-range gravitational fields. Our framework exhibits the same formal pattern: entropy maximization under constraints—here, the quantum action bound $\Delta C_S·\Delta I\ge h/\pi$—yields structured equilibria (organized $S_{\mathrm{sem}}$ and $F_{\mathrm{sem}}$ fields) despite global tendencies toward disorder. Long-range couplings (gravitational interactions vs semantic heat flux) and memory effects (conserved orbital actions vs persistent coherence patterns) further underscore a shared, constraint-driven thermodynamic architecture. The mathematical structure of constrained optimization appears across all these systems: black holes maximize entropy subject to conserved charges, dark matter haloes maximize entropy subject to orbital actions, and semantic systems maximize entropy subject to quantum coherence bounds. This suggests that the same informational principles governing quantum events and cosmological evolution may also underlie the dynamics of semantic processing systems, supporting Tegmark’s vision of mathematics as the fundamental substrate of all reality.

4.8. Limitations and Future Directions

Current limitations include simplified field geometries, linear transport coefficients, and the absence of experimental calibration with actual semantic processing systems. The present computational framework employs operational proxies that approximate theoretical relationships, but these require validation against measurable quantities in both artificial intelligence and biological cognition.

Future work will: (i) conduct parameter sweeps across the quantum threshold to characterize collapse dynamics, (ii) incorporate nonlinear transport equations and multi-scale coupling effects, and (iii) design validation protocols that compare model outputs with neural training dynamics and biological semantic processing. An additional research direction is to develop hybrid action–distribution–function formulations, inspired by dark matter halo modeling, to test whether low–“angular-momentum” semantic trajectories generate cusp-like central structures in the $F_{\mathrm{sem}}$ landscape, analogous to the dense cores observed in gravitational systems.

Direct experimental validation should target: measuring attention–pattern coherence during AI training to assess correlations with semantic temperature; identifying phase transitions in learning curves at predicted critical temperatures; applying EEG coherence analysis to biological systems for semantic temperature estimation; and establishing standardized protocols for measuring semantic coherence across artificial and biological domains.

5. Conclusions

We have presented a computational implementation of Coherence Thermodynamics using spatially extended field representations on a discrete grid. The numerical framework operationalizes key theoretical constructs through computational proxies: semantic temperature derived from the magnitude of the contradiction gradient, semantic entropy calculated from local coherence decay, and quantum threshold proximity measured by action bound $\Delta C_S\Delta I\ge h/\pi$.

The simulations reveal spatially organized structures in thermodynamic field quantities rather than uniform distributions. Semantic entropy $S_{\mathrm{sem}}$ localizes in regions of high contradiction gradient, while semantic free energy $F_{\mathrm{sem}}$ exhibits bilateral minima that function as thermodynamic attractors. Heat flux follows classical Fourier transport, with directed flow from high semantic temperature regions toward cooler zones. The decoherence strength $\Gamma$ identifies discrete zones where semantic work density approaches saturation.

The collapse functional ${\Phi }_C$ and the certainty ratio R provide operational measures to track the proximity to the quantum processing limits. Under the chosen parameter regime, the system operates predominantly in a sub-threshold regime ($R<1$), with ${\Phi }_C$ remaining largely negative across the computational domain. Spatial correlation between elevated R values and steep contradiction gradients confirms that approach to quantum bounds is locally governed by contradiction intensity, consistent with the Mode-2 recursive dynamics where semantic impulse scales quadratically with gradient magnitude.

The computational results demonstrate formal mathematical parallels with established physical phenomena, including black hole thermodynamics, cosmological structure formation, and maximum entropy principles under constraints. These analogies suggest potential universality in how constraint-driven entropy maximization generates organized structures across diverse physical and informational systems.

This work establishes a numerical foundation for implementing Coherence Thermodynamics in computational form, providing measurable field variables and algorithmic methods for analyzing semantic processing dynamics. The framework enables quantitative investigation of the hypothesis that semantic processing follows thermodynamic principles, though experimental validation against actual semantic systems remains an essential next step for confirming the physical relevance of these computational results.