Weibull Distribution with Linear Shape Function

1. Introduction

Without any particular exaggeration, one may say that nearly everything in a lifetime data analysis revolves around the hazard rate function (HRF). Lifetime models (LTMs) are categorized according to the shapes of their HRFs. Special attention is paid to LTMs of “flat-bottomed” HRFs that are commonly named bathtub HRFs. Unfortunately, over time, this name has been used to describe any HRF having a minimum but evidently not being flat-bottomed. The true, i.e. flat-bottomed bathtub hazard rate, is specific to a non-homogeneous population. This population consists of subpopulations of “weak” and “strong” items.

Categorized roughly, LTMs may fall into monolithic or hybrid categories. The most representative monolithic LTMs to be recalled here seem to be the Weibull (W), Gamma (G) and Gamma Weibull (GW). Their failure density functions (FDFs) are

$$f_W\left(t\right)=S_F\left(t-\tau \right){\displaystyle \frac{b}{a}}{\left({\displaystyle \frac{t-\tau }{a}}\right)}^{b-1}exp\left[-{\left({\displaystyle \frac{t-\tau }{a}}\right)}^b\right]\left(t>0\right),$$

(1)

$$f_G\left(t\right)={\displaystyle \frac{1}{a\Gamma \left(c\right)}}{\left({\displaystyle \frac{t}{a}}\right)}^{c-1}exp\left[-\left({\displaystyle \frac{t}{a}}\right)\right],$$

(2)

$$f_{WG}\left(t\right)={\displaystyle \frac{b}{a\Gamma \left(c\right)}}{\left({\displaystyle \frac{t}{a}}\right)}^{bc-1}exp\left[-{\left({\displaystyle \frac{t}{a}}\right)}^b\right],$$

(3)

where $a>0$ is the scale parameter, $b,c>0$ are the shape parameters, $\tau \ge 0$ is the failure free time parameter and $S_F$ is the step function defined as

$$S_F\left(x\right)=1·I\left(x\ge 0\right)+0·I\left(x<0\right).$$

(4)

Please note that (3) LTM came into being by embedding (1) into (2). It makes (3) more flexible than both (1) and (2) owing to the second shape parameter, namely$c$. However, none of LTMs in question is sufficiently flexible to be applicable to non-homogeneous populations. It is because they cannot be bimodal. The reader may check it on their own.

The prime example of hybrid LTM is the compound Weibull (CW) proposed by [48]. Its FDF is given by

$$\begin{array}{ccc}\hfill f_{CW}\left(t\right)& =& \omega {\displaystyle \frac{b_1}{a_1}}{\left({\displaystyle \frac{t}{a_1}}\right)}^{b_1-1}exp\left[-{\left({\displaystyle \frac{t}{a_1}}\right)}^{b_1}\right]+\hfill \\ & +& (1-\omega ){\displaystyle \frac{S_F(t-\tau )b_2}{a_2}}{\left({\displaystyle \frac{t-\tau }{a_2}}\right)}^{b_2-1}exp\left[-{\left({\displaystyle \frac{t-\tau }{a_2}}\right)}^{b_2}\right].\hfill \end{array}$$

(5)

where $a_1,a_2,b_1,b_2>0;\tau \ge 0;\omega \in \left(0,1\right)$.

There is no doubt that (5) can be regarded as an extension of (1) however far-reaching.

As mentioned above, monolithic LTMs are unimodal. In contrast, hybrid LTMs may be bimodal. Of course, they can also be unimodal when (1) or (2), to the great surprise of the analyst, turns out to be inapplicable to a homogeneous population. Struck by the superiority of (5) over (1), (2), (3) one must not overlook the fact that (5) has twice as many parameters than (3). Therefore, employing (5) one should have at its disposal much more input data than employing (3). It is essential to guarantee that (5) and (3) sets of estimates are at the same level of accuracy. We face the problem of equilibrating flexibility and data consumption.

To familiarize ourselves with the problem, let us consider the results of the following simple, but very instructive, Monte Carlo experiment. A set of input data that comprises one hundred samples each of 30 items were drawn from the exponential population. The population scale parameter was set equal to one. Then (1), (2), (3) LTMs were sequentially fitted to the data set. Parameters were estimated with the Maximum Likelihood (ML) Method. Table 1 shows standard deviations of scale parameter estimates.

The (3) LTM produced scale parameter estimates of standard deviation more than five times greater than the (1) LTM did. The explanation is simple. Saying freely, “underfeeding” of the scale parameter took place because the shape parameters have “eaten” most of the input data for their estimation purposes.

In general, no one disputes the need for LTM to be flexible. On the other hand, does LTM need to have as many as 8 parameters? The LTM below, called Kumaraswamy transmuted exponentiated additive Weibull (KTEAW) [66], satisfies the mentioned criterion. Cumulative failure function (CFF) of the KTEAW is defined as

$$F_{KTEAW}\left(t\right)=1-{\left\{1-{\displaystyle \frac{{\left[1-exp\left(-c{t}^d-a{t}^b\right)\right]}^{eg}}{{\left[1+f-f{\left(1-exp\left(-c{t}^d-a{t}^b\right)\right)}^e\right]}^{-g}}}\right\}}^h,$$

(6)

where $\left(t>0;a,c,d,e,f,g,h>0;b>1\right).$

In general, there are currently two techniques to increase flexibility of LTM: In the formula of the failure density function there are embed more parameters or the same parameter are embedded in more than one place. The reader is prompted to compare (1) with (2). The Weibull distribution turned out to be a little more flexible than the Gamma distribution in Monte Carlo experiments.

The shape parameter can be called static in a sense that it shapes the LTM identically at each time point. In this paper, we will be able to shape LTM dynamically owing to the following modification: we replace the shape parameter with the shape function. This is an innovative idea. The subject of modification, of course, will be the Weibull LTM further named the Weibull distribution with shape function (WDSF). The CFF and FDF take forms:

$$F\left(t\right)=1-exp\left[-{\left({\displaystyle \frac{t}{a}}\right)}^{w\left(t\right)}\right],$$

(7)

$$f\left(t\right)={\displaystyle \frac{w\left(t\right)}{a}}·{\left({\displaystyle \frac{t}{a}}\right)}^{w\left(t\right)-1}·e^{-{\left({\displaystyle \frac{t}{a}}\right)}^{w\left(t\right)}}+w^{\prime }\left(t\right)·ln\left({\displaystyle \frac{t}{a}}\right)·{\left({\displaystyle \frac{t}{a}}\right)}^{w\left(t\right)}·e^{-{\left({\displaystyle \frac{t}{a}}\right)}^{w\left(t\right)}}.$$

(8)

The above FDF is a sum of two components. This is a unique property of the LTM in question. Although born as a monolithic LTM the WDSF turns out to be hybrid-like LTM. Please note that WDSF is free of the fraction parameter $\omega$, which is a data guzzler in (5). As it is easy to guess, we, further in this paper, consider the simplest version of WDSF that involves a linear shape function.

By the end of this section, let us return to the very origins of the reliability domain. Let us recall two books published by reliability pathfinders of that time. These are [39] and [46]. A device stops working properly, not because the Finger of Fate points it out and says “fail”. It does it because physical failure process reached its critical level. In mentioned books, commonly used LTM have assigned a particular mathematical failure mechanism or process.

For instance, both books assign the Weibull LTM to the model of weakest link of the chain of elements forming a very long series reliability structure. This point of view appears to be timeless. Therefore, in this paper we have the courage to extend the Weibull LTM assigning the following failure process: As time flows and wear-out process advances, series reliability structure steadily elongates causing device reliability to decrease. Referential mathematical consideration will be presented in Section Properties of Weibull distribution with shape function.

The main goal of our work is to complement the literature on the theory of reliability models by introducing a new distribution with a linear shape function, which is a modification of the Weibull LTM. The additional goal of our paper is to define an estimation method that measures the absolute values of the differences between the empirical and theoretical reliability functions (RF) (see Section Estimation methods).

The rest of the paper is organized as follows. Section A review of modified Weibull distributions is devoted to the review of modified Weibull distributions. The properties of the two-version WDSF such as the CFF, RF, FDF, HRF, hazard rate average function (HRAF), quantile (Q) and pseudo-random number generator (PRNG) are described in Section Properties of Weibull distribution with shape function. Used estimation methods are described in Section Estimation methods. Illustrative examples of applicability and flexibility of the WDSF are presented in Section Applications. Concluding remarks are provided in Conclusions. CFF formulas of bimodal LTMs defined with 5–8 parameters and having a bathtub HRF are provided in Appendix A. As the popularity of the R environment has increased significantly recently, main properties of the new distribution have been implemented in R software [75]. Their full codes are in Appendix B.

2. A Review of Modified Weibull Distributions

Generalized Weibull distributions can be constructed in many ways. The first, and in our opinion, the most important way is to define distributions with the Weibull distribution as their special case (including a mixture of two or more Weibull variables). Other ways are i.e.: adding a constant to the hazard rate of the Weibull model; transformations (linear, inverse or log) of the Weibull random variable; transformations of the CFF or survival function of the Weibull models in such a way that the new models remains a CFF or survival function. More details can be found in [54].

By reviewing the statistical literature, we found 165 generalized Weibull distributions with 2 – 8 parameters. Among them, four distributions have a domain different from $t>0$. There are: reflected Weibull distribution [26] defined for $t<0$ as well as the Log-Weibull [41]; [11], modified odd Weibull Normal [25] and extended odd Weibull normal [7] distributions defined for $t\in R$.

In the rest of the Section, we will focus on such generalized Weibull distributions, for which the Swedish research’s distribution is their special case. In this case, the large family of generalized Weibull distributions reduces to 71 distributions with 3–8 parameters, named by the authors as modified Weibull distributions.

Modified Weibull distributions are divided into six groups, according to the number of their parameters. The list of these models is presented below. Information on hazard rate function shapes is provided in the superscript (¹unimodal, ²increasing, ³decreasing, ⁴bathub). Pseudo-bimodal lifetime models with bathtub hazard rate function are in underline (22 models). Bimodal lifetime models with bathtub hazard rate function are in bold (7 models) and their CFFs are presented in Appendix A.

The group I includes 19 models with three parameters. There are: generalized gamma or gamma Weibull¹⁻⁴ [87], generalization of gamma Weibull¹⁻⁴ [88], exponentiated Weibull¹⁻⁴ [60], Generalized Weibull¹⁻⁴ [61], exponentiated Weibull¹⁻⁴ [62], power generalized Weibull¹⁻⁴ [20], modified Weibull extension²⁻⁴ [95], modified Weibull²⁻⁴ [52], Marshall-Olkin Extended Weibull¹⁻⁴ [40], extended Weibull type^1,4 [15], generalized power Weibull²⁻⁴ [65], Extended Weibull¹⁻⁴ [96], Sarhan and Zaindin’s Modified Weibull^2,3 [78], Weibull Geometric¹⁻⁴ [23], transmuted Weibull¹⁻⁴ [16], complementary Weibull geometric¹⁻⁴ [91], Alpha power Weibull¹⁻⁴ [63], MIT Weibull¹⁻⁴ [55] and Semi Modified Alpha Power Weibull Distribution [18].

The group II includes 18 models with four parameters. There are: four-parameter generalized gamma¹⁻⁴ [42], additive Weibull²⁻⁴ [93], Generalized Modified Weibull^1,2,4 [24], Kumaraswamy Weibull¹⁻⁴ [27], Exponentiated Generalized Gamma^1,4 [28], exponentiated modified Weibull¹⁻⁴ [36], Transmuted modified Weibull² [50], Exponentiated transmuted Weibull²⁻⁴ [34], Generalized Weibull- Exponential [77]¹⁻³, Weibull Lomax^2,3 [89], generalized power generalized Weibull¹⁻⁴ [80], Generalization of Generalized Gamma¹⁻⁴ [84], Weibull Lomax²⁻⁴ [69], additive Chen-Weibull^2,4 [90], Poisson modified Weibull¹⁻⁴ [2], modified power generalized Weibull¹⁻⁴ [83], Generalized New Extended Weibull [13] and new modified exponentiated Weibull (NMEW) [74]^2,4.

The group III includes 27 models with five parameters. There are: Beta modified Weibull¹⁻⁴ [86], Kumaraswamy generalized gamma¹⁻⁴ [73], beta generalized Weibull¹⁻⁴ [85], Transmuted Exponentiated Modified Weibull^2,3 [38], Beta Generalized Gamma¹⁻⁴ [29], transmuted additive Weibull^2,4 [37], Exponentiated Kumaraswamy Weibull¹⁻⁴ [35], new modified Weibull²⁻⁴ [10], Kumaraswamy modified Weibull¹⁻⁴ [31], beta transmuted Weibull¹⁻³ [70], McDonald Weibull¹⁻⁴ (McW)[30], Exponentiated Transmuted Modified Weibull^1,2.4 [71], exponentiated generalized modified Weibull^2,4 [17], gamma generalized modified Weibull[67], generalized modified Weibull geometric⁴ [21], additive modified Weibull²⁻⁴ [44], transmuted exponentiated Weibull geometric¹⁻⁴ [76], transmuted new generalized Weibull²⁻³ [51], Burr XII modified Weibull¹⁻⁴ [56], log-logistic modified Weibull^1,2,4 [68], Kumaraswamy alpha power Weibull¹⁻⁴ [57], exponentiated additive Weibull¹⁻⁴ (EAW) [9]; [4], generalized extended exponential Weibull¹⁻⁴ [82], generalized Weibull generalized exponential [19]¹⁻², new generalized modified Weibull¹⁻⁴ [8] and improved modified Weibull^3,4 [47].

The group IV includes 7 models with six parameters. There are: the mixture of two Weibull⁴ [48], McDonald modified Weibull¹⁻⁴ (McMW) [58], McDonald extended Weibull¹⁻⁴ (McEW) [43], Additive Weibull log logistic¹⁻⁴ [45], underbarBeta exponentiated modified Weibull¹⁻⁴ [81], exponentiated power generalized Weibull binomial¹⁻⁴ [6], and McDonald Generalized Power Weibull¹⁻⁴ (McGPW) [79].

Concluding the review of modified Weibull distributions, we would like to mention two distributions with seven and eight parameters, respectively. Kumaraswamy transmuted exponentiated modified Weibull¹⁻⁴ (KTEMW) with 54 special cases forms group V [5]. Kumaraswamy transmuted exponentiated additive Weibull¹⁻⁴ (KTEAW) [66] with 79 special cases (including KTEMW) forms group VI.

3. Properties of Weibull Distribution with Shape Function

The main goal of the paper is to present the two-version Weibull distribution with the shape function previously denoted as WDSF. This section describes its properties such as CFF, RF, FDF, HRF, hazard rate average function (HRAF), quantile (Q), and pseudorandom number generator (PRNG). Both versions of our model will be used in Section Applications.

We assume that the device of our interest has a long series reliability structure. It makes the real lifetime distribution close to the Weibull distribution. The formula below is the Weibull LTM with the elongation coefficient of the device’s reliability structure.

$$R\left(t\right)=e^{-{\left({\displaystyle \frac{t}{a}}\right)}^{b}N\left(t\right)}$$

We impose two weak conditions on $N\left(t\right)$ with $dN\left(t\right)/dt\ge 0;t\in R^{+}$ and $N\left(0\right)=1$. Owing to such weak conditions, a wide scope open itself for defining $N\left(t\right)$ functions not only of reasonable forms but also of monstrous ones. One reasonable form is $N\left(t\right)={\left(t/a\right)}^{ct}$ because it introduces only one parameter into the Weibull LTM and therefore equilibrates flexibility and data consumption. Thus, we get:

$$R\left(t\right)=e^{-{\left({\displaystyle \frac{t}{a}}\right)}^b·{\left({\displaystyle \frac{t}{a}}\right)}^{ct}}=e^{-{\left({\displaystyle \frac{t}{a}}\right)}^{b+c·t}·}$$

Definition 1.

Let $w\left(t\right)$ from (7) or (8) be a linear shape function with two parameters given by $w\left(t;b,c\right)=b+ct$ then the CFF of the Weibull distribution with linear shape function in the first version (WDSF^I) is defined as

$$F^I\left(t;\mathit{\vartheta }\right)=1-exp\left[-{\left({\displaystyle \frac{t}{a}}\right)}^{b+ct}\right]\left(t>0\right),$$

(9)

where $\mathit{\vartheta }=\left(a,b,c\right)$, $a>0$ is the scale parameter, $b>0,c\ge 0$ are the shape parameters and ${\displaystyle \frac{b}{ac}}\ge -{\displaystyle \frac{t}{a}}\left[1+ln\left({\displaystyle \frac{t}{a}}\right)\right]$ (see the proof of Theorem 2). If $c=0$ then we get the Weibull distribution.

Definition 2.

Let $w\left(t\right)$ from (7) or (8) be a linear shape function with three parameters given by $w\left(t;b,c,\tau \right)=b+c{\left(t-\tau \right)S}_F\left(t-\tau \right)$ then the CFF of the Weibull distribution with linear shape function in the second version (WDSF^II) has the form

$$F^{II}\left(t;\mathit{\theta }\right)=1-exp\left[-{\left({\displaystyle \frac{t}{a}}\right)}^{b+c{\left(t-\tau \right)S}_F\left(t-\tau \right)}\right],$$

(10)

where $\mathit{\theta }=\left(a,b,c,\tau \right)$, $\tau \ge 0$ is the failure free time parameter, $S_F$ is the step function (4) and ${\displaystyle \frac{b-\tau }{ac}}\ge -{\displaystyle \frac{t}{a}}\left[1+ln\left({\displaystyle \frac{t}{a}}\right)\right]$ (see the proof of Theorem 2). If $\tau =0$ then we get the first vesion of our proposal.

Theorem 1.

The RFs of the WDSF^I and WDSF^II are defined, respectively, as

$$R^I\left(t;\mathit{\vartheta }\right)=exp\left[-{\left({\displaystyle \frac{t}{a}}\right)}^{b+ct}\right],$$

(11)

$$R^{II}\left(t;\mathit{\theta }\right)=exp\left[-{\left({\displaystyle \frac{t}{a}}\right)}^{b+c\left(t-\tau \right)S_F\left(t-\tau \right)}\right].$$

(12)

Proof of Theorem 1.

The proof based on the RF definition is trivial. □

Theorem 2.

The FDFs of the WDSF^I and WDSF^II are respectively given by

$$f^I\left(t;\mathit{\vartheta }\right)=exp\left[-{\left({\displaystyle \frac{t}{a}}\right)}^{b+ct}\right]{\left({\displaystyle \frac{t}{a}}\right)}^{b+ct-1}\left[{\displaystyle \frac{b+ct}{a}}+{\displaystyle \frac{tc}{a}}ln\left({\displaystyle \frac{t}{a}}\right)\right],$$

(13)

$$f^{II}\left(t;\mathit{\theta }\right)=exp\left[-u\left(t;\mathit{\theta }\right){\displaystyle \frac{t}{a}}\right]u\left(t;\mathit{\theta }\right)\left[{\displaystyle \frac{b+c\left(t-\tau \right)S_F\left(t-\tau \right)}{a}}+{\displaystyle \frac{{ctS}_F\left(t-\tau \right)}{a}}ln\left({\displaystyle \frac{t}{a}}\right)\right],$$

(14)

where $u\left(t;\mathit{\theta }\right)={\left({\displaystyle \frac{t}{a}}\right)}^{b+c\left(t-\tau \right)S_F\left(t-\tau \right)-1}$.

Proof of Theorem 2.

By computing the derivatives based on (9) and (10) with respect to the lifetime t, we easily obtain formulas (13) and (14). Recall that $t,a,b,c>0$ and the formulas (13)-(14) are non-negative.

Let $z=t/a$, then we have from (13)

$${\displaystyle \frac{b}{a}}+cz+czln\left(z\right)\ge 0\Rightarrow {\displaystyle \frac{b}{ac}}\ge -z\left[1+ln\left(z\right)\right].$$

Let $t-\tau \ge 0$, then we have from (14)

$${\displaystyle \frac{b+c\left(t-\tau \right)}{a}}+{\displaystyle \frac{ct}{a}}ln\left({\displaystyle \frac{t}{a}}\right)\ge 0\Rightarrow {\displaystyle \frac{b-\tau }{ac}}\ge -z\left[1+ln\left(z\right)\right]$$

□

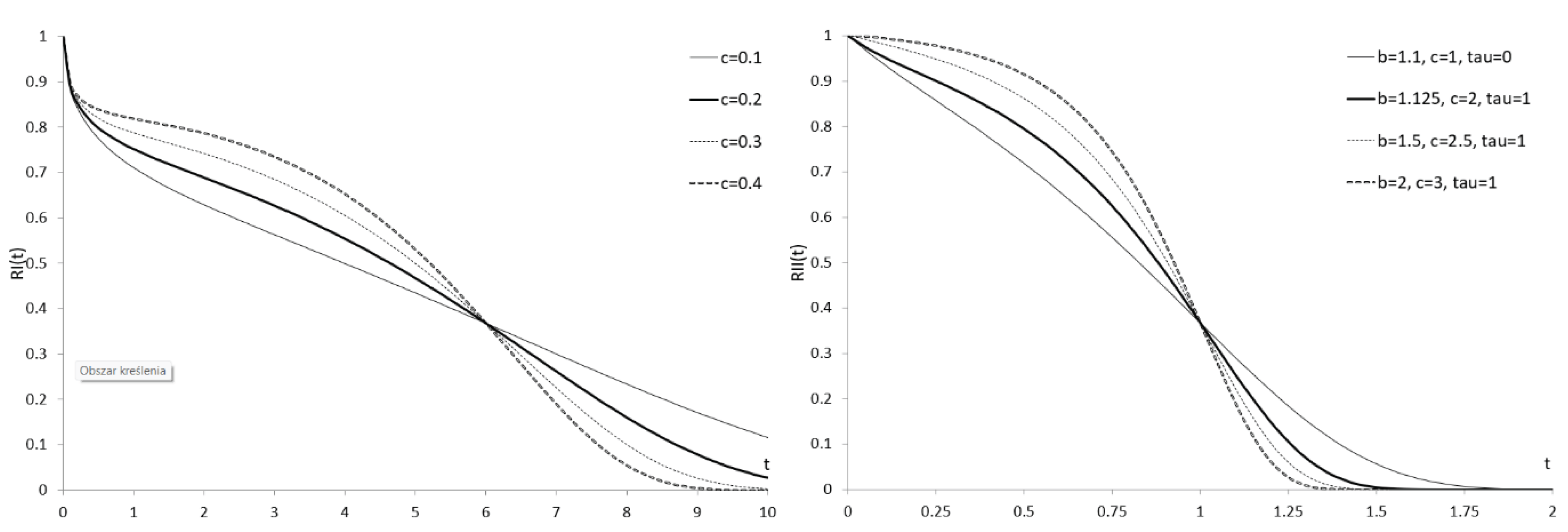
Figure 1 shows the RF of the WDSF^I and WDSF^II. Pseudo-bimodality or bimodality is visible here. The R codes (R Core Team 2021) for calculating the RF values of the WDSF^II are provided in Appendix B.

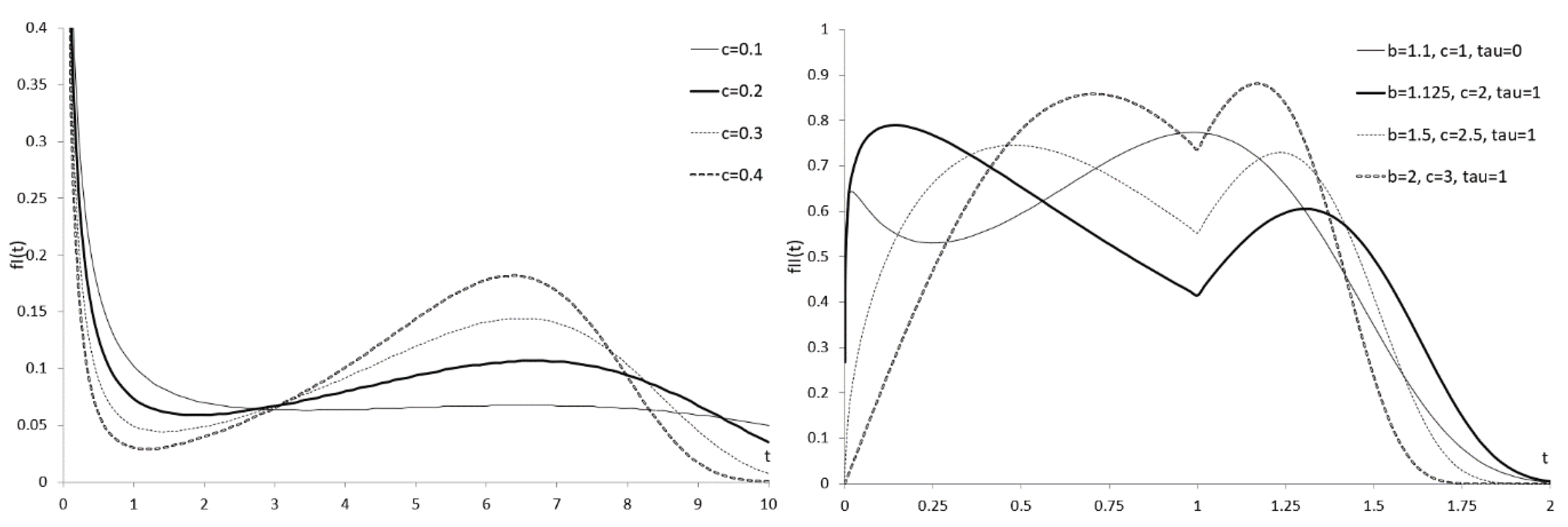
Figure 2 shows the FDF of the WDSF^I and WDSF^II. We see the pseudo-bimodality (on the left) and bimodality (on the right). The R codes for calculating the FDF values of WDSF^II are provided in Appendix B.

Theorem 3.

The HRFs of the WDSF^I and WDSF^II have respectively form

$$h^I\left(t;\mathit{\vartheta }\right)={\left({\displaystyle \frac{t}{a}}\right)}^{b+ct}\left[{\displaystyle \frac{b+ct}{t}}+cln\left({\displaystyle \frac{t}{a}}\right)\right],$$

(15)

$$h^{II}\left(t;\mathit{\theta }\right)=\left[{\displaystyle \frac{b+c\left(t-\tau \right)S_F\left(t-\tau \right)}{t}}+c{S}_F\left(t-\tau \right)ln\left({\displaystyle \frac{t}{a}}\right)\right]{\left({\displaystyle \frac{t}{a}}\right)}^{b+c{\left(t-\tau \right)S}_F\left(t-\tau \right)}.$$

(16)

Proof of Theorem 3.

The proof based on the HRF defintion is trivial. □

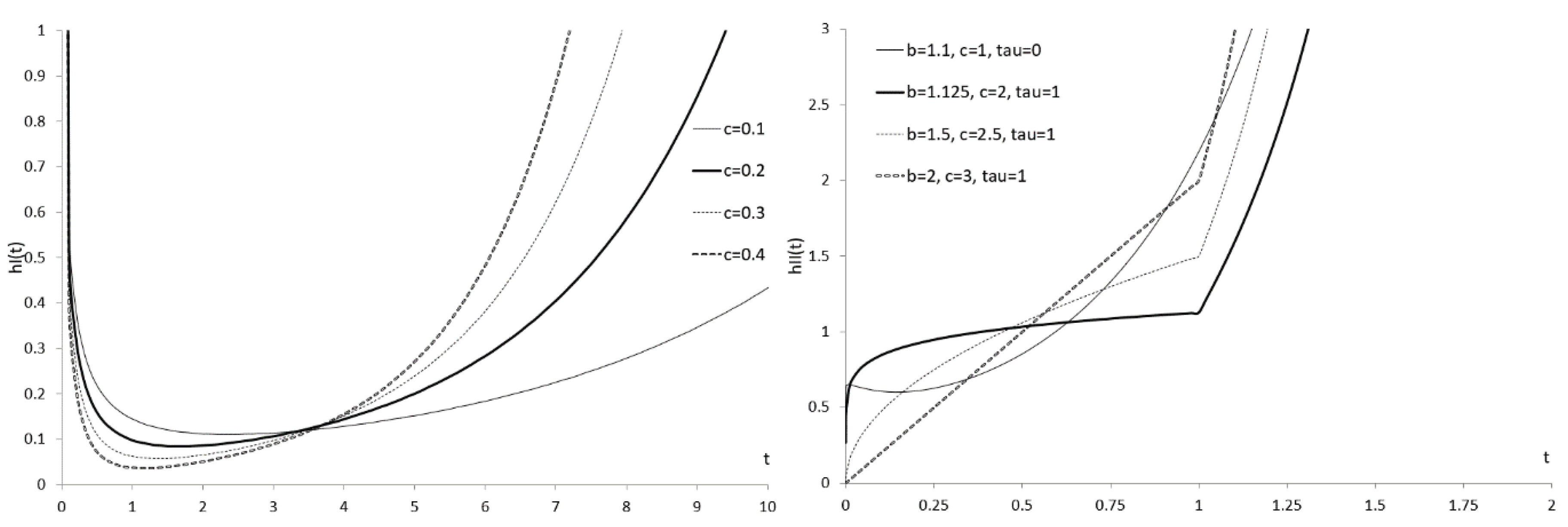
Figure 3 shows the bathtub HRF of the WDSF^I and WDSF^II. The curves flatten as c decreases. The R codes for calculating the HRF values of WDSF^II are provided in Appendix B.

Theorem 4.

The HRAFs of the WDSF^I and WDSF^II are respectively defined as (Barlow and Proschan 1996)

$${ha}^I\left(t;\mathit{\vartheta }\right)={\displaystyle \frac{1}{t}}{\left({\displaystyle \frac{t}{a}}\right)}^{b+ct},$$

(17)

$${ha}^{II}\left(t;\mathit{\theta }\right)={\displaystyle \frac{1}{t}}{\left({\displaystyle \frac{t}{a}}\right)}^{b+c{\left(t-\tau \right)S}_F\left(t-\tau \right)}.$$

(18)

Proof of Theorem 4.

The proof based on the formula $ha\left(t\right)=-\left(1/t\right)ln\left[R\left(t\right)\right]$ is trivial. □

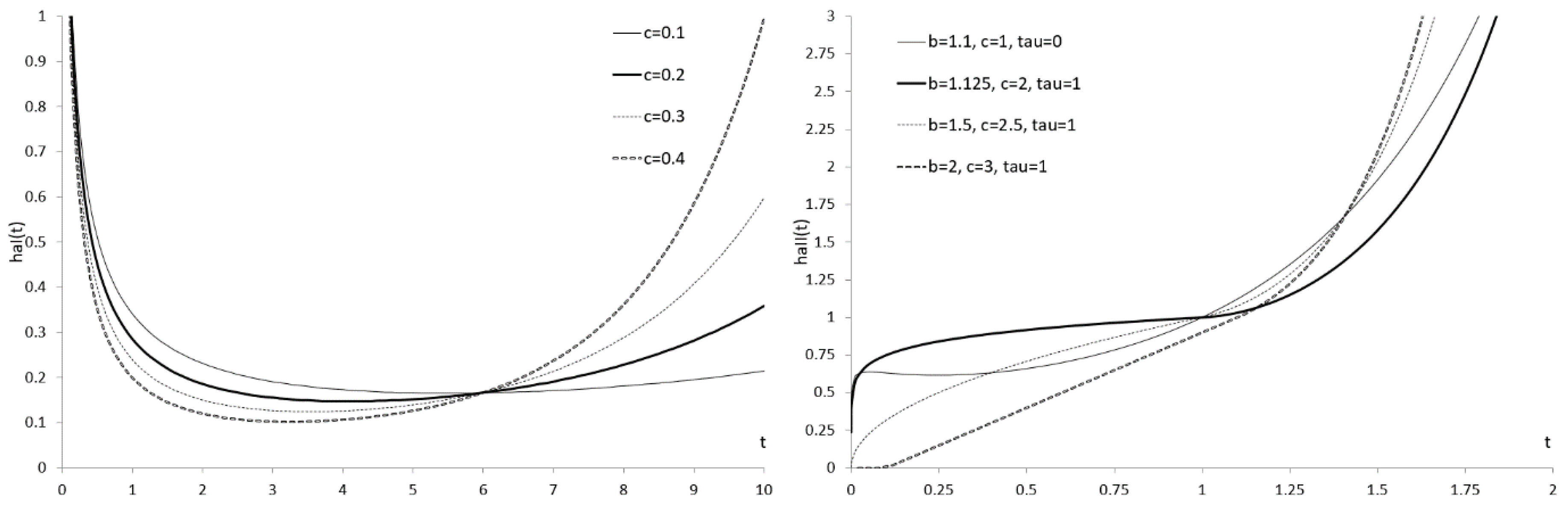
Figure 4 shows the bathtub HRAF of the WDSF^I and WDSF^II. HRAF curves are flatter than HRF curves. The R codes for calculating the HARF values of WDSF^II are provided in Appendix B.

Theorem 5.

Let $0<p<1$. The Qs $q_p^I$ and $q_p^{II}$ of the WDSF^I and WDSF^II are respectively solutions of the equations

$${\left({\displaystyle \frac{q_p^I}{a}}\right)}^{b+c{q}_p^I}+ln\left(1-p\right)=0,$$

(19)

$${\left({\displaystyle \frac{q_p^{II}}{a}}\right)}^{b+c\left(q_p^{II}-\tau \right)S_F\left(q_p^{II}-\tau \right)}+ln\left(1-p\right)=0.$$

(20)

Proof of Theorem 5.

The proof based on (9) and (10) is easy. □

The R codes for calculating the $q_p^{II}$ values of WDSF^II are provided in Appendix B.

Theorem 6.

Let $R\sim Unif\left(0,1\right)$, $T^I$ and $T^{II}$ follow the WDSF^I and WDSF^II, respectively. We can obtain the $T^I$ and $T^{II}$ in two ways.

The first way. The $T^I$ and $T^{II}$ are respectively solutions of the equations

$${\left({\displaystyle \frac{T^I}{a}}\right)}^{b+c{T}^I}+ln\left(1-R\right)=0,$$

(21)

$${\left({\displaystyle \frac{T^{II}}{a}}\right)}^{b+c\left(T^{II}-\tau \right)S_F\left(T^{II}-\tau \right)}+ln\left(1-R\right)=0.$$

(22)

The second way. The algorithm for obtaining the $T^I$ and $T^{II}$ is as follows:

1.

Let $\epsilon ={10}^{-10}$, $k=0$, $T_0^I=0,T_0^{II}=0$.

2.

Let $k=k+1$

3.

$T_{k+1}^I={a\left[-ln\left(R\right)\right]}^{{\left[b+c{T}_k^I\right]}^{-1}}$, $T_{k+1}^{II}={a\left[-ln\left(R\right)\right]}^{{\left[b+c{S}_F\left(T_{k+1}^{II}-\tau \right)\left(T_k^{II}-\tau \right)\right]}^{-1}}$.

4.

If $\left|T_{k+1}^I-T_k^I\right|\ge \epsilon$, $\left|T_{k+1}^{II}-T_k^{II}\right|\ge \epsilon$ then go to step 2.

5.

Return $T^I=T_{k+1}^I$, $T^{II}=T_{k+1}^{II}$.

Proof of Theorem 6.

Based on (9) we get

$$exp\left[-{\left({\displaystyle \frac{T^I}{a}}\right)}^{b+c{T}^I}\right]=1-R$$

(23)

and after taking logarithm on both sides (23) we have (21). Similarly, based on (10), we obtain (22). Recursive formulas in step 3 of the algorithm are obtained based on (9) and (10) using the CFF inversion method. □

The R codes for the PRNG of the WDSF^II are provided in Appendix B.

4. Estimation Methods

Additional goal for this article is outlined in this Section.

Looking through the literature in search of distributions that are modifications of the Weibull distribution, we find that the most dominant method of parameter estimation is the maximum likelihood (ML) method. However, the question remains whether this choice is right. The younger the paper, the more often the parameters are estimated using other methods, e.g. the ordinary least-squares (LS) and weighted least-squares (WLS) ones, see e.g. [3]; [64]; [14]; [12]; [83].

Let $\mathit{\vartheta }=\left(a,b,c\right),\mathit{\theta }=\left(a,b,c,\tau \right)$be parameter vectors and $t_1^{*},t_2^{*},...,t_n^{*}$ be a random sample of size n from the WDSF^I and WDSF^II. To estimate unknown values of parameters, we use estimation methods such as the ML, LS, WLS and least absolute values (LAW). The LAW, which is the first additional goal of the work, measures the absolute values of the differences between the empirical and theoretical RFs.

The likelihood functions (LFs) of the WDSF^I and WDSF^II, based on (13-14), are given by, respectively

$$L^I\left(t_i^{*};\mathit{\vartheta }\right)=\prod _{i=1}^{n}exp\left[-{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{t}_i^{*}}\right]{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{t}_i^{*}-1}\left[{\displaystyle \frac{b+c{t}_i^{*}}{a}}+{\displaystyle \frac{c{t}_i^{*}}{a}}ln\left({\displaystyle \frac{t_i^{*}}{a}}\right)\right],$$

(24)

$$\begin{array}{ccc}\hfill L^{II}\left(t_i^{*};\mathit{\theta }\right)& =& \prod _{i=1}^{n}exp\left[-u\left(t_i^{*};\mathit{\theta }\right){\displaystyle \frac{t_i^{*}}{a}}\right]·u\left(t_i^{*};\mathit{\theta }\right)·\hfill \\ & & ·\left[{\displaystyle \frac{b+c\left(t_i^{*}-\tau \right)S_F\left(t_i^{*}-\tau \right)}{a}}+{\displaystyle \frac{c{t}_i^{*}{S}_F\left(t_i^{*}-\tau \right)}{a}}ln\left({\displaystyle \frac{t_i^{*}}{a}}\right)\right],\hfill \end{array}$$

(25)

where $u\left(t_i^{*};\mathit{\theta }\right)={\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c\left(t_i^{*}-\tau \right)S_F\left(t_i^{*}-\tau \right)-1}$.

The log-likelihood functions (LLFs) of the WDSF^I and WDSF^II, based on ((25)-(26)), are defined as, respectively

$$l^I\left(t_i^{*};\mathit{\vartheta }\right)=-\sum _{i=1}^n{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{t}_i^{*}}+\sum _{i=1}^n\left(b+c{t}_i^{*}-1\right)ln\left({\displaystyle \frac{t_i^{*}}{a}}\right)+\sum _{i=1}^{n}ln\left[{\displaystyle \frac{b+c{t}_i^{*}}{a}}+{\displaystyle \frac{c{t}_i^{*}}{a}}ln\left({\displaystyle \frac{t_i^{*}}{a}}\right)\right],$$

(26)

$$\begin{array}{cc}\hfill l^{II}=& -\sum _{i=1}^n{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c\left(t_i^{*}-\tau \right)S_F\left(t_i^{*}-\tau \right)}+\hfill \\ \hfill & +\sum _{i=1}^n\left(b+c\left(t_i^{*}-\tau \right)S_F\left(t_i^{*}-\tau \right)-1\right)ln\left({\displaystyle \frac{t_i^{*}}{a}}\right)+\hfill \\ \hfill & +\sum _{i=1}^{n}ln\left[{\displaystyle \frac{b+c\left(t_i^{*}-\tau \right)S_F\left(t_i^{*}-\tau \right)}{a}}+{\displaystyle \frac{c{t}_i^{*}{S}_F\left(t_i^{*}-\tau \right)}{a}}ln\left({\displaystyle \frac{t_i^{*}}{a}}\right)\right].\hfill \end{array}$$

(27)

Formulas ${\displaystyle \frac{d{l}^I}{d\mathit{\vartheta }}},{\displaystyle \frac{d{l}^{II}}{d\mathit{\theta }}}$ have complex forms, so in practice we maximize the LF (27-28) or the LLFs (29-30) to obtain the ML estimates.

To obtain the OLS estimates of the WDSF^I and WDSF^II parameters, we minimize the following objective functions, respectively

$${OLS}^I=\sum _{i=1}^n{\left\{{\displaystyle \frac{i-n-1}{n+1}}+exp\left[-{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{t}_i^{*}}\right]\right\}}^2,$$

(28)

$${OLS}^{II}=\sum _{i=1}^n{\left\{{\displaystyle \frac{i-n-1}{n+1}}+exp\left[-{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{\left(t_i^{*}-\tau \right)S}_F\left(t_i^{*}-\tau \right)}\right]\right\}}^2.$$

(29)

To obtain the WLS estimates of the WDSF^I and WDSF^II parameters, we minimize the following objective functions, respectively

$${WLS}^I=\sum _{i=1}^n{\displaystyle \frac{{\left(n+1\right)}^2\left(n+2\right)}{i\left(n-i+1\right)}}{\left\{{\displaystyle \frac{i-n-1}{n+1}}+exp\left[-{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{t}_i^{*}}\right]\right\}}^2,$$

(30)

$${WLS}^{II}=\sum _{i=1}^n{\displaystyle \frac{{\left(n+1\right)}^2\left(n+2\right)}{i\left(n-i+1\right)}}{\left\{{\displaystyle \frac{i-n-1}{n+1}}+exp\left[-{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{\left(t_i^{*}-\tau \right)S}_F\left(t_i^{*}-\tau \right)}\right]\right\}}^2.$$

(31)

Let $R_e\left(i\right)=1-{\displaystyle \frac{i}{n+1}}$ is the empirical RF. To obtain the LAW estimates of the WDSF^I and WDSF^II parameters, we minimize the following objective functions, respectively

$${LAW}^I=\sum _{i=1}^n\left|R_e\left(i\right)-R^I\left(t;\mathit{\vartheta }\right)\right|=\sum _{i=1}^n\left|{\displaystyle \frac{i-n-1}{n+1}}+exp\left[-{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{t}_i^{*}}\right]\right|,$$

(32)

$${LAW}^{II}=\sum _{i=1}^n\left|R_e\left(i\right)-R^{II}\left(t;\mathit{\theta }\right)\right|=\sum _{i=1}^n\left|{\displaystyle \frac{i-n-1}{n+1}}+exp\left[-{\left({\displaystyle \frac{t_i^{*}}{a}}\right)}^{b+c{\left(t_i^{*}-\tau \right)S}_F\left(t_i^{*}-\tau \right)}\right]\right|.$$

(33)

Simulation study was performed with ${10}^3$ samples with a size of $50,100,200$. The samples were drawn from the WDSF^II with $\mathit{\theta }=\left(1,1,c,0\right)$, where $c=\left(1,2,3\right)$. To obtain highly accurate parameter estimates, the optimization procedure was run ${10}^2$ times with random initial values of $Unif(0.75,1.25)$ for $a,b,c$ and $Unif(0,0.25)$ for $\tau$. Our estimates for a given sample are the values that minimize (29), (31), (33) and maximize (27).

The biases and the root mean squared errors (RMSEs) of the WDSF^II estimates are shown in Table 2. We observe that as the sample size increases, the estimates approach the true values, which means that the estimates are consistent. Biases and RMSE values are the lowest for $\widehat{a}$. The biases are the largest for $\widehat{\tau }$ ($c=1)$ and $\widehat{b}$ ($c=2,3)$. The RMSEs are the highest for $\widehat{c}$. The biases increase with the value of c for $\widehat{b}$. The RMSEs increase with the value of c for $\widehat{b},\widehat{c}$ and decrease for $\widehat{a}$. The biases are the lowest for the ML method associated with $\widehat{\tau }$. The biases are lowest for the ML method associated with $\widehat{b},\widehat{c}$. The ML method is not suitable for estimating scale parameters.

5. Applications

In this section, we illustrate the importance of the WDSFI and WDSFII distributions using three real life data sets. The new models are compared with bimodal LTMs, characterized by unimodal, increasing, decreasing and bathub HRF, such as: exponentiated additive Weibull, McDonald Weibull, McDonald modified Weibull, McDonald extended Weibull, McDonald generalized Power Weibull, Compound Weibull, Kumaraswamy transmuted exponentiated modified Weibull, Kumaraswamy transmuted exponentiated additive Weibull. CFFs of mentioned models are presented in Appendix.

All calculations for comparison were performed in R software. To avoid local maxima, the optimization procedure was run ${10}^3$ times with random starting model parameter values that are widely scattered in the parameter space. The final parameter estimates are those parameter values that best maximize the log-likelihood function. AIC, BIC, HQIC criteria and the Kolmogorov-Smirnov (KS) statistic are calculated.

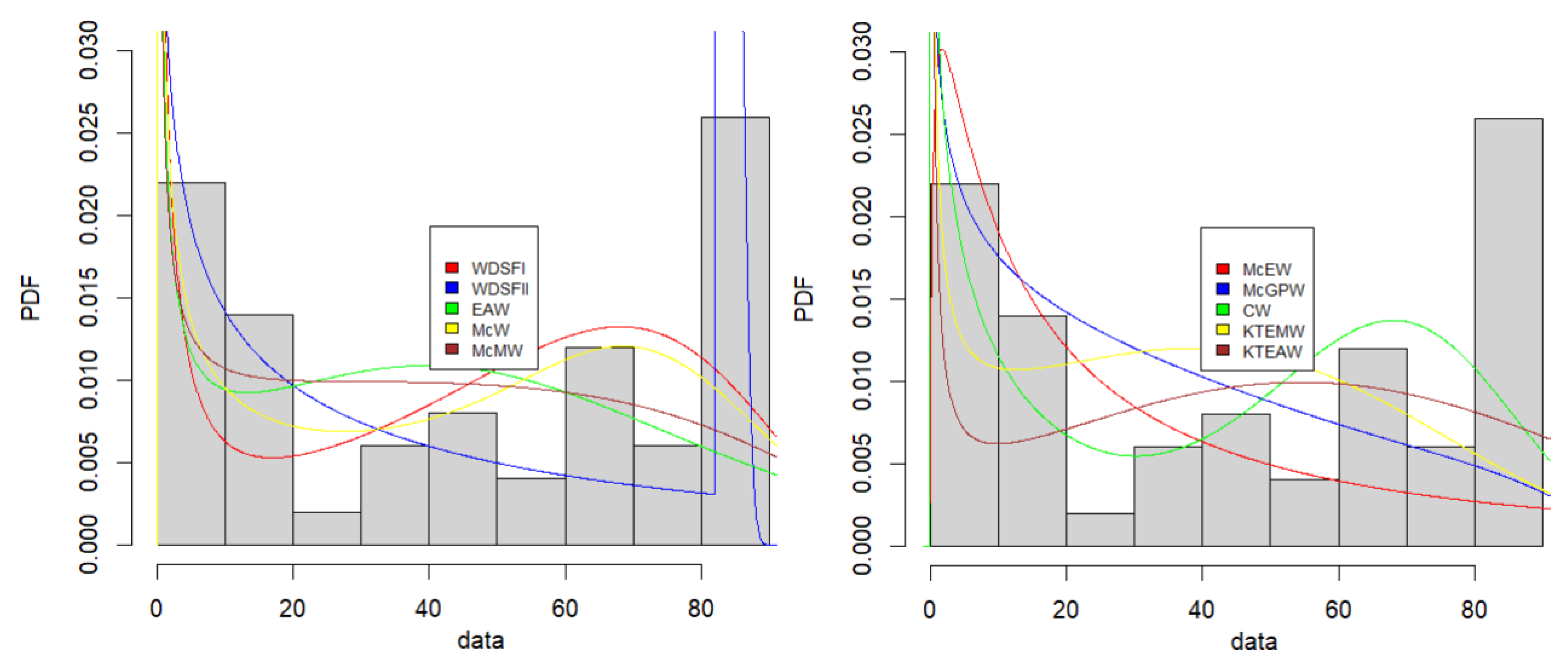
5.1. Failure times of devices

As the first real dataset, 50 failure times of devices ([1]; [53]) presented in Appendix C, is used. ML estimates (MLEs), AIC, BIC, HQIC and KS values are given in Table 3. Better values are marked in bold. Figure 5 shows the estimated FDFs for compared models. The WDSF^II model is more appropriate based on information criteria and KS values. The adaptability of the WDSF^II model can also be observed in Figure 5.

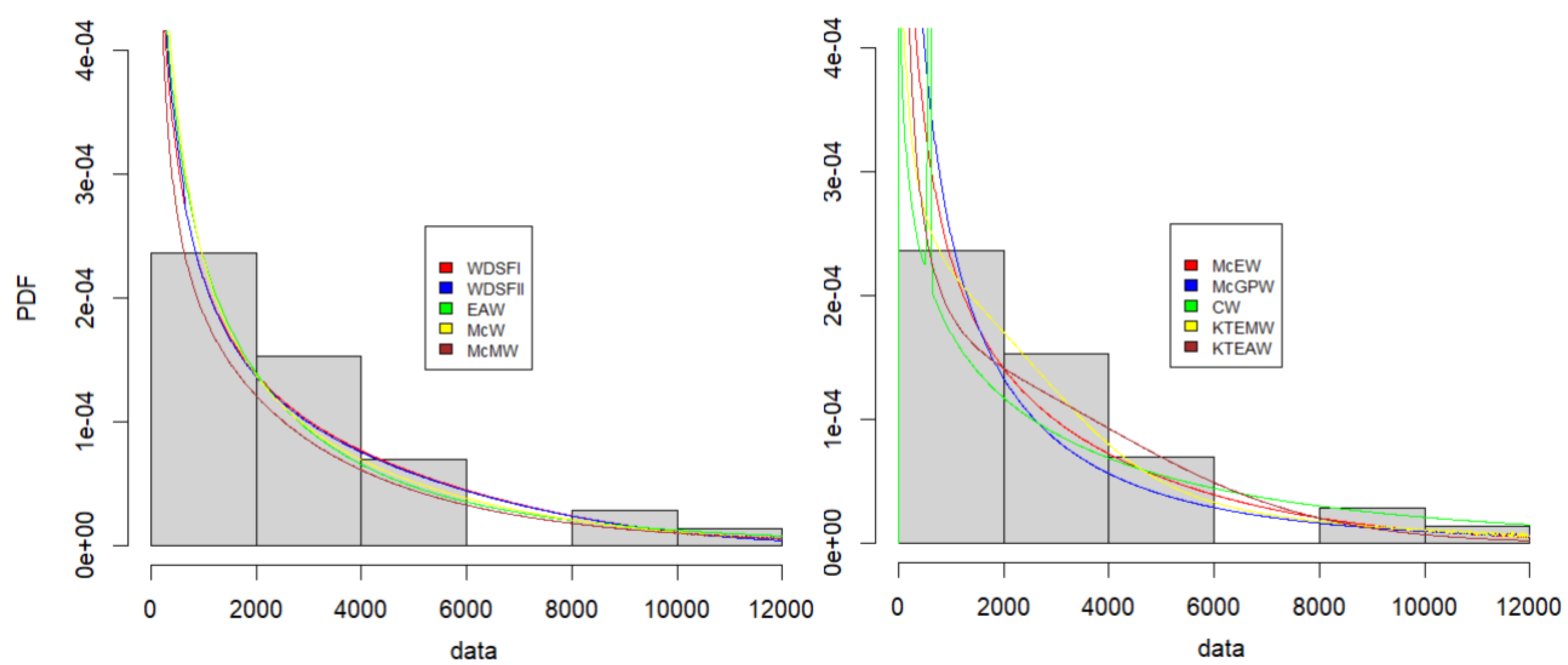
5.2. 500 MW generators

As the second real dataset, 36 times to the first failure of 500 MW generators collected over a 6-year period ([33]; [53]) presented in Appendix C, is used. ML estimates (MLE), AIC, BIC, HQIC and KS values are given in Table 4. The WDSF^I model is more appropriate based on information criteria. The adaptability of the WDSF^I model can also be observed in Figure 6.

6. Discussion

The results obtained in this study demonstrate that the proposed WDSF^I and WDSF^II models provide a flexible and accurate framework for modeling full-life-cycle data with a wide range of hazard ratio shapes, including monotonic, bathtub, and pseudobimodal patterns. Parameter estimation using OLS, WLS, and LAW methods yielded consistent results, with the LAW approach often demonstrating improved robustness in the presence of irregularities in the empirical reliability function.

From the perspective of previous research, our findings are consistent with, and even extend, previous work on generalizations of the Weibull distribution and its modified forms. Similar to these studies, we observed that introducing additional parameters can significantly improve model fit, allowing for more complex hazard ratio shapes. However, the WDSF^I and WDSF^II models differ in structure, offering better adaptation to datasets where existing models still exhibit systematic biases.

Regarding our working hypotheses, empirical analyses support the assumption that additional flexibility in scale structure and distribution shape leads to better data representation without sacrificing interpretability. The models’ performance on real-world datasets suggests they may be particularly well-suited for applications in engineering reliability, biomedical survival analysis, and materials degradation studies, where multi-phase failure mechanisms are present.

In a broader context, these findings contribute to the growing literature on extended-life models and highlight the continuing need for statistical tools capable of capturing a variety of hazardous behaviors. Such tools are crucial for risk assessment, preventive maintenance planning, and decision-making in safety-critical systems.

Future research directions include:

• Extending the proposed models to more precisely process censored, truncated, and interval data.
• Investigation of Bayesian inference methods to incorporate a priori information and quantify uncertainty.
• Development of multivariate or concatenated life-cycle models to capture inter-component dependencies.
• Incorporation of models into regression frameworks, such as proportional hazards or accelerated failure time models, to assess the impact of interdependent variables.

Overall, this study confirms the practical value of the WDSF^I and WDSF^II models and opens promising avenues for both theoretical development and applied research in reliability and survival analysis.

7. Conclusions

This article presents a three- and four-parameter flexible modified Weibull LTM called the Weibull distribution with a linear shape function. An innovative idea is to replace the Weibull shape parameter with a shape function. An estimation method based on theoretical and empirical reliability functions is proposed. An extensive literature review was performed, taking into account the modalities and shapes of the risk rate function. The simulation study is carried out using ML, LS, WLS and LAW methods. Furthermore, to check the suitability and flexibility, the new LTMs are validated with two real datasets and compared with other bimodal LTMs with a bathtub HRF.

The paper shows that even a three-parameter distribution can compete in data modeling with LTM distributions that have two or even almost three times more parameters.