1. Introduction
As the regulation for CO
2 reduction and fuel efficiency improvement increases, electrified systems have been widely used such as power train and chassis system [
1,
2,
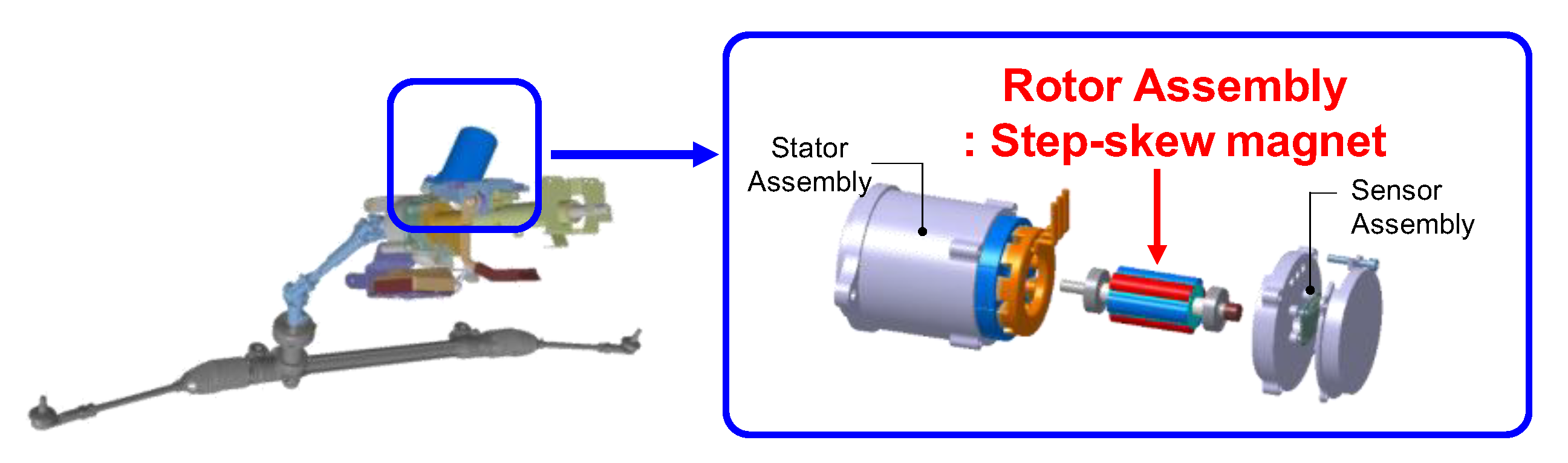
3]. In electrified system in vehicle, EPS (Electric Power Steering) is the most representative electrified system in chassis system as shown in
Figure 1 [
4,
5]. In EPS system, PMSM (Permanent Magnet Synchronous Motor) has been mainly adopted due to high torque density and efficiency [
6].
However, cogging torque reduction is the key design quality factor to enhance steering feeling and driving stability at high speed in EPS system [
7]. In this reason, SPMSM (Surface Permanent Magnet Synchronous Motor) which has magnet outside rotor core has been widely used to reduce cogging torque, compared to IPMSM (Internal Permanent Magnet Synchronous Motor) which has magnets inside rotor core. Compared to SPMSM, IPMSM has a weakness in terms of reducing cogging due to saliency of rotor structure [
8].
Cogging torque is a torque pulsation due to the change of magnetic resistance at no-load drive. This cogging torque depends on the shapes and material properties of the rotor, stator, and magnet [
9,
10]. In this reason, design methods to reduce cogging has been studied extensively in various ways. Previous studies for cogging torque reduction are mainly classified into magnet shape and skew design for the rotor assembly of SPMSM used in EPS system. In case of magnet shape design, applying eccentricity to the magnet shape has been widely used to improve cogging torque reduction [
11,
12].
In addition to the magnet shape design, skew design for cogging torque reduction is classified into continuous and step skew. Although continuous skew has more strength than step-skew to reduce cogging torque, step-skew design for rotor assembly has been in mass-production of EPS system for the manufacturing cost reduction [
13,
14,
15]. Generally, the combination design with eccentric magnet shape and step-skew for rotor assembly have been applied [
16].
In past studies, cycloid curves have been widely applied in mechanical fields, e.g., in speed reducers and oil pumps [
17,
18,
19]. However, in the study by Park, Lim, and Lee [
20], the cycloid curve was applied to the rotor of a motor. In their study, it was also verified that cogging torque was improved for a motor to which a cycloid curve was applied. However, the combination method for cycloidal curve on the magnet shape and step-skew design is not reported and its effectiveness is not also verified.
Furthermore, robust design has been required to guarantee the quality and maintenance of motors after mass-production [
21,
22,
23]. Especially, robust design has been strictly conducted to meet the required variance of cogging torque considering manufacturing disturbances for mass production [
24,
25,
26].
In this study, a cycloid curve on the magnet shape is used to reduce the cogging torque with the combination methods for rotor step skew design. Based on the same rotor step-skew design, an evaluation index δq is used and determined to compare the proposed and conventional magnet shape design. Robust design with cogging torque reduction for the proposed and conventional model are compared and verified through analytical method and prototype tests. using numerical method.
Figure 1.
EPS (Electric Power Steering) system in vehicle: (a) Configuration of EPS system; (b) SPMSM (Surface Permanent Magnet Synchronous Motor) used in EPS system.
Figure 1.
EPS (Electric Power Steering) system in vehicle: (a) Configuration of EPS system; (b) SPMSM (Surface Permanent Magnet Synchronous Motor) used in EPS system.
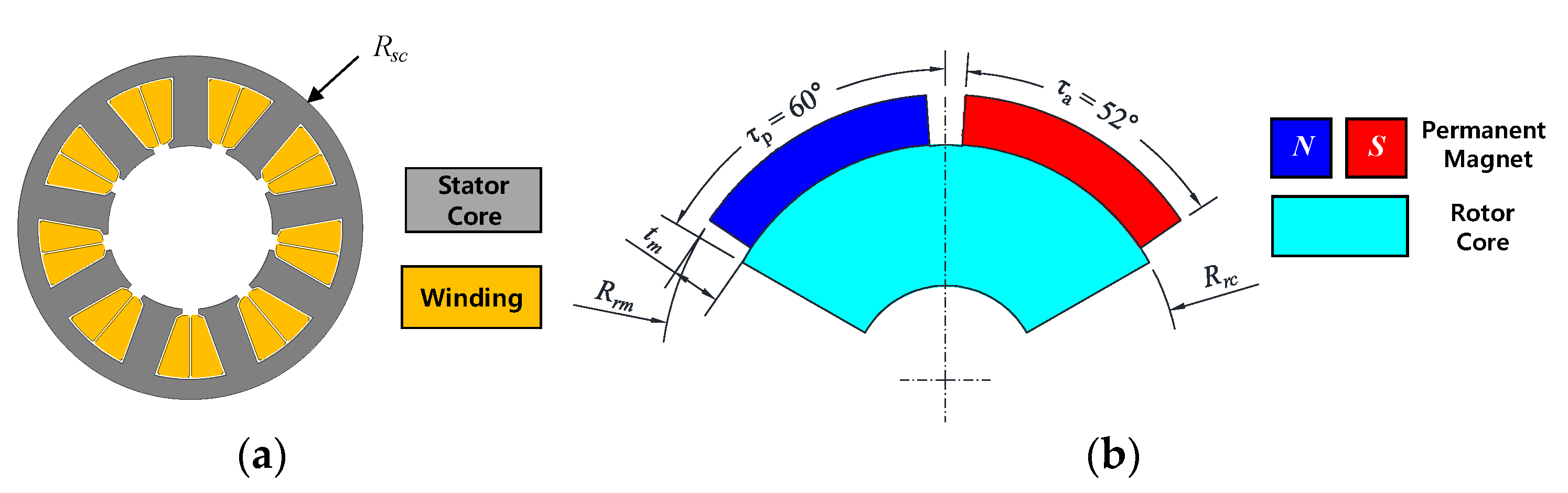
3. Proposed Model for Magnet Shape
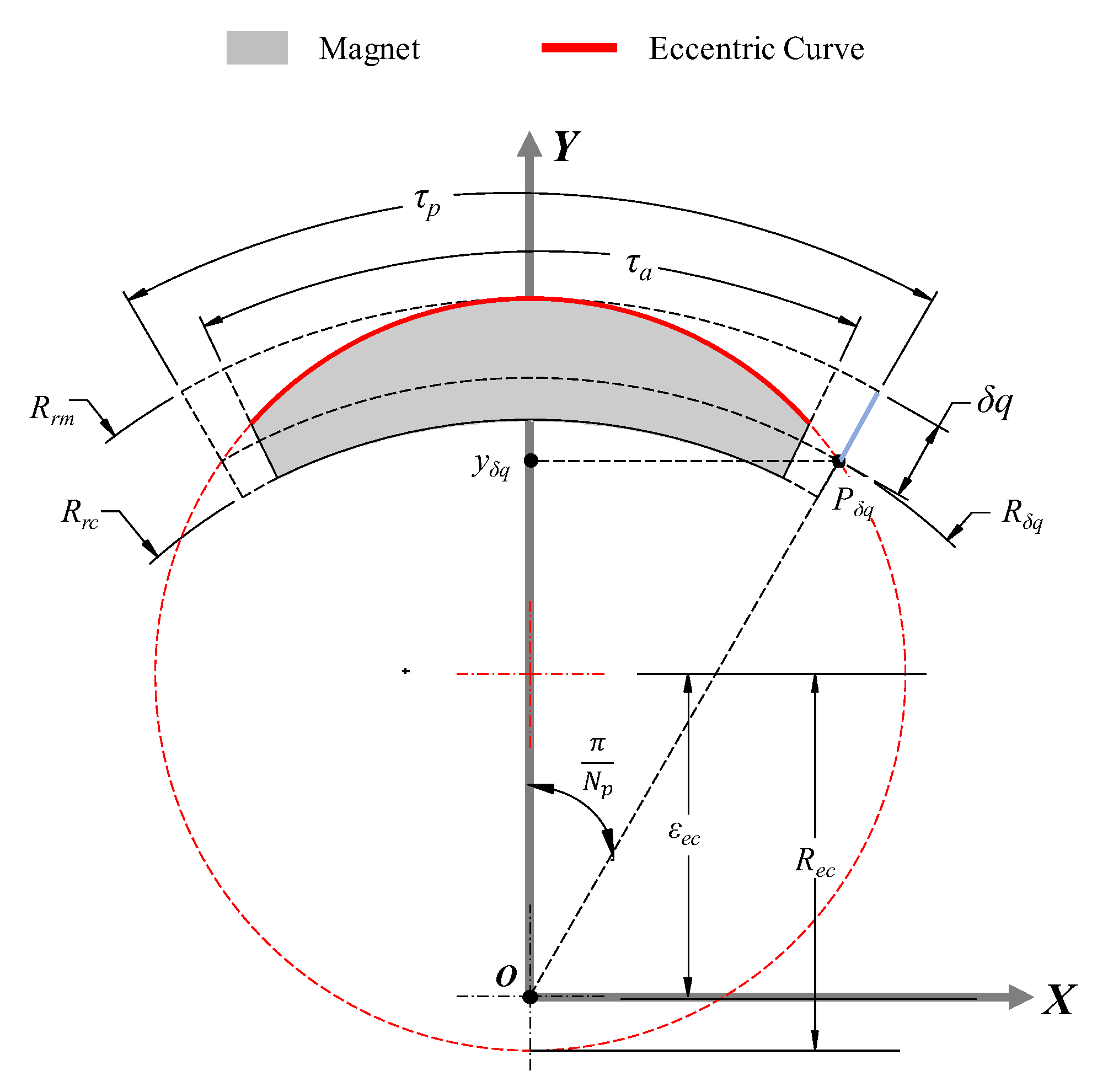
The eccentric curve has been generally used in the magnet shape of SPMSM to reduce cogging torque and torque ripple [
11,
12]. In this study, the eccentric curve, which has an eccentricity from its center, is used to com-pare the proposed curve on the magnet shape as shown in
Figure 4. In order to apply the eccentric circle to the magnet shape, the known parameters are decided. The known parameters are
δq ,
Rrm ,
tm and
Np (The numbers of pole). The unknown parameters of eccentric circle radius Rec and eccentricity
εec can be calculated by using geometrical relation as shown in
Figure 4 [
20].
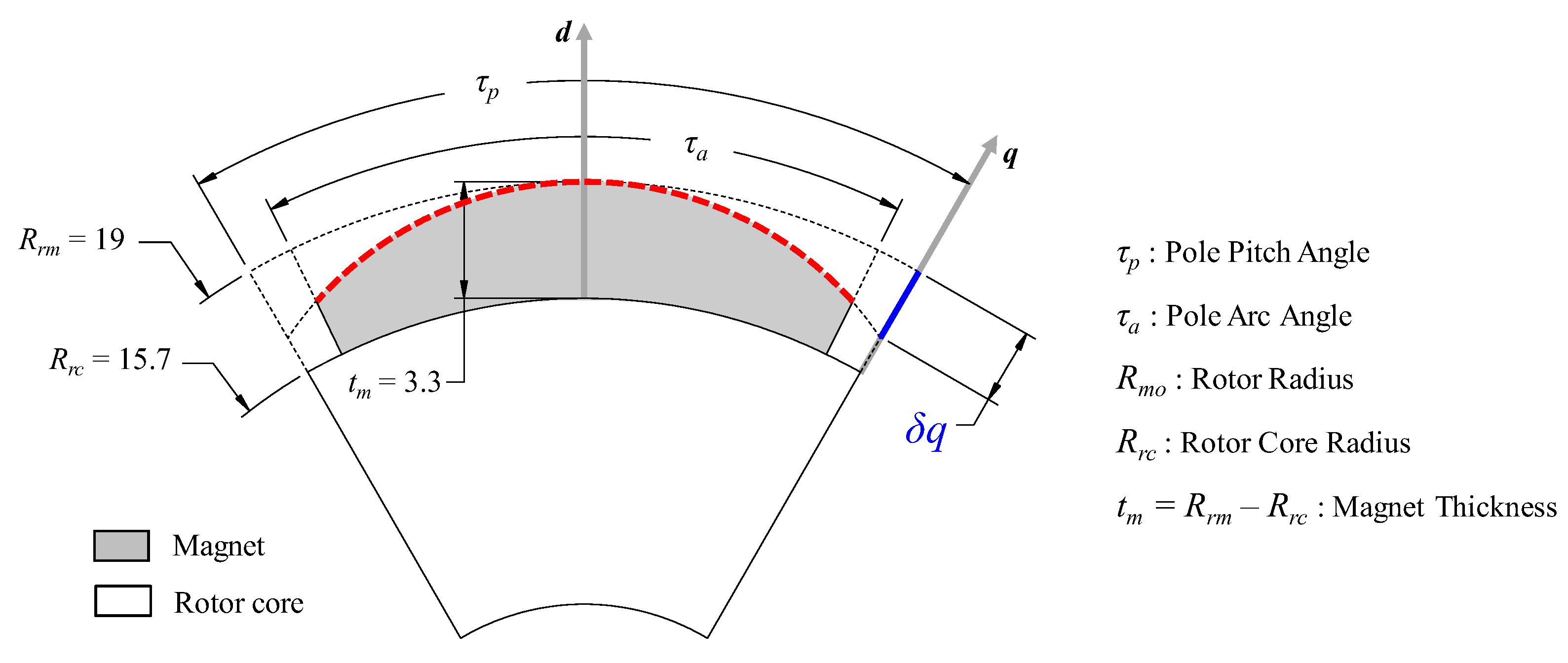
Figure 4.
Definition of eccentric curve for the conventional curve on the magnet.
Figure 4.
Definition of eccentric curve for the conventional curve on the magnet.
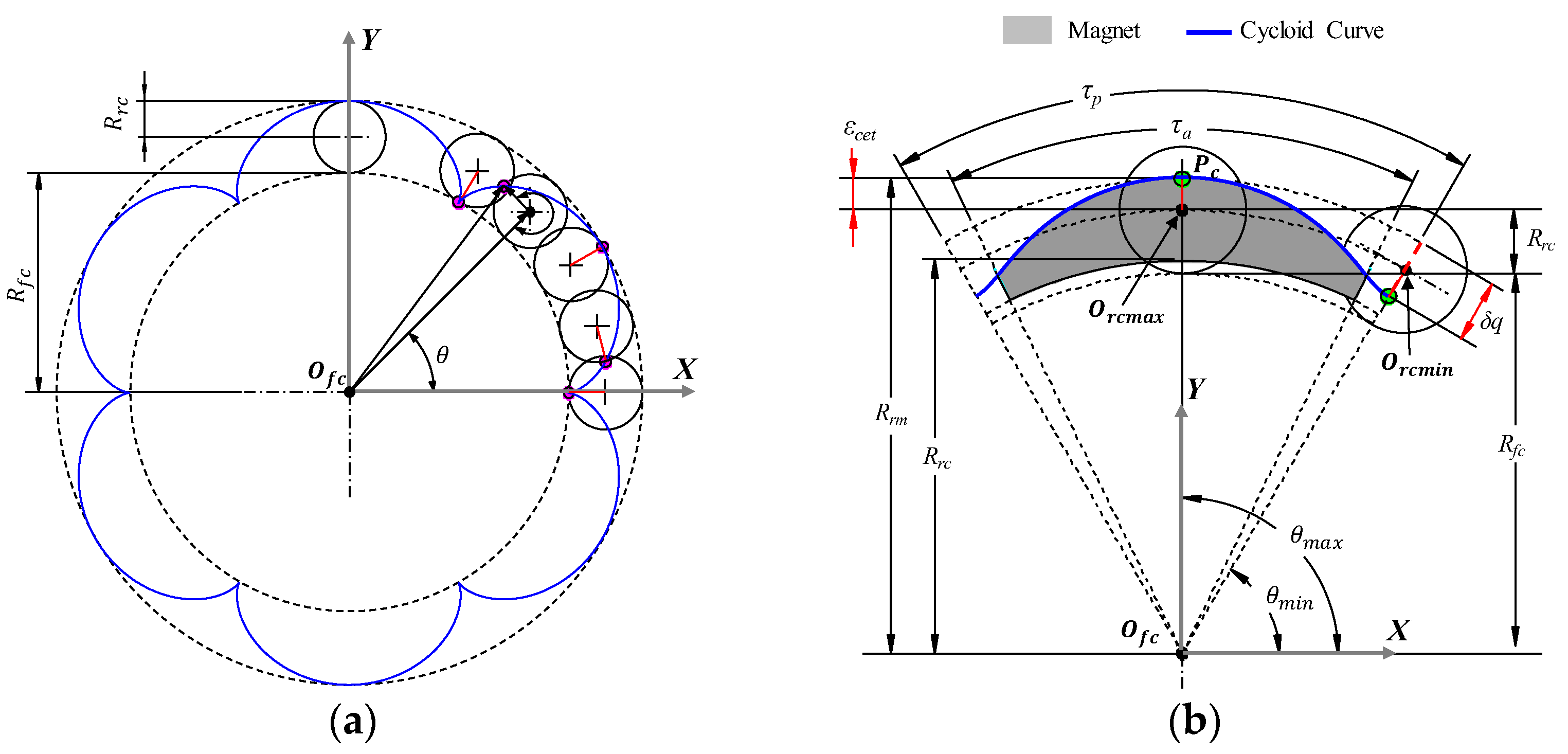
The proposed curve for the magnet shape is cycloid curve. A cycloid is the curve traced by a point in or on rolling circle with radius
Rrc as the rolling circle rolls along a fixed circle with radius
Rfc without slippage as shown in
Figure 5 (a). In order to apply cycloid curve to the magnet shape in the same procedure of eccentric cure, the known parameters are also decided. The known parameters are those of eccentric curve such as
δq ,
Rrm , tm and Np. The unknown parameters of
Rfc ,
Rrc , and eccentricity of cycloid curve
εecc can be also calculated by using geometrical relationship as shown in
Figure 5 (b) [
20].
Figure 4 shows the cycloidal curve trajectory of 6 poles magnet for the rotor model given in
Figure 2 (b). In addition,
Figure 4 (a) shows the trajectory of cycloid curve for 6 poles of rotor without
δq. In contrast to
Figure 4(a),
Figure 4 (b) shows the trajectory of cycloid curve with a certain value of
δq for 1 pole of rotor.
Figure 5.
Definition of cycloid curve for the conventional curve on the magnet: (a) Trajectory of cycloid curve for 6 poles of rotor; (b) Trajectory of cycloid curve on the magnet with 1 pole and δq.
Figure 5.
Definition of cycloid curve for the conventional curve on the magnet: (a) Trajectory of cycloid curve for 6 poles of rotor; (b) Trajectory of cycloid curve on the magnet with 1 pole and δq.
Based on the design procedure of the conventional and proposed curve on the magnet for a given value of
δq , the calculation of cogging torque is conducted. As described in chapter.1 of Introduction section, a cogging torque is a torque pulsation due to the change of magnetic resistance at no-load drive. Generally, the equation of cogging torque
Tcog is expressed in Equation 1 [
11,
12].
In Equation 1,
θ is the rotational position of rotor,
Lstk is the stack length of motor core,
μair is the permeability of air, r is the radius of rotor, 2π is the 1 period of cogging toque pulsation,
Br is the magnetic flux density into radial direction and
Bθ is the magnetic flux density into tangential direction. Additionally, Cogging torque has also the period of torque pulsation for a given number of pole and slot as shown in Equation 2.
In Equation 2, θcog is the mechanical angle of 1 period for cogging torque pulsation, Np and Ns denote the number of pole and slot respectively and LCM means Least Common Multiple. In order to calculate cogging torque, analytical method is a possible solution as shown Equation 1. However, it is relatively difficult to calculate cogging torque as following. First, non-linear properties of magnetic materials such as permanent magnet and electric core. Second, complex geometry of magnet shape such as conventional and proposed curve. In this study, Numerical analysis of FEM (Finite Element Method) is used in order to analyze cogging torque.
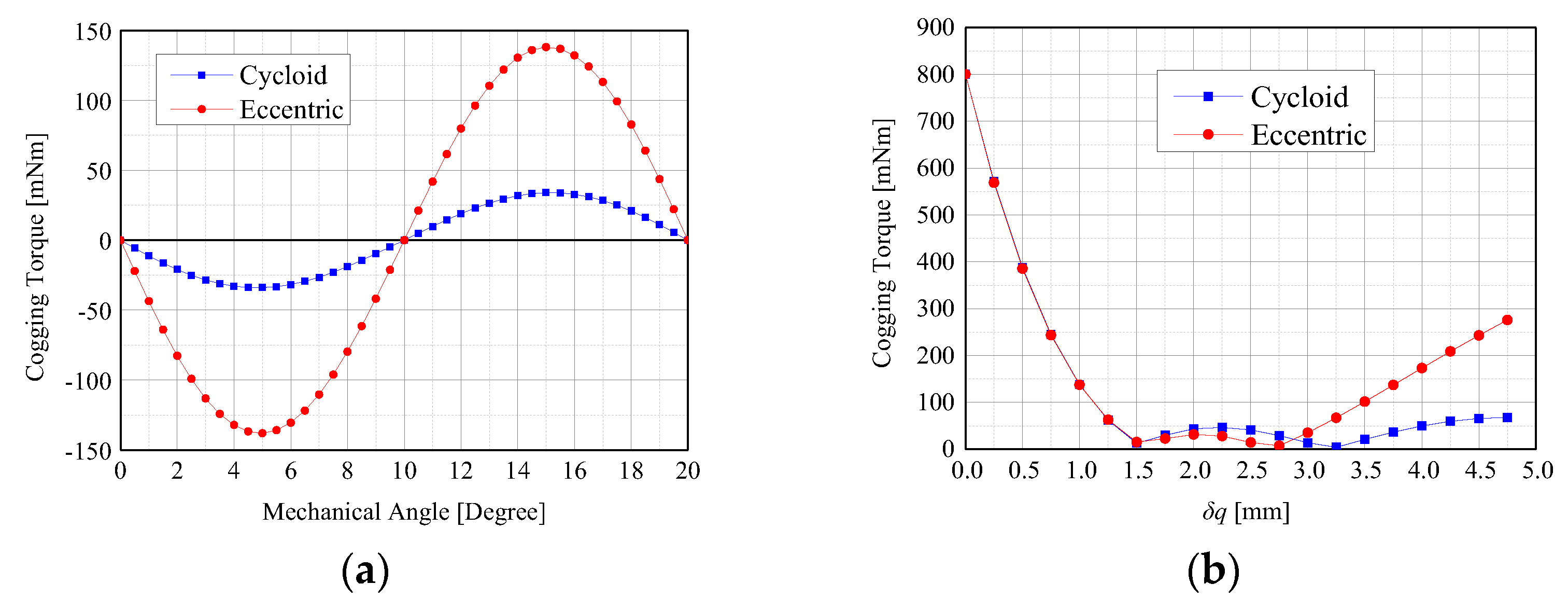
Figure 6 shows the calculation results of cogging torque.
Figure 6 (a) shows the wave form of 1 period for cogging torque pulsation. As described in Equation (2), the mechanical angle of cogging torque
θcog for
Figure 6 (a) is 20° at
δq = 4.75mm with 6 Poles and 9 Slots for this analysis model in
Table 1.
Figure 6 (b) shows the peak to peak values of cogging torque at
δq (0 ≤
δq ≤ 4.75).
Figure 6.
Calculation results of cogging torque: (a) Wave form of 1 period for cogging torque pulsation; (b) Peak to peak values of cogging torque at δq (0 ≤ δq ≤ 4.75).
Figure 6.
Calculation results of cogging torque: (a) Wave form of 1 period for cogging torque pulsation; (b) Peak to peak values of cogging torque at δq (0 ≤ δq ≤ 4.75).
Based on the conventional and prosed curve on the magnet shape, the step skew design, which is the method of cogging torque reduction as explained in chapter 1 of Introduction, is described to reduce cogging torque additionally. Step skew angle
θNskew is found by dividing by
Nstep in Equation (2). Equation (3) shows the calculation of
θNskew.
In Equation (3),
Nstep is the number of step and
θNskew is the step-skew angle with
Nstep. In this study, 3 step-skew is used to compare the conventional and proposed curve on the magnet shape.
Figure 7 (a) and (b) show Skew angle
θcog = 20˚ in Equation (2) and Step Skew Angle
θskew = 6.67° in Equation (3) with 6 poles and 9 slots for
Lstk = 57mm respectively.
Figure 7.
Skew angle and Step-skew angle for 6 poles and 9 slots: (a) Skew Angle θcog = 20˚; (b) Step Skew Angle θ3skew = 6.67°.
Figure 7.
Skew angle and Step-skew angle for 6 poles and 9 slots: (a) Skew Angle θcog = 20˚; (b) Step Skew Angle θ3skew = 6.67°.
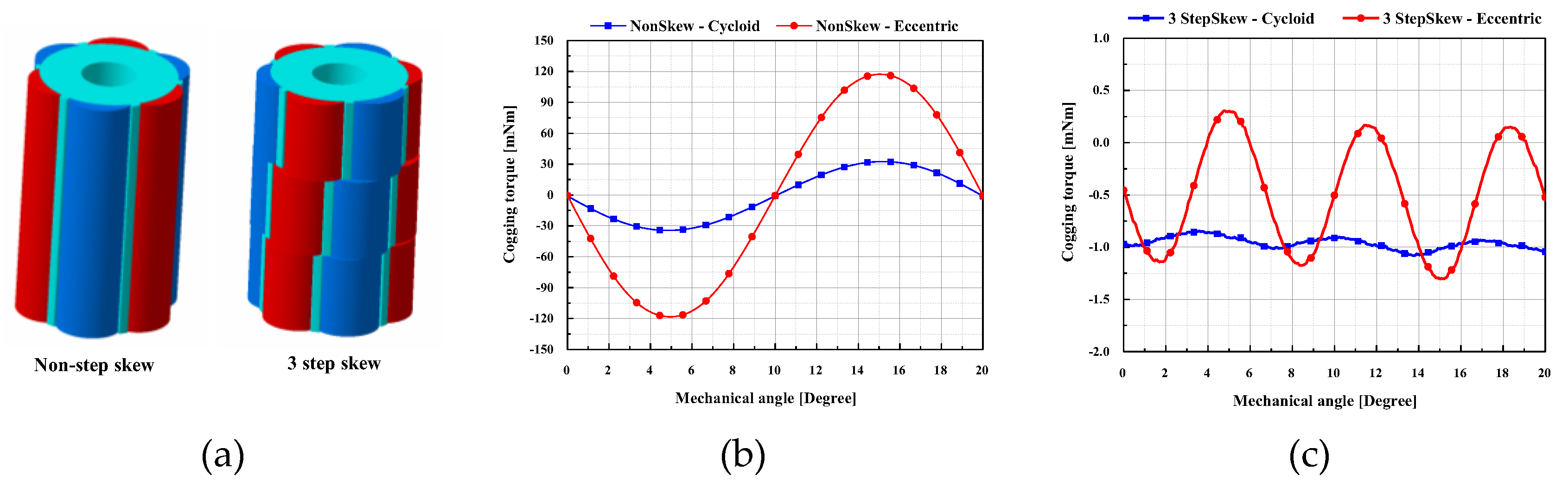
In this study,
δq is selected as 4.5 considering the performance variation due to the manufacturing tolerances. 3D models for the cycloid curve on the shape magnet is shown in
Figure 8 (a) with 3 step-skew of
Figure 7. In
Figure 8 (b) and (c), the wave-forms of 1 period for cogging torque pulsation is shown for non-skew and 3 step-skew model of the eccentric and proposed curve at
δq =4.5, respectively.
Figure 8.
3 step-skew model and calculation results: (a) 3D models of Non-step skew and 3 step-skew for the cycloid curve at δq =4.5; (b) Wave-forms of cogging torque for non-skew model at δq = 4.5; (c) Wave-forms of cogging torque for 3 step-skew model at δq = 4.5.
Figure 8.
3 step-skew model and calculation results: (a) 3D models of Non-step skew and 3 step-skew for the cycloid curve at δq =4.5; (b) Wave-forms of cogging torque for non-skew model at δq = 4.5; (c) Wave-forms of cogging torque for 3 step-skew model at δq = 4.5.
Table 2 shows the peak to peak values of cogging for the Non-skew and 3 step-skew model with the eccentric and cycloid curve on the magnet
δq = 4.5.
Table 2.
Cogging torque for the Non-skew and 3 step-skew model δq = 4.5.
Table 2.
Cogging torque for the Non-skew and 3 step-skew model δq = 4.5.
| Skew model |
Cycloid model
(Proposed model) |
Eccentric model
(Conventional model) |
Unit |
| Non-skew |
64 |
236 |
mNm |
| 3 step-skew |
0.2 |
1.6 |
mNm |
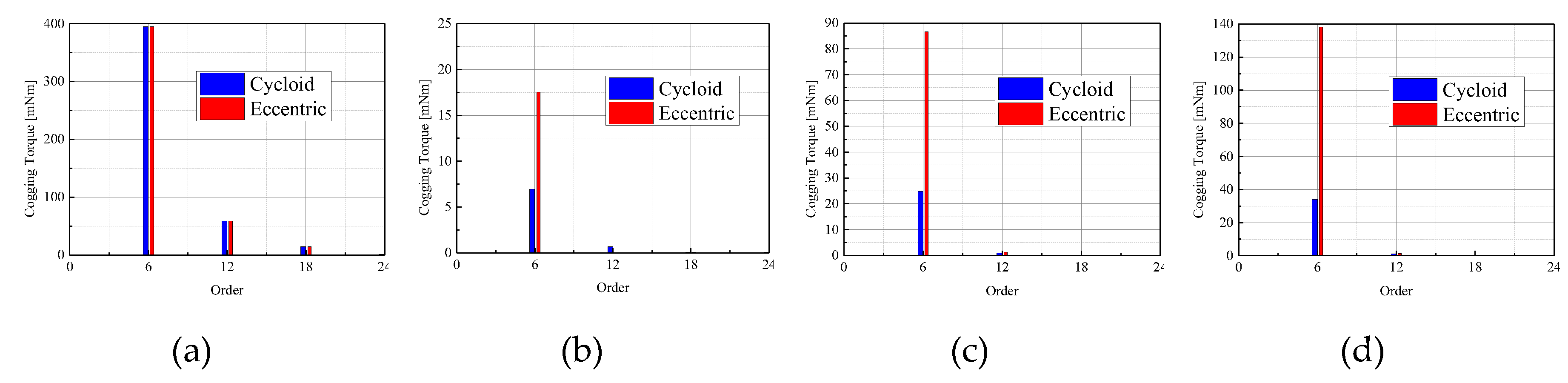
In order to explain the effective cogging reduction mechanism for the cycloid curve on the magnet, order analyses are conducted for the eccentric and cycloid curve on the magnet with the non-skew step rotor. The electric fundamental order of PMSM with 6 poles and 9 slots in
Table 1 is 6 for the 360-mechanical degree. In addition to the fundamental order, the 6n orders with the positive integer value
n are also generated.
Figure 9 shows the order analysis results of cogging torque wave-form for the non-skew model with 6’th
n orders in
Figure 8.
Figure 9.
6n’th cogging torque for the eccentric and cycloid curve on the magnet : (a) δq = 0.0 ; (b) δq = 3.0 ; (c) δq = 4.0 ; (d) δq = 4.75
Figure 9.
6n’th cogging torque for the eccentric and cycloid curve on the magnet : (a) δq = 0.0 ; (b) δq = 3.0 ; (c) δq = 4.0 ; (d) δq = 4.75
As shown in
Figure 9, the 6’th orders are dominant orders for the cogging torque at the given values of
δq.
Figure 10 (a) and (b) show the cogging torque of 6’th and 12’th order for the value of
δq. As shown in
Figure 10 (a), the 6’th order of cogging torque for the eccentric curve on the magnet increases sharply after
δq = 3.0. In this reason, the 6’th and 12’th order of cogging torque are the main orders for the cogging torque generation for the eccentric and cycloid model. Compared the eccentric curve model, the 6’th and 12’th order of cogging torque for the cycloid model are decreased as the values of
δq increases.
Figure 10.
cogging torque (peak to peak value) of the 6’th and 12’th order for the eccentric and cycloid curve on the magnet : (a) 6’th order cogging torque; (b) 12’th order cogging torque.
Figure 10.
cogging torque (peak to peak value) of the 6’th and 12’th order for the eccentric and cycloid curve on the magnet : (a) 6’th order cogging torque; (b) 12’th order cogging torque.
4. Validation
In order to validate the cogging torque reduction for the proposed model, the prototypes are built for the proposed and conventional model as shown in
Figure 11. In
Figure 11 (c), the reference model has the value of
δq = 4.5 as shown in
Figure 11 (a) and (b). The reference model was also built to compare the effectiveness for the proposed and conventional model in Figure (c) with
δq = 0 for the conventional model.
Figure 11.
Protypes for the proposed and conventional model at δq = 4.5 : (a) cycloid for the proposed model ; (b) eccentric for the conventional model; (c) reference model.
Figure 11.
Protypes for the proposed and conventional model at δq = 4.5 : (a) cycloid for the proposed model ; (b) eccentric for the conventional model; (c) reference model.
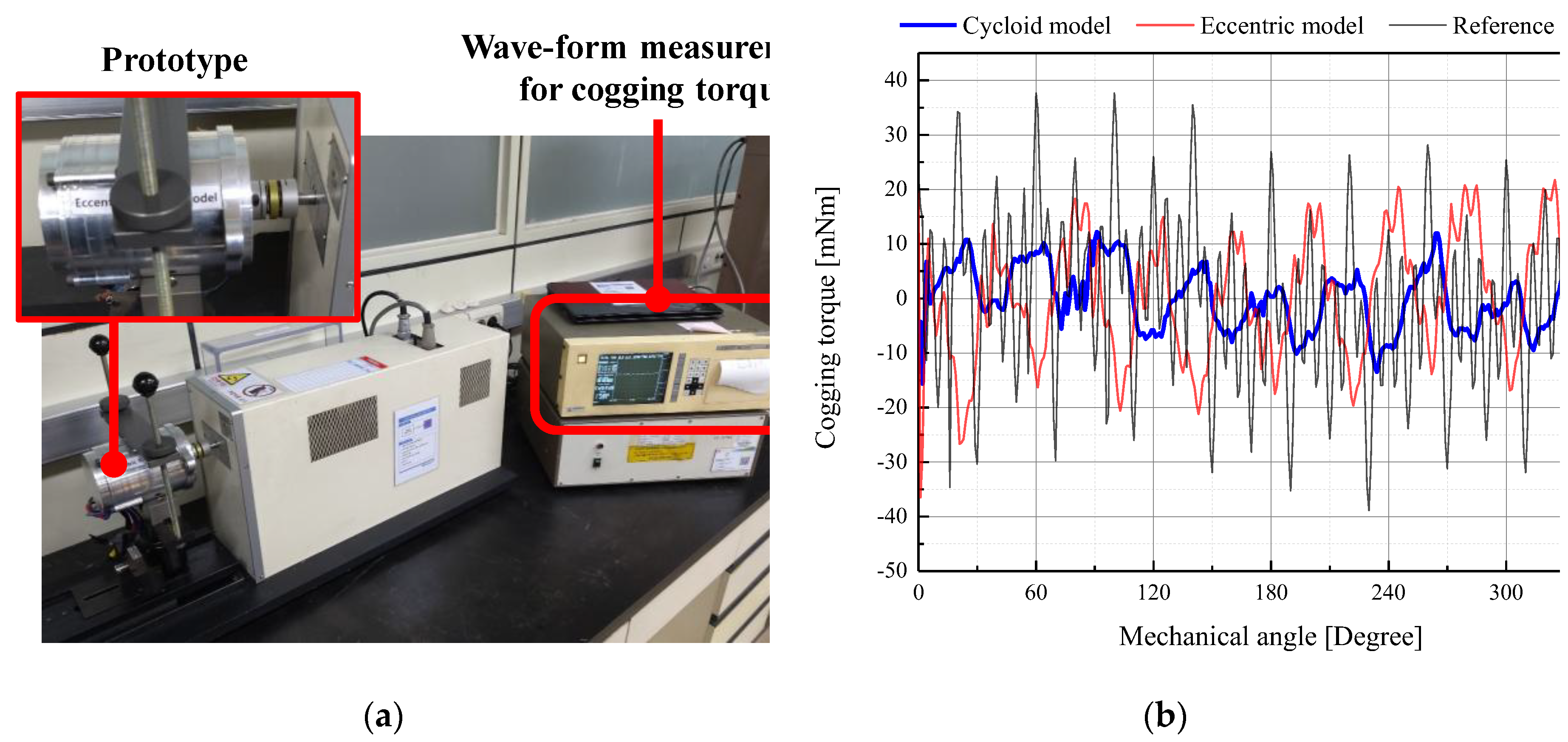
Figure 12 (a) and (b) shows the measurement equipment to measure the wave-forms of cogging torque and the measurement results of cogging torque wave-forms for the prototypes as shown in
Figure 11.
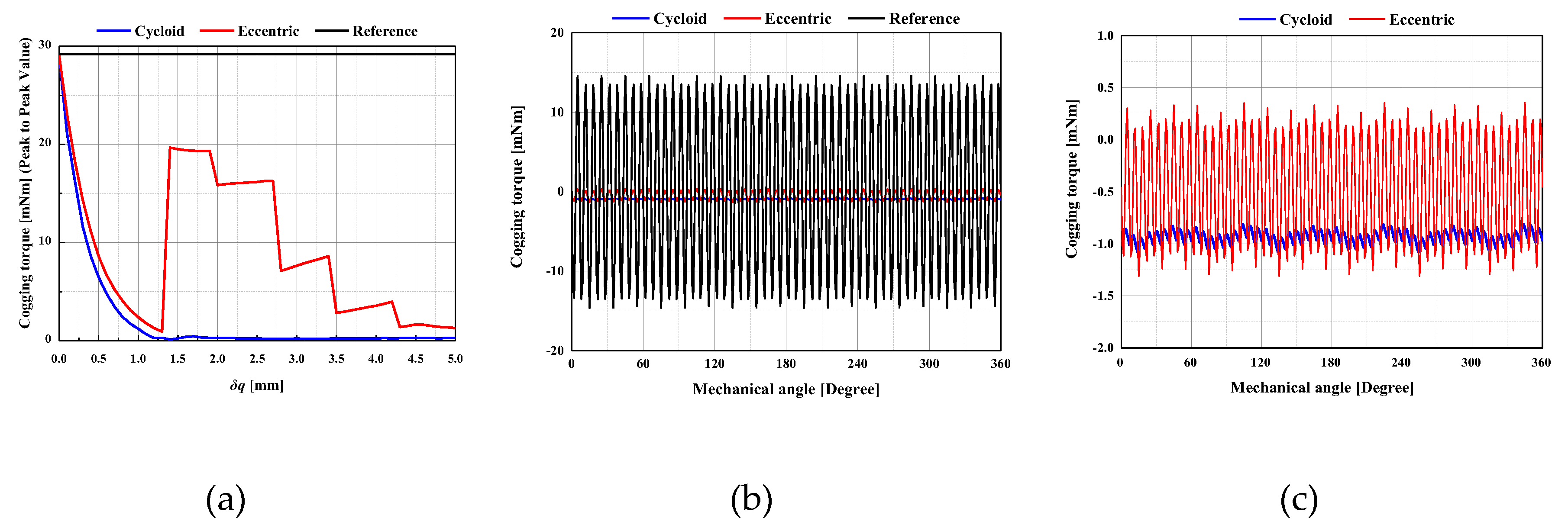
Figure 13 (b) shows the analysis results of cogging torque wave-forms for the prototypes as shown in
Figure 11. Figure (c) shows the extended cogging torque wave-forms for the cycloid and eccentric model in
Figure 13 (b).
Based on the analysis and tests results as shown in
Figure 12 and
Figure 13, the peak to peak values of cogging torque for the prototypes in
Figure 11 are shown in
Table 3. The effectiveness of cogging torque reduction for the proposed model with the cycloid was verified through the results of analysis and tests results as shown in
Figure 12,
Figure 13 and
Table 3.
However, there are considerable differences of the peak to peak values of cogging torque between the analysis and test results in
Table 3. In this study, the motor used in EPS system was dealt with a high precision motor used in EPS system are dealt with the strict cogging torque limit in the unit of mNm. In this reason, these considerable differences of cogging torque for the analysis and test results are affected by the manufacturing deteriorations [
20,
22,
23].
Figure 12.
Measurement equipment and test results : (a) Measurement equipment ; (b) Test results of cogging torque wave-forms for the 3 prototypes with the 360 degree of mechanical angle.
Figure 12.
Measurement equipment and test results : (a) Measurement equipment ; (b) Test results of cogging torque wave-forms for the 3 prototypes with the 360 degree of mechanical angle.
Figure 13.
FEM results : (a) cogging torque (peak to peak value) for the δq ; (b) wave-forms of cogging torque for the cycloid, eccentric and reference model for the 360 degree of mechanical angle ; (b) wave-forms of cogging torque for the cycloid and eccentric model for the 360 degree of mechanical angle.
Figure 13.
FEM results : (a) cogging torque (peak to peak value) for the δq ; (b) wave-forms of cogging torque for the cycloid, eccentric and reference model for the 360 degree of mechanical angle ; (b) wave-forms of cogging torque for the cycloid and eccentric model for the 360 degree of mechanical angle.
Table 3.
Cogging torque for the Non-skew and 3 step-skew model δq = 4.5.
Table 3.
Cogging torque for the Non-skew and 3 step-skew model δq = 4.5.
Cogging Torque
(Peak to peak value) |
Proposed model
(Cycloid model) |
Conventional model
(Eccentric model) |
Reference model |
Unit |
| Analysis (FEM) |
0.2 |
1.6 |
29.2 |
mNm |
| Test |
27.8 |
58.2 |
76.5 |
Although there are considerable differences between analysis and test results, the peak to peak values of cogging torque for the proposed model has little variation for the
δq from 1.0 to 5.0 as shown in
Figure 10 (a) and
Figure 13 (a). In this reason, the proposed model for the non-skew and skew model are verified as the robust model for the manufacturing deteriorations compared to the conventional model.