Improving the Explicit Formula for the Riemann Zeta Zeros Using Nonlinear Corrections

1. Introduction

The counting function for zeros of the Riemann zeta function $\zeta \left(s\right)$ along the critical line is classically approximated by the Riemann–von Mangoldt formula [1]. For zeros $\rho ={\displaystyle \frac{1}{2}}+i\gamma$, the classical smooth term is given by:

$$N_{\mathrm{smooth}}\left(t\right)={\displaystyle \frac{t}{2\pi }}log{\displaystyle \frac{t}{2\pi }}-{\displaystyle \frac{t}{2\pi }}+{\displaystyle \frac{7}{8}}.$$

(1)

Explicit prime sum corrections typically reduce deviations [2], but residual errors persist. We propose a novel nonlinear correction to further reduce this error.

2. Explicit Formula with Nonlinear Correction

Define the explicit prime sum correction as:

$$S\left(t\right)=\sum _{p\le P_{\max }}{\displaystyle \frac{sin(tlogp)}{p^{1/2}logp}},$$

(2)

where the sum is over primes $p\le P_{\max }$.

We propose a nonlinear transformation using the shifted sine integral function $\mathrm{ssinint}\left(x\right)=\mathrm{Si}\left(x\right)-{\displaystyle \frac{\pi }{2}}$:

$$N_{\mathrm{explicit}}\left(t\right)=N_{\mathrm{smooth}}\left(t\right)-{\displaystyle \frac{1}{\pi }}\mathrm{ssinint}\left(S\left(t\right)\right).$$

(3)

We evaluated the deviations numerically using sets of nontrivial zeta zeros ${\gamma }_j$:

$$\mathrm{err}\left(j\right)=N_{\mathrm{explicit}}\left({\gamma }_j\right)-j.$$

(4)

We chose the shifted sine integral $\mathrm{ssinint}\left(x\right)=\mathrm{Si}\left(x\right)-{\displaystyle \frac{\pi }{2}}$ as the nonlinear correction due to its natural appearance in Fourier-analytic treatments of oscillatory prime sums [3]. Its kernel ${\displaystyle \frac{sinu}{u}}$ is closely related to the oscillatory structure underlying the explicit formula, reflecting interference patterns between primes and zeros of $\zeta \left(s\right)$. This makes $\mathrm{ssinint}$ a natural candidate to smooth and rephase the prime sum contribution while preserving the arithmetic oscillations that encode zero distribution.

3. Numerical Results

For various subsets of zeros (up to $N=100,000$), maximum deviations consistently improved relative to the smooth term alone. Representative results:

• $N=200$: max deviation $\sim 0.25$.
• $N=2000$: max deviation $\sim 0.482$.
• $N=5000$: max deviation $\sim 0.609$.
• $N=100,000$: max deviation $\sim 0.716$.

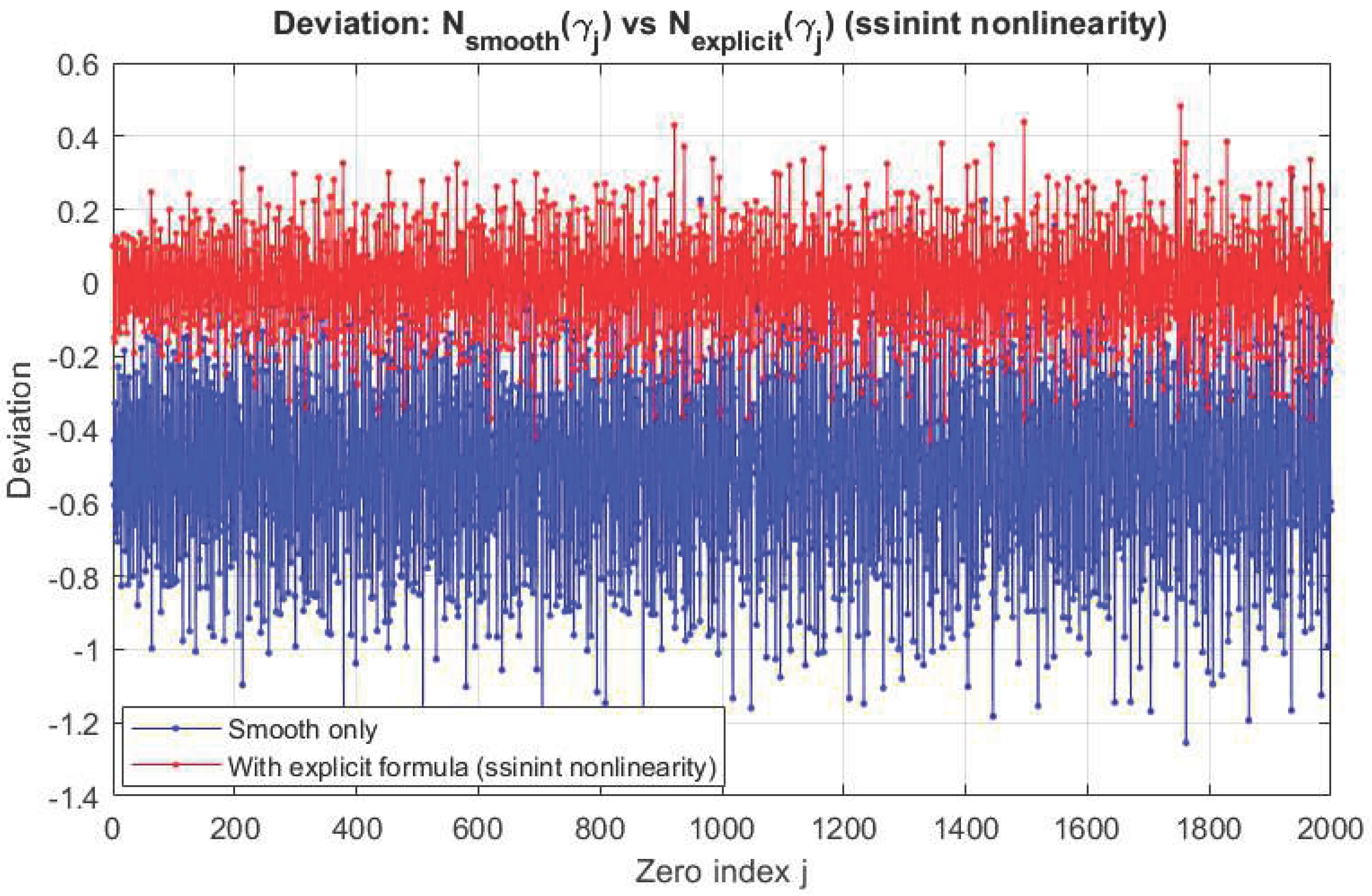
Figure 1. Deviation comparison between the smooth Riemann–von Mangoldt counting function $N_{\mathrm{smooth}}\left({\gamma }_j\right)$ (blue) and the explicitly corrected version with shifted sine integral (ssinint) nonlinearity $N_{\mathrm{explicit}}\left({\gamma }_j\right)$ (red), evaluated over the first 2000 nontrivial zeros of the Riemann zeta function.

Figure 1. Deviation comparison between the smooth Riemann–von Mangoldt counting function $N_{\mathrm{smooth}}\left({\gamma }_j\right)$ (blue) and the explicitly corrected version with shifted sine integral (ssinint) nonlinearity $N_{\mathrm{explicit}}\left({\gamma }_j\right)$ (red), evaluated over the first 2000 nontrivial zeros of the Riemann zeta function.

To assess robustness, we performed Monte Carlo experiments by selecting multiple random subsets of consecutive zeros (size $N=5000$) from the dataset. For each subset, deviations were computed for both the smooth term and the nonlinear explicit formula. Statistics including mean, root-mean-square (RMS), and maximum deviation were recorded across trials, confirming consistent improvement and stability of the nonlinear correction. Increasing $P_{\max }$ logarithmically reduced errors, confirming expected asymptotic behavior. Here we present an extra robustness test which include the Standard (explicit) formula :

Robustness Test Results

The following table presents the mean, maximum, and root-mean-square (RMS) deviations for three methods used to estimate the number of non-trivial zeros of the Riemann zeta function, based on 20 random subsets of $N=1000$ zeros. The methods compared are the classic Riemann–von Mangoldt smooth term, the standard explicit formula, and the explicit formula with a nonlinear correction (ssinint).

Table 1. Deviation Metrics for Robustness Tests (20 Random Subsets, $N=1000$).

Method	Mean Deviation	Max Deviation	RMS Deviation
Classic (smooth)	0.518	1.468	0.600
Standard (explicit)	0.501	1.116	0.537
Explicit (ssinint)	0.160	0.652	0.199

Table 1. Deviation Metrics for Robustness Tests (20 Random Subsets, $N=1000$).

Method	Mean Deviation	Max Deviation	RMS Deviation
Classic (smooth)	0.518	1.468	0.600
Standard (explicit)	0.501	1.116	0.537
Explicit (ssinint)	0.160	0.652	0.199

4. Discussion and Implications

The observed sublinear growth and apparent error saturation at large N suggest a deeper connection with spectral barriers or conjectures related to the distribution of prime numbers and zeros of the zeta function. This warrants further analytic investigation, potentially linking this numerical behavior to known spectral limits in analytic number theory.

5. Conclusion

Introducing a nonlinear correction significantly improves explicit formulas for counting Riemann zeta zeros. Numerical experiments robustly confirm the reduction in deviations and hint at new theoretical insights.