Submitted:
02 December 2025
Posted:
09 December 2025
Read the latest preprint version here
Abstract
Keywords:
MSC: 03D20; 11U05
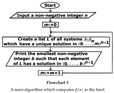
1. The Collatz Problem Leads to a Short Computer Program That Computes in the Limit a Function of Unknown Computability
input("Input a non-negative integer n",n):
while TRUE do
print(sign(n)):
n:=sign(n-1)*(2*n+(1-(-1)^n)*(5*n+2))/4:
end_while:
2. A Limit-Computable Function Which Eventually Dominates Every Computable Function
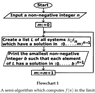
3. The First Undecidable Decision Problem on an Ordered Pair of Non-Negative Integers
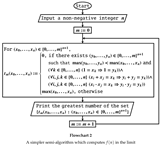
4. A Short Program inMuPADThat Computes f in the Limit
input("Input a non-negative integer n",n):
m:=0:
while TRUE do
X:=combinat::cartesianProduct([s $s=0..m] $t=0..n):
Y:=[max(op(X[u])) $u=1..(m+1)^(n+1)]:
for p from 1 to (m+1)^(n+1) do
for q from 1 to (m+1)^(n+1) do
v:=1:
for k from 1 to n+1 do
if 1=X[p][k] and 1<>X[q][k] then v:=0 end_if:
for i from 1 to n+1 do
for j from i to n+1 do
if X[p][i]+X[p][j]=X[p][k] and X[q][i]+X[q][j]<>X[q][k] then v:=0 end_if:
if X[p][i]*X[p][j]=X[p][k] and X[q][i]*X[q][j]<>X[q][k] then v:=0 end_if:
end_for:
end_for:
end_for:
if max(op(X[q]))<max(op(X[p])) and v=1 then Y[p]:=0 end_if:
end_for:
end_for:
print(max(op(Y))):
m:=m+1:
end_while:
5. The Second Undecidable Decision Problem on an Ordered Pair of Non-Negative Integers
6. A Limit-Computable Function of Unknown Computability Which Eventually Dominates Every Function with a Single-Fold Diophantine Representation
7. A Short Program inMuPADThat Computes in the Limit
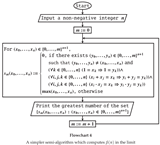
input("Input a non-negative integer n",n):
m:=0:
while TRUE do
X:=combinat::cartesianProduct([s $s=0..m] $t=0..n):
Y:=[max(op(X[u])) $u=1..(m+1)^(n+1)]:
for p from 1 to (m+1)^(n+1) do
for q from 1 to (m+1)^(n+1) do
v:=1:
for k from 1 to n+1 do
if 1=X[p][k] and 1<>X[q][k] then v:=0 end_if:
for i from 1 to n+1 do
for j from i to n+1 do
if X[p][i]+X[p][j]=X[p][k] and X[q][i]+X[q][j]<>X[q][k] then v:=0 end_if:
if X[p][i]*X[p][j]=X[p][k] and X[q][i]*X[q][j]<>X[q][k] then v:=0 end_if:
end_for:
end_for:
end_for:
if q<>p and v=1 then Y[p]:=0 end_if:
end_for:
end_for:
print(max(op(Y))):
m:=m+1:
end_while:
References
- Calude, C. S. To halt or not to halt? That is the question; World Scientific: Singapore, 2024. [Google Scholar]
- Cantone, D.; Casagrande, A.; Fabris, F.; Omodeo, E. The quest for Diophantine finite-fold-ness . Matematiche (Catania) 2021, 76(no. 1), 133–160. [Google Scholar] [CrossRef]
- Cantone, D.; Cuzziol, L.; Omodeo, E. G. On Diophantine singlefold specifications . Matematiche (Catania) 2024, 79(no. 2), 585–620. Available online: https://lematematiche.dmi.unict.it/index.php/lematematiche/article/view/2703/1218.
- Cantone, D.; Omodeo, E. G. “One equation to rule them all”, revisited . Rend. Istit. Mat. Univ. Trieste 2021, 53 Art.(No. 28), 32 pp. [Google Scholar] [CrossRef]
- Davis, M.; Matiyasevich, Yu.; Robinson, J. Hilbert’s tenth problem, Diophantine equations: positive aspects of a negative solution; in: Mathematical developments arising from Hilbert problems (ed. F. E. Browder). Feferman). In Proc. Sympos. Pure Math.; Amer. Math. Soc.: Providence, RI; Amer. Math. Soc.: Providence, RI, 1976; vol. 28, Part 2, p. 323–378 269–324. [Google Scholar] [CrossRef]
- Matiyasevich, Yu. Matiyasevich, Hilbert’s tenth problem; MIT Press: Cambridge, MA, 1993. [Google Scholar]
- Matiyasevich, Yu. Hilbert’s tenth problem: what was done and what is to be done . In Proceedings of the Workshop on Hilbert’s tenth problem: relations with arithmetic and algebraic geometry (Ghent, 1999) Contemp. Math. 270; Amer. Math. Soc.: Providence, RI, 2000; pp. 1–47. [Google Scholar] [CrossRef]
- Matiyasevich, Yu. Towards finite-fold Diophantine representations . J. Math. Sci. (N. Y.) 2010, vol. 171(no. 6), 745–752. [Google Scholar] [CrossRef]
- Royer, J. S.; Case, J. Subrecursive Programming Systems: Complexity and Succinctness; Birkhäuser: Boston, 1994. [Google Scholar]
- Soare, R. I. Interactive computing and relativized computability . In Computability: Turing, Gödel, Church and beyond; Copeland, B. J., Posy, C. J., Shagrir, O., Eds.; MIT Press: Cambridge, MA, 2013; pp. 203–260. [Google Scholar]
- Tyszka, A. A hypothetical upper bound on the heights of the solutions of a Diophantine equation with a finite number of solutions . Open Comput. Sci. 2018, 8(no. 1), 109–114. [Google Scholar] [CrossRef]
- Tyszka, A. All functions g:N→N which have a single-fold Diophantine representation are dominated by a limit-computable function f:N∖{0}→N which is implemented in MuPAD and whose computability is an open problem . In Computation, cryptography, and network security; Daras, N. J., Rassias, M. Th., Eds.; Springer: Cham, 2015; pp. 577–590. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).