A Short Computer Program Which Computes in the Limit a Non-Computable Function from N to N

Apoloniusz Tyszka

doi:10.20944/preprints202508.0363.v1

Submitted:

04 August 2025

Posted:

05 August 2025

Read the latest preprint version here

Abstract

For n∈N, f(n) denotes the smallest b∈N such that if a system of equations S⊆{1=x_k, x_i+x_j=x_k, x_i·x_j=x_k: i,j,k∈{0,...,n}} has a solution in N^{n+1}, then S has a solution in {0,...,b}^{n+1}. The author proved earlier that the function f:N→N is computable in the limit and eventually dominates every computable function g:N→N. We present a simple program in MuPAD which for n∈N prints the sequence {f_i(n)}_{i=0}^∞ of non-negative integers converging to f(n). The previously known computer programs by other authors do not compute in the limit non-computable functions from N to N.

Keywords:

computable function

;

eventual domination

;

limit-computable function

;

MuPAD

;

noncomputable function

;

semi-algorithm

Subject:

Computer Science and Mathematics - Computer Science

For

n \in N

, let

E_{n} = {1 = x_{k}, x_{i} + x_{j} = x_{k}, x_{i} \cdot x_{j} = x_{k} : i, j, k \in {0, \dots, n}}

Theorem 1

([1] p. 118). There exists a limit-computable function

f : N \to N

which eventually dominates every computable function

g : N \to N

.

We present an alternative proof of Theorem 1. For

n \in N

,

f (n)

denotes the smallest

b \in N

such that if a system of equations

S \subseteq E_{n}

has a solution in

N^{n + 1}

, then

S

has a solution in

{0, \dots, b}^{n + 1}

. The function

f : N \to N

is computable in the limit and eventually dominates every computable function

g : N \to N

, see [2]. Flowchart 1 shows a semi-algorithm which computes

f (n)

in the limit, see [2].

A semi-algorithm which computes

f (n)

in the limit

Flowchart 2 shows a simpler semi-algorithm which computes

f (n)

in the limit.

A simpler semi-algorithm which computes

f (n)

in the limit

Lemma 1.

For every

n, m \in N

, the number printed by Flowchart 2 does not exceed the number printed by Flowchart 1.

Proof.

For every

(a_{0}, \dots, a_{n}) \in {0, \dots, m}^{n + 1}

,

E_{n} \supseteq {1 = x_{k} : (k \in {0, \dots, n}) \land (1 = a_{k})} \cup

{x_{i} + x_{j} = x_{k} : (i, j, k \in {0, \dots, n}) \land (a_{i} + a_{j} = a_{k})} \cup

{x_{i} \cdot x_{j} = x_{k} : (i, j, k \in {0, \dots, n}) \land (a_{i} \cdot a_{j} = a_{k})}

□

Lemma 2.

For every

n, m \in N

, the number printed by Flowchart 1 does not exceed the number printed by Flowchart 2.

Proof.

Let

n, m \in N

. For every system of equations

S \subseteq E_{n}

, if

(a_{0}, \dots, a_{n}) \in {0, \dots, m}^{n + 1}

and

(a_{0}, \dots, a_{n})

solves

S

, then

(a_{0}, \dots, a_{n})

solves the system of equations

\tilde{S} : = {1 = x_{k} : (k \in {0, \dots, n}) \land (1 = a_{k})} \cup

{x_{i} + x_{j} = x_{k} : (i, j, k \in {0, \dots, n}) \land (a_{i} + a_{j} = a_{k})} \cup

{x_{i} \cdot x_{j} = x_{k} : (i, j, k \in {0, \dots, n}) \land (a_{i} \cdot a_{j} = a_{k})}

□

Theorem 2.

For every

n, m \in N

, Flowcharts 1 and 2 print the same number.

Proof.

It follows from Lemmas 1 and 2. □

MuPAD is a part of the Symbolic Math Toolbox in MATLAB R2019b. The following program in MuPAD implements the semi-algorithm shown in Flowchart 2.

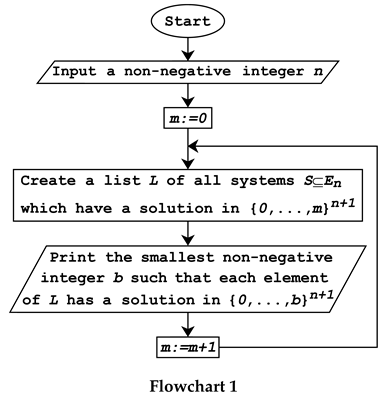
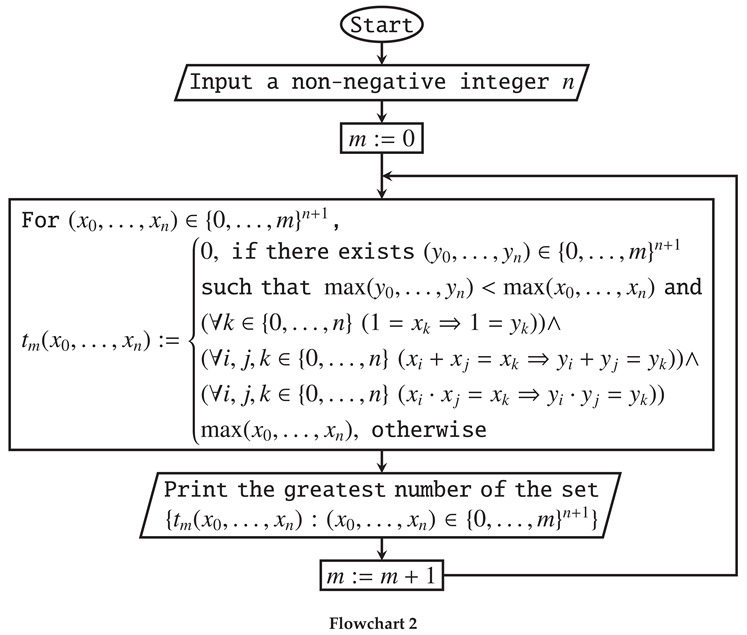
input("Input a non-negative integer n",n):

m:=0:

while TRUE do

X:=combinat::cartesianProduct([s $s=0..m] $t=0..n):

Y:=[max(op(X[u])) $u=1..(m+1)^(n+1)]:

for p from 1 to (m+1)^(n+1) do

for q from 1 to (m+1)^(n+1) do

v:=1:

for k from 1 to n+1 do

if 1=X[p][k] and 1<>X[q][k] then v:=0 end_if:

for i from 1 to n+1 do

for j from i to n+1 do

if X[p][i]+X[p][j]=X[p][k] and X[q][i]+X[q][j]<>X[q][k] then v:=0 end_if:

if X[p][i]*X[p][j]=X[p][k] and X[q][i]*X[q][j]<>X[q][k] then v:=0 end_if:

end_for:

if max(op(X[q]))<max(op(X[p])) and v=1 then Y[p]:=0 end_if:

end_for:

print(max(op(Y))):

m:=m+1:

end_while:

For

n \in N

,

h (n)

denotes the smallest

b \in N

such that if a system of equations

S \subseteq {x_{i} + 1 = x_{k}, x_{i} \cdot x_{j} = x_{k} : i, j, k \in {0, \dots, n}}

has a solution in

N^{n + 1}

, then

S

has a solution in

{0, \dots, b}^{n + 1}

. From [2] and Lemma 3 in [3], it follows that the function

h : N \to N

is computable in the limit and eventually dominates every computable function

g : N \to N

. A bit shorter program in MuPAD computes h in the limit.

The author is not aware about computer programs by other authors which compute in the limit non-computable functions from

N

to

N

.

References

J. S. Royer and J. Case, Subrecursive Programming Systems: Complexity and Succinctness, Birkhäuser, Boston, 1994.
A. Tyszka, All functions g:N→N which have a single-fold Diophantine representation are dominated by a limit-computable function f:N∖{0}→N which is implemented in MuPAD and whose computability is an open problem, in: Computation, cryptography, and network security (eds. N. J. Daras, M. Th. Rassias), Springer, Cham, 2015, 577–590, https://doi.org/10.1007/978-3-319-18275-9_24.
A. Tyszka, A hypothetical upper bound on the heights of the solutions of a Diophantine equation with a finite number of solutions, Open Comput. Sci. 8 (2018), no. 1, 109–114, https://dx.doi.org/10.1515/comp-2018-0012.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.