Recoil Energy in Electron Capture Beta Decay and the Search for Sterile Neutrinos

1. Introduction

Neutrinos and antineutrinos are the most elusive and mysterious elementary particles in contemporary physics. We begin our paper with a brief review of the properties of these particles. Neutrinos are always observed to have left-handed helicity (the spin angular momentum is directed opposite to the linear momentum), while antineutrinos always have right-handed helicity (the spin angular momentum is directed parallel to the linear momentum). The precise nature of the difference between a neutrino and an antineutrino is unresolved. A real distinction exists if the neutrino and the antineutrino are spin ½ “Dirac fermions”. In this case the neutrino and antineutrino are different particles, described by different quantum fields. However, these two particles may also be spin ½ “Majorana fermions”, described by the same quantum field. In this case neutrinos and antineutrinos are the same particles with different helicities, analogous to left and right-circularly polarized photons.

There are three different flavors (i.e., types) of neutrinos and antineutrinos: electron, muon, and tau. The most abundant in the Universe are, probably, the relic neutrinos, which decoupled from the other fundamental particles about 1 s after the Big Bang. The relic neutrinos are expected to contain all three flavors in approximately equal proportion [1]. Currently, the energy of these relic neutrinos is insufficient for their direct detection. However, the relic neutrinos influence the spatial fluctuations of the cosmic microwave background, and this influence was detected [2].

Nuclear reactors generate large numbers of electron antineutrinos. The fission of heavy nuclei, e.g., ²³⁵U, produces neutron-rich daughter nuclei, which undergo beta-decay:

$$\mathrm{Z}\to \left(\mathrm{Z}+1\right)+{\mathrm{e}}^{-}+{\overline{\nu }}_{\mathrm{e}},$$

(1)

Here Z is the atomic number of the parent nucleus and e^- and ${\overline{\nu }}_{\mathrm{e}}$are the electron and the electron antineutrino. This reaction shows that, inside the nucleus, a neutron decays into a proton while radiating an electron and an electron antineutrino. On a more fundamental level, inside the neutron, a down quark (d) with negative electric charge (-1/3)e transforms into an up quark (u) with positive charge (2/3)e while radiating a W^- boson of charge (-e). The W^- boson mediates the weak interaction. It decays by radiating an electron and an electron antineutrino. Due to such beta-decays, about 4.5% of the fission energy released in nuclear reactors is radiated away as electron antineutrinos [3]. First observed in the 1950s, these antineutrinos are now detected routinely. The maximum energy of an antineutrino radiated by nuclear reactors is about 10 MeV. Radioactive isotopes present in the Earth, e.g., ²³⁸U, also produce electron antineutrinos in beta decay processes [4].

Collisions between cosmic rays (typically protons) and atoms in the atmosphere generate atmospheric neutrinos and antineutrinos of both electron and muon flavors, with a wide range of energies up to at least 200 TeV [5]. The process of generation is the following. Byproducts of such collisions, e.g., positively charged pions, decay into positively charged antimuons μ⁺ and muon neutrinos ν_μ:

$${\pi }^{+}\to {\mu }^{+}+{\nu }_{\mu }.$$

(2)

A positively charged pion, or pi meson, has zero spin and consists of an up quark (u) of charge (2/3)e and a down antiquark$\overline{\mathrm{d}}$of charge (1/3)e: π⁺ = u$\overline{\mathrm{d}}$. In the same way, a negatively charged antipion π^-, which consists of up antiquark and down quark, decays into a negatively charged muon μ^- and a muon antineutrino ${\overline{\nu }}_{\mu }$. A muon decays into an electron, a muon neutrino, and an electron antineutrino, while an antimuon decays into a positron (antielectron), an electron neutrino, and a muon antineutrino:

$${\mu }^{-}\to {\mathrm{e}}^{-}+{\nu }_{\mu }+{\overline{\nu }}_{\mathrm{e}},$$

$${\mu }^{+}\to {\mathrm{e}}^{+}+{\overline{\nu }}_{\mu }+{\nu }_{\mathrm{e}}.$$

(3)

A typical particle accelerator may produce a beam of muon neutrinos and antineutrinos with energies in the range from MeV to GeV [6]. For example, if an accelerated proton beam hits a stationary target, positively charged pions π⁺ are produced and can be separated from other particles. Then, the positively charged pions decay in flight into antimuons μ⁺ and muon neutrinos, as shown in formula (2). At the Large Hadron Collider (LHC), neutrinos and antineutrinos of all flavors with energies in the TeV region have been detected in the ForwArd Search ExpeRiment (FASER) [7]. In the LHC, two counter-propagating beams of protons collide producing other hadrons (particles composed from quarks and antiquarks) which decay producing neutrinos and antineutrinos, similar to the processes shown in formulas (2) and (3).

The largest source of neutrinos near the Earth’s surface is the core of the Sun [8]. The nuclear reaction generating the overwhelming majority of solar neutrinos is the fusion of two protons into a deuteron ²H, which contains one proton and one neutron. This reaction generates a positron and an electron neutrino:

$${\mathrm{p}}^{+}+{\mathrm{p}}^{+}{\to }^2\mathrm{H}+{\mathrm{e}}^{+}+{\nu }_{\mathrm{e}}.$$

(4)

The energy of the solar neutrinos produced by this reaction (“pp neutrinos”) is relatively small (below 420 keV) but other nuclear reactions occurring in the core of the Sun produce neutrinos of energy up to 18 MeV [8]. Neutrinos and antineutrinos with energies below 100 MeV are also generated during the core collapse of massive stars [9]. In the process of the collapse, protons and electrons fuse, forming neutrons while radiating electron neutrinos. Also, the initial temperature of the collapsed core is very high (about 10¹¹ K), and thermal energy is converted into neutrinos through pair production of neutrinos and antineutrinos of all the flavors.

An intriguing property of the different neutrino flavors is that each flavor$|{\nu }_{\alpha }⟩$, where α denotes a flavor (α = e,μ,τ), is a superposition of at least three “neutrino mass states”, which for simplicity we denote as $|1⟩$, $|2⟩$, and $|3⟩$. The mass states are the states with definite rest mass values, labeled m₁, m₂, and m₃. A major consequence of this property is the phenomenon of neutrino oscillations. During flight through free space, a neutrino of one flavor may transform into another flavor. For example, the muon neutrino produced in a pion decay may transform in flight into an electron or a tau neutrino. In order to understand neutrino oscillations, it is instructive to consider an analogy with electron spin precession.

Consider a neutral atom in an electronic ground S-state with a single unpaired electron (e.g., lithium) passing through a Stern-Gerlach apparatus which measures the x-component of the atomic spin. After passing through the Stern-Gerlach apparatus, the electron spin of the atom points either in the positive or negative x-direction. We can call these two states the (+x) flavor ($|$+$⟩$state) and (-x) flavor ($|$-$⟩$state). Suppose that after passing through the Stern-Gerlach apparatus, the spin has the (+x) flavor. Let the atom then propagate through a region where a magnetic field points in the negative z-direction. (We choose the negative z-direction for the magnetic field because in the ground state, the electron spin points opposite to the magnetic field.) In the magnetic field, the “energy states”$\left|0\right.⟩$and $\left|1\right.⟩$, which correspond to the definite values of energy, correspond to the (+z) and (-z) spin directions. The original spin flavor (+x) is then a superposition of the two energy states:

$$|+⟩=2^{-\frac{1}{2}}(|0⟩+|1⟩).$$

(5)

When the atom experiences the magnetic field, its spin state$\left|\psi \right.⟩$must change because the flavor state$|$+$⟩$is not a stationary energy state:

$$\left|\psi \right.⟩=2^{-\frac{1}{2}}\left\{\exp \left(\frac{\mathrm{i}\omega \mathrm{t}}{2}\right)\right\}\left|0\right.⟩+\exp \left\{\left(\frac{-\mathrm{i}\omega \mathrm{t}}{2}\right)\right\}\left|1\right.⟩=\cos \left(\frac{\omega \mathrm{t}}{2}\right)\left|+\right.⟩+\mathrm{i}\ast \sin \left(\frac{\omega \mathrm{t}}{2}\right)\left|-\right.⟩.$$

(6)

Here, ω = γ_eB is the frequency of the Larmor precession, which is equal to the transition frequency between the electron spin states $\left|0\right.⟩$and$\left|1\right.⟩$, γ_e is the electron gyromagnetic ratio, and B is the magnitude of the magnetic field. If one uses a second Stern-Gerlach device to measure the flavor of the spin at a distance (d) from the first apparatus, the probability to get the (+x) flavor will be P+ = cos²(ωd/2v), where v is the speed of the atom, and the time t in expression (6) equals d/v. Correspondingly, the probability to observe the (-x) flavor P- = sin²(ωd/2v). The phase difference ωt between the two energy states increases with distance d, and the two probabilities oscillate. For example, with ωd/2v = π/4, the probability to observe the (-x) spin flavor is P- = P+ = ½, and for, ωd/2v = π/2, we have P+ = 0, P- = 1, i.e., the +x flavor changes to the -x flavor.

Just as happens in the case of an electron spin propagating in a magnetic field, when neutrinos propagate in free space, the phase differences between the mass states change, which is detectable as a change in the neutrino flavor. However, unlike the oscillations of the “spin flavor”, in the case of neutrino oscillations we have not two, but three mass states with definite values of rest energy m_kc², where k = 1, 2, 3. The important consequence of neutrino oscillations is that they represent a significant deviation from the Standard Model of particle physics [10]. In the Standard Model, neutrinos have zero rest mass (like a photon) and all propagate with the speed of light.

Mathematically, the neutrino flavor states are expressed in terms of the mass states using the 3x3 lepton mixing matrix U_αk [11]:

$$\left|{\nu }_{\alpha }\right.⟩=\sum {\mathrm{U}}_{\alpha \mathrm{k}}^{\ast }\left|\mathrm{k}\right.⟩.$$

(7)

In this and following expressions, the sum is taken over the mass index k = 1, 2, 3. If a neutrino is created in the flavor state$\left|\alpha \right.⟩$, the probability of observing it in a flavor state $\left|\alpha \prime \right.⟩$ is given by the expression:

$${\mathrm{P}}_{\alpha {\alpha }^{\prime }}={\left|\sum {\mathrm{U}}_{\alpha \mathrm{k}}^{\ast }{\mathrm{U}}_{{\alpha }^{\prime }\mathrm{k}}\exp \left(-\frac{{\mathrm{i}\mathrm{m}}_{\mathrm{k}}^2{\mathrm{c}}^3\mathrm{d}}{\mathrm{ħ}\mathrm{E}}\right)\right|}^2.$$

(8)

Here d is the distance from the neutrino source and E is the total relativistic neutrino energy. Note that equation (8) was derived assuming the ultra-relativistic limit: m_kc² << E.

Neutrino oscillation experiments reliably indicate that the three mass states have squared rest energy differences Δ(m²c⁴) ≈ 7.4x10^-5 (eV)² and Δ(m²c⁴) ≈ 2.5x10^-3 (eV)² [12]. This implies that the mass states have a maximum rest energy greater than 50 meV. Analysis of the available cosmological data provides the following bounds on the sum of the masses of these states: 60 meV < (m₁ + m₂ + m₃)c² < 110 meV [13]. The measurement of the absolute value of the neutrino and antineutrino masses is a notoriously complicated problem. The most advanced Karlsruhe Tritium Neutrino (KATRIN) experiment measures the energy distribution of electrons emitted in the process of tritium beta decay. The latest report gives an upper limit for the electron antineutrino rest energy of 450 meV [14]. Note that there are two possible arrangements for the values of the mass states: 1) m₁ < m₂ < m₃ (normal ordering), and 2) m₃ < m₁ < m₂ (inverted ordering). For both orderings the minimum mass difference refers to the difference between m₁ and m₂: c⁴(m₂² – m₁²) ≈ 7.4x10^-5 (eV)². Current experiments cannot determine which ordering is correct.

A non-zero neutrino mass poses serious challenges for the theory of neutrinos. First of all, for massless particles, the helicity, i.e., the spin component relative to the particle’s momentum, is equivalent to chirality, which is a fundamental property associated with the asymmetry between a quantum field and its mirror image [15]. For a massive particle, which moves with a speed less than the speed of light, the helicity depends on the reference frame, while the chirality does not depend on the reference frame. The weak interaction generates Dirac neutrinos of definite chirality: left-handed Dirac neutrinos and right-handed Dirac antineutrinos. In principle, for a massive neutrino, the helicity may be different from the chirality, i.e., the weak interaction may produce neutrinos with left-handed chirality but right-handed helicity. However, for ultra-relativistic neutrinos (m_kc² << E) the probability of this event is negligible. Secondly, unlike helicity, the chirality of a massive free neutrino is not conserved. Thus, a neutrino with left-handed chirality and left-handed helicity, while moving through free space, may transform into a neutrino with right-handed chirality and left-handed helicity. A neutrino with right-handed chirality does not participate in the weak interaction. Again, the probability of this transformation is negligible for ultra-relativistic neutrinos. In conclusion, for ultra-relativistic neutrinos and antineutrinos, one can safely ignore the fundamental difference between chirality and helicity.

Various extensions of the Standard Model of particle physics predict the existence of additional flavors of right-handed “sterile neutrinos” and left-handed “sterile antineutrinos,” which do not participate in the weak interaction [16,17,18]. While difficult to estimate, the rest masses of sterile neutrinos are expected to be much greater than the mean rest masses of the “active neutrinos”, i.e., the electron, muon and tau neutrinos. If neutrinos are Majorana fermions, then in nuclear decays the active Majorana neutrinos with left-handed chirality could be generated with a small admixture of sterile neutrinos with right-handed chirality.

The search for sterile neutrinos is an important area of research. Experiments with the Los Alamos Liquid Scintillator Detector (LSND) and the Mini Booster Neutrino Experiment (MiniBooNE) indicated the existence of sterile neutrinos with rest energy about 1 eV, but these results were not confirmed by other experiments [19]. The well-known cosmic X-ray line radiation, with energy of approximately 3.5 keV, was found to be consistent with dark matter sterile neutrinos of 7 keV rest energy [20]. The constraints on sterile neutrinos with rest energy in MeV – GeV scale are discussed, for example, in ref. [21]. In our paper we will concentrate on the search for sterile neutrinos using electron capture beta-decay.

In electron capture beta decay, an atomic nucleus of atomic number Z and electric charge Ze absorbs an electron from one of the atomic S-orbitals, transforming into a nucleus of atomic number (Z – 1) and radiating an electron neutrino:

$$\mathrm{Z}+{\mathrm{e}}^{-}\to (\mathrm{Z}-1)+{\nu }_{\mathrm{e}}.$$

(9)

This means that a proton in the nucleus absorbs an electron, transforms into a neutron, and radiates an electron neutrino. On a more fundamental level, due to the weak interaction, an up quark in the proton absorbs an electron and transforms into a down quark while radiating an electron neutrino. It has been suggested that the electron neutrino radiated in this process may have a small admixture of a sterile neutrino [22]. Indeed, assume that the mass of the sterile neutrino is smaller than the nuclear decay energy released in the capture process (i.e., the Q value). Also, assume that the change of the recoil energy, associated with the radiation of a sterile rather than an active electron neutrino, is much greater than the measurement uncertainty of the recoil energy. Under these conditions we may detect the emission of a massive sterile neutrino. Even if the amplitude of the sterile neutrino in the original wave function is very small, there will be a finite probability that the atom radiates a heavy sterile neutrino. In this case, the recoil energy of the daughter atom will be smaller than that in the case of radiation of an electron neutrino. In ref. [22] the authors reported a search for sterile neutrinos of rest energy from 370 keV to 640 keV using the electron capture beta decay ³⁷Ar → ³⁷Cl. In this decay, the atomic number Z changes from 18 to 17. The recoil energies of the daughter ³⁷Cl atoms were measured in the region of 3.6 eV to 7.6 eV. Electron capture beta decays ⁷Be → ⁷Li and ¹³¹Cs → ¹³¹Xe have been identified as the best candidates for the search of sterile neutrinos [23]. In particular, ⁷Be is the lightest atom which decays by electron capture. The daughter ⁷Li atom has a relatively large recoil energy, which is very important in the search for a sterile neutrino.

Improvements in detector technology and the ability to implant radioisotopes directly into the detectors has triggered a resurgence of nuclear recoil experiments (see for example [24]). In ref. [25], the authors used the Isotope Separator and Accelerator (ISAC) in Vancouver, Canada, to implant ⁷Be atoms into superconducting tunnel junction sensors (STJ). In a STJ, two superconductors are separated by a barrier, like in a Josephson junction. When a daughter ⁷Li atom deposits its recoil energy in the detector, electrons are excited above the small (about 1 meV) superconducting energy gap. The increase in current due to the excited electrons is proportional to the recoil energy. This technique allowed the authors of [25] to carry out a search for sterile neutrinos with rest energy in the region of 100 keV to 850 keV.

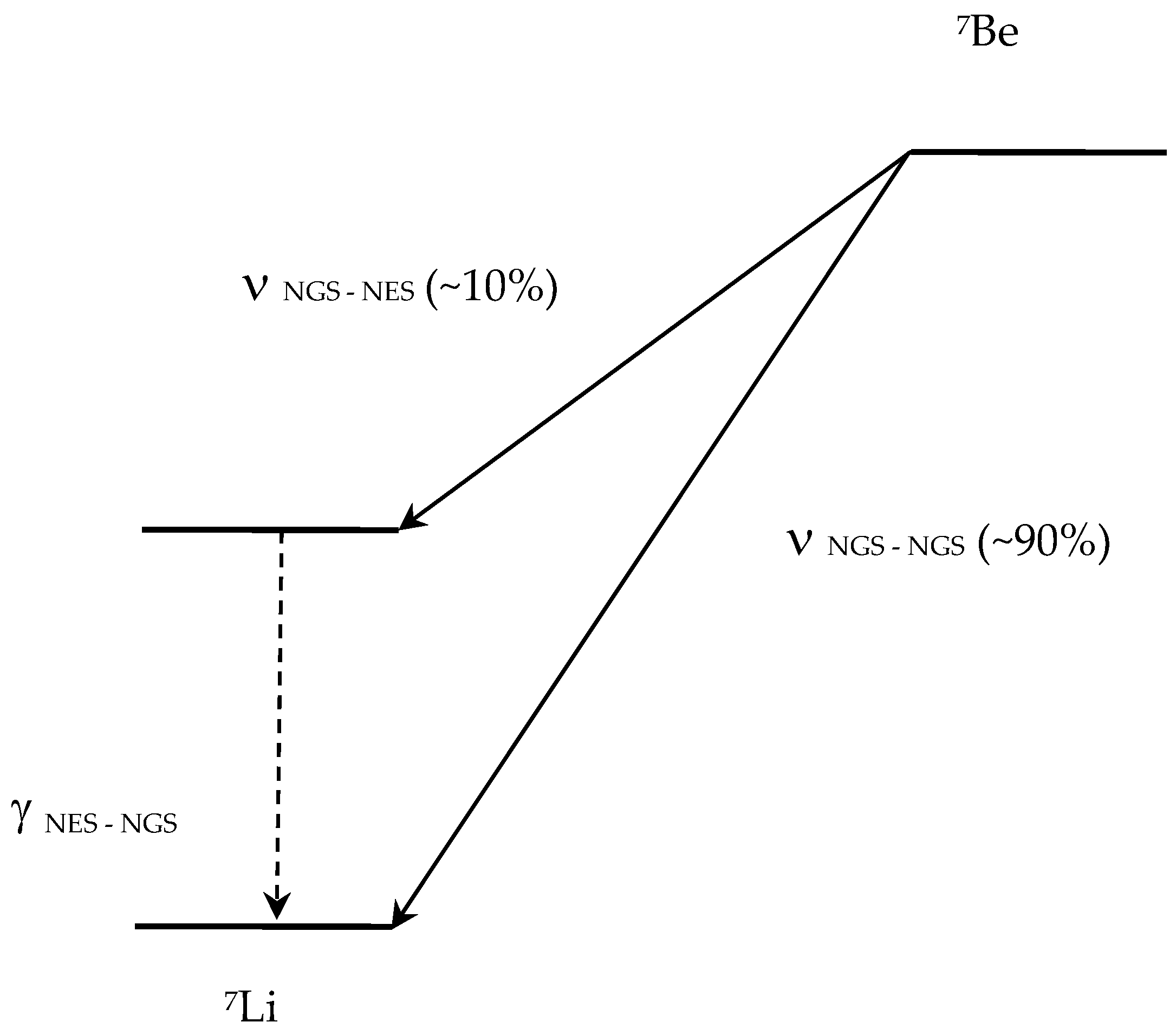
In this paper we report a comprehensive analysis of the two channels of ⁷Be electron capture beta decay. In the first (one-step) channel, the ⁷Be nucleus captures an electron and decays to the nuclear ground state of the daughter ⁷Li atom radiating a neutrino. In the second (two-step) channel, the ⁷Be nucleus captures an electron and decays to the excited state of the ⁷Li nucleus radiating a neutrino and then the ⁷Li nucleus transfers to its ground state, radiating a γ-ray photon. For both channels, we find the recoil energy assuming radiation of a massive neutrino. We derive analytical expressions for the recoil energy and discuss opportunities for searches for sterile neutrinos in electron capture beta decays.

2. Materials and Methods

We consider the electron capture beta decay ⁷Be → ⁷Li, illustrated in Figure 1.

About 90% of ⁷Be nuclei decay to the nuclear ground state of ⁷Li (_NGS-NGS), while about 10% decay into the nuclear excited state (_NGS-NES) and then transition to the nuclear ground state, radiating a γ-ray photon (_NES-NGS). We will consider the recoil energies of the daughter ⁷Li atoms for these two channels.

Firstly, we consider a one-step decay: an electron capture in a parent ⁷Be atom with a direct decay to the nuclear ground state of the daughter ⁷Li atom. The conceptually simplest situation occurs for an L-capture, i.e., the capture of an outer 2s-electron. After the capture of an outer L electron, the electronic system of the daughter atom will likely be in its ground state 1s²2s¹. After a K-capture, i.e., the capture of a 1s-electron, the nucleus transfers to its ground state, but the electronic system will likely be in the excited state 1s¹2s². We will focus on these two final electronic states and omit consideration of complicating situations where the daughter is left in some higher excited state (shake-ups) or is ionized (shake-offs). Recent experiments resolved the K and L recoil spectra and identified shake-up and shake-off contributions [25,26] allowing use of the results of our computations for both K- and L-captures.

To begin, we assume that a radioactive ⁷Be atom at rest absorbs an s-electron, radiating a neutrino. Let the rest mass of the daughter ⁷Li atom with the nucleus in the ground state be $M_{Li}$_, the rest mass of the emitted neutrino be$M_{\nu }$_, the energy difference between the initial rest energy of the parent ⁷Be atom and the final rest energy of the daughter atom be$Q$, the relativistic energy of the emitted neutrino be$E_{\nu }$, and the relativistic energy of the recoiling daughter atom be$E_{Li}$. From energy conservation we obtain

$$M_{Li}{c}^2+Q=E_{\nu }+E_{Li}.$$

(10)

Let the magnitude of the neutrino momentum be$p_{\nu }$and the magnitude of the recoil momentum of the ⁷Li atom be$p_{Li}$. Then the relativistic energies of a neutrino of rest mass$M_{\nu }$, and the daughter atom of rest mass$M_{Li}$, are given by the expressions

$$E_{\nu }=\sqrt{M_{\nu }^2{c}^4+p_{\nu }^2{c}^2},E_{Li}=\sqrt{M_{Li}^2{c}^4+p_{Li}^2{c}^2}.$$

(11)

From momentum conservation, the magnitude of the neutrino momentum equals the magnitude of the atomic recoil momentum:$p_{Li}=p_{\nu }$.

Secondly, we consider the two-step decay: the ⁷Be nucleus captures an s-electron, radiates a neutrino, and decays to the nuclear excited state of ⁷Li. Then, the ⁷Li nucleus promptly transfers to its ground state radiating a γ-ray photon. We assume that the lifetime of the nuclear excited state is much shorter than the measurement time of the recoil energy of the ⁷Li atom. After the neutrino radiation, the nucleus of the daughter ⁷Li atom will be in its excited state. The rest mass of the ⁷Li atom after neutrino radiation we will denote as $M_{L{i}^{\ast }}$, the momentum $p_{L{i}^{\ast }}$, and the relativistic energy $E_{L{i}^{\ast }}$. The relation between the energy, rest mass, and momentum of the ⁷Li atom in the excited nuclear state is described by the relativistic expression

$$E_{L{i}^{\ast }}=\sqrt{M_{L{i}^{\ast }}^2{c}^4+c^2{p}_{L{i}^{\ast }}^2}.$$

(12)

                   From energy conservation we have,

$$M_{Li}{c}^2+Q=E_{\nu }+E_{L{i}^{\ast }},$$

(13)

and, from momentum conservation, $p_{L{i}^{\ast }}=p_{\nu }.$

After radiation of the γ-ray photon, the ⁷Li nucleus transfers to its ground state. For the ⁷Li atom, with its nucleus in the ground state, we will use the same notations$E_{Li}$ and$p_{Li}$as we did for the one step channel. If we denote the momentum of the radiated photon as$p_{\gamma }$, and its energy as$E_{\gamma }=c{p}_{\gamma }$, then from energy conservation we have

$$E_{L{i}^{\ast }}=E_{Li}+E_{\gamma }.$$

(14)

From momentum conservation we obtain the vector equation,

$$\overrightarrow{p_{L{i}^{\ast }}}=\overrightarrow{p_{Li}}+\overrightarrow{p_{\gamma }}.$$

(15)

Taking into consideration that $p_{L{i}^{\ast }}=$ $p_{\nu }$, we obtain from Equation (15):

$$p_{Li}=\sqrt{{\left(p_{\nu }+p_{\gamma }\cos \theta \right)}^2+p_{\gamma }^2{\sin }^2\theta },$$

(16)

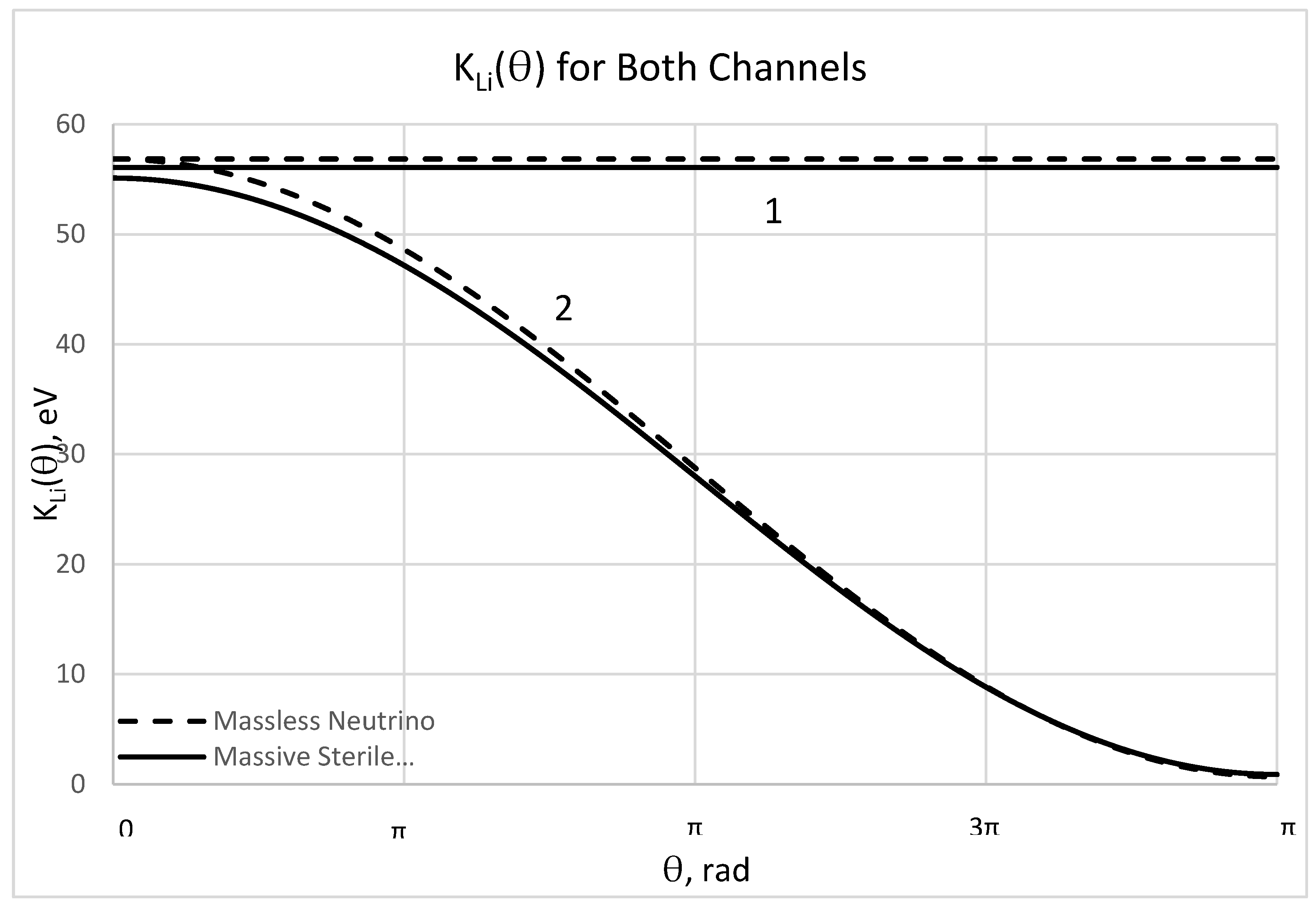
where$\theta$is the angle between the directions of motion of the neutrino and the photon, such that$\theta =0$corresponds to the case where the neutrino and the photon are emitted in the same direction. In the next section, based only on the conservation of energy and momentum, we will obtain exact analytical expressions for the recoil energy of the daughter ⁷Li atom in both channels.

3. Results

In this section we perform analytical computations and numerical estimations of the recoil kinetic energy of the daughter ⁷Li atom.

3.1. Derivation of the Analytical Expressions for the Recoil Energy in the One-Step Decay Channel

3.1.1. Massless Neutrino

Firstly, we will obtain the analytical formula for the recoil energy of the ⁷Li atom assuming that a massive neutrino does not exist. In this case, we can ignore the neutrino mass and take $M_{\nu }=0$. We begin with the equation,

$$M_{Li}{c}^2+Q=p_{\nu }c+E_{Li}.$$

(17)

By rearranging this equation and squaring, we obtain,

$${\left(M_{Li}{c}^2+Q-E_{Li}\right)}^2=p_{\nu }^2{c}^2.$$

(18)

Taking$p_{\nu }^2{c}^2$from the formula, $E_{Li}=\sqrt{M_{Li}^2{c}^4+p_{\nu }^2{c}^2}$, and expanding we find

$${\left(M_{Li}{c}^2+Q\right)}^2-2E_{Li}\left(M_{Li}{c}^2+Q\right)+E_{Li}^2=E_{Li}^2-M_{Li}^2{c}^4.$$

(19)

From this equation we have,

$${\left(M_{Li}{c}^2+Q\right)}^2+M_{Li}^2{c}^4=2E_{Li}\left(M_{Li}{c}^2+Q\right).$$

(20)

Finally, we obtain the expression for the relativistic energy of the ⁷Li atom:

$$E_{Li}=\frac{{\left(M_{Li}{c}^2+Q\right)}^2+M_{Li}^2{c}^4}{2(M_{Li}{c}^2+Q)}.$$

(21)

The kinetic recoil energy of the ⁷Li atom ${\mathrm{K}}_{\mathrm{L}\mathrm{i}}$can be found by subtracting its rest energy:

$$K_{Li}=E_{Li}-M_{Li}{c}^2.$$

(22)

Therefore,

$$K_{Li}=\frac{{\left(M_{Li}{c}^2+Q\right)}^2+M_{Li}^2{c}^4}{2(M_{Li}{c}^2+Q)}-M_{Li}{c}^2.$$

(23)

It can be rewritten as

$$K_{Li}=\frac{Q^2}{2(M_{Li}{c}^2+Q)},$$

(24)

giving a compact expression for the recoil kinetic energy of a massless neutrino single-step decay.

3.1.2. Recoil Energy after Radiation of a Massive Neutrino

The single-step channel with emission of a massive neutrino is governed by the three equations:

$$E_{\nu }=\sqrt{M_{\nu }^2{c}^4+p_{\nu }^2{c}^2},E_{Li}=\sqrt{M_{Li}^2{c}^4+p_{\nu }^2{c}^2},M_{Li}{c}^2+Q=E_{\nu }+E_{Li}.$$

(25)

From the first two equations in (25) we notice that

$$E_{Li}^2-M_{Li}^2{c}^4+M_{\nu }^2{c}^4=E_{\nu }^2.$$

(26)

From the third equation in (25) we obtain,

$${\left(M_{Li}{c}^2+Q-E_{Li}\right)}^2=E_{\nu }^2.$$

(27)

Expanding this expression and using Equation (26) we find,

$${\left(M_{Li}{c}^2+Q\right)}^2-2E_{Li}\left(M_{Li}{c}^2+Q\right)+E_{Li}^2=E_{Li}^2-M_{Li}^2{c}^4+M_{\nu }^2{c}^4.$$

(28)

The last equation can be simplified to give:

$${\left(M_{Li}{c}^2+Q\right)}^2+M_{Li}^2{c}^4-M_{\nu }^2{c}^4=2E_{Li}\left(M_{Li}{c}^2+Q\right).$$

(29)

From here we obtain the expression for the relativistic energy of the ⁷Li atom:

$$E_{Li}=\frac{{\left(M_{Li}{c}^2+Q\right)}^2+M_{Li}^2{c}^4-M_{\nu }^2{c}^4}{2(M_{Li}{c}^2+Q)}.$$

(30)

The recoil kinetic energy of the ⁷Li atom is given by,

$$K_{Li}=E_{Li}-M_{Li}{c}^2=\frac{Q^2-M_{\nu }^2{c}^4}{2\left(M_{Li}{c}^2+Q\right)}.$$

(31)

This expression is the same as that already available in the literature [25]. Note that the recoil kinetic energy approaches zero when the rest neutrino energy$M_{\nu }{c}^2$approaches$Q$. When $M_{\nu }{c}^2=Q$the entire energy of nuclear decay transforms into the rest energy of the neutrino with no residual kinetic energy. The rest energy of a radiated massive neutrino certainly cannot be greater than$Q.$

3.2. Derivation of the Analytical Expressions for the Recoil Energy in the Two-Step Decay Channel

In this subsection we obtain analytical expressions describing the recoil energy in the two-step channel. Firstly, we consider the decay with radiation of a neutrino with zero rest mass, and secondly with radiation of a massive neutrino.

3.2.1. Recoil Energy with a Massless neutrino

We will find the final recoil kinetic energy of the daughter atom after radiation of a massless neutrino and a γ-ray photon. After radiation of a massless neutrino, we have from energy conservation:

$$M_{Li}{c}^2+Q=p_{\nu }c+E_{L{i}^{\ast }}.$$

(32)

From this equation we obtain,

$${\left(M_{Li}{c}^2+Q-E_{L{i}^{\ast }}\right)}^2=p_{\nu }^2{c}^2.$$

(33)

Using Equation (12) for the relativistic energy$E_{L{i}^{\ast }}$, we express$p_{\nu }^2{c}^2$in terms of$E_{L{i}^{\ast }}$to obtain

$${\left(M_{Li}{c}^2+Q\right)}^2-2E_{L{i}^{\ast }}\left(M_{Li}{c}^2+Q\right)+E_{L{i}^{\ast }}^2=E_{L{i}^{\ast }}^2-M_{L{i}^{\ast }}^2{c}^4.$$

(34)

We can rewrite this equation in the following form:

$${\left(M_{Li}{c}^2+Q\right)}^2+M_{L{i}^{\ast }}^2{c}^4=2E_{L{i}^{\ast }}\left(M_{Li}{c}^2+Q\right).$$

(35)

From the last equation we obtain an expression for the relativistic energy$E_{L{i}^{\ast }}$:

$$E_{L{i}^{\ast }}=\frac{{\left(M_{Li}{c}^2+Q\right)}^2+M_{L{i}^{\ast }}^2{c}^4}{2(M_{Li}{c}^2+Q)}.$$

(36)

A similar derivation will provide the expression for$p_{\nu }c$. Beginning from Equation (32), we obtain

$${\left(M_{Li}{c}^2+Q-p_{\nu }c\right)}^2=E_{L{i}^{\ast }}^2.$$

(37)

Substituting expression (12) for the relativistic energy$E_{L{i}^{\ast }}$we obtain,

$${\left(M_{Li}{c}^2+Q\right)}^2-2p_{\nu }c\left(M_{Li}{c}^2+Q\right)+p_{\nu }^2{c}^2=p_{\nu }^2{c}^2+M_{L{i}^{\ast }}^2{c}^4.$$

(38)

We can rewrite the last equation in the form,

$${\left(M_{Li}{c}^2+Q\right)}^2-M_{L{i}^{\ast }}^2{c}^4=2p_{\nu }c\left(M_{Li}{c}^2+Q\right).$$

(39)

From here we obtain an expression for$p_{\nu }c$:

$$p_{\nu }c=\frac{{\left(M_{Li}{c}^2+Q\right)}^2-M_{L{i}^{\ast }}^2{c}^4}{2(M_{Li}{c}^2+Q)}.$$

(40)

Now, we will consider the second step of the decay, ultimately arriving at an expression for $K_{Li}$. From the energy conservation,

$$E_{L{i}^{\ast }}=E_{Li}+p_{\gamma }c.$$

(41)

We will rewrite this equation in the form

$${\left(E_{L{i}^{\ast }}-p_{\gamma }c\right)}^2=E_{Li}^2.$$

(42)

Substituting the expression for the relativistic energy$E_{Li}$we find

$$E_{L{i}^{\ast }}^2-2p_{\gamma }c{E}_{L{i}^{\ast }}+p_{\gamma }^2{c}^2=M_{Li}^2{c}^4+p_{Li}^2{c}^2.$$

(43)

Substituting Equation (16) for$p_{Li}$we obtain

$$E_{L{i}^{\ast }}^2-2p_{\gamma }c{E}_{L{i}^{\ast }}+p_{\gamma }^2{c}^2=M_{Li}^2{c}^4+{\left(p_{\nu }+p_{\gamma }\mathit{cos}\theta \right)}^2{c}^2+p_{\gamma }^2{c}^2{\mathit{sin}}^2\theta .$$

(44)

We simplify this equation to get

$$2p_{\gamma }c{E}_{L{i}^{\ast }}+2p_{\nu }{p}_{\gamma }{c}^2\cos \theta =E_{L{i}^{\ast }}^2-M_{Li}^2{c}^4-p_{\nu }^2{c}^2.$$

(45)

Substituting Equation (12) for the relativistic energy$E_{L{i}^{\ast }},$we obtain

$$2p_{\gamma }c\ast (E_{L{i}^{\ast }}+p_{\nu }c\cos \theta )=M_{L{i}^{\ast }}^2{c}^4-M_{Li}^2{c}^4.$$

(46)

From here we find an expression for$p_{\gamma }c$:

$$p_{\gamma }c=\frac{M_{L{i}^{\ast }}^2{c}^4-M_{Li}^2{c}^4}{{2(E}_{L{i}^{\ast }}+p_{\nu }c\cos \theta )}.$$

(47)

where$E_{L{i}^{\ast }}$is given by Equation (36) and$p_{\nu }c$by Equation (40).

Now that the expression for$p_{\gamma }c$is derived, the relativistic energy$E_{Li}$can be easily found using Equation (41):

$$E_{Li}=E_{L{i}^{\ast }}-p_{\gamma }c.$$

(48)

The recoil kinetic energy$K_{Li}$is then given by:

$$K_{Li}=E_{L{i}^{\ast }}-p_{\gamma }c-M_{Li}{c}^2,$$

(49)

where the first term on the right side of the formula is given by Equation (36) and the second term by Equation (47).

We now consider the special case of the maximum recoil kinetic energy when a photon is radiated in the same direction as the neutrino:$\theta =0$. We will use our expressions (49), (47), and (36) with$\theta =0$. Substituting expressions (47) and (36) for$p_{\gamma }c$and$E_{L{i}^{\ast }}$ to Equation (49), we obtain,

$$K_{Li}=\frac{{\left(M_{Li}{c}^2+Q\right)}^2+M_{L{i}^{\ast }}^2{c}^4}{2(M_{Li}{c}^2+Q)}-\frac{M_{L{i}^{\ast }}^2{c}^4-M_{Li}^2{c}^4}{{2(E}_{L{i}^{\ast }}+p_{\nu }c\cos 0)}-M_{Li}{c}^2.$$

(50)

From Equation (32), we can rewrite the denominator in the second term on the right side of this equation:

$$K_{Li}=\frac{{\left(M_{Li}{c}^2+Q\right)}^2+M_{L{i}^{\ast }}^2{c}^4}{2(M_{Li}{c}^2+Q)}-\frac{M_{L{i}^{\ast }}^2{c}^4-M_{Li}^2{c}^4}{2(M_{Li}{c}^2+Q)}-M_{Li}{c}^2.$$

(51)

The last equation can then be written as

$$K_{Li}=\frac{{\left(M_{Li}{c}^2+Q\right)}^2+M_{Li}^2{c}^4}{2(M_{Li}{c}^2+Q)}-M_{Li}{c}^2,$$

(52)

which simplifies to expression (24). Thus, we have obtained the same formula as for the recoil kinetic energy in the one-step decay. This means that, for a neutrino with zero rest mass, the maximum recoil energy in the two-step decay exactly equals the recoil energy in the one-step decay.

3.2.2. Recoil Kinetic Energy in a Two-Step Decay with Radiation of a Massive Neutrino and a γ-Ray Photon

Now we consider the situation when a radioactive ⁷Be nucleus decays to a ⁷Li nucleus in its excited state radiating a massive neutrino, then the ⁷Li nucleus transfers to its ground state, radiating a γ-ray photon. We will analyze the first step, then the second step, and then derive an expression for the final recoil kinetic energy. Beginning from expressions for the relativistic energies (11) and (12) we obtain,

$$E_{{Li}^{\ast }}^2-M_{L{i}^{\ast }}^2{c}^4+M_{\nu }^2{c}^4=E_{\nu }^2.$$

(53)

Next, from the conservation of energy (Equation (13)) we have,

$${\left(M_{Li}{c}^2+Q-E_{L{i}^{\ast }}\right)}^2=E_{\nu }^2.$$

(54)

From these two equations,

$${\left(M_{Li}{c}^2+Q\right)}^2-2E_{L{i}^{\ast }}\left(M_{Li}{c}^2+Q\right)+E_{L{i}^{\ast }}^2=E_{L{i}^{\ast }}^2-M_{L{i}^{\ast }}^2{c}^4+M_{\nu }^2{c}^4.$$

(55)

We can write the last equation in the form,

$${\left(M_{Li}{c}^2+Q\right)}^2+M_{L{i}^{\ast }}^2{c}^4-M_{\nu }^2{c}^4=2E_{L{i}^{\ast }}\left(M_{Li}{c}^2+Q\right).$$

(56)

From here we find the equation for$E_{L{i}^{\ast }}$:

$$E_{L{i}^{\ast }}=\frac{{\left(M_{Li}{c}^2+Q\right)}^2+M_{L{i}^{\ast }}^2{c}^4-M_{\nu }^2{c}^4}{2(M_{Li}{c}^2+Q)}.$$

(57)

A similar derivation provides an expression for$E_{\nu }$. From Equation (13) we obtain

$${\left(M_{Li}{c}^2+Q-E_{\nu }\right)}^2=E_{L{i}^{\ast }}^2.$$

(58)

Substituting expression (53) for$E_{L{i}^{\ast }}^2$we have

$${\left(M_{Li}{c}^2+Q\right)}^2-2E_{\nu }\left(M_{Li}{c}^2+Q\right)+E_{\nu }^2=E_{\nu }^2-M_{\nu }^2{c}^4+M_{L{i}^{\ast }}^2{c}^4.$$

(59)

The last equation we can rewrite in the form

$${\left(M_{Li}{c}^2+Q\right)}^2-M_{L{i}^{\ast }}^2{c}^4+M_{\nu }^2{c}^4=2E_{\nu }\left(M_{Li}{c}^2+Q\right).$$

(60)

From here we obtain the expression for$E_{\nu }$:

$$E_{\nu }=\frac{{\left(M_{Li}{c}^2+Q\right)}^2-M_{L{i}^{\ast }}^2{c}^4+M_{\nu }^2{c}^4}{2(M_{Li}{c}^2+Q)}.$$

(61)

Now, we will consider the second step of the decay, ultimately arriving at an expression for$K_{Li}$. Again, we begin with conservation of energy,

$$E_{L{i}^{\ast }}=E_{Li}+p_{\gamma }c.$$

(62)

By rearranging the equation and squaring,

$${\left(E_{L{i}^{\ast }}-p_{\gamma }c\right)}^2=E_{Li}^2.$$

(63)

Substituting Equation (11) for$E_{Li}$we obtain,

$$E_{L{i}^{\ast }}^2-2p_{\gamma }c{E}_{L{i}^{\ast }}+p_{\gamma }^2{c}^2=M_{Li}^2{c}^4+p_{Li}^2{c}^2.$$

(64)

Next, substituting Equation (16) for$p_{Li}$, we have

$$E_{L{i}^{\ast }}^2-2p_{\gamma }c{E}_{L{i}^{\ast }}+p_{\gamma }^2{c}^2=M_{Li}^2{c}^4+{\left(p_{\nu }+p_{\gamma }\mathit{cos}\theta \right)}^2{c}^2+p_{\gamma }^2{c}^2{\mathit{sin}}^2\theta .$$

(65)

Expanding, we obtain,

$$E_{L{i}^{\ast }}^2-2p_{\gamma }c{E}_{L{i}^{\ast }}+p_{\gamma }^2{c}^2=M_{Li}^2{c}^4+p_{\nu }^2{c}^2+2p_{\nu }{p}_{\gamma }{c}^2\cos \theta +p_{\gamma }^2{c}^2{\mathit{cos}}^2\theta +p_{\gamma }^2{c}^2{\sin }^2\theta .$$

(66)

From the last equation we obtain

$$2p_{\gamma }c{E}_{L{i}^{\ast }}+2p_{\nu }{p}_{\gamma }{c}^2\cos \theta =E_{L{i}^{\ast }}^2-M_{Li}^2{c}^4-p_{\nu }^2{c}^2.$$

(67)

Substituting Equation (12) for$E_{L{i}^{\ast }}^2,$ where$p_{L{i}^{\ast }}=p_{\nu }$, we find the equation

$$2p_{\gamma }c\ast \left(E_{L{i}^{\ast }}+p_{\nu }c\cos \theta \right)=M_{L{i}^{\ast }}^2{c}^4-M_{Li}^2{c}^4.$$

(68)

where$p_{\nu }c=\sqrt{E_{\nu }^2-M_{\nu }^2{c}^4}$.

This equation yields an expression for$p_{\gamma }c$:

$$p_{\gamma }c=\frac{M_{L{i}^{\ast }}^2{c}^4-M_{Li}^2{c}^4}{{2(E}_{L{i}^{\ast }}+\sqrt{E_{\nu }^2-M_{\nu }^2{c}^4}·\cos \theta )}.$$

(69)

Now that an expression for$p_{\gamma }c$has been derived, the relativistic energy$E_{Li}$can be easily computed:

$$E_{Li}=E_{L{i}^{\ast }}-p_{\gamma }c.$$

(70)

Finally, the recoil kinetic energy$K_{Li}$for the two-step decay is given by Equation (49), where$E_{L{i}^{\ast }}$can be found from Equation (57) and$p_{\gamma }c$from Equation (69).

3.3. Numerical Estimates

In this subsection we estimate the recoil kinetic energy of the ⁷Li atom assuming the rest energy of the postulated sterile neutrino is$M_{\nu }{c}^2=100\mathrm{k}\mathrm{e}\mathrm{V}$. We will use the following values of parameters available in literature [27]: the rest energy difference between the original state of the ⁷Be atom and the final state of the ⁷Li atom$Q\approx 862\mathrm{k}\mathrm{e}\mathrm{V}$, the rest energy difference between the ⁷Li atom with the excited nuclear state and the final state of the ⁷Li atom

$${(M}_{L{i}^{\ast }}-M_{Li})c^2=478\mathrm{k}\mathrm{e}\mathrm{V},$$

(71)

and the rest energy of the final state of the ⁷Li atom$M_{Li}{c}^2=6.535$GeV.

Using these values, for the one-step decay, we obtain the following estimates: after radiation of a massless neutrino,$K_{Li}\approx 56.8\mathrm{e}\mathrm{V}$, and after radiation of a 100 keV massive sterile neutrino,$K_{Li}\approx 56.1\mathrm{e}\mathrm{V}$.

For the two-step decay we present the recoil kinetic energy of the ⁷Li atom as a function of the angle

between the directions of propagation of the neutrino and the photon (see Figure 2). The recoil energy monotonically decreases as increases. The solid lines show the recoil energy after emission of a 100 keV neutrino, and the dashed lines show the recoil energy after emission of a massless neutrino. The horizontal lines show the values of the recoil energy for the one-step decay, and the curves show the values of the recoil energy for the two-step decay.

As we have shown previously, in the case of radiation of a massless neutrino, at$\theta =0$, the final recoil energy of the ⁷Li atom for the two-step decay is exactly the same as the recoil energy for the one-step decay (the value of the recoil energy is, approximately, 56.8 eV). At$\theta =\pi$, corresponding to the photon and the massless neutrino being emitted in opposite directions, the recoil kinetic energy,$K_{Li}\approx 0.68\mathrm{e}\mathrm{V}$. If a 100 keV sterile neutrino is radiated, then for the two-step decay, at$\theta =0$, we obtain:$K_{Li}\approx 55.1$eV, and at$\theta =\pi$, we have$K_{Li}\approx 0.88\mathrm{e}\mathrm{V}$.

4. Discussion

In this work we studied the recoil energy of the ⁷Li atom after the electron capture beta-decay of a radioactive ⁷Be atom. We were interested in the opportunity to use the recoil energy in the search for a massive right-handed sterile neutrino, which could be mixed with the electron neutrino radiated in the nuclear decay process. We have considered two channels of the decay. In the first one-step channel, the ⁷Be nucleus directly decays to the ground state of the ⁷Li nucleus, radiating a neutrino. In the second two-step channel, the ⁷Be nucleus decays to the excited state of the ⁷Li nucleus radiating a neutrino, then the ⁷Li nucleus transfers to its ground state, radiating a γ-ray photon. We assume that in both channels the recoil energy of the ⁷Li atom is measured after the ⁷Li nucleus comes to its ground state. For the case of an L-capture (capture of a 2s-electron), after the nuclear decay, the electron shell of the daughter ⁷Li atom likely comes to its ground state 1s²2s¹. For the case of the K-capture (capture of a 1s-electron), the electron shell likely comes to its excited state 1s¹2s² which is usually followed by emission of an Auger electron [25]. For the one-step channel our result confirms the formula published previously in [25]. For the two-step channel, to the best of our knowledge, the exact analytical expressions for the recoil kinetic energy have not been published before.

Based on our results, we wish to discuss the opportunities to detect a sterile neutrino by measuring the recoil energy of the daughter ⁷Li atom. If the rest energy of the sterile neutrino is smaller than the total energy $Q$ released in the electron capture beta-decay, then we expect a small but finite probability that the electron neutrino generated in the nuclear decay collapses into a sterile neutrino. The simplest way to detect a sterile neutrino is to observe the change of the recoil kinetic energy of the daughter ⁷Li atom in the one-step decay. However, we wish to attract the attention of experimentalists to other options. We pointed out already that the difference between the recoil energy in the one-step decay and maximum recoil energy in the two-step decay is exactly zero for emission of massless neutrinos. A finite value of this difference would indicate the radiation of a massive neutrino. In addition, the difference between the maximum and the minimum recoil energy in the two-step decay may also be exploited in detection schemes.