Molecular Design of H2 Storage/Release Devices: A Direct ab initio MD Study

1. Introduction

Carbon materials are among the most promising candidates for hydrogen (H₂) storage due to their lightweight nature and chemical stability.[1,2,3] For instance, the interactions between carbon nanotubes (CNTs) and H₂,[4,5,6] as well as between graphene (GR) and H₂, have been extensively studied.[7,8,9] However, the binding energies of H₂ to these carbon materials are typically less than 1 kcal/mol,[10,11] which results in low hydrogen storage efficiency for pristine carbon materials.

To address this limitation, alkali metals such as lithium atoms or ions have been doped onto carbon surfaces. For example, lithium-doped graphene (GR-Li) has been shown to increase the adsorption energy of H₂ to approximately 5–6 kcal/mol.[12,13] Moreover, it has been reported that up to 10 H₂ molecules per Li atom can be efficiently bound to GR-Li. Other metals, such as Na, K, Mg, and Al, have also been shown to have hydrogen storage capacity.[14,15,16,17]

In the present study, we theoretically explore the potential of hydrogen storage via chemical bonding between GR nanoflakes and hydrogen atoms. One known approach for chemical hydrogen storage is the hydrogenation of aromatic hydrocarbons (organic chemical hydride method), which allows for both the storage and transport of hydrogen in a chemically bound form. A representative example is the hydrogenation of benzene to cyclohexane:[18,19,20,21]

benzene + 3 H₂ → C₆H₁₂ (cyclohexane)

Cyclohexane is produced by the addition of hydrogen atoms to the π-bonds of the benzene ring. This product can be transported, and hydrogen can later be released via catalytic dehydrogenation. Thus, both metal doping and chemical hydrogenation are considered viable strategies for H₂ storage.

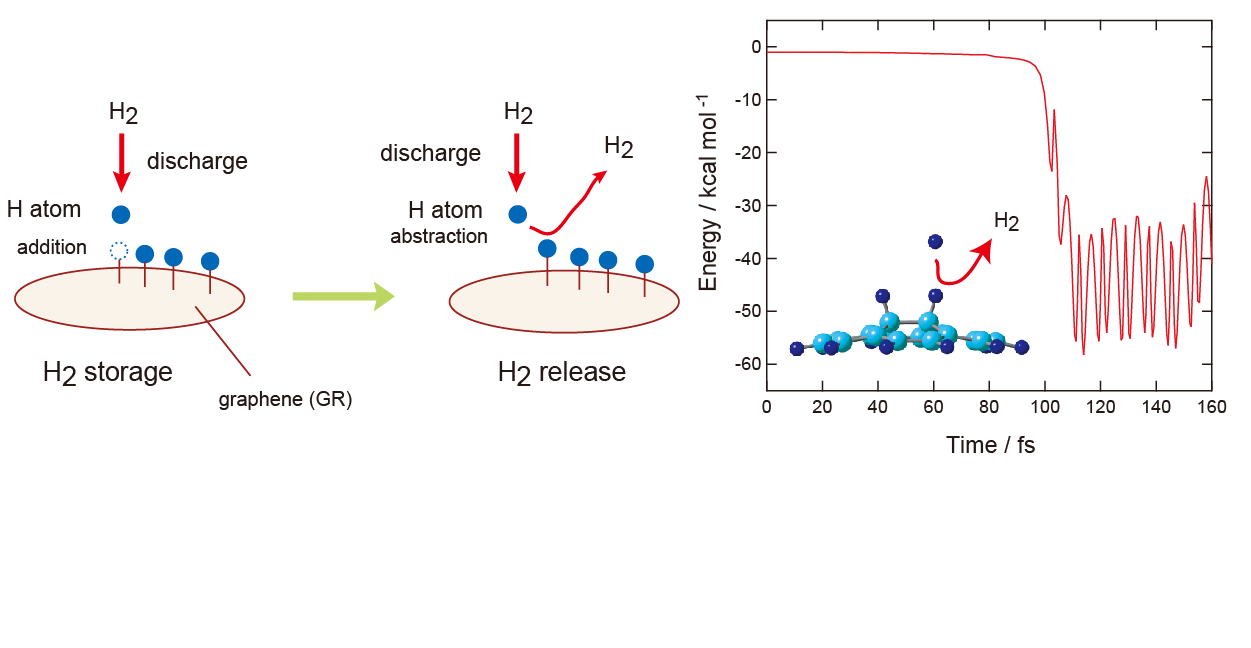
In the present study, we perform a molecular-level design of a GR-based hydrogen storage system using direct ab initio molecular dynamics (AIMD) simulations. Figure 1 shows a schematic illustration of the reaction model investigated in this study. The overall process can be described as follows:

H₂　+　hν (discharge) → H + H

Molecular hydrogen (H₂) is readily dissociated into atomic hydrogen via electrical discharge. The resulting hydrogen atoms are then introduced to the graphene surface, where they react with carbon atoms to form C–H bonds on GR surface:

GR + H → GR–H  (hydrogen atom addition)
  GR–H + H → H–(GR)–H  (H₂storage)

Through this process, H₂ is stored on GR surface in the form of two hydrogen atoms (H₂storage). The release of hydrogen can occur via the following reactions:

H–GR–H + H → GR–H + H₂  (H₂ release)
  GR–H + H → GR + H₂

The H-atom, generated by discharge, attacks to the C-H hydrogen of H-(GR)-H, and then H₂ is formed (H₂ molecule). The primary reaction of interest in this study is the hydrogen release process (H₂ release):

H–(GR)–H + H → GR–H + H₂

(Reaction I)

For comparison, we also investigate the energetics of the hydrogen addition reaction:

GR + H → GR–H

(Reaction II)

Both the energetics and the reaction times for hydrogen storage and release are evaluated using direct AIMD simulations.

For Reaction II,[22,23] we investigated previously the activation and reaction energies by means of DFT methods. Also, direct H₂ addition reaction to GR, H₂ + GR → H-(GR)-H 　(Reaction III), were investigated.[24] The activation energies of Reactions II and III were calculated to be 5-7 and 80 kcal/mol, respectively.[22,23,24] These results indicated that the direct H₂ addition to GR (Reaction III) is impossible under the normal condition. In contrast, Reaction II is possible in normal condition if H-atom is generated.

2. Computational Details

2.1. Ab Initio Calculations

Four types of graphene nanoflake composed of 7, 14, and 19 benzene rings were used in this study, and are referred to as “GR04, GR07, GR14, and GR19” hereafter, respectively. Figure 2A shows the structures of GRs used in this calculations. DFT calculations were performed using the CAM-B3LYP Coulomb-attenuating exchange-correlation energy functional[25] with the 6-31G(d) and 6-311G(d,p) basis sets.[26] The structure of GRs ware first optimized, after which one or two hydrogen atom was placed in the central region of the GR. The mono- and di-hydrogenated GRs were expressed as GR-H and H-(GR)-H, respectively. The structures of GR-H and H-(GR)-H were then fully optimized. The binding energy of the H atom to GR is defined as follows:

$$-E_{bind}=E\left(GR-H\right)-[E\left(H\right)+E\left(GR\right)]$$

(1)

where E(X) is the total energy of X. The H atom binds exothermally to the GR when E_bind(H) is positive.

Atomic charges were calculated using the natural bond population analysis (NPA) algorithm.[27] All calculations were performed using the Gaussian 09 software package.[28] We previously investigated interactions between graphene and various molecules using DFT at the same level of theory.[13,17,29,30] A similar technique was used for the H-(GR)-H system in this study.

2.2. Direct AIMD Calculations

Figure 2B shows the initial configuration of the collision reaction system. For the direct AIMD calculations, the H-(GR)-H cluster were optimized at the CAM-B3LYP/6-31G(d) level. Subsequently, H atom was positioned above the cluster at a distance of r1=4.0–4.5 Å; the trajectory began from this position. The collision energies of H-atom (E_coll) were set to 1-15 kcal/mol at time zero. The near collinear collision was assumed: impact parameter (b) was b=0-0.5 Å. The excess energy, momentum vector, and rotational temperature of the reaction system were assumed to be zero (at 0 fs). The equations of motion for N atoms in the reaction system are given by

$$\begin{array}{l}{\displaystyle \frac{d{Q}_j}{dt}}={\displaystyle \frac{\partial H}{\partial P_j}}\\ {\displaystyle \frac{d{P}_j}{dt}}=-{\displaystyle \frac{\partial H}{\partial Q_j}}=-{\displaystyle \frac{\partial U}{\partial Q_j}}\end{array}$$

(2)

where j = 1–3N, H is the classical Hamiltonian, Q_j is the Cartesian coordinate of the j-th mode, U is the potential energy, and P_j is the conjugated momentum; these equations were numerically solved (NVE ensemble). The velocity Verlet algorithm, with a time step of 0.10–0.25 fs, was used to solve the equations of motion for the system. The maximum simulation time was 2.0 ps. The total energy drift in all trajectory calculations was <0.01 kcal/mol. The numbers of trajectory runs were 22 (E_coll = 1.0), and 5 (E_coll = 2.0-15), respectively. The effects of the functional on the reaction mechanism were investigated using the APFD functional and compared with those of the CAM-B3LYP functional. Direct AIMD calculations were performed using custom-made AIMD codes.[31,32,33,34]

3. Results

• Structures at stationary points for the hydrogen abstraction reaction.

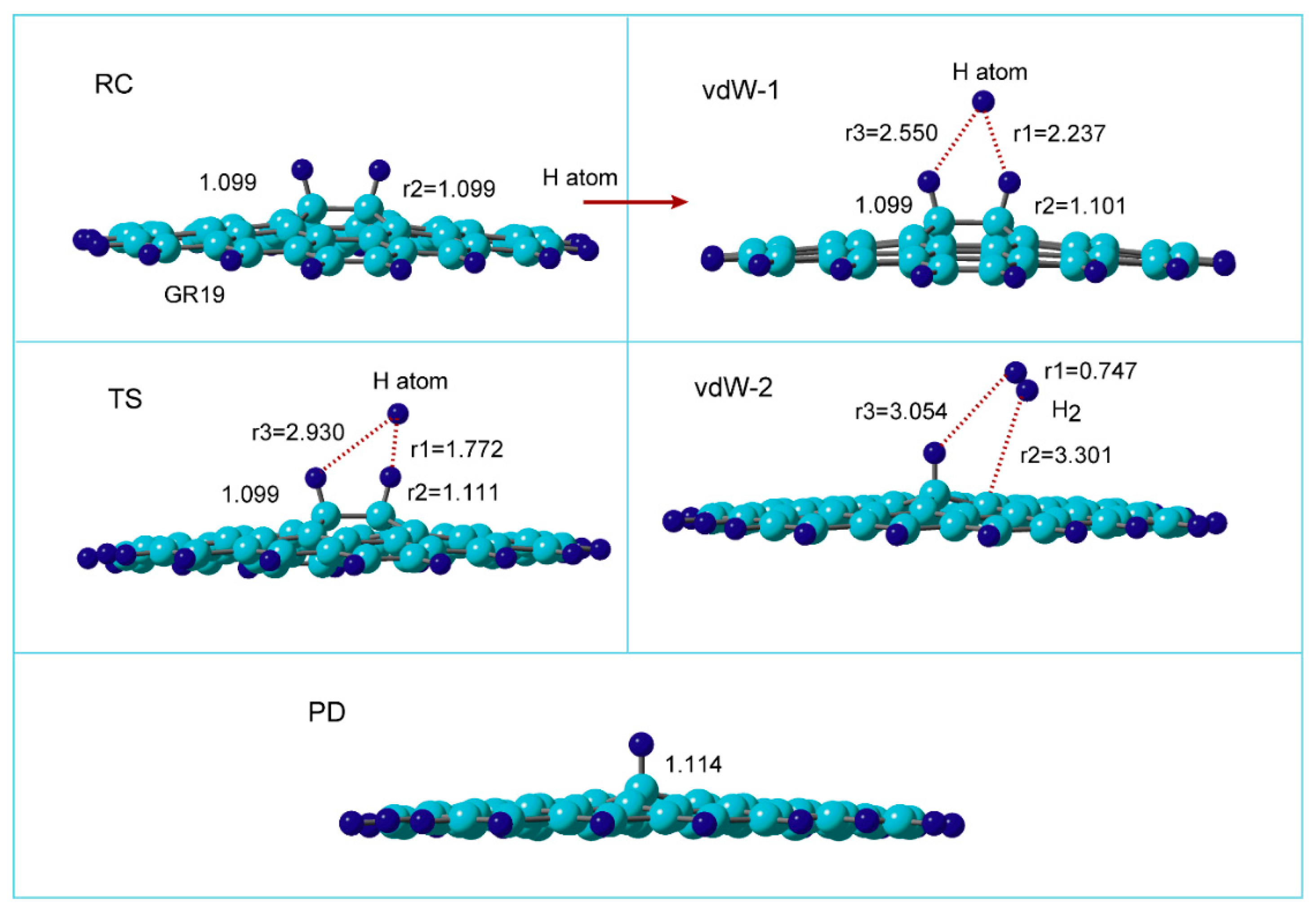
Figure 3 shows the optimized structures along the reaction coordinate for the reaction:

H-(GR)-H + H → H-(GR) + H₂,

where H-(GR)-H means hydrogenated GR (two H-atoms are added to the surface of GR).

At reactant state (RC), the C-H bond length was calculated to be r2=1.099 Å. After the injection of hydrogen (H) atom to H-(GR)-H, van der Waals (vdW) complex was first formed on the surface in the initial state of the reaction (denoted to vdW-1). The H-atom was located between two surface C-H sites and made the bridge structure composed of C-H--H--H-C (r1=2.237 and r3=2.550 Å). The C-H bond was slightly elongated by the interaction with the H-atom (the C-H bond length was changed from r2= 1.099 to 1.101 Å).

Next, the reaction reached to transition state (TS) via vdW-1. The H-atom was located at r1=1.772, and r3=2.930 Å at TS. The C-H bond of the surface C-H site was elongated at TS (r2=1.111 Å). The H-H bond (r1=1.772 Å) was significantly longer than that of H₂ molecule in gas phase (r(H-H)= 0.746 Å). After TS, H₂ molecule was formed by the H-atom abstraction.

In the final state of the reaction, vdW complex was formed (vdW-2), where H₂ was weakly bound to the radical site of the surface. H₂ was located at r2=3.301 Å from the surface. The H-H bond of H₂ was r1=0.747 Å, which is a normal bond length of H₂ molecule. After the H₂ reduction from H-(GR)-H, the product (PD) was remained as H-(GR).

B.

Energy diagram for the hydrogen abstraction reaction

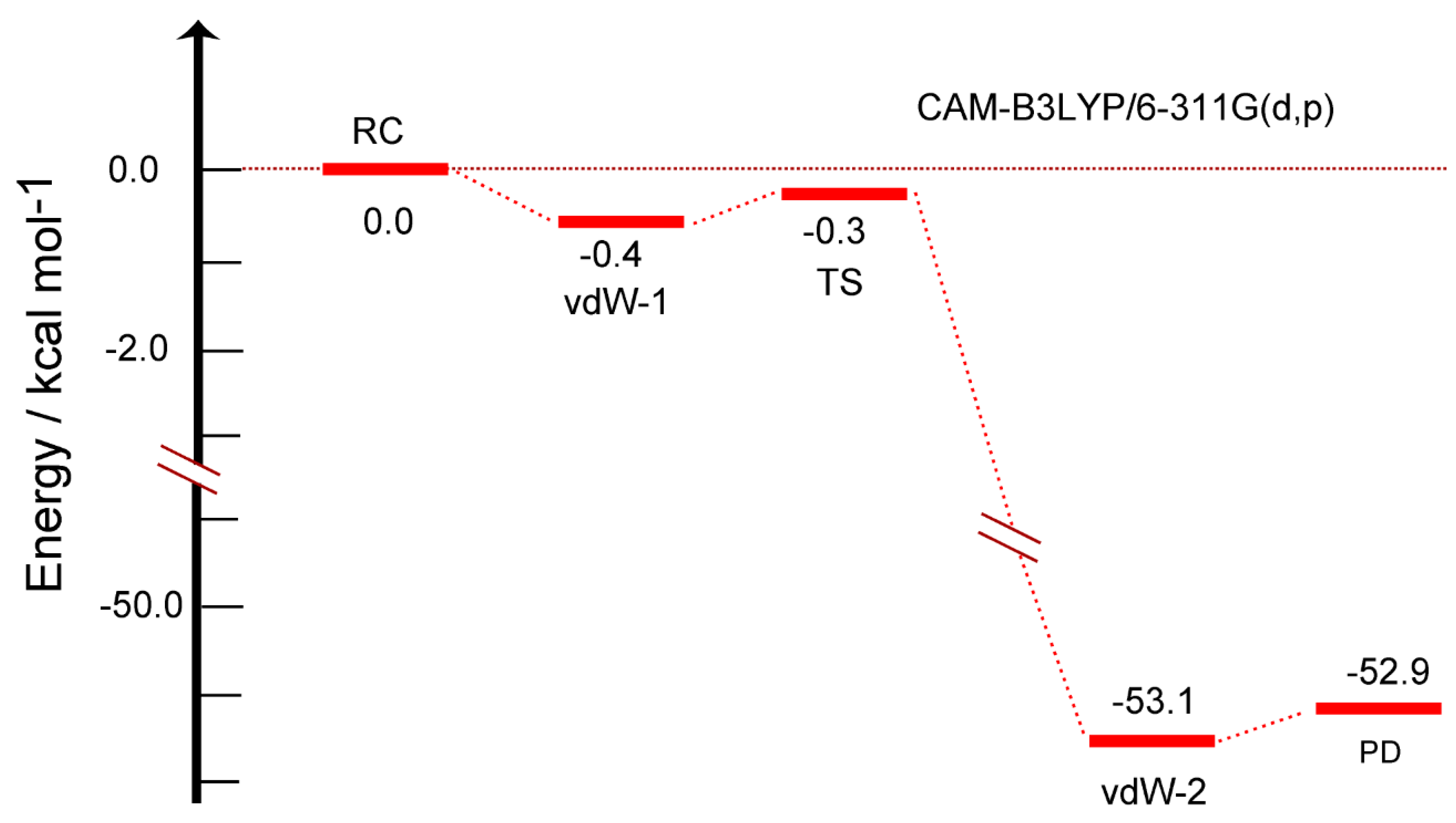
The energy diagram for the reaction is given in Figure 4. The energy level of RC corresponds to the total energy of H-GR-H + H. The initial vdW state (vdW-1) was -0.4 kcal/mol lower in energy than that of RC (zero level). The energy of TS was -0.3 kcal/mol, indicating that the hydrogen abstraction reaction can proceed without activation energy.

After TS of the H-abstraction, the energy of reaction system decreased largely to -53.1 kcal/mol because the H-H bond was newly formed by the formation of H₂. The energy level of vdW state at the PD state was -53.1 kcal/mol (vdW-2). The energy of product state (PD) (-52.9 kcal/mol) was slightly higher than that of vdW-2, where H₂ was dissociated from the surface. The reaction can be expressed as:

RC[H(radical) + H-(GR19)-H] → vdW-1 → TS → vdW2 → PD[(GR19)-H + H₂]. This reaction spontaneously occurs without activation barrier.

C.

Intrinsic reaction coordinate

The intrinsic reaction coordinate (IRC) for the hydrogen abstraction reaction from H-(GR)-H was calculated at the CAM-B3LYP/6-31G(d) level. The result is given in Figure S1 (in supporting information: SI). The point at s=0.0 in (amu)^1/2Bohr corresponds to TS structure in the reaction, and the points at s= -0.5 and s=3.0 indicate the reactant and product regions, respectively. The shape of IRC suggested that the energy decreases drastically after the TS point because the H₂ molecule with a strong H-H bond is formed. The structure at s= -0.5 was close to that of vdW-1. After TS, the energy decreased largely to -23.0 kcal/mol (s=1.2) and -55.0 kcal/mol (s =3.2). At s=3.2, H₂ molecule dissociated from H-GR as H₂ molecule. This IRC calculation indicated that the TS structure connected between RC and PD states for the H-abstraction reaction.

D.

Reaction dynamics

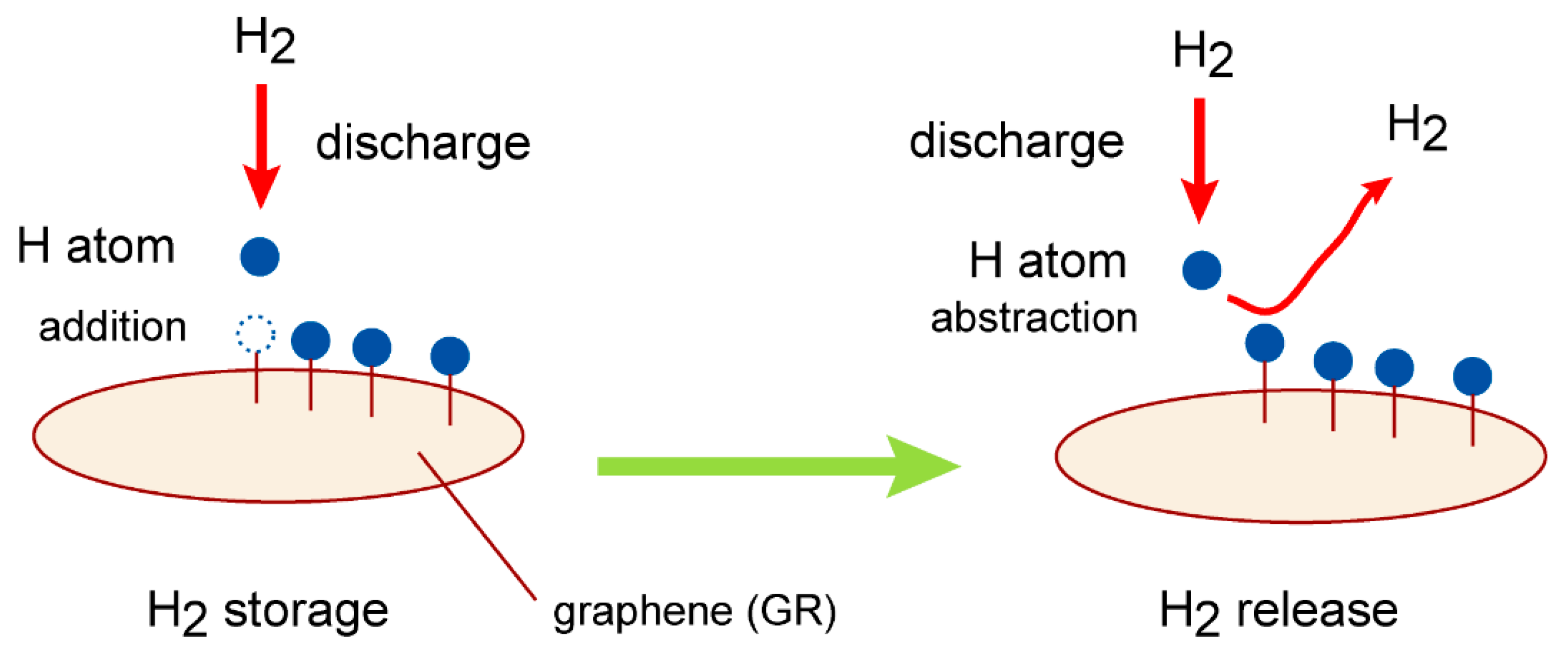
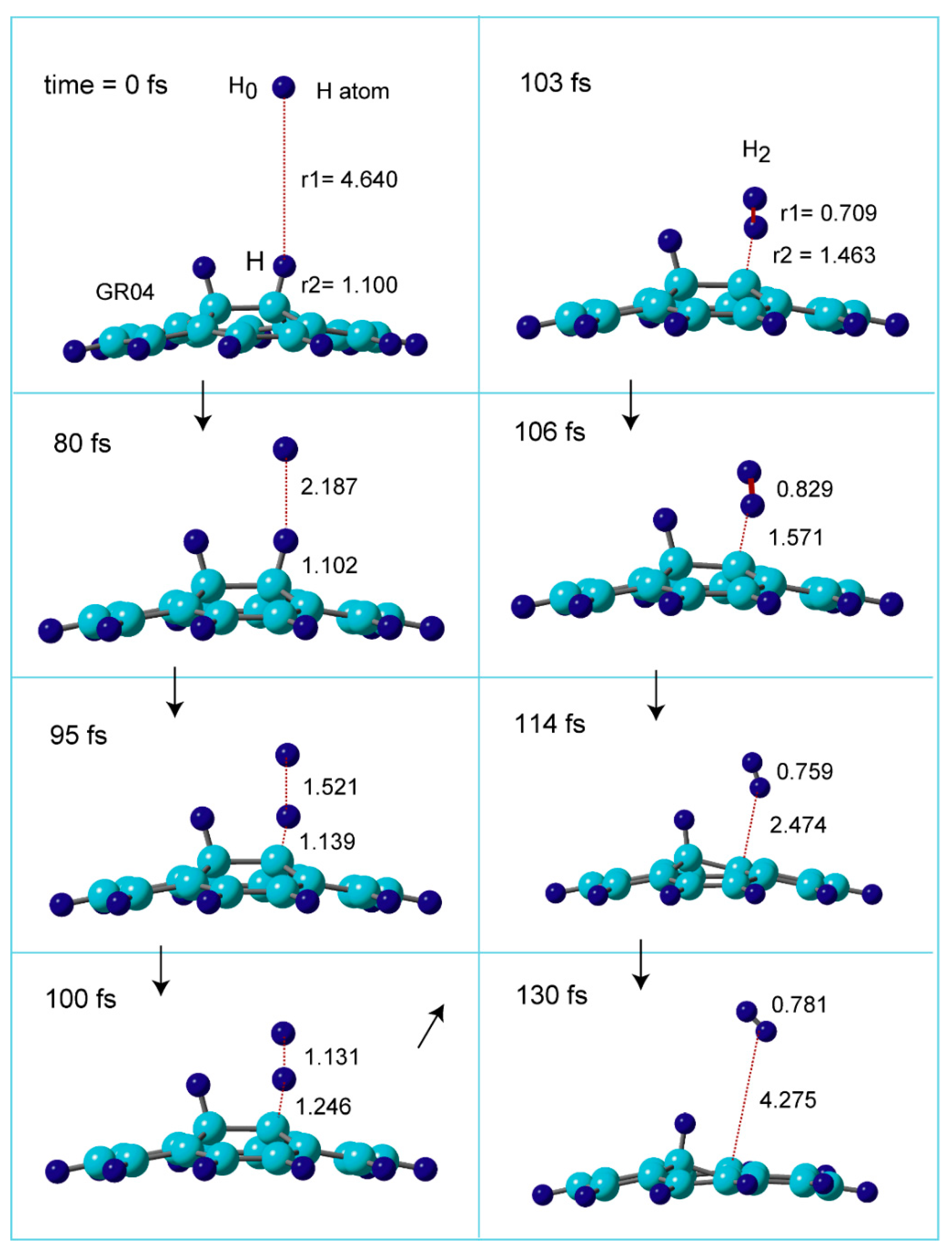
The direct AIMD calculations were carried out at the CAM/6-31G(d) level of theory. GR07 was used as graphene nanoflake. The collision energy was E_coll=1.0 kcal/mol. The snapshots of hydrogen abstraction reaction on GR are illustrated in Figure 5, where the reaction is expressed as H + H-(GR)-H → H-(GR) + H₂.

In the initial structure at time = 0.0 fs, the H-atom was located at r1=4.640 Å. The C-H distance of surface as r2=1.100 Å. At time = 80 fs, the H-atom was located at r1=2.187 Å, and the C-H bond was r2=1.102 Å. The H-atom was more closed to the C-H (r1=1.521 and r2=1.139 Å) at 95 fs. At 100 fs, the structure was close to that of TS (r1=1.131 and r2=1.246 Å), indicating that the C-H bond was largely elongated by the H-abstraction (1.246 Å). At 103 fs, H₂ molecule was completely formed: H-H bond length was r1=0.709 Å and H₂ was located at r2=1.463 Å from the surface. The distances of H₂ from the surface were changed to 1.571 Å (106 fs), 2.474 Å (114 fs), 4.275 Å (130 fs), suggesting that H₂ leaved rapidly from the surface. Thus, the H-abstraction and H₂ formation reactions were completed at 130 fs.

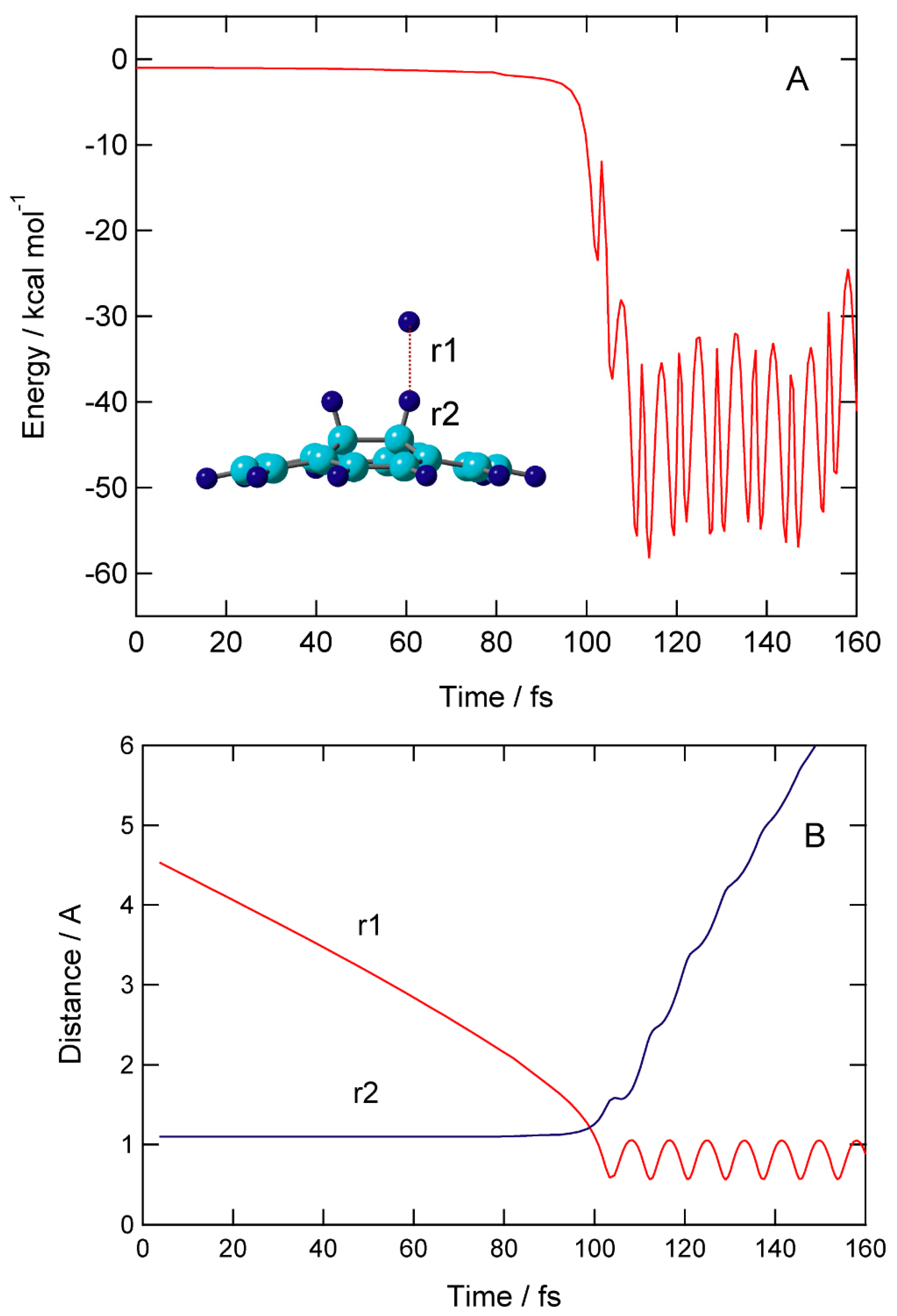
Time evolution of potential energy (PE) and interatomic distances (r1 and r2) are given in Figure 6.

At time zero, the H atom started from r1=4.640 Å above the surface of H-(GR)-H. The H atom gradually approached to C-H site of H-(GR)-H: distances (r1, r2)= (3.460, 1.100) at 40 fs, (2.827, 1.101) at 60 fs, and (2.187, 1.102) at 80 fs. PE was slightly decreased: -0.5 kcal/mol at 80 fs. PE drastically changed around time= 100 fs, where the hydrogen abstraction rapidly occurred a time 95-105 fs. The H-H bond was newly formed after the abstraction, and H₂ molecule was formed at this time. After the H₂ formation, H₂ was rapidly dissociated from the surface: the distances of H₂ from the surface were 3.2 Å (120 fs) and 5.0 Å (140 fs). PE vibrated largely in the ranges (-40) - (-55) kcal/mol after the H₂ dissociation.

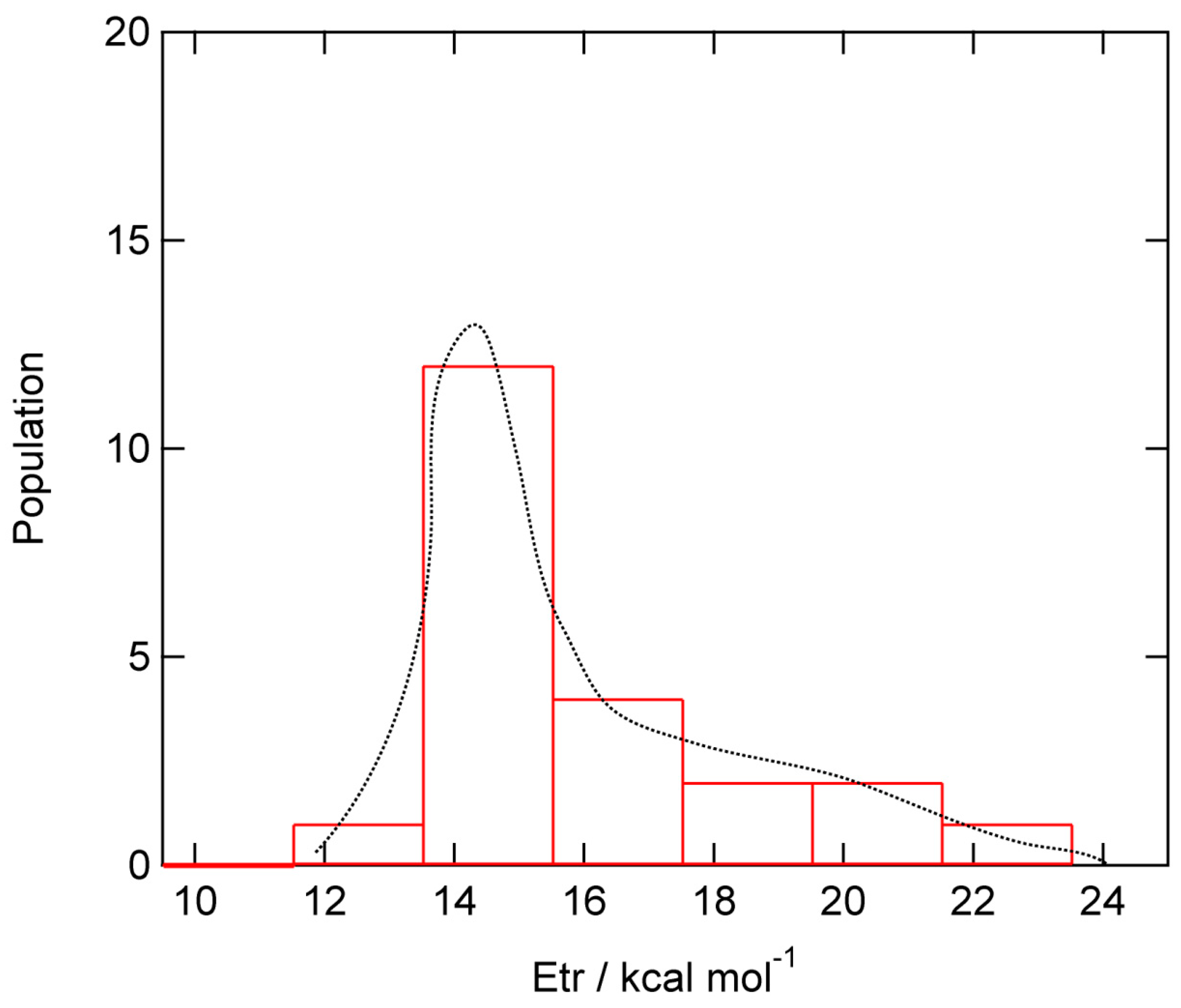
A total of 22 trajectories were run at collision energy of E_coll =1.0 kcal/mol. The translational energies of product H₂ (E_trans) formed by the H-abstraction reaction (H-(GR)-H + H → H-(GR) + H₂) are given in Figure 7. E_trans’s were distributed in the ranges 12.0-22.0 kcal/mol with the peak of E_trans =15.0 kcal/mol. The average of E_trans was 14.9 kcal/mol, which is 26 % of total available energy. The remained energies were transferred into the vibrational modes of H₂-streetching mode and deformation modes of GR.

The time evolution of PE for selected five trajectories are given in Figure S2. Also, the results of DFT-APFD functional are given in Figure S3 for comparison. The similar results were obtained in both methods.

E.

Hydrogen addition reaction to GR surface

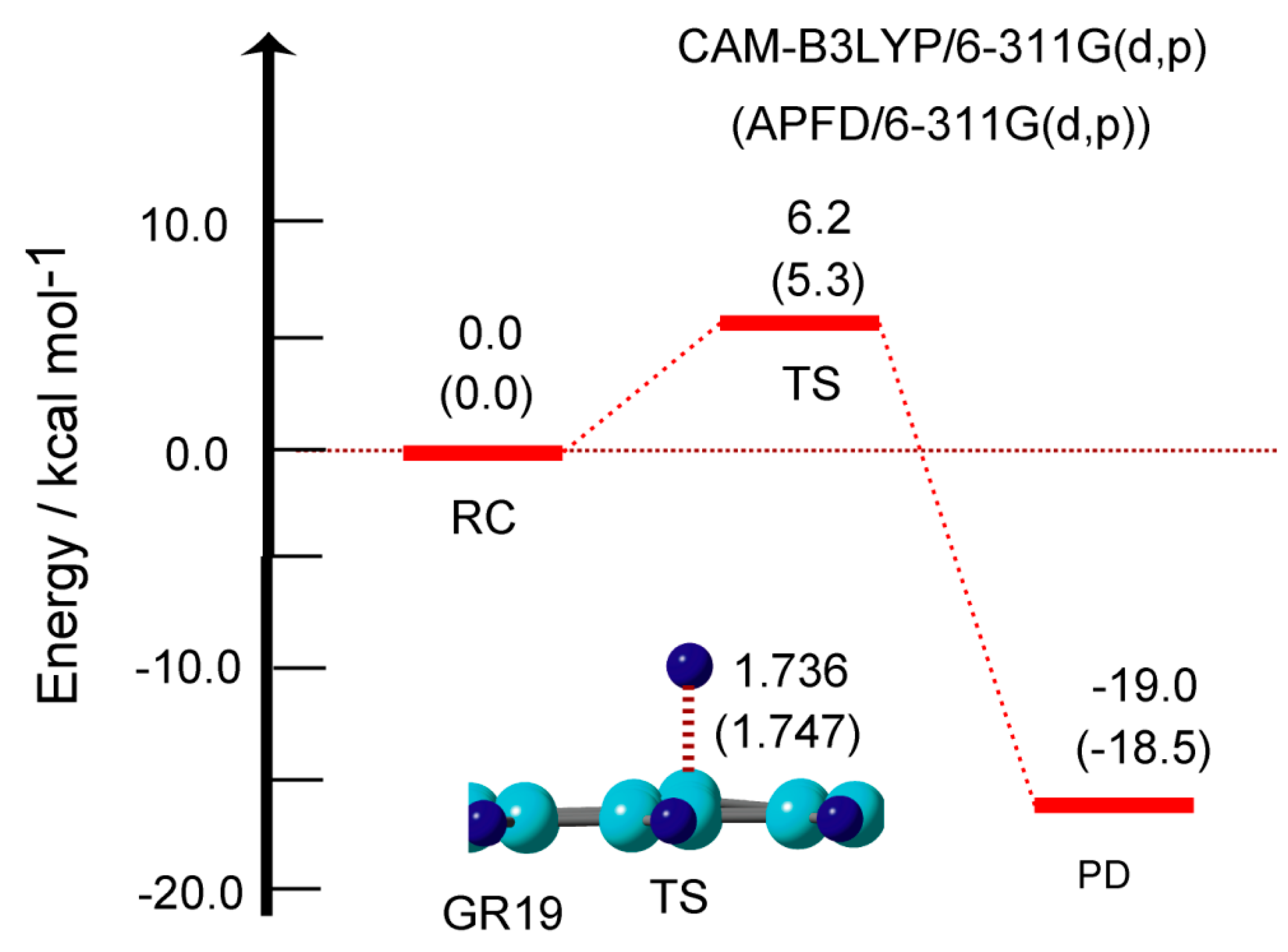
In previous sections, the hydrogen abstraction reaction was calculated and discussed. In this section, the hydrogen addition to the GR surface was re-examined. The reaction is expressed as GR + H → GR-H. In previous papers, we calculated the activation energies for the H-atom addition reaction to the GR surface using CAM-B3LYP functional. In this section, the energies were re-calculated using the APFD functional. The energy diagram and structure of TS for the H addition to the GR surface are given in Figure 8.

At TS, the H atom was located at 1.736 Å from the surface. In case of GR19, the activation energy was calculated to be Ea= 6.2 kcal/mol (CAM-B3LYP) and 5.3 kcal/mol (APFD). The calculated activation energies for several sized GRs are given in Table 1. The activation energies were 6.8 kcal/mol (GR04), 6.6 (GR07), and 5.6 (GR14), indicating that the activation energies were very low (Ea= 5-7 kcal/mol). This low activation barrier is due to the fact that the binding energies of H addition to the GR surface were large in the ranges 14.7-22.4 kcal/mol, as shown in Table 1. The similar results were obtained by the APFD functional. These results indicated that both H-addition and abstraction reactions proceed under low activation energy on GR.

4. Discussion and Conclusions

• Theoretical design of H₂ storage/release device

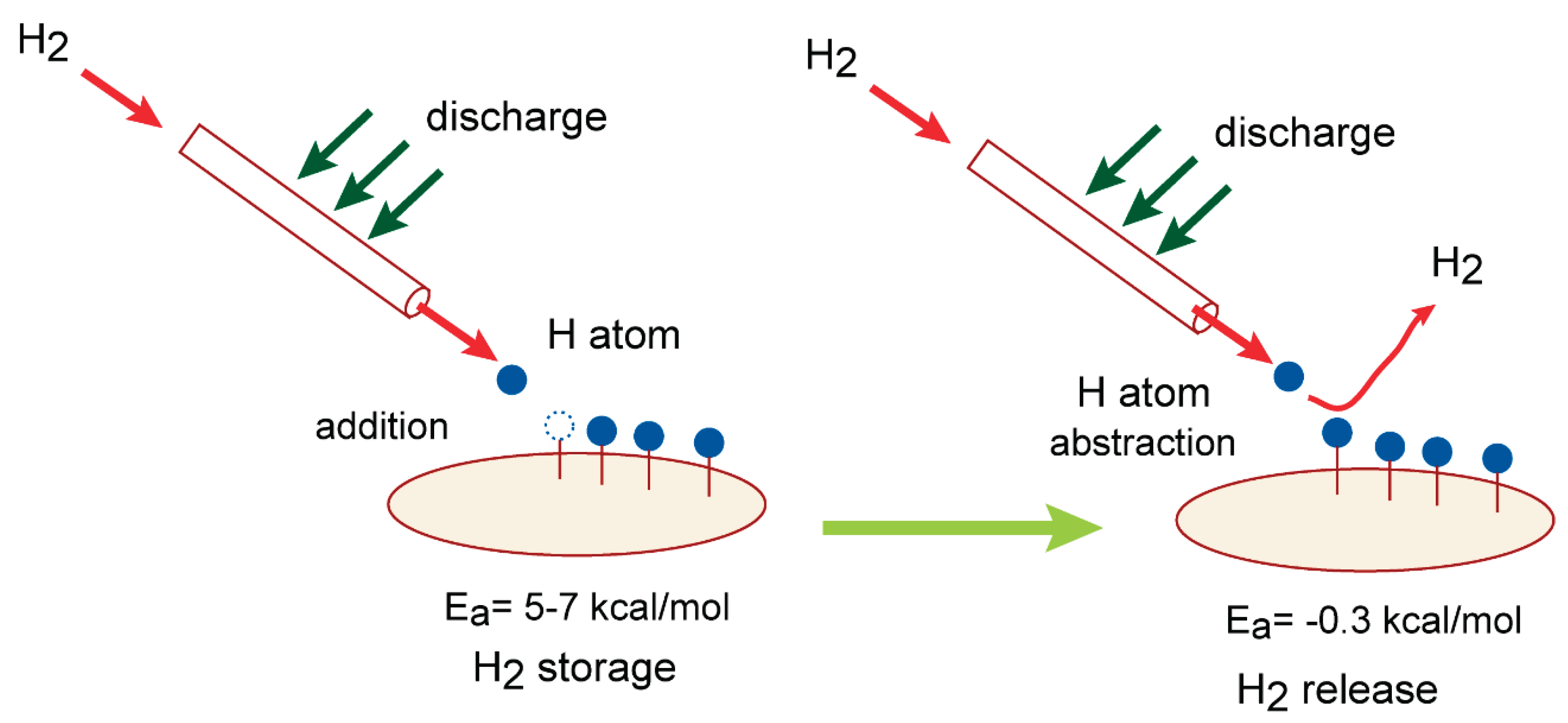
On the basis of the present calculations, the H₂ storage and release device is designed in this section. A schematic illustration H₂ storage/release device is given in Figure 9.

In case of H₂ storage process, first, the H₂ gas is introduces into the reaction tube and H₂ is discharged. The hydrogen atom (H-atom) is easily generated: H₂ + discharge → H + H. The H-atom reacts with carbon atom of GR surface and GR-H (hydrogenated graphene) is formed:

GR + H → GR–H

GR-H + H → H-(GR)–H

This reaction can proceed with a low activation energy (Ea=5-7 kcal/mol). The hydrogen molecule (H₂) is chemically captures as H-atoms on GR surface. The present calculations indicated that H₂ storage process proceeds with low activation energy of 5-7 kcal/mol after the discharge.

In case of H₂ release process, H-tom is generated again by discharge of H₂. The H-atom reacts with H-atom on the GR surface and H₂ is easily formed by the H abstraction reaction:

H + H-(GR)-H → H₂ + H-(GR)

This reaction can proceed also without activation energy (Ea= -0.3 kcal/mol: negative activation energy). The represent study thus designed the H₂ storage/release device composed of graphene.

B.

Conclusion

The development of hydrogen storage and release materials is one of the key themes in the development of a hydrogen society. In the present study, we theoretically designed hydrogen storage and release devices based on graphene (GR)—a lightweight and chemically stable material—using a direct AIMD approach. The calculations showed that the hydrogen addition reaction (H₂ storage):

H + GR → (GR)-H

proceeds with low activation energy (5-7 kcal/mol). Also, the hydrogen abstraction from hydrogenated graphene (H₂ release):

H + H-(GR)-H → H₂ + H-(GR)

occurs without activation energy. The direct AIMD calculations indicate that H-atom abstraction proceeds without the reaction barrier. The model designed in this study could be a new hydrogen storage/release device.