State-Selective Differential Cross Sections for Single-Electron Capture in Slow He⁺-He Collisions

1. Introduction

Charge exchange is not only a fundamental process in atomic physics, but also possesses extensive applications in fields such as astrophysics and fusion plasma physics. In terms of applications, astrophysical studies have shown that the soft X-rays detected from comets can be attributed to the charge exchange processes between solar wind ions and the cometary atmosphere [1,2,3,4,5,6]. The collision between He⁺ and He atoms, as a typical ion-atom interaction system involving three electrons, has been the focus of extensive experimental and theoretical research. This is because it can exhibit the main inelastic reactions (such as electron capture, excitation, ionization, etc.) in ion-atom collisions [7,8,9,10,11]. This collision system has important applications in astrophysics (such as the interaction between the solar wind and planetary atmospheres) and laboratory plasmas (such as the diagnosis of tokamak fusion devices), and its cross-section data are key bases for modeling radiation processes and plasma evolution [12,13].

Early studies were predominantly focused on the measurement of total cross sections. For example, Hegerberg $et$$al$. measured the total cross section for symmetric charge transfer in He⁺-He collisions within the energy range of 1–10 keV [14], and DuBois reported the total cross sections for single electron capture in the range of 3–500 keV [15]. However, they offered only limited information regarding detailed reaction dynamics, which is included in differential cross sections such as angular distributions and state-selective cross sections. With the advancement of experimental techniques, the application of high-resolution methods especially Cold Target Recoil Ion Momentum Spectroscopy (COLTRIMS) has made it possible to measure state-selective differential cross sections and angular differential cross sections, providing a powerful tool for studying dynamics of ion-atom collisions [16,17].

On the theoretical perspective, early coupled-channel calculations such as the three-electron model proposed by Sural $et$$al$. considered only a limited number of channels (6 channels) and neglected momentum transfer phases, making it difficult to describe complex many-body interactions [18]. Subsequently, extended models, e.g., the 128-channel calculation by Hildenbrand $et$$al$. improved computational accuracy but retained limitations, as they have not accounted for the coupling between s- and p-states [19]. In recent years, the application of methods such as the two-center atomic orbital close-coupling (TC-AOCC) and four-body continuum distorted-wave (CDW-4B) has significantly enhanced the ability to describe state-selective cross sections and angular distributions [20,21]. However, despite numerous studies, state-selective differential cross-section data in the low-energy region remain scarce, and different theoretical models show significant discrepancies in prediction of angular distributions [20]. For instance, the classical trajectory Monte Carlo (CTMC) method has limitations in describing quantum effects in the low-energy region [22,23], while quantum mechanical methods [24], although more accurate, incur high computational costs.

Since the angular differential cross section contains more abundant collision information, it can effectively verify the accuracy of the theoretical models for electron capture processes. One of the characteristics of He⁺-He collisions lies in the unique dynamic behaviors induced by their symmetry. Specifically, due to the resonance properties, the ground-state transfer process dominates in the low-energy region, and its angular differential cross section often exhibits oscillatory structures, which makes this collision system an ideal object for testing theoretical models [7,8,10]. Using COLTRIMS setup, this study systematically measured state-selective single-electron capture in the 0.5-5 keV/u He⁺-He collision system. Fully differential cross sections for the reaction process are obtained. Obvious oscillatory structures are observed in the angular differential cross sections of the ground-state capture ($1s-1s$) process. Within the measured energy range, the TCAOCC theoretical method well explained these oscillations [20], but the Fraunhofer diffraction theory only shows good agreement at small scattering angles. In addition, our research is compared with the experimental data and theoretical results of Gao et al. [25], and the two studies show good consistency.

2. Experimental Setup

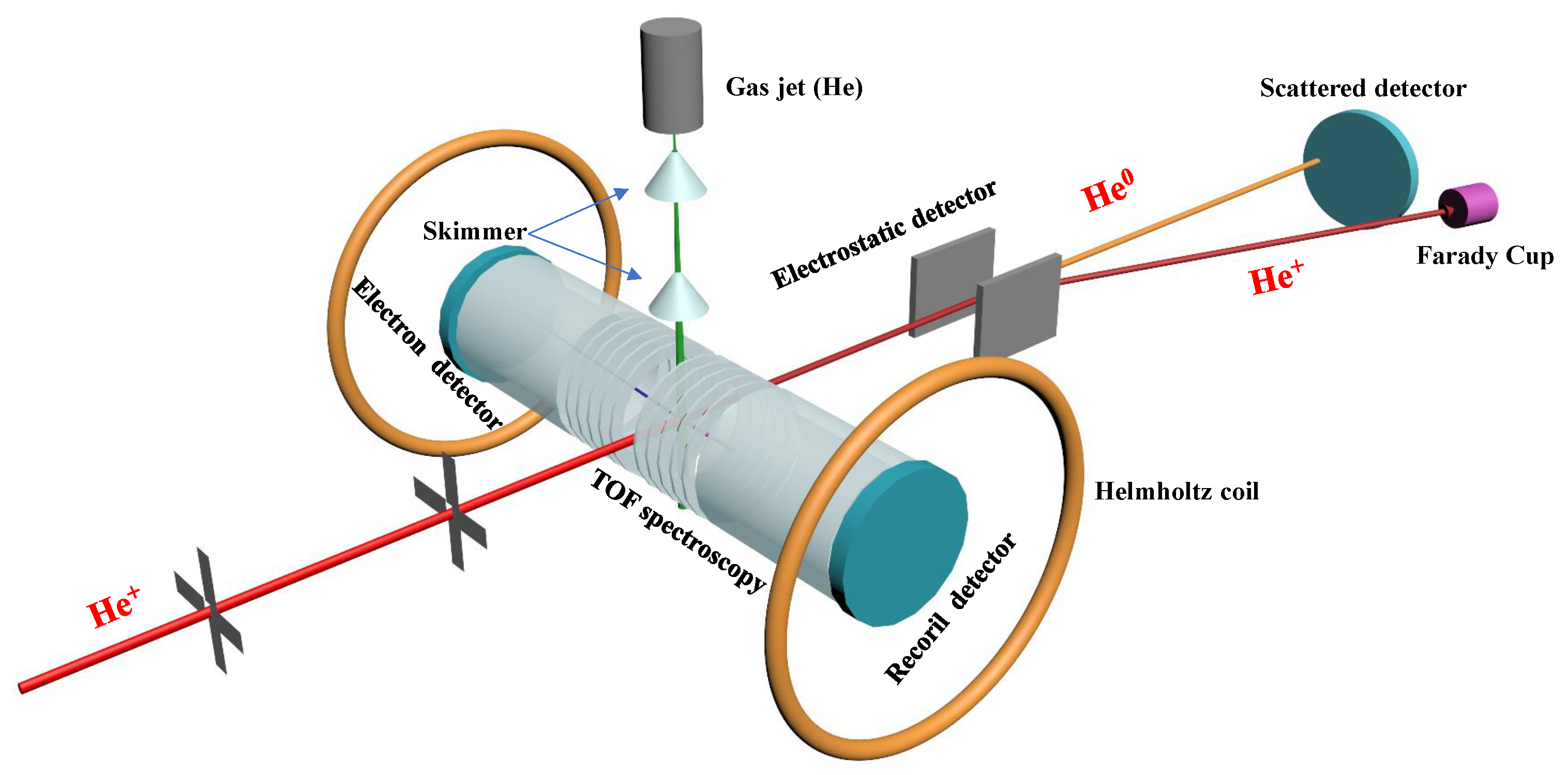
This experiment was conducted on the EBIS platform of the Institute of Modern Physics, Chinese Academy of Sciences as depicted in Figure 1. Detailed information have been provided elsewhere, [26,27,28,29,30,31]. Briefly, helium is introduced into the EBIS to generate helium ions with varying charge states. These ions are then extracted and sorted by a charge state analyzer to isolate the He⁺ ion beam essential for the experiment. Subsequently, the ions are adjusted to the requisite energy for the experiment, passing through a two-dimensional beam-limiting diaphragm and entering a target chamber to collide perpendicularly with the supersonic He target located at the central axis of the Time-of-Flight (TOF) spectrometer. Recoil target ions produced from these collisions are extracted by a uniform electric field oriented perpendicular to both the beam and target directions. They are then detected by a two-dimensional, position-sensitive microchannel plate detector. Post-reaction, scattered projectile ions with various charge states are analyzed by an electrostatic analyzer downstream of the reaction point. Projectiles with reduced charge states are identified by another position-sensitive detector positioned behind the beam, while unreacted projectiles are collected by the Faraday Cup. The TOF spectrometer comprises an acceleration region and a drift region, used to measure the TOF of recoil ions. The experiment utilizes a dual coincidence measurement technique between scattered ions and recoil ions, coupled with an event recording mode measurement. Through analysis of the two-dimensional correlation spectrum between ion positions on the scattering detector and the TOF of the recoil ions, identification of reaction channels like single-electron capture and multiple-electron capture becomes feasible. For specific reaction channels, analyzing the recoil ion positions on the recoil detector and measuring their time of flight enables the reconstruction of the three-dimensional momentum of the recoil ions.

Illustrated in Figure 1, the momentum measured along the beam’s current direction defines the longitudinal momentum of the recoil ion ($P_{\mathrm{long}}$), while the momentum perpendicular to the beam’s direction defines the transverse momentum of the recoil ion ($P_{\mathrm{trans}}$). The fundamental principle of COLTRIMS relies on establishing a relationship between the recoil-ion momentum and two crucial parameters: the Q value representing the binding energy change before and after the collision, and the scattering angle $\theta$ of the projectile ion. [16,17] This capture process can be conceptually viewed as an inelastic two-body collision in terms of kinetics. Hence, adhering to the conservation laws of energy and momentum, a simple relation can be derived for small scattering angles:

$$P_{long}=-{\displaystyle \frac{Q}{v_o}}-{\displaystyle \frac{n}{2}}·v_o$$

(1)

$$\theta ={\displaystyle \frac{P_{trans}}{P_o}}$$

(2)

Here, Q encapsulates details regarding the alteration in binding energy, offering insights into the state populated on the projectile due to the capture process. The variables $v_o$, n, $P_o$, and $\theta$ denote the projectile velocity, the number of electrons captured by the projectile, the initial momentum of the projectile ion, and the scattering angle of the projectile ion, respectively. It is important to note that all quantities in the equations above are presented in atomic units.

3. Theoretical Method

3.1. Integrated Cross Sections

The application of TC-AOCC method to ion-atom collision system requires determination of the single-center electronic state. The total wave function of the system can be expanded in terms of the electronic states which are centered on the target and projectile, respectively. Inserting the total wave function into the time-dependent Schr$\ddot{\mathrm{o}}$dinger equation, one can obtain the coupled equations of the scattering amplitudes [32]. To determine the bound electronic state with Debye–H$\ddot{\mathrm{u}}$ckel potential on either of the two centers, Liu et al. used the variational method with even-tempered trial functions by taking the trial functions in the form [33,34,35]

$$\begin{array}{cc}\hfill {\chi }_{klm}\left(\overrightarrow{r}\right)& =N_l\left({\xi }_k\right)r^l{\mathrm{e}}^{-{\xi }_{k}r}{Y}_{lm}\left(\widehat{\overrightarrow{r}}\right),\hfill \\ \hfill {\xi }_k& =\alpha {\beta }^k,k=1,2,...,N\hfill \end{array}$$

(3)

where $N_l\left({\xi }_k\right)$ is a normalization constant, $Y_{lm}\left(\overrightarrow{r}\right)$ are the spherical harmonics and $\alpha$ and $\beta$ are variational parameters. The atomic states ${\varphi }_{nlm}\left(\overrightarrow{r}\right)$ are then obtained linear combination.

$${\varphi }_{nlm}\left(\overrightarrow{r}\right)=\sum _k{c}_{nk}{\chi }_{klm}\left(\overrightarrow{r}\right),$$

(4)

where the expansion coefficients $c_{nk}$ are determined by diagonalization of single-centre Hamiltonian. This diagonalization yields the energies $E_{nl}\left(\alpha \right)$ of atomic states.

Within the semiclassical approximation, the electron wave function of the He⁺+He($1s^2$) collision system $\mathsf{\Psi }(\overrightarrow{r},t)$ satisfies the equation [20]

$$\left(H-i{\displaystyle \frac{\partial }{\partial t}}\right)\mathsf{\Psi }(\overrightarrow{r},t)=0,$$

(5)

where

$$H=-{\displaystyle \frac{1}{2}}{\nabla }_r^2+V_A\left(r_A\right)+V_B\left(r_B\right),$$

(6)

and $V_B\left(r_B\right)$ are the interactions of the active electron with the projectile (He⁺) and target (He) ion core, respectively. The relative motion of the nuclei is described classically by a rectilinear trajectory with a constant velocity v ($(R(t)=\overrightarrow{b}+\overrightarrow{v}t$, b being the impact parameter). The time-dependent two-center electron wave function is expanded as

$$\mathsf{\Psi }(\overrightarrow{r},t)=\sum _i{a}_i\left(t\right){\varphi }_i^A(\overrightarrow{r},t)+\sum _j{b}_j\left(t\right){\varphi }_j^B(\overrightarrow{r},t),$$

(7)

where ${\varphi }_i^A(\overrightarrow{r},t)$ and ${\varphi }_j^B(\overrightarrow{r},t)$ are traveling (i.e. containing plane-wave electron translational factors) atomic orbitals centered on the target (A) and the projectile (B). Substituting these into Eq. (5), one obtains the system of coupled equations for the amplitudes $a_i\left(t\right)$ and $b_j\left(t\right)$ [32],

$$\begin{array}{cc}\hfill \mathrm{i}(\dot{A}+S\dot{B})& =HA+KB,\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill \mathrm{i}(\dot{B}+S^{†}\dot{A})& =\overline{K}A+\overline{H}B.\hfill \end{array}$$

(8b)

where A and B are vectors representing the amplitudes $a_i$ ($i=1,2,...,N_A$) and $b_j$ ($j=1,2,...,N_B$), respectively. S is the overlap matrix ($S^{†}$ is its transposed form), H and $\overline{H}$ are direct coupling matrices and K and $\overline{K}$ are the electron-exchange matrices. Equations (8) are solved under the initial conditions

$$a_i(-\infty )={\delta }_{1i},b_j(-\infty )=0.$$

(9)

After solving the system of coupled Eq. (6), the cross section for $1\to j$ electron capture transition is calculated as

$${\sigma }_{cx,j}=2\pi {\int }_0^{\infty }{\left|b_j(+\infty )\right|}^{2}bdb,$$

(10)

The sum of ${\sigma }_{cx,j}$ over j gives the corresponding total electron capture cross section.

3.2. Differential Cross Sections

The angular-differential cross sections for an inelastic transition from the initial state i to a final state j can be written as

$${\displaystyle \frac{\mathrm{d}{\sigma }_{ji}}{\mathrm{d}\theta }}=2\pi sin\theta {\left|A_{ji}\right|}^2,$$

(11)

where $A_{ji}$ is the scattering amplitude at a given angle $\theta$. In the eikonal approximation the scattering amplitude is given by

$$A_{ji}{(\theta =\mu \nu (-i)}^{|m_j-m_i|+1}{\int }_0^{+\infty }bF\left(b\right)\mathrm{d}b{J}_{|m_j-m_i|}\times (2b\mu \nu sin{\displaystyle \frac{\theta }{2}}),$$

(12)

$$F\left(b\right)=C_{ji}(b,+\infty ){\mathrm{e}}^{2(i/\nu )Z_T{Z}_{P}lnb},$$

(13)

where $\mu$ is the reduced mass, $\nu$ is the relative collision velocity, and $m_j\left(m_i\right)$ is the magnetic quantum number of the final (initial) state. The function $J_{|}{m}_j-m_i|$ is the Bessel function of the first kind and $C_{ji}$ is the semiclassical transition amplitude for a given impact parameter b. For the considered electron capture process, in the notation of the preceding subsection, $C_{ji}=b_{ij}=b_j(i=1)$ The factor ${\mathrm{e}}^{2(i/\nu )Z_T{Z}_{P}lnb}$ is the eikonal phase, $Z_T$ and $Z_P$ being the projectile and target ion-core effective charges, respectively. It is to be noted that the eikonal approximation is valid for small scattering angles (i.e. at collision energies significantly higher than the interaction energy).

4. Results and Discussion

4.1. State-Selective Electron-Capture Process

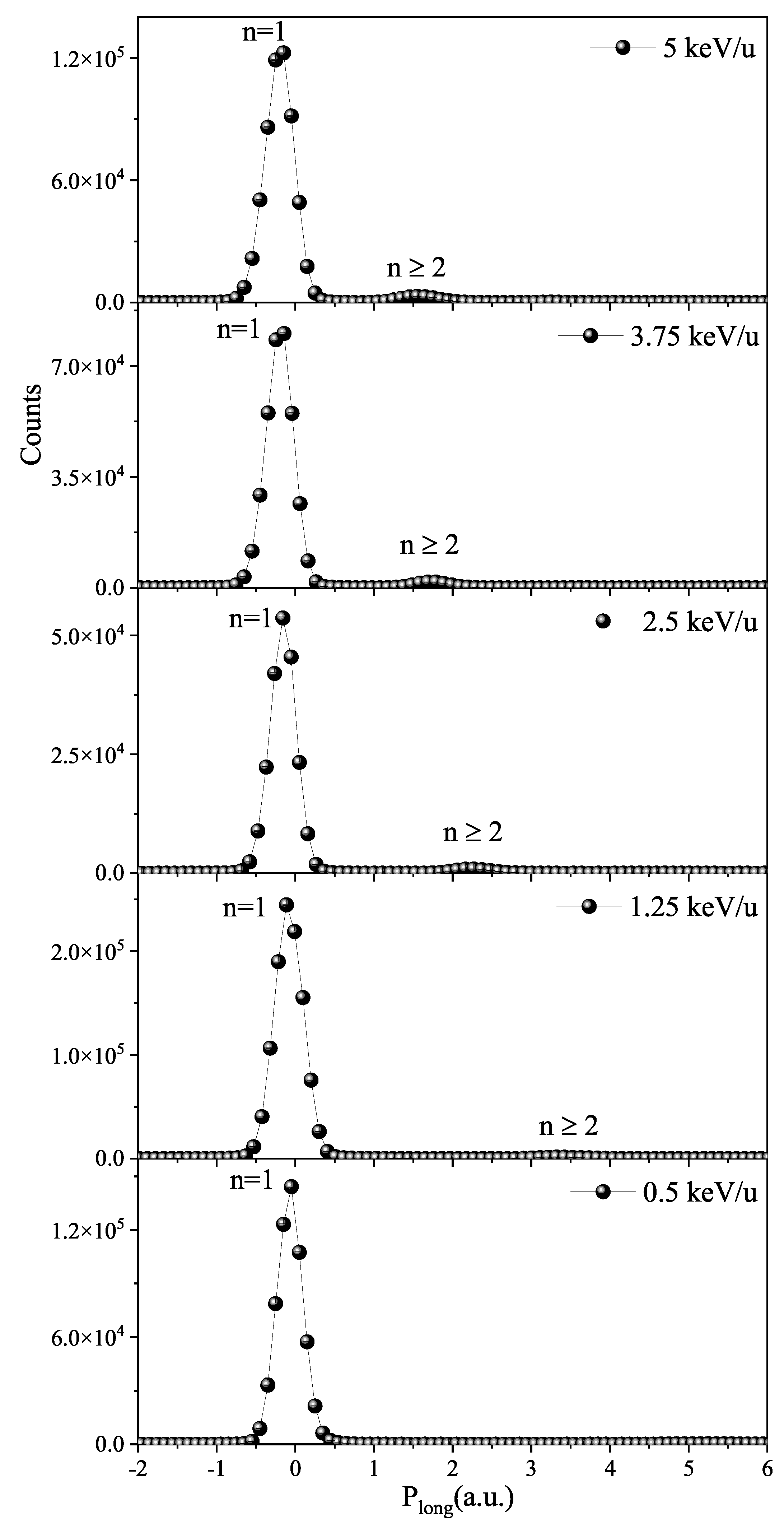
The longitudinal recoil ion momentum distributions are shown in Figure 2 and the relative cross sections are listed in Table 1. The absolute scale of momentum was calibrated using the well-defined single electron capture process in He⁺-He collisions. Different peaks correspond to different final capture states (where n represents the principal quantum number of the captured electron), with the recoil ions being in the ground state. Within the measured energy range, the experimental results indicate that the process of single electron capture into the ground state ($n=1$) of the projectile is dominant, which is consistent with the consideration of "energy matching". This is a common feature of symmetric ion-atom charge transfer processes, as the ground state transfer in He⁺-He collisions is a resonant charge transfer process with a binding energy difference of 0 before and after the reaction. With the increase of projectile energy, in addition to the dominant reaction channel, contributions from excited state transfer (i.e., target electrons captured into states with $n\ge 2$) can be identified, and the relative contribution of this process increases with increasing energy.

4.2. Angular Differential Cross Sections

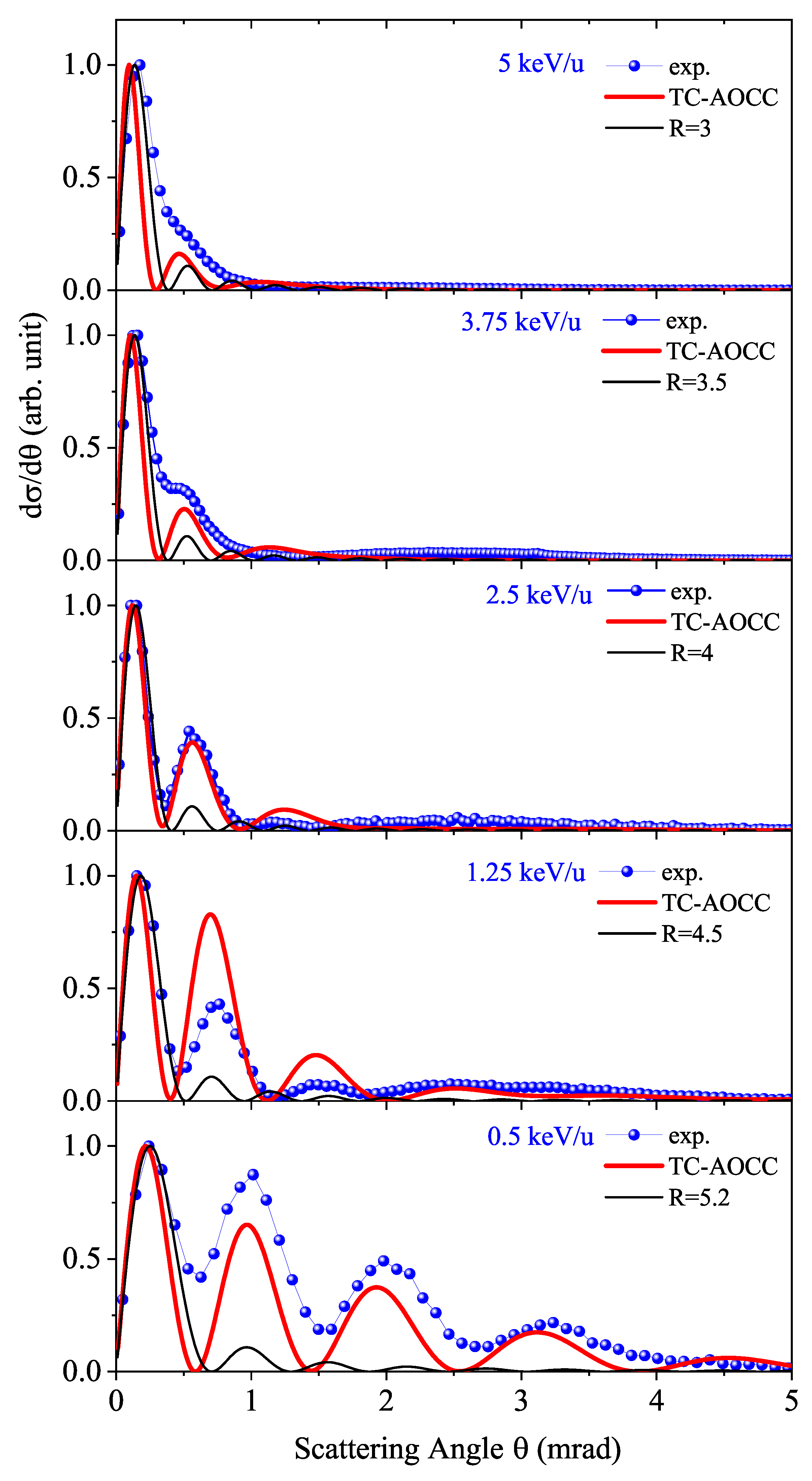
In Figure 3, we present the projectile angular distributions of ground-state transfer in the single-electron capture process of He⁺-He collisions at energies ranging from 0.25 keV/u to 5 keV/u. The blue solid dots in the figure represent experimental values, the red solid line represents the theoretical calculation results using the TC-AOCC method [20], and the black solid line represents the theoretical calculation results of Fraunhofer-type diffraction [36,37,38]. In the figure, R is the maximum collision parameter calculated (equivalent to the Fraunhofer diffraction aperture radius). Within the entire studied energy range, the angular differential cross sections of ground-state capture exhibit obvious oscillatory structures. In the past, various mechanisms have been proposed to explain the oscillatory structures observed in angular differential cross sections, such as the interference between gerade and ungerade scattering amplitudes in the quasi-molecular description [25], dynamic effects caused by projectile-electron scattering [39], and diffraction phenomena of matter waves on atoms [38,40]. This explanation for the oscillatory structures in the angular differential cross sections of elastic and resonant electron capture processes in low-energy collisions of all ion-atom nuclear-symmetric collision systems is widely accepted.

It can be observed in Figure 3 that within the energy range of this study, the calculation results of the Fraunhofer diffraction theory agree well with the experimental results only at the first maximum; the degree of agreement between the first minimum, the second maximum and the experimental results gradually improves as the collision energy increases. Within this energy range, the Fraunhofer diffraction theory shows an obvious energy dependence and cannot describe the situation of large scattering angles. This characteristic has also been confirmed in the study by Guo et al. [7]. In the study by Gao et al. [10], there was also a deviation between the experimental value and the second minimum, which they attributed to the limitations of the Fraunhofer-type model: first, the interaction region where electron transfer occurs is not an ideal circular aperture; second, at larger scattering angles, the contribution of hard (small impact parameter) collisions becomes dominant, and there exists a significant internuclear repulsive interaction, which will mask the diffraction pattern.

In Figure 3, we also present the angular-differential cross sections calculated by the TC-AOCC (Two-Center Atomic Orbital Close-Coupling) method and compare them with the experimental measurement data at the same collision energy. Within the energy range of this study, both the experimental results and the TC-AOCC theoretical results exhibit rich irregular oscillatory structures within the selected angular range. Specifically, for the collision energy E = 0.5 keV/u, the TC-AOCC results agree well with the experimental data when the scattering angle is less than 1.5 mrad; for E = 1.25 keV/u, 2.5 keV/u, 3.75 keV/u, and 5 keV/u, the TC-AOCC results show good agreement with the experimental data for scattering angles less than 1 mrad. For larger scattering angles, the TC-AOCC results underestimate the cross sections.

Within this energy range, the TC-AOCC calculations also have a good ability to predict the positions of the cross section maxima and minima (especially when $\theta <2$ mrad). In the angular range of $\theta <1$ mrad, the calculated oscillation maxima are also in good agreement with the experimental results, but for larger deflection angles, the calculated values tend to be smaller, which is consistent with the research results of Zhao et al. [20]. Compared with the Fraunhofer diffraction theory, the TC-AOCC theory is more suitable for calculating angular-differential cross sections at lower collision energies.

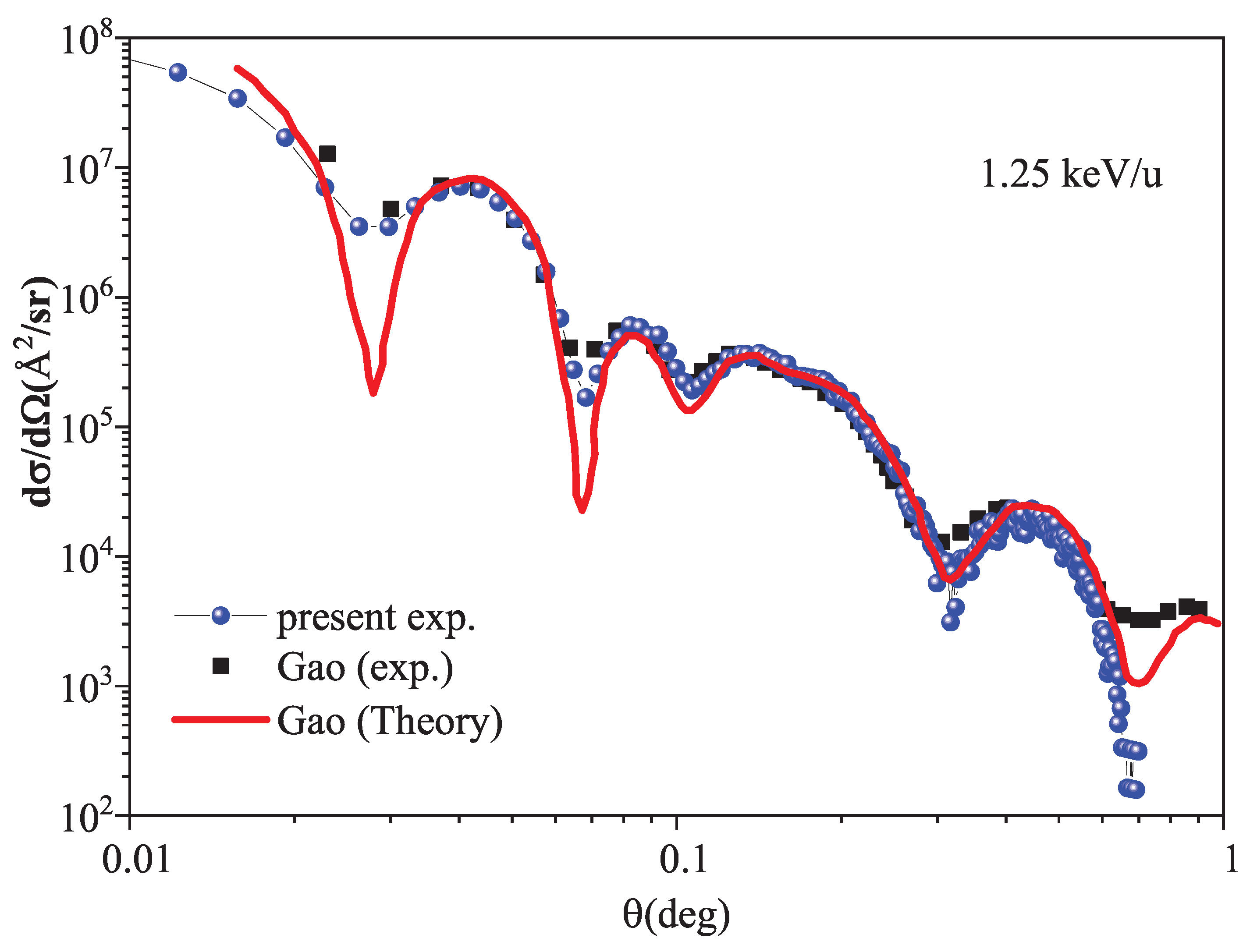
Figure 4 shows the calculated differential cross sections for He⁺-He collisions at an energy of 1.25 keV/u, as well as the experimental and theoretical results of Gao et al. [25]. For easier comparison with the experimental data of Gao et al., we adjusted the second maximum of our own experimental data to correspond to the position of the second maximum reported in the study by Gao et al. At this collision energy, our experimental results, along with the experimental and theoretical results of Gao et al., all exhibit rich irregular oscillatory structures within the selected angular range. Among them, the structure of our experimental results at the minima is clearer, which indicates that the resolution of this experiment is higher than that of Gao et al.’s experiment. It can be seen from the figure that our experimental data are in good agreement with the experimental and theoretical results of Gao et al. over the entire studied angular range. In addition, the TC-AOCC calculation results at the energy of 1.25 keV/u and the research results of Gao et al. have been presented in the article by Zhao et al. [20].

5. Conclusions

In this work, we conducted a combined experimental and theoretical investigation on the single-electron capture process in He⁺-He collisions within the energy range of 0.5–5 keV/u. Using the cold target recoil ion momentum spectroscopy (COLTRIMS) technique, we successfully obtained state-selective cross sections and angular differential cross sections for the collision process. Experimental results show that the ground-state resonant transfer ($1s\to 1s$) is the dominant channel throughout the studied energy range, which is a typical feature of symmetric ion-atom charge transfer reactions. With the increase of collision energy, the relative contribution of excited-state transfer channels (electrons captured to $n\ge 2$ states) gradually increases, reflecting the evolution of collision dynamics from resonant to non-resonant mechanisms.

The angular differential cross sections of ground-state capture exhibit obvious oscillatory structures, which are closely related to the quantum interference effect in the collision process. Theoretical calculations based on the two-center atomic orbital close-coupling (TC-AOCC) method well reproduce the oscillatory characteristics of the angular differential cross sections, especially in the small scattering angle range ($\theta <1$ mrad). The TC-AOCC results not only accurately predict the positions of the cross section maxima and minima but also effectively describe the trend of the cross sections with collision energy, confirming that the oscillatory structures originate from the correlation between the impact parameter dependence of electron capture probability and the matter wave diffraction of the projectile. A comparison with the Fraunhofer diffraction model shows that although the latter can explain the first maximum of the angular differential cross section, it has limitations in describing the oscillatory structures at larger angles.

Overall, this work provides reliable experimental data for the single-electron capture process in He⁺-He collisions at low energies and verifies the applicability of the TC-AOCC method in describing such collision systems. The results deepen the understanding of the microscopic mechanisms of ion-atom charge transfer, especially the quantum interference and diffraction effects in low-energy collisions, and can provide important reference for related studies in astrophysics and plasma physics.