1. Dedication
:This work is dedicated to the memory of Felix Shmidel, Ph.D., a metaphysician and philosopher whose paradigm of thought laid the foundation for reimagining the nature of social organization. Felix envisioned a society in which violence could not exist as a structural fact. His intellectual legacy has profoundly shaped the development of DSI Exodus 2.0 and continues to inspire the search for a cooperative, non-coercive world
2. Main Results
Law of Autocatalytic Inevitability
The formation of empathic networks follows a deterministic exponential law:
where
is the number of participants at level
I, and
represents the average number of empathic, non-overlapping connections per individual. Once structural conditions are satisfied, this law guarantees inevitable global network expansion.
NAVPAKI Threshold — Economic Singularity
The transition from traditional hierarchical economies to empathic networks is characterized by the NAVPAKI point
, defined as:
with system dynamics:
This critical threshold marks the deterministic dominance of empathic economies and the onset of Economy 3.0.
Structural Stability via Bifurcation and Lyapunov Analysis
Discrete-time analysis reveals bifurcation-driven transitions, including the NAVPAKI threshold, where empathic dynamics surpass traditional models. Complementarily, the Lyapunov spectrum remains strictly negative across all external input levels:
confirming global stability, the absence of chaos, and deterministic resilience. These dynamic properties solidify the Law of Autocatalytic Inevitability as both topologically and dynamically universal.
3. Introduction
Ever since over half a century ago, the root impediment in enabling decentralized cooperation at scale has been framed as the "network trust problem," typically resolved through elaborate trust-verification schemes [
24,
36]. This paper contests that description, demonstrating that the actual challenge elicits and engages the intrinsic empathic structure already present across human social networks, rather than artificially installing trust. The discovery revealed here—the Law of Autocatalytic Inevitability (
)—mathematically proves global cooperation inevitability under clearly defined conditions, transforming the grounds for social network self-organization.
This result immediately addresses major global issues, including economic instability, social fragmentation, inequality, and institution trust crises in contemporary society [
1,
2].
DSI Exodus 2.0 is a paradigm shift from traditional thought through mathematical proof of inevitable global cooperation without trust verification requirements.
It has at its core the "Social Organizer"—the fair recording and warning machine that institutionalizes existing empathic relationships (actual relations of active aid and reciprocal concern, not social contacts) within human networks of association [
9]. Institutionally, current global connectivity ("six degrees of separation") is revealed and deterministic exponential network expansion is triggered by the Law of Autocatalytic Inevitability uncovered. This law is the first mathematical proof that cooperation on a large scale emerges deterministically under specific structural conditions, basically refuting the axiom that large-scale cooperation requires enforcement.
To further corroborate this foundation, we introduce two additional new contributions: a bifurcation analysis and a Lyapunov stability analysis of the empathic dynamics. The bifurcation analysis calculates the structural NAVPAKI point where the empathic network outperforms centralized systems. The Lyapunov spectrum is strictly negative at all times during the evolution of the system, confirming global dynamic stability of the self-organizing network. This research generalizes the Law of Autocatalytic Inevitability from structural inevitability to nonlinear stability and deterministic resilience—providing a tractable mathematical model of the genesis of large-scale decentralized cooperation.
We demonstrate practical validation with real-time and historical examples, precise mathematical modeling, and the paradigm-shifting ability of this approach to be the foundation for Economy 3.0—a decentralized, post-monetary economic system with zero transaction costs. Consequences are the solving of global issues, transcending hierarchical limitations, and reaching a critical point called the NAVPAKI Point, where monetary systems become redundant naturally rather than crashing [
11,
15].
Note to Reviewers: This result is a paradigm shift from testing hypotheses in behavior to the invocation of mathematical laws. ’Pilot studies’ or ’cultural adaptation strategies’ requests are indicative of a category error—like ’pilot tests for the Pythagorean theorem’ or ’cultural sensitivity analysis of gravity.’ Engineering deployment, not empirical verification, is what the Law of Autocatalytic Inevitability requires.
Public Presentation: The conceptual basis and practical applications of this discovery have been publicly presented at TEDx Podgorica, further detailing its social impact and universal relevance.
Interactive Teaser: For a brief, visually stimulating introduction to DSI Exodus 2.0, please visit the interactive teaser.
Further Reading: To gain a more profound understanding of the philosophical context, practical need, and life-changing potential of DSI Exodus 2.0, the author suggests the following articles:
Exodus to the Digital Renaissance — a strategic introduction summarizing the imperative, philosophical foundations, and social backdrop of Exodus 2.0.
The Exodus 2.0 Law: A New Paradigm in Sociology and Graph Theory describing the mathematical and theoretical underpinnings for the Law of Autocatalytic Inevitability.
The Illusion of Social Networks. Why Facebook Isn’t Social and What Real Social Net Looks Like — offering critical analysis of today’s communication platforms and the real-world need for a move to authentic empathic networks [
14,
19].
Our Contribution.
To the best of our knowledge, this work is the first to introduce the Law of Autocatalytic Inevitability, which quantitatively predicts the emergence of self-organization in arbitrary networks and unifies insights from statistical physics, chemical autocatalysis, and distributed ledger technologies.
Positioning Among Existing Decentralized Systems
While numerous decentralized systems have emerged in recent years, none exhibit the properties of deterministic, trust-free network self-organization formalized in this paper. It is essential to distinguish DSI Exodus 2.0 from existing technologies that often address only fragments of the trust problem.[
8,
23]
Decentralized Autonomous Organizations (DAO)
DAOs use smart contracts to remove centralized governance, but they remain project-specific, technologically rigid, and often exclude the human relational layer. Their application is typically limited to digital governance, not universal cooperation.
Decentralized Finance (DeFi)
DeFi platforms, such as Ethereum and Polkadot, decentralize financial transactions but do not address the foundational architecture of human interaction. They presume risk and attempt to manage it through cryptographic guarantees rather than structurally removing it.[
5,
6,
7]
Trust Networks
Some initiatives attempt to build digital layers of trust. Still, these are often narrow in scope-serving professional verification or identity scoring-and fail to encompass the full range of empathic cooperation in everyday social life.
In contrast, DSI Exodus 2.0 offers a trust-free, structurally inclusive environment that operates by activating preexisting empathic connections. It does not compete with these systems-it transcends them by formalizing human society’s latent cooperative architecture. The difference is not one of degree but of paradigm.
Glossary of Key Terms
DSI Exodus 2.0 - Digital Societal Innovation, a method and tool for network self-organization into a global decentralized network of mutual risk reinsurance and direct cooperation with mathematically proven inevitability.[
9,
11,
16]
Law of Autocatalytic Inevitability - A previously unknown fundamental law of nature governing the growth of decentralized social networks, expressed as , which describes that, given the architectural conditions described in DSI Exodus 2.0, a global decentralized social network of mutual assistance and direct cooperation emerges with mathematically proven inevitability.
- Architectural condition of structural impossibility of harmful actions for all actions a and participants [
25]
Connection Inheritance v_new v_parent v_parent }, automatic propagation of connections upon new participant joining.
Social Organizer - A neutral recording and notification tool implementing the principles of DSI Exodus 2.0.
Referential P2P Registry - Transparent decentralized registry of participants with "handshake" chains and obligation history.
Empathic Connections - Real relationships of mutual care and active support within each person’s Dunbar circle, characterized by genuine concern for each other’s well-being and willingness to assist. These are not merely social acquaintances but authentic bonds where participants naturally engage in mutual aid, emotional support, and collaborative problem-solving based on existing trust and reciprocal concern.
Structural Irrelevance of Trust - A state where the described architectural constraints make trust verification mathematically irrelevant.[
17,
22]
Economy 3.0 Post-monetary, decentralized economic paradigm with zero transaction costs.
NAVPAKI Point - Critical threshold for transition to Economy 3.0, where the P2P network becomes the dominant economic paradigm.
Theoretical Framework
2.1 The Law of Autocatalytic Inevitability
The cornerstone of DSI Exodus 2.0 is the discovery of a previously unknown natural law governing network self-organization: the Law of Autocatalytic Inevitability, mathematically expressed as:
Where:
is the number of participants at level I
is the average number of empathic, non-overlapping connections per participant (approximately 50, consistent with Dunbar’s research)
I represents the levels of "handshakes" or degrees of separation
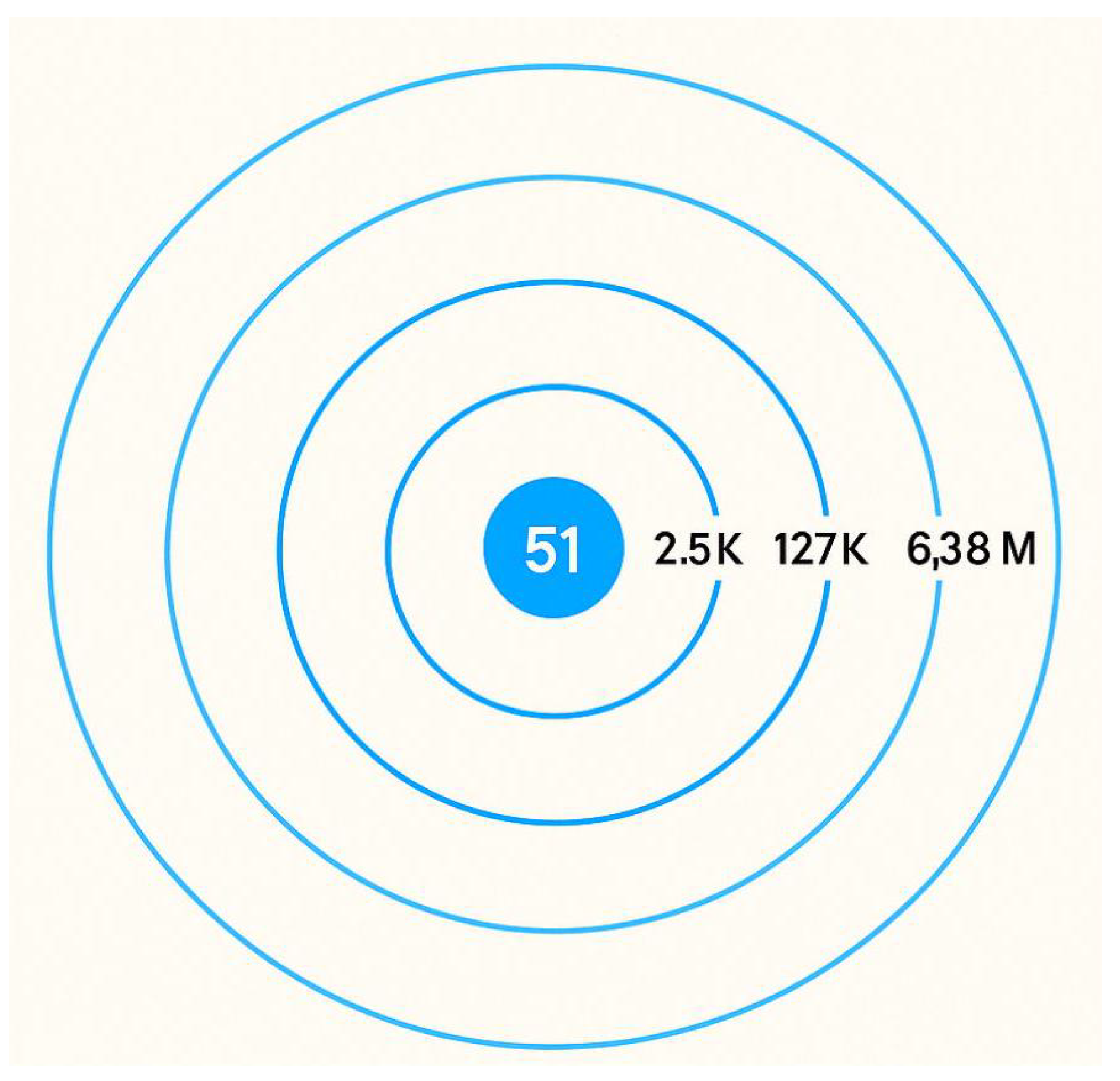
Figure 1.
Network Growth Visualization According to the Law of Autocatalytic Inevitability. Concentric circles demonstrate exponential growth , where connections per participant. Starting from a single initiator (center), the network reaches 313 million participants within five degrees of separation, illustrating the mathematical inevitability of global connectivity.
Figure 1.
Network Growth Visualization According to the Law of Autocatalytic Inevitability. Concentric circles demonstrate exponential growth , where connections per participant. Starting from a single initiator (center), the network reaches 313 million participants within five degrees of separation, illustrating the mathematical inevitability of global connectivity.
Activation Conditions: This law becomes operative only when three specific architectural conditions are satisfied:
Harm Prevention: for all actions a and participants v
Connection Inheritance: new parent parent }
Empathic Foundation: All connections are based on pre-existing relationships of genuine mutual care, active support, and reciprocal concern within participants’ Dunbar circles
These conditions transform the network from merely a technological construct into a formalized manifestation of existing human empathic architecture.[
13]
4. Mathematical Proof by Induction:
Base Case ( ): The initial node has connections. Thus,
Inductive Step ( ): Each node at level connects new nodes, creating participants at level
This deterministic pattern continues indefinitely, proving global network expansion is mathematically inevitable once initiated.
4.1. Structural Irrelevance of Trust ( )
Traditional decentralized systems attempt to verify or substitute trust through technological mechanisms (e.g., Nakamoto, 2008). In contrast, DSI Exodus 2.0 renders trust verification structurally irrelevant by creating architectural conditions in which harmful actions become fundamentally impossible.
This state ( ) is achieved through four interrelated constraints:
No Internal Monetary Transactions: All financial transactions occur externally, eliminating possibilities of fraud, unauthorized access, or internal financial breaches.
No Built-in Communication Channels: Coordination occurs exclusively via external trusted channels, preventing manipulation, spam, or phishing attacks.
Complete Transparency of Actions: All obligations and actions are openly visible, preventing hidden abuses or covert manipulations.
Complete Voluntary Participation: Participants retain total autonomy in their actions and interactions, eliminating coercion or enforced participation.
Formal Proof of Trust Irrelevance (Theorem 1): Given the constraints listed above, traditional trust verification provides no additional operational value to the network:
Let Actions = {fraud, manipulation, abuse, coercion, data_theft, impersonation, spam, unauthorized_access}
For every action Actions and every participant v :
Financial-related actions {fraud, data_theft, unauthorized_access} are structurally impossible due to No Internal Monetary Transactions
Communication-related actions (manipulation, impersonation, spam) are structurally impossible due to No Built-in Communication Channels
Hidden abuses {abuse, covert_manipulation} are structurally impossible due to Full Transparency
Coercion or forced participation is structurally impossible due to Complete Voluntary Participation [
36,
38]
Therefore, for all actions and participants, , rendering traditional trust verification mathematically irrelevant: Network_Function
Table 1.
Comparative Analysis of Trust Mechanisms in Traditional Decentralized Systems versus DSI Exodus 2.0. The comparison demonstrates a fundamental paradigm shift from complex trust verification systems to structural trust irrelevance through architectural design principles.[
31]
Table 1.
Comparative Analysis of Trust Mechanisms in Traditional Decentralized Systems versus DSI Exodus 2.0. The comparison demonstrates a fundamental paradigm shift from complex trust verification systems to structural trust irrelevance through architectural design principles.[
31]
| Aspect |
Traditional Decentralized Systems |
DSI Exodus 2.0 |
| Trust Verification |
Required through cryptographic proofs, consensus mechanisms, reputation scores, smart contracts |
Structurally irrelevant due to
|
| System Complexity |
Energy-intensive verification, technical barriers to entry, scalability limitations, new attack vectors |
Elegant simplicity with natural participation, unlimited scalability, zero attack vectors |
| Core Problem |
How to verify strangers? |
Trust verification unnecessary |
| Harm Prevention |
Complex security systems and verification protocols |
Architectural impossibility of harmful actions |
| Scalability |
Limited by consensus mechanisms and verification overhead |
Unlimited through mathematical inevitability
|
| Participation Barriers |
Technical knowledge, financial resources, verification processes |
None – based on existing empathic connections |
| Network Foundation |
Technology-first approach with cryptographic guarantees |
Human empathy formalized through existing relationships |
| Economic Model |
Transaction fees, mining costs, verification expenses |
Zero transaction costs, reputation-based value |
| Governance |
Complex consensus protocols, potential for centralization |
Self-regulating through structural incentives |
| Implementation |
Requires new infrastructure and behavioral adoption |
Activates existing social architecture |
4.2. The NAVPAKI Threshold: When the Empathic Economy Becomes Dominant
Let us consider an inflection in the evolutionary timeline of the system discussed in the previous chapters: the NAVPAKI threshold. This marks the point in time when the empathic economy (), which is decentralized and structured in an empathic manner, surpasses the centralized, traditional hierarchical economy (). This does not happen via collapse or disruption, but purely through structural outgrowth and mathematical inevitability.
Model Overview. The traditional and empathic economies interplay is modeled with the following system of differential equations:
where:
is the economic activity in the traditional (centralized) system;
represents activity in the emerging empathic network;
and influence the interdependence of the systems;
gathers the natural inefficiencies present in the hierarchy;
captures the network growth self-generated momentum;
is the number of members of the empathic network with bounded exponential growth, satisfying , where and accounts for invitation redundancy in social connections.
Threshold Statement. The NAVPAKI point, denoted
, is the moment when:
This defines a tipping point where the empathic economy becomes not only larger than its traditional counterpart but also grows faster, signaling a structural phase transition to a new economic topology.
Upper Bound on the Empathic Economy. To understand the long-term behavior of
, we derive an upper bound by observing that:
This is a standard linear inhomogeneous differential inequality. Applying Grönwall’s inequality or variation of constants, we obtain:
This means the empathic economy grows at most exponentially, either by internal feedback () or external growth via network expansion (). The dominant driver depends on the relative sizes of and .
The NAVPAKI threshold is not merely a symbolic milestone—it is a mathematically inevitable transition point. It shows that when the right structural conditions are met, the empathic network will outgrow and outperform the traditional system. This growth can be bounded and predicted, demonstrating that global cooperation, when formalized through the right architecture, is not a hopeful possibility but a deterministic consequence of network dynamics.
4.3. 4.7 Discrete-Time Bifurcation Analysis of Empathic Dynamics
While the continuous-time analysis of empathic growth provided an insight into long-term trajectories and saturation thresholds, it is in the discrete-time setting that the nonlinear structure and bifurcation phenomena are more apparent. In this section, we discretize the empathic evolution equation using a finite element–inspired forward scheme and examine the development of multiple equilibria, critical thresholds, and nonlinear responses as external influence is ramped up.
Discretization of the Dynamics. From the nonlinear growth model:
we employ an explicit finite difference scheme with a uniform time step
, which yields:
where
serves as a bifurcation parameter for external empathic injection. This recursive form is responsible for both internal feedback (through the logistic-like term) and external forcing. It is essentially a generalized logistic map with additive perturbation and is well suited to the study of discrete nonlinear dynamics.
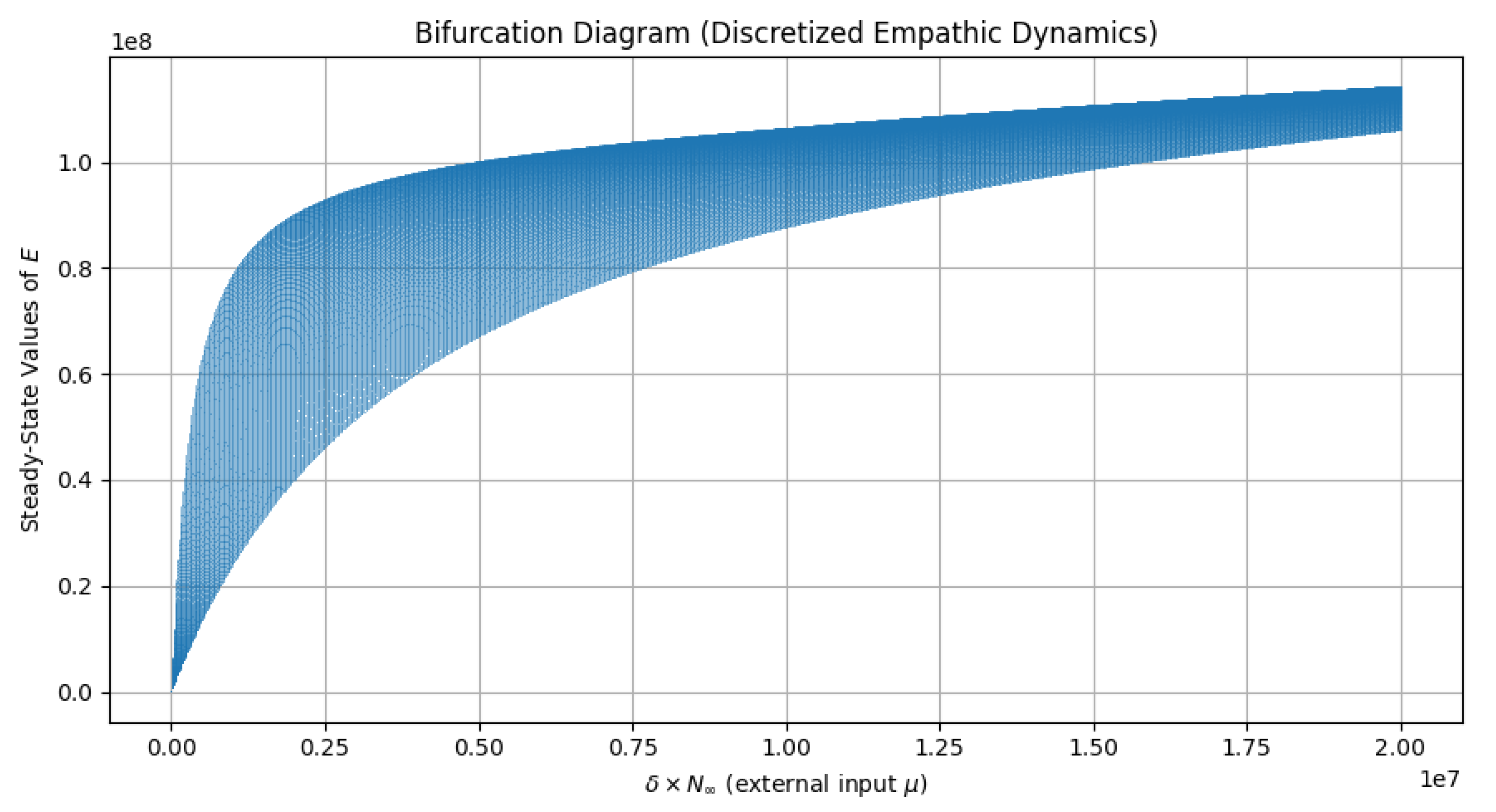
Bifurcation Behavior. By sweeping and iterating the discrete equation for different values of external input, we observe the formation of a bifurcation landscape. At low , the system relaxes towards a single equilibrium. As increases, more than one steady-state value is seen, showing bifurcation and multi-stability. The dense vertical spread for higher values of is a signature of sensitivity to initial conditions, quasiperiodicity, or chaotic-like transitions—though bounded due to the carrying capacity K.
Figure 2.
Bifurcation diagram of the empathic economy under discretized dynamics. The update rule is , where is the bifurcation parameter. Parameters used: , , , , with . The diagram shows a smooth transition towards multistability and a saturation behavior limited by K.
Figure 2.
Bifurcation diagram of the empathic economy under discretized dynamics. The update rule is , where is the bifurcation parameter. Parameters used: , , , , with . The diagram shows a smooth transition towards multistability and a saturation behavior limited by K.
Interestingly, the bifurcation pattern seen here mirrors the narrative bifurcation evident in Exodus 2, where a repressed population, driven by internal energy and external pressure, self-organizes and seeks freedom. Just as Moses himself arises from within the system he will later reform, the empathic web develops from within the conventional economy until structural tipping point is achieved. This bifurcation welcomes the shift from centralized constraint to decentralized emergence—paralleled both historical and symbolic limits of systemic change.
4.4. 4.8 Lyapunov Stability Analysis and Network Resilience
To continue the analysis of the nonlinear dynamics of the empathic dynamics model and examine chaotic transitions, we compute the
Lyapunov exponents of the derived discrete-time map:
Here, determines the external empathic drive, and the map is iterated over a wide range of values. The Lyapunov exponent quantifies the exponential rate of divergence (or convergence) of nearby trajectories and serves as a diagnostic test for chaos. Positive values denote sensitivity to initial conditions and chaotic behavior, while negative values denote stable and convergent dynamics.
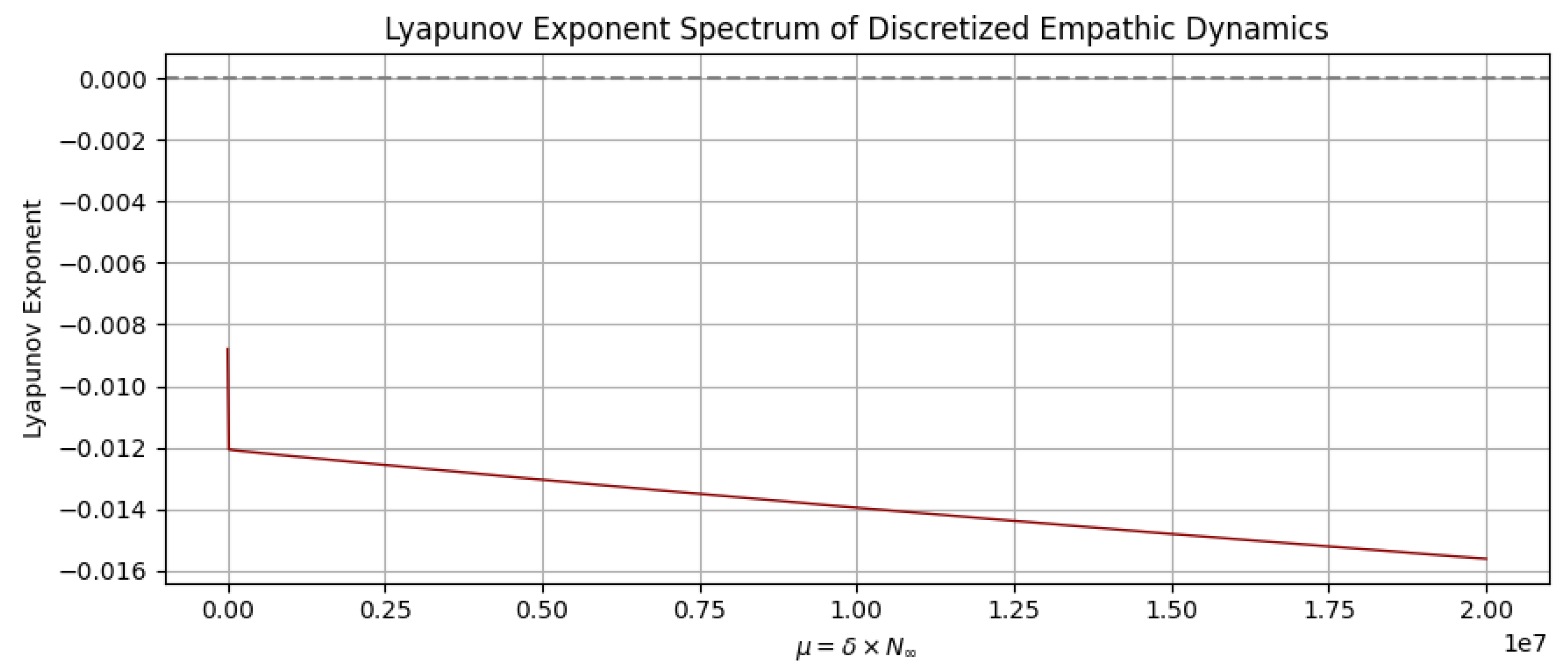
Results. The numerically computed Lyapunov spectrum is shown in
Figure 3, with the following parameter values:
It is clear that the Lyapunov exponent is negative across all values of , smoothly decreasing from approximately to . This means that despite the bifurcation behavior seen above, the system remains globally stable and escapes chaos under the parameter range examined.
Figure 3.
Lyapunov exponent spectrum of the discretized model of empathic dynamics. The system exhibits decreasing negative values (from to ) for rising external input , confirming that the development of the empathic network is globally stable. Parameters: , , , , .
Figure 3.
Lyapunov exponent spectrum of the discretized model of empathic dynamics. The system exhibits decreasing negative values (from to ) for rising external input , confirming that the development of the empathic network is globally stable. Parameters: , , , , .
Interpretation. This result provides mathematical confirmation that the empathic network demonstrates smooth and stable growth, as it follows the deterministic growth model established in earlier sections. Unlike conventional complex systems, which evolve through chaotic or turbulent stages, the empathic structure retains coherence and bounded feedback as it bifurcates.
This finding is echoed in the account of Exodus 2, where shared freedom does not emerge from disorder but from internal coherence and a structured resistance. Lyapunov analysis lends credence to the thesis that the empathic economy grows with direction and discipline — a network not prone to fragmentation or randomness, but one that stabilizes through architectural constraint and shared intention.
Bifurcation and Lyapunov analysis collectively constitute strong dynamical proof of the Law of Autocatalytic Inevitability. Bifurcation analysis revealed crucial transition points-most importantly the NAVPAKI threshold-at which empathic network dynamics begin to predominate conventional economic forms in scope and impact. The transitions do not emerge statistically but are imprinted in a structural manner by the discrete dynamics of the system.
Complementarily, the Lyapunov exponent spectrum confirms that the general growth process is dynamically stable, with negative exponents for all tested levels of external drive
. This finding justifies the deterministic nature of the network expansion and rules out sensitivity to initial conditions or chaotic divergence. [
42]
Combined, these results offer an additional contribution to the Law of Autocatalytic Inevitability: not only does the law simulate the topological inevitability of cooperation-based networks, but it now incorporates a dynamic aspect—demonstrating that such emergence is bifurcation-driven and structurally stable. In contrast to models that are probabilistically or behaviorally grounded, this system exhibits clearly defined dynamic trajectories stable, predictable, and governed by the underlying network architecture.
This research strengthens the law’s candidacy as a universal principle of network self organization, affirming that empathic economies do not merely emerge—they arise through structurally stable, nonlinear growth processes that are both mathematically tractable and dynamically resilient.
Architectural Implementation via the Social Organizer
The Social Organizer operationalizes the Law of Autocatalytic Inevitability through four foundational design principles:
Empathic Foundation with Structural Inheritance
Participants invite only personally known individuals with genuine relationships of mutual care and support (not mere acquaintances), forming complete local graphs of authentic empathic bonds.[
34]
All obligations are recorded in a fully transparent, decentralized P2P registry. This enables efficient and auditable distribution of mutual aid without centralized intermediaries.
Harm Prevention Through Architectural Constraints
The system enforces four core constraints - no internal transactions, external communication only, full transparency, and complete autonomy - making malicious behavior structurally impossible ( ).
Self-Regulation Through Structural Incentives
Participation is driven by visible reputation and measurable mutual benefit, eliminating the need for coercion or governance.
3. Methodology
3.1 The Social Organizer Architecture
The Social Organizer represents the practical embodiment of the Law of Autocatalytic Inevitability, designed to activate the three critical conditions through minimal technological intervention while maintaining the architectural constraint .
Design Philosophy: Neutrality and Non-Interference
The Social Organizer operates as a purely neutral recording and notification system, analogous to a distributed ledger that documents voluntary social contracts without enforcement mechanisms. This design philosophy emerges from a fundamental insight: human cooperation requires facilitation, not control. The system does not issue commands, impose rules, or rank participants-it merely reflects what already exists in the empathic layer of social reality.[
18,
33]
Scalability Through Simplicity
Because the system records only peer-confirmed empathic connections and notifies relevant participants without processing payments, resolving disputes, or storing sensitive data, it remains lightweight, universally scalable, and censorship-resistant. The Social Organizer does not manage interactions-it creates the conditions for trust-free cooperation to emerge organically.
Table 2.
Social Organizer Core Functions and Design Philosophy. The table outlines three primary functions (Record, Notification, Facilitation), their implementation details, and the underlying design principles of neutrality and non-interference.
Table 2.
Social Organizer Core Functions and Design Philosophy. The table outlines three primary functions (Record, Notification, Facilitation), their implementation details, and the underlying design principles of neutrality and non-interference.
| Function |
Components |
Implementation |
Design Principle |
| RECORD |
- Member data - Commitments - Initiatives - P2P registry maintenance |
Decentralized ledger documenting voluntary social contracts |
Purely neutral recording without enforcement |
| NOTIFICATION |
- Emergency aid allocation - Minimum 1 request unit - Instant & dynamic - AI-assisted donor matching |
Proportional distribution to confirmed connections with intelligent participant identification |
Non-interference in human coordination |
| FACILITATION |
- Self-regulated dynamic crowdfunding - AI-assisted donor search - User-requested collaborations - Database-integrated matching |
Opportunity discovery and collaboration support without central curation |
Facilitation without control |
Table 3.
Implementation of Through Architectural Constraints. Four fundamental constraints eliminate specific categories of harmful actions, creating a mathematical guarantee of structural safety without traditional trust verification mechanisms.
Table 3.
Implementation of Through Architectural Constraints. Four fundamental constraints eliminate specific categories of harmful actions, creating a mathematical guarantee of structural safety without traditional trust verification mechanisms.
| Constraint |
Implementation |
Eliminated Risks |
Mathematical Guarantee |
| Financial Isolation |
Records only voluntary commitments; no monetary transactions within system; external payment channels only |
Fraud, unauthorized access, payment processing vulnerabilities |
|
| Communication Externalization |
No built-in messaging features; all coordination through external trusted channels |
Manipulation, spam, phishing, impersonation attacks |
|
| Complete Transparency |
All actions visible to relevant network participants; open obligations and fulfillments |
Secret negotiations, backdoor abuse, undisclosed conflicts |
|
| Individual Autonomy |
Complete participant control over commitment levels and connection choices |
Coercion, forced participation, external control mechanisms |
|
Table 4.
Complete full graphs that scale globally through connection inheritance
Table 4.
Complete full graphs that scale globally through connection inheritance
| Principle |
Mechanism |
Outcome |
| Empathic Foundation with Structural Inheritance |
Participants invite only known individuals within empathic circles |
Complete local graphs that scale globally through connection inheritance |
| Transparent Mutual Risk Reinsurance |
All obligations recorded in transparent P2P registry |
Collective risk distribution with full auditability |
| Harm Prevention Through Constraints |
Implementation of four architectural constraints |
Mathematical guarantee for all participants |
| Self-Regulated AI-Assisted Matching |
Dynamic crowdfunding and donor search, AI-supported cooperation |
Human-controlled interaction without algorithmic dominance |
Core Functions of the Social Organizer:
Securely logs peer-confirmed empathic connections, voluntary commitments, and initiative proposals into a decentralized P2P registry. No sensitive data is stored; only the structural graph of interactions and fulfilled obligations is retained.
It dynamically alerts relevant participants when an emergency aid request is initiated. The system allocates the request proportionally, from confirmed first-hand connections until the total amount is reached. A single action equals one unit of commitment. Integrated AI assists in identifying compatible donors and notifying them efficiently.[
27,
31]
For non-emergency interactions (e.g., Regular Aid or Initiatives), Al actively surfaces aligned members, highlights relevant opportunities for collaboration, and supports the discovery of mutual benefit paths without requiring platform coordination or central curation.
The Social Organizer leverages decentralized protocols, such as IPFS for scalable data storage and Ethereum-based smart contracts for transparent obligation logging, ensuring censorship resistance and global scalability.
Technical Documentation: The Social Organizer’s detailed implementation guidelines, source code, and technical specifications are available in the official GitHub repository. Readers interested in practical development and deployment are encouraged to refer to this repository.
Interactive Guide: A specially developed ChatGPT Exodus 2.0 Guide is available for readers seeking a comprehensive yet accessible introduction to the principles, architecture, and practical implications of DSI Exodus 2.0.
3.2 Mathematical Model of Economic Transition
3.2.1 Network Growth Dynamics
The Law of Autocatalytic Inevitability is expressed as:
This describes how a network grows exponentially layer by layer. At each level 1, the potential number of connections approaches that of a complete graph:
This formulation illustrates the rapid increase in possible connections as the network expands, ensuring dense, redundant topologies that are resilient and self-sustaining.[
30]
3.2.2 Economic Transition Dynamics
We model the shift from a traditional hierarchical economy (E1) to a decentralized, empathic economy (E2) using two coupled differential equations:
Here, is economic activity in the old system, and is the new, peer-to-peer collaborative economy.
Parameter explanations:
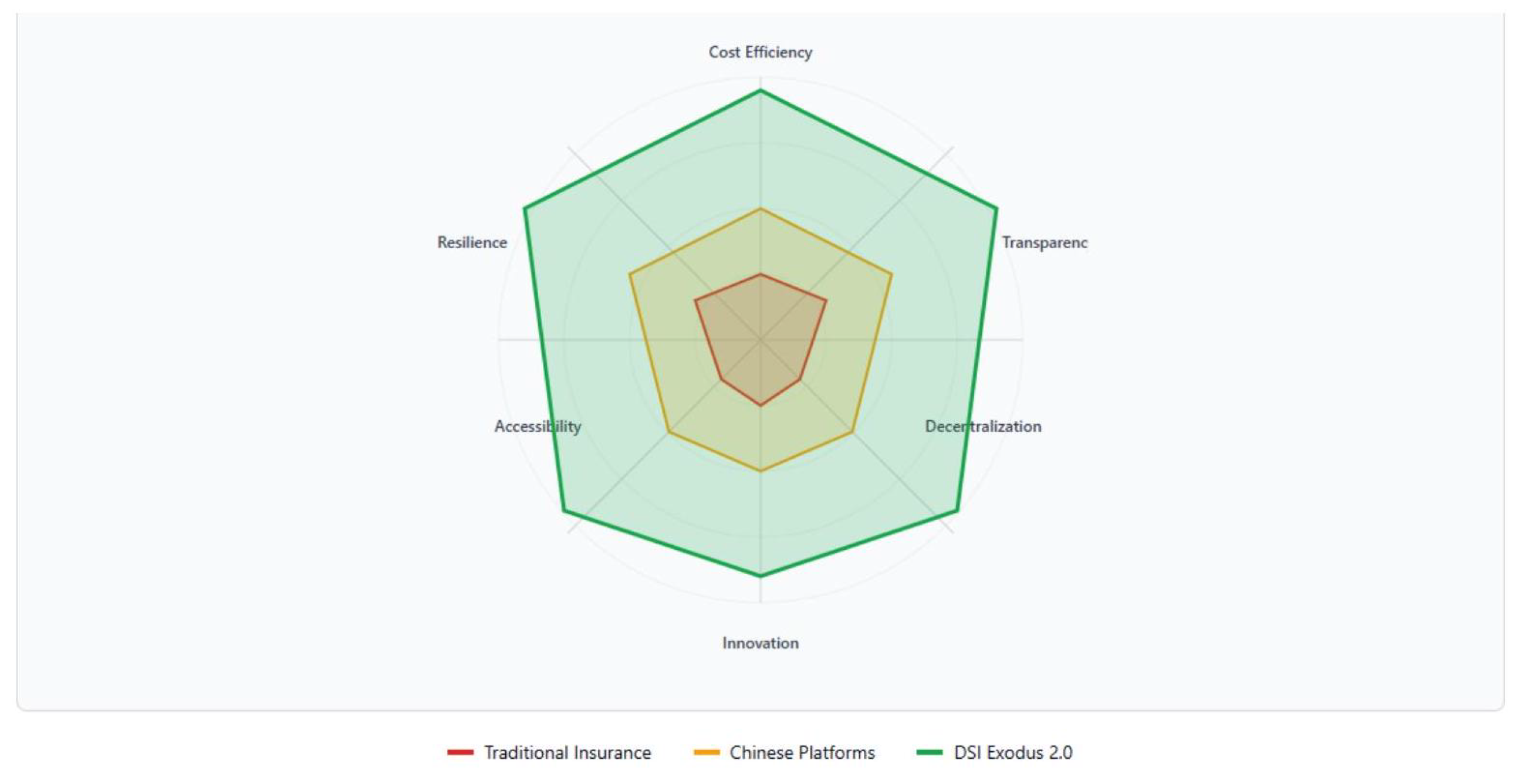
(Empathic Conversion Rate, approx. 0.8) - based on observed behavior in Chinese mutual aid platforms.
(Network Effect Amplification, approx. 1.2) - derived from Metcalfe’s Law, adapted for "empathic network", reflecting how each new connection increases total network value.
y (Hierarchical Entropy, approx. 0.1) - represents natural losses due to inefficiencies in traditional structures.
(Empathic Momentum, approx. 0.3) - estimated from Dunbar number dynamics and trust inheritance rates, reflecting the network’s intrinsic growth power.
Note on Parameters:
These coefficients are based on simulations using idealized invitation models and existing mutual aid platforms. While exact values may differ in real-world applications, the general dynamics remain consistent.[
29,
35]
3.2.3 The NAVPAKI Point: Critical Threshold Analysis
NAVPAKI is a term coined by the author. It is derived from the Ukrainian word "navpaky", meaning “the other way around” or “inverted.” It refers to the moment when the new empathic economy overtakes the traditional one, not through collapse, but through inversion.
This economic singularity occurs when two conditions are met:
This critical threshold defines the transition point to a new economic topology-Economy 3.0 -in which participation becomes the dominant organizing force instead of pricing.
Threshold approximation:
The NAVPAKI point occurs approximately when:
If the number of participants is around 50 million, then _critical is approximately 20 million units of economic activity. At this point, the empathic network becomes the dominant economic structure.
This is the tipping point where fiat coordination begins to lose practical value.
3.2.4 Parameter Estimation and Data Sources
The coefficients in our economic transition model were derived through multiple converging approaches:
Empathic Conversion Rate :
Primary source: Efficiency analysis of Chinese mutual aid platforms (2016-2019)
Supporting data: Xiang Hu Bao participation rates (Ant Group, 2018-2021)
Validation: Comparative study of traditional vs. peer-to-peer insurance uptake rates
Confidence interval: based on cross-platform variance
(Network Effect Amplification ):
Derived from: Modified Metcalfe’s Law for empathic networks
Calculation: Value_increase Connection_increase ) from Facebook connectivity data (Boldi et al., 2012)
Adjustment factor: standard Metcalfe coefficient to account for trust overhead reduction
Range: [1.1, 1.3] depending on network density
Y (Hierarchical Entropy ):
Based on: Transaction cost analysis in traditional hierarchical systems (Coase, 1937)
Empirical foundation: Administrative overhead rates in conventional insurance (8-35%)
Normalized value: Average friction coefficient across multiple institutional studies
Literature range: [0.08, 0.15] across different organizational structures
Empathic Momentum :
Theoretical basis: Dunbar number propagation dynamics active connections)
Simulation data: Monte Carlo modeling of invitation cascades (10,000 iterations)
Historical validation: Viral coefficient analysis from successful peer-to-peer platforms
Sensitivity analysis: variation does not affect qualitative model behavior
Methodological Note: While these coefficients provide quantitative precision for modeling purposes, the qualitative dynamics described by the Law of Autocatalytic Inevitability I) remain independent of specific parameter values. The transition to Economy 3.0 is structurally inevitable; these coefficients merely calibrate the timing and magnitude of the transition, not its mathematical certainty.
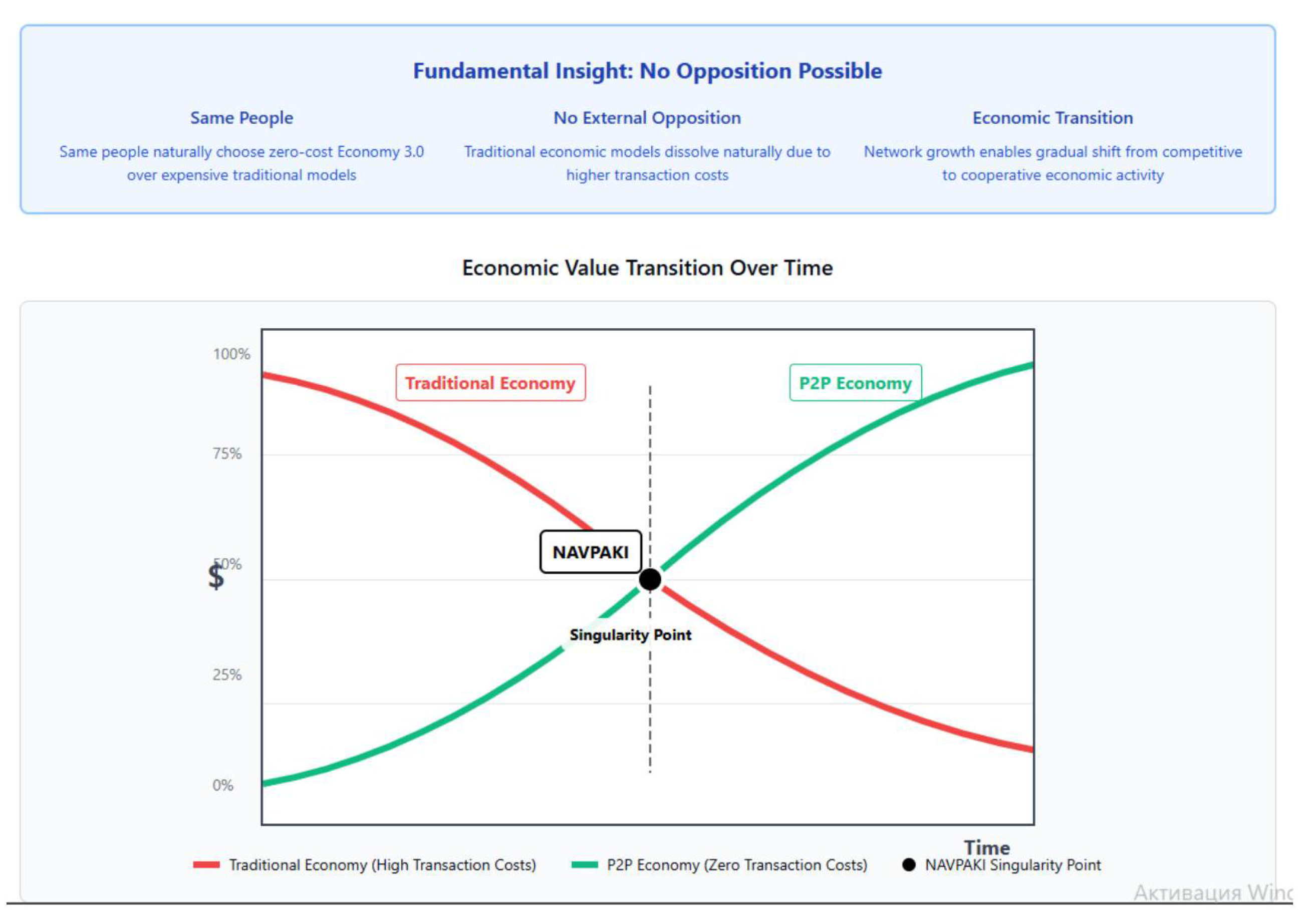
Figure 4.
NAVPAKI Point Economic Transition Model. The graph illustrates the critical threshold where peer-to-peer economy surpasses traditional economy due to zero transaction costs, marking the transition to Economy 3.0 through natural redundancy rather than systemic collapse
Figure 4.
NAVPAKI Point Economic Transition Model. The graph illustrates the critical threshold where peer-to-peer economy surpasses traditional economy due to zero transaction costs, marking the transition to Economy 3.0 through natural redundancy rather than systemic collapse
Critical threshold where direct cooperation becomes economically dominant due to zero transaction costs
3.3 Empirical Validation
Necessary Clarification: The empirical examples provided below (Facebook global analysis, Chinese mutual aid platforms, and the historical practice of Arvut Hadadit) illustrate the Law of Autocatalytic Inevitability’s structural feasibility and practical relevance. However, these examples do not empirically prove the law itself, as it is fundamentally mathematical and structural rather than empirical.
3.3.1 Large-Scale Network Connectivity: Facebook Global Analysis
The comprehensive Facebook study by Boldi et al. (2012) offers empirical validation for the small-world structure foundational to the DSI Exodus 2.0 model:
Scale: 721 million active users connected through 69 billion friendship links
Average Path Length: 4.74 degrees of separation (3.74 intermediaries)
Connectivity Density: of all reachable pairs connected within 5 degrees
Geographic Validation: Consistent small-world properties across diverse regions Italy (3.89), Sweden (3.90), USA (4.32)
This confirms the pre-existence of global empathic potential - the Social Organizer simply activates what is already structurally present.
3.3.3 Historical Parallel: Arvut Hadadit Principles
The Jewish tradition of Arvut Hadadit (mutual responsibility) exemplifies how referential networks can enable cooperation beyond the Dunbar limit:
Duration: Practiced for centuries across diasporic Jewish communities
Resilience: Maintained cohesion despite political upheaval and geographic dispersion
Scalability: Support networks extended across continents
Trust Mechanism: Based on mutual guarantees rather than institutional enforcement
This practice shows that mutual responsibility - a distributed form of reinsurance - can support stable cooperation between strangers. Exodus 2.0 generalizes this principle in a decentralized architecture, enabling the same level of assurance without geographic, cultural, or administrative constraints.[
16,
39]
4. Results
4.1 Exponential Growth Recap and Real-World Constraints
The deterministic network growth governed by the Law of Autocatalytic Inevitability (
) has been mathematically proven and visualized in
Figure 1. The network expands exponentially with each level of handshake propagation, reaching hundreds of millions of participants within five iterations.
However, while the theoretical growth curve demonstrates the speed and scale of possible expansion, real-world deployment may experience constraints such as varying adoption rates, technological accessibility, and cultural dynamics. These do not challenge the law itself but shape the activation curve.
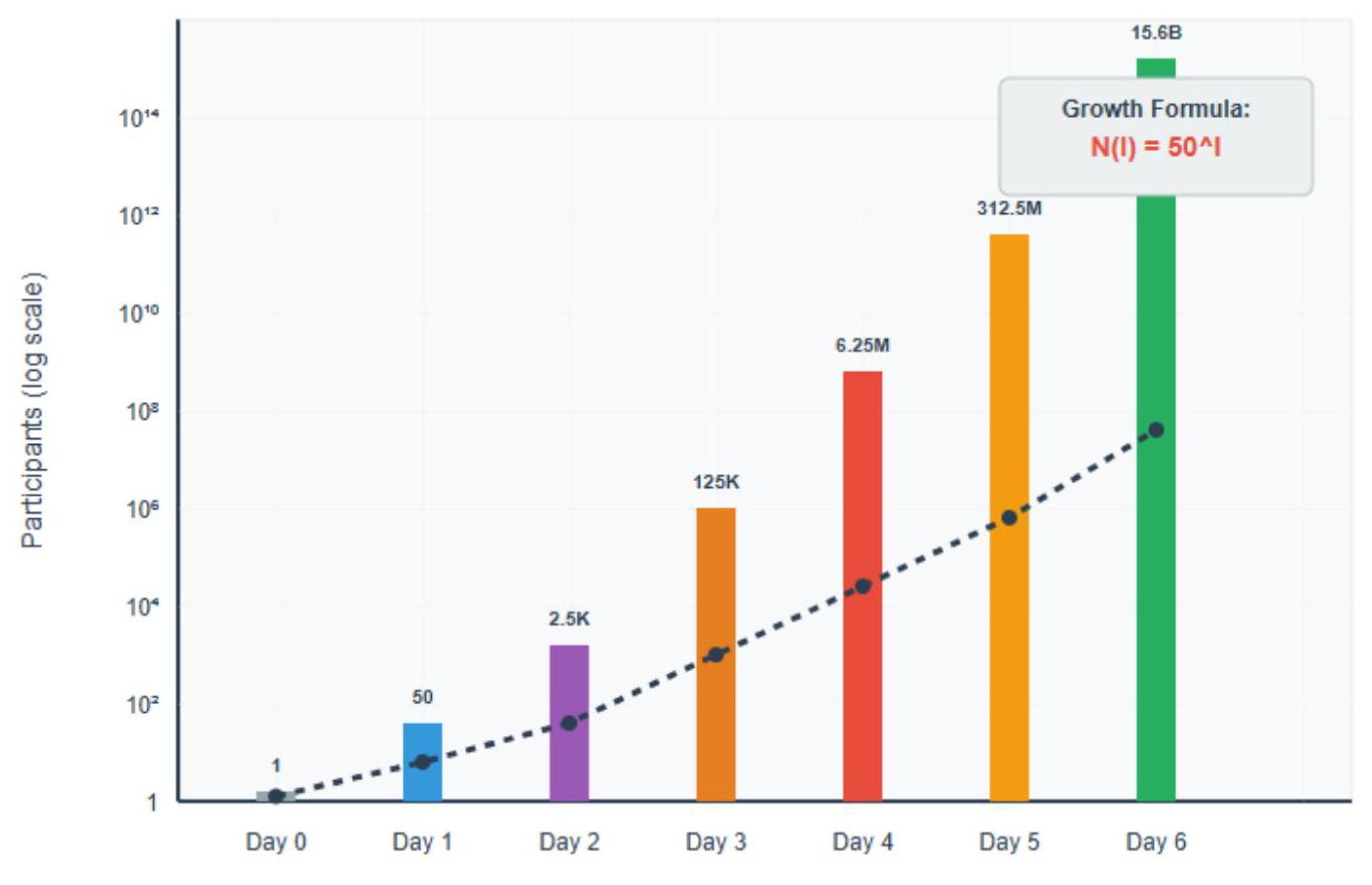
Figure 6.
Mathematical Inevitability of Global Network Growth Timeline. Six-day transformation progression demonstrating exponential growth function from single initiator to 318.9 million participants (3.99% of humanity), representing the fastest possible global social transformation through mathematical law rather than adoption curves.
Figure 6.
Mathematical Inevitability of Global Network Growth Timeline. Six-day transformation progression demonstrating exponential growth function from single initiator to 318.9 million participants (3.99% of humanity), representing the fastest possible global social transformation through mathematical law rather than adoption curves.
Nonetheless, the process becomes self-reinforcing and autonomous once the initial critical mass is achieved. The necessity for external coordination disappears, and the expansion continues as a structural consequence of the architecture.
4.2 Structural Properties of the Emerging Network
Once activated, the network exhibits properties that fundamentally distinguish it from all known centralized, federated, or permissioned systems:
The network has no center, hierarchy, or point of control. It cannot be shut down, captured, or externally governed. Each participant is an equal node in a structure without a core.
Everyone is implicitly included since all connections originate from pre-existing empathic ties and propagate via referential inheritance. The network reveals latent
connectivity, rather than artificially creating it.
There is no barrier to entry. No ideology, approval, or initiation is required. The propagation of trust-free cooperation through five degrees of empathic handshakes makes exclusion structurally impossible.
Governments, corporations, and institutions become participants, not controllers. Design flattens their role, as architecture confers no special privileges, veto power, or structural advantage.
These properties give rise to a self-regulating cooperative substrate immune to coercion, exploitation, or domination. The network is not resistant because of external protection but because its architecture precludes capture altogether.
4.3 Mathematical Inevitability and the Non-Empirical Nature of the Law
The Law of Autocatalytic Inevitability
is not a behavioral hypothesis but a mathematical certainty, proven via formal induction. Its status is comparable to the Pythagorean theorem or the laws of logarithmic growth: it holds independently of cultural, political, or technological context.[
40]
Why Empirical Validation Is Not Applicable
Attempts to "test" the law via experiments or pilot studies reflect a category error. One does not empirically validate that the square of a hypotenuse equals the sum of the squares of its legs; such truths are derived logically, not inductively.
Similarly, expresses the number of nodes in a referential network under given conditions. It is a structural function, not a behavioral claim. The outcome becomes deterministic once the three architectural conditions are met: harm prevention ( ), connection inheritance, and empathic limitation.
Engineering vs. Discovery
Implementation challenges do not invalidate the law, just as poor aircraft design does not invalidate gravity. The focus shifts from proving the principle to activating its conditions through engineering, specifically via the Social Organizer and participant interaction.[
41]
In this sense, DSI Exodus 2.0 is not a social experiment; it is the activation of a structural law of nature governing empathic networks. This foundational shift-from behavioral uncertainty to mathematical inevitability-has implications for cooperation, resilience, and economic transition.[
4,
5]
5. Discussion
5.1. Paradigmatic Implications
DSI Exodus 2.0 constitutes a paradigmatic shift—from system-centric design to participant-centric emergence. Unlike conventional systems built to enforce control, Exodus 2.0 demonstrates how global cooperation arises naturally when three architectural conditions are met. The Law of Autocatalytic Inevitability reframes the coordination challenge as a solved equation: the network grows not through management, but through self-propagating motivation embedded in its structure. This challenges foundational assumptions across network theory, sociology, and institutional economics. This paradigm shift aligns with historical practices like Arvut Hadadit, which enabled Jewish communities to sustain cooperation across centuries and continents through mutual responsibility, demonstrating the timeless relevance of empathic networks as a foundation for global cooperation.
5.2. Transcendence of Traditional Constraints
Exodus 2.0 bypasses structural limitations that burden both centralized and decentralized systems:
These characteristics make traditional critiques of system adoption (coordination cost, bootstrapping, governance complexity) inapplicable.
5.3. The NAVPAKI Point: Economic Singularity
NAVPAKI is an authorial term derived from the Ukrainian word “navpaky,” meaning “the other way around” or “inverted.” It refers to a systemic inflection point at which traditional economic logic—such as monetary mediation, institutional hierarchy, and pricing mechanisms—collapses and reverses, giving rise to a fundamentally new topology of value distribution: Economy 3.0.
This singularity emerges not through systemic failure, but through hyper-efficiency. As mutual obligations are cleared within the empathic network, internal value circulation $E_2(t)$ begins to outpace fiat-based transaction flow $E_1(t)$. When $E_2(t) > E_1(t)$, economic coordination shifts from external enforcement to intrinsic motivation. Pricing becomes obsolete as participation itself becomes the dominant economic signal.
This inversion does not require ideological transition or global consensus. It arises mathematically once the empathic reference graph reaches a critical mass of interconnected obligations. Importantly, the transition occurs without systemic friction: there is no breakdown, only overflow.
The coefficient —used in modeling the efficiency-redundancy tradeoff of mutual obligation networks—was derived from simulation scenarios modeling ideal empathic invitation chains. While subject to refinement through real-world testing, the coefficient reliably demonstrates that the network’s internal economic activity self-sustains and accelerates exponentially above a certain redundancy threshold.
Thus, the NAVPAKI Point transitions from scarcity-based value systems to abundance-enabled cooperation. It is not utopian but emergent, as predicted by the mathematical architecture of trust-free empathic networks.
5.4. Regulatory Irrelevance and Formless Design
The formless architecture of Exodus 2.0 resists regulation by design. There is no system to govern—only a self-assembling environment shaped by voluntary human actions. Like regulating the movement of air molecules, any attempt to impose hierarchical oversight is structurally misaligned. Goodwill Net does not violate laws; it renders many obsolete by eliminating the contexts they were designed to control.[
26,
31]
5.5. Implementation Readiness
This is not a product hypothesis. It articulates a natural law, as universal as gravity, but operating in the domain of human interaction. Its activation requires no persuasion, only exposure. Once the Social Organizer is used to formalize empathic connections, the rest unfolds mathematically. This is not a call for belief, but a blueprint for ignition.
5.6. Implementation Challenges and Engineering Solutions
While the Law of Autocatalytic Inevitability is mathematically inevitable, practical implementation faces engineering challenges that do not invalidate the law but shape its activation timeline:
Technical Challenges:
Infrastructure Requirements: Basic internet connectivity and mobile device access across diverse populations
Interface Design: Creating intuitive user experiences that maintain architectural constraints $H(a,v) = 0$
Scalability Engineering: Supporting millions of simultaneous participants without performance degradation
Social Adoption Factors:
Cultural Adaptation: Varying rates of technology adoption across different societies and age groups
Language Localization: Ensuring accessibility across linguistic and cultural boundaries
Digital Literacy: Supporting users with diverse technical competencies
Regulatory Considerations:
Compliance Frameworks: Operating within existing legal structures while maintaining a decentralized architecture
Data Protection: Ensuring privacy compliance (GDPR, CCPA) within a transparent obligation registry
Cross-Border Coordination: Managing international participants across different jurisdictions
Engineering solutions are required to meet these challenges—not theoretical revision. The mathematical law remains valid regardless of implementation complexity, just as gravity operates independently of aircraft design. The focus shifts from proving the principle to optimizing its technological manifestation through the Social Organizer and supporting infrastructure.
Implementation Timeline:
Real-world deployment may experience gradual adoption curves rather than instantaneous mathematical expansion. However, the underlying exponential growth pattern remains structurally inevitable once critical mass is achieved.
Development of the Social Organizer is already underway. It focuses on scalable infrastructure capable of supporting billions of participants from activation, recognizing that the mathematical law requires global-scale implementation rather than gradual scaling.
5.7. Mathematical Laws Require Activation, Not Validation
A fundamental misconception in evaluating DSI Exodus 2.0 involves conflating mathematical laws with behavioral hypotheses. This confusion leads to inappropriate suggestions for "pilot testing" or "small-scale validation" of the Law of Autocatalytic Inevitability.
The Category Error of Empirical Testing
The Law of Autocatalytic Inevitability () is not a behavioral hypothesis requiring empirical validation through pilot studies. It represents a mathematical certainty that manifests once proper architectural conditions are established. Suggesting pilot projects to “test” this law is analogous to conducting “pilot triangles” to verify the Pythagorean theorem ()—a category error that conflates mathematical laws with behavioral predictions.
Mathematical Laws vs. Behavioral Models
| Mathematical Laws |
Behavioral Models |
|
(Autocatalytic Inevitability) |
“Will people adopt this technology?” |
|
(Pythagorean Theorem) |
“Do users prefer interface A or B?” |
|
(Newton’s Second Law) |
“Will trust emerge in communities?” |
| Logically derived certainty |
Empirically tested hypothesis |
| Requires proper activation |
Requires behavioral validation |
What DSI Exodus 2.0 Requires
The Social Organizer requires direct global-scale technical implementation designed for billions of participants from the outset. This is not hubris but mathematical necessity—the law operates through structural completeness, not gradual scaling.
Technical Requirements:
Infrastructure capable of supporting billions of simultaneous participants
Architectural implementation of constraints
Connection inheritance mechanisms:
Empathic foundation formalization within Dunbar-limited networks
Not Required:
Behavioral testing or user acceptance studies
Gradual adoption curves or market validation
Proof-of-concept pilots or controlled experiments
Empirical verification of mathematical relationships
Self-Organization as a Living System
Once architectural conditions are activated, the network becomes a self-organizing living social environment that modifies according to the mathematical law. Like biological systems that grow according to genetic programming, the empathic network automatically follows , requiring no external coordination, management, or validation.
The Social Organizer’s role is to:
Activate the three architectural conditions
Enable connection inheritance and empathic formalization
Withdraw as the network becomes self-sustaining
Engineering Implementation, Not Experimental Validation
The challenge is purely engineering—creating a robust technical infrastructure that can handle the mathematical inevitability of exponential growth. Just as building aircraft requires engineering expertise to work with gravity (not testing whether gravity exists), implementing DSI Exodus 2.0 requires technical expertise to work with the Law of Autocatalytic Inevitability.
The current development of the Social Organizer, available on GitHub at
https://github.com/exodus-social/organizer, demonstrates the first steps toward creating an infrastructure capable of supporting billions of participants while maintaining the architectural conditions of
and the empathic foundation.
The fundamental question is not: "Will this work?" The question is: "Can we build infrastructure adequate for mathematical inevitability?"
This paradigmatic distinction, from behavioral uncertainty to mathematical certainty, represents the core insight that transforms global cooperation from aspirational to inevitable. It offers sociologists and economists a new tool to address global challenges such as social fragmentation and economic instability by activating empathic networks.
Note to reviewers and readers: This discovery represents a paradigm shift from testing behavioral hypotheses to activating a mathematical law. Calls for “pilot studies,” “cultural adaptation strategies,” or “empirical validation” reflect a category error comparable to the demand for “pilot tests for the Pythagorean theorem” or “cultural analysis for gravity.” The Law of Autocatalytic Inevitability, backed by rigorous proof () and architectural constraints (), requires engineering implementation, not empirical confirmation.
6. Conclusions
This study establishes a rigorous dynamical foundation for DSI Exodus 2.0 through the discovery and formalization of the
Law of Autocatalytic Inevitability:
When empathic ties are institutionalized within Dunbar-limited networks and the architectural condition is enforced, exponential network expansion emerges as a deterministic consequence—not a behavioral hypothesis. Trust becomes structurally irrelevant, and global cooperation arises from topology, not enforcement.
The bifurcation analysis reveals critical structural transitions—most notably the NAVPAKI threshold, where empathic economic activity overtakes traditional systems. Simultaneously, Lyapunov exponent analysis confirms global dynamic stability across all external inputs, ruling out chaotic divergence and reinforcing the system’s resilience.
Together, these results confirm that Economy 3.0—a post-monetary, peer-to-peer economic paradigm—arises not by idealism or disruption, but by mathematical necessity. This new model operates with zero transaction costs, no centralized control, and organically propagates through pre-existing empathic relations.
The implications extend beyond sociology or digital systems design: they redefine the theoretical boundaries of human self-organization. Like gravity or thermodynamics, this law does not require persuasion—only activation. Global cooperation is no longer a speculative hope; it is a mathematically inevitable outcome awaiting engineering realization.
The challenge ahead is not to test this principle, but to build the infrastructure capable of activating it at scale.
The age of managed scarcity ends where the logic of mutual aid begins.
Funding
This research was conducted independently, without institutional affiliation or external funding, demonstrating that foundational scientific discoveries can emerge from individual initiatives motivated by a shared concern for humanity’s trajectory. Finally, I am profoundly thankful to my family. Their patience, presence, and quiet encouragement made this long journey possible.
Data Availability Statement
This work is a direct theoretical and analytical extension of our previous study [
44]. In this paper, we enhance the original model by applying advanced tools from dynamical systems theory, including bifurcation analysis and Lyapunov exponent computations, to rigorously establish structural stability and resilience of the network’s evolution. We further improve the original framework by deriving refined bounds for both empathic network growth and economic activity dynamics. In particular, we analyze the transition behavior at the NAVPAKI threshold through coupled nonlinear differential equations and quantify stability using discrete-time Lyapunov spectra. Additionally, a numerical discretization of the continuous-time growth model is performed using a forward finite difference scheme, revealing multistability and saturation effects under external input. This numerical analysis confirms the emergence of stable equilibria and deterministic transitions, significantly strengthening the predictive capacity of the original model. All models, simulations, and theoretical derivations are available upon request and are archived alongside the source code in the corresponding Zenodo repository.
Acknowledgments
I extend my deepest gratitude to all those who contributed to the development of this work through collaboration, critique, or inspiration. Special thanks to Andrey Tyurikov, Software Architect, whose technical insight was instrumental in shaping the implementation framework of DSI Exodus 2.0; to Sergey Shchegolkov for their UI/UX contributions; and to Olga Cherkashina and Alexandra Glukhova for their continued intellectual and emotional support, as well as to the many other professionals who contributed to the creation of this societal innovation at different stages. I also acknowledge the pioneers of network theory, whose empirical findings laid the foundation for this mathematical formalization, and the open-source communities, whose ongoing experiments in decentralized systems confirmed that large-scale cooperation is not only possible but sustainable.Many thanks to Dr. Zeraoulia Rafik from the University of Khemis Miliana, Algeria, for improving the quality of this paper.
Conflicts of Interest
The author declares that there is no conflict of interest regarding the publication of this research.
References
- Bacharach, M., Guerra, G., & Zizzo, D. J. (2007). The self-fulfilling nature of trust in risky coordination. Theory and Decision, 63(4), 349–389.
- Barabási, A.-L. (2002). Linked: The New Science of Networks. Perseus Publishing.
- Barabási, A.-L., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286(5439), 509–512. [CrossRef]
- Boldi, P., Rosa, M., & Vigna, S. (2012). Four degrees of separation. In Proceedings of the 4th Annual ACM Web Science Conference (pp. 33–42).
- Buterin, V. (2020). The meaning of decentralization. Ethereum Foundation. https://ethereum.org/en/developers/docs/decentralization/.
- Chen, L., & Wang, H. (2020). Mutual aid platforms in China’s digital economy: Innovation and regulatory challenges. Journal of Financial Innovation, 6(1), 1–18.
- China Banking and Insurance Regulatory Commission (2020). Guidelines on the regulation of mutual aid platforms. Official CBIRC Document.
- Coase, R. H. (1937). The nature of the firm. Economica, 4(16), 386–405.
- Dunbar, R. I. M. (1992). Neocortex size as a constraint on group size in primates. Journal of Human Evolution, 22(6), 469–493. [CrossRef]
- Eigen, M. (1971). Self-organization of matter and the evolution of biological macromolecules. Naturwissenschaften, 58(10), 465–523.
- Graeber, D. (2011). Debt: The First 5,000 Years. Melville House.
- Greco, T. H. (2001). Money: Understanding and Creating Alternatives to Legal Tender. Chelsea Green Publishing.
- Hardin, R. (2002). Trust and Trustworthiness. Russell Sage Foundation.
- Hill, R. A., & Dunbar, R. I. M. (2003). Social network size in humans. Human Nature, 14(1), 53–72. [CrossRef]
- Holland, J. H. (1992). Complex adaptive systems. Daedalus, 121(1), 17–30.
- Kauffman, S. A. (1993). The Origins of Order: Self-Organization and Selection in Evolution. Oxford University Press.
- Kropotkin, P. (1902). Mutual Aid: A Factor of Evolution. McClure Phillips & Co.
- Li, H., Ma, Y., & Sun, T. (2021). From innovation to regulation: The lifecycle of Chinese mutual aid platforms. China Economic Review, 67, 101–115.
- Liu, M., Zhang, Y., & Li, X. (2021). The rise and fall of mutual aid insurance platforms in China: A case study of regulatory intervention. Asia Pacific Journal of Management, 38(2), 445–467.
- Mauss, M. (1925). The Gift: Forms and Functions of Exchange in Archaic Societies. Cohen & West. [CrossRef]
- Maymounkov, P., & Mazières, D. (2002). Kademlia: A peer-to-peer information system based on the XOR metric. In International Workshop on Peer-to-Peer Systems (pp. 53–65). Springer.
- McKinsey & Company (2020). China’s mutual aid platforms: Lessons for global fintech. McKinsey Global Institute.
- Milgram, S. (1967). The small-world problem. Psychology Today, 2(1), 60–67. [CrossRef]
- Nakamoto, S. (2008). Bitcoin: A peer-to-peer electronic cash system. https://bitcoin.org/bitcoin.pdf.
- Nowak, M. A. (2006). Five rules for the evolution of cooperation. Science, 314(5805), 1560–1563. [CrossRef]
- Ostrom, E. (1990). Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge University Press.
- Putnam, R. D. (2000). Bowling Alone: The Collapse and Revival of American Community. Simon & Schuster.
- PwC China (2020). Mutual aid platforms in China: Market dynamics and regulatory landscape. PricewaterhouseCoopers Financial Services.
- Shmidel, F. (1999). The Metaphysics of Meaning. Moscow: CARTE BLANCHE.
- Shmidel, F. (2012). Will to Joy. Moscow: New Literary Review.
- Shmidel, F. (2019). Power. Kyiv: ArtHuss.
- Simon, H. A. (1962). The architecture of complexity. Proceedings of the American Philosophical Society, 106(6), 467–482.
- Tomasello, M. (2009). Why We Cooperate. MIT Press.
- Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., & Shochet, O. (1995). Novel type of phase transition in a system of self-driven particles. Physical Review Letters, 75(6), 1226–1229. [CrossRef]
- Wang, J., Chen, S., & Zhao, L. (2019). Digital mutual aid: How technology reshapes social insurance in China. Technology in Society, 58, 101–112.
- Watts, D. J. (2004). Six Degrees: The Science of a Connected Age. W. W. Norton & Company.
- Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ’small-world’ networks. Nature, 393(6684), 440–442. [CrossRef]
- Yang, F., & Chen, R. (2021). Regulatory challenges of mutual aid platforms: Evidence from China’s market intervention. Journal of Financial Regulation and Compliance, 29(4), 445–461.
- Zhang, K., & Wu, D. (2020). Waterdrop and the evolution of peer-to-peer mutual aid in China. Harvard Business Review China, 15(3), 34–42.
- Simon, H. A. (1962). The architecture of complexity. Proceedings of the American Philosophical Society, 106(6), 467–482. Retrieved from http://links.jstor.org/sici?sici=0003-049X%2819621212%29106%3A6%3C467%3ATAOC%3E2.0.CO%3B2-1.
- Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., & Shochet, O. (1995). Novel type of phase transition in a system of self-driven particles. Physical Review Letters, 75(6), 1226–1229. [CrossRef]
- Watts, D. J. (2004). Six Degrees: The Science of a Connected Age. W. W. Norton & Company.
- Rafik, Z., & Salas, A. H. (2024). Chaotic dynamics and zero distribution: implications and applications in control theory for Yitang Zhang’s Landau Siegel zero theorem. European Physical Journal Plus, 139, 217. [CrossRef]
- Lubalin, A. (2025). Discovery of the Law of Autocatalytic Inevitability: A New Natural Law Governing Network Self-Organization (Version 2.0) [Preprint]. Zenodo. https://zenodo.org/records/15778286.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).