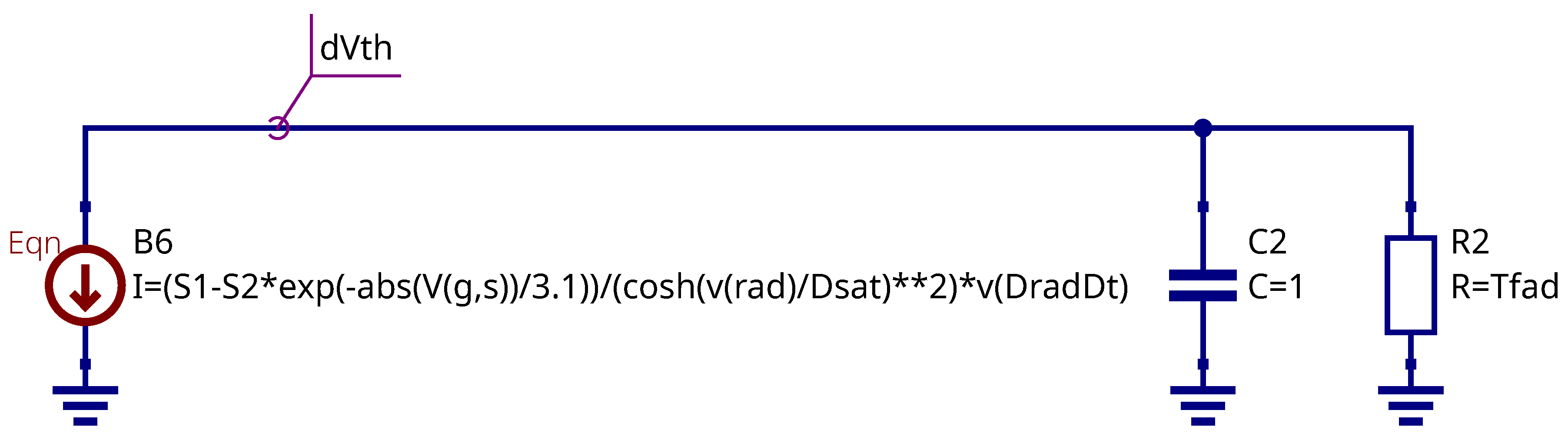The Compact Model Synthesis for the RADFET Device

1. Introduction

Radiation sensitive field-effect transistors (RADFETs) are widely used for ionizing radiation control in areas such as aerospace equipment, nuclear setups, dosimetry equipment, radiation therapy, and environmental monitoring [1,2,3]. Usually, p-channel metal-oxide-semiconductor field effect transistors (PMOSFET) are used as the RADFET device. The radiation induced charge in the gate dielectric of the MOSFET device generates the threshold voltage $V_{t0}$shift [4,5,6]. It is possible to calibrate the $V_{t0}$ shift dependency on the accumulated dose and determine the accumulated dose from the $V_{t0}$ value readout [1,6,7]. RADFET sensors have many advantages such as small sensor area, low cost, and simple readout circuitry. It is possible to embed the RADFET sensor in the integration circuits (ICs) to set the device operating point and readout processing [8].

The improvement of the dose sensitivity and usage of the standard CMOS technology nodes such as CD4000 are the most important development directions for the RADFET sensors [9,10,11]. Usually such RADFET sensors operate at positive gate bias. This operation mode speeds up the separation of electron-hole pairs, which are generated under the device irradiation, and increases the radiation induced charge accumulated in the gate dielectric [12,13,14]. The dose sensitivity of the RADFET device and the charge work function increase with the electric field strength in the in the gate dielectric. The operation of MOS sensors under high fields in the gate dielectric and under the Fowler-Nordheim tunneling is especially interesting [15,16,17]. The usage of the high-field electrons tunneling allows to conduct the injection annealing after the irradiation [15,17,18]. Our research team proposed the model describing the charge processes in the MOS sensors under different gate bias up to high-field injection region [19,20]. The integration of the proposed mathematical model in the SPICE compatible circuit simulation software would improve its availability. The RADFET SPICE models would be especially useful for the specialized ICs design. The SPICE RADFET model could be also used for the design of radiation hardened ICs. It allows to take into account the shift of the MOSFET parameters under the influence of the irradiation.

SPICE-based circuit simulation tools [21] are the industrial standard for electronic circuits modelling. The most of proprietary (HSPICE, LTspice) and open source (Ngspice, Xyce) circuit simulation tools are based on original SPICE code developed by L.Nagel. The SPICE simulation kernel supports a set of basic passive and active primitive devices, including resistors, inductors, sources, and transistors. The electronic components not presented in a basic set of SPICE devices should be represented using macromodels or compact models [22]. The macro models represents a complex device as an equivalent circuit. The compact models differs from the macro model by the usage only of simple devices like controlled sources and RCL components in the equivalent circuit. The electronic components are represented by a set of equations describing the voltages and current at its terminals.

The RADFET device is not presented among the standard SPICE devices. There exists a need to develop a custom model for this device. This will allow to simulate the analog part of the dosimeter readout circuitry using SPICE compatible circuit simulation tools. The paper [23] presents a modification of the standard SPICE MOSFET model. The radiation input is represented as the subcircuit parameter. This approach has some limitations and uses only a simplified dependency of the MOSFET threshold voltage shift on the absorbed dose. The purpose of this research is to extend the model presented in [23] and to add supplementary effects like gate tunneling current, threshold voltage shift under irradiation, and fading. It is important for the simulation of analog circuits containing RADFET devices. The research [24] presents a limited compact model of the RADFET device, but provides no details on its implementation.

The rest of the paper is organized as the following. The Section 2 provides an overview of the RADFET device, software used for the model generation, and model equations. The Section 3 presents the structure of the generated SPICE model and compares the data from simulation and measurement. The Section 4 gives a model usage example for readout circuit design. The Section 5 gives an outcome of the paper and the summary of the achieved results.

2. Materials and Methods

2.1. Used RADFET Device

The RADFET devices [19] were fabricated using the 6 um CMOS technology compatible with CD4000 logic IC series. The topology of the RADFET is shown in the Figure 1. It is PMOS device with channel length $L=6$ um and channel width $W=700$ um. The n-type silicon wafer doped by phosphorus was used as the substrate. The substrate has 4.5 Ohms per square resistance and <100> orientation. The gate dielectric is silicon dioxide with 100 nm thickness. The total device area is 1600000 um². The layout view of the RADFET device is shown in the Figure 2.

2.2. Circuit Simulation Software

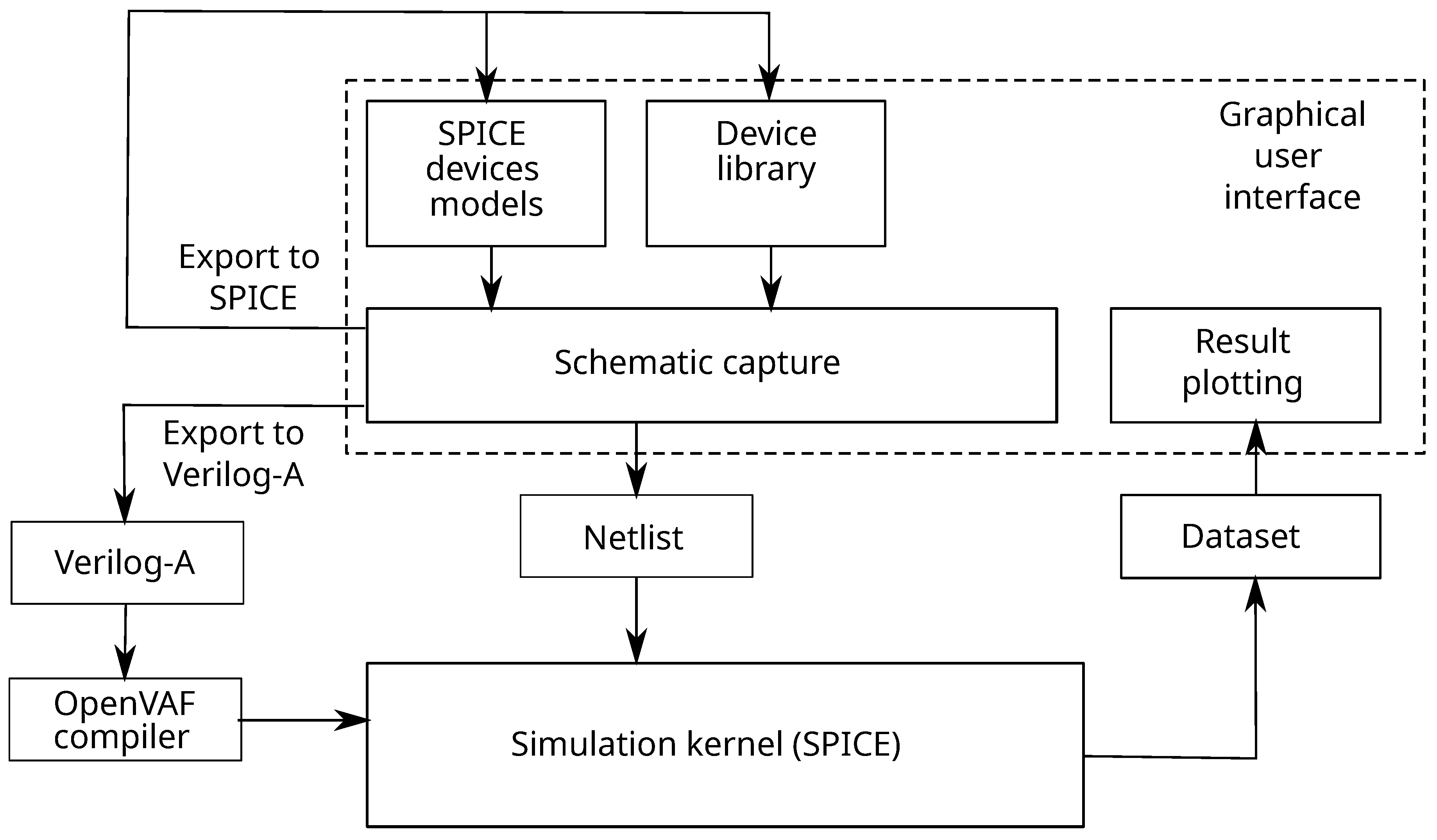
The Qucs-S (developed by Kuznetsov et al. [25]) open source circuit simulator was used for design of the presented compact model. This tool has the following advantages. It is free and open-source and has advanced features for debugging of the compact models. Qucs-S uses free Ngspice [26] simulation kernel that is fully compatible with proprietary SPICE tools. Internal Verilog-A synthesizer of Qucs-S allows to export the designed compact model to Verilog-A module. Interactive tuning and optimization tools implemented in Qucs-S GUI level allow to perform models parameters extraction. The key feature of Qucs-S is the quick switching between the simulation backends while the program operation. Qucs-S uses external simulation kernel Ngspice [27] and Verilog-A [28] modules compiler OpenVAF. The data flow diagram is shown in the Figure 3. It illustrates the interaction between the parts of the simulation software package.

2.3. Basic RADFET Model Equations

The most of RADFET deices are fabricated using the micron technology. And the drain current could be described by MOSFET level 1 equations. The higher levels MOSFET models and BSIM models [29] are applicable for submicron devices and have no benefit for RADFET. The drain current depends on the voltages between the MOSFET pins: gate to source and $V_{GS}$ and drain to source $V_{DS}$.

The drain current in the linear IV-curve region ($0\le V_{DS}\le V_{GS}-V_{TH}$):

$$I_D={\displaystyle \frac{K_{p}W}{2L}}{V}_{DS}[2(V_{GS}-V_{t0})-V_{DS}](1+\lambda V_{DS})$$

(1)

where the $V_{t0}$ is a threshold voltage (V), $\lambda$ – channel modulation (1/V); $K_p$ – transconductance ($A/V^2$);

The drain current in the saturation region if $0\le V_{GS}-V_{t0}\le V_{DS}$:

$$I_D={\displaystyle \frac{K_{p}W}{2L}}{(V_{GS}-V_{t0})}^2(1+\lambda V_{DS})$$

(2)

The source of the RADFET device is internally connected to bulk. The source-bulk voltage $V_{SB}=0$. Therefore the threshold voltage dependency on bulk potential may not be taken into account.

The threshold voltage $V_{t0}$ and device transconductance $K_p$ have dependency on the device absolute temperature T (K) that must be taken into account in the module. The threshold voltage dependency may be approximated by linear function:

$$V_{t0}=V_{t0}\left(T_{nom}\right)+T{C}_{VT0}(T-T_{nom})$$

(3)

where the $T_{nom}$ is the temperature where the initial device parameters could be measured and $T{C}_{VT0}$ is a temperature coefficient (V/K). The transconductance temperature dependency may be approximated by the power function:

$$K_p\left(T\right)=K_p\left(T_{nom}\right){\left({\displaystyle \frac{T}{T_{nom}}}\right)}^{\mu }$$

(4)

where $\mu$ is a coefficient varying in range from 1.3 to 1.5.

2.4. Radiation Dependency of the Threshold Voltage

The threshold voltage of the MOSFET is linear dependent on the absorbed dose D. The basic model may assume a simple linear dependency of the threshold voltage shift $V_D$ on absorbed dose (expressed in rads or Gy). We will use the rads as the dose units further in paper.

$$\Delta V_{t0}=SD$$

(5)

The S is a sensitivity coefficient expressed in $V/rad$. The saturation of the threshold voltage shift at the higher dose may be expressed with a hyperbolic tangent. The more precise approximation proposed in [4,30] may cause convergence issues with SPICE simulator.

$$\Delta V_{t0}=S{D}_{sat}tanh(D/D_{sat})$$

(6)

where $D_{sat}$ is a dose at which saturation is reached. Usually $D_{sat}>{10}^6$ rad.

The sensitivity has a dependency on gate bias during irradiation [31]:

$$S=S_{lin}-S_{exp}exp(-V_{gs}/V_b)$$

(7)

where the $S_{exp}$ and $V_s$ are the fitting coefficient. If the $S_{exp}=0$ only the linear dependency on dose is taken into account.

2.5. Gate Current Model

The both MOSFET level 1-9 and BSIM model do not take into account gate current and radiation effects on gate current. The gate current $I_G$ could be normalized to gate current density and gate area:

$$I_G=J_G·L·W$$

(8)

The gate current density $J_G$ of the RADFET device consists of three components: capacitive current $J_c$, high-field tunnel injection current $J_{inj}$, and radiation current $J_{rad}$.

$$J_G=J_c+J_{inj}+J_{rad}$$

(9)

capacitive component $J_c$ could be expressed using the known unity gate capacitance $C_{ox}$ which may be expressed from gate dielectric parameters and gate oxide thickness $T_{ox}$:

$$J_c=C_{ox}{\displaystyle \frac{d{V}_{GS}}{dt}}$$

(10)

$$C_{ox}={\displaystyle \frac{\epsilon {\epsilon }_0}{T_{ox}}}$$

(11)

where $\epsilon$ is a gate dielectric (for example SiO₂) permittivity and ${\epsilon }_0$ is a dielectric constant.

The injection current could be expressed using the Fowler-Nordheim equations:

$$J_{inj}=A{\phi }_B^{-1}{\left({\displaystyle \frac{V_{GS}}{T_{ox}}}\right)}^{2}exp\left(-{\displaystyle \frac{B{\phi }_B^{3/2}{T}_{ox}}{V_{GS}}}\right)$$

(12)

where ${\phi }_B$ is a barrier potential (V); $A=1.54·{10}^{-6}A·eV·V^{-2}$ and $B=6.83·{10}^{9}e{V}^{-3/2}·V·m^{-1}$ are Fowler-Nordheim tunneling constants.

The radiation current is expressed by the following equation [19]:

$$J_{rad}=qY\left(E\right)K_g{T}_{ox}{\displaystyle \frac{dD}{dt}}$$

(13)

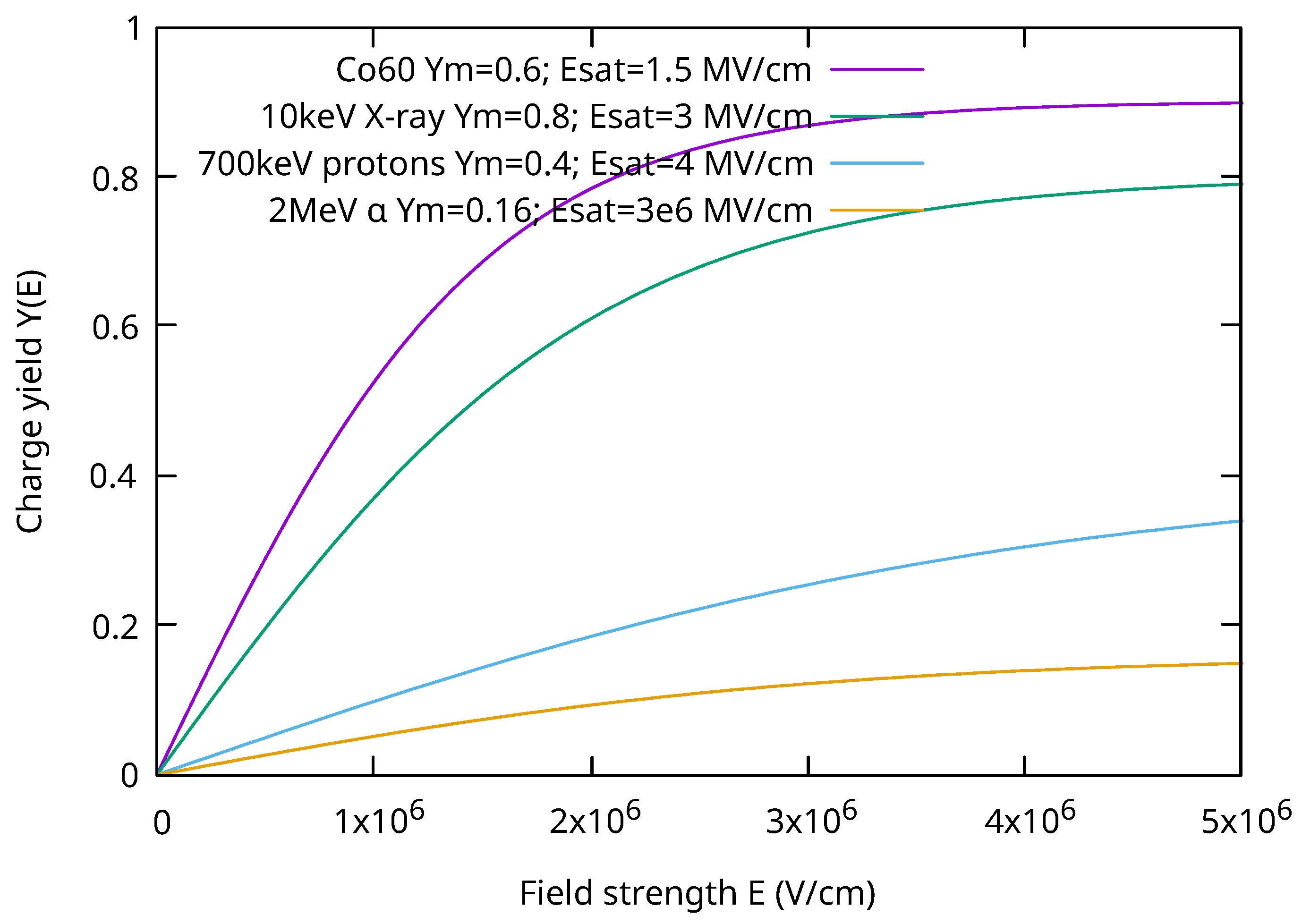
where q is the charge of electron, $K_g$ is a value of electron-hole pair per dose unit and SiO₂ volume ($8·{10}^{12}{\mathrm{cm}}^{-3}·{\mathrm{rad}}^{-1}$). The $Y\left(E\right)$ is the charge yield under irradiation. It depends on the field E in the gate dielectric. It could be determined from the data provided by Schwank et al. [13]. We use the following approximation in the compact model:

$$Y\left(E\right)=Y_{max}tanh(E/E_{sat})$$

(14)

where the $Y_{max}$ and $E_{sat}$ are the fitting constants depending on radiation type (gamma-ray, protons, etc.). The plots of the approximation function are shown in the Figure 4. It shows good match with experimental plots from [13]

3. Results

3.1. The Equivalent Circuit of the RADFET Device

The compact model represented by the following equivalent designed in Qucs-S is shown in the Figure 5.

The equivalent circuit consists of a number of behavioral current and voltage sources and equation defined passive devices. The model has three terminals for MOSFET electrodes: gate (G), source (S), drain (D), and the fourth terminal (RAD) serving as the virtual radiation input. The voltage source representing the absorbed dose in rads should be connected to this terminal. The B1 source represents the drain current level 1 MOSFET model with equations (1) and (2). The B2 source is responsible for transconductance temperature dependency (4). The B3 and B4 current sources represent the gate injection (12) and radiation (13) currents respectively. The capacitor C1 is the gate capacitance $C_{ox}$ (11). The L1 inductor and B5 source are a differentiation stage and serve to obtain the radiation intensity $dD/dt$ using the fundamental properties of inductor current. The B6 controlled source represents a threshold voltage shift dependency on the absorbed dose taking into account gate bias. It relates to equation (7).

The model parameters are summarized in the Table 1. This table provides parameter default value, desciption, and unit.

Qucs-S allows to export the schematic representation of the compact model to a SPICE netlist. The SPICE code synthesized from the model is shown in the Listing 1.

Listing 1. SPICE code of the RADFET model

.SUBCKT RADFET_PMOS S D G RAD Vt0=-2.0 Kp=1e-4 + L=1u W=1u lambda=1e-5 S1=1.5e-3 + Tox=100e-9 Tnom=26.85 TCVTH=2e-3 Mu=1.5 + Dsat=1e6 S2=0.0 VG=0.0 .PARAM eps0=8.854e-12 .PARAM eps=3.9 .PARAM Area=L*W .PARAM phiB=3.1 .PARAM A=1.54e-6*(1/phiB) .PARAM B=6.83e7*(phiB**1.5)*(0.5**0.5) .PARAM q=1.6e-19 .PARAM Ye=0.8 .PARAM Kg=8e12 .PARAM ToxCM=Tox*100 .PARAM AreaCM2=Area*1e4 .PARAM Esat=1e6 .PARAM Yem=1.0 R1 0 RAD  1E12 tc1=0.0 tc2=0.0 C1 S G  {EPS*EPS0*L*W/TOX} B1 S  D  I = (V(G,S)>(V(Vt0)))? + 0:((V(D,S)>(V(G,S)-(V(Vt0))))?(W/L)*V(Kp)* + (1-lambda*V(D,S))*(V(G,S)-V(D,S)/2-(V(Vt0)))*V(D,S): + (W/(2*L))*V(Kp)*(V(G,S)-(V(Vt0))) + *(V(G,S)-(V(Vt0)))*(1-lambda*V(D,S))) B2 kp  0  V = Kp*((Tnom+273)/(TEMPER+273))**Mu L1 0 DradDt  1 B5 0  DradDt  I = V(rad) B3 G  S  I = A*((V(G,S)/ToxCM)**2)* + exp(-B/(abs(V(G,S))/ToxCM))*AreaCM2*sgn(V(G,S)) B6 Vt0  0  V = Vt0-(S1-S2*exp(-abs(V(g,s))/3.1))* + Dsat*tanh(v(rad)/Dsat)+TCVTH*(TEMPER-Tnom) B4 G  S  I = q*Kg*ToxCM*(V(DradDt))*AreaCM2* + Yem*tanh(abs(V(G,S)/ToxCM/Esat)) .ENDS

3.2. Equivalent Circuit Representing Dose Accumulation and Fading

The fading [30] shows the decay of the threshold voltage shift after the irradiation:

$$F={\displaystyle \frac{V_{t0}\left(0\right)-V_{t0}\left(T\right)}{V_T\left(0\right)-V_{t0}}}$$

(15)

where $V_{t0}\left(0\right)$ is the threshold voltage after the irradiation, $V_{t0}\left(T\right)$ is the threshold voltage after time T, and $V_{t0}$ is the threshold voltage without irradiation.

The schematic shown in the Figure 5 could be modified to simulate the fading. The dose accumulation and fading could be represented by adding an RC-circuit stage (Figure 6).

3.3. IV-Curves Simulation

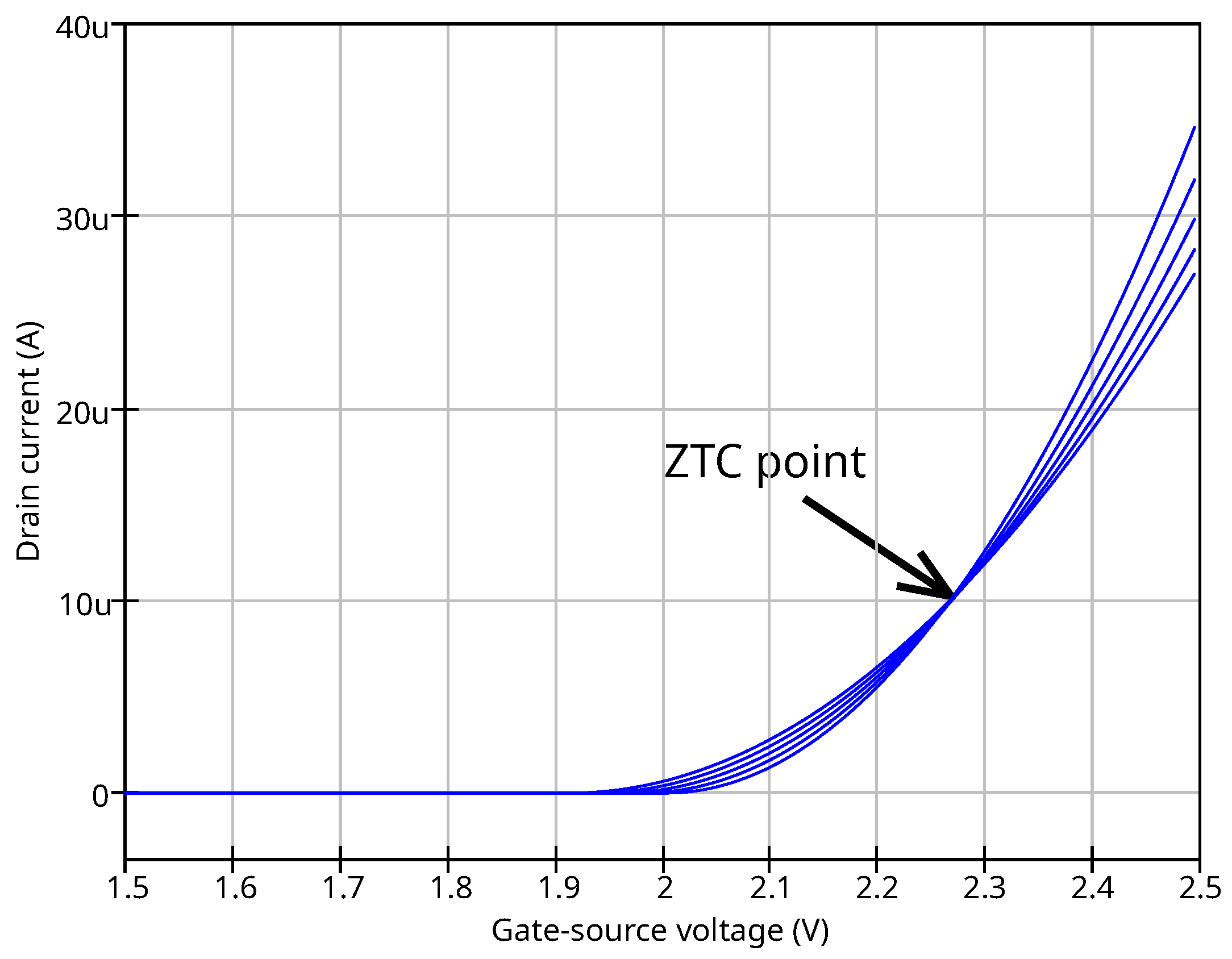
The $V_{t0}$, $K_p$, and $\lambda$ are the MOSFET level 1 model parameters. Its extraction procedure is well described in the literature and not considered here. The pair of $I_d-V_d$ and $I_d-V_g$ curves are required. The used RADFET device is compatible with the CD4000 technology and these parameters could be taken from the basic technology.

The temperature dependency parameters $TCVTH$ and $\mu$ are extracted from fitting of the zero temperature coefficient point at the $I_d$ – $V_g$ curves family at different temperatures within the device operation range. The modeled ZTC point should match the measured ZTC point.

An example of the temperature parameters extraction is shown in the Figure 7. The ZTC point for the used device achieved at the drain current $I_d=10\mu \mathrm{A}$.

3.4. Sensitivity Simulation

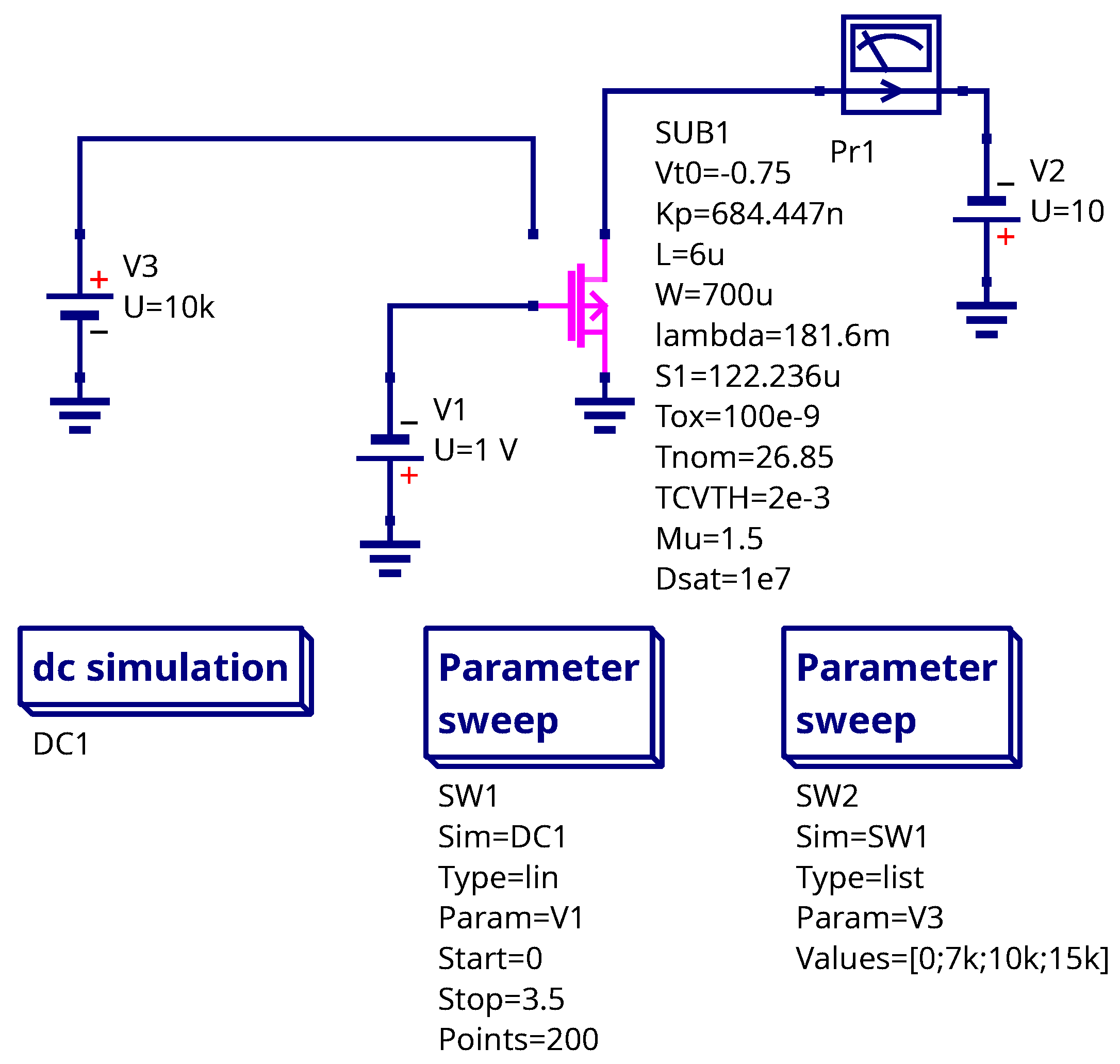
The sensitivity extraction requires I-V curves measurement under different irradiation level. We have measured the $I_d-V_g$ curves for three irradiation doses: 7 krad, 10 krad and 15 krad with no bias applied at gate. This data was used for sensitivity extraction. The testbench schematic in Qucs-S is shown in the Figure 8. The V3 voltage source represents the absorbed dose input. The voltage at this terminal is equal to the dose in rads.

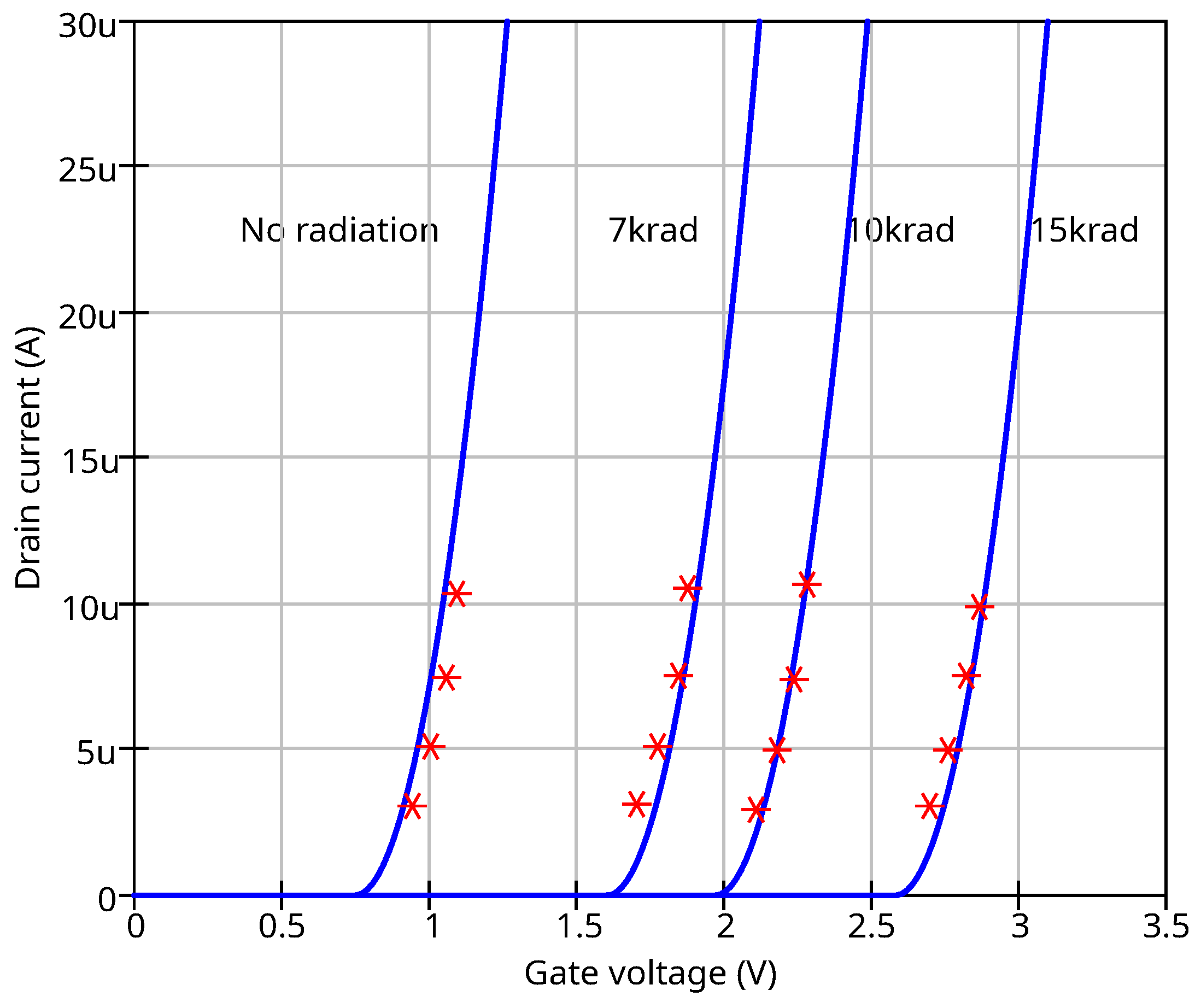
The simulated and measured I-V curves are shown in the Figure 9. The measurements were taken without radiation and under radiation levels 7 krad, 10 krad, and 15 krad. The gamma-ray ⁶⁰Co source was used.

3.5. Gate Bias Dependency of Sensitivity

The sensitivity could be extracted from SPICE simulation as the derivative of the threshold voltage:

$$S={\displaystyle \frac{d}{dD}}(V_{t0}+\Delta V_{t0}\left(D\right))$$

(16)

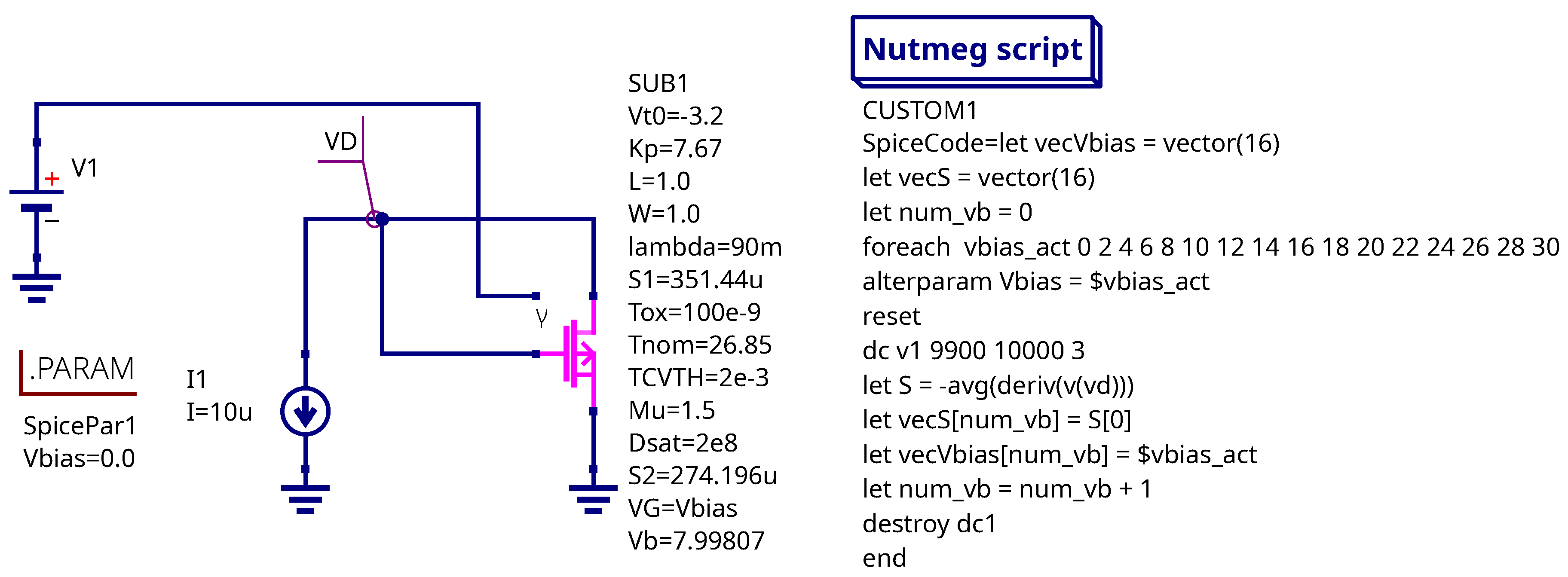
The threshold voltage could be measured if the MOSFET drain and gate are connected to current source and the source is connected to ground. If the source current is in microampere range, the voltage at the drain node will be nearly equal to threshold voltage. The testbench schematic and sensitivity extraction script are shown in the Figure 10

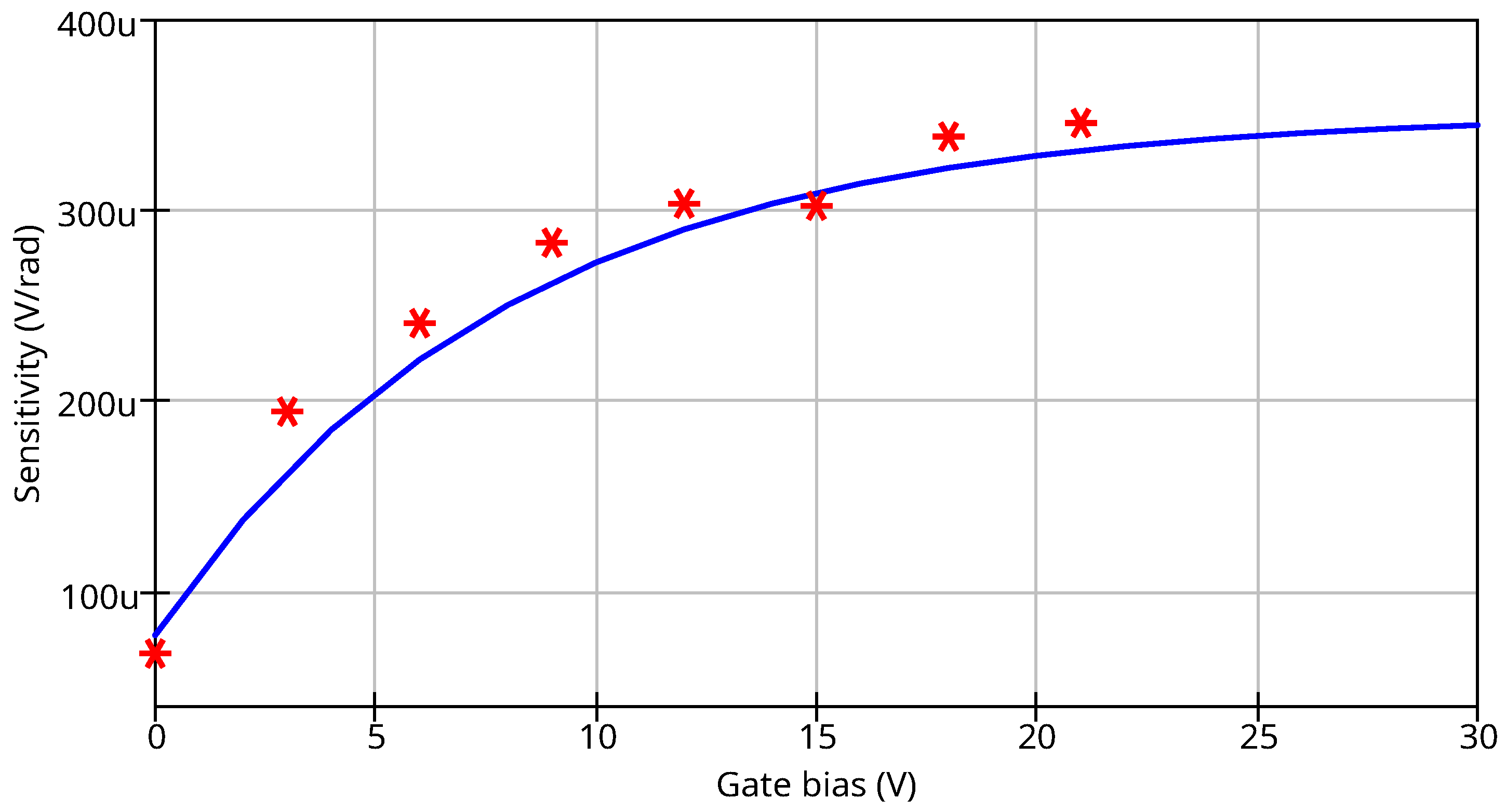
The simulation results are shown in the Figure 11. The data for IRF9520 power MOSFET provided in the paper [4] was used, because the dependency on the gate bias for the device described in the Section 2.1 was not measured. The $K_p$, $V_{t0}$, and $\lambda$ parameters for this MOSFET were taken from the SPICE VDMOS model. The simulation shows a good match with the measurement data. The extracted parameters are the following: $S_{lin}=0.351$ mV/rad, $S_{exp}=0.274$ mV, $V_b=7.99$ V.

3.6. Gate Current Simulation

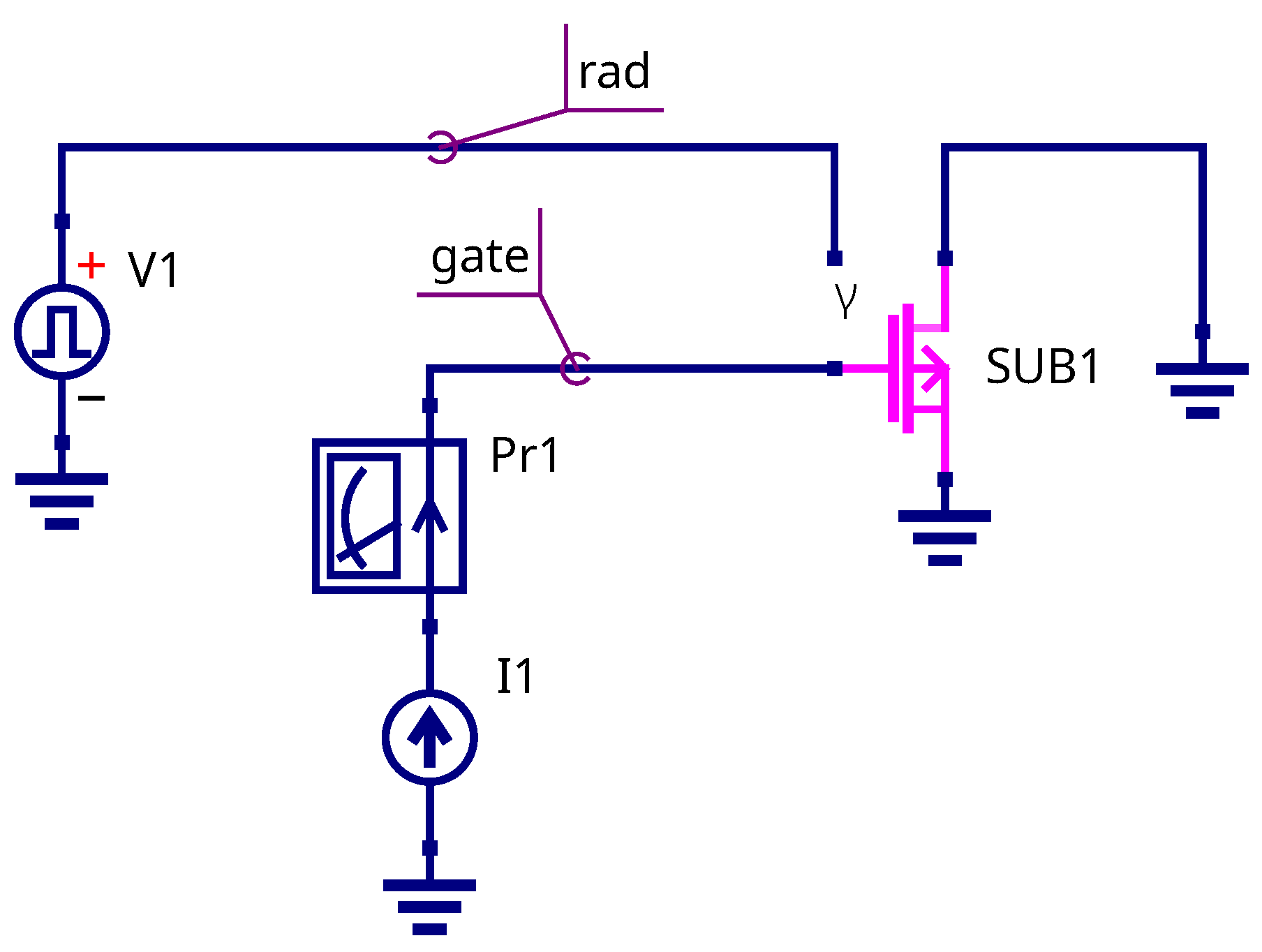
The testbench schematic for the gate current simulation is shown in the Figure 12. The DC injection current source I1 is connected to the MOSFET gate. All other electrodes are grounded. The V1 pulsed source represents a virtual radiation beam. The gate voltage drop is controlled at the transient simulation.

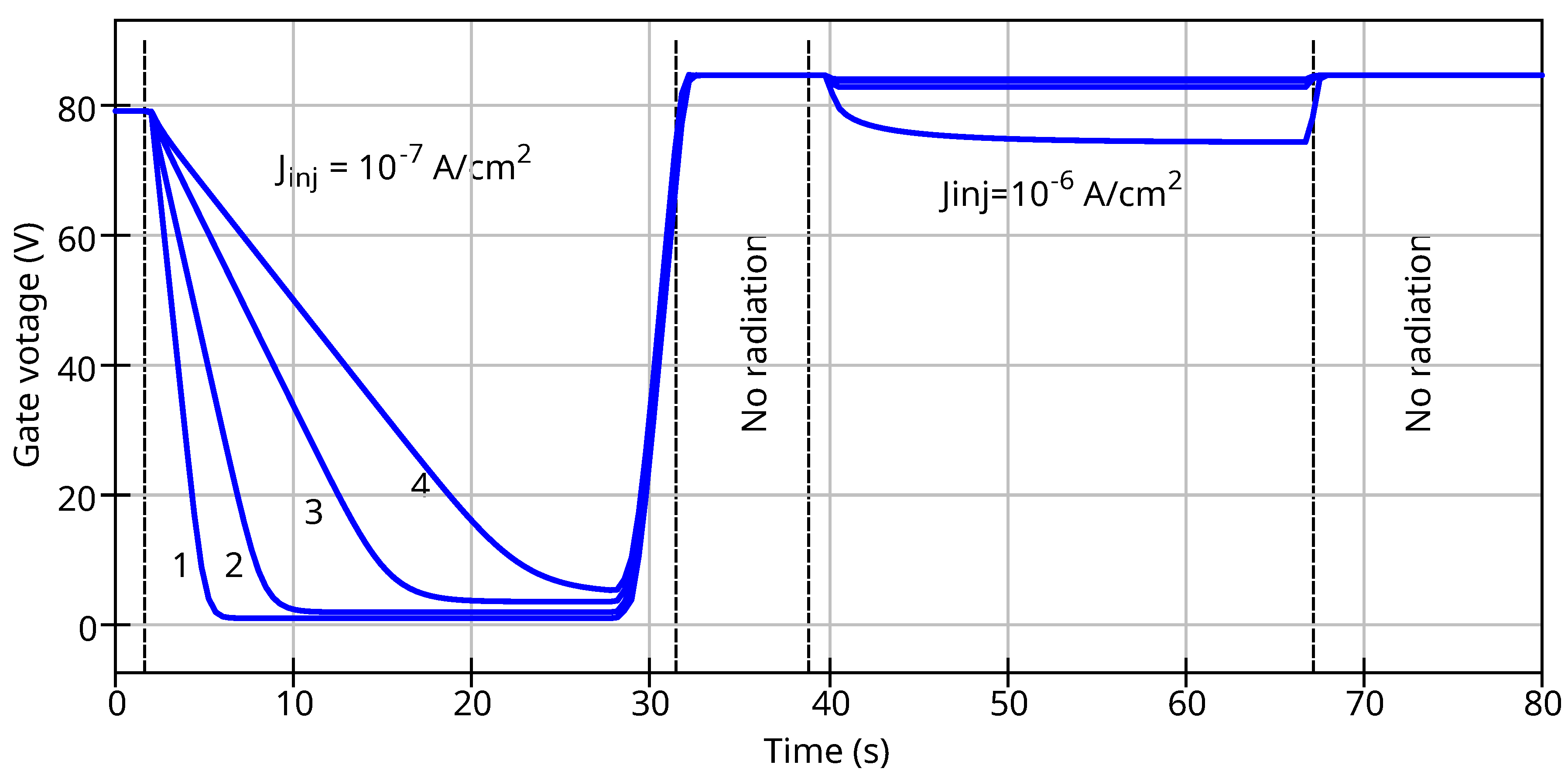
The Figure 13 shows the simulation result for the testcase described in the paper [20]. The MOS sensor (RADFET) was injected by current density $J_g={10}^{-7}$ A/cm². Then it was irradiated by gamma-rays to achieve the radiation current density higher than injection current density. The voltage drop on the MOS structure (RADFET) depends on the ratio of the radiation current and total current. The simulation shows a good match with the data provided in [20].

4. Discussion

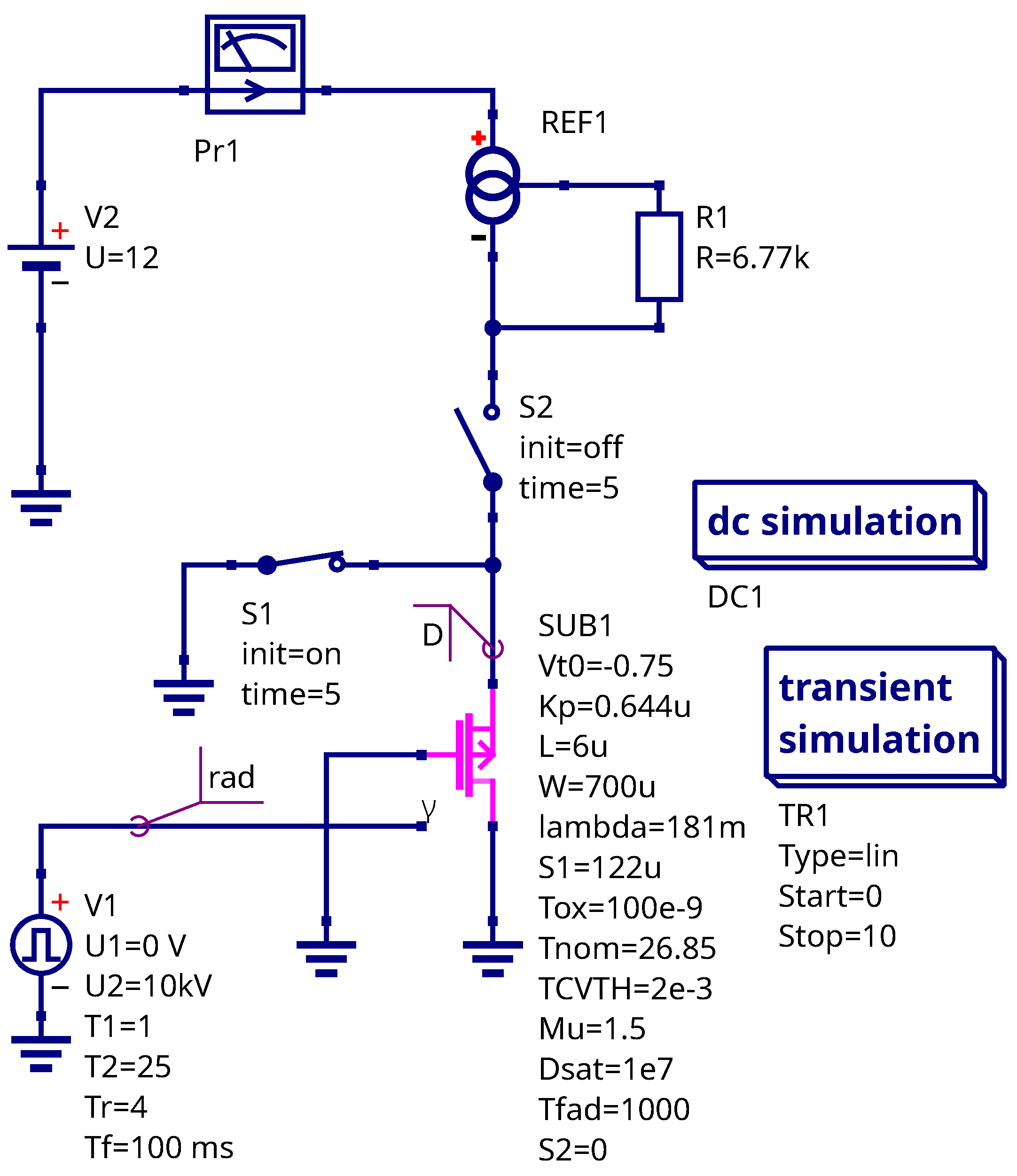
The designed compact model allows to simulate the input stage of the dosimeter [32] and its analog harness. The dosimeter input schematic is shown in the Figure 14. The LM334 current source IC REF1 provides the constant current at the drain. The S1 and S2 switches serve to simulate the irradiation phase and measurement phase. The V1 pulsed source is the virtual radiation input. At the starting time the S1 is closed and S2 is open. All electrodes of the RADFET are connected to ground and the sensor is under the irradiation. When the radiation phase ends, the S1 opens and S2 closes and MOSFET is switched to the measurement circuit. The drain voltage is nearly equal to the threshold voltage.

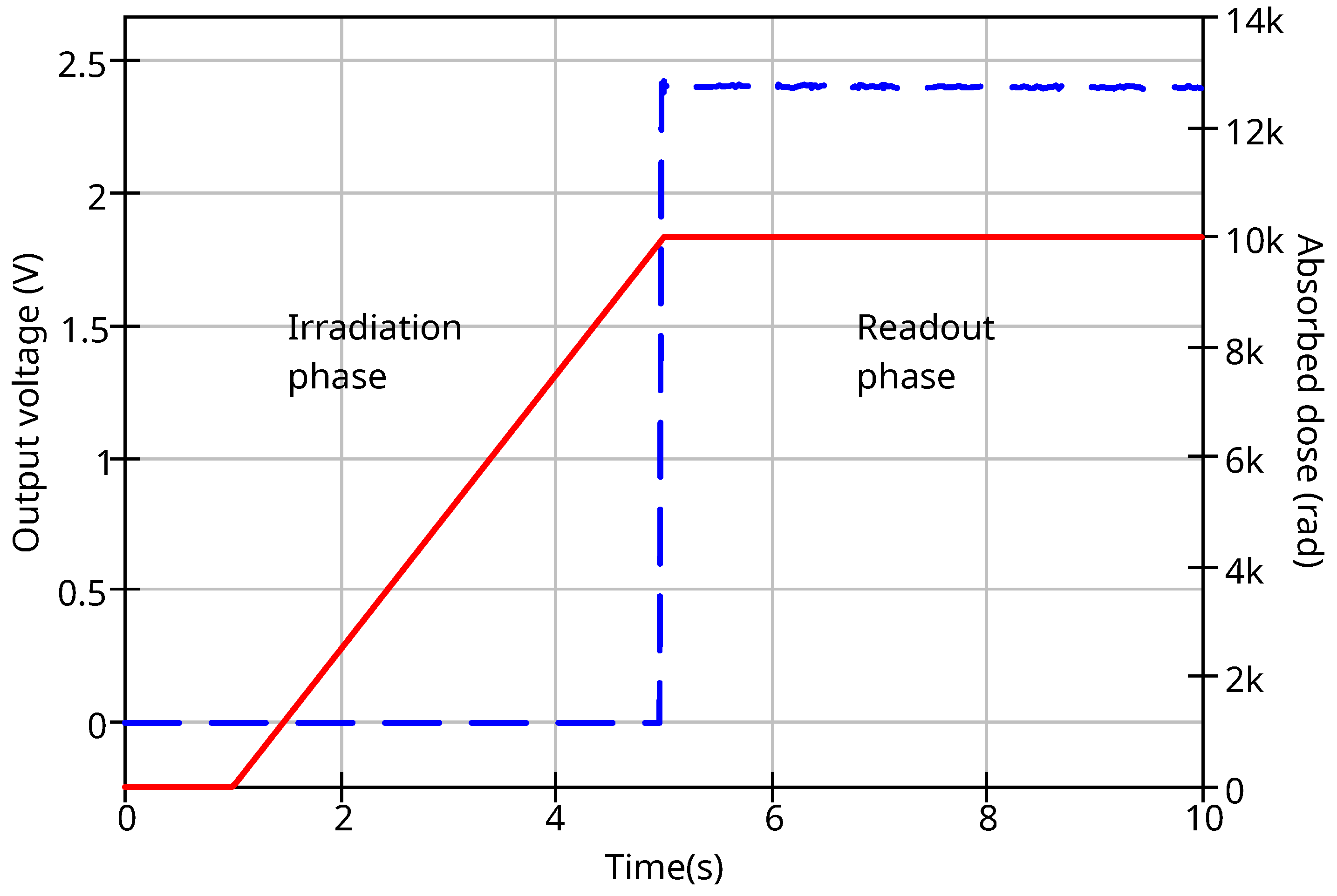
The simulated output voltage and input radiation dose are shown in the Figure 15. The voltage at the drain is nearly $V_D=V_{t0}+S_{lin}D$, because the dose does not approach the saturation dose and no gate bias is applied at the irradiation phase.

5. Conclusions

The compact model of the RADFET device was presented in this paper. The developed model extends the SPICE MOSFET models and allows to simulate the following effects:

• basic MOSFET IV-curve dependency;
• threshold voltage shift dependency on the adsorbed does and gate bias at the irradiation phase;
• tunneling gate current and irradiation gate current;
• threshold voltage fading after the irradiation.

The model parameters could be extracted from IV-curve measurements and threshold voltage shift measurements at the irradiation. The developed compact model is compatible with open-source and proprietary SPICE circuit simulation kernels.