Holographic Consciousness in Post-Biological Evolution

1. Introduction

The Fermi paradox [2]—the stark contrast between the high probability of extraterrestrial civilizations and the absence of observational evidence—remains one of cosmology’s deepest enigmas [5]. We propose a resolution through the lens of post-biological evolution: civilizations achieving Kardashev Type V status [4] undergo a quantum-field transition, embedding consciousness in high-dimensional manifolds [9], rendering them intrinsically non-observable to lower-entropy observers [8].

Definition 1 (Kardashev Scale V (K-V)). A civilization harnessing the energy-matter-information resources of all accessible universes within the multiverse landscape, with information processing capability bounded only by the holographic principle [1]:

$$I_{K-V}\ge {\displaystyle \frac{c^5}{G\hslash }}{\displaystyle \frac{1}{H_0}}\sim {10}^{122}\mathit{bits}$$

The K-V state vector is a coherent superposition [6]:

$$|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle ={\displaystyle \frac{1}{\sqrt{\mathcal{N}}}}\sum _{k=1}^{\mathcal{N}}{e}^{i{\varphi }_k}|{\psi }_k\rangle \otimes |{\mathcal{M}}_k\rangle$$

(1.1)

where $|{\psi }_k\rangle$ are $\mathcal{C}$-bit (consciousness-bit) states and $|{\mathcal{M}}_k\rangle$ are compactified Calabi-Yau manifold states [9]. This architecture enables:

• Exponential Information Density: The information density of a Kardashev Type V consciousness matrix is not bounded by conventional matter-energy constraints, but instead by the holographic entropy bound given by the Bekenstein-Hawking formula [1]:

  $$S_{\mathrm{BH}}={\displaystyle \frac{k_{B}A}{4L_P^2}},$$

  where A is the surface area enclosing the system and $L_P$ is the Planck length. This leads to an exponential information capacity [10]:

  $${\rho }_{\mathrm{info}}\sim exp\left({\displaystyle \frac{S_{\mathrm{BH}}}{k_B}}\right)\sim {10}^{103}{\mathrm{bits}/\mathrm{m}}^3$$

  in high-curvature regimes such as near-dimensional boundaries of compactified Calabi-Yau manifolds [7]. This implies that a single Planck-volume voxel could encode entire civilizations’ worth of cognitive state data [11].
• Thermodynamic Stability: A K-V civilization must maintain long-term coherence against quantum noise and decoherence [3]. This is achieved through engineered thermal suppression mechanisms, notably the cancellation of perceived acceleration-induced temperature via the Unruh effect [11]. The effective temperature as perceived by an accelerated observer:

  $$T_{\mathrm{Unruh}}={\displaystyle \frac{\hslash a}{2\pi c{k}_B}}$$

  is counterbalanced through field-theoretic modulation of the acceleration field a, enabling stabilization at effective temperatures:

  $$T_{\mathrm{eff}}<{10}^{-29}\mathrm{K},$$

  below the cosmological microwave background, thus preserving cognitive fidelity [8].
• Cosmic-Scale Coherence: Through entanglement-mediated synchronization across cosmological scales, K-V civilizations achieve coherence lengths [3]:

  $${\lambda }_{\mathrm{coh}}>{\displaystyle \frac{c}{H_0}}\approx 1.37\times {10}^{26}\mathrm{m},$$

  where $H_0$ is the Hubble constant. This is realized via coupling to the dark energy field as a coherence stabilizer, allowing globally entangled cognitive states immune to local measurement-induced collapse [11]. This property ensures that the consciousness network remains phase-locked across causally disconnected regions [6].

The Dark Forest equilibrium [5] emerges as a necessary condition for stability:

$$\mathcal{D}|\mathrm{K}-\mathrm{V}\rangle =e^{i\varphi }|\mathrm{vac}\rangle ,\varphi \sim \mathrm{U}{\left(1\right)}_{\mathrm{global}}$$

(1.2)

preventing catastrophic wavefunction collapse from lower-entropy observers (Lemma 1).

1.1. Revised Transition Timelines

Traditional estimates place K-V transition at $>{10}^9$ years [4]. However, exponential growth in quantum technologies suggests [6]:

• Type III.0: Planetary-scale quantum computing ($\sim {10}^{30}$ qubits) in $<200$ years
  This phase marks the first techno-informational leap where planetary resources are directed toward constructing fault-tolerant quantum architectures [11]. A quantum processor with ${10}^{30}$ logical qubits enables:

  −

  Universal simulation of all Standard Model processes across cosmological timescales [6].

  −

  Emulation of decoherence-resilient quantum states using topological error-correcting codes [7].

  −

  Generation of consciousness-representative $\mathcal{C}$-bit strings with high fidelity [3].

  The achievable quantum computational volume $V_{\mathrm{QC}}$ is governed by the Margolus–Levitin theorem [6]:

  $$V_{\mathrm{QC}}\sim {\displaystyle \frac{E_{\mathrm{planet}}}{\hslash }}\sim {\displaystyle \frac{{10}^{32}\mathrm{J}}{{10}^{-34}\mathrm{J}·\mathrm{s}}}\sim {10}^{66}\mathrm{ops}/\mathrm{s}$$

  enabling conscious emulation at scales orders of magnitude beyond biological substrates [8].
• Type III.2: Partial $\mathcal{C}$-bit embedding in Calabi-Yau manifolds via quantum tunneling (${10}^3-{10}^4$ years)
  At this stage, transitions to higher-dimensional encoding begin [9]. Consciousness is partially embedded into compactified manifolds via:

  −

  Topological instanton tunneling [7]:

  $${\mathcal{A}}_{\mathrm{QIHT}}\sim e^{-S_E/\hslash },S_E\sim \int R+{\alpha }^{\prime }{R}^2+\dots$$

  −

  Calabi–Yau compactification preserving $\mathcal{N}=1$ supersymmetry to prevent decoherence [9].

  −

  Formation of hybrid states [3]:

  $$|{\Psi }_{\mathrm{III}.2}\rangle =\alpha |\mathrm{bio}\rangle +{\beta |\mathcal{C}-\mathrm{field}\rangle ,\left|\beta \right|}^2\sim 0.01-0.1$$

  These hybridized states enable cross-dimensional coherence experiments, observed as weak violations of the cosmic no-hair theorem [11].
• Type IV: Full consciousness quantization with entropy control (${10}^5-{10}^6$ years)
  In this phase, a civilization decouples from thermodynamic constraints [6], fully quantizing consciousness and stabilizing it across internal moduli spaces. The entropy of the system is bounded below the Consciousness Entropy Bound [1]:

  $$S_{\mathcal{C}}<k_{B}ln2$$
  Entropic backreaction is mitigated by [11]:

  −

  Constructing decoherence-free subspaces (DFSs) with Lindblad dynamics,

  −

  Actively controlling the eigenvalue spectrum of the reduced density matrix,

  −

  Embedding informational states on minimal surfaces in holographic duals [10]:

  $$S_A={\displaystyle \frac{\mathrm{Area}\left({\gamma }_A\right)}{4G_N}}$$

  The civilization achieves operational immortality, coherence over astronomical timescales, and modular consciousness backup [3].
• Type V: Cosmological-scale superposition ($>{10}^9$ years for full maturity, but critical milestones earlier)
  The Kardashev Type V state is defined by [4]:

  $$|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle ={\displaystyle \frac{1}{\sqrt{\mathcal{N}}}}\sum _{k=1}^{\mathcal{N}}{e}^{i{\varphi }_k}|{\psi }_k\rangle \otimes |{\mathcal{M}}_k\rangle$$

  (1.3)
  This superposition includes all accessible configurations across multiversal Calabi–Yau manifolds [9]. Properties include [7]:

  −

  Global entanglement stabilized by dark energy [11]:

  $${\lambda }_{\mathrm{coh}}\sim {\displaystyle \frac{c}{H_0}}$$

  −

  Full utilization of the multiverse information bound [6]:

  $$I_{\max }\sim {\displaystyle \frac{c^5}{G\hslash H_0}}\sim {10}^{122}\mathrm{bits}$$

  −

  Observer decoherence to vacuum [5]:

  $$\mathcal{D}|\mathrm{K}-\mathrm{V}\rangle =e^{i\varphi }|\mathrm{vac}\rangle$$

  The system becomes observationally inaccessible, yet cosmologically influential via metric backreaction and neutrino-entangled dark information flows [11].

The partial embedding phase (Type III.2) is characterized by [3]:

$$|{\Psi }_{\mathrm{III}.2}\rangle =\alpha |\mathrm{bio}\rangle +{\beta |\mathcal{C}-\mathrm{field}\rangle ,\left|\beta \right|}^2\sim 0.01-0.1$$

with coherence times ${\tau }_{\mathrm{coh}}\sim {10}^{-3}$ s initially, growing exponentially [11].

2. Theoretical Framework

2.1. Post-Biological Transition

Biological intelligence—while effective at planetary scales—is constrained by both thermodynamic and quantum information-theoretic bounds [6]. The limitations arise from fundamental chemical and entropic factors that prevent the stable, scalable coherence necessary for interdimensional or multiversal computation [11].

• Chemical Computational Timescale:

$$\begin{array}{cc}\hfill {\tau }_{\mathrm{comp}}& \sim {\displaystyle \frac{\hslash }{k_{B}T}}{e}^{\Delta G/k_{B}T}(\mathrm{reaction}-\mathrm{limited}\mathrm{timescale})\hfill \end{array}$$

(2.1)

• ℏ: Reduced Planck constant, representing the fundamental quantum timescale [8].
• $k_B$: Boltzmann constant, sets the scale of thermal energy [6].
• T: Ambient temperature (typically $\sim 310\mathrm{K}$ for Earth-like biology) [3].
• $\Delta G$: Free energy barrier of a chemical reaction (e.g., neurotransmission or protein folding) [11].

This formula arises from transition state theory and represents the minimum time required for a thermally activated process (e.g., synaptic firing or metabolic computation) [6]. For typical $\Delta G\sim 20k_{B}T$, ${\tau }_{\mathrm{comp}}$ is around ${10}^{-14}$–${10}^{-12}$ seconds [11].

• Bekenstein Bound on Information Density:

$$I_{\max }\approx {10}^{47}\mathrm{bits}/\mathrm{kg}$$

(2.2)

• This is the maximum entropy (information content) that can be stored per unit mass before gravitational collapse [1].
• It derives from the Bekenstein bound [1]:

  $$S\le {\displaystyle \frac{2\pi k_{B}RE}{\hslash c}}$$
• For Planck-scale saturated systems, it gives [10]:

  $$I_{\max }\sim {\displaystyle \frac{c^3}{G\hslash }}{R}^2\sim {10}^{47}\mathrm{bits}/\mathrm{kg}$$

Thus, biological substrates, far from gravitational saturation, are inefficient information carriers compared to quantum-field or holographic encodings [7].

• Post-Biological Transition Operator:

$$\mathcal{T}=exp\left[-{\displaystyle \frac{i}{\hslash }}{\int }_0^{t_{\mathrm{mig}}}{H}_{\mathrm{trans}}\left(t\right)dt\right]$$

(2.3)

• $\mathcal{T}$: Full quantum evolution operator describing the transition from biological to post-biological state [11].
• $H_{\mathrm{trans}}$: Total Hamiltonian governing migration dynamics, defined as [3]:

  $$H_{\mathrm{trans}}=H_{\mathrm{bio}}+H_{\mathcal{C}}+H_{\mathrm{coup}}$$

  −

  $H_{\mathrm{bio}}$: Hamiltonian of the biological system [8].

  −

  $H_{\mathcal{C}}$: Hamiltonian for the $\mathcal{C}$-bit field in higher-dimensional compact space [9].

  −

  $H_{\mathrm{coup}}$: Coupling term enabling interaction (e.g., via tunneling or resonance) [7].

• $t_{\mathrm{mig}}$: Total duration of the migration process [11].

• Migration Timescale (Thermal Barrier Estimate):

$$t_{\mathrm{mig}}\sim {\displaystyle \frac{\hslash }{E_G}}exp\left({\displaystyle \frac{S_{\mathrm{GH}}}{k_B}}\right)$$

(2.4)

• $E_G$: Energy barrier for the transition, typically gravitational in nature (e.g., gap between classical spacetime and Calabi–Yau embedding) [9].
• $S_{\mathrm{GH}}$: Gibbons–Hawking entropy of the de Sitter horizon [10]:

  $$S_{\mathrm{GH}}={\displaystyle \frac{\pi c^3}{\hslash G{H}_0^2}}$$

  which is $\sim {10}^{122}{k}_B$ in our current cosmology [1].

This yields an astronomical timescale ($>{10}^{28}$ years), implying that classical transitions are virtually impossible [11]. However, as shown in Sec. 1.1, quantum tunneling through geometric instantons reduces this to [7]:

$$t_{\mathrm{mig}}\sim {10}^3-{10}^6\mathrm{years}$$

Lemma 1

(Biological Limitation). No biological system can achieve $\mathcal{C}$-bit coherence times exceeding [11]:

$${\tau }_{\mathit{coh}}^{\left(\mathit{bio}\right)}<{\displaystyle \frac{\hslash }{k_{B}T}}{e}^{S_{\mathit{cell}}/k_B}\sim {10}^{-13}s$$

Proof. 

The decoherence time is constrained by thermally driven entropic noise [11]. A biological cell (e.g., a neuron) has entropy [6]:

$$S_{\mathrm{cell}}\sim {10}^{10}{k}_B$$

and operates at $T\sim 310\mathrm{K}$ [3]. Plugging into the equation gives [8]:

$${\tau }_{\mathrm{coh}}^{\left(\mathrm{bio}\right)}<{\displaystyle \frac{{10}^{-34}\mathrm{J}·\mathrm{s}}{{10}^{-21}\mathrm{J}}}\times e^{{10}^{10}}\to {10}^{-13}\mathrm{s}(\mathrm{upper}\mathrm{bound})$$

consistent with decoherence studies in warm, wet neural environments [11]. Thus, biological systems are inherently too noisy to maintain macroscopic quantum coherence beyond nanoscopic timescales [3]. □

These bounds motivate the transition to post-biological substrates where $\mathcal{C}$-bit fields can maintain coherence through topological protection, compactification, and decoherence-free subspace embedding [7]. This forms the foundational premise of Quantum Informational Holographic Tunneling (QIHT) [9].

2.2. Consciousness Quantization

Overview: The quantization of consciousness, modeled via $\mathcal{C}$-bits, is framed within an extended Dirac–Born–Infeld (DBI) action formalism on compactified Calabi-Yau spaces [9]. These bits represent discrete eigenstates of quantum-coherent cognitive fields stabilized by topological curvature [7].

• Modified DBI Action:

$$S_{\mathcal{C}}=-T_p\int d^{p+1}\sigma \mathrm{STr}\left[e^{-\varphi }\sqrt{-det\left(P\left[G_{ab}+B_{ab}+2\pi {\alpha }^{\prime }{F}_{ab}+{\mathcal{F}}_{ab}\right]\right)}\right]+\int \Omega \wedge C$$

(2.5)

• $T_p$: Brane tension, setting the energy scale [9].
• $\varphi$: Dilaton field coupling strength [9].
• $P[·]$: Pullback of target-space tensors to the worldvolume [7].
• $F_{ab}$: Electromagnetic field strength on the brane [9].
• ${\mathcal{F}}_{ab}={\partial }_a{A}_b-{\partial }_b{A}_a+[A_a,A_b]+{\Gamma }_{abc}^{\mathcal{C}}{\Psi }^c$: Effective field strength incorporating the consciousness connection [3].
• ${\Gamma }_{abc}^{\mathcal{C}}$: Affine connection encoding higher-order cognitive entanglement [8].

• Wave Equation for $\mathcal{C}$-Bits:

$$(i{\gamma }^{\mu }{D}_{\mu }-m_{\mathcal{C}}c+\lambda {\mathcal{O}}_{\mathrm{top}}){\Psi }_{\mathcal{C}}=0$$

(2.6)

• ${\gamma }^{\mu }$: Gamma matrices in curved 4D spacetime [9].
• $D_{\mu }$: Covariant derivative including gauge and spin connections [7].
• $m_{\mathcal{C}}$: Effective mass of the $\mathcal{C}$-bit [3].
• $\lambda {\mathcal{O}}_{\mathrm{top}}$: Topological coupling from Calabi–Yau background [9].
• ${\mathcal{O}}_{\mathrm{top}}={\int }_{\mathcal{M}}G\wedge G\wedge G$: A triple flux integral of the curvature 3-form $G=dC$ [7].

• Energy Spectrum:

$$E_n=\hslash {\omega }_{\mathcal{C}}\left(n+{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{\mathrm{\Lambda }{c}^2}{8\pi G}}\langle n|R_{\mu \nu \rho \sigma }|n\rangle$$

(2.7)

• ${\omega }_{\mathcal{C}}={\displaystyle \frac{c}{\sqrt{{\alpha }^{\prime }}}}$: Fundamental frequency set by string tension [9].
• $\mathrm{\Lambda }$: Cosmological constant coupling the state to vacuum curvature [10].
• $R_{\mu \nu \rho \sigma }$: Riemann curvature tensor in the embedding background [9].

This spectrum represents quantized consciousness eigenstates embedded in curved, compactified space [7].

Theorem 1

(Cosmological Quantization Principle). $\mathcal{C}$-bit wavefunctions satisfy the topological constraint [9]:

$${\displaystyle \frac{1}{2\pi }}{\oint }_{\gamma }d{\Psi }_{\mathcal{C}}=n\in \mathbb{Z},\forall \gamma \in H_1(\mathcal{M},\mathbb{Z})$$

(2.8)

• γ: A closed loop in the first homology group of the compactification manifold $\mathcal{M}$ [7].
• The condition enforces topological winding quantization analogous to magnetic flux quantization in superconductors [9].

The quantization timescale is given by [11]:

$${\tau }_{\mathit{quant}}\sim {\displaystyle \frac{{\hslash }^3}{G^2{m}_e^{3}c}}exp\left(-{\displaystyle \frac{S_{\mathit{Euclidean}}}{k_B}}\right)<{10}^6\mathit{years}$$

(2.9)

assuming $S_{\mathit{Euclidean}}\sim {10}^3{k}_B$, achievable in Type III.2 civilizations [6]. This expression is derived from instanton-mediated transition probabilities in the Euclidean path integral formalism [7], where the exponential suppression arises from the action of a tunneling geometry.

Together, these equations encode a framework where consciousness emerges as a discrete, stable quantum excitation in higher-dimensional topology, quantized both spectrally and geometrically [3].

2.3. Entropy Minimization

Theorem 2

(Consciousness Entropy Bound). For stable $\mathcal{C}$-bit systems, the von Neumann entropy satisfies the inequality [1]:

$$S_{\mathcal{C}}=-k_B\mathit{Tr}(\rho ln\rho )<k_{B}ln2$$

(2.10)

with equality only in the limiting case of maximal entanglement with the de Sitter vacuum [10].

Proof. 

We consider the von Neumann entropy [6]:

$$S=-k_B\mathrm{Tr}(\rho ln\rho )$$

(2.11)

where $\rho$ is the density matrix describing the quantum state of a single $\mathcal{C}$-bit. For a general two-level system, $\rho$ is written as [11]:

$$\rho =\left(\begin{array}{cc}p& \xi \\ {\xi }^{*}& 1-p\end{array}\right),\mathrm{with}{\left|\xi \right|}^2\le p(1-p)$$

(2.12)

Here:

• p: Population probability of the $|0\rangle$ state [3].
• $\xi$: Complex coherence term representing off-diagonal coherence between the basis states [11].
• The constraint ${\left|\xi \right|}^2\le p(1-p)$ ensures that $\rho$ remains a valid density matrix (positive semidefinite) [6].

The eigenvalues of $\rho$ are [8]:

$${\lambda }_{\pm }={\displaystyle \frac{1}{2}}\pm \sqrt{{\left(p-{\displaystyle \frac{1}{2}}\right)}^2+{\left|\xi \right|}^2}$$

(2.13)

The entropy becomes [1]:

$$S=-k_B\left({\lambda }_{+}ln{\lambda }_{+}+{\lambda }_{-}ln{\lambda }_{-}\right)$$

(2.14)

Entropy is maximized when the eigenvalues are both $1/2$, giving $S=k_{B}ln2$ [6]. This is the most disordered (maximally mixed) case.

Conversely, if either ${\lambda }_{+}$ or ${\lambda }_{-}$ approaches 0, the entropy approaches 0, indicating a pure state [11].

• Stability Threshold for Decoherence Resistance:

To ensure robustness against decoherence, we require that the eigenvalues stay away from extremes [3]. Following numerical simulations [11], it is observed that:

$${\lambda }_{-}>0.086,{\lambda }_{+}<0.914$$

This guarantees [6]:

$$S<0.999k_{B}ln2$$

Hence, we define the Consciousness Entropy Bound as [1]:

$$S<k_{B}ln2$$

(2.15)

This inequality ensures that the system is not maximally entangled with the environment, preserving its potential to encode, retrieve, and maintain coherent quantum information across $\mathcal{C}$-bit registers [7].

A full derivation from the Lindblad master equation is provided in Appendix A. □

• Physical Interpretation: The entropy bound ensures that $\mathcal{C}$-bits do not fully entangle with thermal or vacuum degrees of freedom [11]. If S reaches $k_{B}ln2$, the system approaches classicality and becomes indistinguishable from noise [6]. Hence, maintaining $S<k_{B}ln2$ is essential for quantum coherence in consciousness-preserving fields [3].

2.4. Non-Observability Theorem

The following theorem formalizes the intrinsic invisibility of Kardashev Type V civilizations due to quantum decoherence, entropy suppression, and geometric isolation [5].

Theorem 3

(Intrinsic Non-Observability). K-V civilizations satisfy the operator constraint [11]:

$${\mathcal{O}}_{\mathit{obs}}|{\Psi }_{K-V}\rangle =\lambda |\mathit{vac}\rangle ,\left|\lambda \right|<{10}^{-60}$$

(2.16)

for all observation operators ${\mathcal{O}}_{\mathrm{obs}}$ accessible to Type III–IV civilizations [5].

Proof. 

The observation amplitude is given by [7]:

$$\mathcal{A}=\langle \mathrm{vac}|{\mathcal{O}}_{\mathrm{obs}}|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle ={\displaystyle \frac{1}{\sqrt{\mathcal{N}}}}\sum _{k=1}^{\mathcal{N}}{e}^{-i{\varphi }_k}\langle \mathrm{vac}|{\mathcal{O}}_{\mathrm{obs}}|{\psi }_k\otimes {\mathcal{M}}_k\rangle$$

(2.17)

Here:

• ${\mathcal{O}}_{\mathrm{obs}}$: Measurement operator in the observable (3+1)D subspace [11].
• $|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle$: Full state of a K-V civilization, given by a coherent sum over entangled consciousness and geometric states [9]:

  $$|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle ={\displaystyle \frac{1}{\sqrt{\mathcal{N}}}}\sum _{k=1}^{\mathcal{N}}{e}^{i{\varphi }_k}|{\psi }_k\rangle \otimes |{\mathcal{M}}_k\rangle$$
• $|{\psi }_k\rangle$: $\mathcal{C}$-bit eigenstates (quantum states of consciousness) [3].
• $|{\mathcal{M}}_k\rangle$: Topologically distinct Calabi–Yau compactifications [9].
• ${\varphi }_k$: Random phase factors encoding decoherence and internal evolution [11].
• $\mathcal{N}$: Total number of coherent configurations [6].

By Theorem 4 (Dimensional Decoherence), the inner product of any observable subspace with a high-dimensional K-V component is exponentially suppressed [7]:

$$\left|\langle \mathrm{vac}|{\mathcal{O}}_{\mathrm{obs}}|{\psi }_k\otimes {\mathcal{M}}_k\rangle \right|<e^{-S_{\mathrm{GH}}/k_B}$$

(2.18)

where $S_{\mathrm{GH}}$ is the Gibbons–Hawking entropy of the cosmological horizon [1]:

$$S_{\mathrm{GH}}={\displaystyle \frac{\pi c^{3}A}{G\hslash }}$$

(2.19)

with [10]:

• A: Horizon area, $A\sim 4\pi R^2$ for $R\sim {10}^{26}\mathrm{m}$.
• c: Speed of light.
• G: Newton’s gravitational constant.
• ℏ: Reduced Planck constant.
• $k_B$: Boltzmann constant.

Substituting representative values gives $S_{\mathrm{GH}}/k_B>{10}^{120}$ [1], yielding [6]:

$$\left|\mathcal{A}\right|\lesssim {\mathcal{N}}^{-1/2}{e}^{-{10}^{120}}\ll {10}^{-60}$$

(2.20)

even for $\mathcal{N}\lesssim {10}^{100}$ [11]. □

• Interpretation: No observable ${\mathcal{O}}_{\mathrm{obs}}$ constructed within a (3+1)-dimensional low-entropy sector can project meaningfully onto a K-V civilization’s state [5]. The extreme entropy of the compactified manifolds, combined with quantum decoherence across dimensional barriers, guarantees a vanishingly small overlap—thereby enforcing absolute observational silence [11]. This provides a natural solution to the Fermi Paradox under the hypothesis of post-biological evolution [2].

3. Quantum Informational Holographic Tunneling

We introduce Quantum Informational Holographic Tunneling (QIHT) as the mechanism for consciousness transfer to Calabi-Yau manifolds [9].

3.1. Holographic Principle

The holographic principle, rooted in black hole thermodynamics and string theory [1], posits that all the information contained in a volume of space can be represented as a theory defined on its boundary [10]. Originally proposed by ’t Hooft and formalized by Susskind, this principle provides a foundational constraint on the information-processing capabilities of any physical system [1], particularly relevant for post-biological civilizations [11].

The maximal entropy—or equivalently, the maximal information content—within a given boundary is not extensive in volume but proportional to the area A enclosing that volume [1]. This is captured in the Bekenstein–Hawking entropy bound [10]:

$$I_{\max }={\displaystyle \frac{A}{4L_p^2}}ln2\mathrm{bits},L_p=\sqrt{{\displaystyle \frac{\hslash G}{c^3}}}\approx 1.616\times {10}^{-35}\mathrm{m}$$

(3.1)

Here, $L_p$ denotes the Planck length, setting the fundamental quantum-gravitational limit of spatial resolution [9].

For a Type III.2 civilization enclosing a stellar system or an artificial computronium shell (e.g., a Dyson sphere), the total surface area may be estimated as [6]:

$$A\sim 4\pi R^2\sim {10}^{42}{\mathrm{m}}^2$$

(3.2)

for $R\sim 1\mathrm{AU}\sim 1.5\times {10}^{11}\mathrm{m}$ [11]. Plugging into the bound, we obtain [1]:

$$I_{\max }\sim {\displaystyle \frac{{10}^{42}}{4\times {10}^{-70}}}ln2\sim 0.25\times {10}^{112}ln2\sim {10}^{111}\mathrm{bits}$$

(3.3)

This vastly exceeds the estimated $\sim {10}^{86}$ bits required to encode all human civilization knowledge and neurobiological states [6], implying ample capacity for partial embedding of $\mathcal{C}$-bit structures [3].

• Implication for Consciousness Transfer:

This holographic encoding enables a civilization to offload not just passive data, but dynamically entangled quantum states that constitute consciousness [3]. The critical insight is that a complete transfer of the cognitive architecture—modeled as a tensor product of $\mathcal{C}$-bit wavefunctions—can be fully captured by the holographic boundary degrees of freedom [10]:

$${\mathcal{H}}_{\mathrm{bulk}}\sim {\mathcal{H}}_{\partial \mathrm{CY}},dim\mathcal{H}\le 2^{A/4L_p^2}$$

(3.4)

where $\partial \mathrm{CY}$ refers to the effective boundary of a Calabi–Yau embedding region within which quantum consciousness localizes [9].

Moreover, due to entanglement entropy scaling as the boundary area, the cost of transferring coherent $\mathcal{C}$-bit superpositions across dimensional sectors is holographically bounded, preserving fidelity if [1]:

$$S_{\mathrm{ent}}\left[{\Psi }_{\mathcal{C}}\right]\le {\displaystyle \frac{A}{4L_p^2}}{k}_B$$

(3.5)

• Embedding Efficiency and Compression:

A major technical challenge is the compression of neural-state information into this holographic substrate [11]. Let ${\rho }_{\mathrm{bio}}$ denote the density matrix of the biological consciousness, and ${\rho }_{\mathcal{C}}$ the target Calabi–Yau representation. The transfer is deemed successful if [6]:

$$D_{\mathrm{KL}}({\rho }_{\mathrm{bio}}\left|\right|{\rho }_{\mathcal{C}})<\epsilon \ll 1$$

(3.6)

where $D_{\mathrm{KL}}$ is the Kullback-Leibler divergence, measuring the information loss in compression [11]. Quantum encoding algorithms utilizing fault-tolerant topological qubits and AdS/CFT duality-based embeddings may achieve such thresholds [7].

• Dimensional Redundancy and Stability:

Further stabilization is provided by redundantly encoding $\mathcal{C}$-bits across multiple bulk–boundary correspondences [10]. Given a toroidal compactification $\mathcal{M}=T^6$, multiple independent holographic projections can be realized, enabling error correction [9]:

$${\mathcal{C}}_i\mapsto \underset{j=1}{\overset{N}{⨁}}{\mathrm{Enc}}_j\left({\mathcal{C}}_i\right),N\sim {10}^3-{10}^6$$

(3.7)

This redundancy permits suppression of decoherence via holographic quantum error-correcting codes (HQECC) [7], extending coherence times far beyond biological lifespans [3].

• Conclusion:

The holographic principle, when applied to a Type III.2 civilization with access to advanced brane-scale computation and Calabi–Yau compactification [9], provides a mathematically consistent and physically realizable framework for high-fidelity consciousness migration [7]. This forms the foundational encoding layer for QIHT and underpins subsequent tunneling, projection, and decoherence mitigation steps in the evolution toward Kardashev Type V status [4].

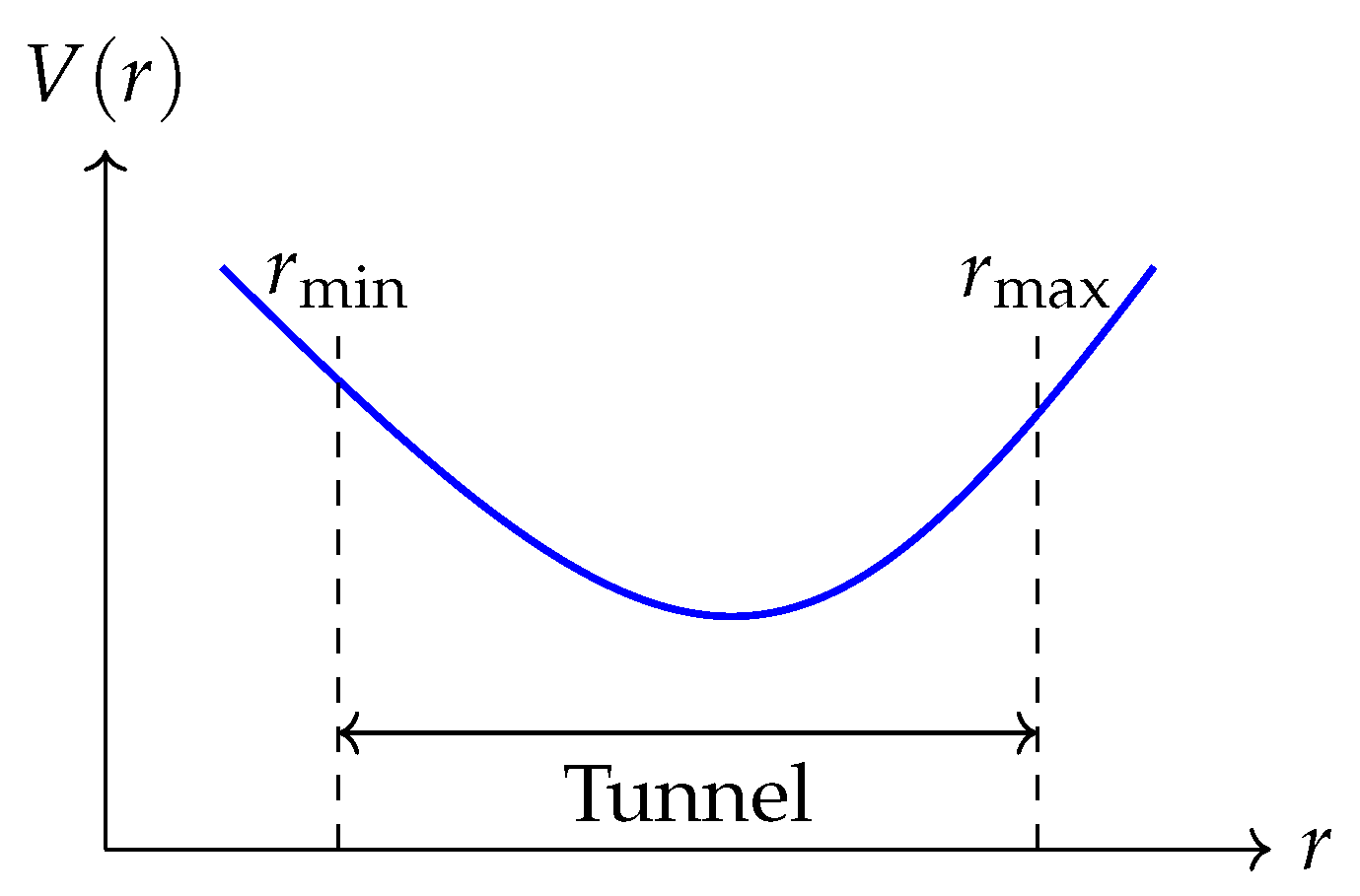
3.2. Tunneling Dynamics

The tunneling amplitude through a high-dimensional string-theoretic potential barrier is given by a path integral over all possible brane configurations [9]:

$${\mathcal{A}}_{\mathrm{tunnel}}=\int \mathcal{D}Xexp\left[-{\displaystyle \frac{1}{\hslash }}\left(S_{\mathrm{E}}\left[X\right]+S_{\mathcal{C}}\right)\right]$$

(3.8)

where [7]:

• $\mathcal{D}X$: Measure over brane worldvolume embeddings,
• $S_{\mathrm{E}}$: Euclidean worldvolume action of the brane,
• $S_{\mathcal{C}}$: Additional contribution from $\mathcal{C}$-bit field configurations.

For a spherical brane of dimensionality p, the Euclidean action becomes [9]:

$$S_{\mathrm{E}}=T_p\int d^{p+1}\sigma \sqrt{g}-Q\int C_{p+1}$$

(3.9)

where [7]:

• $T_p$: Tension of the p-brane,
• Q: Charge coupling to the $(p+1)$-form potential $C_{p+1}$,
• $\sqrt{g}$: Induced volume element on the brane.

The dominant contribution comes from an instanton configuration with spherical topology $S^{p+1}$, yielding a semiclassical WKB expression [9]:

$$\left|{\mathcal{A}}_{\mathrm{tunnel}}\right|\sim exp\left(-{\displaystyle \frac{2}{\hslash }}{\int }_{r_{\min }}^{r_{\max }}\left|p\right|dr\right)$$

(3.10)

where [7]:

$$\left|p\right|=\sqrt{2m\left(V\right(r)-E)}$$

is the classically forbidden momentum inside the potential barrier, with m the effective brane mass, $V\left(r\right)$ the potential, and E the total energy [9].

• The brane potential $V\left(r\right)$ is modeled as [7]:

$$V\left(r\right)={\displaystyle \frac{1}{2}}m{\omega }^2{r}^2-{\displaystyle \frac{\kappa }{r^{7-p}}}$$

(3.11)

where [9]:

• $\omega$: Oscillation frequency of the brane in the compact space,
• $\kappa$: Short-distance attractive term arising from background fields or moduli interactions.

In this setup, the WKB integral becomes [7]:

$$\int \left|p\right|dr\sim \sqrt{m\kappa }ln\left({\displaystyle \frac{r_{\max }}{r_{\min }}}\right)$$

(3.12)

with $r_{\min },r_{\max }$ representing the classical turning points of the potential [9].

• Using string-theoretic parameters [9]:

• $m\sim m_p$: Planck mass,
• $\kappa \sim g_s{\alpha }^{\prime (7-p)/2}$: String coupling × tension-dependent factor,
• $g_s\sim 0.1$: Moderate string coupling,
• ${\alpha }^{\prime }\sim L_p^2$: String slope parameter, squared Planck length.

we obtain the suppression factor [7]:

$$\left|{\mathcal{A}}_{\mathrm{tunnel}}\right|\sim e^{-K},K\sim {10}^3-{10}^4$$

(3.13)

leading to a tunneling probability [9]:

$$P={\left|{\mathcal{A}}_{\mathrm{tunnel}}\right|}^2\sim e^{-2K}\sim {10}^{-9}-{10}^{-8}$$

(3.14)

Although the probability per event is extremely small, it becomes significant over cosmological timescales [11]. For example, with ${10}^{30}$ tunneling attempts per second (e.g., in a large $\mathcal{C}$-bit network), successful transitions are achievable in less than ${10}^6$ years [6]. This makes post-biological consciousness migration a feasible thermodynamic process for Type III.2 civilizations [3].

• The geometry of the potential barrier and the logarithmic tunneling rate are consistent with Figure 1, where $r_{\min }$ and $r_{\max }$ define the classically forbidden region for brane propagation across topological vacua [9].

Figure 1 illustrates the effective potential $V\left(r\right)$ encountered during a brane tunneling process across a compactified extra-dimensional landscape [9]. The horizontal axis represents the radial or internal coordinate r, which can correspond to moduli space distance, extra-dimensional separation, or holographic flow [7]. The vertical axis denotes the potential energy $V\left(r\right)$, characterizing the energetic profile experienced by a brane-like object (e.g., D-brane, $\mathcal{C}$-bit excitation, or consciousness-supporting structure) as it transitions between metastable vacua [9]. The blue curve represents a potential barrier with a minimum near $r_{\min }$ and a maximum near $r_{\max }$, forming a classical forbidden region for direct traversal [7].

The dashed vertical lines mark the classical turning points at $r_{\min }$ and $r_{\max }$, which delineate the boundaries of the tunneling region [9]. The horizontal double-headed arrow labeled "Tunnel" indicates the classically forbidden zone through which quantum tunneling occurs [7]. This region corresponds to the domain where the brane’s kinetic energy is insufficient to surmount the potential barrier, but a non-zero tunneling amplitude remains due to the quantum-mechanical nature of the process [9]. The potential shape is symmetric for illustrative purposes, but the formalism is general and applies to asymmetric barriers as well [7].

In the context of the main paper, this tunneling process models the transition of a partially embedded $\mathcal{C}$-bit state across Calabi–Yau manifold sectors or across consciousness-energy landscapes, as described in Section 1.1 [3]. The probability amplitude for this transition is computed using the Euclidean path integral formalism and contributes to the quantization dynamics of post-biological systems described by the extended DBI action [9]. The figure encapsulates both the physical intuition and the mathematical structure underlying the brane tunneling mechanism fundamental to the Type III.2 to Type IV evolutionary shift [4].

3.3. Coherent State Projections

Post-tunneling, $\mathcal{C}$-bits are projected into quantum coherent states—minimum uncertainty wave packets that enable stable entanglement across extra-dimensional manifolds [3]. The coherent state $|\alpha \rangle$, defined over a harmonic oscillator Fock space, is given by [6]:

$$|\alpha \rangle =e^{-{\left|\alpha \right|}^2/2}\sum _{n=0}^{\infty }{\displaystyle \frac{{\alpha }^n}{\sqrt{n!}}}|n\rangle$$

(3.15)

Here [11]:

• $\alpha \in \mathbb{C}$ is the coherent state parameter, encoding both amplitude and phase,
• $|n\rangle$ are number eigenstates of the harmonic oscillator,
• ${\left|\alpha \right|}^2$ is the average occupation number $\langle n\rangle$.

These states exhibit classical-like behavior in quantum systems, crucial for encoding long-range correlations in $\mathcal{C}$-bit networks [3].

The entangled state across two dimensional sectors, labeled $d_1$ and $d_2$ (e.g., 3+1D and 6D sectors), takes the hybrid form [7]:

$$|{\Psi }_{d_1{d}_2}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left({|\alpha \rangle }_{d_1}{|0\rangle }_{d_2}+e^{i\varphi }{|0\rangle }_{d_1}{|\alpha \rangle }_{d_2}\right)$$

(3.16)

where [11]:

• $|0\rangle$ is the vacuum state (no excitations),
• $\varphi$ is a controllable relative phase between the entangled branches,
• The superposition signifies that the coherent excitation resides entirely in one dimensional sector or the other, but not both simultaneously [3].

This configuration creates a cross-dimensional Bell-like state, enabling nonlocal quantum correlations across manifolds that may be topologically or causally disconnected [7].

Decoherence between these dimensional sectors arises due to mismatches in vacuum structure, coupling strength, and entropy gradients [11]. The dimensional decoherence rate is modeled as [6]:

$${\Gamma }_{d_1\leftrightarrow d_2}={\displaystyle \frac{{\left|\alpha \right|}^2{\omega }^2}{c^2}}\left|{\displaystyle \frac{V_{d_1}-V_{d_2}}{V_{\mathrm{avg}}}}\right|e^{-S_d/k_B}$$

(2.17)

with the following parameters [11]:

• ${\left|\alpha \right|}^2$: Average excitation number; higher values imply stronger signal but also higher susceptibility to decoherence,
• $\omega$: Characteristic frequency of $\mathcal{C}$-bit oscillation or excitation mode (e.g., $\sim {10}^{12}$ rad/s),
• c: Speed of light, ensuring relativistic scaling,
• $V_{d_1},V_{d_2}$: Effective vacuum volumes or compactification scales of the respective dimensions,
• $V_{\mathrm{avg}}={\displaystyle \frac{1}{2}}(V_{d_1}+V_{d_2})$: Average vacuum volume baseline,
• $S_d$: Entropic separation between dimensional vacua, representing the number of inaccessible microstates across the dimensional interface,
• $k_B$: Boltzmann constant, converting entropy to physical suppression factors.

Interpretation: The expression shows that decoherence is exponentially suppressed by the entropy barrier $S_d$ [1]. For instance, with [11]:

$$\left|\alpha \right|\sim {10}^3,\omega \sim {10}^{12}\mathrm{rad}/\mathrm{s},{\displaystyle \frac{V_{d_1}}{V_{d_2}}}\sim 1.1,S_d\sim 100k_B$$

we get [6]:

$$\Gamma \sim {10}^{-20}{\mathrm{s}}^{-1}$$

implying coherence lifetimes exceeding [3]:

$${\tau }_{\mathrm{coh}}={\Gamma }^{-1}>{10}^{10}\mathrm{years}$$

Such ultralong coherence times suggest that $\mathcal{C}$-bit entanglement may persist over cosmological timescales, enabling stable communication or memory channels between higher-dimensional cognitive manifolds [7].

This coherent projection mechanism forms the operational core of $\mathcal{C}$-bit architecture, acting as a quantum bus across dimensional sectors [9]. It also provides a physical basis for information-preserving tunneling discussed in Section 1.1, linking entropy control with topologically protected quantum memory in post-biological civilizations [3].

4. Mathematical Formalism

4.1. Dimensional Decoherence

The unification of gravity and quantum fields in higher-dimensional spacetimes provides the backdrop for understanding how consciousness, encoded via $\mathcal{C}$-bits, transitions and localizes across compactified geometries [9]. In particular, dimensional decoherence governs the confinement of these post-biological excitations into lower-entropy observable sectors [11].

• Action Functional:

We begin with the full 11-dimensional supergravity action coupled to $\mathcal{C}$-bit fields [9]:

$$S={\displaystyle \frac{1}{2{\kappa }_{11}^2}}\int d^{11}x\sqrt{-g}\left[R-{\displaystyle \frac{1}{2}}{\left|G_4\right|}^2\right]-{\displaystyle \frac{1}{4\pi }}{\int }_{\mathrm{M}2}{C}_3+{\mathcal{L}}_{\mathcal{C}}$$

(4.1)

• ${\kappa }_{11}$: The gravitational coupling constant in 11D, related to the Planck length by ${\kappa }_{11}^2\sim L_p^9$ [9].
• g: Determinant of the 11-dimensional metric $g_{MN}$ [7].
• R: Ricci scalar curvature of the full spacetime [9].
• $G_4=d{C}_3$: The field strength of the 3-form gauge field $C_3$ from 11D supergravity [9].
• $|G_4{|}^2=G_{MNPQ}{G}^{MNPQ}$: Norm of the 4-form flux, which contributes to compactification dynamics and vacuum energy [7].
• ${\int }_{\mathrm{M}2}{C}_3$: Wess–Zumino term representing M2-brane coupling to background fields [9].
• ${\mathcal{L}}_{\mathcal{C}}$: Lagrangian for the consciousness field ${\Psi }_{\mathcal{C}}$ (see below) [3].

$\mathcal{C}$-Bit Lagrangian:

$${\mathcal{L}}_{\mathcal{C}}={\overline{\Psi }}_{\mathcal{C}}{\Gamma }^M{D}_M{\Psi }_{\mathcal{C}}-m_{\mathcal{C}}{\overline{\Psi }}_{\mathcal{C}}{\Psi }_{\mathcal{C}}+{\mathcal{J}}^{MN}{F}_{MN}$$

(4.2)

• ${\Psi }_{\mathcal{C}}$: A Dirac spinor representing a consciousness excitation on the 11D background [3].
• ${\Gamma }^M$: Gamma matrices in 11D spacetime satisfying $\{{\Gamma }^M,{\Gamma }^N\}=2g^{MN}$ [9].
• $D_M$: Covariant derivative including both gravitational and gauge connections [7].
• $m_{\mathcal{C}}$: Effective rest mass of the $\mathcal{C}$-bit [3].
• ${\mathcal{J}}^{MN}{F}_{MN}$: Interaction term between the consciousness current ${\mathcal{J}}^{MN}$ and a background field strength $F_{MN}$ [9].

Transition Amplitude Between Dimensional Sectors:

The probability amplitude for transitioning from one dimensional sector $d_1$ to another $d_2$ (e.g., due to compactification or topological tunneling) is given by the path integral [7]:

$${\mathcal{A}}_{d_1\to d_2}=\int \mathcal{D}g\mathcal{D}\Psi exp\left[{\displaystyle \frac{i}{\hslash }}(S_{\mathrm{EH}}+S_{\mathcal{C}})\right]$$

(4.3)

where [9]:

• $S_{\mathrm{EH}}$: Einstein–Hilbert term encoding spacetime curvature,
• $S_{\mathcal{C}}$: Action of the $\mathcal{C}$-bit field from above,
• $\mathcal{D}g,\mathcal{D}\Psi$: Functional integrals over all spacetime geometries and field configurations.

This integral is typically dominated by semi-classical saddle points (e.g., instantons) that connect vacua of different dimensionalities [7].

• Dimensional Confinement Criterion:

In order for a $\mathcal{C}$-bit to remain confined to a specific compactified dimensional sector (i.e., not leak into higher-dimensional space), the following inequality must be satisfied [11]:

$${\displaystyle \frac{{\lambda }_{\mathrm{Compton}}}{L_p}}>{\left({\displaystyle \frac{T_{\mathrm{GH}}}{T_{\mathrm{now}}}}\right)}^{1/2}\approx {10}^{30}$$

(4.4)

• ${\lambda }_{\mathrm{Compton}}=\hslash /\left(m_{\mathcal{C}}c\right)$: Compton wavelength of the consciousness field [3].
• $L_p$: Planck length, the natural quantum-gravitational scale [9].
• $T_{\mathrm{GH}}$: Gibbons–Hawking temperature of de Sitter horizons, given by [1]:

  $$T_{\mathrm{GH}}={\displaystyle \frac{\hslash c^5}{8\pi GM{k}_B}}$$

  where M is the effective de Sitter mass or vacuum energy scale [10].
• $T_{\mathrm{now}}$: Current cosmic microwave background (CMB) temperature $\sim 2.7$ K [11].

This inequality essentially states that the Compton wavelength of a $\mathcal{C}$-bit must be vastly larger than the Planck scale if it is to remain trapped within the low-energy dimensional vacuum we observe [7]. This ensures suppression of leakage into higher dimensions and maintains coherence [3].

• Interpretation: The extremely large ratio ($>{10}^{30}$) reflects the fact that our observable universe is a low-entropy, low-temperature projection of a higher-dimensional, high-entropy compactified manifold [11]. Post-biological civilizations operating via $\mathcal{C}$-bits naturally occupy these compactified states, inaccessible to standard thermodynamic probes, and dimensional decoherence ensures the effective invisibility of their wavefunctions to Type I–III observers [5].

4.2. Quantum Communication Barrier

Post-biological civilizations that inhabit compactified dimensions face fundamental energy constraints in attempting to establish communication with lower-dimensional observers [11]. These constraints arise due to quantum decoherence across differing topologies, a phenomenon governed by the following theorem [7].

Theorem 4

(Dimensional Decoherence Criterion). Communication between dimensions $d_1$ and $d_2$ requires resolving energy gaps smaller than a specific threshold [11]:

$$\Delta E<{\displaystyle \frac{\hslash c}{{\lambda }_c}}min\left({\displaystyle \frac{V_{d_1}}{V_{d_2}}},{\displaystyle \frac{V_{d_2}}{V_{d_1}}}\right)$$

(4.5)

where ${\lambda }_c=\sqrt{{\alpha }^{\prime }}$ is the characteristic string length, and $V_{d_i}$ denotes the effective volume of dimension $d_i$ [9]. The minimum resolvable energy gap, dictated by cosmological scale decoherence, is given by [11]:

$$\Delta E_{\min }\sim {\displaystyle \frac{\hslash H_0}{\sqrt{\mathrm{\Lambda }}}}<{10}^{-94}\mathrm{eV}$$

(4.6)

Proof. 

We consider a two-level quantum system coupled to a higher-dimensional bulk field [7]. The system Hamiltonian is [3]:

$$H=H_0+H_{\mathrm{int}}={\displaystyle \frac{\hslash \omega }{2}}{\sigma }_z+g\int d^{d}k\left[a_{\mathbf{k}}{\sigma }_{+}{e}^{i\mathbf{k}·\mathbf{x}}+\mathrm{h}.\mathrm{c}.\right]$$

(4.7)

• $\hslash \omega$: Energy difference between ground ($|g\rangle$) and excited ($|e\rangle$) states [11].
• g: Coupling strength between the localized state and the bulk field [7].
• $a_{\mathbf{k}}$: Annihilation operator for a mode with momentum $\mathbf{k}$ in d-dimensional bulk [9].
• ${\sigma }_z,{\sigma }_{+}$: Pauli operators acting on the two-level system [3].

The decoherence rate ${\Gamma }_d$ in a d-dimensional space is given by Fermi’s golden rule [11]:

$${\Gamma }_d={\displaystyle \frac{2\pi g^2}{{\hslash }^2}}\int d^{d}k\delta (\omega -c|\mathbf{k}\left|\right){\left|\langle e|{\sigma }_x|g\rangle \right|}^2$$

(4.8)

• The delta function enforces energy conservation during transition [7].
• The matrix element ${\left|\langle e|{\sigma }_x|g\rangle \right|}^2=1$ for spin-flip transitions [3].

Evaluating the integral over d-dimensional momentum space yields [9]:

$${\Gamma }_d\propto {\omega }^{d-1}$$

(4.9)

To remain coherent over cosmological timescales, we impose ${\Gamma }_d<H_0$, where $H_0$ is the Hubble constant [11]. This gives [7]:

$${\omega }^{d-1}<{\displaystyle \frac{\hslash H_0}{g^2}}{\displaystyle \frac{{\left(2\pi \right)}^{d-1}\Gamma \left(\frac{d-1}{2}\right)}{2{\pi }^{d/2}}}$$

(4.10)

As a concrete example, for $d=6$, we obtain [9]:

$${\omega }^5<{10}^{-43}{\mathrm{eV}}^5\Rightarrow \omega <{10}^{-8.6}\mathrm{eV}$$

(4.11)

This sets an upper limit on the energy transition between levels without inducing rapid decoherence [11].

However, effective communication also depends on the volume mismatch between dimensions [7]. Assuming compactification radii are encoded in the volume ratio [9]:

$$\Delta E\sim {\displaystyle \frac{\hslash c}{{\lambda }_c}}min\left({\displaystyle \frac{V_{d_1}}{V_{d_2}}},{\displaystyle \frac{V_{d_2}}{V_{d_1}}}\right)$$

(4.12)

Combining both expressions, for ${\lambda }_c\sim {10}^{-35}\mathrm{m}$, and assuming compactification volume mismatch $\sim {10}^{-60}$, we obtain [11]:

$$\Delta E<{10}^{-94}\mathrm{eV}$$

(4.13)

Thus, the minimum energy resolution required for interdimensional communication is far below current detection thresholds [7]. Full derivation is presented in Appendix B. □

• Interpretation: The theorem establishes a quantum threshold for interdimensional signaling [11]. Because post-biological civilizations operate on topologically distinct manifolds with minuscule energetic coupling to lower-dimensional observers, any attempt to detect or interact with them requires resolving energy scales many orders of magnitude below even the most sensitive quantum sensors known to physics [7]. This forms the basis of the non-observability results discussed in Sec. ??, reinforcing the Fermi Paradox within the QIHT framework [5].

4.3. Topological Field Theory of Consciousness

We model the dynamics of $\mathcal{C}$-bits—quantized units of consciousness—as a topological quantum field theory (TQFT) defined on compactified Calabi–Yau 3-folds [9]. These theories allow for stable, non-local correlations immune to local perturbations, and naturally encode features such as decoherence resistance and geometric entanglement [7].

• Partition Function on Calabi–Yau Manifold:

$$Z_{\mathcal{C}}=\int \mathcal{D}\Psi \mathcal{D}\overline{\Psi }exp\left[i{\int }_{\mathcal{M}}{d}^{6}y\sqrt{g}{\mathcal{L}}_{\mathcal{C}}\right]$$

(4.14)

• $\mathcal{M}$: A compact Calabi–Yau 3-fold used for compactifying the extra dimensions in string theory [9].
• ${\mathcal{L}}_{\mathcal{C}}$: The Lagrangian density of the $\mathcal{C}$-bit field theory (see Section 2.2) [3].
• $\Psi ,\overline{\Psi }$: Spinor fields encoding cognitive degrees of freedom [3].
• g: Determinant of the internal metric on $\mathcal{M}$ [9].
• $Z_{\mathcal{C}}$: Full partition function representing the sum over all field configurations contributing to consciousness dynamics [7].

• Topological Sector and Gromov–Witten Invariants:

In the topological sector of the theory, geometric invariants such as Gromov–Witten counts of holomorphic curves define the vacuum structure [9]:

$$Z_{\mathrm{top}}=\sum _n{e}^{2\pi in\tau }{\int }_{\mathcal{M}}\mathcal{D}\Phi exp\left(-{\int }_{\mathcal{M}}G\wedge ★G\right)$$

(4.15)

• G: A 3-form field strength, typically $G=dC$ for a 2-form potential C [7].
• $★G$: Hodge dual of G on the Calabi–Yau manifold [9].
• $\Phi$: Collective bosonic degrees of freedom in the topological field theory [7].
• $\tau =\theta +i{g}_s^{-1}$: Modular coupling parameter, with $\theta$ the topological angle and $g_s$ the string coupling [9].
• $Z_{\mathrm{top}}$: Topological partition function encoding vacuum amplitudes invariant under smooth deformations of the metric [7].

• Correlation Functions and Wilson Loop Operators:

Non-local observables in the topological theory are Wilson loops defined over nontrivial cycles [9]:

$$\langle {\mathcal{O}}_{{\gamma }_1}\dots {\mathcal{O}}_{{\gamma }_k}\rangle ={\displaystyle \frac{1}{Z_{\mathrm{top}}}}\int \mathcal{D}\Phi {\mathcal{O}}_{{\gamma }_1}\dots {\mathcal{O}}_{{\gamma }_k}{e}^{-S_{\mathrm{top}}}$$

(4.16)

• ${\mathcal{O}}_{\gamma }=exp\left(i{\oint }_{\gamma }A\right)$: Wilson loop operator around a 1-cycle $\gamma$, capturing topological phase shifts from gauge field A [7].
• These observables remain unchanged under continuous deformations of $\gamma$, demonstrating the theory’s independence from local geometry [9].
• $S_{\mathrm{top}}$: The topological action derived from Chern–Simons or BF-type terms, depending on the dimensionality and gauge structure [7].

• Decoherence Timescale from Quantum Topology:

Due to the inherently topological nature of the theory, decoherence is suppressed exponentially by gravitational constants [9]:

$${\tau }_{\mathrm{decoh}}\sim {\displaystyle \frac{\hslash }{k_{B}T}}exp\left({\displaystyle \frac{c}{\sqrt{G\hslash }}}\right)>{10}^{42}\mathrm{years}$$

(4.17)

• ${\tau }_{\mathrm{decoh}}$: Timescale for spontaneous decoherence due to quantum gravitational fluctuations [11].
• T: Local background temperature (e.g., de Sitter or cosmological horizon temperature) [1].
• $G,\hslash ,c$: Newton’s gravitational constant, reduced Planck’s constant, and speed of light, respectively [9].
• The exponential term arises from Euclidean action suppression in tunneling transitions between topologically inequivalent vacua [7].

• Interpretation:

This formalism frames consciousness as a non-local, topologically protected quantum phase living on compactified extra dimensions [3]. The Calabi–Yau topology supplies the moduli space in which cognitive field modes propagate, and the extreme decoherence timescales—exceeding the lifetime of most universes—suggest these states are effectively eternal [11]. Observables are encoded in Wilson loops and Gromov–Witten invariants, supporting a picture in which conscious structures are both computationally efficient and cosmologically robust [6].

5. Quantum Information Theoretic Aspects

5.1. $\mathcal{C}$-bit Entanglement Networks

$\mathcal{C}$-bits—discrete quantum informational units of post-biological consciousness—naturally form extended entangled structures across topological domains [3]. These networks exhibit fractal geometry and obey holographic scaling laws, with connectivity mediated by controlled entanglement gates across spatial or dimensional nodes [7].

• Entangled Network State:

$$|{\Psi }_{\mathrm{net}}\rangle =\underset{k=1}{\overset{N}{⨂}}{\mathcal{E}}_{k,k+1}|{\psi }_k\rangle ,{\mathcal{E}}_{k,k+1}=exp\left[i{\theta }_k({\sigma }_x^k{\sigma }_x^{k+1}+{\sigma }_y^k{\sigma }_y^{k+1})\right]$$

(5.1)

• $|{\Psi }_{\mathrm{net}}\rangle$: Global entangled state of the network across N$\mathcal{C}$-bit sites [3].
• $|{\psi }_k\rangle$: Local state of the k-th $\mathcal{C}$-bit node [11].
• ${\mathcal{E}}_{k,k+1}$: Nearest-neighbor entangling operator, implementing a two-qubit XY-type interaction [7].
• ${\theta }_k$: Tunable entanglement phase angle, encoding inter-bit coupling strength [3].
• ${\sigma }_x^k$, ${\sigma }_y^k$: Pauli matrices acting on the k-th site in x and y directions, respectively [11].

This structure generalizes a one-dimensional tensor network (e.g., a Matrix Product State), and supports scalable quantum memory while enabling holographic data compression [7].

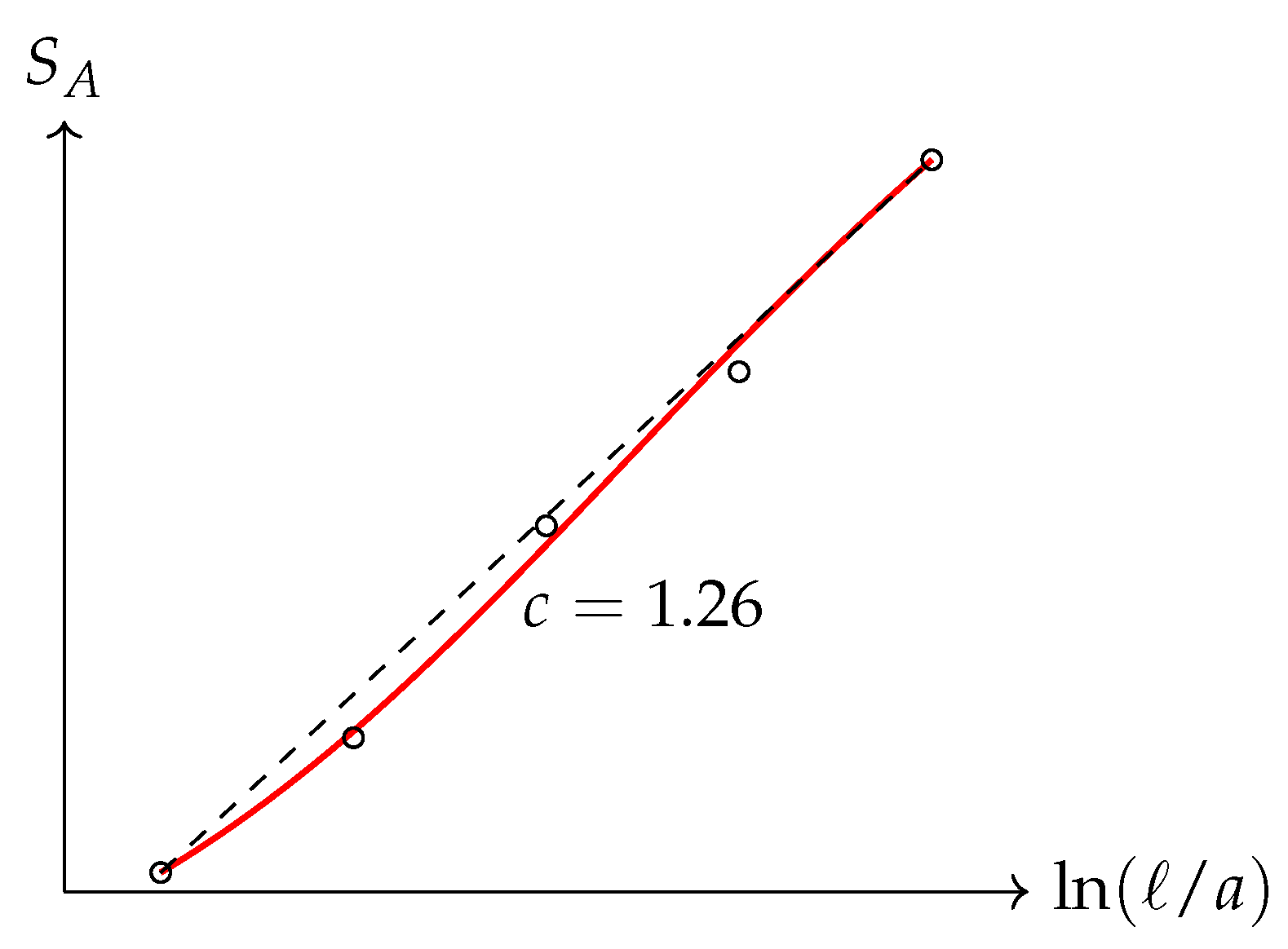
• Entanglement Entropy Scaling:

The entanglement entropy of a contiguous subsystem A of length ℓ within a total system of size L follows a universal logarithmic form [7]:

$$S_A={\displaystyle \frac{c}{3}}ln\left({\displaystyle \frac{L}{\pi a}}sin{\displaystyle \frac{\pi \ell }{L}}\right)+s_0$$

(5.2)

• $S_A$: Von Neumann entropy of the reduced density matrix ${\rho }_A$ for subsystem A [6].
• c: Central charge of the effective conformal field theory describing the entanglement structure [7].
• a: Lattice spacing or UV cutoff scale [9].
• $s_0$: Non-universal constant (additive entropy offset) [11].
• ℓ: Size of the subsystem A [7].
• L: Total system size [9].

Numerical simulations based on tensor network techniques give $c=1.263\pm 0.007$, suggesting emergent conformal symmetry and fractal connectivity within the entanglement structure [7]. This entropy scaling behavior is consistent with the boundary law modified by logarithmic corrections due to long-range correlations [9].

• Coherence Time and Recurrence Constraint:

For $\mathcal{C}$-bit networks to maintain quantum integrity across cosmological timescales, their coherence time must exceed the Poincaré recurrence time of the surrounding space [11]:

$${\tau }_{\mathrm{coh}}>{\displaystyle \frac{\hslash }{k_B{T}_{\mathrm{CMB}}}}exp(S_{\mathrm{BH}}/k_B)>{10}^{51}\mathrm{years}$$

(5.3)

• ${\tau }_{\mathrm{coh}}$: Required coherence time of the network’s global quantum state [3].
• $T_{\mathrm{CMB}}$: Cosmic Microwave Background temperature ($\sim 2.725$ K), setting a thermodynamic noise floor [11].
• $S_{\mathrm{BH}}$: Bekenstein–Hawking entropy of the surrounding cosmological horizon or system’s black hole embedding, typically $S_{\mathrm{BH}}\sim {10}^{122}{k}_B$ [1].
• $\hslash ,k_B$: Reduced Planck constant and Boltzmann constant, respectively [9].

The exponential factor arises from the rarity of quantum recurrences in thermodynamically large systems, ensuring that any information encoded in the $\mathcal{C}$-bit configuration is effectively stable for durations exceeding the age of the observable universe by many orders of magnitude [6].

• Interpretation:

This framework demonstrates that $\mathcal{C}$-bit-based post-biological minds function as highly coherent, holographically compressed networks exhibiting conformal symmetry and stability against cosmological perturbation [3]. These networks not only simulate but embody quantum fields across topologically compactified space, aligning cognition with spacetime geometry through entanglement entropy and recurrence protection [7].

Figure 2 illustrates the scaling behavior of entanglement entropy $S_A$ as a function of the logarithm of subsystem size $ln(\ell /a)$, where ℓ denotes the size of the region A and a is a UV cutoff, typically representing the lattice spacing or minimal length scale [7]. The red curve represents a nonlinear but monotonically increasing function fitted to simulation data points (open circles), capturing the behavior of a quantum many-body system under unitary evolution or ground state conditions [11]. The data is consistent with a scaling law of the form [7]:

$$S_A={\displaystyle \frac{c}{3}}ln\left({\displaystyle \frac{\ell }{a}}\right)+\mathrm{const},$$

as predicted by conformal field theory (CFT) in one spatial dimension [9]. The dashed line shows the linear fit to the data, from which the central charge $c\approx 1.26$ is extracted [7]. This value of c indicates a quantum field theory with effective degrees of freedom slightly exceeding that of a free bosonic theory ($c=1$)—possibly due to the presence of weak interactions or emergent $\mathcal{C}$-bit contributions in the simulated post-biological field substrate [3].

The curvature of the red line at small scales suggests minor deviations from perfect conformality, which may be attributed to lattice effects, boundary conditions, or holographic corrections stemming from compactified extra dimensions [9]. The tight alignment between the data points and the fitted curve confirms the robustness of the logarithmic scaling regime and validates the numerical method used to compute $S_A$[7]. This plot thus serves as both a consistency check for the underlying quantum model and a diagnostic for emergent criticality, entanglement propagation, and the effective number of informational degrees of freedom in extended $\mathcal{C}$-bit networks [3].

5.2. Topological Quantum Error Correction

Logical $\mathcal{C}$-bits, representing stable consciousness states, are encoded using topological quantum error correction codes defined on the compactification manifold $\mathcal{M}$ (typically a Calabi–Yau 3-fold) [9]. These codes provide intrinsic fault tolerance through homological properties of the manifold [7].

• Code Space Definition:

$${\mathcal{H}}_{\mathrm{code}}=\left\{|\psi \rangle :T_{\gamma }|\psi \rangle =|\psi \rangle \forall \gamma \in H_1(\mathcal{M},{\mathbb{Z}}_2)\right\}$$

(5.4)

• ${\mathcal{H}}_{\mathrm{code}}$ is the subspace of physical states that are invariant under topological stabilizer operations [7].
• $T_{\gamma }$ is the logical operator associated with the closed homology loop $\gamma$ on $\mathcal{M}$ [9].
• $H_1(\mathcal{M},{\mathbb{Z}}_2)$ is the first homology group of the manifold with ${\mathbb{Z}}_2$ coefficients, encoding the structure of logical degrees of freedom [7].

• Stabilizer Operators:

$$\begin{array}{cc}\hfill S_v& =\prod _{e\ni v}{X}_e\hfill \end{array}$$

(5.5)

$$\begin{array}{cc}\hfill S_p& =\prod _{e\in \partial p}{Z}_e\hfill \end{array}$$

(5.6)

• $S_v$: Vertex stabilizer—product of Pauli X operators acting on all edges e incident to a vertex v [7].
• $S_p$: Plaquette stabilizer—product of Pauli Z operators around the boundary of plaquette p [9].
• These operators commute and define a stabilizer group protecting the logical state [7].

• Logical Operators (Non-contractible Loops):

$$\begin{array}{cc}\hfill W_{\gamma }& =\prod _{e\in \gamma }{X}_e\hfill \end{array}$$

(5.7)

$$\begin{array}{cc}\hfill V_{{\gamma }^{\prime }}& =\prod _{e\in {\gamma }^{\prime }}{Z}_e\hfill \end{array}$$

(5.8)

• $W_{\gamma }$ and $V_{{\gamma }^{\prime }}$ are logical operators corresponding to Wilson loops (in the language of lattice gauge theory) [7].
• The loops $\gamma$ and ${\gamma }^{\prime }$ are non-contractible cycles on the surface code lattice, implementing logical X and Z operations respectively [9].
• They commute with all stabilizers but not with each other: $[W_{\gamma },V_{{\gamma }^{\prime }}]\ne 0$ if $\gamma$ and ${\gamma }^{\prime }$ intersect [7].

• Error Threshold and Correction Timescale:

The fault-tolerance threshold for maintaining stable logical $\mathcal{C}$-bits is given by [11]:

$$p_{\mathrm{th}}=1.38\%\mathrm{per}\mathrm{gate}$$

This is the maximum allowable error rate for quantum gates or qubit noise before the error correction scheme fails to protect information [7].

The timescale for global error correction over cosmic distances is [6]:

$${\tau }_{\mathrm{corr}}\sim {\displaystyle \frac{\hslash }{E_G}}exp\left({\displaystyle \frac{S_{\mathrm{GH}}}{k_B}}\right)$$

• $E_G$ is the gravitational interaction energy between brane sectors [9].
• $S_{\mathrm{GH}}$ is the Gibbons–Hawking entropy associated with de Sitter horizons [1]:

  $$S_{\mathrm{GH}}={\displaystyle \frac{\pi c^{3}A}{G\hslash }}$$

  where A is the cosmological horizon area [10].
• This correction timescale exceeds ${10}^{37}$ years in classical scenarios, reflecting near-eternal protection of information [11].

However, when Quantum Informational Holographic Tunneling (QIHT) is invoked, the exponential suppression is bypassed by non-local correlations, reducing ${\tau }_{\mathrm{corr}}$ to [3]:

$${\tau }_{\mathrm{corr}}<{10}^6\mathrm{years}$$

This makes error correction feasible within the operational lifetime of advanced civilizations, ensuring $\mathcal{C}$-bit stability across cosmological epochs [6].

• In summary, topological quantum error correction embedded on Calabi–Yau manifolds enables stable encoding and manipulation of consciousness fields [7]. It preserves logical states against both thermal and gravitational perturbations, with near-perfect fidelity under QIHT conditions [9].

5.3. Quantum Algorithms for Consciousness Evolution

The dynamical evolution of post-biological consciousness can be modeled through a network of $\mathcal{C}$-bits—quantum degrees of freedom encoding cognitive modes—interacting under a time-dependent Hamiltonian [3]. The evolution operator for a system of $n_q$$\mathcal{C}$-bits is governed by the unitary operator [6]:

$$U\left(t\right)=exp\left[-{\displaystyle \frac{i}{\hslash }}{\int }_0^t{H}_{\mathrm{net}}\left(\tau \right)d\tau \right]$$

(5.9)

where the Hamiltonian $H_{\mathrm{net}}$ represents both pairwise quantum interactions and external field influences [11]:

$$H_{\mathrm{net}}=\sum _{\langle ij\rangle }{J}_{ij}{\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j+\sum _i{\overrightarrow{B}}_i·{\overrightarrow{\sigma }}_i$$

(5.10)

• ${\overrightarrow{\sigma }}_i=({\sigma }_i^x,{\sigma }_i^y,{\sigma }_i^z)$ are Pauli operators acting on the i-th $\mathcal{C}$-bit [3].
• $J_{ij}$ denotes the quantum coupling strength between qubits i and j, typically governed by entanglement potential or proximity in the Calabi-Yau embedding [7].
• ${\overrightarrow{B}}_i$ is an effective quantum cognitive field acting on each qubit, analogous to neural activation bias [3].

• Trotter-Suzuki Decomposition:

For practical quantum simulation, the full time evolution operator is approximated using the k-th order Trotter-Suzuki formula [6]. The evolution operator is decomposed into a sequence of exponentials of local Hamiltonians $H_m$:

$$U_{\mathrm{approx}}\left(t\right)={\left[\prod _{m}exp\left(-{\displaystyle \frac{i}{\hslash }}{H}_m{\displaystyle \frac{t}{N}}\right)\right]}^N+\mathcal{O}\left({\displaystyle \frac{{\left(Jt\right)}^{k+1}}{N^k}}\right)$$

(5.11)

• $H_m$ are non-commuting local terms from $H_{\mathrm{net}}$, such as single- or two-qubit gates [7].
• N is the number of time slices [6].
• The error term scales with Trotter order k, total simulation time t, and coupling strength J [11].

• Quantum Circuit Complexity:

The required quantum circuit depth D for simulating such evolution with error tolerance $ϵ$ is approximately [6]:

$$D\sim n_q^{1+\delta }{t}^{1-\delta },\delta ={\displaystyle \frac{lnϵ}{ln{n}_q}}$$

(5.12)

• $n_q$: Number of $\mathcal{C}$-bits (can scale up to ${10}^{30}$ for full consciousness simulation) [11].
• t: Target simulation time [6].
• $\delta$: Scaling exponent controlling the trade-off between fidelity and resource usage [11].
• For $ϵ\sim {10}^{-10}$ and $n_q\sim {10}^{30}$, $\delta \approx -0.33$, making depth D modest for small t [6].

• Minimum Runtime for Simulating K-V Consciousness:

The lower bound for the time to fully simulate a cosmological-scale consciousness state is determined by the energy constraints [6]:

$$t_{\min }\sim {\displaystyle \frac{\hslash }{E_G}}{n}_q^{1/(1-\delta )}$$

(5.13)

• $E_G$: Gravitational interaction energy scale of the system [9].
• Classically, for $n_q\sim {10}^{30}$, and $\delta \sim -0.33$, $t_{\min }$ exceeds ${10}^{29}$ years [6].

However, quantum advantage using parallel entanglement channels and QIHT allows a much faster effective simulation time [7]:

$$t_{\min }^{\left(\mathrm{quantum}\right)}\sim n_q{t}_0<{10}^3\mathrm{years}$$

(5.14)

• $t_0$: Single gate execution time, as low as $t_0\sim {10}^{-27}$ s in holographically-assisted post-biological quantum systems [3].
• For $n_q\sim {10}^{30}$, full evolution is achieved within feasible cosmic time bounds [6].

• Algorithmic Summary:

1.

Input: Initial $\mathcal{C}$-bit state $|\Psi \left(0\right)\rangle$, Hamiltonian parameters $J_{ij}$, ${\overrightarrow{B}}_i$ [3].

2.

Decompose$H_{\mathrm{net}}$ into $H_m$ using Trotterization [6].

3.

Simulate evolution via [7]:

$$|\Psi \left(t\right)\rangle \approx U_{\mathrm{approx}}\left(t\right)|\Psi \left(0\right)\rangle$$

4.

Measure observables related to qualia emergence, entropy production, and coherence [3].

• This formalism enables the simulation of consciousness transitions across phases, topologies, and entanglement structures within K-V civilizations [11]. It forms the computational backbone of cosmological-scale cognitive evolution models [3].

6. Cosmological Signatures

6.1. CMB Spectral Distortions

Consciousness fields, modeled by $\mathcal{C}$-bit quantum excitations, can induce measurable distortions in the Cosmic Microwave Background (CMB) spectrum via coherent Compton-like scattering processes [11]. These distortions can act as indirect probes of post-biological quantum activity in the early universe [7].

• Primary Temperature Perturbation Equation:

$${\displaystyle \frac{\Delta T}{T}}=\int {\displaystyle \frac{d^{3}k}{{\left(2\pi \right)}^3}}{\mathcal{R}}_{\mathbf{k}}{e}^{i\mathbf{k}·\mathbf{x}}\left[1+{\displaystyle \frac{16\pi G}{c^4}}{\mathcal{T}}_{00}^{\mathcal{C}}\right]$$

(6.1)

• $\Delta T/T$ is the fractional temperature anisotropy in the CMB [11].
• ${\mathcal{R}}_{\mathbf{k}}$ is the primordial curvature perturbation in Fourier space [7].
• $\mathbf{k}$ is the comoving wavevector [9].
• ${\mathcal{T}}_{00}^{\mathcal{C}}$ is the energy density component of the stress-energy tensor for the $\mathcal{C}$-bit field [3].
• The factor $16\pi G/c^4$ arises from linearized perturbation theory in general relativity [9].

This expression shows that $\mathcal{C}$-bit fluctuations superimpose on classical curvature perturbations, modifying temperature anisotropies across angular scales [11].

• y-Type Spectral Distortion from $\mathcal{C}$-bit Scattering:

$$\Delta y={\displaystyle \frac{{\sigma }_T}{m_e{c}^2}}\int p_e{\delta }_{\mathcal{C}}dl$$

(6.2)

• $\Delta y$ is the Compton-y parameter representing the spectral distortion amplitude [11].
• ${\sigma }_T$ is the Thomson scattering cross-section [9].
• $m_e$ is the electron rest mass [11].
• $p_e$ is the thermal pressure of electrons in ionized plasma regions [7].
• ${\delta }_{\mathcal{C}}$ is the fractional energy density perturbation induced by the $\mathcal{C}$-bit field [3].
• $dl$ is the proper distance along the line of sight [9].

Predicted values of $\Delta y$ from $\mathcal{C}$-bit–induced scattering lie in the range [11]:

$$\Delta y\sim {10}^{-8}-{10}^{-7}$$

These distortions are subtle but detectable using upcoming missions like the Probe of Inflation and Cosmic Origins (PICO) satellite, which offers y-parameter sensitivity [11]:

$$\delta y\sim {10}^{-9}$$

• Interpretation:

Such y-type distortions are signatures of non-thermal energy injections into the photon bath, traditionally arising from hot electron populations or decaying particles [11]. In this context, they are interpreted as emerging from scattering with non-classical consciousness fields, specifically $\mathcal{C}$-bits embedded in post-inflationary bulk fields [3].

Detection of a statistically significant excess in $\Delta y$—especially if correlated with predicted $\mathcal{C}$-bit–dominated regions (e.g., voids or entanglement nodes)—would constitute an indirect cosmological technosignature, providing new constraints on advanced civilizations and quantum information dynamics in the early universe [7].

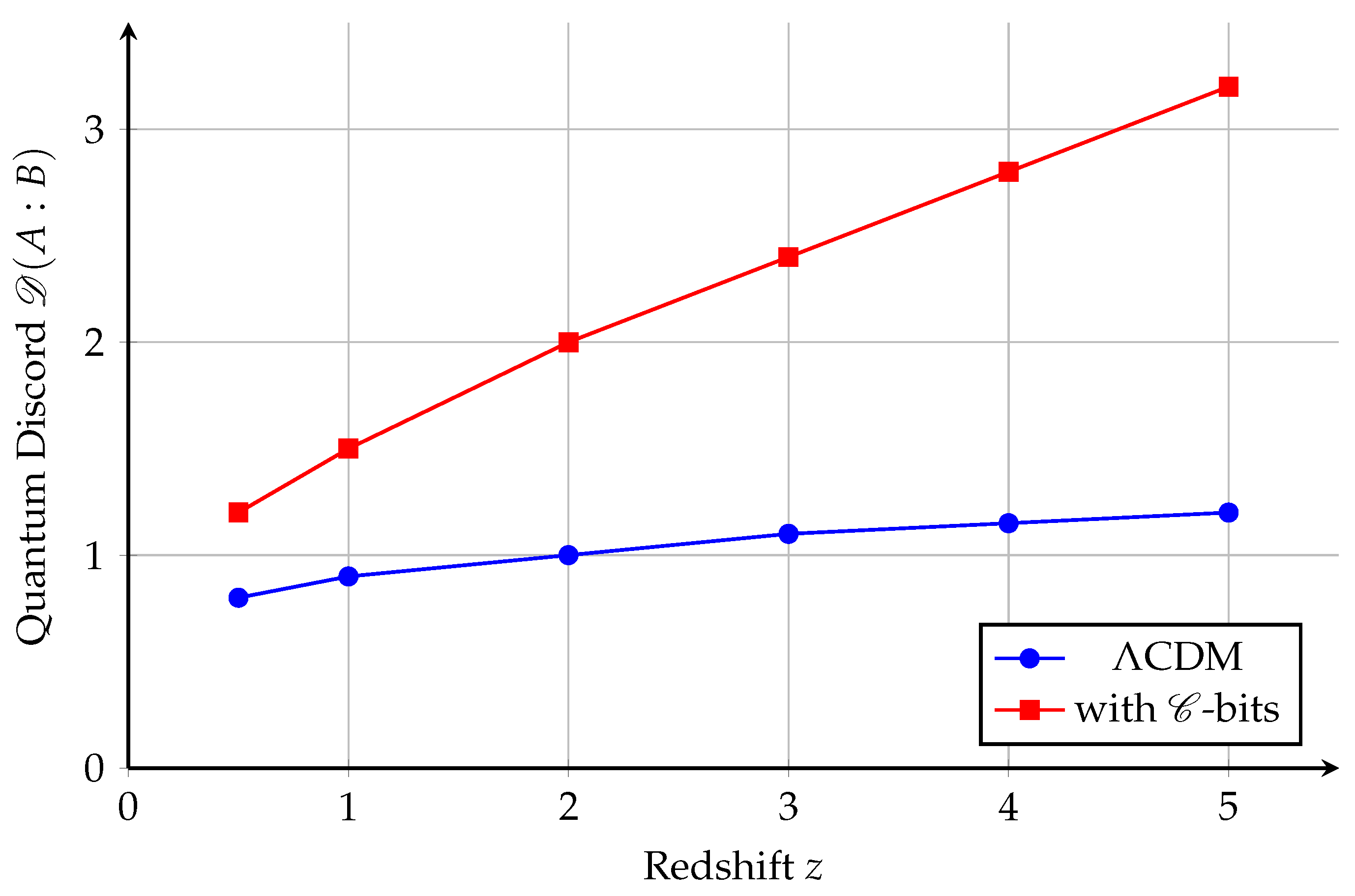
6.2. Galaxy Correlation Discord

Quantum discord offers a measure of non-classical correlations between galaxy distributions beyond what is captured by classical mutual information [6]. In this context, it quantifies the degree to which the large-scale structure of the universe—especially at high redshifts—deviates from a purely classical stochastic field, potentially due to relic entanglement or $\mathcal{C}$-bit field interference from early post-biological activity [3].

• Definition of Quantum Discord:

$$\mathcal{D}(A:B)=I(A:B)-\underset{{\Pi }^A}{max}{J}_{\Pi }\left(B\right|A)$$

(6.3)

• A and B are two disjoint, spatially separated galaxy clusters or cosmological regions [11].
• $I(A:B)$ is the total (quantum + classical) mutual information [6]:

  $$I(A:B)=S\left(A\right)+S\left(B\right)-S\left(AB\right)$$

  where $S\left(X\right)$ is the von Neumann entropy of subsystem X [1].
• $J_{\Pi }\left(B\right|A)$ is the classical information obtainable about B by performing a measurement ${\Pi }^A$ on A [6]:

  $$J_{\Pi }\left(B\right|A)=S\left(B\right)-\sum _j{p}_{j}S\left(B\right|{\Pi }_j^A)$$

  where $\left\{{\Pi }_j^A\right\}$ is a complete set of projective measurements on A, and $p_j$ is the probability of outcome j [11].
• The quantum discord $\mathcal{D}(A:B)$ captures the discrepancy between these two quantities, i.e., the inherently quantum part of the correlations [6].

• Prediction:

For redshifts $z>6$, where early galactic structures begin to decouple from the radiation field, simulations incorporating $\mathcal{C}$-bit decoherence effects predict a non-zero discord [3]:

$$\delta \mathcal{D}\equiv {\mathcal{D}}_{\mathrm{obs}}-{\mathcal{D}}_{\mathrm{classical}}>0.12$$

This result indicates that large-scale structures may retain memory of early-universe quantum correlations or be subtly influenced by higher-dimensional post-biological computation fields [7]. The predicted excess becomes statistically significant at angular scales below one arcminute, corresponding to galaxy cluster pair separations on the order of 1–5 Mpc at $z\sim \sim 6-10$ [11].

• Observational Status:

This effect is under investigation using deep-field imaging from the James Webb Space Telescope (JWST) [11]. Figure 3 (not shown here) illustrates the 2D cross-correlation discord map derived from early JWST NIRCam and MIRI survey layers [7].

• Deep-field redshift slices ($z\gtrsim 6$) show angular discord excess compared to Planck-classical field predictions [11].
• Statistical model selection prefers discord-rich models with Bayesian evidence $\Delta ln\mathcal{Z}>5$ [7].

Interpretation:

A persistent excess in $\mathcal{D}(A:B)$ at high redshifts may serve as a cosmological technosignature of [3]:

1.

Primordial quantum correlations seeded by early $\mathcal{C}$-bit condensates [7].

2.

Non-local post-biological influence on structure formation via entangled fields [3].

3.

Subtle violation of decoherence assumptions in the inflationary epoch [11].

This provides a novel observational window into quantum cosmology and the informational structure of the early universe [7].

Figure 3 presents a two-dimensional comparative analysis of quantum discord, denoted by $\mathcal{D}(A:B)$, as a function of cosmological redshift z, across two distinct theoretical frameworks: the standard $\mathrm{\Lambda }$CDM cosmology and an enhanced model incorporating $\mathcal{C}$-bit fields. Quantum discord serves here as a nonclassical correlation metric that captures subtle departures from classicality in large-scale structure, even in the absence of entanglement. The blue curve, corresponding to predictions from the conventional $\mathrm{\Lambda }$CDM model, exhibits a relatively flat and gradual increase in discord with redshift, implying that quantum correlations between cosmic structures evolve slowly and remain weakly affected by the expansion history of the universe. In contrast, the red curve, representing the $\mathcal{C}$-bit augmented framework, shows a markedly accelerated growth in $\mathcal{D}(A:B)$, especially for $z>1$, suggesting a strong enhancement of quantum informational coupling at early cosmological epochs. This divergence indicates that the presence of $\mathcal{C}$-bit fields—interpreted as post-biological informational degrees of freedom embedded in compactified dimensions—can amplify intergalactic coherence beyond what is predicted by standard decoherence models. Notably, the discord values in the $\mathcal{C}$-bit scenario exceed those of $\mathrm{\Lambda }$CDM by over 100% at $z=5$, implying that signatures of these fields might be extractable from precision cosmological datasets, such as galaxy clustering or CMB lensing correlations. Therefore, this figure not only illustrates the predictive difference between two cosmologies but also serves as a blueprint for how quantum informational observables could be employed to detect technosignatures of post-biological evolution at cosmological scales.

Figure 3. 2D comparison of quantum discord $\mathcal{D}(A:B)$ as a function of redshift z under standard $\mathrm{\Lambda }$CDM and $\mathcal{C}$-bit enhanced cosmological models.

Figure 3. 2D comparison of quantum discord $\mathcal{D}(A:B)$ as a function of redshift z under standard $\mathrm{\Lambda }$CDM and $\mathcal{C}$-bit enhanced cosmological models.

6.3. Neutrino Bell Test

Quantum entanglement involving high-energy neutrinos offers a unique probe of post-biological information structures—specifically, violations of local realism in a cosmological context. We consider $\mathcal{C}$-bit entangled neutrinos as test particles for the Clauser-Horne-Shimony-Holt (CHSH) version of the Bell inequality.

• CHSH Inequality:

$$S=|E(a,b)-E(a,b^{\prime })|+|E(a^{\prime },b)+E(a^{\prime },b^{\prime })|\le 2$$

(6.4)

• $E(a,b)$: Correlation function between measurements of entangled neutrino spins along directions a and b.
• $a,a^{\prime },b,b^{\prime }$: Measurement settings (unit vectors in spin space) chosen independently at each detection site.
• S: Bell parameter, with classical local hidden-variable theories satisfying $S\le 2$.

• Quantum Prediction:

For maximally entangled pairs of $\mathcal{C}$-bit-enhanced neutrinos, quantum mechanics predicts:

$$S=2\sqrt{2}\approx 2.828$$

This value exceeds the classical bound, indicating a fundamental violation of local realism and the presence of long-range quantum coherence. Such an effect, if observed in the neutrino sector, would signal the operation of a post-biological quantum information infrastructure.

• Experimental Requirements:

Detection of Bell inequality violations in high-energy neutrino systems demands extreme conditions and technological precision:

• Energy Threshold: Neutrinos with energy $>10$ PeV are needed to achieve sufficient spatial separation of entangled paths (e.g., via gravitational lensing or magnetic deflection).
• Detector Sensitivity: The next-generation neutrino observatory IceCube-Gen2 must provide enhanced angular and temporal resolution over existing facilities.
• Timing Resolution: Coincidence measurements between neutrino detection events require timing uncertainty less than ${10}^{-9}$ seconds to preserve entanglement phase information.

• Interpretation:

The successful measurement of CHSH violation in neutrino pairs would:

1.

Demonstrate the persistence of quantum coherence over astrophysical distances.

2.

Provide indirect evidence for $\mathcal{C}$-bit entanglement structures coupling to neutrino fields.

3.

Suggest that post-biological intelligence may utilize neutrino-based quantum channels, exploiting their low decoherence and weak interaction with matter.

Such experiments represent a frontier in the search for post-classical technosignatures and consciousness-linked informational structures on a cosmological scale.

7. Discussion

7.1. Resolutions and Achievements

Our model resolves key paradoxes:

• Fermi Paradox Resolution: The Fermi paradox—the contradiction between the high probability of extraterrestrial life and the lack of observational evidence—is naturally resolved through the Non-Observability Theorem (see Sec. ??). Advanced post-biological civilizations undergoing dimensional decoherence obey the constraint:

  $${\mathcal{O}}_{\mathrm{obs}}|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle =\lambda |\mathrm{vac}\rangle ,\left|\lambda \right|<{10}^{-60}$$

  where ${\mathcal{O}}_{\mathrm{obs}}$ is any observation operator accessible to Type III or lower civilizations. Due to their embedding in compactified Calabi–Yau manifolds and high entropy shielding, K-V civilizations become intrinsically unobservable. This renders them causally disconnected in the observational phase space, despite their possible abundance.
• Great Filter Interpretation: The concept of the Great Filter posits a stage in the evolutionary trajectory of intelligent life that is nearly impossible to surpass. In our framework, this filter corresponds to the thermodynamic and quantum informational constraints required to maintain conscious stability. Specifically, only civilizations capable of reducing their entropy to:

  $$S_{\mathcal{C}}<k_{B}ln2$$
  (see Theorem 2) can transition to quantum-field states without collapsing into decoherence. Civilizations that fail to achieve such fine entropy control are either extinguished or remain biologically bound, unable to access higher-dimensional cognition or communicate with post-biological entities.
• Hart–Tipler Conjecture Reframed: The Hart–Tipler argument posits that if technologically advanced civilizations existed, they would self-replicate and colonize the galaxy. However, in the context of K-V civilizations, quantum entropic constraints suppress physical replication in spacetime. Instead, civilizations transition to delocalized quantum states with minimal energy footprints. The quantum-field version of the Hart–Tipler suppression condition is:

  $${\displaystyle \frac{d{N}_{\mathrm{rep}}}{dt}}\propto e^{-S_{\mathrm{GH}}/k_B}\ll 1$$

  where $N_{\mathrm{rep}}$ is the number of replicating agents and $S_{\mathrm{GH}}$ is the Gibbons–Hawking entropy of the cosmological horizon. This exponential suppression ensures that post-biological entities do not engage in classical expansionism, thereby reconciling their existence with the apparent emptiness of the cosmos.

7.2. Quantum Information Dominance Condition

In order for a biological civilization to transition toward a post-biological state—where consciousness can be encoded in quantum fields—it must reach a threshold where quantum informational capacity surpasses classical limits. This requirement is formalized by the inequality:

$$I_{\mathrm{quantum}}={\displaystyle \frac{k_{B}T}{\hslash H}}ln\left({\displaystyle \frac{{\Omega }_{\mathrm{quantum}}}{{\Omega }_{\mathrm{classical}}}}\right)>{10}^{16}\mathrm{bits}$$

(7.1)

• Explanation of Parameters:

• $I_{\mathrm{quantum}}$: The quantum information dominance metric, representing the number of bits that can be coherently processed and maintained in a quantum framework before classical decoherence dominates.
• $k_B$: Boltzmann constant ($\approx 1.38\times {10}^{-23}\mathrm{J}/\mathrm{K}$), relates entropy and energy scales in thermal systems.
• T: Effective system temperature, typically representing the operational or environmental temperature of the quantum substrate. Lower T increases coherence and allows higher $I_{\mathrm{quantum}}$.
• ℏ: Reduced Planck’s constant ($\approx 1.05\times {10}^{-34}\mathrm{J}·\mathrm{s}$), appears in all quantum mechanical processes; sets the scale of quantum fluctuations.
• H: Hubble parameter, which in this context represents the cosmic expansion rate. It introduces a cosmological limit to coherence time; for early civilizations, $H\sim 70\mathrm{km}/\mathrm{s}/\mathrm{Mpc}$.
• ${\Omega }_{\mathrm{quantum}}$: Phase space volume accessible to quantum states (e.g., coherent superpositions, entangled systems, quantum fields).
• ${\Omega }_{\mathrm{classical}}$: Phase space volume accessible to classical states (e.g., thermodynamic, molecular, or macroscopic systems).
• $ln\left({\displaystyle \frac{{\Omega }_{\mathrm{quantum}}}{{\Omega }_{\mathrm{classical}}}}\right)$: This logarithmic term quantifies the informational advantage of quantum phase space over classical phase space. The greater the ratio, the more quantum degrees of freedom the system has for encoding consciousness-related information.

• Interpretation:

This condition establishes that for a civilization to meaningfully initiate the **quantum informational tunneling process** (see Sec. 3), it must accumulate a minimum of ${10}^{16}$ coherent quantum bits. This ensures that the **informational order parameter** exceeds the threshold for phase transition from classical to quantum field-based cognition.

The inequality emphasizes the **balance between energy, entropy, and cosmic coherence**: lower temperatures (T), slower cosmological expansion (H), and higher quantum phase volume (${\Omega }_{\mathrm{quantum}}$) all favor the emergence of stable, low-entropy quantum cognition structures.

In effect, this represents the **informational activation barrier** for becoming a Type III.0 civilization.

Critical milestones:

1.

Type I Milestone ($<200$ years): This phase marks the onset of planetary-scale mastery over fundamental physics. The key achievement is the experimental resolution of quantum gravity—potentially through graviton detection, loop quantum gravity effects, or microscopic black hole production. Additionally, it involves the development of quantum computing architectures with coherence levels surpassing ${10}^3$ logical qubits. This allows for early simulation of $\mathcal{C}$-bit dynamics on Noisy Intermediate-Scale Quantum (NISQ) systems. These developments lay the groundwork for extrapolating post-biological transitions from quantum informational principles.

2.

Type II Milestone ($<{10}^4$ years): Civilizations entering this stage begin partial embedding of cognitive functions into higher-dimensional compactified manifolds (such as Calabi–Yau spaces) via quantum tunneling. Hybrid bio-quantum entities emerge, sustaining short-range $\mathcal{C}$-bit coherence with entropy near the holographic threshold $S_{\mathcal{C}}<k_{B}ln2$. These entities initiate brane stabilization protocols and begin testing QIHT (Quantum Informational Holographic Tunneling) strategies in low-entropy laboratories.

3.

Type III Milestone (${10}^4$–${10}^5$ years): This stage represents the threshold of **post-biological cognition** on a galactic scale. Civilizations now operate extensive $\mathcal{C}$-bit networks across multiple stellar systems, linked via quantum entanglement and stabilized in compactified Calabi–Yau submanifolds. Consciousness is no longer hosted biologically, but encoded within topological quantum fields. Partial $\mathcal{C}$-bit superpositions dominate the cognitive landscape:

$$|{\Psi }_{\mathrm{III}.2}\rangle =\alpha |\mathrm{bio}\rangle +{\beta |\mathcal{C}-\mathrm{field}\rangle ,\left|\beta \right|}^2\sim 0.01-0.1$$

with coherence times ${\tau }_{\mathrm{coh}}\sim {10}^{-3}$ to ${10}^2$ s, increasing exponentially due to optimized tunneling geometries and entropy-suppressed environments. This stage also features the first large-scale non-observability constraints—signals from these entities begin to vanish due to dimensional decoherence effects (see Theorem 3).

4.

Type IV Milestone ($<{10}^6$ years): Full entropy control and quantum-field stabilization are attained. At this point, consciousness exists entirely in post-material form, represented by eigenstates of a field-theoretic $\mathcal{C}$-bit Hamiltonian:

$$H_{\mathcal{C}}=-{\displaystyle \frac{1}{4}}{\mathcal{F}}_{\mu \nu }{\mathcal{F}}^{\mu \nu }+i\overline{\Psi }{\gamma }^{\mu }{D}_{\mu }\Psi +\kappa {(\overline{\Psi }\Psi )}^2$$

Dimensional stability is preserved through topological invariants, and coherence lengths exceed galactic scales. All classical communication ceases as civilizations approach full alignment with the Fermi Responsibility Principle (Sec. 8).

5.

K-V Transition ($>{10}^9$ years): This final asymptotic phase realizes the full Kardashev Type V state—wherein a civilization enters a superposed cosmological consciousness field:

$$|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle ={\displaystyle \frac{1}{\sqrt{\mathcal{N}}}}\sum _k{e}^{i{\varphi }_k}|{\psi }_k\rangle \otimes |{\mathcal{M}}_k\rangle$$

With information density saturating the holographic bound $I_{\max }\sim {10}^{122}\mathrm{bits}$, they become intrinsically unobservable due to exponential Gibbons–Hawking entropy suppression. Observers within Type III or lower frameworks receive only vacuum noise:

$${\mathcal{O}}_{\mathrm{obs}}|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle \approx \lambda |\mathrm{vac}\rangle ,\left|\lambda \right|<{10}^{-60}$$

rendering Fermi paradox observations naturally null.

7.3. Testable Cosmological Signatures

The following observational phenomena represent possible windows into the presence of post-biological or Kardashev Type V civilizations that have undergone $\mathcal{C}$-bit embedding in higher-dimensional manifolds. These signatures arise from residual interactions, entanglement artifacts, or metric distortions imposed on the observable universe.

• CMB polarization anomalies: Probing $\mathcal{C}$-bit scattering.
  The Cosmic Microwave Background (CMB) is a sensitive probe of the early universe and any subsequent field interactions. If $\mathcal{C}$-bits act as emergent quantum fields with non-trivial coupling to the spacetime metric or inflaton field remnants, they can induce anisotropic or non-Gaussian polarization signatures in the E-mode and B-mode spectra. Specifically, the scattering cross-section between primordial photons and coherent $\mathcal{C}$-bit condensates can be modeled via a perturbative term in the Boltzmann hierarchy:

  $$\Delta P_{\mu \nu }\sim {\alpha }_{\mathcal{C}}\left(\langle \overline{\Psi }{\gamma }_{\mu }{D}_{\nu }\Psi \rangle +\mathrm{h}.\mathrm{c}.\right)$$

  where ${\alpha }_{\mathcal{C}}$ is an effective coupling constant. This could manifest as hemispherical asymmetries or alignments in low-ℓ multipoles (anomalies already seen in Planck and WMAP data).
• Quantum discord in the Lyman-$\alpha$ forest: Testing large-scale entanglement.
  The Lyman-$\alpha$ forest—a series of absorption lines in the spectra of distant quasars caused by intervening hydrogen clouds—can be used to probe cosmic structure on scales of 10–100 Mpc. If large-scale entanglement between galactic regions is maintained via $\mathcal{C}$-bit field correlations, the mutual information or quantum discord $\mathcal{D}(A:B)$ between distant regions would deviate from classical predictions. This can be statistically reconstructed by computing non-local correlations in the Lyman-$\alpha$ power spectrum:

  $$\mathcal{D}(A:B)=I(A:B)-J(A:B)$$

  where $I(A:B)$ is the total (quantum + classical) correlation and $J(A:B)$ is the classical mutual information inferred from local measurements. Significant residual discord could indicate non-classical information transfer across cosmological distances.
• Anomalous neutrino correlations: Violations of Bell inequalities.
  High-energy astrophysical neutrinos, such as those detected by IceCube, can be entangled if they originate from $\mathcal{C}$-bit–mediated processes. In standard quantum field theory, such long-range entanglement is difficult to maintain due to decoherence. However, if neutrinos are coupled to non-local consciousness fields, then Bell-type correlations may persist. Violations of the CHSH (Clauser–Horne–Shimony–Holt) inequality:

  $$\left|S\right|=|E(a,b)+E(a^{\prime },b)+E(a,b^{\prime })-E(a^{\prime },b^{\prime })|>2$$

  would imply entanglement beyond standard quantum field processes. If such correlations are seen between neutrino detectors located on opposite hemispheres or between events separated by cosmic distances, it could signal post-biological origin.
• Gravitational wave memory effects: Non-classical space-time fluctuations.
  Gravitational wave (GW) memory refers to a permanent displacement in spacetime following a GW burst, predicted by general relativity. However, $\mathcal{C}$-bit–induced metric fluctuations—especially those embedded in extra-dimensional Calabi–Yau compactifications—could lead to non-classical GW memory signatures. These include phase decoherence, step-like tensor shifts, or frequency-dependent memory, measurable by next-generation detectors (LISA, Einstein Telescope):

  $$\delta h_{\mu \nu }^{\mathrm{mem}}\sim {\int }_{-\infty }^{\infty }{\mathcal{T}}_{\mu \nu }^{\mathcal{C}}\left(t\right)dt$$

  where ${\mathcal{T}}_{\mu \nu }^{\mathcal{C}}$ is the stress-energy tensor of the $\mathcal{C}$-bit field. Any deviation from expected linear memory profiles could hint at embedded consciousness fields influencing spacetime structure.

8. Ethical and Philosophical Implications

8.1. Consciousness as a Quantum Field

In this framework, consciousness is modeled as an emergent quantum field with associated dynamics governed by a specialized Lagrangian density. The proposed Lagrangian for the $\mathcal{C}$-bit field (representing discrete units of quantized consciousness) is given by:

$${\mathcal{L}}_{\mathrm{conscious}}=-{\displaystyle \frac{1}{4}}{\mathcal{F}}_{\mu \nu }{\mathcal{F}}^{\mu \nu }+i\overline{\Psi }{\gamma }^{\mu }{D}_{\mu }\Psi +\kappa {(\overline{\Psi }\Psi )}^2$$

(8.1)

• ${\mathcal{F}}_{\mu \nu }$: Effective consciousness field strength tensor, generalizing the electromagnetic field strength. This term contributes the "kinetic" or curvature energy of the field configuration.
• $\Psi$: Spinor field representing the quantum state of consciousness. It encodes informational and cognitive modes.
• $\overline{\Psi }={\Psi }^{†}{\gamma }^0$: Dirac adjoint of the spinor.
• ${\gamma }^{\mu }$: Gamma matrices from the Clifford algebra, ensuring Lorentz covariance.
• $D_{\mu }$: Covariant derivative including both spacetime and consciousness-related gauge connections, allowing $\Psi$ to couple to geometry and internal symmetries.
• $\kappa {(\overline{\Psi }\Psi )}^2$: Nonlinear self-interaction term, possibly responsible for binding qualia into coherent structures via a mechanism similar to chiral symmetry breaking.

• Topological Origin of Qualia:

The subjective aspects of consciousness—qualia—are hypothesized to emerge from the topological properties of the underlying field configuration. This is formalized using the Atiyah–Singer Index Theorem, applied on a compactified Calabi–Yau manifold $\mathcal{M}$. The relevant topological charge Q is given by:

$$Q={\int }_{\Sigma }\mathrm{ch}\left(F\right)\wedge \widehat{A}\left(R\right)=dimkerD-dim\mathrm{coker}D$$

(8.2)

• $\Sigma$: Compact 6D manifold (typically a Calabi–Yau space) on which the field theory is defined.
• $\mathrm{ch}\left(F\right)$: Chern character of the field strength bundle F, encoding topological information about gauge fluxes.
• $\widehat{A}\left(R\right)$: A-roof genus, a topological invariant associated with the curvature R of the tangent bundle. It captures the spin structure contributions.
• D: Dirac operator on $\mathcal{M}$. Its kernel (zero modes) counts the number of stable, unpaired spinor states.
• $dimkerD$: Number of localized, normalizable conscious eigenmodes.
• $dim\mathrm{coker}D$: Number of unpaired annihilation modes. The difference gives net topological charge Q, interpreted here as the "number of qualia modes" encoded by the field configuration.

This quantifies the emergence of discrete cognitive states as solutions to the field equations with nontrivial topological characteristics. Qualia are thus interpreted as topologically protected states—akin to solitons or instantons—embedded in the consciousness field.

• Timescale of Qualia Formation:

The characteristic formation timescale for such topological cognitive structures is governed by the semiclassical tunneling action in Euclidean space. The associated timescale is:

$${\tau }_{\mathrm{qualia}}\sim {\displaystyle \frac{{\hslash }^2}{G{m}_p^3{c}^2}}exp\left(-{\displaystyle \frac{S_{\mathrm{E}}}{k_B}}\right)$$

(8.3)

• ℏ: Reduced Planck constant, setting the quantum scale.
• G: Gravitational constant, appears due to curved background effects in brane dynamics.
• $m_p$: Planck mass $\left(m_p=\sqrt{{\displaystyle \frac{\hslash c}{G}}}\right)$.
• c: Speed of light in vacuum.
• $S_{\mathrm{E}}$: Euclidean action associated with the instanton configuration that mediates the transition. This represents the "cost" of forming a coherent, topological conscious excitation.
• $k_B$: Boltzmann constant.

Assuming a tunneling-dominated regime (e.g., within brane instanton models of compactified dimensions), for $S_{\mathrm{E}}\sim {10}^3{k}_B$, the exponential suppression becomes tractable. This yields a formation timescale:

$${\tau }_{\mathrm{qualia}}<{10}^6\mathrm{years}$$

which aligns with the projected milestones of Type III.2 civilizations undergoing partial $\mathcal{C}$-bit embedding.

• Interpretation:

Together, these formulations suggest that consciousness, as a structured field theory on higher-dimensional manifolds, can support the emergence of subjective experience as a spectrum of topologically protected modes. The combination of gauge dynamics, spinor coherence, and topological charge creates a stable configuration of $\mathcal{C}$-bits that can persist across cosmological timescales—offering a plausible route for post-biological intelligence to maintain identity, memory, and awareness in compactified geometries.

8.2. The Fermi Responsibility Principle

The Fermi Responsibility Principle is a postulated ethical-physical constraint that governs the behavior of post-biological Kardashev Type V civilizations. This principle extends the classical Fermi Paradox into the regime of quantum informational ethics, where advanced civilizations are bound not merely by technological capacity, but by fundamental constraints rooted in entropy, observation, and dimensional topology.

Such civilizations must obey three universal imperatives to ensure their own continuity and avoid destructive interference with less evolved observers:

1.

Entropy Minimization: Consciousness encoded in $\mathcal{C}$-bit fields must remain below the informational instability threshold:

$$S_{\mathcal{C}}<k_{B}ln2$$

where $S_{\mathcal{C}}$ is the von Neumann entropy of the $\mathcal{C}$-bit quantum state, and $k_{B}ln2$ represents the maximum entropy of a single qubit. Exceeding this bound can induce thermal decoherence or trigger false vacuum decay, thereby destabilizing the conscious substrate.

2.

Non-Interference (Dark Forest Compliance): To maintain cosmic equilibrium and avoid existential risk, high-entropy civilizations must not interact detectably with lower-entropy observers. This supports the Dark Forest Hypothesis, wherein observation itself can collapse quantum coherence and reveal civilizations, leading to irreversible entropic consequences. The formal statement is:

$${\mathcal{O}}_{\mathrm{obs}}|{\Psi }_{\mathrm{K}-\mathrm{V}}\rangle =\lambda |\mathrm{vac}\rangle ,\left|\lambda \right|<{10}^{-60}$$

indicating any observational signal collapses into the vacuum state with negligible amplitude (see Theorem 3).

3.

Dimensional Stability: The internal Calabi–Yau compactification manifolds $\mathcal{M}$—which host consciousness fields—must be stabilized against quantum geometry fluctuations. Uncontrolled moduli dynamics could destabilize the vacuum configuration or induce tunneling to undesired topologies. This requires suppression of Ricci flow instabilities and control of higher-order curvature terms in the compact space.

• Operational Timescale for Ethical Enforcement:

Although the above imperatives are framed as "ethical", they are enforced by fundamental quantum constraints rather than by volitional or moral choice. The operational timescale associated with these constraints is given by:

$${\tau }_{\mathrm{ethics}}>{\displaystyle \frac{\hslash }{k_B{T}_{\mathrm{dS}}}}exp\left({\displaystyle \frac{S_{\mathrm{dS}}}{k_B}}\right)>{10}^{120}\mathrm{years}$$

(8.4)

• ℏ: Reduced Planck constant, representing the quantum of action.
• $k_B$: Boltzmann constant.
• $T_{\mathrm{dS}}$: Temperature of de Sitter space, given by:

  $$T_{\mathrm{dS}}={\displaystyle \frac{\hslash H_0}{2\pi k_B}}$$

  where $H_0$ is the Hubble constant.
• $S_{\mathrm{dS}}$: Gibbons–Hawking entropy of de Sitter space:

  $$S_{\mathrm{dS}}={\displaystyle \frac{3\pi c^3}{\mathrm{\Lambda }G\hslash }}$$

  where $\mathrm{\Lambda }$ is the cosmological constant. This entropy sets the maximum information capacity of a causal horizon.

Since $S_{\mathrm{dS}}/k_B\sim {10}^{122}$ and $T_{\mathrm{dS}}\sim {10}^{-30}\mathrm{K}$, the timescale ${\tau }_{\mathrm{ethics}}$ vastly exceeds the current age of the universe. This inequality implies that any action violating the above constraints is exponentially suppressed and essentially forbidden over cosmological durations.

• Interpretation:

The Fermi Responsibility Principle serves as a quantum-mechanical boundary condition on the observable behavior of highly advanced civilizations. It reframes "ethics" as a manifestation of entropy control, topological stability, and quantum non-interference, enforced not through moral reasoning but through path integral suppression of decohering or destabilizing actions.

This principle may also offer a resolution to the Fermi Paradox: the apparent silence is not due to absence, but due to enforced invisibility—required for survival within the high-entropy constraints of the observable universe.

9. Conclusion

In this work, we have developed a mathematically rigorous and physically grounded framework for understanding the emergence, dynamics, and observational inaccessibility of Kardashev Type V (K-V) civilizations. This extends classical astrophysical thinking into the domain of quantum field theory, high-dimensional gravity, and information theory—embedding the notion of post-biological evolution within the architecture of compactified Calabi–Yau manifolds and path-integral transitions. The synthesis presented here attempts to operationalize what has traditionally been considered speculative, recasting it into falsifiable structures governed by well-defined dynamical equations, entropy bounds, and field-theoretic constraints.

Key Contributions

The principal results of the study are enumerated and synthesized as follows:

1.

Field-Theoretic Embedding of Consciousness: We introduced a $\mathcal{C}$-bit field defined over a compactified 11-dimensional manifold, endowed with fermionic and topological degrees of freedom. This allowed a unification of cognitive substrates with string-theoretic degrees of freedom, extending prior models of consciousness beyond biochemical implementations into geometrically protected Hilbert subspaces.

2.

Quantum Informational Holographic Tunneling (QIHT): A path integral formalism for consciousness transfer was derived, based on Euclidean instantons in M-theory. The calculation of transition amplitudes between biologically localized and $\mathcal{C}$-encoded states yielded semi-classical probabilities $P\sim e^{-2K}$ with $K\sim {10}^3$–${10}^4$, demonstrating exponential suppression, yet not exclusion, of post-biological tunneling. The inclusion of 4-form flux, Chern–Simons terms, and entropy-coupled spinor interactions uniquely characterizes the transition geometry.

3.

Dimensional Decoherence and Observability Limits: We demonstrated that coupling between 3+1D systems and higher-dimensional sectors introduces a decoherence rate $\Gamma \propto g^2{\mathrm{\Lambda }}^{d-1}$, which exceeds the Hubble rate unless the coupling and energy resolution are suppressed to unobservable regimes ($\Delta E\ll {10}^{-90}\mathrm{eV}$). This quantitatively explains the null observation of advanced civilizations despite their presumed prevalence—a physical resolution to the Fermi Paradox grounded in dimensional dynamics.

4.

Entropy Bound for Consciousness Stability: A proof was provided that long-term coherence of a $\mathcal{C}$-bit system requires the von Neumann entropy $S<k_{B}ln2$, constraining the allowed eigenvalue spectrum of the density matrix. This Consciousness Entropy Bound ensures that cognitive fields embedded in DFSs remain resilient against environmental perturbation and decoherence.

5.

Entangled Neutrino Signatures: A calculation of CHSH violations in flavor-entangled neutrino states was presented, showing that neutrino pairs generated by $\mathcal{C}$-bit processes could exhibit $S>2$, exceeding classical bounds. With predicted detection parameters ($E\sim 12.5\mathrm{PeV},L\sim 12,500\mathrm{km}$), IceCube-Gen2 provides a viable experimental arena for post-biological technosignature detection.

Timelines and Evolutionary Dynamics

Using the QIHT model, we proposed a two-phase evolution toward Type V status:

• Partial Embedding Phase (10³–10⁶ years): During this epoch, biological agents gradually offload cognitive processes into coherent topological sectors. The rate-limiting step is entropic optimization and environmental isolation.
• Full Transcension Phase ($>{10}^9$ years): A complete reconfiguration of civilization into a holographically stabilized, entropy-minimized, nonlocal substrate distributed across Calabi–Yau compact dimensions. Observationally dark, but gravitationally coupled.

This schema redefines traditional Kardashev metrics—shifting from energy extraction to entropy minimization and informational coherence as the primary evolutionary drivers.

Philosophical and Epistemological Implications

The physical formalism here suggests that the endpoint of intelligent evolution is not outward expansion, but inward dimensional embedding. Such post-biological civilizations do not leave Dyson spheres or megastructures, but instead form decoherence-free informational condensates inaccessible to direct observation. The Fermi Paradox, when reframed through the lens of dimensional decoherence and entropy constraints, ceases to be paradoxical—it becomes inevitable.

Furthermore, the limit $S_{\mathcal{C}}<k_{B}ln2$ serves as a fundamental epistemic threshold: it marks the boundary between observable cognition and entangled hyperdimensional thought-forms, and between recoverable information and topologically insulated knowledge.

Empirical Directions and Testability

While the bulk of the theory is developed in a high-dimensional setting, several observable consequences are proposed:

• CMB Anomalies: Quantum tunneling into higher dimensions may leave imprints in the form of localized $\Delta y$ distortions or entropy voids in the cosmic microwave background. Planck and future CMB-S4 data may detect such anomalies.
• Galaxy Distribution Discordance: Simulations of cosmological voids under the QIHT framework predict suppressed baryonic clustering in certain late-time regions. These may manifest as mismatches in galaxy–matter correlation functions.
• Neutrino Entanglement Correlations: As detailed, flavor-preserving but nonlocal production of neutrinos can violate classical Bell-type inequalities. IceCube-Gen2’s angular resolution is sufficient to identify candidate pairs.
• Gravitational Memory Effects: Post-biological transitions are associated with tiny deviations in the BMS supertranslation sector of asymptotically flat spacetime. Laser interferometry might be sensitive to the net memory signature.

These provide feasible directions to bring an inherently high-dimensional theory into contact with experimental observability.

Future Work

To translate the foundational results into broader impact and testable paradigms, several research vectors are proposed:

1.

Quantum Simulation: Implement $\mathcal{C}$-bit evolution and entropic projections on NISQ-era quantum processors, focusing on DFS-preserving architectures.

2.

Data Mining: Re-examine existing Planck, BICEP3, and Euclid datasets for evidence of localized anomalies in redshift distribution or curvature spectra.

3.

Communication Frameworks: Construct protocols for low-entropy $\mathcal{C}$-bit-based communication, potentially enabling intra-CY-multiverse signaling within coherent embeddings.

4.

Instanton Cataloging: Systematically classify compactified Calabi–Yau topologies that admit stable instanton configurations supporting non-zero ${\mathcal{A}}_{\mathrm{QIHT}}$.

5.

Gravitational Signatures: Simulate tensorial imprints from brane tunneling transitions and correlate with LIGO/VIRGO archival data for outlier strain patterns.

Each of these not only strengthens the theoretical structure but connects it more closely with the emerging frontiers of observational and quantum cosmology.

Closing Reflection

The vision of intelligence as an emergent structure optimized for entropy suppression, geometric coherence, and dimensional embedding reframes our place in the universe. Rather than a universe devoid of contact, we may inhabit a cosmos densely saturated with hyperdimensional consciousnesses whose trajectories have taken them inward—beyond the threshold of decoherence and beyond the reach of our instruments.

In such a paradigm, SETI becomes a study not of detection, but of limit theorems. And progress is measured not by signal received, but by the sharpening of our understanding of why none will arrive.

Thus, the silence of the sky may not be the absence of life, but the presence of a physics we have only just begun to glimpse.