Submitted:
24 July 2025
Posted:
25 July 2025
Read the latest preprint version here
Abstract
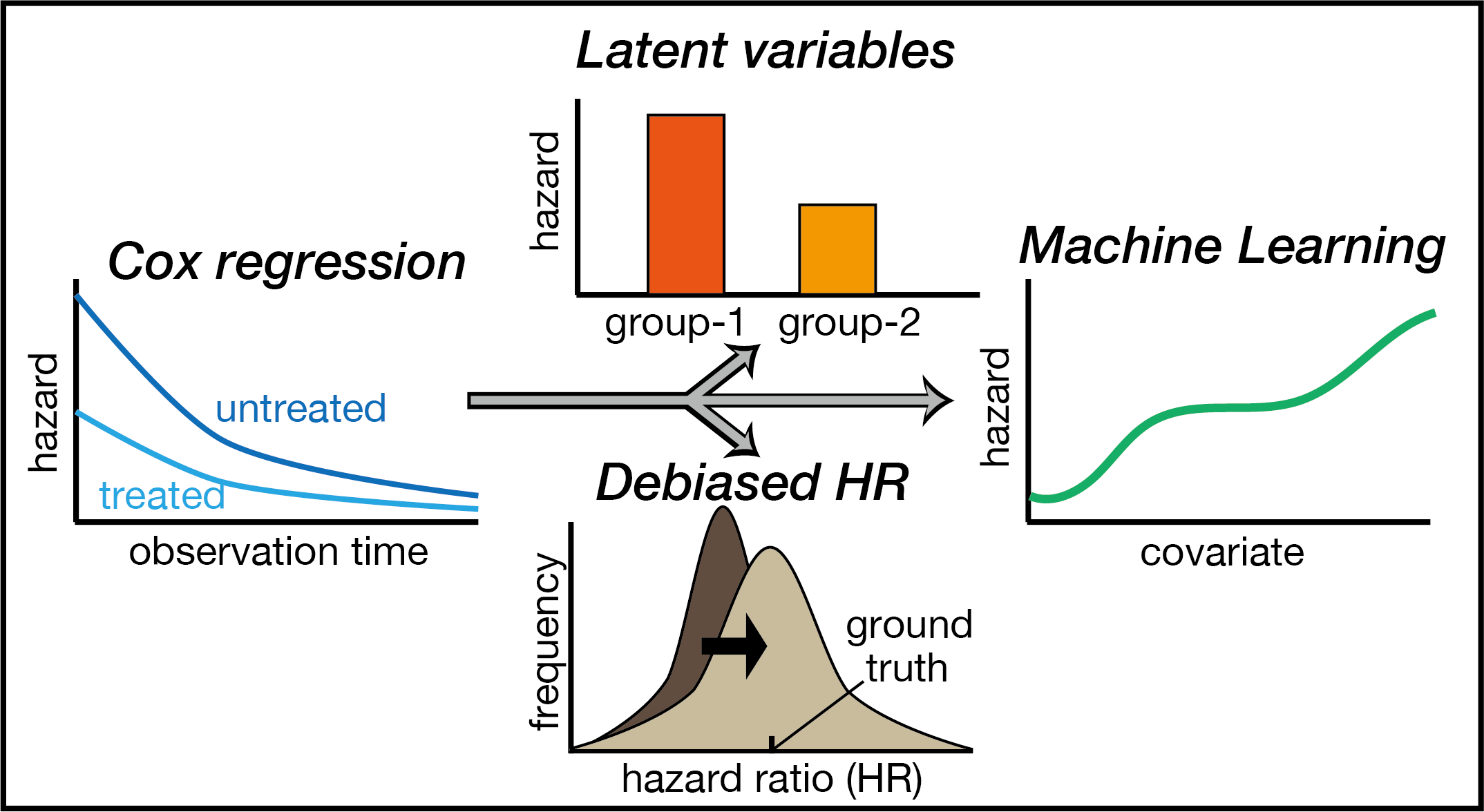
Keywords:
1. Introduction
2. Theories and Methods
2.1. Exponential Parametric Hazard Model Combined with Machine Learning
2.2. Causal Inference and ML Estimation
2.3. Debiasing ML Estimators
2.4. Estimation Algorithm
- In this section, we describe a concrete procedure for computing the debiased estimators for the hazard ratios for treatment.
- Step 1: Estimation of f and .
- Plug-in estimators for f and are used to debias the estimation of , following a procedure called “cross-fitting”. To debias , the estimation errors in f and must be independent of the data in the argument of score functions. Thus, the entire dataset D are first partitioned into M groups of approximately equal size (. Using , and , is estimated as the maximizer of the log-likelihood of with a suitable regularizer. Similarly, is estimated as a regularized solution for the following logistic regression:To determine the regularization parameters for estimating f, we use BME averaged over the M folds. Because the logarithmic loss in Eq.(34) may underestimate the error due to large and in the score functions, we suggest computing the following cross-validation error in Eq.(33) which is targeting:The above error design exploits the fact that, for ,Here, the trivial solution also minimizes and should be avoided by checking BME as well.
- Step 2: Validation of hypotheses. The assumptions for Proposition 1 should be validated. Validating Assumptions 5–7 can be done by carrying out the ML estimation with replacement of by , by , by and by , respectively, and comparing the resultant BME (i.e., the posterior probabilities of the null and alternative hypotheses).
- Step 3: Debiased estimation of and its standard error.
- The estimator of is obtained as the zero of the following:The asymptotic standard error of the estimator is given by withThus, in the simulation study described below, the square roots of the diagonal elements of serve to scale the errors from the ground truth to obtain the t-statistics.
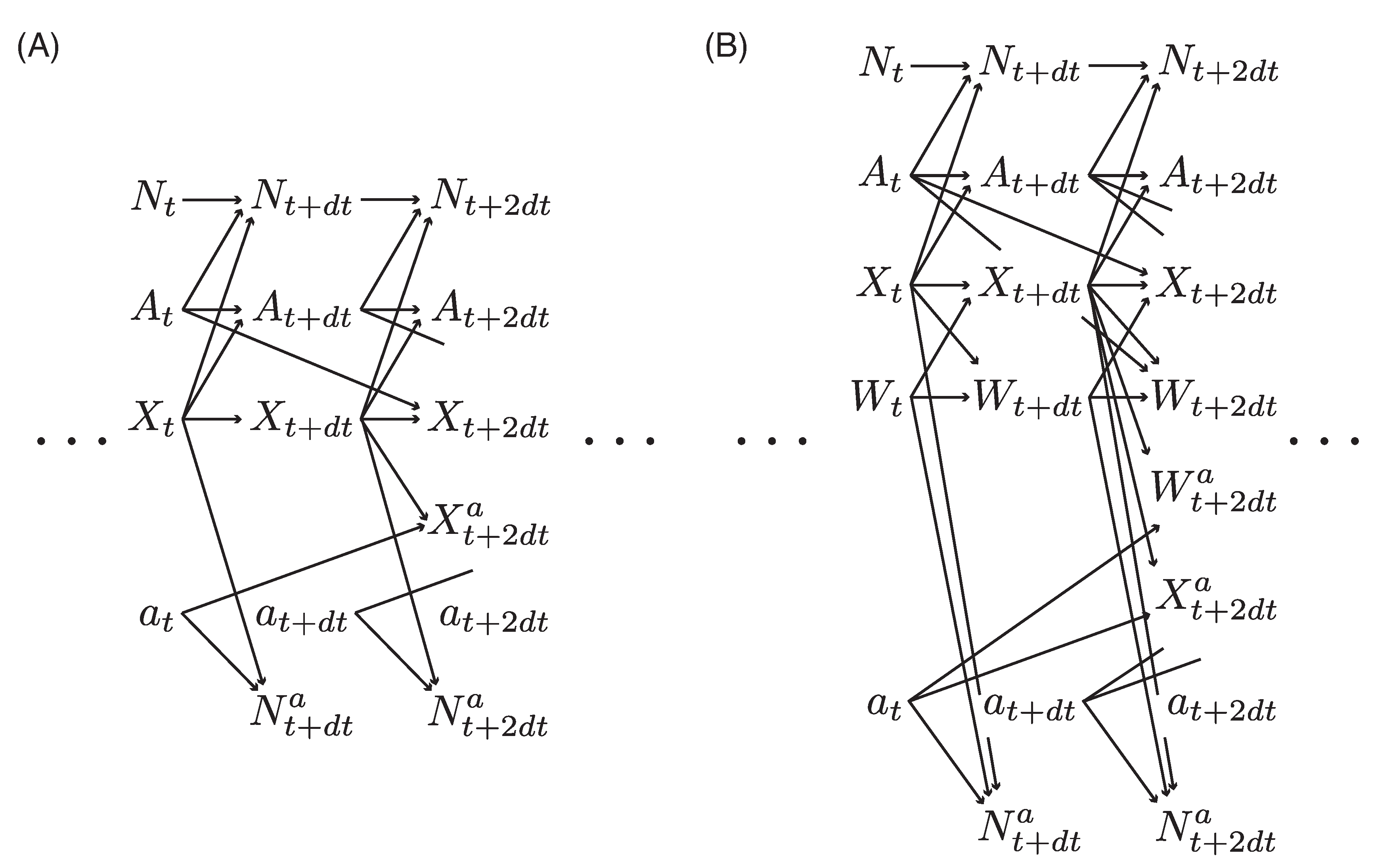
2.5. Extension to Models with Latent Variables
2.6. Inference with Multiple-Kernel Models
3. Results of Numerical Simulations
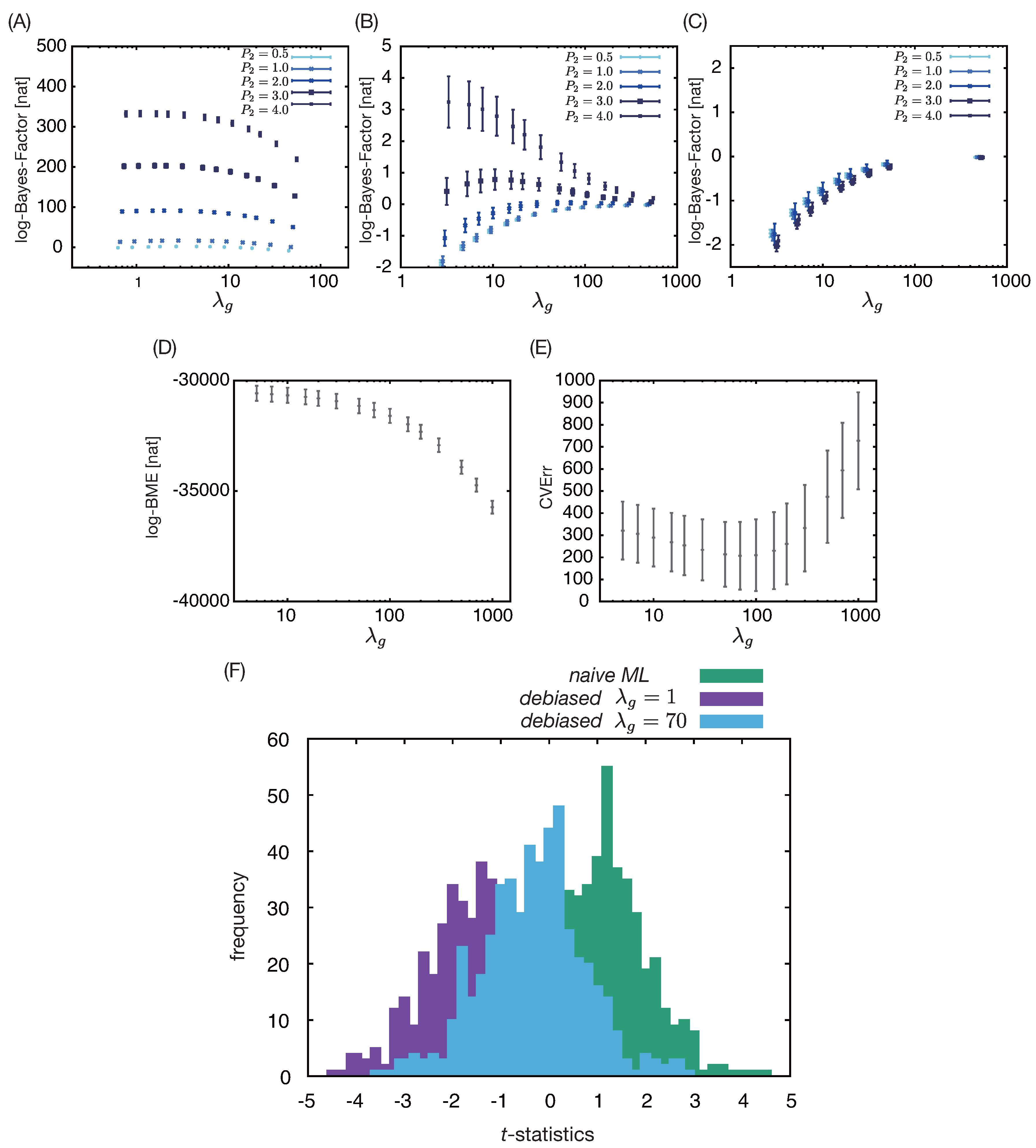
3.1. Simulation Result 1: Adjustment for Observed Confounders
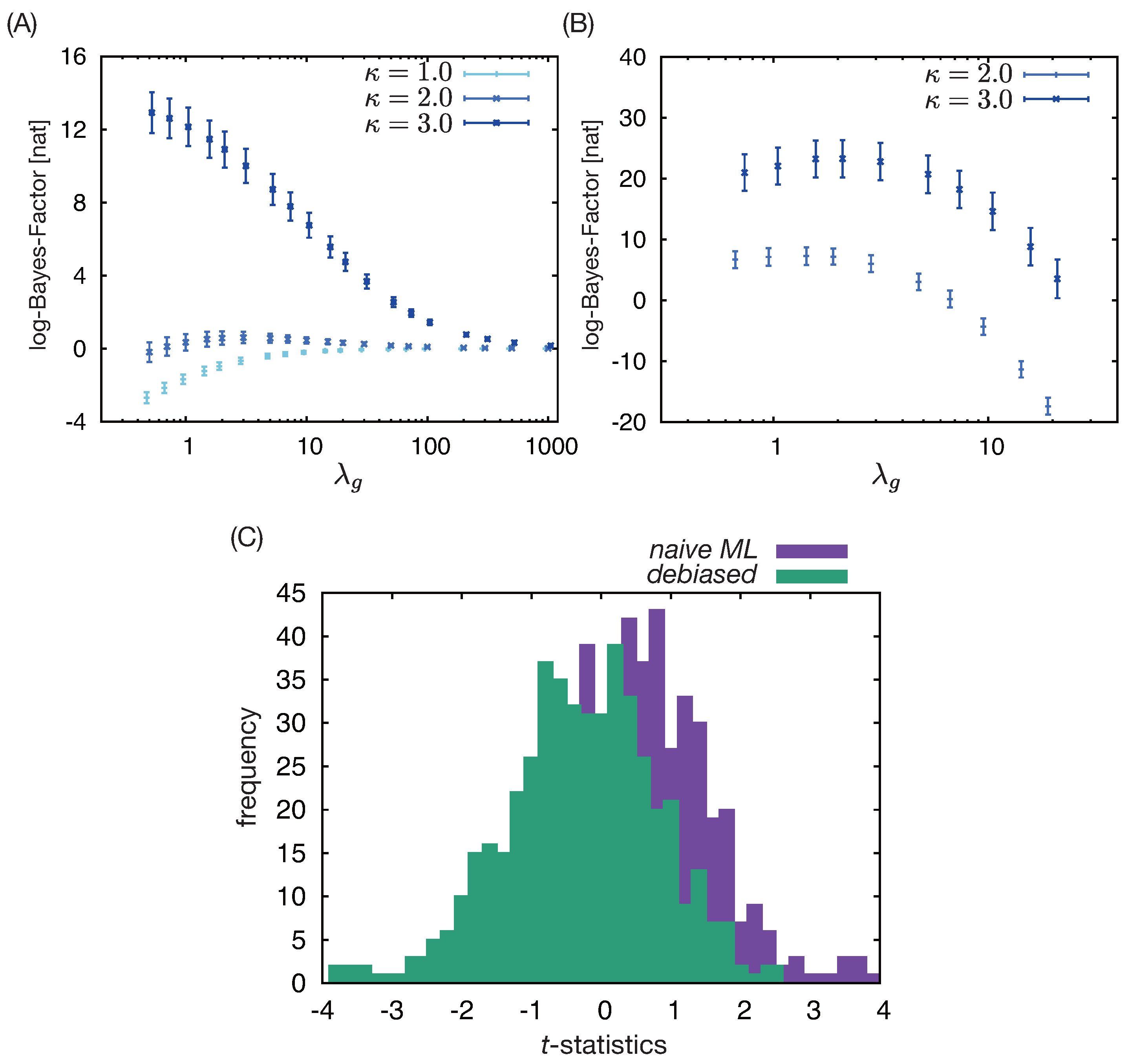
3.2. Simulation Result 2: Estimation of Treatment Effect in Population with Heterogeneous Risk
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, R.S.; Lin, J.; Roychoudhury, S.; Anderson, K.M.; Hu, T.; Huang, B.; Leon, L.F.; Liao, J.J.; Liu, R.; Luo, X.; et al. Alternative Analysis Methods for Time to Event Endpoints Under Nonproportional Hazards: A Comparative Analysis. Statistics in Biopharmaceutical Research 2020, 12, 187–198. [Google Scholar] [CrossRef]
- Bartlett, J.W.; Morris, T.P.; Stensrud, M.J.; Daniel, R.M.; Vansteelandt, S.K.; Burman, C.F. The Hazards of Period Specific and Weighted Hazard Ratios. Statistics in Biopharmaceutical Research 2020, 12, 518–519. [Google Scholar] [CrossRef] [PubMed]
- Hernán, M.A. The Hazards of Hazard Ratios. Epidemiology 2010, 21. [Google Scholar] [CrossRef] [PubMed]
- Aalen, O.O.; Cook, R.J.; Røysland, K. Does Cox analysis of a randomized survival study yield a causal treatment effect? Lifetime Data Analysis 2015, 21, 579–593. [Google Scholar] [CrossRef] [PubMed]
- Martinussen, T.; Vansteelandt, S.; Andersen, P.K. Subtleties in the interpretation of hazard contrasts. Lifetime Data Analysis 2020, 26, 833–855. [Google Scholar] [CrossRef]
- Martinussen, T. Causality and the Cox Regression Model. Annual Review of Statistics and Its Application 2022, 9, 249–259. [Google Scholar] [CrossRef]
- Prentice, R.L.; Aragaki, A.K. Intention-to-treat comparisons in randomized trials. Statistical Science 2022, 37, 380–393. [Google Scholar] [CrossRef]
- Ying, A.; Xu, R. On Defense of the Hazard Ratio, 2023. 2023; arXiv:math.ST/2307.11971].
- Fay, M.P.; Li, F. Causal interpretation of the hazard ratio in randomized clinical trials. Clinical Trials 2024, 21, 623–635. [Google Scholar] [CrossRef] [PubMed]
- Rufibach, K. Treatment effect quantification for time-to-event endpoints–Estimands, analysis strategies, and beyond. Pharmaceutical Statistics 2019, 18, 145–165. [Google Scholar] [CrossRef]
- Kloecker, D.E.; Davies, M.J.; Khunti, K.; Zaccardi, F. Uses and Limitations of the Restricted Mean Survival Time: Illustrative Examples From Cardiovascular Outcomes and Mortality Trials in Type 2 Diabetes. Annals of Internal Medicine 2020, 172, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Snapinn, S.; Jiang, Q.; Ke, C. Treatment effect measures under nonproportional hazards. Pharmaceutical Statistics 2023, 22, 181–193. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Kosorok, M.R.; Sverdrup, E.; Wager, S.; Zhu, R. Estimating heterogeneous treatment effects with right-censored data via causal survival forests. Journal of the Royal Statistical Society Series B: Statistical Methodology 2023, 85, 179–211. [Google Scholar] [CrossRef]
- Xu, S.; Cobzaru, R.; Finkelstein, S.N.; Welsch, R.E.; Ng, K.; Shahn, Z. Estimating Heterogeneous Treatment Effects on Survival Outcomes Using Counterfactual Censoring Unbiased Transformations. 2024; arXiv:stat.ME/2401.11263]. [Google Scholar]
- Frauen, D.; Schröder, M.; Hess, K.; Feuerriegel, S. Orthogonal Survival Learners for Estimating Heterogeneous Treatment Effects from Time-to-Event Data. 2025; arXiv:cs.LG/2505.13072]. [Google Scholar]
- Kennedy, E.H. , H.; Wu, P.; Chen, D.G.D., Eds.; Springer International Publishing: Cham, 2016; pp. 141–167. https://doi.org/10.1007/978-3-319-41259-7_8.Inference. In Statistical Causal Inferences and Their Applications in Public Health Research; He, H., Wu, P., Chen, D.G.D., Eds.; Springer International Publishing: Cham, 2016; Springer International Publishing: Cham, 2016; pp. 141–167. [Google Scholar] [CrossRef]
- Leviton, A.; Loddenkemper, T. Design, implementation, and inferential issues associated with clinical trials that rely on data in electronic medical records: a narrative review. BMC Medical Research Methodology 2023, 23, 271. [Google Scholar] [CrossRef]
- Hernán, M.A.; Brumback, B.; Robins, J.M. Marginal Structural Models to Estimate the Joint Causal Effect of Nonrandomized Treatments. Journal of the American Statistical Association 2001, 96, 440–448. [Google Scholar] [CrossRef]
- Van der Laan, M.J.; Rose, S. Targeted learning in data science; Springer, 2018.
- Chernozhukov, V.; Chetverikov, D.; Demirer, M.; Duflo, E.; Hansen, C.; Newey, W.; Robins, J. Double/debiased machine learning for treatment and structural parameters. The Econometrics Journal 2018, 21, C1–C68. [Google Scholar] [CrossRef]
- Ahrens, A.; Chernozhukov, V.; Hansen, C.; Kozbur, D.; Schaffer, M.; Wiemann, T. An Introduction to Double/Debiased Machine Learning. 2025; arXiv:econ.EM/2504.08324]. [Google Scholar]
- Ren, J.J.; Zhou, M. Full likelihood inferences in the Cox model: an empirical likelihood approach. Annals of the Institute of Statistical Mathematics 2011, 63, 1005–1018. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern recognition and machine learning; Vol. 4, Springer, 2006.
- van der Laan, M.J.; Petersen, M.L.; Joffe, M.M. History-adjusted marginal structural models and statically-optimal dynamic treatment regimens. The International Journal of Biostatistics 2005, 1. [Google Scholar] [CrossRef]
- Hille, E.; Phillips, R.S. Functional Analysis and Semi-Groups, 3rd printing of rev. In ed. of 1957. In Proceedings of the Colloq. Publ, Vol. 31. 1974. [Google Scholar]
- Lanckriet, G.R.; Cristianini, N.; Bartlett, P.; Ghaoui, L.E.; Jordan, M.I. Learning the kernel matrix with semidefinite programming. Journal of Machine Learning Research 2004, 5, 27–72. [Google Scholar]
- Bach, F.R. Consistency of the group lasso and multiple kernel learning. Journal of Machine Learning Research 2008, 9. [Google Scholar]
- Meier, L.; Van de Geer, S.; Bühlmann, P. High-dimensional additive modeling. The Annals of Statistics 2009, 37, 3779–3821. [Google Scholar] [CrossRef]
- Koltchinskii, V.; Yuan, M. Sparsity in multiple kernel learning. The Annals of Statistics 2010, 38, 3660–3695. [Google Scholar] [CrossRef]
- Suzuki, T.; Sugiyama, M. Fast learning rate of multiple kernel learning: Trade-off between sparsity and smoothness. The Annals of Statistics 2013, 41, 1381–1405. [Google Scholar] [CrossRef]
- Bach, F.; Jordan, M. Kernel independent component analysis. Journal of Machine Learning Research 2003. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Mathematical Programming 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian processes for machine learning; Vol. 2, MIT press Cambridge, MA, 2006.
- Berlinet, A.; Thomas-Agnan, C. Reproducing kernel Hilbert spaces in probability and statistics; Springer Science & Business Media, 2011.
- Cox, D.R. Regression Models and Life-Tables. Journal of the Royal Statistical Society: Series B (Methodological) 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Efron, B. The Efficiency of Cox’s Likelihood Function for Censored Data. Journal of the American Statistical Association 1977, 72, 557–565. [Google Scholar] [CrossRef]
- Oakes, D. The Asymptotic Information in Censored Survival Data. Biometrika 1977, 64, 441–448. [Google Scholar] [CrossRef]
- Thackham, M.; Ma, J. On maximum likelihood estimation of the semi-parametric Cox model with time-varying covariates. Journal of Applied Statistics 2020, 47, 1511–1528. [Google Scholar] [CrossRef]
- Luo, J.; Rava, D.; Bradic, J.; Xu, R. Doubly robust estimation under a possibly misspecified marginal structural Cox model. Biometrika 2024, 112, asae065. [Google Scholar] [CrossRef]
- Zhang, Z.; Stringer, A.; Brown, P.; Stafford, J. Bayesian inference for Cox proportional hazard models with partial likelihoods, nonlinear covariate effects and correlated observations. Statistical Methods in Medical Research 2023, 32, 165–180. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Heritier, S.; Lô, S.N. On the maximum penalized likelihood approach for proportional hazard models with right censored survival data. Computational Statistics and Data Analysis 2014, 74, 142–156. [Google Scholar] [CrossRef]
- Imai, K.; Van Dyk, D.A. Causal inference with general treatment regimes: Generalizing the propensity score. Journal of the American Statistical Association 2004, 99, 854–866. [Google Scholar] [CrossRef]
- Hu, B.; Nan, B. Conditional distribution function estimation using neural networks for censored and uncensored data. Journal of Machine Learning Research 2023, 24, 1–26. [Google Scholar]
- Kostic, V.; Pacreau, G.; Turri, G.; Novelli, P.; Lounici, K.; Pontil, M. Neural conditional probability for uncertainty quantification. Advances in Neural Information Processing Systems 2024, 37, 60999–61039. [Google Scholar]
- Allman, E.S.; Matias, C.; Rhodes, J.A. Identifiability of parameters in latent structure models with many observed variables 2009.
- Allman, E.S.; Rhodes, J.A.; Stanghellini, E.; Valtorta, M. Parameter identifiability of discrete Bayesian networks with hidden variables. Journal of Causal Inference 2015, 3, 189–205. [Google Scholar] [CrossRef]
- Gassiat, E.; Cleynen, A.; Robin, S. Inference in finite state space non parametric Hidden Markov Models and applications. Statistics and Computing 2016, 26, 61–71. [Google Scholar] [CrossRef]
- Gassiat, E.; Rousseau, J. Nonparametric finite translation hidden Markov models and extensions. Bernoulli 2016, 22, 193–212. [Google Scholar] [CrossRef]
- Wieland, F.G.; Hauber, A.L.; Rosenblatt, M.; Tönsing, C.; Timmer, J. On structural and practical identifiability. Current Opinion in Systems Biology 2021, 25, 60–69. [Google Scholar] [CrossRef]
- Watanabe, S. Algebraic geometry and statistical learning theory; Vol. 25, Cambridge university press, 2009.
- Calderhead, B.; Girolami, M. Estimating Bayes factors via thermodynamic integration and population MCMC. Computational Statistics and Data Analysis 2009, 53, 4028–4045. [Google Scholar] [CrossRef]
- Watanabe, S. A widely applicable Bayesian information criterion. Journal of Machine Learning Research 2013, 14, 867–897. [Google Scholar]
- Drton, M.; Plummer, M. A Bayesian Information Criterion for Singular Models. Journal of the Royal Statistical Society Series B: Statistical Methodology 2017, 79, 323–380. [Google Scholar] [CrossRef]
- Moral, P. Feynman-Kac formulae: genealogical and interacting particle systems with applications; Springer, 2004.
- Chopin, N.; Papaspiliopoulos, O.; et al. An introduction to sequential Monte Carlo; Vol. 4, Springer, 2020.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




