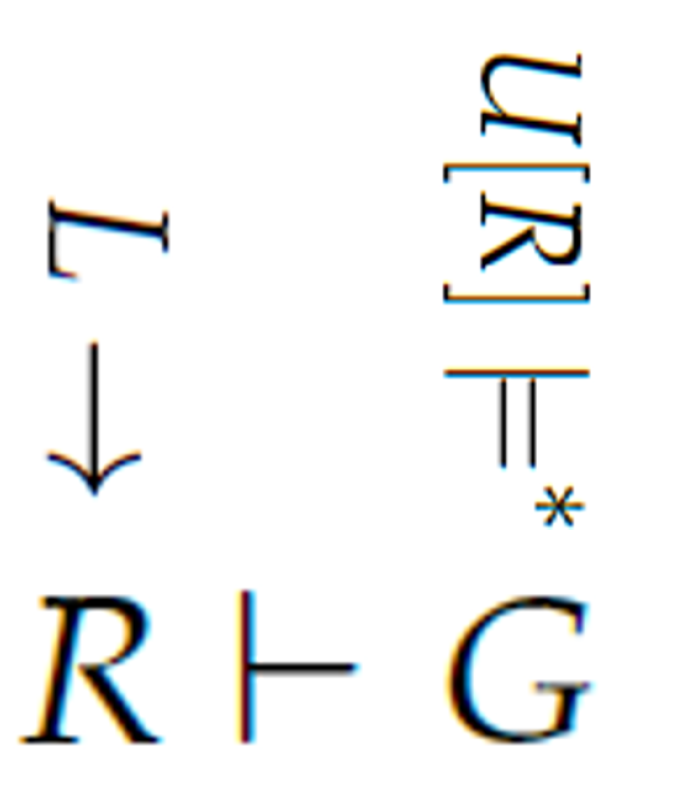A Multimodal AI System: Comparing LLMs and Theorem Proving Systems

1. Introduction and Motivation

This section introduces the motivation for this paper. It also includes the background that informed our approach to this work.

Neural Tax Networks [1,2] is building a proof-of-technology for a multimodal AI system. The first modality is based on automated theorem-proving for first-order logic systems. This is realized by using the logic programming language ErgoAI [3] for proving statements in tax law. The second modality is expected to use LLMs (Large Language Models) in two ways. The initial application of LLMs is to help users input information into the system and understand the system’s output or answer. This application of LLMs is the focus of our comparison of modalities of LLMs and first-order logical theorem-proving systems. The second application of LLMs will target the translation of tax law into ErgoAI code. Both of these applications of LLMs are challenging and have not yet been fully tried and tested.

This paper leverages logical model theory to better understand the limits of applying these two modalities together. Particularly, this paper gives insight into the limits on combining LLMs and theorem proving systems into a single system capable of both reading and analyzing U.S. tax law. We make a key assumption: the LLMs work with an uncountable number of words over all time. We argue this is not an unreasonable assumption since deeper specialization in new areas of the law or new areas of human understanding often requires either the creation of new words or the assignment of new, additional meanings to existing words. These new word meanings differ from previous word meanings. Moreover, (1) LLMs are based on very large amounts of data that is occasionally updated, (2) linguistic models such as Heaps’ law [4] allows partial estimates of the number of unique words in a document based on the document’s size and does not have an explicit bound, and (3) natural language usage by speakers adds new words, or creates additional meanings of words over time, while fewer words fall out of use or represent irrelevant concepts.

We will highlight a special case of the upward Löwenheim–Skolem Theorem that indicates if we have a countable infinite number of word meanings for our system, then we have an uncountable set of word meanings. Alternatively, we can take a limit over all time providing an uncountable number of word meanings over an infinite number of years.

We argue that resolution theorem-proving systems, unlike LLMs, have domains that contain at most a countable number of words and word meanings. Particularly, these words and word meanings are established when the rules and facts are set. In addition, for applications of theorem-proving systems to legal reasoning, the rules are often set with specific word meanings in mind.

A key question we work on is: Suppose a theorem-proving system (such as a system designed to analyze U.S. tax law) does not add any new rules while new word meanings are added to the system’s domain by an LLM. This LLM essentially “feeds” the words represented by LLM tokens into the theorem-proving system. For example, suppose a theorem proving system based on U.S. tax law is required to answer a question input by the user using a word tokenized by the LLM as having a certain meaning but which word is not contained in the text of the tax law that otherwise would apply to the user’s question. In this case, the theorem proving system’s rules would work the same for the original domain (i.e., the domain of words contained in the tax law when it was enacted) while being required to deal with the new words that are tokenized from an LLM. To address this in our analysis we assume an uncountable domain of word meanings, a subset of which may be supplied to the theorem-proving system by the LLMs.

A novel application of the Löwenheim–Skolem (L-S) Theorems and elementary logical model equivalence, see Theorems 8 and 7, indicates that the same rules of the theorem proving system can still work even when an uncountable number of word meanings are in the theorem-proving system’s domain. Another view is from the Lefschetz Principle of first-order logic [5]. This indicates the same first-order logic sentences can be true given specific models with different cardinalities. For instance, one model may have cardinality ${\aleph }_0$ and another may have cardinality ${\aleph }_1$.

1.1. Technical Background

ChatGPT was the first publicly available LLM. ChatGPT and many other similar models are based on [6]. Surveys of LLMs include [7,8].

This paper seeks insight on multimodal AI systems based on the foundations of computing and mathematics. To do so we analyze the effects of the combination of a first-order logic theorem proving system with LLMs.

LLMs have been augmented with logical reasoning [9]. Our work uses logical reasoning systems to augment LLMs. There has also been work on the formalization of AI based on the foundations of computing. For example, standard notions of learnability can neither be proven nor disproven [10]. This result leverages foundations of machine learning and a classical result of the independence of the continuum hypothesis. The Turing test can be viewed as version of an interactive proof system brining the Turing test to key foundations of computational complexity [11].

1.2. Technical Approach

The domain of an LLM is the specific area of knowledge or expertise that the model is focused on. It’s essentially the context in which the LLM is trained and applied. Thus it determines the types of tasks it can perform and the kind of information it can process and generate.

Applying LLMs are in the next phase of our proof-of-technology. We already have basic theorem proving working in ErgoAI with several tax rules. It is the practical combination of these modalities that will allow complex questions to be precisely answered. Ideally, given the capabilities of LLMs, the users will be able to easily work with the system.

Many theorem proving systems supply answers with explanations. In our case, these explanations are proofs from the logic-programming system ErgoAI. Of course, the Neural Tax Networks system assumes all facts entered by a user are true.

ErgoAI is an advanced multi-paradigm logic-programming system by Coherent Knowledge LLC [3,12]. It is Prolog-based and includes non-monotonic logics, among other advanced logics and features. For instance, ErgoAI supports defeasible reasoning. Defeasible reasoning allows a logical conclusion to be defeated by new information. This is sometimes how law is interpreted: If a new law is passed, then any older conclusions that the new law contradicts are dis-allowed.

The idea that proofs are syntactic and model theory is semantic goes back to, at least, the start of logical model theory. Of course, the semantics of model theory or LLMs may not align with the linguistic or philosophical semantics of language.

Table 1. List of symbols and their definitions

Symbol	Definition
$R_t$	Root of a proof tree
$G=<N,\Sigma ,P,S>$	A context-free grammar
${\aleph }_0$	Countable infinite cardinality
${\aleph }_1$	Uncountable infinite cardinality
${\mathcal{M}}_{orig}$	Logical model of first-order theorem-proving system with originalism
${\mathcal{N}}_{llm}$	Logical model of LLMs
$\mathbb{N}$	The set of natural numbers $\{1,2,\dots \}$
$\mathbb{Q}$	Field of rational numbers
$\overline{\mathbb{Q}}$	Field of all solutions to polynomial quations with coefficients from $\mathbb{Q}$
$\mathbb{R}$	The set of real numbers
$\mathbb{C}$	The set of complex numbers

Table 1. List of symbols and their definitions

Symbol	Definition
$R_t$	Root of a proof tree
$G=<N,\Sigma ,P,S>$	A context-free grammar
${\aleph }_0$	Countable infinite cardinality
${\aleph }_1$	Uncountable infinite cardinality
${\mathcal{M}}_{orig}$	Logical model of first-order theorem-proving system with originalism
${\mathcal{N}}_{llm}$	Logical model of LLMs
$\mathbb{N}$	The set of natural numbers $\{1,2,\dots \}$
$\mathbb{Q}$	Field of rational numbers
$\overline{\mathbb{Q}}$	Field of all solutions to polynomial quations with coefficients from $\mathbb{Q}$
$\mathbb{R}$	The set of real numbers
$\mathbb{C}$	The set of complex numbers

1.3. Structure of This Paper

Section 2 discusses select previous work on multimodality and the law. It briefly reviews expert systems and approaches where LLMs can perform some level of legal reasoning. Section 3 gives a logic background illustrated by select ErgoAI statements. This section shows ErgoAI or Prolog have at most a countably infinite number of atoms that may be substituted for variables. We argue each of these atoms has a finite number of meanings. Section 4 introduces logical model theory and gives a high-level view of how our system works. Section 5 discusses the upward and downward Löwenheim-Skolem theorems as well as elementary equivalence from logical model theory. We give results based on these foundations to show (1) LLMs have uncountable models under certain circumstances, and (2) Models of both LLMs and the first-order logic theorem proving systems cannot be distinguished by first-order logic expressions.

2. Multimodality and the Law

This section reviews work relevant to automated legal reasoning.

2.1. Expert Systems

This subsection gives background of expert systems and programming languages for the law.

Expert systems simulate the decision-making and reasoning of human experts. These systems use a knowledge base with domain specific information and rules. The knowledge base, domain specific information, and rules help these systems solve complex problems.

A legal expert system is an expert system that uses artificial intelligence for legal reasoning. These AI systems mimic human experts in the law. They can offer guidance on specific legal issues or tasks. These systems can help lawyers, legal professionals, or the public navigate legal processes, understand legal concepts, and complete legal forms. On one hand, several papers have been published discussing the limitations of expert systems when applied to the law [13,14,15]. On the other hand, several LLM-based legal expert systems are now on the market. See for example [16]. Work is also occuring to develop programming languages specifically designed for the law. ErgoAI, developed by Coherent Knowledge LLC, is one example of a programming language that can be easily applied to legal reasoning for expert systems. Another is Catala, a programming language designed specifically for programming law [17]. Its initial focus was on US and French law and it targets the construction of legal reasoning or expert systems.

2.2. Knowledge, Rule Bases and Inference Engines

This subsection highlights details of legal expert systems. It also discusses the importance of explainability for legal arguments.

For tax law expert systems, the knowledge base is usually derived from statues enacted by legislatures. Statutes are essentially legal rules written in precise natural language. In the USA, regulations and clarifications are added by the U.S. Treasury Department and comparable state and local institutions. Rulings on the application of law to specific facts are given in case law and, occasionally, in private letter rulings issued by the U.S. Treasury Department. These cases and rulings are opinions governing how the language of statutes is to be interpreted and applied. Case law and governmental rulings are written in natural language.

An expert system’s inference engine applies the system’s rules and facts to the facts provided by the user to produce conclusions. Ideally, in the case of a tax law expert system the conclusions reached by the system are the same as those which would be reached by a court or administrative body that considered the same question. Those conclusions are based on the facts of a particular situation. These facts are provided to the system and are intended to be the same facts that would be provided to a court or a government regulator if a court or regulator were to consider the same set of facts and the same question. The objective, in our case, is to derive percise conclusions that are provably accurate from the given facts.

An important requirement for the tax law system is full explainability: the answer to a query should contain the entire formal proof that leads to the conclusion. As this allows the user to understand, and have confidence, in the conclusion to an extent not possible with systems that rely solely on LLM technology.

2.3. LLMs and Other Approaches to Legal Reasoning

This subsection discusses applying LLMs to legal reasoning. Particularly, it briefly touches on methods that augment LLMs to help justify legal arguments.

Large language models can be used to answer tax questions, but the responses they provide may be inaccurate. Even so, there are many applications of AI and LLMs to the law. These legal applications include decision support systems, legal document analysis, and litigation risk assessment [18].

LLMs often struggle with logical reasonings tasks. This is not surprising because LLMs are essentially artificial neural networks trained on huge corpora of data to generate answers to natural language queries. Empirical distributions or probability play roles in LLM training. LLMs alone do not give any reasoning to justify their conclusions. Explainability for LLMs often requires other methods, or tools, and is often multimodal.

Chain-of-thought (CoT) prompting [19,20] is a prompt engineering technique designed to improve LLMs’ performance on tasks requiring logic, calculation, and decision-making. CoT prompting does this by structuring the input prompt to mimic human reasoning. To construct a CoT prompt, insert something like “Describe your reasoning in steps” or “Explain your answer step by step” to an LLM query. In essence, this prompting technique asks the LLM both generate a result and also to provide detailed steps it used to arrive at the result.

CoT prompting can give reasoning from LLMs for simple logical reasoning tasks. These tasks may require a few reasoning steps. However, CoT often fails in complex logical reasoning tasks. CoT prompting may not provide explicit proofs. To address this weakness of CoT prompting, several neurosymbolic approaches use LLMs with theorem proving systems on complex logical reasoning tasks [21,22] .

Symbolic Chain-of-Thought (SymbCoT) also uses multimodality to handle the logical reasoning combined with LLMs [19]. Such LLM-based frameworks integrate symbolic expressions and logic rules with CoT prompting. This is because CoT’s reliance on natural language is insufficient for precise logical calculations. SymbCoT works to overcome this by using LLMs to translate natural language queries into symbolic formats, create reasoning plans, and verify their accuracy. This multimodal combination of symbolic logic and natural language processing works so LLMs answers are more logically explainable.

Multimodal approaches typically have the steps: (1) translation (e.g., using LLMs) from a natural language statement to a logical reasoning problem as a set of first-order logic formulas, (2) planning and execution the reasoning steps by a symbolic solver or a theorem-proving system to answer the logical reasoning problem, and (3) translation (e.g., using LLMs) of the solution of the logical reasoning problem, from the last step, back to natural language.

Another approach is to use directly explainable AI techniques for LLMs. For instance, Shapley values or Integrated Gradients may compute attributions of features impacting results of AI. For an NLP application see [23]. The Shapley values method is implemented in the shap Python library [24]. This library is integrated with gradient methods and implemented in Tensorflow [25] and Captum [26]. Other discussions of explainability in AI include

[27,28,29].

2.4. Tax Preparation Systems

This subsection gives highlights of some tax preparation systems.

There are several commercial tax preparation software systems. These systems do not provide proofs of their conclusions. Rather they are highly structured in their data entry. These systems focus on filling out tax forms.

LLMs are directly used to analyze taxes [30]. There are some systems that offer multimodal combinations of LLMs and logical proof systems. See for example [31].

3. First-Order Logic Systems

This section reviews first-order logic. It discusses aspects of legal reasoning as it may be implemented in ErgoAI.

First-order logic expressions have logical connectives $\wedge ,\vee$ and a unary symbol ¬. They also have variables and quantifiers $\forall ,\exists$. These quantifiers only apply to the variables. We also discuss functions and predicates in first-order logic. It is the variables, functions, and predicates that differentiates first-order logic from more basic logics. Functions and predicates represent relationships. The logical connectives, functions, and predicates all can apply to the variables. We assume all logic expressions are well-formed, finite, and in first-order logic.

Proofs are syntactic structures. A proof of a logic formula may be concisely expressed as a directed acyclic graph. First-order logic proofs can be laid out as trees. If the proof’s goal is to establish an expression $R_t$ is provable, then the proof tree has $R_t$ as its root. The vertices of a proof graph are facts, axioms, and expressions. The directed edges connect nodes by an application of an inference rule. The inference rule for Prolog-like theorem proving systems is generally selective linear definite clause resolution. To apply such inference rules may require substitution or unification. If a logical formula is provable, then finding a proof often reduces to trial and error or exhaustive search.

ErgoAI has frame-based syntax which adds structure and includes object oriented features. The ErgoAI or Prolog expression H:-B is a rule. This rule indicates that if the body B is true then conclude the head H is true.

Listing  is an ErgoAI rule for determining if an expenditure is a deduction. The notation ?X is that of a variable. In Listing , ?X is an expenditure that has Boolean typed properties ordinary, necessary, and forBusiness.

Listing 1. A rule in ErgoAI in frame-based syntax

?X:Deduction :-     ?X:Expenditure,     ?X[ordinary => \boolean],     ?X[necessary => \boolean],     ?X[forBusiness => \boolean].

The rule in Listing  has a body indicating that if there is an ?X that is an expenditure with true properties ordinary, necessary, and forBusiness, then ?X is a deduction. This rule is taken as an axiom.

The ErgoAI code in Listing  has three forBusiness expenses. It also has two donations that are not forBusiness. Since these two donations are not explicitly forBusiness, by negation-as-failure ErgoAI and Prolog systems assume they are not forBusiness. The facts are the first five lines. There is a rule on the last line. Together the facts and rules form the database of axioms for an ErgoAI frame-based program.

Listing 2. Axioms in ErgoAI in frame-based syntax

employeeCompensation:forBusiness. rent:forBusiness. robot:forBusiness. foodbank:donation. politicalParty:donation.   ?X:liability :- ?X:forBusiness.

A program in the form of a query of the database in Listing  is in Listing . This listing shows three matches for the variable ?X.

Listing 3. A program in ErgoAI in frame-based syntax.

ErgoAI> ?X:forBusiness.   >> employeeCompensation >> rent >> robot

Hence an ErgoAI system can prove employeeCompensation, rent, and robot all are forBusiness. We can also query the liabilities which gives the same output as the bottom three lines of Listing .

It is interesting that some modern principles of tax law are not all that different from ancient principles of tax law. The principles under-pinning tax law evolve slowly. Certain current tax principles are analogous to some in the Roman Empire in the last 1,900+ years [32,33]. While the meaning of words evolves, ideally the semantics of tax law remains the same over time. Modern tax law is of course much more complex than ancient tax law, in large part because both commercial laws and bookkeeping have improved and become more complex (and more precise) than in ancient times. Modern tax law has both evolved as financial transactions have evolved and has even allowed the creation of more complex financial transactions.

Under the legal theory of Originalism, the words in the tax law should be given the meaning those words had at the time the law was enacted. Scalia and Garner’s book is on how to interpret written laws ([34], p 78). For example, they say,

“Words change meaning over time, and often in unpredictable ways.”

Assumption A1

(Originalism). A law should be interpreted based on the meaning of its words when the law was enacted.

Of course, tax law can be changed quickly by a legislature. Assuming originalism, the meaning of the words in the newly changed laws, when the new laws are enacted, is the basis of understanding these new laws.

Specifying the meanings of words in natural language uses natural language. Specifying meanings or words for theorem-proving systems uses variables that are expressed as atoms. The syntax of variables in most programming languages are specified by regular expressions. Variables can be specified or grouped together using context-free grammars. The same is true for the syntax of atoms in ErgoAI or Prolog. An atom is an identifier that represents a constant, a string, name or value. Atoms are alphbetic characters provided the first character is lower-case or the under-score. Atoms can name predicates, but the focus here is on atoms representing items that are be substituted for variables in first-order expressions.

In tax law, some of the inputs may be parenthesized expressions. For example, some amounts owed to the government are compounded quarterly based on the “applicable federal rate” published by the U.S. Treasury Department. Such an expression may be best written as a parenthesized expression. So, the text of all unique words or inputs for the tax statutes are a subset of certain context free grammars. A context-free grammar can represent paranthesized expressions and atoms in ErgoAI.

Definition 1 (Context-free grammar  (CFG)).A context-free grammar is a 4-tuple G so that $G=<N,\Sigma ,P,S>$ where N is a set of non-terminal variables, Σ is a set of terminals or fixed symbols, P is a set of production rules so $p\in P$ is such that $p:A\Rightarrow \alpha$ where $A\in N$ and $\alpha \in {(N\cup \Sigma )}^{*}$, and $S\in N$ is the start symbol.

The language generated by a context-free grammar is all strings of terminals that are generated by the production rules of a CFG. The number of strings in a language generated by CFGs is at most countably infinite.

Definition 2

(Countable and uncountable numbers). If all elements of any set T of can be counted by some or all of the natural numbers $\mathbb{N}$, then T has cardinality $\left|T\right|\le {\aleph }_0$. Equality holds when there is a bijection between each element of the set T and a non-finite subset of $\mathbb{N}$.

The real numbers $\mathbb{R}$ have cardinality $\left|\mathbb{R}\right|={\aleph }_1$ which is uncountable.

There is a rich set of extensions and results beyond Definition 2, see for example [35,36,37,38]. The next theorem is classical. In our case, this result is useful for applications of the Löwenheim–Skolem (L-S) Theorems. See Theorem 8.

Theorem 1

(Domains from context free grammars). A context free grammar can generate a language of size ${\aleph }_0$.

Proof. 

Consider a context-free grammar $G=(N,\Sigma ,P,S)$ made of a set of non-terminals N, a set of terminals $\Sigma =\{0,1,2,\dots ,9\}$, a set of productions P, and the start symbol S. Let $ϵ\notin \Sigma$, be the empty symbol.

The productions P of interest are:

$$\begin{array}{ccc}\hfill L& ⟹& 0\left|1\right|\dots |9\hfill \\ \hfill L& ⟹& ϵ\hfill \\ \hfill S& ⟹& L|LS\hfill \end{array}$$

Starting from S, the set of all strings of terminals w that can be derived from P is written as,

$$\begin{array}{ccc}\hfill S& \stackrel{*}{⟹}& w.\hfill \end{array}$$

So, the CFG G can generate all strings representing the natural numbers $\mathbb{N}$. All natural numbers form a countably infinite set, completing the proof.    □

The proof of Theorem 1 uses a CFG that generates the language of all integers in $\mathbb{N}$. Each individual word in the domain of all words used in the law can be uniquely numbered by an integer in $\mathbb{N}$. Separately, any numerical values required by computing taxes can also be represented using integers and paranthesized expressions.

Listing  can be expressed in terms of provability. In this regard, consider Listing .

Listing 4. Applying a rule or axiom in pseudo-ErgoAI as a proof

?X:Expenditure ∧?X[ordinary -> \true] ∧ ?X[necessary -> \true] ∧ ?X[forBusiness -> \true] ⊢  ?X:Deduction

So, if there is an ?X that is an expenditure, and it is ordinary, necessary, and forBusiess, then this is accepted as a proof that ?X is a deduction. This is because rules and facts are axioms. So, if the first four lines of the rule in Listing are satisfied, then we have a proof that ?X is a Deduction.

The statement $⊢E$ indicates that E is provable in the logical system at hand. That is, E is a tautology. A tautology is a formula that is always true. For example, given a Boolean variable $X=?X:forBusiness$, then

$$\begin{array}{ccc}\hfill E& =& X\vee \neg X\hfill \end{array}$$

must always be true so it is a tautology. The formula $\neg E=\neg X\wedge X$ is a contradiction. Contradictions are always false.

Consider a formula E and a set of formulas F in the same logical system. If from the formulas in F, axioms made of the facts and rules of the system, and one or more inference rules, then we can prove E, we write $F⊢E$. In other words, from F can we prove E given the database of rules and facts of the sytem an one or more inference rules.

Also, consider a first-order logical system. Suppose E is formula of this system. A formula may have free variables. A free variable is not bound or restricted.

Adding quantification, $Qx\in I,E$ where E is a first-order formula, then this means $\forall x\in I,E$ if $Q=\forall$ or $\exists x\in I,E$ if $Q=\exists$. If a variable is quantified it is not a free variable. Quantification is important to express laws as logic. Theorem proving languages such as ErgoAI or Prolog default to $\forall x$ for any free variable x.

Definition 3

(Logical symbols of a first-order language [37]). The logical symbols of a first-order language are,

(1)

variables $x_1,x_2,\dots$

(2)

logic connectives $\neg ,\vee ,\wedge$

(3)

quantifiers $\exists ,\forall$

(4)

scoping (, ) or [] or such-that :

(5)

equality =

Definition 4

($\mathcal{L}$-language). If $\mathcal{L}=[L,D,\sigma ]$, then this is a first-order $\mathcal{L}$-language where L is the set of logical symbols and connectives, D is the domain, and σ is the signature of the system which is its constants, predicates, and functions.

The signature $\sigma$ of a logical system is the set of all non-logical symbols and operators of a first-order language [37].

A formula f is an expression made from an $\mathcal{L}$-language and we write $f\in \mathcal{L}$. A formula f has no free-variables if each variable in f is quantified by one of ∀ or ∃.

Definition 5

(Sentence). Consider a first-order logic language $\mathcal{L}$ and a formula $f\in \mathcal{L}$. If f has no free variables, then f is a sentence.

An interpretation defines a domain and semantics to functions and predicates for formulas or sentences. An interpretation that makes a formula E true is a model. Given an interpretation, a formula may not be either true or false if the formula has free variables.

Definition 6

(First-order logic interpretation [37]). Consider a first-order logic language $\mathcal{L}=[L,D,\sigma ]$ and a set I. The set I is an interpretation of $\mathcal{L}$ iff the following holds:

• There is a interpretation domain $D_I$ made from the elements in I
• If there is a constant $d\in D$, then it maps uniquely to an element $d_I\in D_I$
• If there is a function symbol $f\in \sigma$ where f takes n arguments, then there is a unique $F_i\in D_I$ where $F_i$ is an n-ary function.
• If there is a predicate symbol $r\in \sigma$ where r takes n arguments, then there is a unique n-ary predicate $R_i\in D_I$.

An interpretation I of a first-order logic language $\mathcal{L}=[L,D,\sigma ]$ includes all of the logical symbols in L. Consider the domain D, signature $\sigma$, and I is an interpretation. The interpretation I can be applied to a sentence. Given any interpretation, then any sentence must be $true$ or $false$.

Definition 7

(Logical model). Consider a first-order $\mathcal{L}$-language $\mathcal{L}=[L,D,\sigma ]$ and an interpretation I of $\mathcal{L}$, then I is a model iff for all $f\in \mathcal{L}$ are so that $F_i\left(I\right)$ is true, where $F_i$ corresponds with f.

Models are denoted $\mathcal{M}$ and $\mathcal{N}$.

The expression $\vDash E$ indicates all interpretations of the system make E true. If an interpretation I in a logical system can express the positive integers $\mathbb{N}=\{1,2,\dots \}$ and the sentence $E=\forall x\in \mathbb{N}[x^2>0]$, then $I\vDash E$ is true. However, if I is updated to include $\left\{0\right\}\cup \mathbb{N}$, then $I\neg \vDash E$.

The expression $I\vDash E$ means we can substitute values from I into E giving $E\left(I\right)$. The sentence $E\left(I\right)$ is true when $I\vDash E$.

Definition 8

(First-order logic definitions). Given any set of first-order logic formulas E and an interpretation I, then E is:

• Validif every interpretation I is so that E is true
• Inconsistent or Unsatisfiableif E is false under all interpretations I
• Consistent or Satisfiableif E is true under at least one interpretation I

The next result is classical, see [36,37].

Theorem 2

(First-order logic is semi-decidable). Consider a set of first-order logic formulas E.

• If E is true, then there is an algorithm that can verify E’s truth in a finite number of steps.
• If E is false, then in the worst case there is no algorithm can verify E’s falsity in a finite number of steps.

Suppose H and C are first-order logic formulas. If H is provable, then it is valid so it satisfies all models.

Theorem 3

(Logical soundness). For any set of first-order logic formulas H and a first-order formula C: If $H⊢C$, then $H\vDash C$.

Gödel’s completeness theorem [37] indicates if a first-order logic formulas is valid, then it is provable. If C satisfies all models H, then C is provable.

Theorem 4

(Logical completeness). For any set of first-order logic formulas H and a first-order logic formula C: If $H\vDash C$, then $H⊢C$.

There are many rules that can be found in tax statutes. Many of these rules are complex. Currently there are about ${10}^6$ word instances in the US Federal tax statutes and about $2\times {10}^6$ word instances in the US Federal case tax law. Of course most of these words are repeated many times.

3.1. Interpretations and Models for Originalism and LLMs

This subsection discusses the interpretation $I_{orig}$ and the model ${\mathcal{M}}_{orig}$. These are used by the remainder of the paper. These interpretations are for first-order theorem-proving systems and LLMs. The focus here is on $I_{orig}$ for ErgoAI.

Theorems 3 and 4 tell us that any first-order sentence that has a valid model can be proved. And symmetrically, any first-order sentence that can be proved has a valid model. These relationships extend to first-order logic in ErgoAI. Recall, all ErgoAI statements are equivalent to first-order sentences. Any ErgoAI statement that has a valid model is provable. Any first-order statement that is provable in ErgoAI has a valid model. Here we sketch a correspondence between ErgoAI statemens and logical interpretations.

The interpretation $I_{orig}$ is for first-order logic programs encoding tax law. Of course, the ideas here can apply to many other areas besides tax law. In any case, the interpretation $I_{orig}$ fixes all word and phrase meanings from when the laws were enacted, see Assumption A1.

• $D_I$ The domain is $D_I=\mathbb{N}\times \mathbb{N}$ where any string can be uniquely represented by its numerical representation, such as characters in UTF-8. All strings in $D_I$ have first element of 1. All integers have a first element of 2.
• Rules A rule $H:-B$ is interpreted as the logic expression $B\Rightarrow H$.
• PredicatesPredicate symbols can be uniquely represented as tuples from $(\mathbb{N}\times \mathbb{N})\times \mathbb{N}$. The first element of a predicate tuple is a 1 indicating the second element represents a string denoting the predicate’s name. The final element is the arity of the predicate.
• Functions Functions are predicates that return elements of the domain. Functions can be built in ErgoAI by having a predicate that returns an element of the domain or by using an if-then-else clause.

An ErgoAI predicate can be expressed as ?D:Refund :- ?D:TaxesOwed, ?D < 0. A facts can be expressed as ?P:NeedTaxAttorney :- true .

All expressions using $I_{orig}$ are sentences. This is because languages, such as ErgoAI or Prolog, assumes universal quantification for any unbound variables.

Unification and negation-as-failure add complexity to first-order logic programming interpretations [43,53]. Handling logic programs database change in first-order logic programming can be done using additional semantics [39].

4. Theorem Proving, Logic Models, and LLMs

This section focuses on logical model theory as it applies to LLMs using logic programming. Logic programming can illustrate logical semantics using the ⊧ symbol. We use first-order logic capabilities of ErgoAI in frame-mode.

If there is an ErgoAI rule or axiom:

$$\begin{array}{ccc}\hfill (?X1,\dots ,?Xn):H& :-& (?X1,\dots ,?Xn):B\hfill \end{array}$$

so that H is the head and B is the body. Where H holds if B is true.

Consider the rule,

$$\begin{array}{ccc}\hfill F(?X)& =& ?X:liability:-?X:forBusiness.\hfill \end{array}$$

(1)

Along with the model,

$$\begin{array}{ccc}\hfill \mathcal{M}& =& \{cloudStorage:forBusiness,virtualMachine:forBusiness\}.\hfill \end{array}$$

Given $\mathcal{M}$ and $F(?X)$, the next statement is true:

$$\begin{array}{ccc}\hfill \mathcal{M}& \vDash & F(?X).\hfill \end{array}$$

That is, the interpretation $\mathcal{M}$ makes $cloudStorage:liability$ and $virtualMachine:liability$ true. Hence $\mathcal{M}$ is a model for $F(?X)$. Alternatively consider,

$${\mathcal{M}}^{\prime }=\{foodbank:donation,politicalParty:donation\},$$

then ${\mathcal{M}}^{\prime }\neg \vDash F(?X)$ is true. This is because there is no ?X so that ?X:forBusiness in $F(?X)$.

In the case of LLMs, words or word fragments are represented by vectors (embeddings) in high-dimensional space. These word or word fragments are tokens. Each feature of a token has a dimension. In many cases there are thousands of dimensions [40]. Similar token vectors have close semantic meanings. This is a central foundation for LLMs [41,42].

The notion of semantics in LLMs is based on the context dependent similarity between token vectors [41]. These similarity measures form an empirical distribution. Over time, such empirical distributions change as the meanings of words evolve. We believe it is reasonable to assume our users will be using the most recent jargon. The most recent jargon may be different from the semantics of the laws when the laws were enacted. See Assumption A1.

In the case of LLMs, we use ${\vDash }^{*}$ to indicate semantics by adding that close word or phrase vectors can be substituted for each other.

Given two word vectors x and y both from the set of all word vectors V and a similarity measure $s:V\times V\to [-1,+1]$. So values close to 1 indicate high similarity and values close to $-1$ indicate vectors whose words have close to the opposite meanings. The function s can be a cosine similarity measure. In any case, suppose there are words $V_x\subseteq V$ where for all $y\in V_x$, then y is similar enough to x so y can be substituted for x given a suitable threshold. We assume similarity measures stringent enough so all $V_x\subseteq V$ are finite. Substitutions can be randomly selected from $V_x$, which may make this AI method seem human-like.

A simplified case for deducting a lunch expense highlights key issues for computing with LLMs. Consider a model

$$\begin{array}{ccc}\hfill \mathcal{M}& =& \left\{salad.ordinary:Expenditure,burger.ordinary:Expenditure\right\}.\hfill \end{array}$$

These terms may be a model for a lunch expenditure. So salad[ordinary -> ] holds. But, a zillion-dollar-frittata, costs about 200 times the cost of a salad or burger. So the zillion-dollar-frittata is not an ordinary expenditure. For example, Listing indicates that the zillion-dollar-frittata property or field ordinary disqualifies it from being deductible. That is, zillion-dollar-frittata[ordinary -> ]. All three of these salad, burger and zillion-dollar-frittata may have some close dimensions, but their cost dimension (feature) is not in alignment.

Definition 9

(Extended logical semantics for LLMs). Consider a first-order logic language $\mathcal{L}=[L,D,\sigma ]$ and a first-order sentence $f\in \mathcal{L}$ with a model $\mathcal{M}$. Then $\mathcal{M}{\vDash }^{*}f$ iff all pairs $\{a,b\}\subset \mathcal{M}$ the similarity $s(a,b)$ is above a suitable threshold.

In Definition 9, since $\mathcal{M}{\vDash }^{*}f$, then given $\mathcal{M}$ the expression f is true.

Definition 10

(Theory for a model). Consider a first-order logic language $\mathcal{L}=[L,D,\sigma ]$ and and a model $\mathcal{M}$ for all sentences in $\mathcal{L}$, then $\mathcal{M}$’s theory is,

$$\begin{array}{ccc}\hfill Th\left(\mathcal{M}\right)& =& \{f\in \mathcal{L}:\mathcal{M}\vDash f\}.\hfill \end{array}$$

Given a model $\mathcal{M}$ of a language $\mathcal{L}$, then the theory $Th\left(\mathcal{M}\right)$ is all true sentences from $\mathcal{L}$. Generating these sentences can be challenging.

Definition 11

(Knowledge Authoring). Consider a set of legal statutes and case-law in natural language L, then finding equivalent first-order rules and facts and putting them all in a set R is expressed as, $L\to R$.

Knowledge authoring is very challenging [44] and this holds true for tax law. We do not have a solution for knowledge authoring of tax law, even using LLMs. Consider the first sentence of US Federal Law defining a business expense [45],

“26 §162 In general - There shall be allowed as a deduction all the ordinary and necessary expenses paid or incurred during the taxable year in carrying on any trade or business, including—”

The full definition, not including references to other sections has many word instances. The semantics of each of the words must be defined in terms of facts and rules. Currently, our proof-of-technology has a basic highly structured user interface that allows a user to enter facts. The proof-of-technology also builds simple queries with the facts. Currently, this is done using our rather standard user interface. Our system has a client-server cloud-based architecture where the proofs are computed by ErgoAI on our backend. A tax situation is entered by a user through the front end. A tax question is expressed by facts. We also add queries, as functions or predicates, based on the user input. The proofs are presented on the front end of our system.

Our goal is to have users enter their questions in a structured subset of natural language with the help of an LLM-based software bot. The user input is the set of natural language expressions U. The logic axioms based on the statues and regulations is the set R. An LLM will help translate these natural language statements U into ErgoAI facts and queries that are compatible with the logic rules and facts R in ErgoAI. Accurate translations of natural language statements into ErgoAI is challenging. We do not yet have an automated way to translate from user entered natural language tax questions into ErgoAI facts and queries. However, Coherent Knowledge LLC has recently announced a product, ErgoText, that may help with this step [46].

Definition 12

(Determining facts for R). Consider a natural language tax query U and its translation into both facts and a query into the expression G that is compatible with the ErgoAI rules R, then $U\left[R\right]{\vDash }^{*}G$.

Using LLMs, Definition 12 depends on natural language word similarity. The words and phrases in user queries must be mapped to a query and facts in our ErgoAI rules R so ErgoAI can work to derive a result.

Definition 11 and Definition 12 can be combined to give the next definition.

Definition 13.

Consider the ErgoAI rules and facts R representing the tax law and the ErgoAI user tax question as a queries and facts $U\left[R\right]$. The query and facts are written as sentences in G where $U\left[R\right]{\vDash }^{*}G$ since they must be compatible with the rules R. The sentences G must be built from $U\left[R\right]$ for R’s theory. Now a theorem prover such as ErgoAI can determine whether, $R⊢G$.

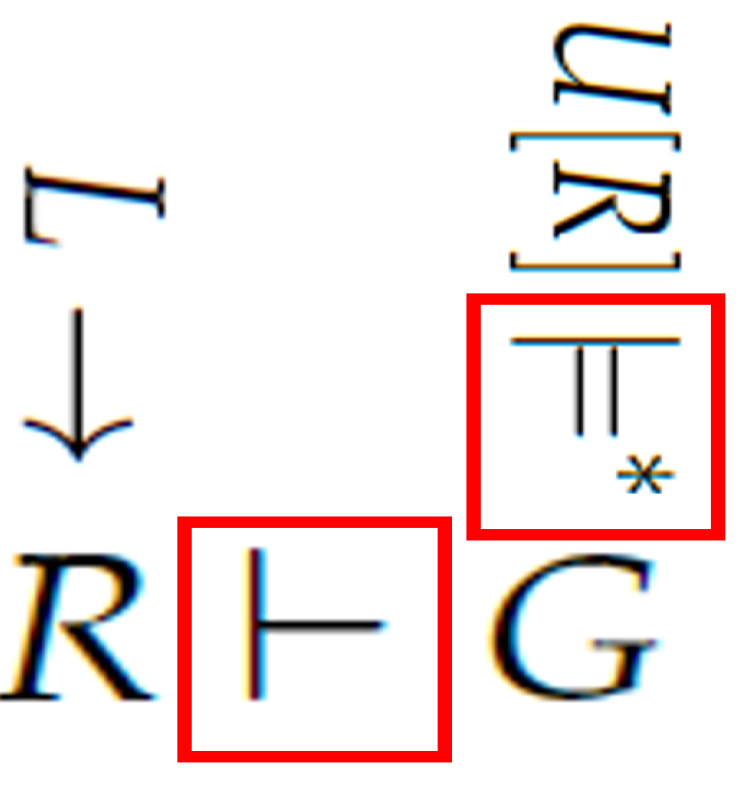
Figure 1 shows our vision of the Neural Tax Networks system. Currently, we are not doing the LLM translations automatically.

This figure depicts knowledge authoring as $L\to R$. Since L is the natural language laws, they are based on the semantics of when the said laws were enacted by Assumption A1. Next, a natural language query U, with its facts, is converted into first-order sentences G which are compatible with R as $U\left[R\right]{\vDash }^{*}G$. Particularly, after computing $U\left[R\right]$ then G is computed so that the expression $U\left[R\right]{\vDash }^{*}G$ is true. This can be repeated for many different user questions U. Finally, the system tries to find a proof $R⊢G$. See Figure 2. The red boxes indicate parts of our processing that may be repeated many times in one user session. This figure highlights knowledge authoring, the semantics of LLMs, and logical deduction.

5. Löwenheim–Skolem Theorems and Elementary Equivalence

This section gives the main results of this paper. As before, our theorem-proving systems prove theorems in first-order logic. These results suppose legal rules and regulations are encoded in a first-order logic legal theorem-proving system. We assume the semantics of the law is at most countable from when the laws were enacted. This is assuming originalism for the rules in a theorem proving system for first-order logic. The culmination of this section then shows: if new semantics are introduced by LLMs, then the first-order theorem-proving system will be able to prove the same results from the origional semantics as well as the new semantics introduced by the LLMs. In traditional logic terms, first-order logic cannot differentiate between the original semantics and the new LLM semantics.

LLMs are trained on many natural language sentences or phrases. Currently, several LLMs are trained on greater than $2\times {10}^{12}$ words instances or tokens. LLMs are trained mostly on very recent meanings of words or phrases.

Theorem 5

(Special-case of the upward Löwenheim–Skolem [37]). Consider a first-order theory E. If E has a countable model, then E has an uncountable model.

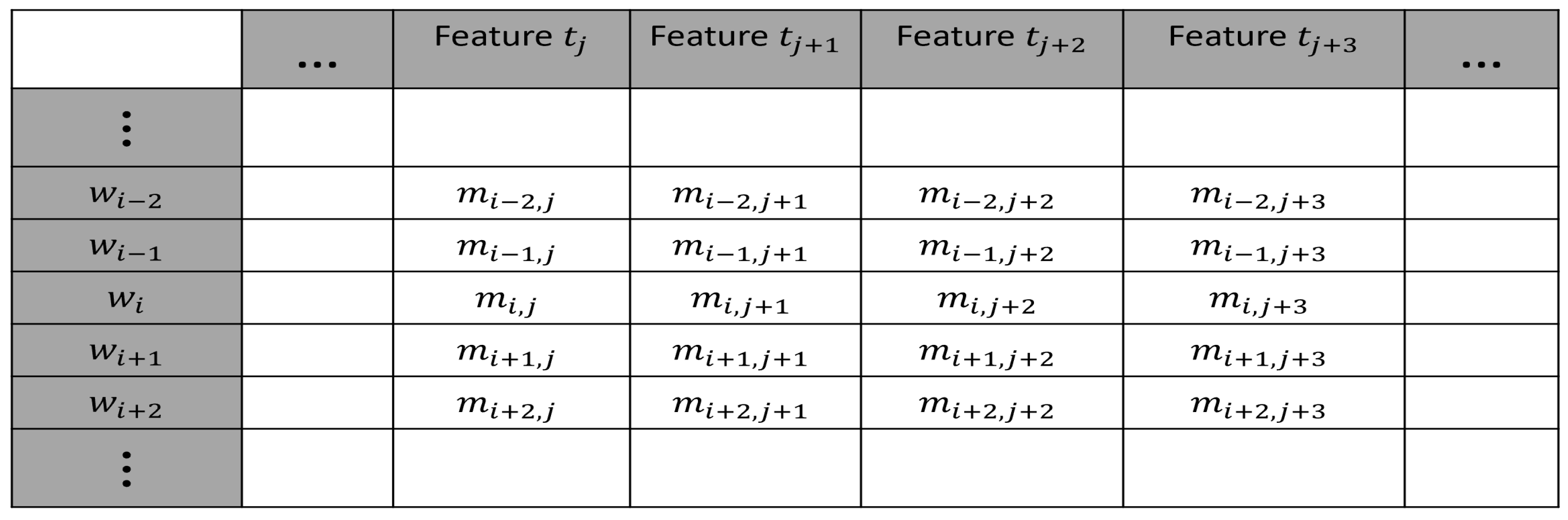
Michel, et al. [48] indicates that English adds about 8,500 new words per year. See also Petersen, et al. [49]. Theorem 6 is based on the idea that new words with new meanings or new meanings are added to current words over time. There are several ways we can represent new meanings: (1) a new meaning can be represented as a set of features with different values from other concepts, or (2) a new meaning may require some new features. See the features in Figure 3. We assume there will always be new meanings that require new features. So the number of feature columns is countable over all time. Just the same, we assume the number of words an LLM is trained on is countable over all time. But the number of meanings of words is uncountable. In summary, over all time, we assume the number of rows of words is countably infinite. Also, we assume the number of feature columns is countably infinite.

Given all of these new words and their new features, they diagonalize. Figure 3 shows a word $w_i$ whose features must be different from any other word with a different meaning. Therefore, any new word with a new meaning or an additional meaning for the same word $w_i$ is $w^{\prime }\ne w_i$. So $w^{\prime }$ will never have the same feature values of any of the other word meanings. So, if there is any countable feature columns and word meaning rows, there must always be additional meanings not listed.

Furthmore, individual words have many feature sets. Each feature set of a single word represents a different meaning.

In the case of Neural Tax Networks, some of these new words represent goods or services that are taxable. Ideally, the tax law statutes will not have to be changed for such new taxable goods or services. These new word meanings will supply new logical interpretations for tax law.

Assumption A2.

Natural language will always add new meanings to workds or add new words with new meanings. Some words or phrases or their particular meanings decline in use.

Old or archaic meanings of words are not lost. Rather, these archaic meanings are often known and recorded.

For LLMs, assuming languages always add new words over time, then it can be argued that natural language has an uncountable model if we take a limit over all time even though this uncountable model may only add a few terms related to tax law each year. To understand the limits of our multimodal system, our assumption is that such language growth and change goes on forever. Some LLMs currently train on ${10}^{12}$ word instances or tokens. This is much larger than the number of words often needed by many theorem proving systems. Comparing countable and uncountable sets in these contexts may give us insight.

For the next theorem, recall Assumption A1 which states the original meaning of words for our theorem-proving system is fixed. In other words, the meaning of the words in law is fixed from when the laws were enacted. These word meanings are captured by the models for our theorem-proving system.

Theorem 1 shows context-free grammars can build infinite domains for theorem proving systems. This is by construting a countable number of atoms. Assumption A2 supposes the set of all words V in an LLM has cardinality ${\aleph }_1$. So using a similarity measure s so that each word token vector x has a finite subset of equivalent words $V_x$ where $|V_x|\le c$, for a constant integer $c\ge 1$. Since this uncountable union of finite sets is indexed by an uncountable set,

$$\begin{array}{c}\hfill \bigcup _{x\in V}{V}_x\end{array}$$

it must be uncountable.

Theorem 6.

Taking a limit over all time, LLMs with constant bounded similarity sets have an ${\aleph }_1$ number tokens.

In some sense, Theorem 6 assumes human knowledge will be extended forever. This assumption is based on the idea that as time progresses new meanings will continually be formed. This appears to be tantamount to assuming social constructs, science, engineering, and applied science will never stop evolving.

The next definitions relate different models to each other.

Definition 14

(Elementary extensions and substructures). Consider a first-order language $\mathcal{L}=[L,D,\sigma ]$. Let $\mathcal{M}$ and $\mathcal{N}$ be models and suppose $\mathcal{M}\subseteq \mathcal{N}$.

Then $\mathcal{N}$ is an elementary extension of $\mathcal{M}$ or $\mathcal{M}⪯\mathcal{N}$ iff every first-order sentence $f\in \mathcal{L}$ is so that

$$\begin{array}{ccc}\hfill \mathcal{M}\vDash f\left(x\right)& \iff & \mathcal{N}\vDash f\left(x\right),and\hfill \end{array}$$

• If $\mathcal{M}⪯\mathcal{N}$, then $\mathcal{N}$ is anelementary extensionof $\mathcal{M}$,
• If $\mathcal{M}⪯\mathcal{N}$, then $\mathcal{M}$ is anelementary substructureof $\mathcal{N}$.

The function $f\in \mathcal{L}$ can have any arity, so x can be considered a tuple for $f\left(x\right)$.

Definition 15

(Elementary equivalence). Consider a first-order language $\mathcal{L}=[L,D,\sigma ]$. Let $\mathcal{M}$ and $\mathcal{N}$ be models of $\mathcal{L}$. Then $\mathcal{N}$ is elementary equivalent to $\mathcal{M}$ so $\mathcal{N}\equiv \mathcal{M}$, iff every first-order sentence $f\in \mathcal{L}$ is so that

$$\begin{array}{ccc}\hfill \mathcal{M}\vDash f\left(x\right)& \iff & \mathcal{N}\vDash f\left(x\right).\hfill \end{array}$$

Given a model $\mathcal{N}$, then $Th\left(\mathcal{N}\right)$ is the complete first-order theory of $\mathcal{N}$. See Definition 10.

Theorem 7

(Elementary and first-order theory equivalence). Consider a first-order language $\mathcal{L}=[L,D,\sigma ]$ and two of its models $\mathcal{M}$ and $\mathcal{N}$, then

$$\begin{array}{ccc}\hfill \mathcal{N}\equiv \mathcal{M}& \iff & Th\left(\mathcal{N}\right)=Th\left(\mathcal{M}\right).\hfill \end{array}$$

Suppose a user input U is compatible with first-order logic rules and regulations R of our theorem proving system. These facts and rules are in the set $U\left[R\right]$. LLMs may help give the semantic expression G where $U\left[R\right]{\vDash }^{*}G$. These formulas G are computed with (e.g., cosine) similarity along with any additional logical rules and facts. This also requires Assumption A2 giving a countable model for G.

The next version of the Löwenheim–Skolem (L-S) Theorems is from [35,50].

(L-S) Theorems).Theorem 8 (Löwenheim–Skolem Consider a first-order language $\mathcal{L}=[L,D,\sigma ]$ with an infinite model $\mathcal{M}$. Then there is a model $\mathcal{N}$ so that $\left|\mathcal{N}\right|=\kappa$ and

• UpwardIf $\kappa \ge \left|\mathcal{M}\right|$, then $\mathcal{N}$ is an elementary extension of $\mathcal{M}$, or $\mathcal{M}⪯\mathcal{N}$,
• DownwardIf $\kappa <\left|\mathcal{M}\right|$, then $\mathcal{N}$ is an elementary substructure of $\mathcal{M}$, or $\mathcal{N}⪯\mathcal{M}$.

A first-order language $\mathcal{L}=[L,D,\sigma ]$ with an countably infinite model ${\mathcal{M}}_{orig}$ can encode tax law.

The next corollary applies to tax law as well as other areas.

Corollary 1

(Application of Upward L-S). Consider a first-order language $\mathcal{L}=[L,D,\sigma ]$ with a countably infinite model ${\mathcal{M}}_{orig}$ for a first-order logic theorem proving system. Suppose this first-order theorem-proving system has a countably infinite domain from a countably infinite model ${\mathcal{M}}_{orig}$ where $|{\mathcal{M}}_{orig}|=\kappa ={\aleph }_0$. Then there is a model $\mathcal{N}$ that is an elementary extension of ${\mathcal{M}}_{orig}$ and $\left|\mathcal{N}\right|\ge {\aleph }_0$.

Proof. 

There is a countably infinite number of constants from the domain $D_I$ from an interpretation of $\mathcal{L}$ if these constants can be specified by Theorem 1. So, apply Theorem 8 (Upward) to the first-order logic theorem proving system for sentences of $\mathcal{L}$, with a countably infinite model ${\mathcal{M}}_{orig}$. The Upper L-S theorem indicates there is a countable infinite model ${\mathcal{M}}_{orig}$ so that $|{\mathcal{M}}_{orig}|=\kappa ={\aleph }_0$. □

For the next result, a precondition is the model ${\mathcal{M}}_{orig}$ is a subset of ${\mathcal{N}}_{llm}$.

Corollary 2

(Application of Downward L-S). Consider a first-order language $\mathcal{L}=[L,D,\sigma ]$ and a countably infinite model ${\mathcal{M}}_{orig}\subseteq {\mathcal{N}}_{llm}$, for a first-order logic theorem proving system. We assume an LLM with ${\vDash }^{*}$ and a model ${\mathcal{N}}_{llm}$ so that $|{\mathcal{N}}_{llm}|=\kappa ={\aleph }_1$. By the downward L-S theorem, ${\mathcal{M}}_{orig}$ is an elementary substructure of ${\mathcal{N}}_{llm}$ and $|{\mathcal{M}}_{orig}|={\aleph }_0$.

Proof. 

Consider a first-order language $\mathcal{L}=[L,D,\sigma ]$ and a first-order logic theorem-proving system with a countably infinite model ${\mathcal{M}}_{orig}$. The elements or atoms of this model can be defined using context-free grammars or a regular language, see Theorem 1. This generates a countably infinite domain for the model so $|{\mathcal{M}}_{orig}|={\aleph }_0$.

Suppose we have an uncountable model ${\mathcal{N}}_{llm}$ based on the uncountablility of LLM models by Theorem 6. That is,

$$\begin{array}{ccc}\hfill |{\mathcal{N}}_{llm}|& =& {\aleph }_1.\hfill \end{array}$$

Then by the downward Löwenheim–Skolem Theorem, there is an elementary substucture ${\mathcal{M}}_{orig}$ of ${\mathcal{N}}_{llm}$ where $|{\mathcal{M}}_{orig}|<|{\mathcal{N}}_{llm}|$. By Theorem 1 there is an infinite number of elements in the origional domain of the first-order theorem proving system so $|{\mathcal{M}}_{orig}|={\aleph }_0$. □

To apply this corollary, suppose the originalism-based legal first-order logic theorem proving system has a model whose elements are a subset of an LLM model. Then there is an equivalence between an LLM’s uncountable model using new words and phrases with new meanings and a first-order countable logic model. This equivalence is based on the logical theory of each of these models. In other words, a consequence of Theorem 7 is next.

Corollary 3.

Consider a language $\mathcal{L}=[L,D,\sigma ]$ and two of its models ${\mathcal{M}}_{orig}$ and ${\mathcal{N}}_{llm}$, where ${\mathcal{M}}_{orig}\subseteq {\mathcal{N}}_{llm}$, then

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{llm}\equiv {\mathcal{M}}_{orig}& \iff & Th\left({\mathcal{N}}_{llm}\right)=Th\left({\mathcal{M}}_{orig}\right).\hfill \end{array}$$

6. Discussion

This paper aims to give a better understanding of relationships between LLMs and first-order logic theorem proving systems. The first-order theorem proving systems we are using are from ErgoAI or Prolog.

The results here assume taking limits over all time. This is an unusual type of limit. Even though all humans are mortal, these results may give insight to their experience due to the large data sets. It is germane, since LLMs train on very large data sets. Currently, they can be as large as ${10}^{12}$ word instances or tokens. In contrast, the number of facts and rules in US tax law requires from ${10}^6$ to $3\times {10}^6$ word instances.

Consider an uncountable model or number of words or concepts from LLMs by Theorem 6. Corollary 2 indicates such an uncountable model can work with a theorem proving system using a countably infinite model. This is very interesting in light of originalism for the law in Assumption A1. Furthermore, some of the rules and concepts of tax law are similar to those from 1,900 years ago. This indicates some semantics remains over a long time, even in different languages and in different eras.

One classical interpretation of the upward Löwenheim–Skolem Theorem is that first-order logic cannot distinguish higher levels of infinity. That is, first-order logic cannot differentiate sets with distinct cardinalities of ${\aleph }_i$, for $i\ge 0$. It is also widely discussed that first-order logic cannot make statements about subsets of its own domain [54].

A special case of the Lefschetz Principle of first-order logic states that the field of rational numbers $\overline{\mathbb{Q}}$ and that of complex numbers $\mathbb{C}$ have an elementary equivalence as described in Theorem 7. See [5,52]. The field $\overline{\mathbb{Q}}$ contains the roots of all polynomials with coefficients from $\mathbb{Q}$. So, $\overline{\mathbb{Q}}$ contains algebraic numbers that may be complex. There are a countable number of polynomials with coefficients from $\mathbb{Q}$, hence $|\overline{\mathbb{Q}}|={\aleph }_0$. There is an uncountable number of complex numbers that are not roots of polynomial equations with coefficients from $\mathbb{Q}$. so $\left|\mathbb{C}\right|={\aleph }_1$.

This means sentences that are true in $\overline{\mathbb{Q}}$ with cardinality ${\aleph }_0$ are also true in $\mathbb{C}$ with cardinality ${\aleph }_1$. That is, by Theorem 7, we have

$$\begin{array}{ccc}\hfill \overline{\mathbb{Q}}\equiv \mathbb{C}& \iff & Th\left(\overline{\mathbb{Q}}\right)=Th\left(\mathbb{C}\right).\hfill \end{array}$$

Our use of the Löwenheim–Skolem Theorems and our discussion of Lefschetz Principle sheds light on originalism.

We also mention the classical notion that there is a countable number of algorithms that can be listed. Yet, it is possible to diagonalize over these algorithms showing algorithms not in this list. This discrepancy is rectified by results based on uncomputable numbers such as part 2 of Theorem 2. Meanings, in the sense we discuss here, may not tie into algorithms.

7. Conclusions

We presented a high-level description of an expert system for tax law to answer tax questions in natural language based on the tax statutes and case law. Already, the results our proof-of-technology system produces are fully explainable, i.e. providing a full proofs of the logical reasoning based on a small subset of tax law. We use the first-order logic theorem-proving system in ErgoAI. To effectively achieve a goal, the system will incorporate a database of all tax laws. It will have an LLM enhanced interface to load the data, translate the questions into logical queries and facts, and translate the generated line of reasoning in natural language. So the answers can be presented as proofs. These syntactic proofs are tied together with the semantics of LLMs extending the theorem-proving semantics. Important theoretical results on the limits of logical reasoning in such systems are presented.