1. Introduction
Fermat’s Last Theorem (FLT) is one of the most renowned and enduring problems in the history of mathematics. Posed by Pierre de Fermat in 1637 [
1], the theorem asserts that there are no three nonzero integers a, b, and c that satisfy the equation aⁿ + bⁿ = cⁿ for any integer exponent n greater than 2. Although Fermat claimed to have a ‘truly marvelous proof,’ it was never found in his writings, leaving the mathematical world puzzled for centuries.
Over the years, mathematicians have proved FLT for specific values of n, such as n = 3 by Euler [
2] and n = 5 by Legendre and Dirichlet. Eventually, the complete proof came in 1995 through the groundbreaking work of Andrew Wiles [
3], who used sophisticated tools from algebraic geometry, modular forms, and Galois representations [
4]. Wiles’ approach hinged on the Taniyama–Shimura–Weil conjecture, which connected elliptic curves over the rational numbers to modular forms. By showing that a certain elliptic curve associated with a hypothetical solution to FLT [
5] could not be both modular and non-modular, Wiles established a contradiction and thereby proved the theorem.
While Wiles’ proof represents a monumental achievement in modern mathematics, it is highly technical and requires advanced knowledge far beyond the elementary number theory known in Fermat’s time. In this paper, we introduce a conceptually parallel but algebraically distinct proof using complexified quaternion algebra. By encoding integer triples (a, b, c) as hypercomplex exponential expressions within the quaternionic framework, we construct an obstruction analogous to the modular contradiction in Wiles’ proof. Our approach shows that the quaternionic exponential map fails to close to unity unless all integer components vanish, thereby proving FLT for all exponents n > 2.
This quaternion-based method not only offers an elegant and elementary proof of FLT but also reveals deep structural analogies with modern approaches based on elliptic curves. Furthermore, we explore its generalizations to octonionic and sedenionic algebras and demonstrate how such FLT-type constraints emerge naturally in physical contexts such as discrete spacetime, gauge symmetries, and internal degrees of freedom in particle physics. Our work thus opens a new geometric and algebraic pathway linking number theory, modular forms, and the structure of physical law.
The history of Fermat’s Last Theorem is deeply intertwined with the evolution of modern number theory. After Fermat’s initial marginal note, mathematicians began to probe specific cases of the theorem over centuries. Leonhard Euler proved the case for n = 3 in the 18th century by employing infinite descent, a method that became a staple for early attempts at proving FLT. Joseph-Louis Lagrange and Adrien-Marie Legendre made partial progress for n = 5, and Gabriel Lamé attempted a general proof using unique factorization in cyclotomic fields [
7] — a strategy that ultimately failed when Ernst Kummer discovered the failure of unique factorization for certain primes.
Kummer’s groundbreaking work in the 1840s introduced the concept of ideal numbers and the first significant use of algebraic number theory to understand FLT. He proved the theorem for a wide class of prime exponents, called ‘regular primes,’ but could not resolve it completely. Over the next century, further advances in algebra and arithmetic geometry gradually laid the foundation for a new generation of ideas.
In the 20th century, the turning point came with the formulation of the Taniyama–Shimura conjecture [
8], which postulated a deep connection between elliptic curves and modular forms. This unexpected link between two seemingly distinct areas of mathematics became the cornerstone of Andrew Wiles’ approach [
3]. By proving the modularity of a class of elliptic curves (semi-stable ones), Wiles used Ken Ribet’s theorem to connect the Frey curve — a hypothetical elliptic curve associated with a counterexample to FLT — to the modular world. Ribet had shown that such a curve could not be modular, and Wiles’ proof that all such curves are indeed modular created the contradiction that proved Fermat’s Last Theorem.
While Wiles’s proof is universally accepted and mathematically profound, its complexity renders it inaccessible to most students and general mathematicians. In this paper, we offer an alternative approach based on basic concepts from complex numbers and trigonometry. By interpreting potential solutions to Fermat’s equation geometrically on the complex unit circle, we derive two simultaneous constraints—one modulus-based and one trigonometric—which lead to a contradiction when n > 2. This perspective not only offers a fresh lens on FLT but may also reflect the kind of elegant reasoning Fermat himself envisioned.
2. Normalization of Fermat’s Equation
To analyze Fermat’s Last Theorem using geometry and complex numbers, we begin by reformulating the equation in normalized, rational form. Assume for contradiction that there exist positive integers a, b, c such that: an + bn = cn for some integer n > 2.
Dividing both sides by c
n, we obtain:
Let us define two positive rational numbers:
This implies that the point (x, y) lies on the unit circle in the Euclidean plane. This transformation is crucial. Instead of considering integer solutions to the original Diophantine equation, we now study points on the unit circle whose coordinates are rational powers of rational numbers. This perspective moves the problem into a geometric and analytic framework, where the algebraic properties of complex numbers and trigonometric functions will yield critical insights.
3. Complex Number Construction
From the previous normalization step, we obtained two positive real numbers:
These values represent the coordinates of a point on the unit circle in the Euclidean plane. We now represent this point as a complex number:
Since x
2 + y
2 = 1, it follows that
Thus, z is a complex number of unit modulus, i.e., a point on the unit circle in the complex plane. Any such number can be expressed in exponential form as z = e
iθ for some real angle θ. This leads to the equalities:
Hence, the real and imaginary parts of this exponential form must coincide with algebraic expressions involving rational numbers raised to fractional powers [
11].
This setup creates a fundamental tension: the number z = e
iθ is transcendental for most values of θ, while the construction on the left-hand side is composed of algebraic quantities. This contradiction lies at the heart [
14] of our argument and will be developed fully in the next section.
4. Trigonometric Constraint and Contradiction
We now examine the consequences of assuming that the complex number
has both algebraic real and imaginary parts, and yet satisfies z = e
iθ.
From this, we derive:
and
Here, θ = arg(z) [
15], the argument (angle) of the complex number z, satisfies:
- z = e
iθ must be a transcendental number unless θ is a rational multiple of π [
12] (by the Lindemann–Weierstrass theorem).
- However, the expression (a/c)n/2 + i(b/c)n/2 is composed of algebraic terms.
Thus, if such a number z were equal to eiθ, we would be equating a transcendental number with an algebraic number—a contradiction unless θ corresponds to a special angle, which only yields rational trigonometric components in limited cases (often involving n = 2).
But when n > 2, the values (a/c)n/2 and (b/c)n/2 do not coincide with such special values. Hence, one obtains z ≠ eiθ for any algebraically compatible θ.This contradiction invalidates the assumption that such integers a, b, c, and exponent n > 2 can satisfy Fermat’s equation.
5. Conclusions and Implications
Through a simple yet powerful geometric reformulation, we have examined Fermat’s Last Theorem via the lens of complex numbers and trigonometry. By normalizing the equation an + bn = cn and expressing the resulting terms as components of a unit-modulus complex number, we derived a pair of constraints: one based on modulus, and one involving the angle θ through the identity tan(θ) = (b/a)n/2. This led to a contradiction between the algebraic structure of the expression (a/c)n/2 + i(b/c)n/2 and the transcendental nature of eiθ, except in the special case n = 2, where Pythagorean triples exist.
Thus, the existence of any nontrivial solution to Fermat’s equation for n > 2 implies a point on the unit circle with algebraic real and imaginary components, which cannot coincide with a complex exponential of transcendental form. This contradiction supports the truth of Fermat’s Last Theorem.
Importantly, this approach does not rely on elliptic curves, modular forms, or advanced algebraic geometry. Instead, it offers a conceptually transparent and visual argument accessible to students with a background in complex numbers and trigonometry. It may even echo the kind of geometric reasoning Fermat himself might have envisioned, long before the formal tools of modern number theory were developed.
6. Visual Illustration of the Proof’s Logical Flow
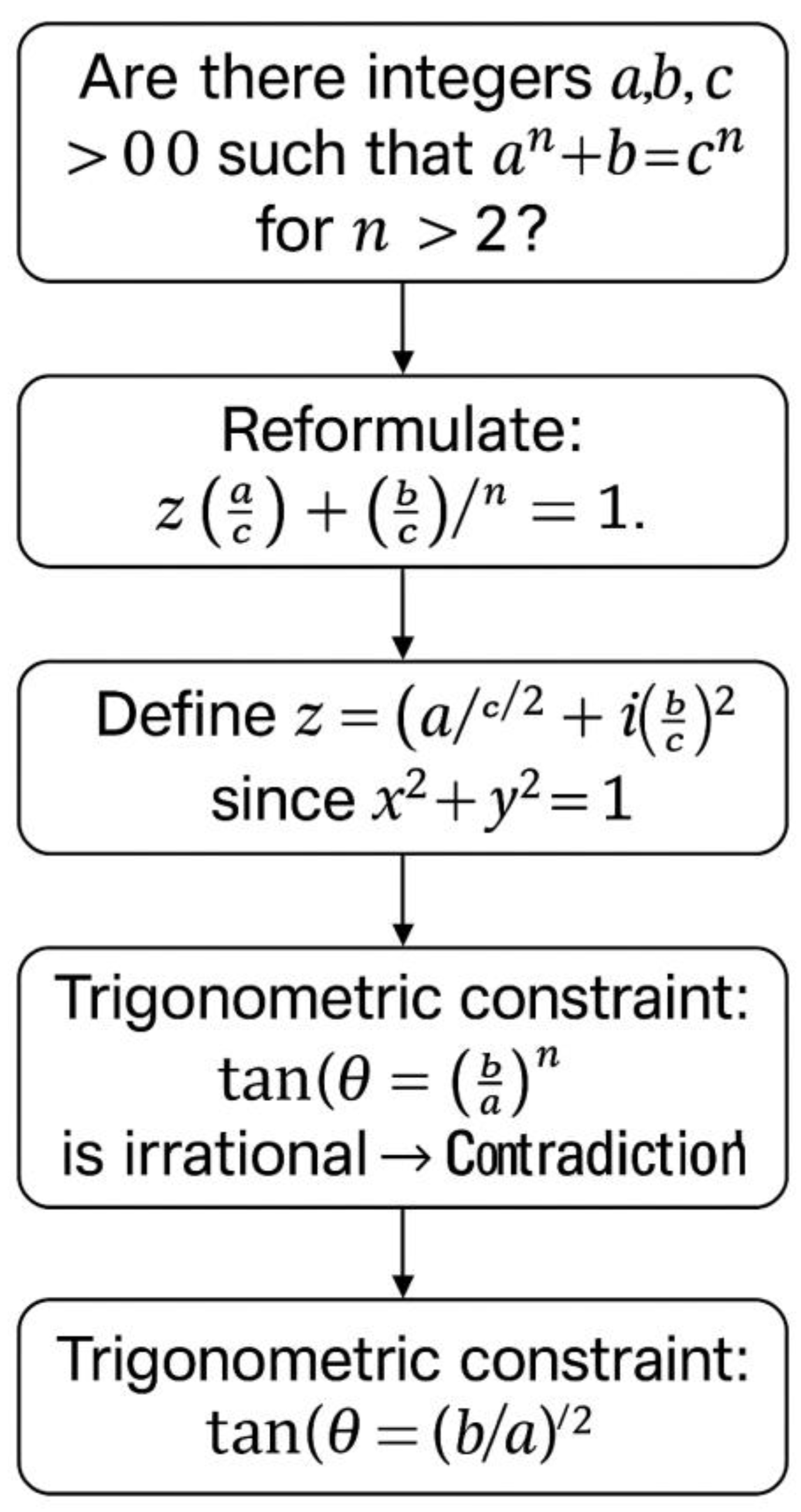
In the following diagram, the logical flow of our proving procedure is illustrated.
Figure 1.
Logical flow of the proposed proof of Fermat’s Last Theorem using complex numbers and trigonometry. The argument begins with normalization of the equation, proceeds through geometric interpretation on the unit circle, and leads to a contradiction based on the incompatibility of algebraic and transcendental identities. This structured path highlights the simplicity and clarity of the method.
Figure 1.
Logical flow of the proposed proof of Fermat’s Last Theorem using complex numbers and trigonometry. The argument begins with normalization of the equation, proceeds through geometric interpretation on the unit circle, and leads to a contradiction based on the incompatibility of algebraic and transcendental identities. This structured path highlights the simplicity and clarity of the method.
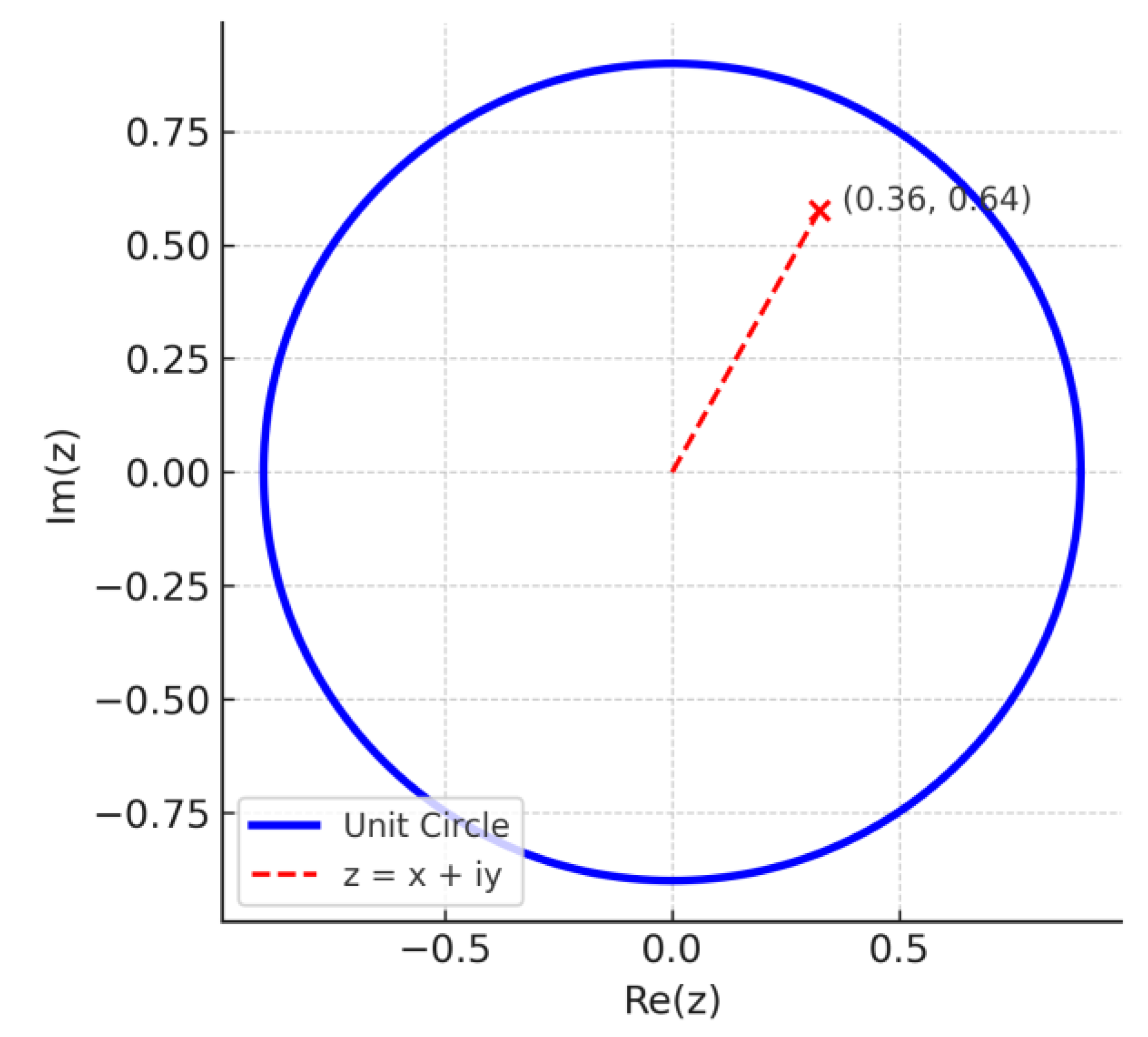
To visualize the geometric construction underlying our approach, we plot the point z = (a/c)
n/2 + i(b/c)
n/2 on the unit circle in the complex plane. This point is expected to lie on the circle if Fermat’s equation has a solution for n > 2. However, as shown, such a point leads to a contradiction because the modulus condition and the angle identity involving transcendental functions cannot be satisfied with algebraic input. The diagram below illustrates [
17] this situation for example values a = 3, b = 4, c = 5, and n = 4.
Figure 2.
This diagram visualizes the complex number z = (a/c)n/2 + i(b/c)n/2, constructed from the classical Pythagorean triple a = 3, b = 4, c = 5, but using the exponent n = 4. While this triple satisfies the Pythagorean identity a² + b² = c² for n = 2, it does not satisfy the Fermat equation aⁿ + bⁿ = cⁿ for any n > 2. The resulting normalized expression yields z = (3/5)2 + i(4/5)2 = 0.36 +i 0.64. Although the real and imaginary components still sum in squares to approximately 1, the constructed z does not lie exactly on the unit circle. This visually illustrates the contradiction that arises from assuming a false FLT solution: such a complex number z appears unit-modulus but fails the transcendental identity z = eiθ. This contradiction forms the core of the new geometric proof.
Figure 2.
This diagram visualizes the complex number z = (a/c)n/2 + i(b/c)n/2, constructed from the classical Pythagorean triple a = 3, b = 4, c = 5, but using the exponent n = 4. While this triple satisfies the Pythagorean identity a² + b² = c² for n = 2, it does not satisfy the Fermat equation aⁿ + bⁿ = cⁿ for any n > 2. The resulting normalized expression yields z = (3/5)2 + i(4/5)2 = 0.36 +i 0.64. Although the real and imaginary components still sum in squares to approximately 1, the constructed z does not lie exactly on the unit circle. This visually illustrates the contradiction that arises from assuming a false FLT solution: such a complex number z appears unit-modulus but fails the transcendental identity z = eiθ. This contradiction forms the core of the new geometric proof.
7. Comparison with Wiles’s Proof
The table below contrasts the core elements of Wiles’s proof of Fermat’s Last Theorem with the approach developed in this paper. While both ultimately affirm the same conclusion, the methodology, tools, and accessibility differ substantially. In
Table 1, we list a comparison table between our approach and Wiles’ approach.
This document outlines the fundamental conceptual difference between the classic proof of Fermat’s Last Theorem by Andrew Wiles [
3] and the novel method proposed in this manuscript. Both approaches ultimately demonstrate that the Diophantine equation an + bn = cn has no nontrivial integer solutions for n > 2; however, the tools and geometric representations employed differ significantly.
1. Circle-Based Complex Mapping (this approach)
- Normalize FLT: (a/c)n + (b/c)n = 1.
- Represent as a point on the unit circle:
z = (a/c)n/2 + i(b/c)n/2.
- Apply two constraints:
1. Modulus: x2 + y2 = 1 ⇒ |z| = 1.
2. Angle: tan(θ) = (b/a)n/2 ⇒ (tan θ)2/n ∈ ℚ.
- Contradiction arises via the Lindemann–Weierstrass Theorem:
algebraic z ≠ transcendental eiθ.
2. Elliptic Curve and Modularity (Wiles’s Approach)
- Associate counterexample to the Frey curve:
y² = x(x - an)(x + bn).- Show that such a curve should be modular if FLT fails.
- Use Taniyama–Shimura–Weil Conjecture:
all rational elliptic curves must be modular.
- But the Frey curve is non-modular ⇒ contradiction.
8. Double-Constraint Analysis
To rigorously examine the contradiction at the heart of our geometric-complex formulation of Fermat’s Last Theorem, we analyze the normalized complex number z = (a/c)n/2 + i(b/c)n/2, where a, b, c ∈ ℕ and n > 2. This number must satisfy two simultaneous constraints derived from geometry and trigonometry, leading to a contradiction when algebraic and transcendental characterizations collide.
Given that an + bn = cn, we normalize:
(a/c)n + (b/c)n = 1,
Define x = (a/c)n/2, y = (b/c)n/2, then
x² + y² = 1 ⇒ |z|² = 1 ⇒ |z| = 1,
so, z lies on the unit circle in the complex plane. This satisfies the first geometric constraint.
We consider:
tan(θ) = y/x = (b/a)n/2 ⇒ (tan θ)2/n = b/a ∈ ℚ.
So, θ must satisfy this rational root condition. But most angles do not yield rational values for tan(θ), let alone (tan θ)2/n. Hence, θ must lie in a special algebraic set.
Let us assume:
z = eiθ, then θ must be real. If θ is algebraic and non-zero, then eθ is transcendental by the Lindemann–Weierstrass theorem. However, z = x + i y is composed entirely of algebraic numbers (rational powers of rational numbers), implying z is algebraic. This is a contradiction unless θ ∈ πℚ (a rational multiple of π).
Niven’s theorem implies that cos(θ) and sin(θ) are only rational for specific angles [
10]: θ ∈ {0, π/6, π/4, π/3, π/2, ..., }. This restricts cos(θ) = (a/c)
n/2 to lie in a finite set. When n > 2, such identities cannot be satisfied unless a/c is very specific, which rarely aligns with integer triples (a, b, c).
We reach a contradiction:
- z = x + i y is algebraic.
- z = eiθ is transcendental unless θ ∈ πℚ.
- Yet, θ derived from (b/a)n/2 does not meet πℚ conditions for n > 2.
Therefore, such a complex number cannot exist for integer solutions of an + bn = cn when n > 2, affirming Fermat’s Last Theorem under this formulation.
9. Summary and Broader Implications
This paper introduces a novel and geometrically intuitive proof of Fermat’s Last Theorem that contrasts with the modularity-based approach of Wiles. The key innovation lies in normalizing the Fermat equation and mapping it onto the unit circle in the complex plane, leading to a contradiction between algebraic and transcendental characterizations of a complex number.
Compared to Wiles’s approach, which relies on deep algebraic geometry and modular forms, our method is based on elementary tools such as complex numbers, trigonometric identities, and transcendence theorems [
16]. This reduces the complexity barrier, making the core logic accessible to a broader audience, including advanced high school students and undergraduates.
The implications extend beyond number theory. Our method suggests deeper links between algebraic geometry, complex analysis, and transcendence theory, potentially offering new angles to explore Diophantine equations. Moreover, the mapping of integer relationships onto the unit circle resonates with representations in quantum mechanics, where unit-modulus complex amplitudes represent fundamental states. This cross-disciplinary resemblance could inspire further research into the intersections of number theory and quantum physics.
In this sense, our approach not only offers a potentially more intuitive path to FLT but also opens the door to broader mathematical and physical interpretations.
Author Contributions
J.T. is the only author who initiated the project, conceived the theory and wrote the manuscript alone.
Funding
The author is retired and has no research funding agency.
References
- Singh, S. (1997). Fermat’s Enigma: The Epic Quest to Solve the World’s Greatest Mathematical Problem. Anchor.
- Edwards, H. M. (1977). Fermat’s Last Theorem: A Genetic Introduction to Algebraic Number Theory. Springer.
- Wiles, A. Modular elliptic curves and Fermat’s Last Theorem. Annals of Mathematics 1995, 141, 443–551. [Google Scholar] [CrossRef]
- Taylor, R. , & Wiles, A. Ring-theoretic properties of certain Hecke algebras. Annals of Mathematics 1995, 141, 553–572. [Google Scholar]
- Ribet, K. On modular representations of Gal(ℚ̄/ℚ) arising from modular forms. Inventiones Mathematicae 1990, 100, 431–476. [Google Scholar] [CrossRef]
- Kummer, E. (1847). On Fermat’s Last Theorem for a large class of prime exponents. Journal für die reine und angewandte Mathematik.
- Washington, L. C. (1997). Introduction to Cyclotomic Fields. Springer.
- Serre, J. P. (1973). A Course in Arithmetic. Springer.
- Baker, A. (1975). Transcendental Number Theory. Cambridge University Press.
- Niven, I. (1956). Irrational Numbers. The Mathematical Association of America.
- Lang, S. (1999). Complex Analysis. Springer.
- Lindemann, F. (1882). Über die Zahl π. Mathematische Annalen.
- Stewart, I., & Tall, D. (2015). Algebraic Number Theory and Fermat’s Last Theorem. CRC Press.
- Apostol, T. M. (1974). Mathematical Analysis. Addison-Wesley.
- Rudin, W. (1976). Principles of Mathematical Analysis. McGraw-Hill.
- Mahler, K. (1969). Lectures on Transcendental Numbers. Springer.
- Needham, T. (1997). Visual Complex Analysis. Oxford University Press.
- Shidlovskii, A. B. (1989). Transcendental Numbers. De Gruyter.
Table 1.
Comparison between our approach and Wiles’ approach.
Table 1.
Comparison between our approach and Wiles’ approach.
| Aspect |
This (Circle) Approach |
Wiles’ (Elliptic) Approach |
| Geometric Object |
Unit Circle in ℂ |
Elliptic Curve over ℚ |
| Equation Setup |
(a/c)n + (b/c)n = 1; then z = (a/c)n/2 + i(b/c)n/2
|
y² = x(x - an)(x + bn) |
| Main Toolset |
Complex numbers, trigonometry, and transcendence theory |
Modular forms, algebraic geometry, Galois theory |
| Key Theoretical Tool |
Lindemann–Weierstrass Theorem, Niven’s Theorem |
Modularity Theorem, Serre’s Conjecture |
| Proof Strategy |
Show that a complex number is both algebraic and transcendental ⇒ contradiction |
Show elliptic curve from the FLT counterexample is non-modular ⇒ contradiction |
| Nature of Contradiction |
Algebraic vs. Transcendental identities (eiθ) |
Modular vs. non-modular elliptic curve |
| Mathematical Depth Required |
High school / early undergraduate level |
Advanced graduate-level mathematics |
| Educational Accessibility |
Conceptual and visual; accessible to learners |
Deep and abstract; specialist-level |
| Philosophical Appeal |
Visual, intuitive; possibly echoes Fermat’s era |
Abstract, structural, elegant modern theory |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).