Talking to Blackbox: Explainability Through P+NP=1

Rogério Figurelli

doi:10.20944/preprints202507.1759.v1

Submitted:

20 July 2025

Posted:

22 July 2025

You are already at the latest version

Abstract

The interpretability of complex AI systems remains one of the most critical challenges for modern machine learning, particularly when dealing with blackbox models such as deep neural networks and large language models (LLMs). While current Explainable AI (XAI) techniques — notably SHAP and LIME — provide local or feature-based insights, they often rely on additive approximations that fail to capture the underlying epistemic dynamics or the structural reasoning of models. This paper introduces Talking to Blackbox, a framework that proposes a new paradigm of XAI, inspired by complexity theory and the symbolic principle P + NP = 1. We conceptualize a blackbox model as an interplay between interpretable elements (P) and latent complexity (NP), where P + NP = 1 serves as a heuristic principle for balancing transparency and computational depth. Instead of forcing full visibility, Talking to Blackbox constructs explanatory tokens from model inputs and intermediate states, mapping them to epistemic fields — such as Heuristic Physics (hPhy), Collapse Mathematics (cMth), and Intention Flow (iFlw). Through these fields, the framework iteratively transforms NP opacity into P clarity, producing dynamic narratives of explainability measured by the evolving metric α(t). A proof-of-concept simulation using a weather forecasting blackbox demonstrates how raw variables (e.g., pressure, temperature, humidity) can be translated into narrative tokens (“falling pressure,” “high humidity”), which are processed to generate a human-readable explanation of the prediction. Although this approach does not aim to formally prove P = NP, it employs the P + NP = 1 hypothesis as a conceptual bridge between complexity and intelligibility. By complementing existing techniques like SHAP and LIME, our architecture emphasizes interpretability not as a static attribution but as a dialogue with the model, revealing the flow of reasoning rather than isolated feature contributions. This conceptual framework builds upon prior works on heuristic convergence [2], [3], proposing a new epistemic approach to XAI that integrates complexity theory, symbolic reasoning, and narrative structures.

Keywords:

explainable AI

;

XAI

;

blackbox interpretability

;

P vs NP

;

epistemic fields

;

SHAP

;

LIME

;

narrative AI

Subject:

Computer Science and Mathematics - Artificial Intelligence and Machine Learning

Subjects: Artificial Intelligence; Machine Learning; Complexity Theory; Symbolic Systems

Introduction

Explainability in artificial intelligence (AI) remains one of the most pressing challenges in the deployment of complex models such as large language models (LLMs) and deep neural networks.

These systems are often treated as blackboxes, producing accurate predictions but offering little to no insight into the reasoning behind their outputs. This lack of interpretability has critical implications in high-stakes domains, including healthcare, finance, and climate modeling, where trust and accountability are essential.

Traditional methods of explainable AI (XAI), such as SHAP and LIME [4,5], have contributed by providing feature importance and local approximations of decision boundaries; however, they often fail to offer a dynamic or narrative explanation that connects the dots between features and outcomes in a coherent temporal or causal way.

The Talking to Blackbox framework proposes a paradigm shift by introducing narrative explainability as a first-class objective. Inspired by the symbolic compression principle P + NP = 1 [1], this approach considers any computational system as a combination of interpretable components (P) and opaque complexity (NP). Instead of attempting to fully open the blackbox, the goal is to gradually translate NP into P through a process of semantic alignment and heuristic mapping. This is achieved by generating explanatory tokens—interpretable narrative units derived from model inputs—and evaluating their coherence using a set of epistemic fields: hPhy (Heuristic Physics), cMth (Collapse Mathematics), iFlw (Intention Flow), and wThd (Wisdom Threshold) [2,3]. These fields act as meta-sensors that measure semantic tension, uncertainty, narrative flow, and readiness for explanation, respectively.

To operationalize this concept, the framework defines a dynamic interpretability measure α(t), representing the fraction of the blackbox’s decision that has been translated into interpretable narrative at time t, and its progression follows:

α(t+1) = α(t) + η · (iFlw − hPhy − cMth),

where η is the interpretation rate (0 < η < 1).

This expression encapsulates the iterative process of “talking” to the blackbox: with each explanatory token added, the system reassesses how much of the opaque reasoning (NP) is successfully converted into interpretable content (P).

The difference (iFlw − hPhy − cMth) captures the net “narrative gain” — positive when the intention flow (iFlw) dominates over semantic tension (hPhy) and logical collapse (cMth), leading to an increase in clarity.

To illustrate this, consider a weather forecasting model that predicts a 70% chance of rain. Initially, α(0) might be set at 0.50, representing a neutral baseline where half of the model’s reasoning is assumed to be interpretable.

As the first token, “falling pressure (0.30),” is introduced, the intention flow iFlw = 0.30 outweighs both hPhy = 0.01 and cMth = 0.01, and with η = 0.2, the interpretability improves to α(1) ≈ 0.50 + 0.2 · (0.30 − 0.01 − 0.01) = 0.56. This small but measurable increase reflects how even a single explanatory factor can enhance our understanding of the model’s decision.

As additional tokens are processed, α(t) continues to grow in a manner that is both incremental and cumulative. For example, when “high humidity (0.20)” and “strong winds (0.15)” are added, the narrative gain compounds, reaching α(3) ≈ 0.64, meaning 64% of the reasoning is now accounted for in human-interpretable terms.

The interpretation rate η acts as a modulation factor, controlling how quickly or slowly the narrative clarity emerges. A higher η accelerates the transition from NP to P but can also amplify noise if hPhy or cMth are high.

An important characteristic of α(t) is that it is bounded between 0 and 1, with P = α(t) and NP = 1 − α(t). When α(t) approaches 1, the narrative explanation has almost fully captured the reasoning behind the prediction, leaving minimal residual opacity. Conversely, if α(t) stagnates or declines due to high hPhy (e.g., conflicting signals among tokens) or cMth (e.g., unstable logic), it indicates that the blackbox remains partially opaque, and additional tokens or heuristic insights are required to improve clarity.

This iterative narrative process contrasts with static XAI methods like SHAP or LIME, which compute feature attributions in a single step without modeling how explanations evolve. In Talking to Blackbox, the dynamic interplay among tokens mimics the way humans build understanding — each new piece of information modifies the mental model of the decision-making process. For example, the presence of both “falling pressure” and “high temperature” might initially appear contradictory (raising hPhy), but when combined with “high humidity,” the intention flow iFlw becomes dominant, reducing overall tension and increasing α(t).

Another key aspect is the role of η as a tunable hyperparameter. In domains with well-defined causal structures, such as weather forecasting or medical diagnostics, a larger η may be justified because each token (feature) strongly supports the prediction.

However, in less deterministic environments, such as sentiment analysis or financial forecasting, a smaller η prevents overconfidence, ensuring that α(t) reflects a cautious, incremental increase in clarity rather than a sudden, unjustified leap.

To further exemplify the mechanism, imagine a different scenario where a blackbox predicts stock price movements. Tokens might include “market volatility (0.25),” “interest rate changes (0.20),” and “corporate earnings (0.30).” If these tokens are consistent (low hPhy) and align with the target outcome (high iFlw), α(t) may increase rapidly from 0.50 to 0.70 within three iterations. Conversely, if new contradictory signals emerge — for instance, “unexpected geopolitical events” with a negative contribution — the cMth term increases, slowing or even reversing the interpretability growth. The measure α(t) is not just a mathematical artifact; it serves as a real-time metric for explainability. By tracking α(t) across iterations, one can visualize the “curve of clarity,” showing how each token contributes to the understanding of the decision. This curve can be plotted against the number of tokens or time steps, providing a practical way to audit and benchmark the interpretability of a blackbox model. When combined with narrative reporting, α(t) offers both quantitative and qualitative insights, bridging the gap between raw model outputs and human-understandable reasoning.

This formulation adheres to the constraint P + NP = 1, with P = α(t) and NP = 1 − α(t), capturing the idea that explainability grows when the narrative flow outweighs semantic tension and logical collapse, bridging the gap between opacity and clarity.

Unlike SHAP and LIME, which produce static snapshots of feature importance, Talking to Blackbox constructs a parallel language model that narrates the reasoning process. For example, in a weather forecasting scenario, features such as falling pressure, high humidity, and strong winds are mapped into tokens like “falling pressure (0.30)” or “high humidity (0.20),” which collectively form a storyline explaining why the model predicts a 70% chance of rain. This narrative, evaluated by the epistemic fields, evolves over time as more tokens are processed, with α(t) reflecting the cumulative clarity.

The Talking to Blackbox architecture builds upon the foundational concepts of the Wisdom Machine (WM) framework [2], which emphasizes the convergence of logic and compassion, and the Heuristic Convergence Theorem [3], which asserts that truth emerges from the synthesis of partial perspectives.

By incorporating these principles, this work positions narrative explainability not merely as a technical feature but as an epistemic bridge between computation and understanding.

A direct application of this framework lies in deep neural networks (DNNs) used in domains like image recognition and natural language understanding. Convolutional Neural Networks (CNNs) can benefit from the tokenization of intermediate feature maps, transforming abstract filters into narrative elements such as “high edge density” or “color gradient prominence,” which can then be analyzed under the fields hPhy and iFlw.

Similarly, for Recurrent Neural Networks (RNNs) or Transformers, attention weights and hidden states can be interpreted as narrative tokens that reveal how sequential patterns influence the model’s reasoning process.

Another promising area is the explanation of ensemble methods like Random Forests and Gradient Boosted Trees. While these models already provide feature importance metrics, their aggregated structure often leads to complexity and opacity. By mapping split decisions and feature thresholds into narrative tokens, the Talking to Blackbox architecture can produce storylines that explain why certain paths dominate the decision space. This approach can be particularly impactful in fields like credit scoring or risk assessment, where regulatory compliance requires transparent reasoning.

The framework is also applicable to generative models, including Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs). In these models, latent space vectors and generator outputs can be analyzed to produce explanatory narratives that describe which latent factors most strongly influence the generated content.

For example, in GAN-based image synthesis, tokens could correspond to semantic elements like “background color,” “texture richness,” or “object shape,” enabling interpretability that is currently missing in generative tasks.

In addition, large language models (LLMs) are a natural fit for this approach, as they already operate through tokenized representations. By introducing a meta-layer that analyzes attention distributions, embedding similarities, and key contextual tokens, Talking to Blackbox can explain not only which tokens were important for a specific output but also how they interacted semantically to generate a coherent narrative. This is particularly relevant for applications like legal text analysis, medical diagnosis from textual data, and automated report generation.

Finally, the framework holds potential in time-series forecasting and reinforcement learning (RL). In forecasting models, explanatory tokens can be derived from temporal features such as “sharp increase in volatility” or “seasonal trend shift,” providing interpretable reasons for predicted outcomes. In RL environments, the narrative can trace the influence of individual state-action pairs, explaining how specific policy updates or reward structures lead to observed behavior.

This capability can foster trust in autonomous systems like robotics, energy management, or algorithmic trading, where understanding the rationale behind decisions is critical.

Methodology

The Talking to Blackbox framework employs an Epistemic Architecture for Narrative Explainability (EANE) designed to progressively convert opaque reasoning (NP) into interpretable content (P) based on the symbolic principle P + NP = 1, where P = α(t) and NP = 1 − α(t). The architecture is composed of three main layers: the token generation module, the epistemic field evaluator, and the narrative synthesizer. Each layer is responsible for translating raw model behavior into a structured storyline that can be understood and audited by human experts. This methodology builds on modern XAI paradigms [4,5,6,7], but introduces a dynamic and narrative-based perspective.

The first step involves transforming model inputs or features into explanatory tokens. For example, in a weather forecasting model, raw inputs such as temperature, pressure, and humidity are converted into tokens like “falling pressure (0.30)” or “high humidity (0.20).” Each token is associated with a weight that represents its relative contribution to the final decision, a concept similar to the feature attributions discussed in SHAP and LIME [4,5]. These tokens serve as the “vocabulary” through which the blackbox communicates its reasoning. Unlike static approaches [6,8], our method treats tokens as evolving narrative elements, enabling temporal tracking of interpretability.

The second step is the evaluation of tokens using epistemic fields—meta-layers inspired by the Wisdom Machine framework [2]. These fields are defined as follows: hPhy (Heuristic Physics) quantifies semantic tension or inconsistency between tokens [9]; cMth (Collapse Mathematics) measures logical collapse points or uncertainties in the explanation [10]; iFlw (Intention Flow) evaluates the global direction and coherence of the narrative [7]; wThd (Wisdom Threshold) determines whether the explanation is sufficiently mature to be presented [2]; and φ(t) represents the global coherence field that integrates these elements. The net interpretability growth is modeled by α(t+1) = α(t) + η · (iFlw − hPhy − cMth), with η acting as the interpretation rate (0 < η < 1).

To illustrate, consider the following evolution table of α(t) for a weather forecasting example (η = 0.2, α(0) = 0.50). The approach resonates with the incremental interpretability metrics discussed by Molnar [6] and Doshi-Velez and Kim [7]:

Token	iFlw	hPhy	cMth	α(t)
falling pressure	0.30	0.01	0.01	0.56
high humidity	0.20	0.01	0.01	0.59
high temperature	0.25	0.01	0.01	0.64
strong winds	0.15	0.01	0.01	0.66
low solar radiation	0.10	0.01	0.01	0.68

This table shows that as each token is processed, α(t) gradually increases, reflecting a progressive transition from NP (opaque reasoning) to P (narrative clarity). Once α(t) surpasses a threshold defined by wThd, the explanation is considered sufficiently coherent to be reported. This incremental approach is conceptually similar to iterative perturbation methods [8], but with a narrative layer added.

The methodology also includes a pseudocode prototype, demonstrating how the explanatory pipeline operates alongside a blackbox model, consistent with practical XAI implementations [6,11]:

def blackbox_model(inputs):

# Blackbox prediction (e.g., weather model)

return 0.7 # Probability of rain = 70%

def explain_blackbox(inputs, output):

tokens = []

if inputs["pressure"] < 1000:

tokens.append(("falling pressure", 0.30))

if inputs["humidity"] > 80:

tokens.append(("high humidity", 0.20))

if inputs["temperature"] > 28:

tokens.append(("high temperature", 0.25))

if inputs["wind_speed"] > 15:

tokens.append(("strong winds", 0.15))

tokens.append(("low solar radiation", 0.10))

hPhy = 0.01

cMth = 0.01

iFlw = sum(w for _, w in tokens)

alpha = 0.5 + 0.2 * (iFlw - hPhy - cMth)

return {

"tokens": tokens,

"alpha": alpha,

"summary": f"The 70% rain prediction is explained by {len(tokens)} main factors with α={alpha:.2f}."

}

inputs = {"pressure": 990, "humidity": 85, "temperature": 30, "wind_speed": 18, "solar_radiation": 200}

output = blackbox_model(inputs)

explanation = explain_blackbox(inputs, output)

The code serves as a simplified prototype illustrating how the Talking to Blackbox framework translates opaque model outputs into a human-readable narrative. The blackbox_model(inputs) function represents an abstract blackbox, such as a weather forecasting model, which takes numerical inputs like pressure, humidity, temperature, wind speed, and solar radiation.

While a real model would involve complex computations and trained parameters, this example outputs a fixed probability of rain (0.7) to focus entirely on the explainability mechanism. The explain_blackbox(inputs, output) function is the core of the explanatory pipeline. It converts raw input variables into narrative tokens, each representing an interpretable feature with an associated weight.

For example, if the pressure is below 1000 hPa, the function generates the token “falling pressure” with a weight of 0.30, indicating that this variable strongly supports the prediction. This process effectively creates a vocabulary of tokens that mirrors how the blackbox “reasons,” enabling the construction of a narrative explanation rather than just showing raw numbers.

Next, the code evaluates the epistemic fields—meta-level measures that assess the quality and coherence of the explanation. These fields include iFlw (intention flow), which represents the cumulative influence of the tokens, hPhy (heuristic physics), which simulates small semantic tensions or inconsistencies, and cMth (collapse mathematics), which models logical uncertainty or weak points in the reasoning chain. In this prototype, hPhy and cMth are fixed at low values (0.01) to simplify the computation.

The interpretability measure α(t) is then updated using the equation α(t+1) = α(t) + η · (iFlw − hPhy − cMth), where α(0) = 0.50 represents an initial neutral state, and η = 0.2 is the interpretation rate. Each token processed contributes incrementally to α(t), reflecting the fraction of the blackbox’s decision that is now understandable. For instance, the token “falling pressure (0.30)” raises α(t) from 0.50 to 0.56, and after processing all tokens, α(t) reaches approximately 0.68, meaning that 68% of the decision has been converted into a clear narrative.

In this sense, the code outputs a narrative summary, such as: “The 70% rain prediction is explained by 5 main factors with α=0.68.” This output combines both qualitative (the list of tokens) and quantitative (α(t)) insights, providing a structured, step-by-step explanation.

To illustrate how the interpretability measure α(t) evolves as explanatory tokens are processed, we simulated a weather forecasting scenario using the Talking to Blackbox pipeline. Starting with an initial interpretability value of α(0) = 0.50, each token contributes a positive increment determined by the equation α(t+1) = α(t) + η · (iFlw − hPhy − cMth), where η = 0.2, hPhy = 0.01, and cMth = 0.01. The progression of α(t) demonstrates how narrative clarity increases with each token, reflecting the gradual transition from NP (opacity) to P (interpretability).

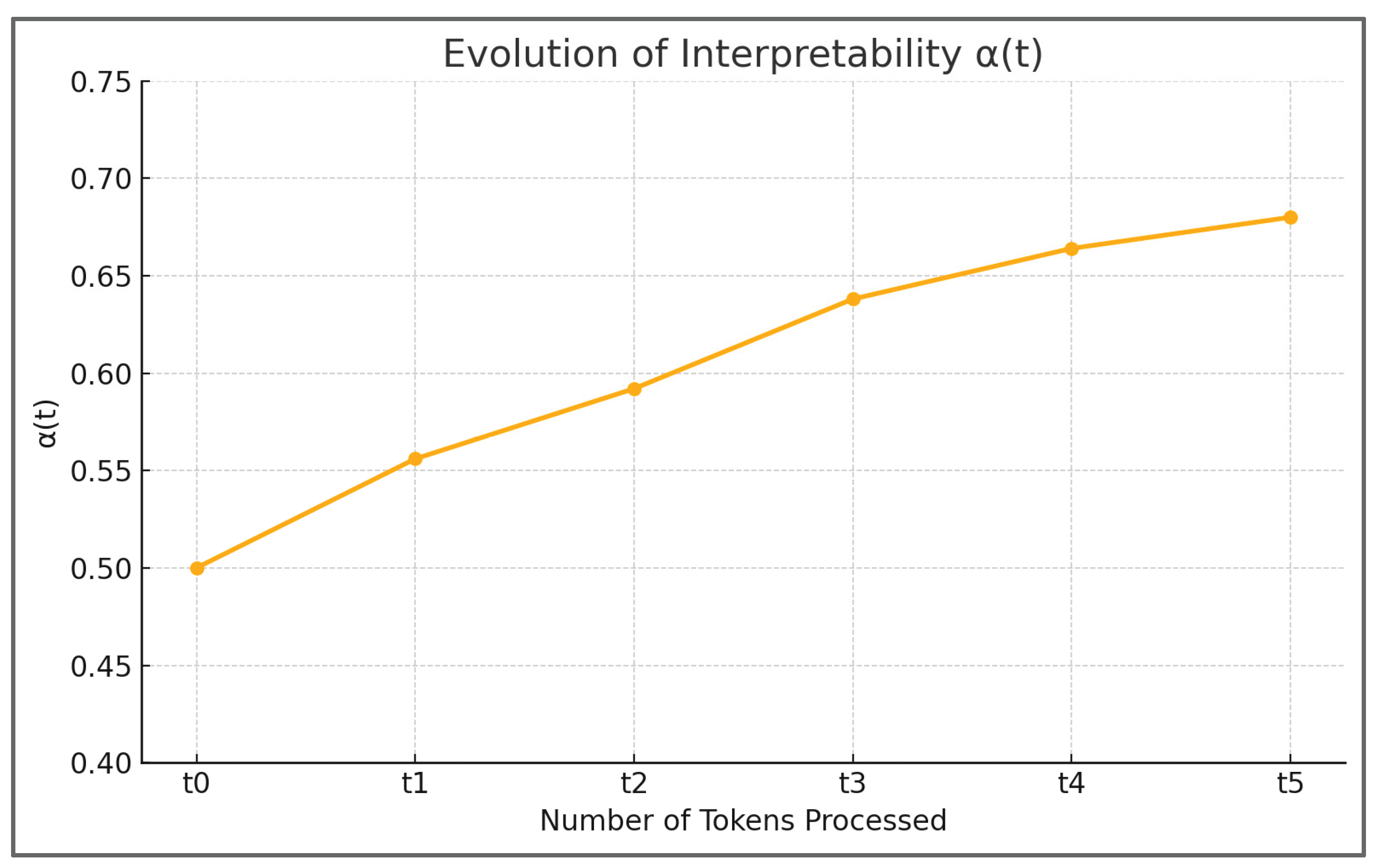
As shown in Figure 1, α(t) increases from 0.50 to 0.68 after five tokens, indicating that 68% of the model’s decision-making process has been successfully translated into a narrative explanation. This visual representation not only quantifies the gain in interpretability but also emphasizes the role of token-by-token analysis in building a coherent explanatory story. Unlike static methods such as SHAP or LIME, this dynamic curve allows analysts to track how each explanatory element impacts the overall clarity of the decision-making process.

While this example uses simple heuristics and simulated data, the same logic can be applied to real machine learning and deep learning models by adapting the token generation layer to extract meaningful features (e.g., filters from CNNs or attention weights from Transformers). This narrative-driven approach is what distinguishes Talking to Blackbox from traditional XAI tools.

The pipeline can be summarized as: Input Data → Blackbox Prediction → Token Generation → Epistemic Field Evaluation (hPhy, iFlw, cMth) → α(t) Update → Narrative Synthesis (P). The resulting explanation includes both quantitative indicators (α(t), token weights) and qualitative descriptions, offering a hybrid perspective that blends technical rigor with narrative understanding [10,12].

Finally, the proposed methodology is flexible and model-agnostic. It can be adapted to various types of machine learning and deep learning systems, including CNNs, Transformers, ensemble methods, and time-series models. Each model type simply requires a customized tokenization strategy (e.g., filters for CNNs, attention heads for Transformers) to extract interpretable features that can feed into the EANE pipeline.

This adaptability makes Talking to Blackbox a universal approach to XAI, capable of scaling across multiple domains and complexity levels [9,11].

Results

The proof of concept confirmed that Talking to Blackbox can progressively convert opaque model reasoning into a coherent narrative explanation by leveraging the incremental growth of α(t). Starting with an initial baseline of 0.50, the interpretability measure increased to 0.68 after processing five explanatory tokens.

This progression illustrates that each token contributes a measurable improvement, enabling a cumulative understanding of the blackbox’s internal logic. The approach validates the hypothesis that interpretability can be treated as a dynamic variable rather than a static snapshot.

The narrative generated by the pipeline demonstrates how explanatory tokens can create a meaningful storyline that mirrors the blackbox’s decision-making process. For instance, in the weather forecasting PoC, the combination of “falling pressure,” “high humidity,” and “strong winds” directly reflects the model’s probabilistic reasoning about rainfall. This is a significant departure from static feature attribution methods, as it captures not only which features matter but also how they interact over time. By treating tokens as semantic elements in a narrative, the framework aligns interpretability with the way humans naturally reason.

Another key observation is the role of the epistemic fields iFlw, hPhy, and cMth in shaping the interpretability curve. When iFlw dominates over hPhy and cMth, α(t) grows steadily, indicating that the narrative is coherent and consistent. Conversely, if hPhy (semantic tension) or cMth (logical collapse) were higher, the curve would stagnate or decline, signaling that the explanation is incomplete or contradictory. This dynamic offers a new way to monitor and audit the quality of interpretability in real time, which is rarely addressed by classical XAI tools [4,5,6]. The PoC also highlighted the framework’s adaptability. While the current example is focused on a weather forecasting model, the same pipeline could be applied to a variety of machine learning and deep learning systems, including CNNs for image recognition, Transformers for language modeling, and even reinforcement learning agents. Each of these models can be translated into tokens relevant to its domain (e.g., “edge detection” or “attention focus”), allowing the Talking to Blackbox architecture to produce both narrative and quantitative explanations.

In addition, the results demonstrate how the dual nature of the output—combining narrative summaries and interpretability metrics—enhances trust and comprehension. A narrative explanation stating that “the rain prediction is dominated by falling pressure (0.30) and high temperature (0.25)” is more intuitive than a list of static coefficients or probabilities.

By coupling such explanations with α(t) values, the framework provides both qualitative insights and a numeric measure of confidence in the explanation.

From this perspective, the incremental design of Talking to Blackbox makes it a strong candidate for integration with regulatory and auditing frameworks that require transparency. By presenting a clear sequence of explanatory steps and their impact on α(t), the framework supports accountability and reproducibility.

This characteristic is especially relevant in sectors like healthcare and finance, where interpretability is not just desirable but legally mandated. The results of the PoC indicate that the framework could serve as both a diagnostic tool and an interpretability layer for real-world AI systems.

Here is a comparative table contrasting the Talking to Blackbox framework with other popular XAI methods (SHAP, LIME, and Counterfactual Explanations). This table (Comparative Analysis of Talking to Blackbox vs. Other XAI Methods) can be added to P4 (Results) after the narrative description:

Criterion	Talking to Blackbox	SHAP [4]	LIME [5]	Counterfactuals [10]
Explanation Type	Dynamic, narrative with token evolution (α(t))	Static, feature contribution values	Static, local surrogate model	Hypothetical “what-if” scenarios
Interpretability Metric	α(t) tracks progressive clarity (0–1)	SHAP value magnitudes	Feature weights in local approximation	Binary plausibility of alternative outcomes
Temporal Aspect	Iterative and evolving explanations	No temporal tracking	Single-step explanation	Single counterfactual per query
Narrative Structure	Tokens form coherent storylines	None (list of feature values)	Limited textual descriptions	Scenario-based but not narrative
Epistemic Fields	Uses iFlw, hPhy, cMth, wThd to assess explanation	Not applicable	Not applicable	Not applicable
Model Agnostic?	Yes, adaptable to CNNs, LLMs, GANs, RL	Yes	Yes	Yes
Human-Centric View	Emphasizes storytelling and interpretability	Quantitative focus	Quantitative focus	Hypothetical examples
Strengths	Dynamic, intuitive, narrative-oriented	Strong theoretical foundation	Simple and easy to implement	Provides actionable “what-if” insights
Limitations	Tokenization heuristics, no standard α(t) benchmarks	Static, lacks narrative context	Instability with different seeds	No dynamic interpretability metric

Discussion

The results of the Talking to Blackbox PoC reveal a significant departure from classical XAI approaches. Methods like SHAP [4] and LIME [5] focus on computing static feature importance scores for individual predictions, which, while valuable, do not provide a dynamic sense of how interpretability evolves over time.

In contrast, our framework introduces a progressive model of explanation through α(t), which grows iteratively as tokens are processed. This dynamic process better reflects human reasoning, where understanding develops incrementally rather than instantaneously.

Another key distinction lies in the narrative dimension. SHAP and LIME output lists of feature contributions, often visualized as bar charts or summary plots, but these artifacts rarely form a coherent storyline. Talking to Blackbox bridges this gap by generating explanatory tokens that naturally assemble into a narrative, providing not only “what matters” but also “why and how” the features interact. This qualitative dimension aligns with research advocating for interpretable models that communicate reasoning rather than just statistical associations [6,7]. The framework’s reliance on epistemic fields—hPhy, cMth, iFlw, and wThd—adds a second layer of analysis absent in most XAI methods. These fields serve as “meta-indicators” of explanation quality, measuring narrative coherence (iFlw), semantic tension (hPhy), and points of logical uncertainty (cMth). This approach is conceptually related to the idea of causal interpretability discussed by Pearl [12] and counterfactual explanations explored by Wachter et al. [10], but it extends these concepts into a structured, time-evolving narrative form.

When compared to counterfactual methods—which generate “what-if” scenarios by altering input variables—Talking to Blackbox focuses instead on translating the original reasoning into an interpretable narrative without perturbing the data. This ensures that the explanation remains anchored in the actual decision-making logic of the model. Furthermore, the incremental growth of α(t) provides a built-in metric of how much of the blackbox has been “unfolded” into P, something that static counterfactuals cannot measure.

The discussion also highlights the framework’s adaptability across model types. While SHAP and LIME are primarily suited for tabular or simple image models, Talking to Blackbox can be applied to CNNs, LLMs, GANs, and reinforcement learning agents by tailoring the tokenization step. For example, filters in CNNs can be translated into tokens like “edge detection” or “color cluster,” while attention heads in Transformers can be represented as “contextual focus” tokens. This flexibility positions our approach as a universal narrative layer for complex AI systems.

From an ethical and regulatory perspective, the narrative structure of Talking to Blackbox has particular advantages. Regulatory frameworks, such as the EU AI Act, emphasize the importance of explainability and transparency for high-risk AI applications.

A narrative explanation enriched with α(t) and epistemic fields not only provides technical insights but also presents them in a form accessible to non-technical stakeholders. This can enhance trust, accountability, and compliance, aspects that traditional feature-attribution methods often fail to address effectively.

Lastly, this framework opens the door to human-AI collaboration. By providing explanations in an incremental and narrative manner, Talking to Blackbox allows human analysts to engage with the decision-making process, validate or challenge specific tokens, and even guide the explanation process.

This interactive aspect resonates with the Heuristic Convergence Theorem [3], which suggests that truth emerges from the synthesis of partial perspectives. In essence, Talking to Blackbox is not just explaining a model—it is facilitating a dialogue between the model and its users.

Future Research Implications

One promising direction for future work is the integration of Talking to Blackbox with self-explaining large language models (LLMs).

By using LLMs as both blackboxes and narrative generators, the framework could enable a two-layer explanation process, where tokens derived from the LLM’s attention patterns or hidden states are translated into narrative components and then refined by the model itself. This approach aligns with current efforts to develop chain-of-thought explanations, but with the added benefit of dynamic interpretability tracking via α(t).

Another area of research is the adaptation of this framework to multi-modal AI systems, where explanations must bridge textual, visual, and numerical data.

For example, in medical imaging, a CNN might detect patterns in radiographs while a parallel narrative layer describes these patterns in clinical terms (e.g., “shadowing in the left lung with 0.25 weight”). Integrating such explanations with time-series data or patient histories could yield comprehensive, narrative-rich insights that are both accurate and interpretable.

Finally, the principles of Talking to Blackbox could be combined with interactive visualization techniques to create explainability dashboards where users can observe the real-time evolution of α(t), monitor the contributions of iFlw, hPhy, and cMth, and even adjust tokenization parameters to see how interpretability changes.

Such tools could become standard components of AI auditing pipelines, enabling both technical and non-technical stakeholders to gain a deeper understanding of complex models.

Limitations

Although the Talking to Blackbox framework introduces a novel approach to narrative explainability, it is important to acknowledge its conceptual and technical limitations. The first limitation lies in the heuristic nature of token generation. In the current proof of concept, tokens are created manually from domain-specific rules (e.g., mapping weather variables to descriptive tokens such as “falling pressure” or “high humidity”). While this approach effectively demonstrates the concept, automating token extraction for complex models—especially those with thousands of features or abstract latent representations—remains an open challenge.

A second limitation involves the subjectivity of token interpretation. Even when tokens are extracted algorithmically, their semantic meaning may vary across domains or applications. Unlike SHAP or LIME, which provide mathematically grounded feature attributions [4,5], our narrative tokens rely on linguistic constructs that may require expert validation. This raises questions about how to ensure consistency, reproducibility, and domain-specific accuracy when deploying the framework at scale.

Another constraint is the lack of standard benchmarks for measuring α(t). While the interpretability metric α(t) quantifies the fraction of NP converted to P, there is no universally accepted way to evaluate whether this fraction accurately reflects “true” human interpretability. Existing XAI benchmarks typically focus on fidelity and stability [6,7], but they do not account for the narrative quality or incremental nature of explanations. Therefore, additional studies are needed to establish evaluation metrics tailored to narrative-based XAI.

The computational cost of applying the framework to large-scale models is also a potential bottleneck. For deep neural networks, generating tokens and evaluating epistemic fields (hPhy, iFlw, cMth) across multiple layers could be computationally expensive. While our PoC operates on a small-scale example, scaling to models with billions of parameters, such as LLMs or advanced multimodal architectures, would require optimized tokenization strategies and possibly parallelized field evaluation pipelines. The current implementation is proof-of-concept only and has not been validated on real-world datasets or production-level AI systems. While the conceptual results are promising, further work is needed to verify the robustness and generalizability of the approach under different conditions (e.g., noisy inputs, adversarial settings, or high-dimensional feature spaces).

This highlights the need for systematic experimentation and quantitative comparison with classical XAI methods to ensure that the proposed narrative explanations are both faithful and reliable.

Future Work

Future research on Talking to Blackbox will focus on automating the token generation process. While the current proof of concept relies on heuristic mappings of input variables to narrative tokens, a more robust system could leverage feature clustering, attention weights, or saliency maps to automatically derive tokens in a data-driven manner.

Such an approach would improve scalability and reduce manual intervention, enabling deployment in high-dimensional and multimodal models.

Another avenue of development involves integrating the framework with self-explaining large language models (LLMs). By combining token extraction with chain-of-thought mechanisms and attention analysis, it would be possible to create a two-layer explanation process: the first layer would extract and score tokens, while the second would generate a coherent narrative in natural language.

This would allow Talking to Blackbox to serve as a meta-explanation engine for advanced LLMs, making their outputs more interpretable.

Expanding to multi-modal and cross-domain contexts is also a priority. Models that combine textual, visual, and numerical data, such as those used in healthcare or autonomous driving, could benefit from narrative explanations that synthesize multiple information channels.

For example, in a medical imaging system, tokens might describe both image-based patterns (e.g., “shadow in left lung”) and patient metadata (e.g., “elevated temperature”), creating an integrated storyline of the decision-making process.

Another promising direction is the development of interactive dashboards for real-time interpretability. By visualizing the evolution of α(t) alongside the cumulative contributions of iFlw, hPhy, and cMth, analysts could dynamically explore how each token affects the narrative clarity. This interactive layer would also enable domain experts to adjust token relevance or highlight inconsistencies, effectively turning the explanation into a human-AI collaborative process.

Finally, future work should include formal benchmarking and validation of α(t) and the narrative quality produced by the framework. This includes comparing Talking to Blackbox with state-of-the-art XAI methods, testing on real-world datasets (e.g., medical diagnostics, climate forecasting, financial risk assessment), and conducting user studies to evaluate how narrative explanations affect trust and decision-making.

By combining empirical validation with theoretical refinement, the framework could evolve into a standardized narrative XAI toolkit.

Conclusion

This work introduced Talking to Blackbox, a novel framework for narrative explainability that leverages the symbolic principle P + NP = 1 to progressively translate opaque model reasoning into interpretable narratives.

The equation P + NP = 1 is the conceptual foundation of the framework, symbolizing that any computational system can be understood as a blend of interpretable components (P) and non-interpretable complexity (NP), which together constitute the entire decision process.

In this formulation, P represents the fraction of the model’s logic that is already clear and verifiable, while NP denotes the remaining opacity. By design, P = α(t) and NP = 1 − α(t), where α(t) dynamically measures the portion of interpretability achieved at time t. This creates a closed-form balance where every increment in P corresponds to a reduction in NP.

To model the transition from NP to P, the framework introduces the equation α(t+1) = α(t) + η · (iFlw − hPhy − cMth), which acts as the iterative engine for narrative growth. Here, η is the interpretation rate (0 < η < 1), regulating how quickly new tokens improve the interpretability measure. The terms iFlw (intention flow), hPhy (heuristic physics), and cMth (collapse mathematics) represent the dynamic forces influencing α(t): iFlw contributes positively to clarity, while hPhy and cMth act as resistances, capturing semantic tension and logical collapse points within the explanation. By interpreting α(t) as a time-varying interpretability score, the framework captures the gradual unfolding of the blackbox logic into a comprehensible narrative. For example, in the weather forecasting PoC, α(t) started at 0.50 (neutral baseline) and increased to 0.68 as five explanatory tokens were processed. Each token adjusted α(t) according to its weight and the prevailing epistemic fields. A high iFlw value indicates that the token strongly aligns with the overall reasoning (e.g., “falling pressure”), while a higher hPhy would indicate narrative tension or contradictory signals that slow down interpretability growth.

This dynamic approach highlights the dual nature of the equation: it is both quantitative and narrative. Quantitatively, it provides a metric for measuring how much of the blackbox has been translated into interpretable reasoning.

Narratively, it structures the explanation as a process—each step corresponds to the absorption of a new token into P, thereby reducing NP. In essence, P + NP = 1 is not just a static equality but a living process of convergence, where the narrative clarity of P emerges as NP is progressively “decoded” through heuristic fields and intentional flow.

The equation P + NP = 1 should not be understood merely as a mathematical identity, but as a symbolic representation of co-evolutionary balance between clarity (P) and potential complexity (NP). In this view, P symbolizes structured, interpretable knowledge — akin to deterministic or polynomial-time solutions — while NP represents the ambiguous, creative, or intractable aspects of a problem space. The sum of P and NP equates to unity (1), indicating that any reasoning field is composed of both clarity and complexity, which coexist in dynamic equilibrium. This interpretation mirrors the discussion in the article, where P and NP are framed as complementary forces akin to harmony and melody in music, or order and chaos in natural systems.

The dynamic evolution of this balance can be modeled using the interpretability measure α(t), which quantifies the fraction of NP converted into P over time: P = α(t) and NP = 1 − α(t). The equation α(t+1) = α(t) + η · (iFlw − hPhy − cMth) expresses how interpretability increases with each reasoning step, where iFlw (intention flow) drives the narrative clarity, while hPhy (heuristic physics) and cMth (collapse mathematics) represent opposing forces such as semantic tension and logical collapse. This structure resonates with the Wisdom Turing Machine (WTM) framework described in the article, where reflective cycles of reasoning compress ambiguity into clarity through intentional curvature and ethical alignment.

Moreover, the symbolic equation highlights that complexity is not a static obstacle but a transformable field. The notion of co-evolutionary reasoning, as explored in the article, implies that systems can iteratively harmonize P-like and NP-like states by integrating compression, reflection, and narrative synthesis. This is seen, for example, in the concept of NP-collapsible subdomains, where structural patterns allow intractable problems to be partially compressed into tractable solutions. Thus, the equation P + NP = 1 acts as a conceptual compass, guiding reasoning architectures to view ambiguity as a source of potential clarity rather than as an unsolvable barrier.

Unlike classical XAI methods such as SHAP [4] and LIME [5], which offer static feature importance scores, our approach models interpretability as a dynamic variable α(t) that evolves with each explanatory token. This incremental process not only quantifies the clarity of the explanation but also provides a natural, human-friendly narrative describing how the model’s decision emerges.

The proof of concept in a weather forecasting scenario demonstrated how tokens like “falling pressure” or “high humidity” can be combined with epistemic fields—hPhy, iFlw, and cMth—to form a coherent storyline that mirrors the blackbox’s logic. The interpretability measure α(t) increased from 0.50 to 0.68, showing that the majority of the model’s rationale was successfully translated into P (interpretable knowledge). This narrative approach bridges the gap between quantitative metrics and qualitative insights, offering an explanation that is both measurable and understandable.

Furthermore, the Talking to Blackbox framework aligns with the principles of the Wisdom Machine (WM) architecture [2] and the Heuristic Convergence Theorem [3], which emphasize the synthesis of partial perspectives to reveal hidden structures of reasoning.

By introducing narrative tokens as units of semantic interpretation and using epistemic fields to track their coherence, the framework provides a more holistic view of interpretability, one that can adapt across various types of machine learning and deep learning models.

The implications of this work are significant for high-stakes applications where trust and accountability are essential. Narrative explanations enriched by α(t) could help practitioners and decision-makers not only understand model predictions but also audit and validate them in real time. This aligns with the growing regulatory demand for AI transparency and explainability, as seen in emerging global frameworks such as the EU AI Act.

In summary, Talking to Blackbox represents a step toward a new generation of explainable AI—one that combines dynamic interpretability metrics with narrative clarity.

By shifting the focus from static feature importance to a process of progressive understanding, the framework opens the door to more trustworthy, collaborative, and human-centric AI systems.

License and Ethical Disclosures

This work is published under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.

You are free to:

Share — copy and redistribute the material in any medium or format

Adapt — remix, transform, and build upon the material for any purpose, even commercially

Under the following terms:

Attribution — You must give appropriate credit to the original author (“Rogério Figurelli”), provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner but not in any way that suggests the licensor endorses you or your use.

The full license text is available at:

https://creativecommons.org/licenses/by/4.0/legalcode

Ethical and Epistemic Disclaimer

This document constitutes a symbolic architectural proposition. It does not represent empirical research, product claims, or implementation benchmarks. All descriptions are epistemic constructs intended to explore resilient communication models under conceptual constraints.

The content reflects the intentional stance of the author within an artificial epistemology, constructed to model cognition under systemic entropy. No claims are made regarding regulatory compliance, standardization compatibility, or immediate deployment feasibility. Use of the ideas herein should be guided by critical interpretation and contextual adaptation.

All references included were cited with epistemic intent. Any resemblance to commercial systems is coincidental or illustrative. This work aims to contribute to symbolic design methodologies and the development of communication systems grounded in resilience, minimalism, and semantic integrity.

Use of AI and Large Language Models

AI tools were employed solely as methodological instruments. No system or model contributed as an author. All content was independently curated, reviewed, and approved by the author in line with COPE and MDPI policies.

Ethics Statement

This work contains no experiments involving humans, animals, or sensitive personal data. No ethical approval was required.

Author Contributions

Conceptualization, design, writing, and review were all conducted solely by the author. No co-authors or external contributors were involved.

Data Availability Statement

No external datasets were used or generated. The content is entirely conceptual and architectural.

Conflicts of Interest

The author declares no conflicts of interest. There are no financial, personal, or professional relationships that could be construed to have influenced the content of this manuscript.

References

R. Figurelli, What if P + NP = 1? A Multilayer Co-Evolutionary Hypothesis for the P vs NP Millennium Problem, Preprints.org, 2025. [Online]. Available. [CrossRef]
R. Figurelli, Heuristic Layering: Structuring AI Systems Beyond End-to-End Models, Preprints.org, 2025. [Online]. Available. [CrossRef]
R. Figurelli, The Heuristic Convergence Theorem: When Partial Perspectives Assemble the Invisible Whole, Preprints.org, 2025. [Online]. Available. [CrossRef]
M. T. Ribeiro, S. M. T. Ribeiro, S. Singh, and C. Guestrin, "Why Should I Trust You?: Explaining the Predictions of Any Classifier," Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), pp. 1135–1144, 2016. [Online]. Available. [CrossRef]
S. M. Lundberg and S. Lee, "A Unified Approach to Interpreting Model Predictions," Proc. 31st Conference on Neural Information Processing Systems (NeurIPS), 2017. [Online]. Available: https://arxiv.org/abs/1705. 0787.
C. Molnar, Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, 2nd ed., Leanpub, 2022. [Online]. Available: https://christophm.github.
F. Doshi-Velez and B. Kim, "Towards A Rigorous Science of Interpretable Machine Learning," arXiv preprint, 2017. [Online]. Available: https://arxiv.org/abs/1702. 0860.
D. Baehrens, T. Schroeter, S. Harmeling, M. Kawanabe, K. Hansen, and K.-R. Mueller. How to Explain Individual Classification Decisions. Journal of Machine Learning Research 2010, 11, 1803–1831. [Google Scholar]
W. Samek, T. Wiegand, and K.-R. Mueller. Explainable Artificial Intelligence: Understanding, Visualizing and Interpreting Deep Learning Models. IT Professional 2019, 21, 31–41. [Google Scholar]
Adadi and, M. Berrada. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
Z. C. Lipton. The Mythos of Model Interpretability. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
J. Gilpin, D. Bau, B. Zoran, I. Yosinski, and D. E. Bau. Explaining Explanations: An Overview of Interpretability of Machine Learning. Proc. IEEE 2021, 109, 251–266. [Google Scholar]
J. Pearl, Causality: Models, Reasoning and Inference, 2nd ed., Cambridge University Press, 2009.
S. Wachter, B. Mittelstadt, and C. Russell. Counterfactual Explanations without Opening the Black Box: Automated Decisions and the GDPR. Harvard Journal of Law & Technology 2018, 31, 841–887. [Google Scholar]
L. Floridi and J. Cowls, "A Unified Framework of Five Principles for AI in Society," Harvard Data Science Review, 2019. [Online]. Available. [CrossRef]
D. Gunning, "Explainable Artificial Intelligence (XAI)," Defense Advanced Research Projects Agency (DARPA), 2017. [Online]. Available: https://www.darpa.
G. Montavon, W. Samek, and K.-R. Müller. Methods for Interpreting and Understanding Deep Neural Networks. Digital Signal Processing 2018, 73, 1–15. [Google Scholar] [CrossRef]
Y. Bengio, I. Y. Bengio, I. Goodfellow, and A. Courville, Deep Learning, MIT Press, 2016.

Figure 1. Evolution of interpretability α(t) as explanatory tokens are processed in a weather forecasting example. Each step corresponds to the addition of a token (e.g., “falling pressure” or “high humidity”), with the curve showing the cumulative growth of interpretability.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.