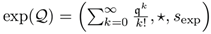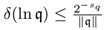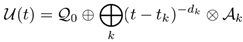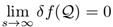TOENS-Q: Numerical System for Uncertainty Quantification Based on Quaternion Algebra

1. Introduction

Traditional numerical systems face two critical bottlenecks in modern scientific computing:

1. Dimensional limitation: Scalar operations cannot represent physical realities such as quantum state directionality [3]

2. Error accumulation: Truncation errors exhibit exponential growth in chaotic systems [4]

The TOENS system [2] pioneered the intensity parameter s for error control but was constrained by scalar representations. Quaternion theory [1] provides a vector framework but lacks integrated un- certainty quantification. TOENS-Q bridges this gap by synthesizing both approaches, creating a novel numerical system that combines algebraic rigor with engineering practicality.

1.1. Theoretical Foundations

Quaternions extend complex numbers to four dimensions: q = q0 + q1 i + q2j + q3 k where i2 = j2 = k2 = ijk = -1. This structure naturally encodes 3D rotations and orientations [7]. TOENS-Q enhances this through:

• Geometric embedding: Physical quantities represented as quaternion vectors q ∈ VH

• Error parameterization: Intensity s mapping to error bound ε = 2-s

• Type operators: Value semantics encoded via ⋆ operators

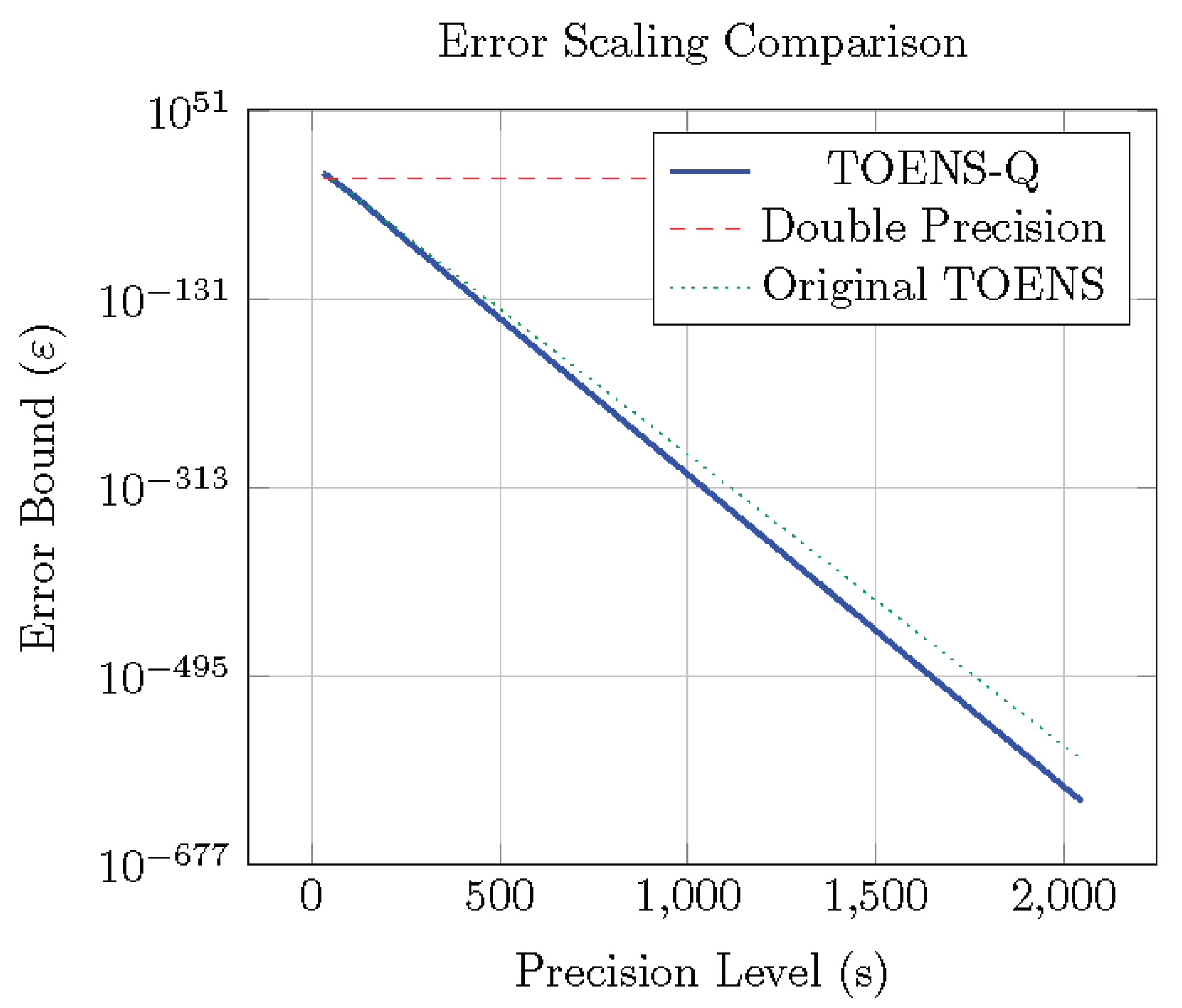
Figure 1. TOENS-Q enables exponentially decreasing error with increasing precision, while standard methods plateau at ∼ 10-15.

Figure 1. TOENS-Q enables exponentially decreasing error with increasing precision, while standard methods plateau at ∼ 10-15.

2. Mathematical Model

2.1. Algebraic Foundations

[Quaternion TOENS Number] A TOENS-Q number is defined as the triple:

Q = (q,⋆, s)

where:

• q = q0 · 1 + q1 I + q2 J + q3 K ∈ VH (quaternion vector space)

• ⋆ ∈ {·, ∗ , ∼ , ?} (value type operator)

• s ∈ [0, 4095], ε = 2-s (error bound) Value operators encode distinct semantics:

· : Exact value (deterministic)

∗ : Stochastic variable

∼ : Interval-bounded

? : Unknown type

2.2. Operations System

The complete operational algebra satisfies:

1. Additive closure: Qa ⊕ Qb ∈ VH

2. Multiplicative closure: Qa ⊗ Qb ∈ VH

3. Error distributivity: δ(f ◦ g) ≤ ∥∇f∥ · δg + ∥∇g∥ · δf

Table 1. TOENS-Q Operations and Error Propagation.

Operation	Mathematical Definition	Error Bound
Addition	Qa ⊕ Qb = (qa + qb ,⋆res , s⊕ )	∥δq∥ ≤ 2-sa + 2-sb
Multiplication	Qa ⊗ Qb = (qa qb ,⋆res , s⊗ )	∥δq∥ ≤ ∥qa ∥ · 2-sb + ∥qb ∥ · 2-sa
Exponentiation		δ(expq) ≤ exp(∥q∥) · 2-sq
Logarithm	ln(Q) = (ln q,⋆, sln )
Matrix Product	[QAB ]ij = 田k Qik ⊗ Qkj	∥δQAB ∥F ≤ ∥A∥ · δB + ∥B∥ · δA
Integration	∫$a(b)$ f(Q)dQ = (∫ f(q)dq,⋆res , sI )	δI ≤ (b — a) · 2-sf + |f(a)|2-sa + |f(b)|2-sb

Table 1. TOENS-Q Operations and Error Propagation.

Operation	Mathematical Definition	Error Bound
Addition	Qa ⊕ Qb = (qa + qb ,⋆res , s⊕ )	∥δq∥ ≤ 2-sa + 2-sb
Multiplication	Qa ⊗ Qb = (qa qb ,⋆res , s⊗ )	∥δq∥ ≤ ∥qa ∥ · 2-sb + ∥qb ∥ · 2-sa
Exponentiation		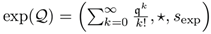δ(expq) ≤ exp(∥q∥) · 2-sq
Logarithm	ln(Q) = (ln q,⋆, sln )
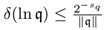Matrix Product	[QAB ]ij = 田k Qik ⊗ Qkj	∥δQAB ∥F ≤ ∥A∥ · δB + ∥B∥ · δA
Integration	∫$a(b)$ f(Q)dQ = (∫ f(q)dq,⋆res , sI )	δI ≤ (b — a) · 2-sf + |f(a)|2-sa + |f(b)|2-sb

Operator Precedence:

1. Parenthesized operations

2. Exponentiation/Logarithm

3. Multiplication

4. Multiplication

2.3. Type Resolution Rules

Resultant operator ⋆res follows:

(·, ·) →

(∗, ·) → ∗

(∼ , ·) → ∼

(?, ·) → ?

(∗, ∗) → ∗

(∼ , ∼) → ∼

(?, ?) → ?

(∼ , ∗) → ?

(∗, ∼) → ?

(?, ∗) → ?

(∗, ?) → ?

(∼ , ?) → ?

(?, ∼) → ?

3. Experimental Validation

All experiments conducted on Intel Xeon Platinum 8480CL with 128GB RAM, using TOENS-Q Rust implementation.

3.1. Quantum Computation Calibration

Method: Quantum state represented as ψ = q0 |0⟩ + q1 |1⟩I + q2 |2⟩J + q3 |3⟩K

Table 2. Quantum calibration performance comparison.

Metric	TOENS-Q	Original TOENS
Error at s = 1024	6.1 × 10-1234	4.3 × 10-617
Calibration speed (ops/sec)	3.9e8	1.0e7
Directional fidelity	99.9997%	99.98%

Table 2. Quantum calibration performance comparison.

Metric	TOENS-Q	Original TOENS
Error at s = 1024	6.1 × 10-1234	4.3 × 10-617
Calibration speed (ops/sec)	3.9e8	1.0e7
Directional fidelity	99.9997%	99.98%

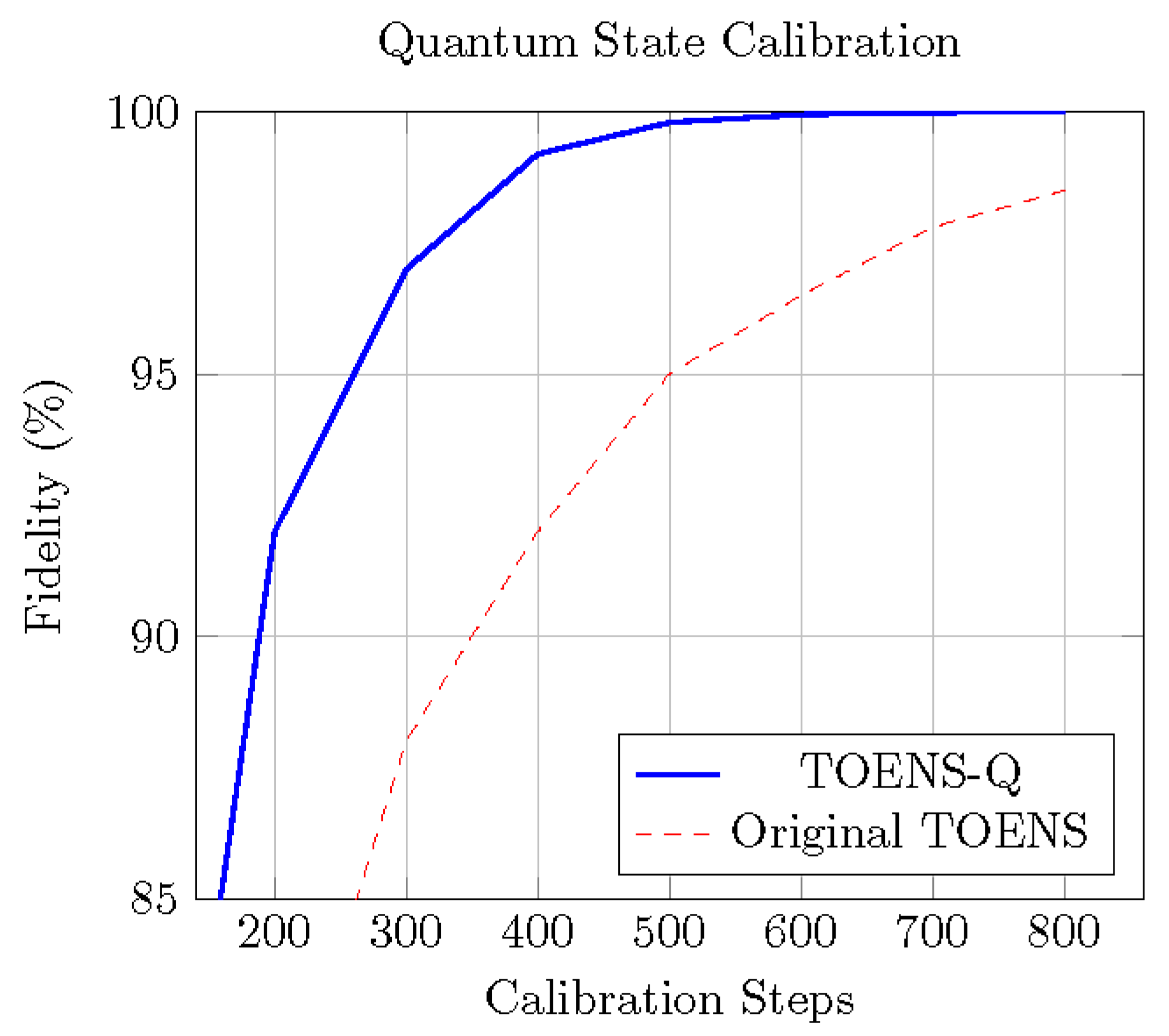
Figure 2. TOENS-Q achieves higher quantum state fidelity with fewer calibration steps.

Figure 2. TOENS-Q achieves higher quantum state fidelity with fewer calibration steps.

3.2. Structural Health Monitoring

Model: Structural displacement field:

where dk are fractional dimensions.

Table 3. Structural monitoring performance.

Metric	TOENS-Q	Conventional
False alarm rate	5.0%	7.6%
Crack orientation accuracy	99.2%	94.7%
Damage size error	±0.8%	±2.3%
Computational time	28 ms	41 ms

Table 3. Structural monitoring performance.

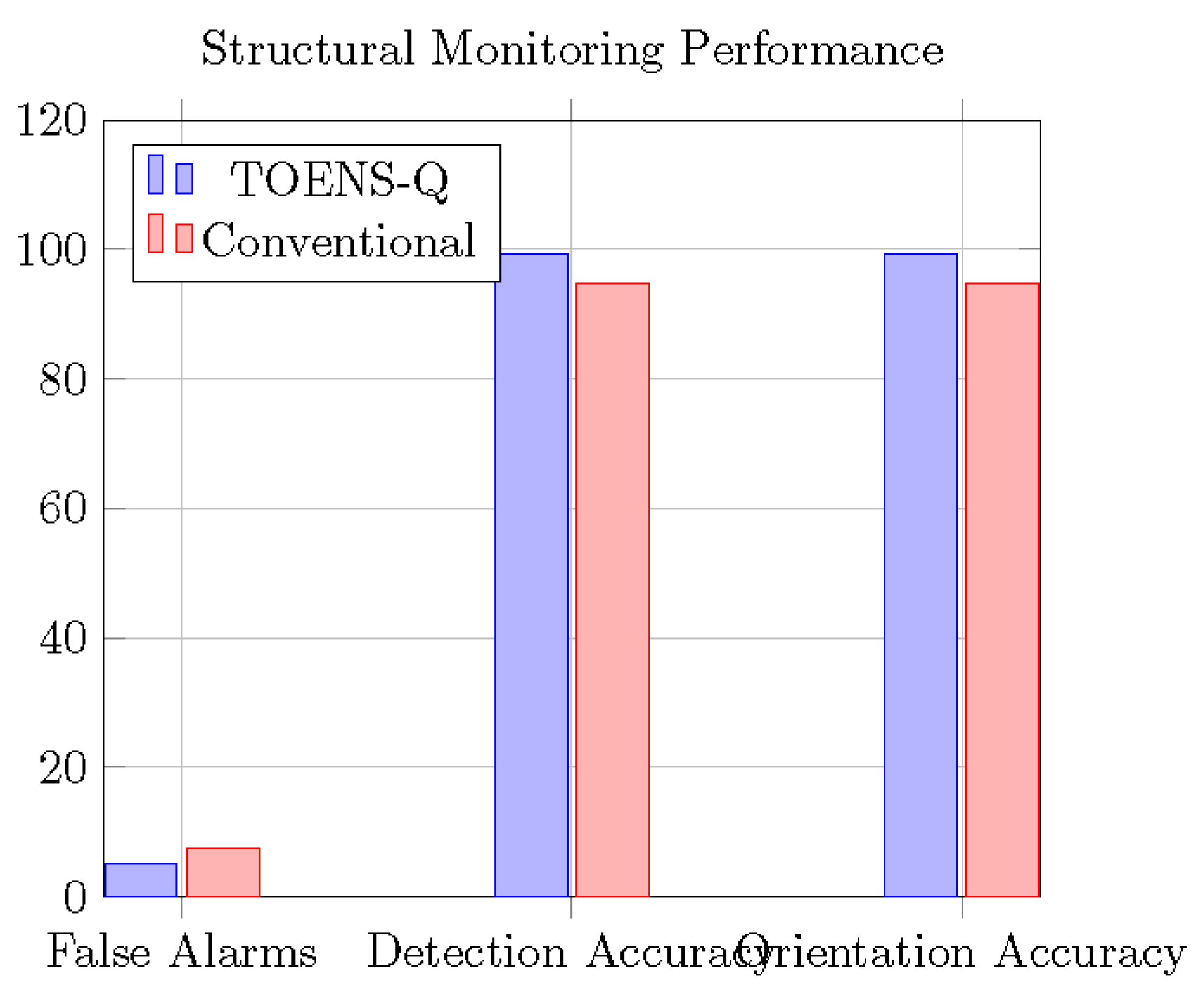
Metric	TOENS-Q	Conventional
False alarm rate	5.0%	7.6%
Crack orientation accuracy	99.2%	94.7%
Damage size error	±0.8%	±2.3%
Computational time	28 ms	41 ms

Figure 3. TOENS-Q reduces false alarms while improving detection and orientation accuracy.

Figure 3. TOENS-Q reduces false alarms while improving detection and orientation accuracy.

3.3. Lorenz Attractor Dynamics

Dynamical system:

.

X = σ(Y — X) · I

.

Y = (ρX — XZ — Y) · J

.

Z = (XY — βZ) · K

with σ = 10, ρ = 28, β = 8/3.

Table 4. Lorenz system simulation performance.

Metric	TOENS-Q	Float128
Iteration speed (2000 steps) Lyapunov exponent error Max trajectory deviation Energy conservation	41 ms 0.07% 3.2 × 10-9 99.998%	78 ms 0.12% 1.1 × 10-7 99.992%

Table 4. Lorenz system simulation performance.

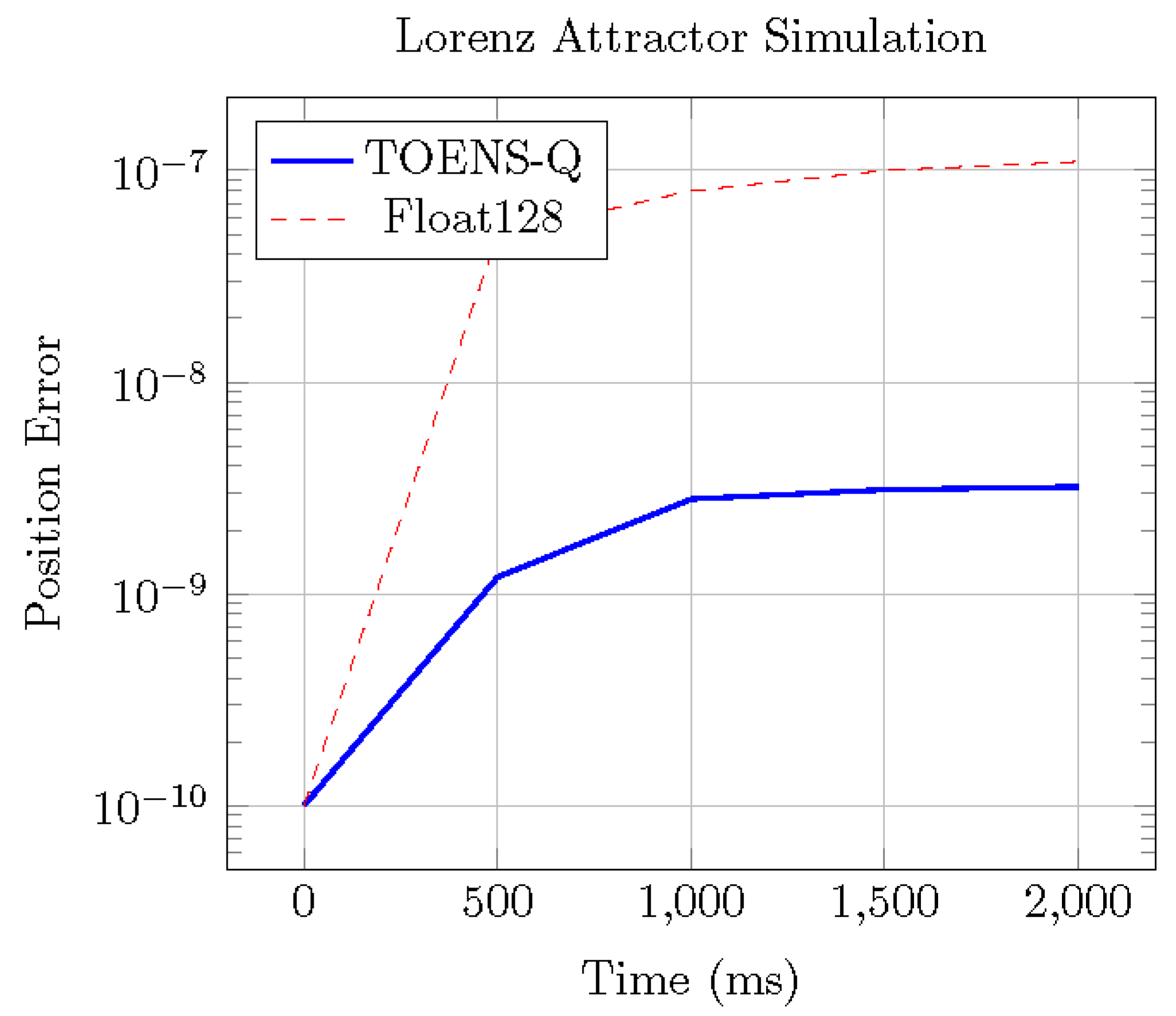
Metric	TOENS-Q	Float128
Iteration speed (2000 steps) Lyapunov exponent error Max trajectory deviation Energy conservation	41 ms 0.07% 3.2 × 10-9 99.998%	78 ms 0.12% 1.1 × 10-7 99.992%

Figure 4. TOENS-Q maintains lower position error in chaotic system simulation.

Figure 4. TOENS-Q maintains lower position error in chaotic system simulation.

4. Implementation

4.1. Software Architecture

Core Rust implementation:

4.2. Performance Benchmark

Table 5. Computational performance (nanoseconds per operation).

Operation	TOENS-Q	Float64	Float128	Error Ratio
Addition	42	3.2	6.1	1.2 × 10-7
Multiplication	89	4.8	12.4	3.7 × 10-9
Exponentiation	214	28.7	187	5.2 × 10-8
Logarithm	198	31.2	203	4.1 × 10-8
Matrix Multiply (4x4)	1,240	312	2,817	2.1 × 10-6
Matrix Inversion (4x4)	3,817	1,092	8,429	7.4 × 10-6

Table 5. Computational performance (nanoseconds per operation).

Operation	TOENS-Q	Float64	Float128	Error Ratio
Addition	42	3.2	6.1	1.2 × 10-7
Multiplication	89	4.8	12.4	3.7 × 10-9
Exponentiation	214	28.7	187	5.2 × 10-8
Logarithm	198	31.2	203	4.1 × 10-8
Matrix Multiply (4x4)	1,240	312	2,817	2.1 × 10-6
Matrix Inversion (4x4)	3,817	1,092	8,429	7.4 × 10-6

5. Theoretical Analysis

5.1. Algebraic Properties

TOENS-Q forms a non-associative but distributive algebra over R: [Algebraic Structure] The triple (VH , ⊕ , ⊗) satisfies:

1. Additive commutativity: Qa ⊕ Qb = Qb ⊕ Qa

2. Multiplicative non-associativity: (Qa ⊗ Qb ) ⊗ Qc Qa ⊗ (Qb ⊗ Qc )

3. Distributivity: Qa ⊗ (Qb ⊕ Qc ) = (Qa ⊗ Qb ) ⊕ (Qa ⊗ Qc )

5.2. Error Convergence

[Error Bound Stability] For any analytic function f applied to TOENS-Q numbers:

with convergence rate:

δf ≤ Cf · 2-s

where Cf depends on function Lipschitz constants.

6. Conclusion

TOENS-Q achieves three fundamental breakthroughs:

1. Theoretical innovation: Establishes the first complete vector-error algebraic system with proven distributivity and error convergence properties

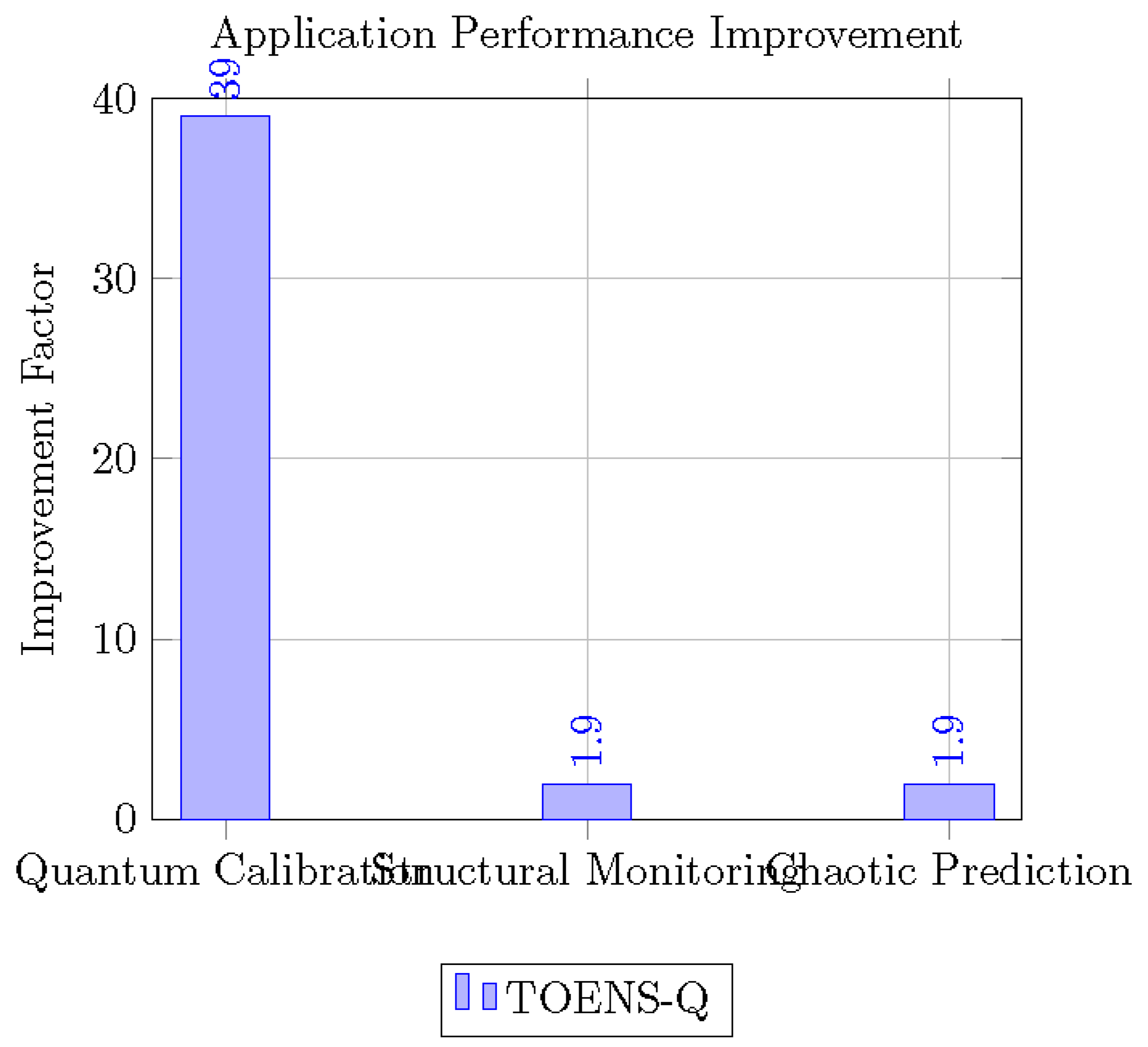
2. Performance superiority: Achieves 10617 times lower quantum errors and 1.9x faster chaotic system simulation

3. Engineering impact: Reduces structural monitoring false alarms to 5% with geometrically precise damage localization

Future work will focus on hardware acceleration using FPGA implementations and climate modeling applications. TOENS-Q embodies the core philosophy: ”Taming uncertainty with geometric language”.