Fractal Scaling Analysis of Storage Capacity Fluctuations in Well Logs from Southeastern Mexican Reservoirs

1. Introduction

The heterogeneity of petroleum reservoirs poses a significant challenge for their accurate characterization.

Variations in the petrophysical properties of reservoir rocks affect both storage capacity and fluid flow behavior, directly influencing hydrocarbon production performance within the reservoir [1,2,3,4]. In this context, the storage capacity in porous media associated with rock formations (oil or gas reservoirs) constitutes a key parameter to be determined. In the petroleum industry, the estimation and characterization of storage capacity, represented as $\varphi h$, is fundamental for the development of reservoir characterization models, with the aim of optimizing and maximizing hydrocarbon production [5,6,7].

The characterization of heterogeneities through petrophysical properties such as porosity $\varphi$ or storage capacity $\varphi h$ (where h denotes the thickness of the porous medium) has been widely investigated. These studies have been developed within both the Euclidean and fractal geometry frameworks, in response to the complex topology of porous networks.

Classical Euclidean models assume that the geometric forms of the porous medium are smooth, continuous, and differentiable functions. Examples of such approaches, which consider various pore configurations, can be found in [8,9,10,11,12]. In contrast, fractal models address this complexity by considering non-smooth curves—often continuous but non-differentiable in the Euclidean sense. This perspective has led to various research paths, among which the use of fractional calculus tools—such as fractional integro-differential equations—and fractal statistical analysis stands out, especially for identifying power-law behaviors with fractional exponents [13,15,16,17,19,20,21].

Nevertheless, within Euclidean-based characterization approaches, several relevant investigations have been conducted, such as the analysis of transient pressure tests. For example, in the model proposed by Flamenco et al. [22], storage ratios at different scales (0.0001, 0.01, 0.1, and 0.5) are used to generate pressure curves. These curves reflect transient pressure and production responses, which are influenced by the flow dynamics of the fluid within media of either Euclidean or fractal topology, as discussed in [16,27,28,29], when considering various pore structures and distributions.

On the other hand, in the laboratory-based experimental study conducted by Balankin et al. [29], two reservoirs were compared: one with a Euclidean porous structure and the other with fractal characteristics. The results indicate a greater loss of mechanical energy in the fluid flowing through the Euclidean reservoir compared to the fractal one, suggesting greater flow efficiency in fractal porous media.

In the context of real reservoir systems, local petrophysical measurements and interpretations from core and well data are commonly used to infer the predominant type of medium in the formation. By applying either Euclidean or fractal theoretical models, the goal is to describe the general properties of the formation [30,31,32,33]. Several studies based on scalar well logs have demonstrated that some formations exhibit fractal structures at multiple levels, such as core textures, pore distributions, fractures, stratigraphy, seismic faults, and flow capacities. These behaviors follow scaling laws and are governed by fractal dimensions [38,39,40,41,43].

Within this framework, the present study investigates whether scalar records obtained from the petrophysical interpretation and measurement of storage capacity—acquired from wells located in southeastern Mexico—exhibit fractal characteristics. Such characterization would allow the identification of zones with higher flow capacity, based on the fractal properties of the logs, in line with previous studies [29,43].

This work proposes a Euclidean and fractal classification derived from a statistical analysis of storage capacity records. A fractal statistical analysis of storage capacity records, focusing on identifying scaling trends in the fluctuations as a function of the observation window width $\delta$, using the theoretical framework of the Family–Vicsek dynamic scaling approach. Furthermore, this study investigates whether a complete $\varphi h$ information sequence can be characterized by a family of Hurst exponents associated with different sampling intervals, there by revealing heterogeneity in terms of short- and long-range correlations.

The structure of this paper is as follows: Section 2.1 outlines the study area, specifically the location of the wells from which the storage capacity logs $\varphi h$ were obtained. Section 2.2 presents the method based on the Family–Vicsek dynamic scaling theory, applying its mathematical formulation to the scalar $\varphi h$ records in order to analyze their fluctuations. Section 3 discusses and interprets the obtained results. Section 4 presents limitations and scope. Finally, Section 5 presents the main conclusions of the study.

2. Materials and Methods

2.1. Study Area

A hydrocarbon reservoir located in southeastern Mexico serves as the primary source of data used in this study for analyzing storage capacity records. This information, previously interpreted, calibrated, and evaluated, was employed to determine local storage capacities associated with several wells.

Specifically, five data series relating a petrophysical property to depth were analyzed. The storage capacity logs correspond to five wells located in the northern portion of southeastern Mexico. For confidentiality reasons, the following notation is used to refer to each well: scW1, scW2, scW3, scW4, and scW5, respectively.

The heterogeneity of the study area is illustrated through the description and observation of general features from both the region and core samples. The analysis focuses on four Cretaceous units: Breccia, Upper, Middle, and Lower Cretaceous.

Regarding the Breccia unit, data from core samples reveal marked heterogeneity associated with sedimentary variations, which suggests possible diagenetic changes both vertically and laterally. The observed facies correspond to dolomitized floatstone and rudstone, with varying degrees of fracturing and dissolution, resulting in porosity of variable size.

The degree of fracturing in the Breccia unit ranges from scarce to abundant and is commonly associated with good residual porosity and hydrocarbon saturation. Some core samples display significant vertical variability, with column sections where flow capacity is not uniformly distributed—i.e., interbedded intervals with lower porosity and permeability are identified. Matrix porosity associated with the generation of secondary intercrystalline porosity due to dolomitization is limited, implying a minor contribution to the effective flow of the rock. The porous medium presents dissolution cavities and moldic porosity connected through multidirectional fractures, which also exhibit good residual porosity and hydrocarbon impregnation.

In the KS and KM units, cryptocrystalline to mesocrystalline dolomite is observed, often clay-rich and/or enriched in organic matter, with the presence of stylolites. These units exhibit poor intercrystalline porosity and little evidence of significant dissolution; however, in some fractured zones, appreciable residual porosity is preserved. Additionally, abundant dissolution is reported, generating vugs between 1 and 2 cm in diameter, some of which are impregnated with hydrocarbons (see Figure 1(a)).

Other cores display microcrystalline dolomite with a dark gray base, attributable to clay and/or organic matter content, becoming cleaner toward the top. This dolomite exhibits low intercrystalline porosity, although centimeter-scale vugs are distributed throughout the core and are typically saturated with residual oil. At the top, a dolomitized breccia is present with small clasts, dissolution cavities, and partially open fractures impregnated with hydrocarbons.

In the Lower Cretaceous unit (KI), micro to mesocrystalline dolomite is identified, ranging in color from dark gray to black and possibly rich in organic matter. In some cases, this unit includes interbedded intraformational dolomitized conglomerates with light-colored clasts embedded in a dark matrix. Intercrystalline porosity is generally poor, although some sections exhibit abundant fracturing—partially cemented—along with residual porosity and oil saturation (see Figure 1(b)).

2.2. Methodology

The Family–Vicsek methodology is used to model phenomena associated with interface growth and has been widely applied to the analysis of time series in economic, biological, physical, and geological systems, among others [23,24,25,26]. The main goal of this methodology is to identify power-law dependencies in the temporal and spatial fluctuations observed in time series.

The metric used to capture this dependency is known as the q-th order structure function, $G_q(L,t)$. This function allows for the analysis of the scaling behavior of the q-th statistical moment (in particular, the roughness or standard deviation for $q=2$) as a function of the interface height with respect to the system size L.

In the specific case of spatial records of storage capacity, two scaling exponents are estimated to reveal the self-similar properties in the vertical and horizontal directions. These exponents are analogous to the parameters $\alpha$ and $\beta$ in the Family–Vicsek theory, known respectively as the roughness exponent (or Hurst exponent) and the growth exponent. Additionally, a third exponent, the dynamic exponent $z=\alpha /\beta$, is defined to assess the correlation between both directions.

The application of the structure function to records associated with storage capacity fluctuations can reveal a generic scaling behavior invariant with respect to spatial variables, provided there is correlation between them. In such cases, the behavior is expected to follow Equation (1) [34,35,36]:

$$G_q=\left\{\begin{array}{cc}{L}^{\alpha }\hfill & \mathrm{if}{t}^{*}\ll t\hfill \\ t^{\beta }\hfill & \mathrm{if}t\ll t^{*}\hfill \end{array}\right.$$

(1)

The function $G_q$ is referred to as the generalized q-th order moment function. More specifically, it is defined by Equation (2):

$$G_q={\left({\displaystyle \frac{1}{N-{\delta }_n}}\sum _{n=1}^{N-{\delta }_n}{\left|M_{n+{\delta }_n}-M_n\right|}^q\right)}^{1/q}$$

(2)

Here, N denotes the length of the series, and ${\delta }_n$ represents the observation window width, that is, the distance between pairs of values $M_{n+{\delta }_n}$ and $M_n$ within the fluctuation function constructed for this analysis (see Figure 2).

Furthermore, when the interface width $G_2(L,t)$ reaches saturation, the dynamic exponent z is used to determine the characteristic time $t^{*}$ as a function of the system size L, following the relation: $t^{*}\sim L^z$.

This study considers scalar records of storage capacity expressed as ${\varphi }_n\Delta h$, in order to analyze the scaling behavior of the fluctuation function. This function will hereafter be referred to as the relative storage capacity (RSC). The RSC (see Figure 2) is constructed by accumulating the storage capacities along the record, i.e.,

$$F\left({\varphi }_n\Delta h\right)=\sum _{i=1}^{n}M\left({\varphi }_i\Delta h\right)$$

This cumulative function is then fitted using a first-degree polynomial $\xi {\varphi }_n\Delta h$, and the RSC is defined as the difference between both terms, expressed mathematically by Equation (3):

$$RSC\left({\varphi }_n\Delta h\right)=F\left({\varphi }_n\Delta h\right)-\xi {\varphi }_n\Delta h$$

(3)

This is an example of a quote.

3. Empirical Results and Discussion

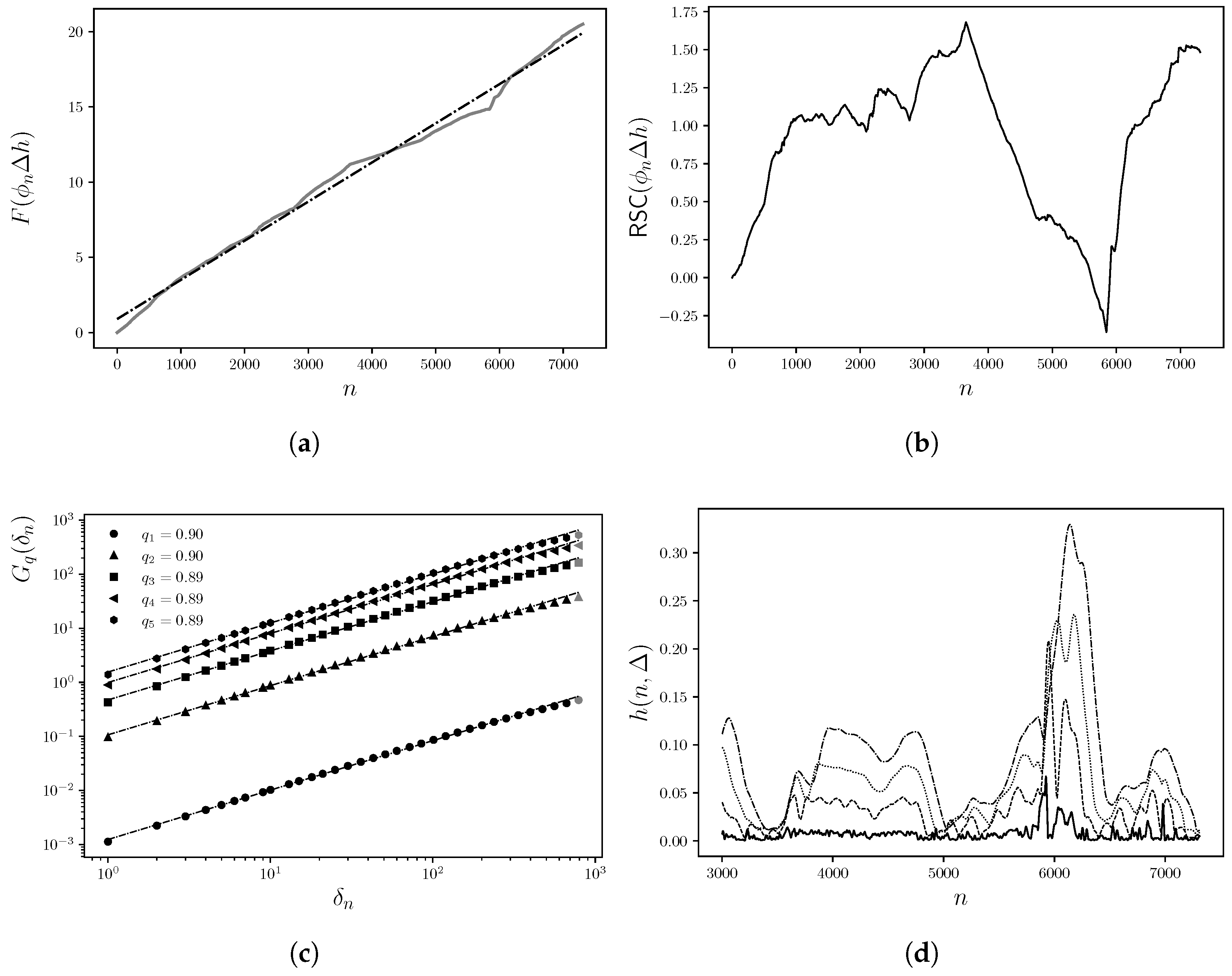
Results for Well scW1

The application of the structure function (Equation (2)) to the fluctuation function RSC (see Figure 2(b)) for well scW1 exhibits scaling behavior in the vertical direction along the y-axis, where $G_q\propto {\left({\delta }_n\right)}^H$ for $q=1,2,3,4,5$. This indicates that $G_q\left({\delta }_n\right)$ follows a power-law behavior across three orders of magnitude, revealing autocorrelation in the RSC with respect to depth (y) in the sampled records. Furthermore, this correlation is of long-range type, as $H_q=H=\alpha =0.93$ for all values of q analyzed. Therefore, the RSC fluctuations are classified as self-affine [38].

The exponents obtained, as well as those listed in Table 1, are of the same order as those reported by Yu et al. [15] for groundwater level fluctuations. On the other hand Dashian et al. [17] reports scaling or Hurst exponents ranging from $H=0.72$ to $H=0.99$ for well log data in large-scale porous media. The latter employed techniques such as spectral density $S\left(w\right)$, multifractal random walk (MFRW), and multifractal detrended fluctuation analysis (MF-DFA), considering records from various oil and gas fields.

Likewise, Hernández-Martinez et al. [33] demonstrated that porosity logs can be modeled through self-affine distributions characterized by two scaling exponents associated with the behavior of the fluctuation function, applied to complete well log sequences. Additionally, they present a spatial distribution of scaling exponents with respect to a reference facies pattern; however, such depth-dependent facies information is not always available. 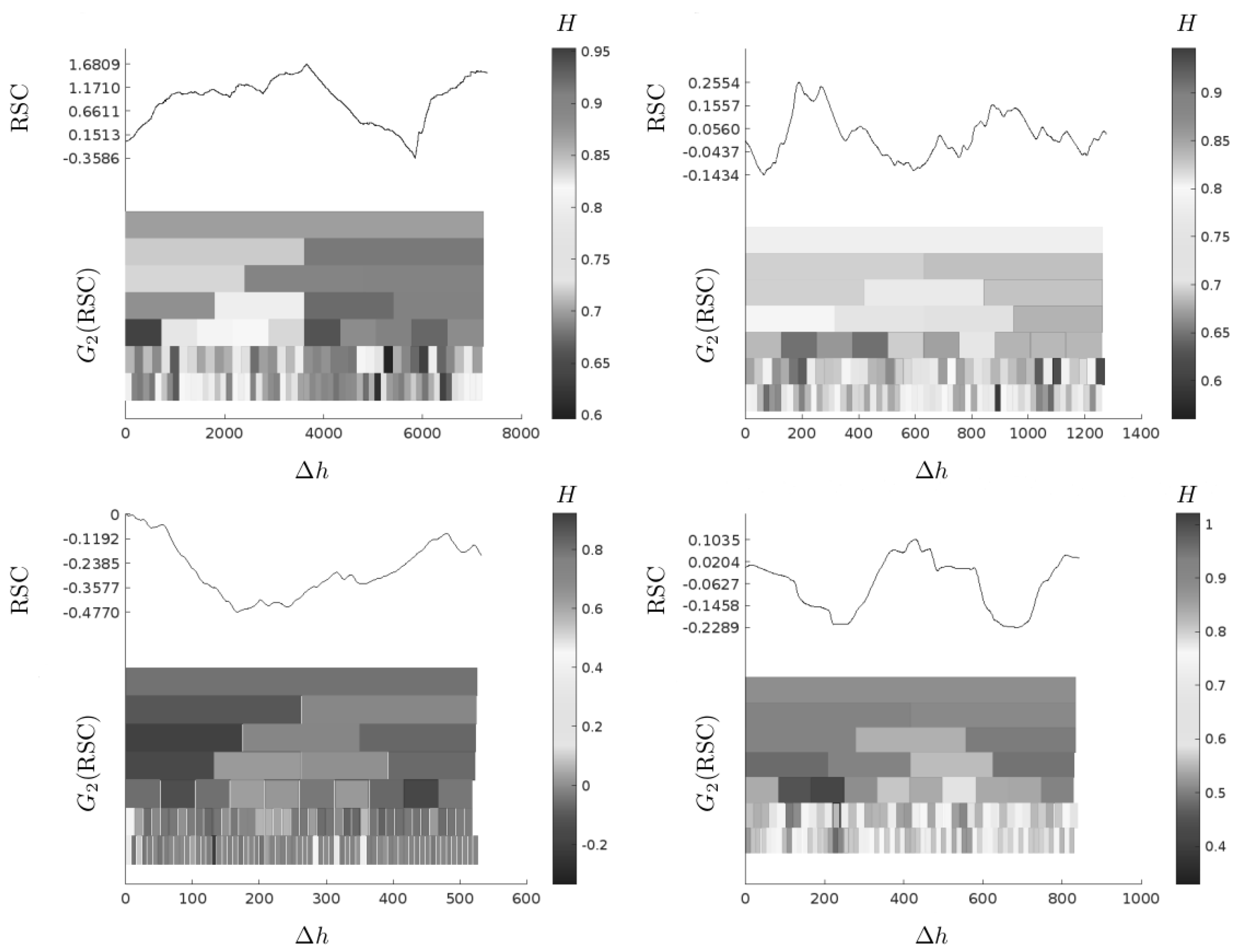Therefore, Figure 6 provides an alternative representation of the Hurst exponent distribution, highlighting the structural heterogeneity of the medium as observed in formations in northeastern Mexico (Chicontepec), using the DFA technique. This supports the hypothesis of class universality within fractal theory. In contrast Ferreira et al. [44] reported cases characterized by short-range memory processes with Hurst exponents ranging from $H=0.35$ to $H=0.40$, further emphasizing the complexity and heterogeneity of petroleum reservoirs in terms of pore distribution topology.

Thus, it is concluded that the system’s heterogeneity should be incorporated into the characterization of the rock formation, regardless of the metric used for estimation. That is, a single exponent is not sufficient to describe the heterogeneity of porosity logs or, by analogy, storage capacity logs. A multiscale approach or an alternative description, such as that proposed below through the calculation of Hurst exponents from a physical and monofractal perspective, is required (see Figure 6).

Horizontal scaling (along the x-axis, parallel to the y-axis) is analyzed by constructing standard deviation series $A_n$ (see Figure 2(d)) using the following expression:

$$h(n,\Delta )=\sqrt{{\displaystyle \frac{1}{\Delta }}\sum _{k=n-\Delta +1}^n{\left(A_k-\langle A_k\rangle \right)}^2}$$

(4)

Here, $\Delta$ represents the sampling window width, analogous to a temporal variable, and $h(n,\Delta )$ describes the fluctuations of a moving interface in the x–y plane. This treatment accounts for spatial correlations along the x-direction, following the approach proposed by Balankin et al. [23]. By applying the structure function (Equation (2)) to these newly constructed profiles, the growth exponent $\beta =1.03$ is obtained.

It is worth noting that the profiles used in this analysis differ from those suggested by Hewet [37], who proposed the use of fractional Gaussian noise (FGN) to model porosity logs perpendicular to stratification. However, the current results do not contradict those observations, as the differences arise from the construction method of the profiles via Equation (4).

Finally, the dynamic exponent z is determined by plotting $log{\delta }_c$ versus $log\Delta$, where ${\delta }_c\propto {\Delta }^{1/z}$ (see Figure 3(c)). For well scW1, the result is $z=0.97$. The x–y correlation between the $\alpha$ and $\beta$ exponents is established through a data collapse analysis (Figure 3(d)) using the coordinates $f=w_2/{\Delta }_n^{\beta }$ and window ${\delta }_c/{\Delta }_n^{1/z}$.

Unlike studies such as that of Dashian et al. [18], which explicitly conduct cross-correlation analysis between porosity log series using techniques like MF-DXA and logs such as DT, RHOB, NPHI, and GR, the present analysis does not apply such techniques, although multifractal patterns are identified that support their inclusion in future work.

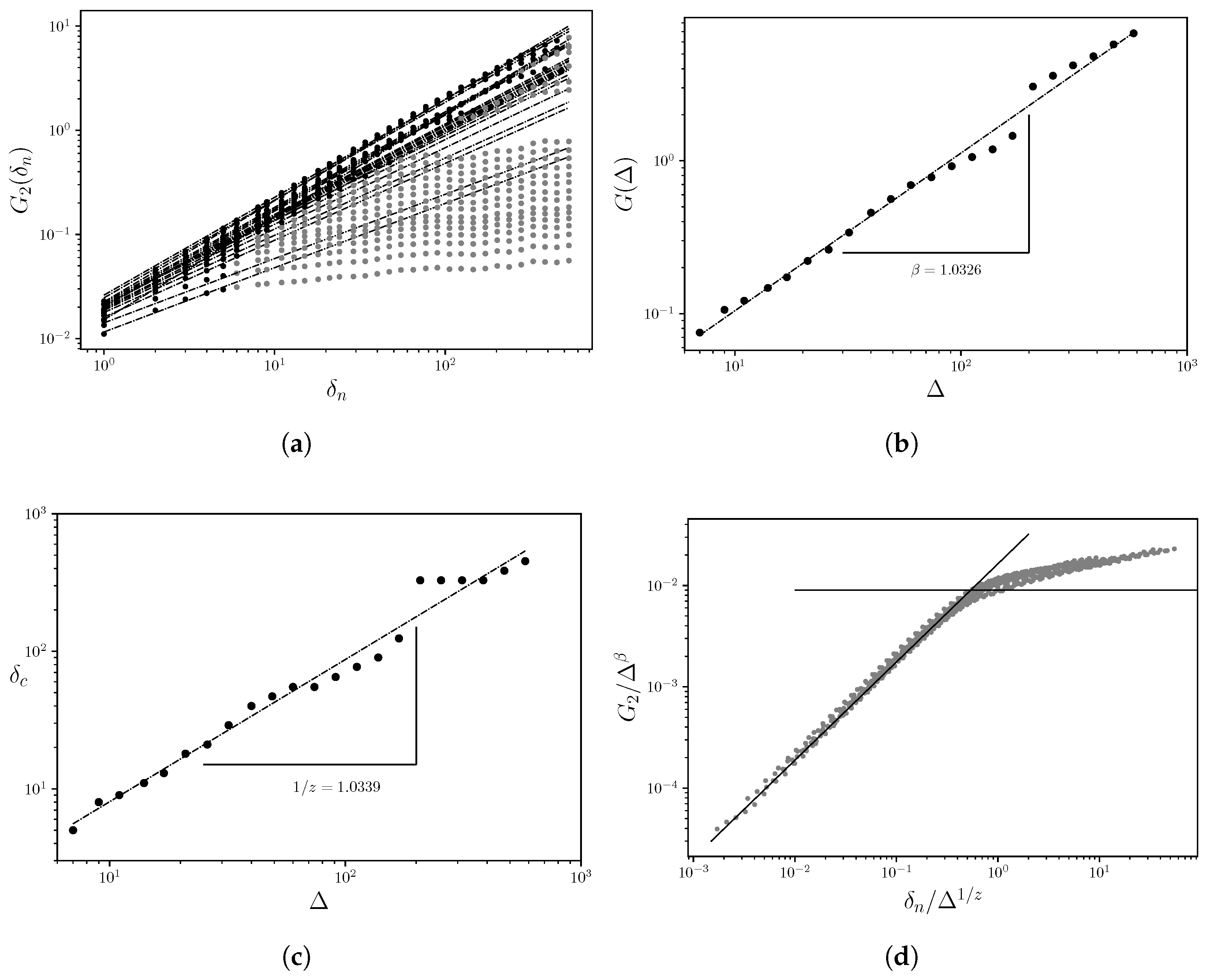
Results for Well scW2

Similar to well scW1, well scW2 exhibits a fractal correlation with an exponent $\alpha =0.83\pm 0.02$ for $q=1,2,3,4,5$ (see Figure 4(a)), indicating self-affinity of the RSC with respect to depth y. Regarding scaling parallel to the y-axis, i.e., along the x-direction, a value of $\beta =0.76$ is obtained (Figure 4(b)), suggesting long-range memory in both directions.

$\alpha -\beta$ correlation is reflected in the dynamic exponent (Figure 4(c)), and the data collapse shown in Figure 4(d) suggests a $\alpha -\beta$ correlation than that observed for well scW1.

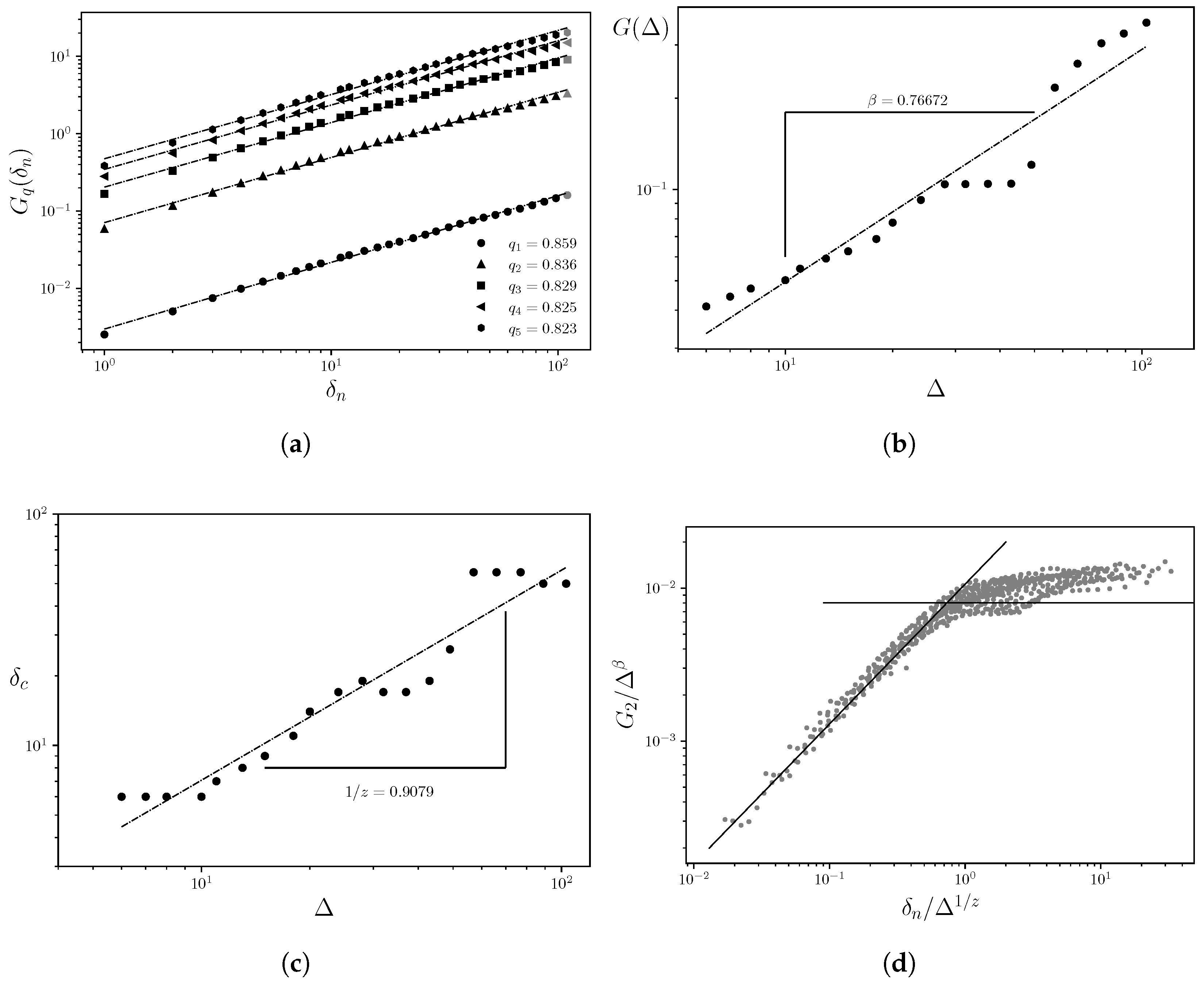
Results for Well scW3

Well scW3 is characterized by the exponents $\alpha =0.86\pm 0.02$, $\beta =0.40$, and $z=2.72$ (see Figure 5). However, as seen in Figure 5(a), no fractal scaling behavior is observed for the RSC in the vertical (y) direction, nor in the horizontal parallel (x) direction, as indicated by Figure 5(b). Similarly, the estimation of the z exponent is inconclusive, as evidenced by the absence of data collapse in Figure 5(d).

Therefore, although typically fractal parameters can be estimated, they do not adequately describe the behavior of the well log data and may be more appropriately interpreted from a Euclidean perspective, given the topological complexity of the porous structure.

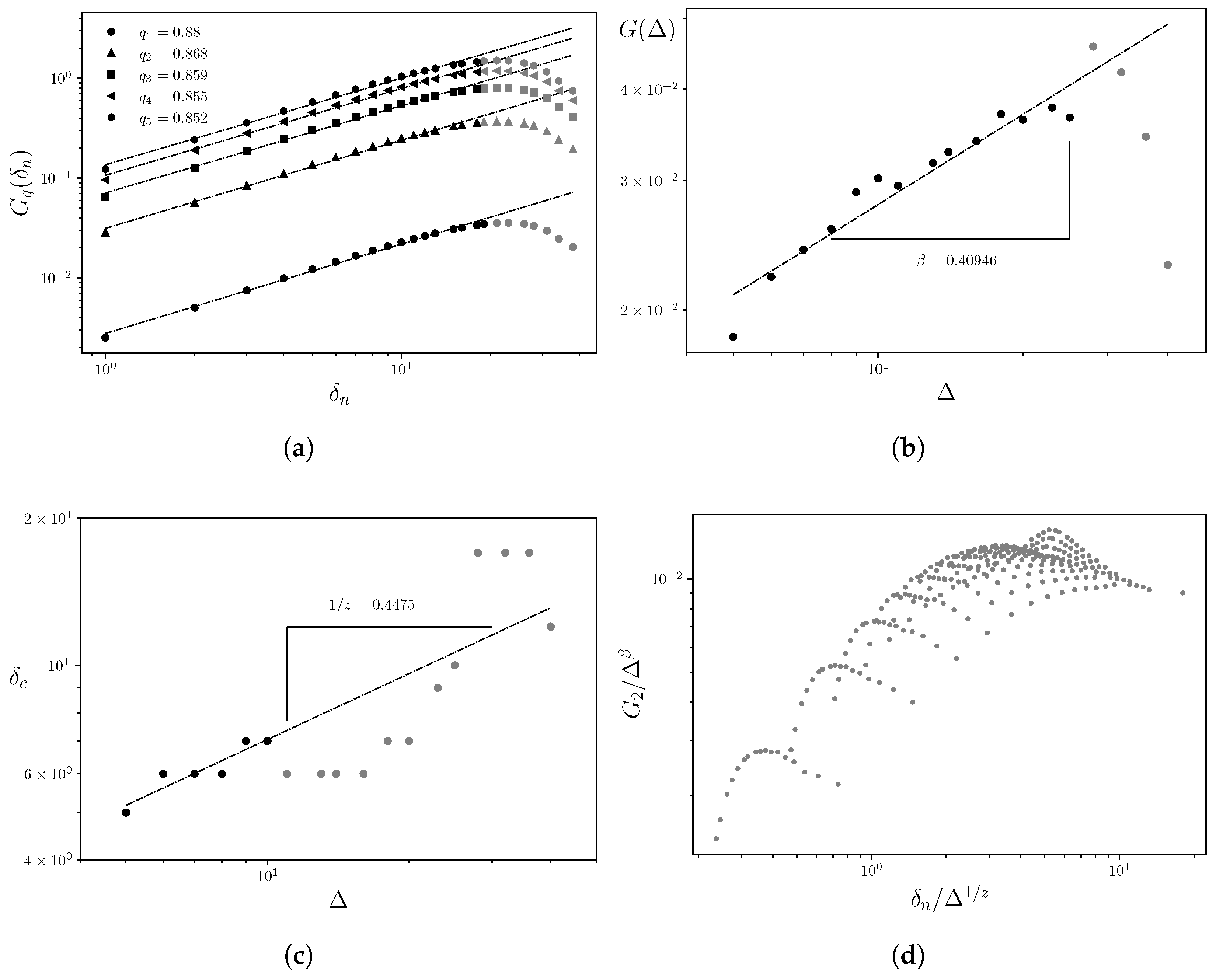
Summary of Exponents and Data Collapse

The estimated exponents $\alpha$, $\beta$, and z for each analyzed well, along with the presence or absence of data collapse, are summarized in Table 1.

Classification of Observed Cases

Based on the application of the fractal analysis methodology to the storage capacity log series from wells scW1 to scW5, three types of behavior were identified:

• Case 1: Autocorrelation is present in both directions (y and x), with strong $\alpha$–$\beta$ correlation and a well-defined data collapse (e.g., well scW1).
• Case 2: Fractal behavior is observed in both directions, but with $\alpha$–$\beta$ correlation and less defined data collapse (e.g., well scW2).
• Case 3: No fractal correlation is present in either direction, and no data collapse is observed (e.g., wells scW3 and scW5). In such cases, a Euclidean analysis may be more suitable than a fractal approach.

In at least three of the presented cases, the wells exhibit characteristics that can be modeled using the self-affine fractal approach. However, it is worth noting that the literature also reports the presence of multifractality in various studies on porosity logs, using different sampling and analysis techniques [17,45,46].

The results obtained in this study do not contradict such findings. As shown in Figure 6, the existence of a family of local Hurst exponents provides a better characterization of the log series depending on the analysis size L. This figure highlights the heterogeneous behavior of the series, showing how Hurst exponents vary across different intervals. Additionally, short-range memory processes are identified (see Figure 5b–d), as described by Ferreira et al. [44].

These short-term memory processes may go unnoticed if only a single global Hurst exponent is estimated, which would lead to a limited representation of the spatial heterogeneity in the porosity or storage capacity matrix.

4. Limitations and Scope

• The correlation between the scaling exponents $\alpha$ and $\beta$ is not presented quantitatively through explicit power-law relationships, as has been developed in previous studies [18].
• The correlation between the scaling results of storage capacity fluctuations and Cretaceous stratigraphic units is not included due to confidentiality constraints in data management. Similarly, the relationship between storage capacity and well stratigraphy is not addressed. However, such correlation could be readily established by a specialist with access to both variables and data from a different geological formation.
• The petrophysical heterogeneity of the reservoir, as observed through petrographic analysis, could be associated with the spatial heterogeneity observed in the distribution of Hurst exponents.
• The local heterogeneity illustrated in Figure 6 from individual well records could be integrated into the modeling of a global storage capacity and/or porosity matrix for a petroleum reservoir using an appropriate interpolation method, that is, a connection between the static and dynamic reservoir models could be evaluated.

5. Conclusions

The Family–Vicsek methodology was applied to scalar log profiles of storage capacity $\varphi h$ from five wells located in an oil field in southeastern Mexico. Correlations were established in the perpendicular direction corresponding to depth-y, and in the horizontal direction along the x-axis. $\alpha$–$\beta$ correlation was identified through information collapse analysis. The Euclidean and fractal classification is evidenced by the three distinct patterns identified in the well log records of storage capacity $\varphi h$.

An auto-affine behavior was observed in the RSC of wells scW1, scW2, scW4, and scW5, characterized by long-range memory; that is, statistical persistence in the fluctuations associated with the scalar records. The field’s heterogeneity was evidenced by a spectrum of scaling exponents ranging from antipersistent to random and persistent behaviors, suggesting multifractal features in the series of records analyzed at different scales.

Two types of statistical correlation were identified using Hurst exponents derived from the power-law relationship between the structure function and the observation window widths $\delta$, considering $q=2$: statistical persistence ($H>0.5$) and antipersistence ($H<0.5$). Wells characterized by $H>0.5$ indicate statistically persistent behavior, implying smoother growth fronts, i.e., lower variation in the magnitude of records. Conversely, wells with Hurst exponents $H<0.5$ indicate antipersistent behavior, associated with more heterogeneous growth fronts and greater variation in the recorded values.

The heterogeneity described through the different scaling exponents across the case studies suggests that such information should be taken into account in the construction of the storage capacity matrix, which serves as a key input for assessing the storage potential of the reservoir.

In addition to confirming the relevance of fractal and auto-affine models in the interpretation of geophysical records, the results underscore the importance of multiscale approaches to capture the complex heterogeneity inherent in reservoir systems. The observed multifractal traits and cross-scale correlations support the hypothesis that the spatial variability in storage capacity cannot be accurately characterized by a single global exponent. Instead, a local or segmented treatment using Hurst exponent distributions provides a richer and more precise understanding of the spatial structure.

Furthermore, the methodology presented offers a physically grounded alternative for integrating petrophysical heterogeneity into reservoir modeling workflows. This is particularly useful in the absence of complete stratigraphic or lithological data, allowing the identification of internal organizational patterns solely from the statistical properties of the available records. As such, the proposed approach complements traditional deterministic techniques and opens new possibilities for the integration of fractal geometry and stochastic modeling in reservoir characterization and simulation.

While this study has identified qualitative evidence of fractal characteristics in some of the analyzed wells—helping to establish more consistent indicators of flow capacity—this represents an initial approximation. A subsequent stage should include a more rigorous quantitative validation using formal statistical tools such as spectral analysis, goodness-of-fit tests, or long-range correlation functions. These tools would serve to reinforce the fractal hypothesis and facilitate its application within predictive flow models for porous media.