Submitted:
15 July 2025
Posted:
16 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Soil Sampling
2.2. Wetting-Drying Cycles and Sample Preparation
2.3. Synchrotron-Based X-Ray Computed Tomography: Image Acquisition and Segmentation
2.4. Morphological Analysis
3. Results and Discussion
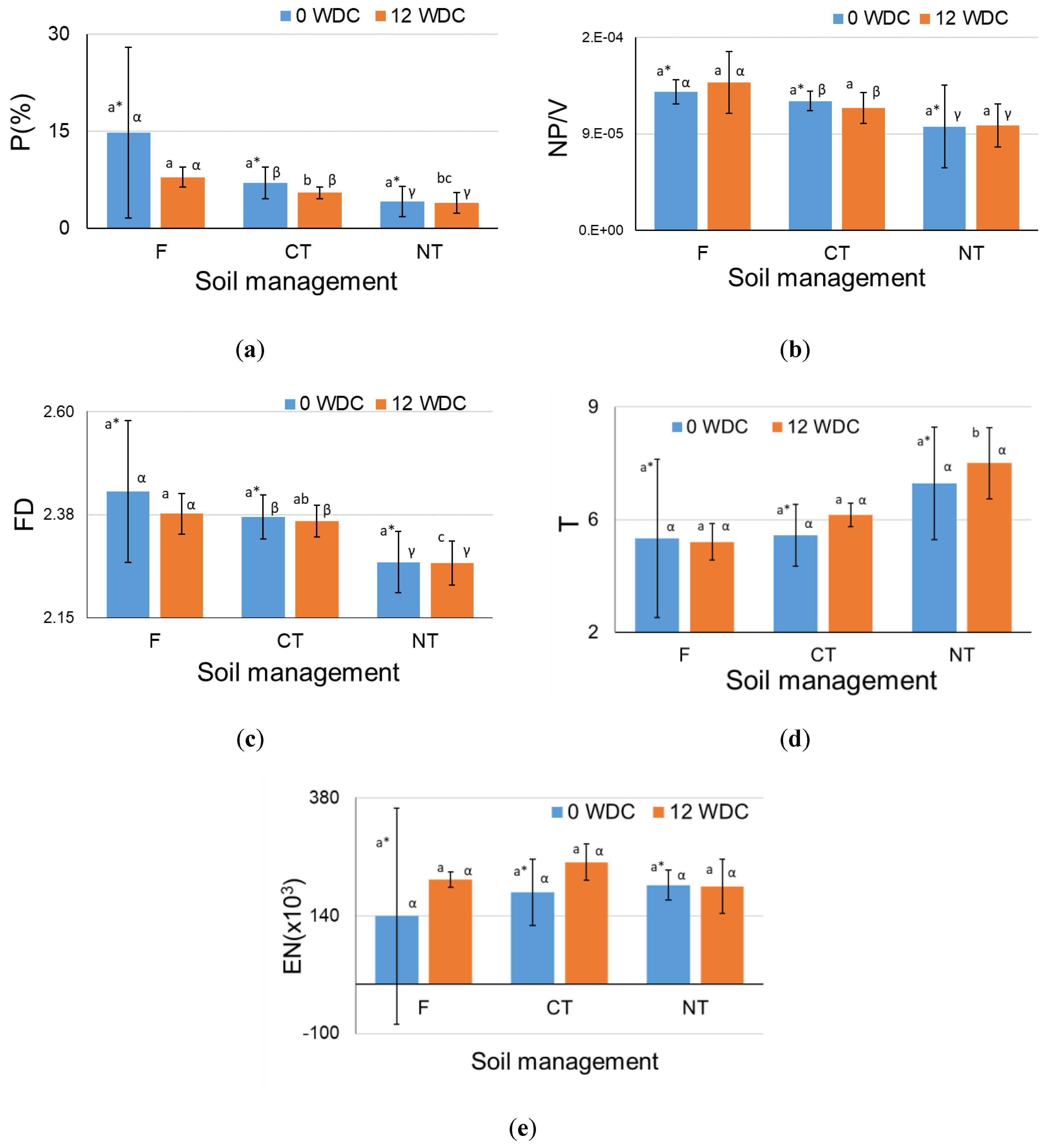
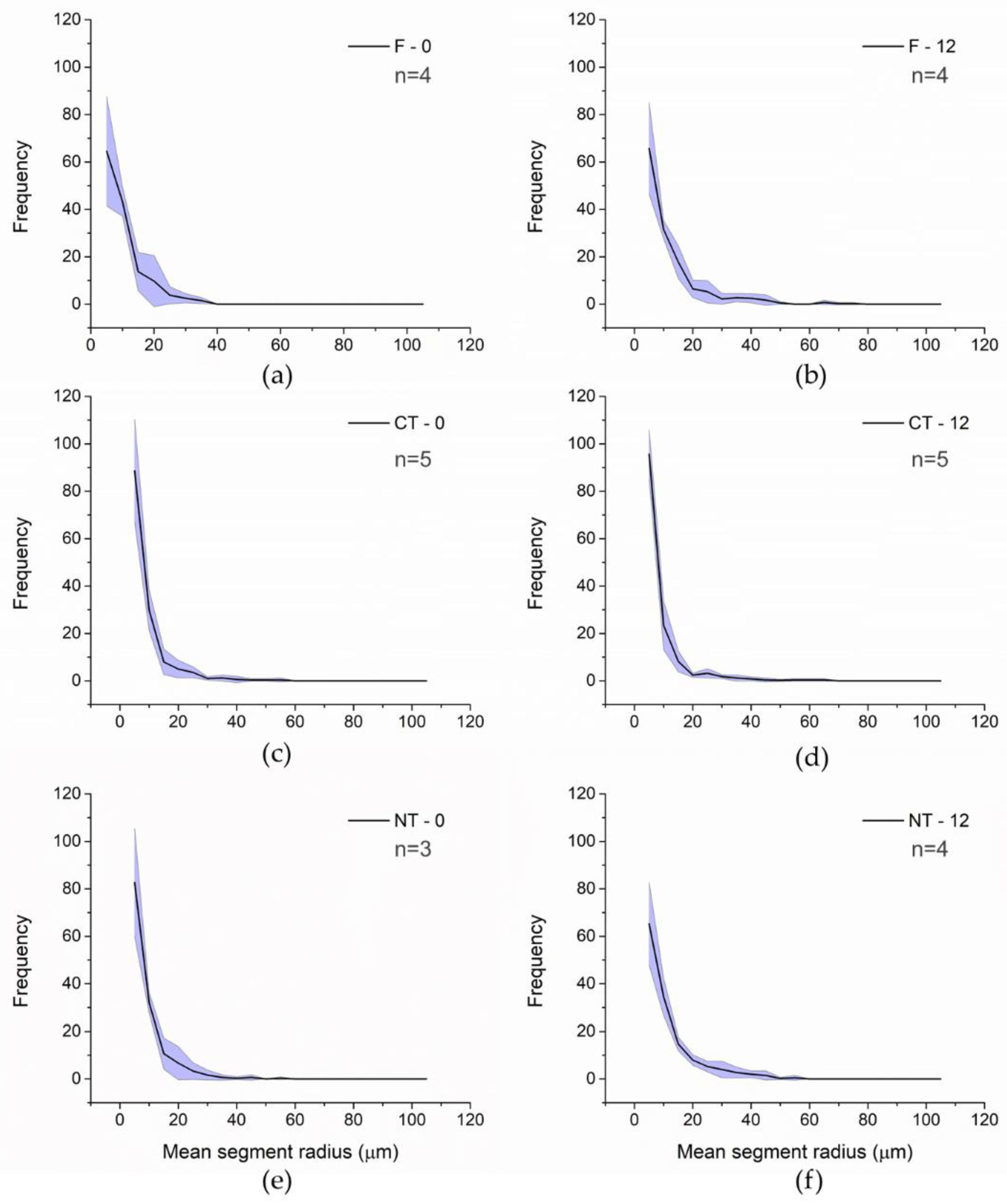
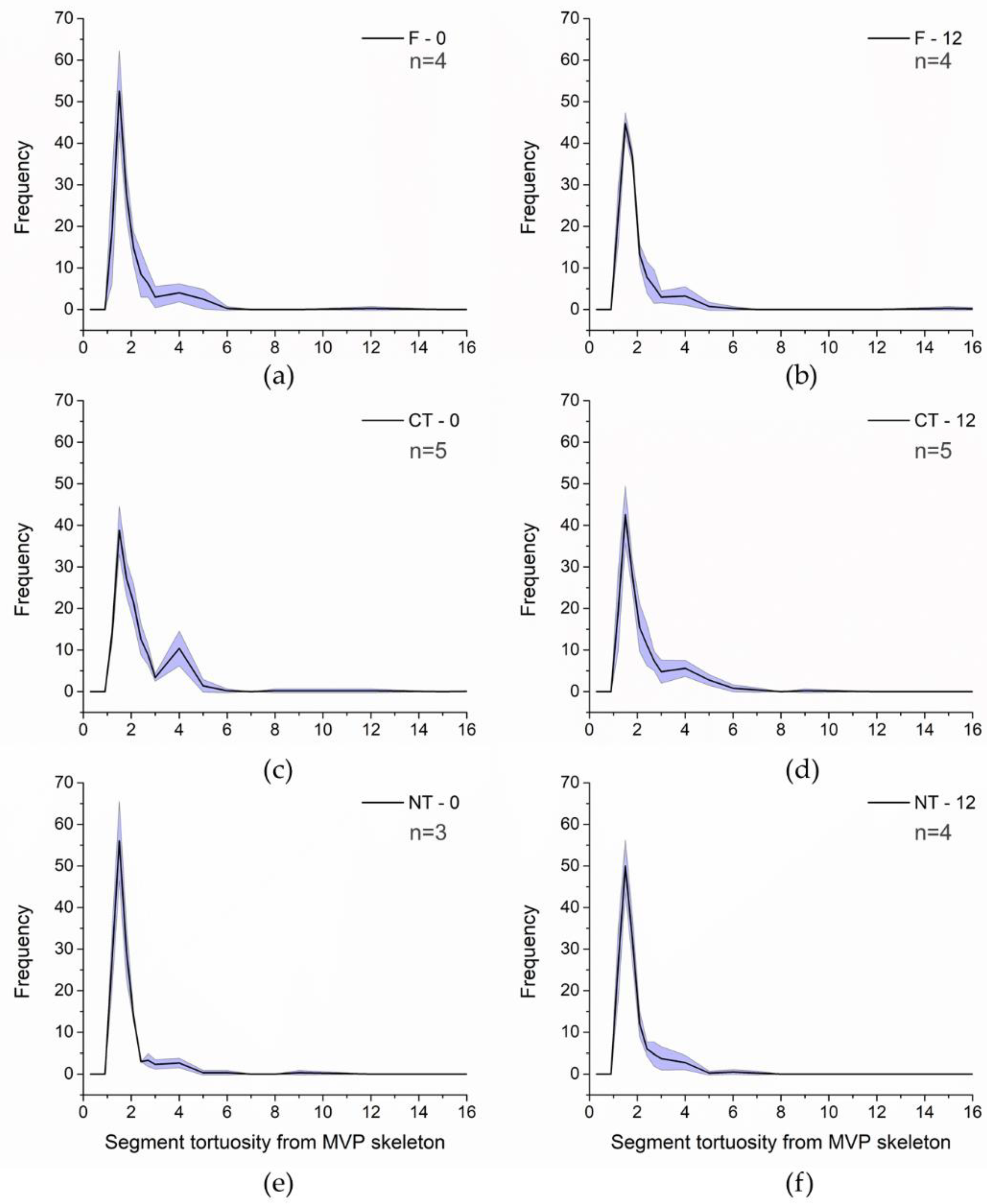
3.1. Morphological Analyzes Considering All Pores in Each Aggregate
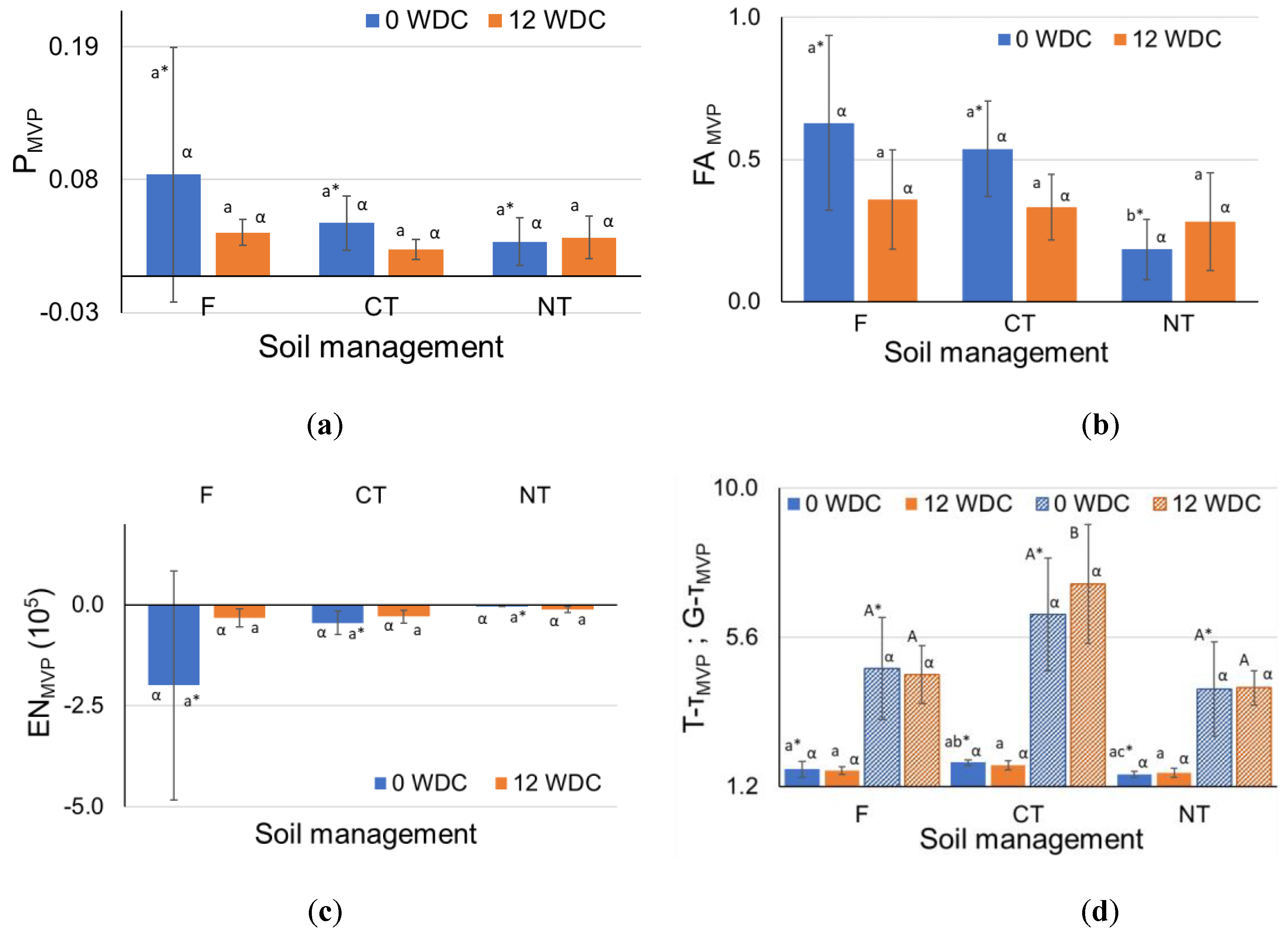
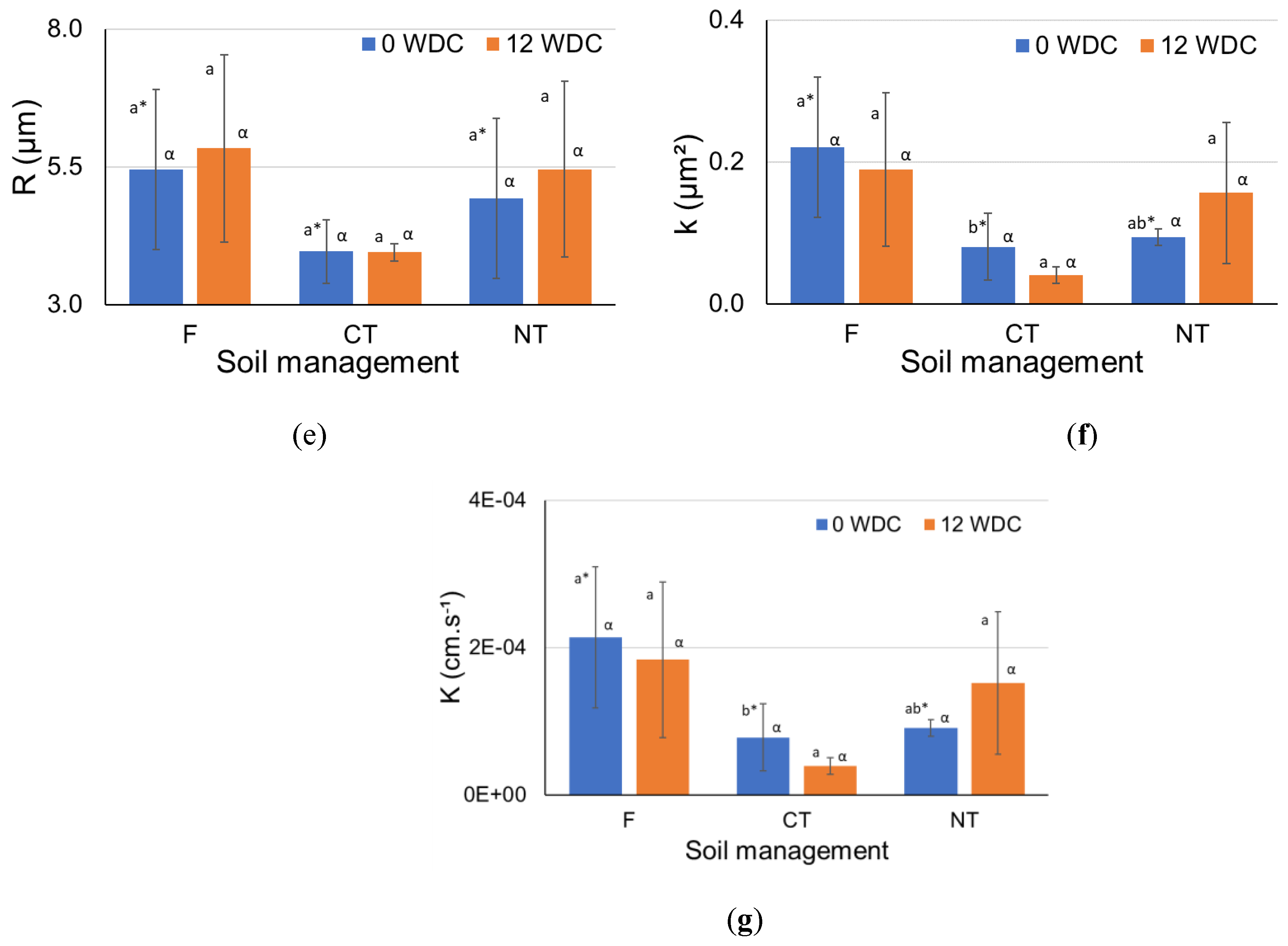
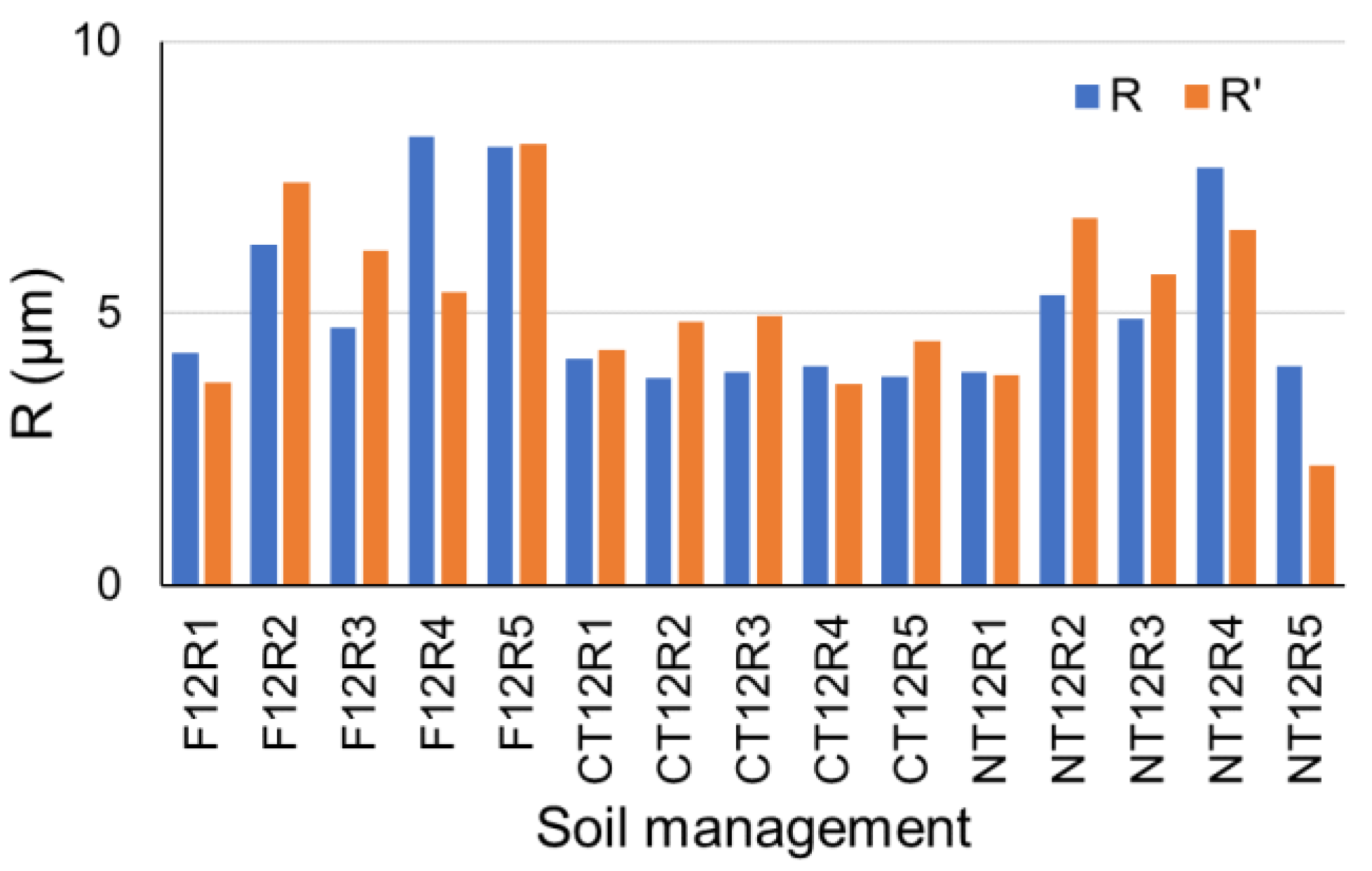
3.2. Permeability and Hydraulic Conductivity Considering the Most Voluminous Pore (MVP) in Each Aggregate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Lampurlanés, J.; Cantero-Martínez, C. Hydraulic conductivity, residue cover and soil surface roughness under different tillage systems in semiarid conditions. Soil and Tillage Research. 2006, 85, 13–26. [Google Scholar] [CrossRef]
- Kumar, V.; Saharawat, Y.; Gathala, M.; Jat, M.; Singh, S.; Chaudhary, N. Effect of different tillage and seeding methods on energy use efficiency and productivity of wheat in the Indo-Gangetic Plains. Field Crops Research. 2013, 142, 1–8. [Google Scholar] [CrossRef]
- Colombo, F.; Macdonald, C.; Jeffries, T.; Powell, J.; Singh, B. Impact of forest management practices on soil bacterial diversity and consequences for soil processes. Soil Biol. Biochem. 2015, 94, 200–210. [Google Scholar] [CrossRef]
- Galindo, V.; Giraldo, C.; Lavelle, P.; Armbrecht, I.; Fonte, S.J. Land use conversion to agriculture impacts biodiversity, erosion control, and key soil properties in an Andean watershed. Ecosphere. 2022, 13, 3979. [Google Scholar] [CrossRef]
- Klooster, D.; Masera, O. Community forest management in Mexico: carbon mitigation and biodiversity conservation through rural development. Global environmental change. 2000, 10, 259–272. [Google Scholar] [CrossRef]
- Houshyar, E.; Grundmann, P. Environmental impacts of energy use in wheat tillage systems: A comparative life cycle assessment (LCA) study in Iran. Energy. 2017, 122, 11–24. [Google Scholar] [CrossRef]
- Lal, R. Restoring soil quality to mitigate soil degradation. Sustainability. 2015, 7, 5875–5895. [Google Scholar] [CrossRef]
- Galdos, M. V.; Pires, L. F.; Cooper, H. V.; Calonego, J. C.; Rosolem, C. A.; Mooney, S. J. Assessing the long-term effects of zero-tillage on the macroporosity of Brazilian soils using X-ray Computed Tomogra-phy. Geoderma. 2019, 337, 1126–1135. [Google Scholar] [CrossRef] [PubMed]
- Morillas, L.; Portillo-estrada, M.; Gallardo, A. Wetting and drying events determine soil N pools in two Mediterranean ecosystems. Applied Soil Ecology. 2013, 72, 161–170. [Google Scholar] [CrossRef]
- Shekhar, S.; Mailapalli, D.; Raghuwanshi, N.; Das, B. Hydrus-1D model for simulating water flow through paddy soils under alternate wetting and drying irrigation practice. Paddy and Water Environment. 2019, 18, 73–85. [Google Scholar] [CrossRef]
- Ma, R.; Cai, C.; Li, Z.; Wang, J.; Xiao, T.; Peng, G.; Yang, W. Evaluation of soil aggregate microstructure and stability under wetting and drying cycles in two Ultisols using synchrotron-based X-ray micro-computed tomography. Soil and Tillage Research. 2015, 149, 1–11. [Google Scholar] [CrossRef]
- Diel, J.; Vogel, H.; Schlüter, S. Impact of wetting and drying cycles on soil structure dynamics. Geoderma 2019, 345, 63–71. [Google Scholar] [CrossRef]
- Fang, H.; Zhou, H.; Norton, G.J.; Price, A.H.; Raffan, A.C.; Mooney, S.J.; Peng, X.; Hallett, P.D. Interaction between contrasting rice genotypes and soil physical conditions induced by hydraulic stresses typical of alternate wetting and drying irrigation of soil. Plant and soil. 2018, 430, 233–243. [Google Scholar] [CrossRef] [PubMed]
- Carrijo, D.R.; Akbar, N.; Reis, A.F.B.; Li, C.; Gaudin, A.C.M.; Parikh, S.J.; Linquist, B.A. Impacts of variable soil drying in alternate wetting and drying rice systems on yields, grain arsenic concentration and soil moisture dynamics. Field Crops Res. 2018, 222, 101–110. [Google Scholar] [CrossRef]
- Price, A.H.; Norton, G.J.; Salt, D.E.; Ebenhoeh, O.; Meharg, A.A.; Meharg, C.; Davies, W.J. Alternate wetting and drying irrigation for rice in Bangladesh: Is it sustainable and has plant breeding something to offer? Food and Energy Security. 2013, 2, 120–129. [Google Scholar] [CrossRef]
- Reddi, L.; Ming, X.; Hajra, M.; Lee, I. Permeability reduction of soil filters due to physical clogging. Journal of geotechnical and geoenvironmental engineering, 2000, 126, 236–246. [Google Scholar] [CrossRef]
- Tseng, C. L.; Alves, M. C.; Crestana, S. Quantifying physical and structural soil properties using X-ray microtomography. Geoderma. 2018, 318, 78–87. [Google Scholar] [CrossRef]
- Soto-Gomez, D.; Perez-Rodriguez, P.; Juiz, L. V.; Paradelo, M.; Lopez-Periago, J. E. 3D multifractal characterization of computed tomography images of soils under different tillage management: Linking multifractal parameters to physical properties. Geoderma. 2020, 363, 114129. [Google Scholar] [CrossRef]
- Piccoli, I.; Camarotto, C.; Lazzaro, B.; Furlan, L.; Morari, F. Conservation agriculture had a poor impact on the soil porosity of Veneto low-lying plain silty soils after a 5-year transition period. Land Degradation & Development. 2017, 28, 2039–2050. [Google Scholar] [CrossRef]
- Carson, J.K.; Gonzalez-Quiñones, V.; Murphy, D.V.; Hinz, C.; Shaw, J.A.; Gleeson, D.B. Low pore connectivity increases bacterial diversity in soil. Appl. Environ. Microbiol. 2010, 76, 3936–3942. [Google Scholar] [CrossRef] [PubMed]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in porous media: a critical review. Soil science society of America journal. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Lu, S.F.; Han, Z.J.; Xu, L.; Lan, T.G.; Wei, X.; Zhao, T.Y. On measuring methods and influencing factors of air permeability of soils: An overview and a preliminary database. Geoderma. 2023, 435, 116509. [Google Scholar] [CrossRef]
- Dal Ferro, N.; Charrier, P.; Morari, F. Dual-scale micro-CT assessment of soil structure in a long-term fertilization experiment. Geoderma 2013, 204, 84–93. [Google Scholar] [CrossRef]
- Kravchenko, A. N.; Negassa, W. C.; Guber, A. K.; Rivers, M. L. Protection of soil carbon within macro-aggregates depends on intra-aggregate pore characteristics. Scientific Reports. 2015, 5(1), 16261. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, N. J.; Larsbo, M.; Koestel, J. Connectivity and percolation of structural pore networks in a cultivated silt loam soil quantified by X-ray tomography. Geoderma. 2017, 287, 71–79. [Google Scholar] [CrossRef]
- Hillel, D. Introduction to environmental soil physic. Elsevier Science, San Diego, California, 2003. [CrossRef]
- Yudina, A.; Kuzyakov, Y. Dual nature of soil structure: The unity of aggregates and pores. Geoderma. 2023, 434, 116478. [Google Scholar] [CrossRef]
- Ferreira, T. R.; Archilha, N. L.; Cássaro, F. A.M.; Pires, L.F. How can pore characteristics of soil aggregates from contrasting tillage systems affect their intrinsic permeability and hydraulic conductivity? Soil & Tillage Research. 2023, 230, 105704. [Google Scholar] [CrossRef]
- Wang, W.; Kravchenko, A. N.; Smucker, A. J. M.; Liang, W.; Rivers, M. L. Intra-aggregate pore characteristics: X-ray computed microtomography analysis. Soil Science Society of America Journal. 2012, 76(4), 1159–1171. [Google Scholar] [CrossRef]
- Tang, C. S.; Cheng, Q.; Gong, X.; Shi, B.; Inyang, H. I. Investigation on microstructure evolution of clayey soils: A review focusing on wetting/drying process. Journal of Rock Mechanics and Geotechnical Engineering. 2023, 15(1), 269–284. [Google Scholar] [CrossRef]
- Borges, J.A.; Pires, L.F.; Cassaro, F.A.; Auler, A.C.; Rosa, J.A.; Heck, R.J.; Roque, W.L. X-ray computed tomography for assessing the effect of tillage systems on topsoil morphological attributes. Soil Tillage Res. 2019, 189, 25–35. [Google Scholar] [CrossRef]
- Pires, L. F.; Ferreira, T. R.; Cássaro, F. A.; Cooper, H. V.; Mooney, S. J. A comparison of the differences in soil structure under long-term conservation agriculture relative to a secondary forest. Agriculture. 2022, 12(11), 1783. [Google Scholar] [CrossRef]
- Soil Survey Staff. Simplified Guide to Soil Taxonomy. 2013, USDA-Natural Resources Conservation Service, National Soil Survey Center, Lincoln, USA. Conservation Service, National Soil Survey Center, Lincoln, USA.
- Shaheb, M.R.; Venkatesh, R.; Shearer, S.A. A review on the effect of soil compaction and its management for sustainable crop production. J. Biosyst. Eng. 2021, 46, 417–439. [Google Scholar] [CrossRef]
- Provenzano, G.; Rallo, G.; Ghazouani, H. Assessing field and laboratory calibration protocols for the diviner 2000 probe in a range of soils with different textures. J. Irrig. Drain. Eng. 2016, 142, 04015040. [Google Scholar] [CrossRef]
- Greenland, D.J. Soil damage by intensive arable cultivation: temporary or permanent? Philosophical Transactions of the Royal Society of London. Biological Sciences. 1977, 281(980), 193–208. [Google Scholar] [CrossRef]
- Spina, T. V.; Vasconcelos, G.J.Q.; Goncalves, H.M.; Libel, G.C.; Pedrini, H.; Carvalho, T.J.; Archilha, N.L. Towards Real Time Segmentation of Large-Scale 4D Micro/Nanotomography Images in the Sirius Synchrotron Light Source. Microsc. Microanal. 2018, 24, 92–93. [Google Scholar] [CrossRef]
- Ferreira, T.R.; Archilha, N.L.; Pires, L.F. An analysis of three XCT-based methods to determine the intrinsic permeability of soil aggregates. Journal of Hydrology. 612, 128024. [CrossRef]
- Lehmann, P.; Wyss, P.; Flisch, A.; Lehmann, E.; Vontobel, P.; Krafczyk, M.; Kaestner, A.; Beckmann, F.; Gygi, A.; Fluhler, H. Tomographical imaging and mathematical description of porous media used for the prediction of fluid distribution. Vadose Zo. 2006, J. 5, 80–97. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irrig. Drain. Div. 1966, 92, 61–88. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Estimation of saturated hydraulic conductivity with pedotransfer functions: A review. J. Hydrol. 2019, 575, 1011–1030. [Google Scholar] [CrossRef]
- Regelink, I. C.; Stoof, C. R.; Rousseva, S.; Weng, L.; Lair, G. J.; Kram, P.; Nikolaidis, N.P.; Kercheva, M.; Banwart, S.; Comans, R. N. Linkages between aggregate formation, porosity and soil chemical properties. Geoderma. 2015, 247, 24–37. [Google Scholar] [CrossRef]
- Fernández-Ugalde, O.; Barré, P.; Hubert, F.; Virto, I.; Girardin, C.; Ferrage, E.; Chenu, C. Clay mineralogy differs qualitatively in aggregate-size classes: clay-mineral-based evidence for aggregate hierarchy in temperate soils. European journal of soil science. 2013, 64(4), 410–422. [Google Scholar] [CrossRef]
- Schlüter, S.; Leuther, F.; Vogler, S.; Vogel, H. J. X-ray microtomography analysis of soil structure deformation caused by centrifugation. Solid Earth. 2016, 7(1), 129–140. [Google Scholar] [CrossRef]
- Spaccini, R.; Zena, A.; Igwe, C. A.; Mbagwu, J. S. C.; Piccolo, A. Car-bohydrates in water-stable aggregates and particle size fractions of forested and cultivated soils in two contrasting tropical ecosystems. Biogeochemistry, 2001, 53, 1–22. [Google Scholar] [CrossRef]
- Su, Z.; Zhang, J.; Wu, W.; Cai, D.; Lv, J.; Jiang, G.; Huang, J.; Gao, J.J.; Hartmann, R.; Gabriels, D. Effects of conservation tillage practices on winter wheat water-use efficiency and crop yield on the Loess Plateau, China. Agricultural Water Management. 2007, 87(3), 307–314. [Google Scholar] [CrossRef]
- Park, E.J.; Smucker, A.J.M. Saturated Hydraulic Conductivity and Porosity within Macroaggregates Modified by Tillage. Soil Science Society of America. 2005, 69, 38–45. [Google Scholar] [CrossRef]
- Guo, X. M.; Guo, N.; Liu, L. Effects of Wetting-Drying Cycles on the CT-Measured Macropore Characteristics under Farmland in Northern China. 2023, Eurasian Soil Science, 1-9. [CrossRef]
- Wen, T.; Chen, X.; Shao, L. Effect of multiple wetting and drying cycles on the macropore structure of granite residual soil. Journal of Hydrology. 2022, 614, 128583. [Google Scholar] [CrossRef]
- de Oliveira, J.A.; Cássaro, F.A.; Posadas, A.N.; Pires, L.F. Soil pore network complexity changes induced by wetting and drying cycles—a study using X-ray microtomography and 3D multifractal analyses. Int. J. Environ. Res. Public Health 2022, 19. [Google Scholar] [CrossRef] [PubMed]
- Gaspareto, J. V.; Oliveira, J. A. D.; Andrade, E.; Pires, L. F. Representative Elementary Volume as a Function of Land Uses and Soil Processes Based on 3D Pore System Analysis. Agriculture. 2013, 13(3), 736. [Google Scholar] [CrossRef]
- Zhang, S. J.; Tang, Q.; Bao, Y. H.; He, X. B.; Tian, F. X.; Lü, F. Y.; Wang, M.F.; Anjum, R. Effects of seasonal water-level fluctuation on soil pore structure in the Three Gorges Reservoir, China. Journal of Mountain Science. 2018, 15(10), 2192–2206. [Google Scholar] [CrossRef]
- Muñoz, F. J.; San Jose Martinez, F.; Caniego, F. J. Fractal parameters of pore space from CT images of soils under contrasting management practices. Fractals. 2014, 22(03), 1440011. [Google Scholar] [CrossRef]
- Ferreira, T. R.; Pires, L. F.; Wildenschild, D.; Brinatti, A. M.; Borges, J. A.; Auler, A. C.; dos Reis, A. M. Lime application effects on soil aggregate properties: Use of the mean weight diameter and synchrotron-based X-ray μCT techniques. Geoderma. 2019, 338, 585–596. [Google Scholar] [CrossRef]
- Lee, B. H.; Lee, S. K. Effects of specific surface area and porosity on cube counting fractal dimension, lacunarity, configurational entropy, and permeability of model porous networks: Random packing simulations and NMR micro-imaging study, Journal of Hydrology. 2013, 496, 122–141. [CrossRef]
- Zhang, Y.; Yang, Z.; Wang, F.; Zhang, X. Comparison of soil tortuosity calculated by different methods. Geoderma. 2021, 402, 115358. [Google Scholar] [CrossRef]
- Matyka, M.; Koza, Z. How to Calculate Tortuosity Easily? AIP Conf. Proc. 2012, 1453, 17–22. [Google Scholar] [CrossRef]
- Duhour, A.; Costa, C.; Momoa, F.; Falco, L.; Malacalza, L. Response of eart worm communities to soil disturbance: Fractal dimension of soil and species’ rank-abundance curves. Applied Soil Ecology. 2009, 43, 83–88. [Google Scholar] [CrossRef]
- Peth, S.; Horn, R.; Beckmann, F.; Donath, T.; Fischer, J.; Smucker, A. J.M. Three-Dimensional Quantification of Intra-Aggregate Pore-Space Features using Synchrotron-Radiation-Based Microtomography. Soil Science Society of America Journal. 2008, 72(4), 897–907. [Google Scholar] [CrossRef]
- Leij, F. J.; Ghezzehei, T. A.; Or, D. Modeling the dynamics of the soil pore-size distribution. Soil and Tillage Research. 2002, 64(1-2), 61-78. [CrossRef]
- Udawatta, R. P.; Anderson, S. H.; Gantzer, C. J.; Garrett, H. E. Agroforestry and grass buffer influence on macropore characteristics: a computed tomography analysis. Soil Science Society of America Journal. 2006, 70(5), 1763–1773. [Google Scholar] [CrossRef]
- Pires, L. F.; Roque, W. L.; Rosa, J. A.; Mooney, S. J. 3D analysis of the soil porous architecture under long term contrasting management systems by X-ray computed tomography. Soil and Tillage Research. 2019, 191, 197–206. [Google Scholar] [CrossRef]
- An, R.; Kong, L.; Zhang, X.; Li, C. Effects of dry-wet cycles on three-dimensional pore structure and permeability characteristics of granite residual soil using X-ray micro computed tomography. J. Rock Mech. Geotech. Eng. 2022, 14, 851–860. [Google Scholar] [CrossRef]
- Zhang, L.; Qi, S.; Ma, L.; Guo, S.; Li, Z. , Li, G., Yang, J.; Zou, Y.; Tonglu Li, T.; Hou, X. Three-dimensional pore characterization of intact loess and compacted loess with micron scale computed tomography and mercury intrusion porosimetry. Scientific Reports. 2020, 10(1), 8511. [Google Scholar] [CrossRef] [PubMed]
- Messing, I.; Jarvis, N. J. Temporal variation in the hydraulic conductivity of a tilled clay soil as measured by tension infiltrometers. Journal of Soil Science. 1993, 44(1), 11–24. [Google Scholar] [CrossRef]
- Holzer, L.; Marmet, P.; Fingerle, M.; Wiegmann, A.; Neumann, M.; Schmidt, V. Tortuosity and Microstructure Effects in Porous Media: Classical Theories, Empirical Data and Modern Methods. Springer. 2023, 333, 198. [Google Scholar] [CrossRef]
- Pagliai, M.; Vignozzi, N.; Pellegrini, S. Soil structure and the effect of management practices. Soil and Tillage Research. 2004, 79, 131–143. [Google Scholar] [CrossRef]
- Lal, R.; Shukla, M.K. Principles of soil physics. 2004. CRC Press. [CrossRef]
- Gerke, K. M. ; Marina V Karsanina. Pore-scale modelling of flow and transport phenomena in soils, 2023. [Google Scholar] [CrossRef]
- Horn, R. Time dependence of soil mechanical properties and pore functions for arable soils. Soil Science Society of America journal. 2004, 68(4), 1131–1137. [Google Scholar] [CrossRef]
- Horn, R.; Dexter, A.R. Dynamics of soil aggregation in an irrigated desert loess. Soil & tillage research. [CrossRef]
- Vogel, H. J. Morphological determination of pore connectivity as a function of pore size using serial sections. European Journal of Soil Science. 1997, 48(3), 365–377. [Google Scholar] [CrossRef]
- Gharedaghloo, B.; Price, J. S.; Rezanezhad, F.; Quinton, W. L. Evaluating the hydraulic and transport properties of peat soil using pore network modeling and X-ray micro computed tomography. Journal of Hydrology. 2018, 561, 494–508. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




