Submitted:
12 July 2025
Posted:
15 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
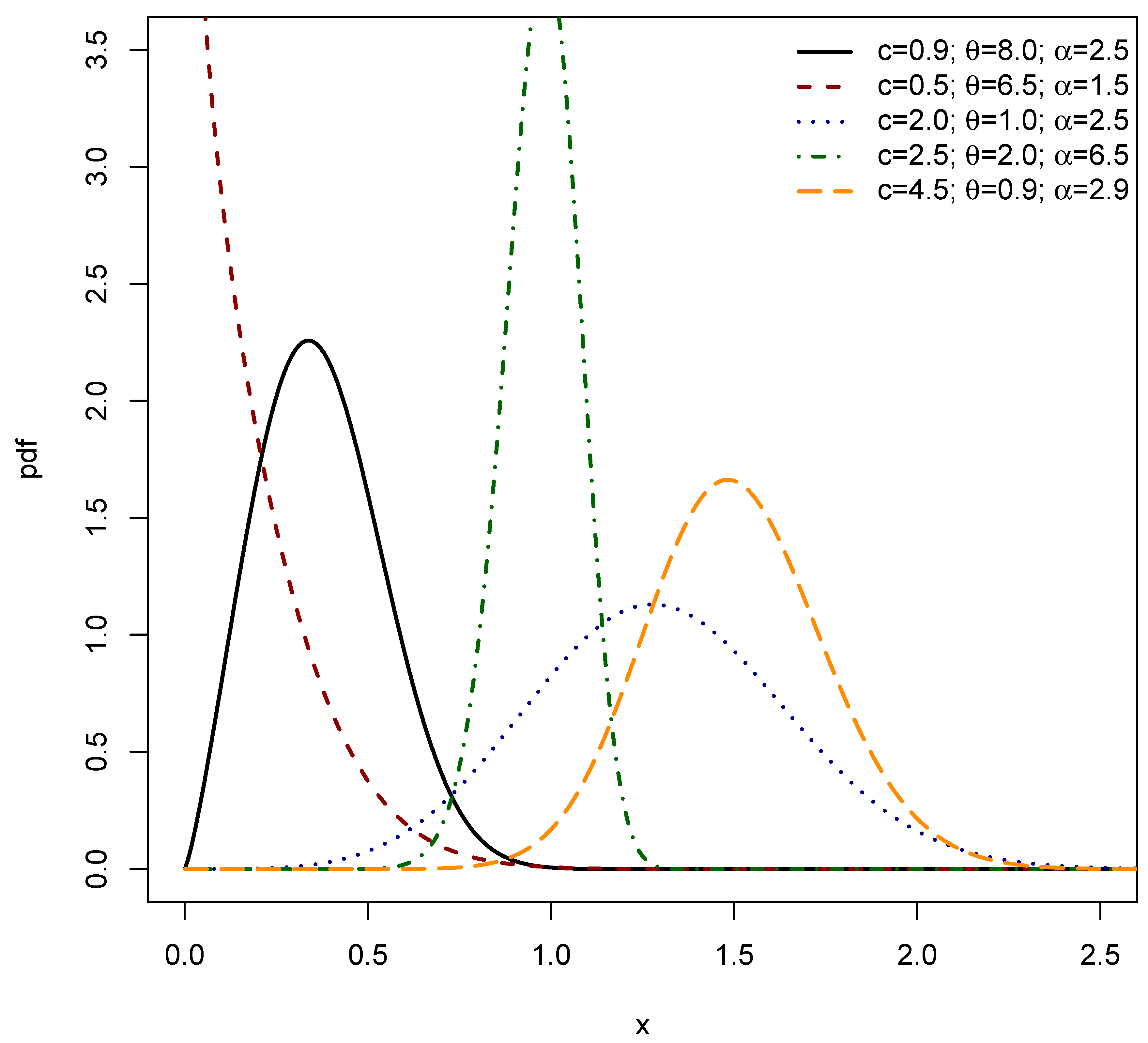
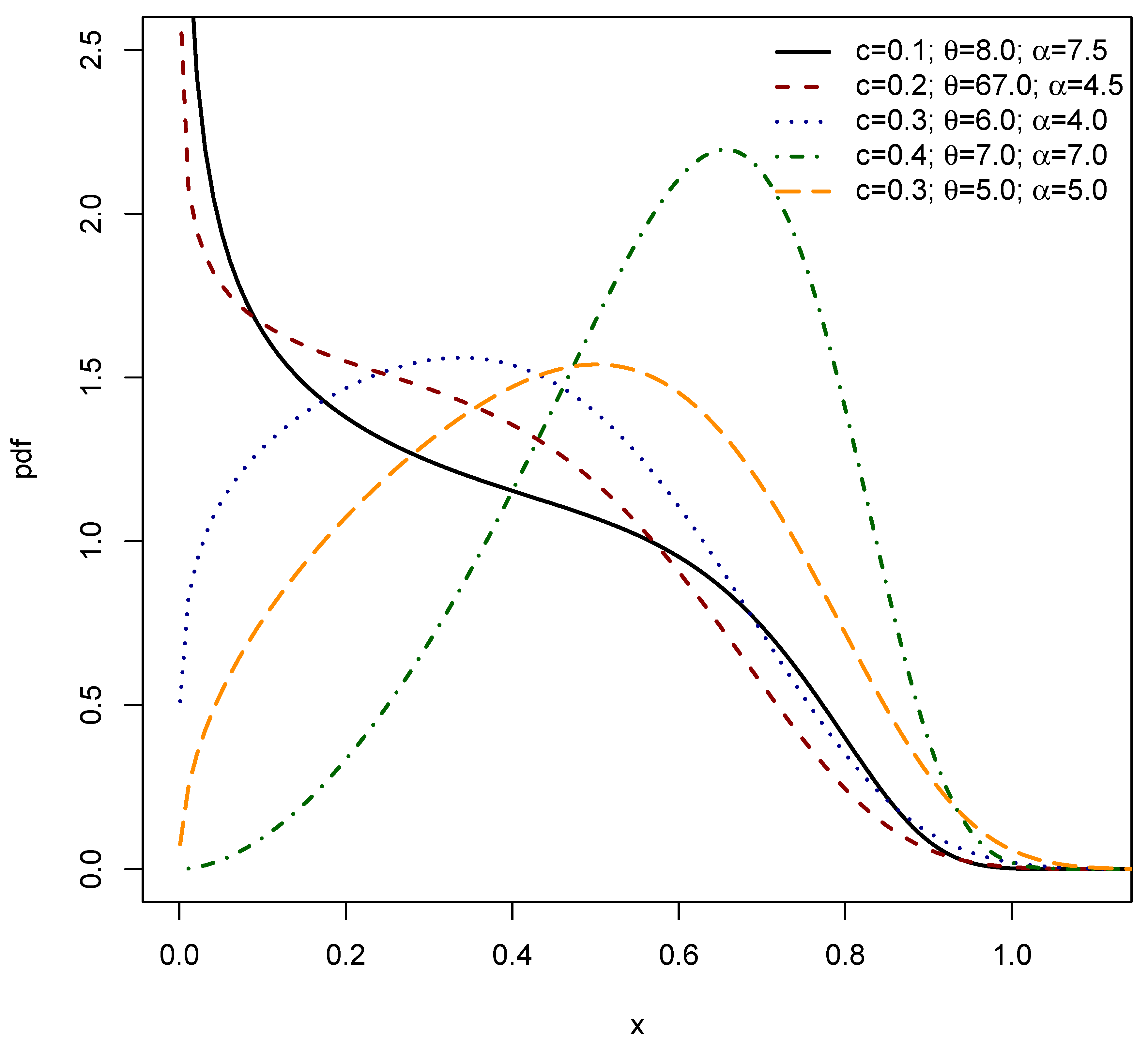
2. The Exponentiated Power Shanker (EPS) Distribution
2.1. Linear Representation
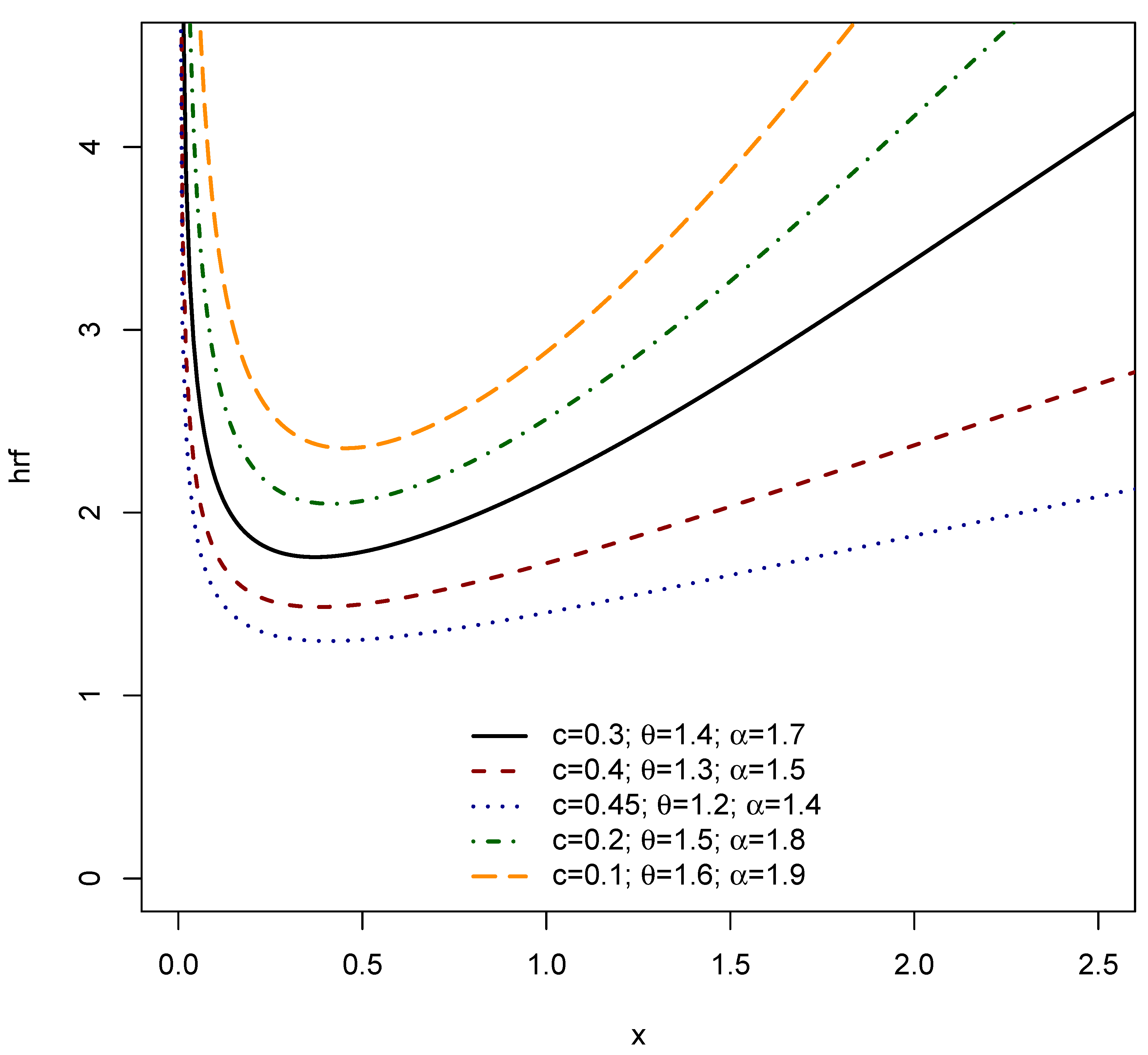
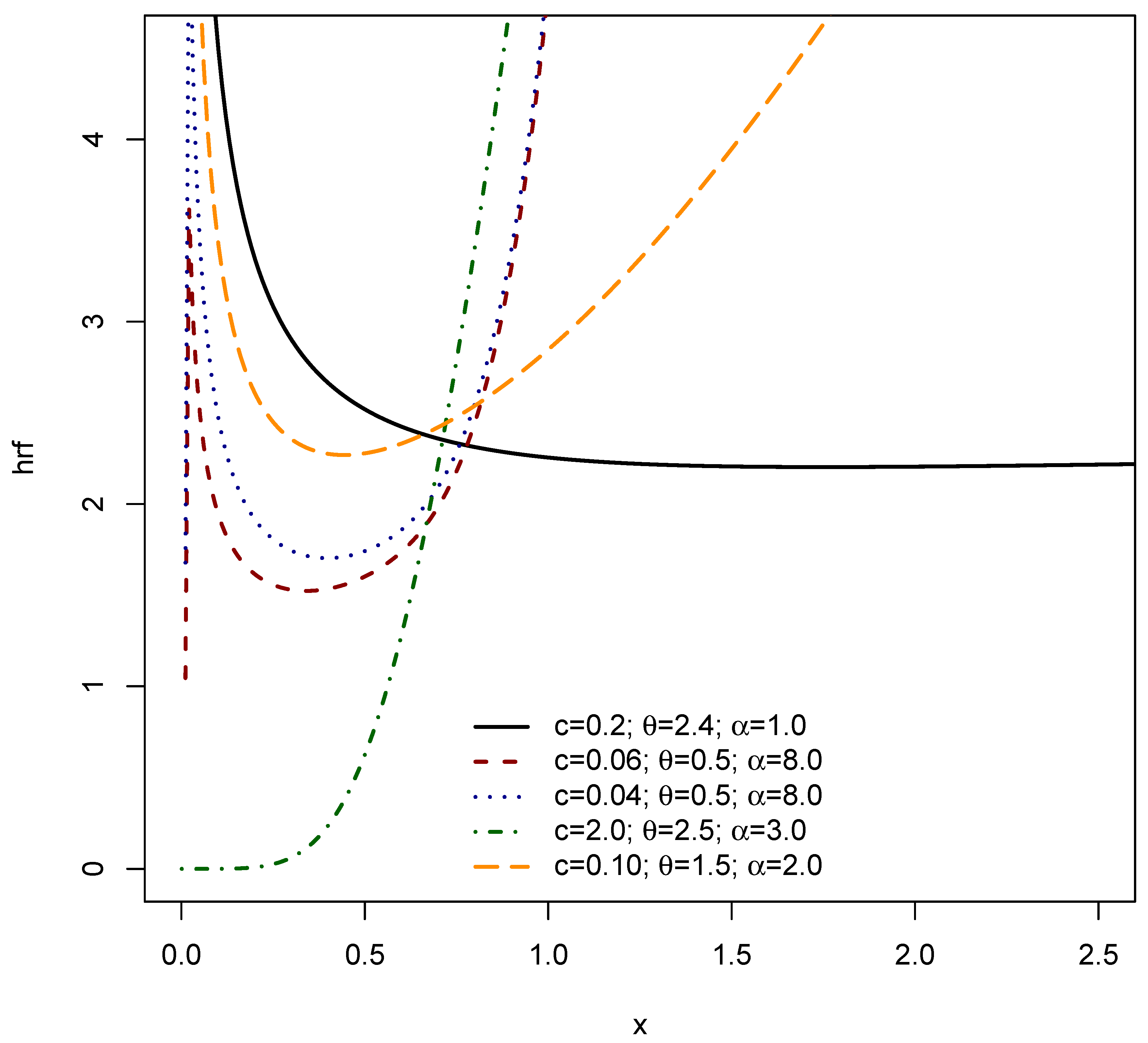
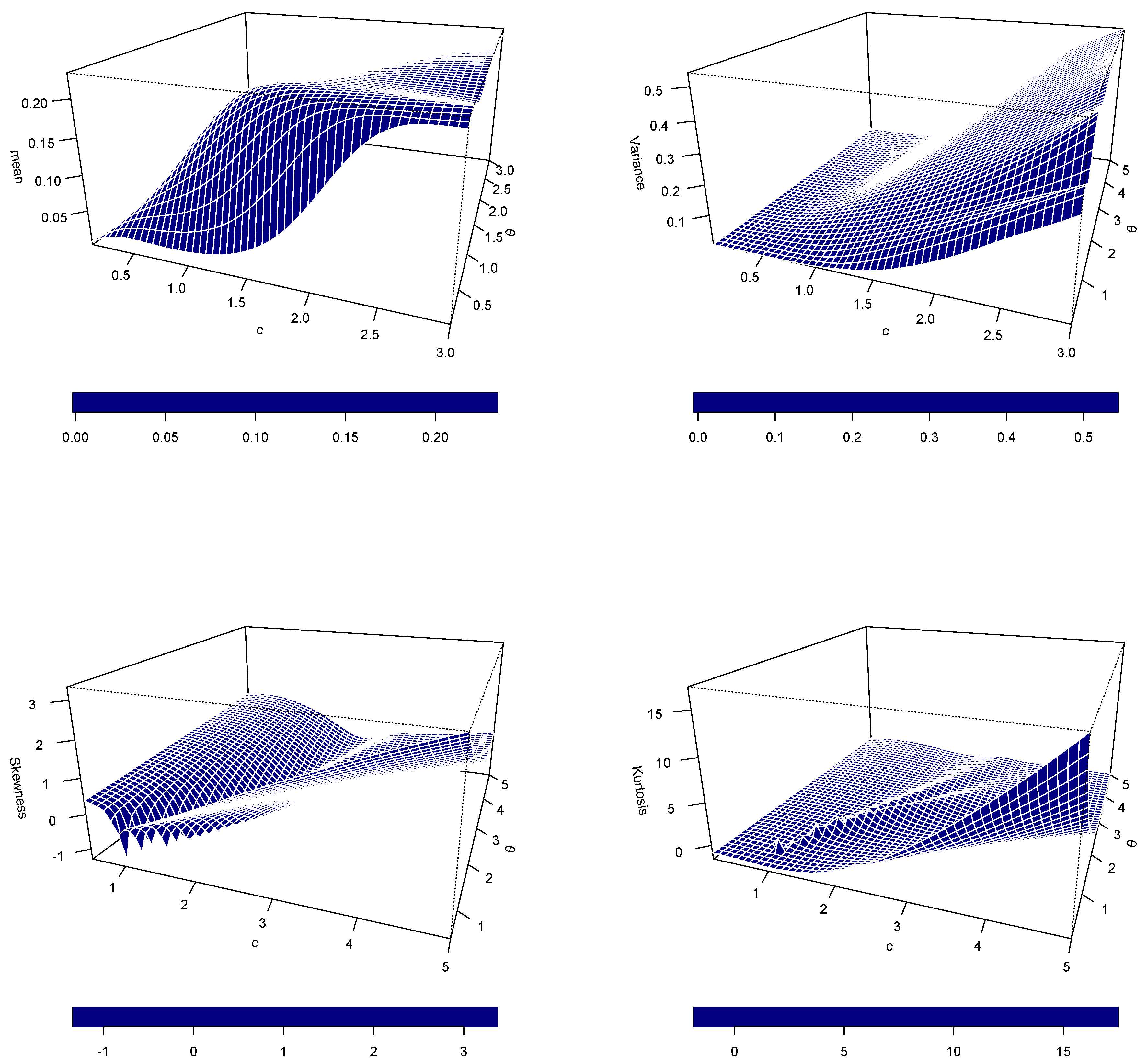
3. Structural Characteristics
4. Maximum Likelihood Estimation
4.1. Conditions for Existence
- The log-likelihood function must be continuous over the parameter space . This ensures that the function does not have "jumps" that would prevent a maximum from being attained. For the EPS distribution, the log-likelihood function is a composite of continuous functions (logarithms, exponentials, sums, products), so it is generally continuous wherever it is defined. However, careful consideration must be given to the domains of logarithmic terms, e.g., , , , , , and the term . These terms imply that , , , , and the argument of the last logarithm must be strictly positive.
-
If the parameter space is a compact set (i.e., closed and bounded), and the log-likelihood function is continuous on , then by the Extreme Value Theorem, a maximum of is guaranteed to exist within . In practice, parameter spaces for distributions are often open (e.g., for scale or shape parameters), which are not compact. In such cases, alternative conditions are needed, such as:
- (a)
- as ℑ approaches the boundary of or goes to infinity: This condition ensures that the maximum does not lie on the boundary or at infinity, forcing it into the interior of the parameter space. For the EPS distribution, for example, as or or , certain terms in tend to , which is a desirable property for ensuring an interior maximum. Similarly, if parameters become excessively large, the likelihood should tend to zero.
4.2. Conditions for Uniqueness
-
If the log-likelihood function is strictly concave over the parameter space , and if a maximum exists, then that maximum is unique. A strictly concave function has at most one global maximum.
- (a)
- Mathematically, strict concavity can be checked by examining the Hessian matrix of the log-likelihood function, . If is negative definite for all , then is strictly concave. This is often the most challenging condition to verify analytically for complex likelihood functions.
- (b)
- For the EPS distribution, one would need to compute the second partial derivatives with respect to c, , and , and then form the Hessian matrix. Demonstrating that this matrix is negative definite across the entire parameter space can be very difficult.
4.3. Implications for the EPS Distribution
- The analytical solution for (Equation 8) implicitly depends on and . This means that exists uniquely given specific values of and . However, the global MLE for c depends on the numerically optimized values of and .
-
Since the likelihood equations for and (Equations 9 and 10 set to zero) do not have closed-form solutions, numerical methods like optim() are necessary. The success and reliability of these numerical methods heavily depend on the underlying properties of the log-likelihood function related to existence and uniqueness:
- (a)
- Local Maxima: If the log-likelihood function for the EPS distribution is not strictly concave, optim() might converge to a local maximum instead of the global maximum. This highlights the importance of choosing good initial values for the optimization (e.g., from moment estimators or a grid search) and potentially running the optimization from multiple starting points to increase confidence in finding the global optimum.
- (b)
- Boundary Issues: The parameters must be positive. The numerical optimization routine must be constrained to respect these bounds (e.g., using method="L-BFGS-B" with lower arguments in R’s optim() function). If the true MLE lies on the boundary of the parameter space, standard derivative-based methods may not apply directly, and the maximum might not be at a point where the gradient is zero.
- (c)
- Identifiability: A fundamental prerequisite for uniqueness is that the model must be identifiable, meaning that different parameter vectors must correspond to different probability distributions. If the EPS distribution is not identifiable (i.e., different combinations of can produce the exact same distribution), then unique MLEs cannot exist. While most well-defined distributions are identifiable, it’s a theoretical point to consider.
5. Regression
5.1. MLE of For Right-Censored Sample
6. Simulation Study
- Generate t from the density
- Generate .
-
Otherwise, return to step 1.
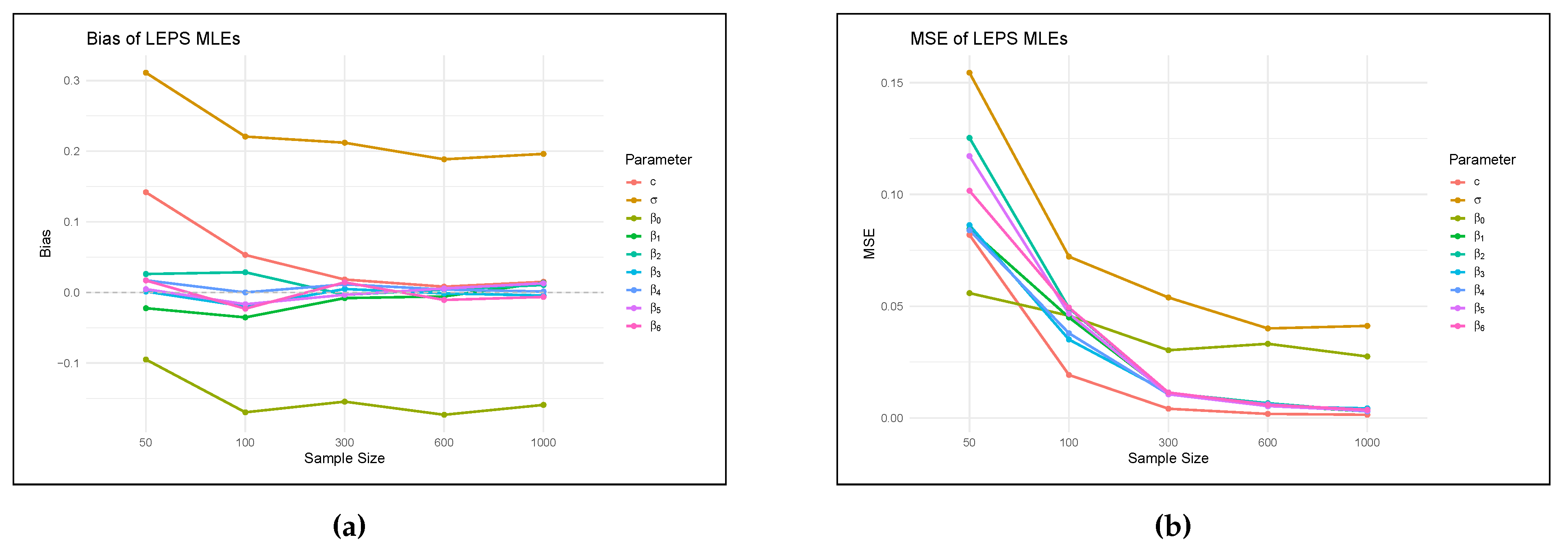
7. Applications
7.1. Fitting LEPS Regression Model to Lifetime of COVID-19 Patients
- (i)
- Intercept (): Estimated lifetime for the baseline patient with all predictors at zero (i.e. youngest age, no heart disease, no asthma, no diabetes, no neurological condition, no obesity) is about 4 years and 6 months.
- (ii)
- Age (): For every additional year of age, the lifetime is expected to decrease by roughly 0.018 years, holding all else equal. This suggests a negative correlation between survival time and age.
- (iii)
- Heart disease (): Patients with heart disease suffers a lifetime reduction by about 0.31 years.
- (iv)
- Asthma (): Asthma appears to be positively correlated with lifetime, increasing it by about 0.088 years but it is not significant statistically since (p-value ).
- (v)
- Diabetes (): lifetime for diabetic patients is significantly low at about 0.54 years, suggesting diabetes seriously reduces the life expectancy of a COVID-19 patient.
- (vi)
- Neurological condition (): Neurological conditions also decrease lifetime by about 0.44 years.
- (vii)
- Obesity (): Obesity has a very weak negative effect on lifetime, but the effect is small and not statistically significant.
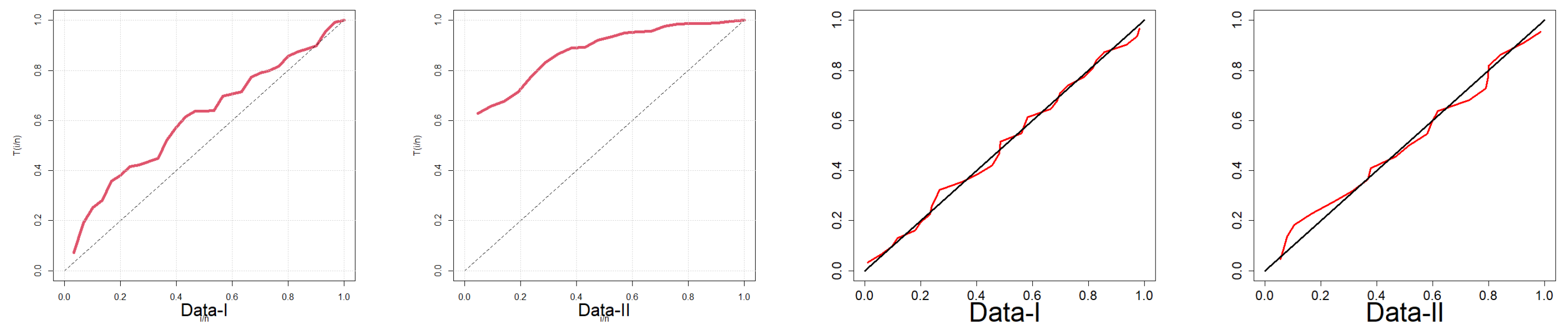
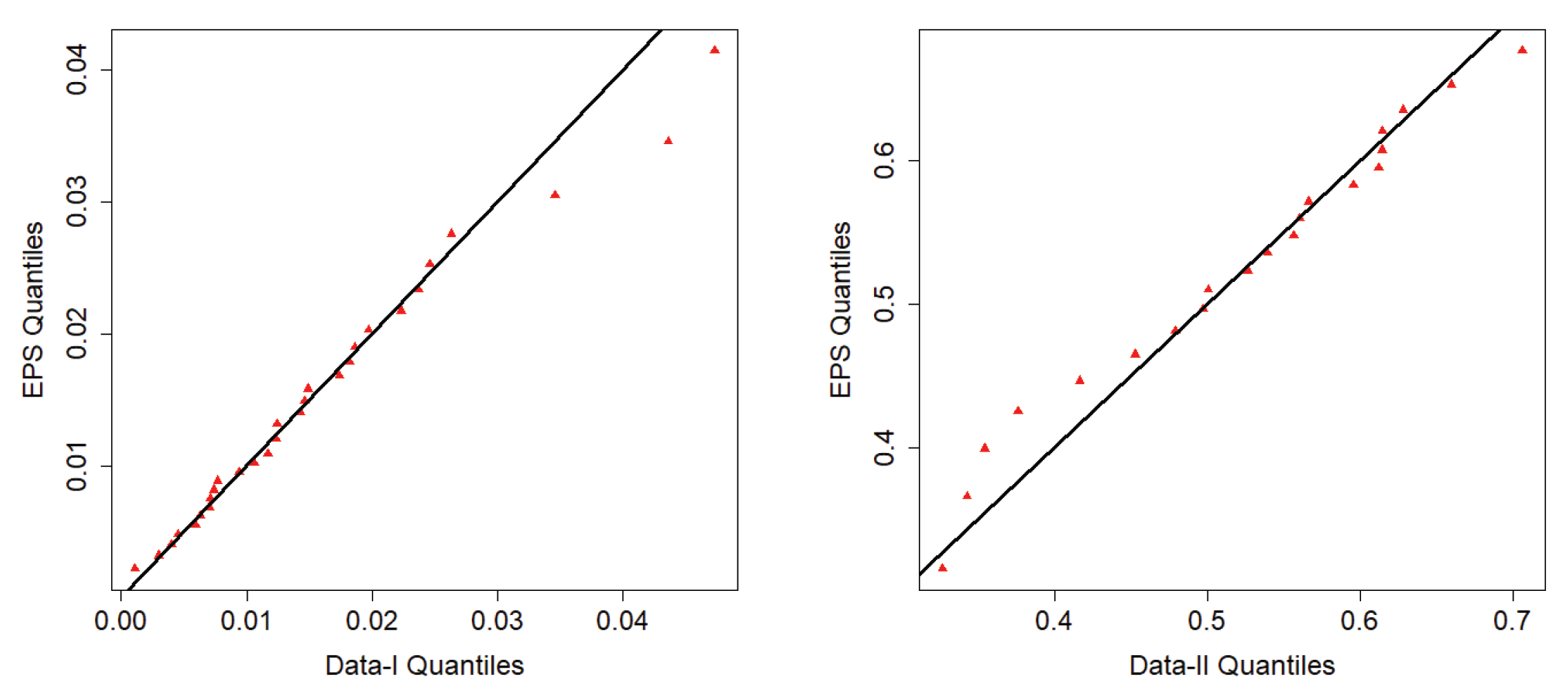
7.2. Fitting EPS to Reliability Data
| Data | Distribution | LL | AIC | CAIC | BIC | HQIC | P-value | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Data-I | EPS | 98.54 | -191.0839 | -190.1608 | -186.8803 | -189.7391 | 0.0178 | 0.1346 | 0.0660 | 0.9995 |
| NGLXTE | 96.82 | -189.6349 | -189.1904 | -186.8325 | -188.7383 | 0.0712 | 0.5074 | 0.1219 | 0.7643 | |
| Logistic-Weibull | 97.74 | -189.4824 | -188.5593 | -185.2788 | -188.1376 | 0.0303 | 0.1958 | 0.0738 | 0.9968 | |
| Power Zeghdoudi | 231.89 | -459.7825 | -459.3380 | -456.9801 | -458.8860 | 0.0189 | 0.1435 | 0.0661 | 0.9994 | |
| Power Ishita | 98.24 | -192.4895 | -192.0450 | -189.6871 | -191.5929 | 0.0280 | 0.2115 | 0.0749 | 0.9960 | |
| Power Prakaamy | 98.24 | -192.4895 | -192.045 | -189.6871 | -191.5929 | 0.0280 | 0.2115 | 0.0749 | 0.9960 | |
| Power Rama | -196.4895 | -192.4895 | -192.045 | -189.6871 | -191.5929 | 0.0220 | 0.2116 | 0.0748 | 0.9960 | |
| Power Lomax | 98.46 | -190.9299 | -190.0068 | -186.7263 | -189.5851 | - | - | 367.17 | ||
| Data-II | EPS | 17.95 | -29.8916 | -28.4798 | -26.7580 | -29.2115 | 0.0225 | 0.1958 | 0.0868 | 0.9932 |
| NGLXTE | 17.84 | -31.6816 | -31.0149 | -29.5925 | -31.2282 | 0.0275 | 0.2202 | 0.0945 | 0.9827 | |
| Logistic-Weibull | 15.77 | -25.5328 | -24.1211 | -22.3993 | -24.8528 | 0.0923 | 0.6032 | 0.1170 | 0.9044 | |
| Power Zeghdoudi | 31.70 | -59.4087 | -58.7420 | -57.3196 | -58.9553 | 0.0466 | 0.3275 | 0.1054 | 0.9546 | |
| Power Ishita | 17.79 | -31.5737 | -30.9070 | -29.4846 | -31.1203 | 0.0326 | 0.2473 | 0.0999 | 0.9710 | |
| Power Prakaamy | 17.79 | -31.5738 | -30.9072 | -29.4848 | -31.1205 | 0.0326 | 0.2473 | 0.0999 | 0.9710 | |
| Power Rama | -35.57 | -31.5714 | -30.9047 | -29.4823 | -31.1180 | 0.0326 | 0.2474 | 0.1000 | 0.9707 | |
| Power Lomax | 17.78 | -29.5634 | -28.1516 | -26.4298 | -28.8833 | 0.0756 | 0.5523 | 0.9074 | 2.2 |
8. Conclusion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shanker, R. Shanker distribution and its applications. International journal of statistics and Applications 2015, 5, 338–348. [Google Scholar] [CrossRef]
- Lindley, D.V. Fiducial distributions and Bayes’ theorem. Journal of the Royal Statistical Society. Series B (Methodological), 1958; 102–107. [Google Scholar]
- Onyekwere, C.K.; Obulezi, O.J. Chris-Jerry distribution and its applications. Asian Journal of Probability and Statistics 2022, 20, 16–30. [Google Scholar] [CrossRef]
- Odom, C.; Ijomah, M. Odoma distribution and its application. Asian journal of probability and statistics 2019, 4, 1–11. [Google Scholar] [CrossRef]
- KK, S. Pranav distribution with properties and its applications. Biom Biostat Int J 2018, 7, 244–254. [Google Scholar]
- Shanker, R. Aradhana distribution and its applications. International Journal of Statistics and Applications 2016, 6, 23–34. [Google Scholar] [CrossRef]
- Ekemezie, D.F.N.; Obulezi, O.J. The Fav-Jerry Distribution: Another Member in the Lindley Class with Applications. Earthline Journal of Mathematical Sciences 2024, 14, 793–816. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Mutairi, D.K.; Balakrishnan, N.; Al-Enezi, L.J. Power Lindley distribution and associated inference. Computational Statistics & Data Analysis 2013, 64, 20–33. [Google Scholar] [CrossRef]
- Shanker, R.; Shukla, K.K. Power Shanker distribution and its application. Türkiye Klinikleri Biyoistatistik 2017, 9, 175–187. [Google Scholar] [CrossRef]
- Embrechts, P.; Klüppelberg, C.; Mikosch, T. Modelling Extremal Events: for Insurance and Finance; Springer, 1997.
- Kotz, S.; Nadarajah, S. Extreme Value Distributions: Theory and Applications; Imperial College Press, 2000.
- Azzalini, A. A class of distributions which includes the normal ones. Scandinavian Journal of Statistics 1985, 12, 171–178. [Google Scholar]
- Aryal, G.R.; Nadarajah, S. Skew t-distribution and its applications. Statistics 2005, 39, 55–76. [Google Scholar]
- McLachlan, G.J.; Peel, D. Finite Mixture Models; Wiley-Interscience, 2000.
- Rasmussen, C.E. The infinite Gaussian mixture model. PhD thesis, University of Cambridge, 1999.
- Lambert, D. Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics 1992, 34, 1–14. [Google Scholar] [CrossRef]
- Ridout, M.S.; Demetrio, C.G.; Hinde, J. Count data models with heterogeneity: An application to claim frequency data. Biometrical Journal 2001, 43, 441–452. [Google Scholar]
- Jones, M.C. Kumaraswamy distribution: properties and applications. International Journal of Statistical Modeling 2009, 8, 281–298. [Google Scholar]
- Cordeiro, G.M.; de Castro, M.H. The beta generalized Kumaraswamy distribution. Journal of Statistical Computation and Simulation 2011, 81, 891–907. [Google Scholar]
- Mudholkar, G.S.; Srivastava, D.K.; Freimer, M. The exponentiated Weibull family: A reanalysis of the bus-motor-failure data. Technometrics 1996, 38, 253–256. [Google Scholar] [CrossRef]
- Aarset, M.V. How to identify a bathtub hazard rate. IEEE Transactions on Reliability 1987, 36, 106–108. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day, 1976.
- Joe, H. Multivariate Models and Dependence Concepts; Chapman and Hall/CRC, 1997.
- Klein, J.P.; Moeschberger, M.L. Survival Analysis: Techniques for Censored and Truncated Data; Springer, 2003.
- Tobin, J. Estimation of relationships for limited dependent variables. Econometrica 1958, 26, 24–36. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman and Hall/CRC, 2013.
- McCulloch, C.E.; Searle, S.R.; Neuhaus, J.M. Generalized, Linear, and Mixed Models; Wiley, 2001.
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. The Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Guan, W.j.; Liang, W.h.; Zhao, Y.; Liang, H.r.; Chen, Z.s.; Li, Y.m.; Liu, X.q.; Chen, R.c.; Tang, C.l.; Wang, T.; et al. Comorbidity and its impact on 1590 patients with COVID-19 in China: a nationwide analysis. European Respiratory Journal 2020, 55. [Google Scholar] [CrossRef]
- Chen, T.; Wu, D.; Chen, H.; Yan, W.; Yang, D.; Chen, G.; Ma, K.; Xu, D.; Yu, H.; Wang, H.; et al. Clinical characteristics of 113 deceased patients with coronavirus disease 2019: retrospective study. BMJ 2020, 368. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. The Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef] [PubMed]
- Sardu, C.; D’Onofrio, N.; Biondi-Zoccai, G.; Ferraraccio, F.; Rizzo, M.R.; Barbieri, M.; Ruggiero, R.; Marfella, R.; Paolisso, G. Outcome of patients with diabetes mellitus affected by COVID-19: experience from an Italian hospital. Diabetes research and clinical practice 2020, 162, 108137. [Google Scholar]
- Durrans, S.R. Distributions of fractional order statistics in hydrology. Water Resources Research 1992, 28, 1649–1655. [Google Scholar] [CrossRef]
- Lehmann, E.L. The power of rank tests; Springer, 2012.
- Ferreira, A.A.; Cordeiro, G.M. The exponentiated power Ishita distribution: Properties, simulations, regression, and applications. Chilean Journal of Statistics (ChJS) 2023, 14. [Google Scholar] [CrossRef]
- Obulezi, O.J.; Ujunwa, O.E.; Anabike, I.C.; Igbokwe, C.P. The exponentiated power Chris-Jerry distribution: properties, regression, simulation and applications to infant mortality rate and lifetime of COVID-19 patients. TWIST 2023, 18, 328–337. [Google Scholar]
- Nwankwo, M.P.; Nwankwo, B.C.; Obulezi, O.J. The Exponentiated Power Akash Distribution: Properties, Regression, and Applications to Infant Mortality Rate and COVID-19 Patients’ Life Cycle. Annals of Biostatistics and Biometric Applications 2023, 5, 1–12. [Google Scholar]
- Murthy, D.P.; Xie, M.; Jiang, R. Weibull models; John Wiley & Sons, 2004.
- Obulezi, O.J.; Obiora-Ilouno, H.O.; Osuji, G.A.; Kayid, M.; Balogun, O.S. A new family of generalized distributions based on logistic-x transformation: sub-model, properties and useful applications. Research in Statistics 2025, 3, 2477232. [Google Scholar] [CrossRef]
- Chaudhary, A.K.; Kumar, V. The Logistic-Weibull distribution with Properties and Applications. IOSR Journal of Mathematics 2021, 17, 32–41. [Google Scholar]
- Messaadia, H.; Zeghdoudi, H. Zeghdoudi distribution and its applications. International Journal of Computing Science and Mathematics 2018, 9, 58–65. [Google Scholar] [CrossRef]
- Shukla, K.K.; Shanker, R. Power Ishita distribution and its application to model lifetime data. Statistics in Transition new series 2018, 19. [Google Scholar] [CrossRef]
- Shukla, K.K.; Shanker, R. Power Prakaamy distribution and its applications. International Journal of Computational and Theoretical Statistics 2020, 7. [Google Scholar]
- Abebe, B.; Tesfay, M.; Eyob, T.; Shanker, R. A two-parameter power Rama distribution with properties and applications. Biometrics and Biostatistics International Journal 2019, 8, 6–11. [Google Scholar]
- Rady, E.H.A.; Hassanein, W.; Elhaddad, T. The power Lomax distribution with an application to bladder cancer data. SpringerPlus 2016, 5, 1–22. [Google Scholar] [CrossRef]

| Behavior | Examples | Standard Limitation | Advanced Models | References |
|---|---|---|---|---|
| Heavy Tails | Financial returns, insurance claims | Normal, exponential decay too quickly | Pareto, t-distribution, Generalized Pareto Distribution (GPD), Log-Cauchy, Stable distributions | [10,11] |
| Skewness | Income, survival times | Normal/logistic are symmetric | Skew-normal, Skew-t, Exponentiated, Transmuted models | [12,13] |
| Multimodality | Gene expression, survey responses | Standard distributions are unimodal | Mixture models, Dirichlet processes, Kernel Density Estimation (KDE) | [14,15] |
| Zero-inflation | Doctor visits, insurance claims | Poisson underestimates zeros | Zero-inflated Poisson, Zero-inflated Negative Binomial | [16,17] |
| Complex bounded shapes | Proportions, rates (0 to 1) | Beta/uniform lack shape flexibility | Kumaraswamy, Beta-Kumaraswamy, Generalized Beta (GB) family | [18,19] |
| Non-monotonic hazard | Reliability/survival data | Weibull assumes monotonic hazard | Exponentiated Weibull, Bathtub models | [20,21] |
| Dependence (Temporal/Spatial) | Sensor data, climate, markets | Assumes independence | ARIMA, GARCH, Spatial Autoregressive (SAR) models, Copulas | [22,23] |
| Censoring or Truncation | Survival, income data | Assumes complete data | Tobit models, Kaplan-Meier estimator, Cox proportional hazards model | [24,25] |
| Nonlinear/Mixed structures | Random or hierarchical effects | Cannot capture heterogeneity | Generalized Linear Mixed Models (GLMMs), Bayesian Hierarchical Models | [26,27] |
| True Population Parameter | n | AE | Bias | MSE | Failure | |
|---|---|---|---|---|---|---|
|
and |
50 | c | 4.01214 | 2.76214 | 1805.52 | 2 |
| 3.21083 | 0.21083 | 1.07584 | ||||
| 2.70836 | 0.45836 | 3.05114 | ||||
| 100 | c | 1.48190 | 0.23193 | 0.94771 | 0 | |
| 3.07120 | 0.07120 | 0.28288 | ||||
| 2.40114 | 0.15114 | 0.58128 | ||||
| 300 | c | 1.29588 | 0.04588 | 0.14002 | 0 | |
| 3.02794 | 0.02794 | 0.07585 | ||||
| 2.30830 | 0.05830 | 0.13499 | ||||
| 600 | c | 1.27276 | 0.02276 | 0.05977 | 0 | |
| 3.01246 | 0.01246 | 0.03454 | ||||
| 2.27485 | 0.02485 | 0.05943 | ||||
|
and |
50 | c | 2.39687 | 1.19687 | 102.66400 | 0 |
| 2.64503 | 0.14503 | 0.74596 | ||||
| 2.06780 | 0.31780 | 1.37844 | ||||
| 100 | c | 1.53352 | 0.33352 | 20.05157 | 0 | |
| 2.55056 | 0.05056 | 0.29395 | ||||
| 1.89479 | 0.14479 | 0.41803 | ||||
| 300 | c | 1.25556 | 0.05556 | 0.13416 | 0 | |
| 2.51623 | 0.01623 | 0.07365 | ||||
| 1.78768 | 0.03768 | 0.07880 | ||||
| 600 | c | 1.22647 | 0.02647 | 0.05145 | 0 | |
| 2.50769 | 0.00769 | 0.03345 | ||||
| 1.76348 | 0.01348 | 0.03225 |
| True Population Parameter | n | AE | Bias | MSE | Failure | |
|---|---|---|---|---|---|---|
|
and |
50 | c | 7.58699 | 5.58699 | 10808.23 | 0 |
| 1.62114 | 0.12114 | 0.61375 | ||||
| 0.53816 | 0.03816 | 0.03435 | ||||
| 100 | c | 2.37108 | 0.37108 | 4.04365 | 0 | |
| 1.52277 | 0.02277 | 0.19236 | ||||
| 0.52169 | 0.02169 | 0.01270 | ||||
| 300 | c | 2.10305 | 0.10305 | 0.42604 | 0 | |
| 1.51435 | 0.01435 | 0.05911 | ||||
| 0.50540 | 0.00540 | 0.00406 | ||||
| 600 | c | 2.05266 | 0.05266 | 0.17822 | 0 | |
| 1.50626 | 0.00626 | 0.02683 | ||||
| 0.50247 | 0.00247 | 0.00183 | ||||
|
and |
50 | c | 5.34962 | 3.59962 | 1355.51 | 0 |
| 2.66720 | 0.16720 | 0.90745 | ||||
| 0.85155 | 0.10155 | 0.18730 | ||||
| 100 | c | 2.33891 | 0.58891 | 7.82254 | 0 | |
| 2.58483 | 0.08483 | 0.36659 | ||||
| 0.79499 | 0.04499 | 0.05807 | ||||
| 300 | c | 1.88049 | 0.13049 | 0.50744 | 0 | |
| 2.52786 | 0.02786 | 0.10010 | ||||
| 0.76031 | 0.01031 | 0.01386 | ||||
| 600 | c | 1.79878 | 0.03978 | 0.14491 | 0 | |
| 2.50497 | 0.00497 | 0.04073 | ||||
| 0.75652 | 0.00652 | 0.00615 |
| n | Parameter | AE | Bias | MSE | Failures |
|---|---|---|---|---|---|
| 50 | c | 0.8419 | 0.1419 | 0.081913 | 0 |
| 1.3111 | 0.3111 | 0.15446 | 0 | ||
| 0.4051 | -0.0949 | 0.055856 | 0 | ||
| -0.4223 | -0.0223 | 0.084558 | 0 | ||
| 0.3261 | 0.0261 | 0.125322 | 0 | ||
| -0.1987 | 0.0013 | 0.086269 | 0 | ||
| 0.1172 | 0.0172 | 0.083993 | 0 | ||
| -0.0953 | 0.0047 | 0.117172 | 0 | ||
| 0.067 | 0.017 | 0.101669 | 0 | ||
| 100 | c | 0.7531 | 0.0531 | 0.019264 | 1 |
| 1.2207 | 0.2207 | 0.072187 | 1 | ||
| 0.3303 | -0.1697 | 0.045762 | 1 | ||
| -0.4353 | -0.0353 | 0.044984 | 1 | ||
| 0.3286 | 0.0286 | 0.049173 | 1 | ||
| -0.2199 | -0.0199 | 0.035101 | 1 | ||
| 0.1 | 0 | 0.037915 | 1 | ||
| -0.1167 | -0.0167 | 0.046636 | 1 | ||
| 0.027 | -0.023 | 0.049399 | 1 | ||
| 300 | c | 0.7183 | 0.0183 | 0.004132 | 0 |
| 1.212 | 0.212 | 0.053904 | 0 | ||
| 0.3454 | -0.1546 | 0.030306 | 0 | ||
| -0.408 | -0.008 | 0.011035 | 0 | ||
| 0.2967 | -0.0033 | 0.011113 | 0 | ||
| -0.1951 | 0.0049 | 0.01142 | 0 | ||
| 0.1115 | 0.0115 | 0.010602 | 0 | ||
| -0.1033 | -0.0033 | 0.010573 | 0 | ||
| 0.0643 | 0.0143 | 0.011398 | 0 | ||
| 600 | c | 0.7082 | 0.0082 | 0.001816 | 0 |
| 1.1885 | 0.1885 | 0.040061 | 0 | ||
| 0.3268 | -0.1732 | 0.033185 | 0 | ||
| -0.4056 | -0.0056 | 0.005568 | 0 | ||
| 0.3041 | 0.0041 | 0.006607 | 0 | ||
| -0.2013 | -0.0013 | 0.00525 | 0 | ||
| 0.1041 | 0.0041 | 0.006256 | 0 | ||
| -0.0944 | 0.0056 | 0.005313 | 0 | ||
| 0.0394 | -0.0106 | 0.005905 | 0 |
| Distribution | AIC | CAIC | BIC | HQIC | Rank |
|---|---|---|---|---|---|
| LEPS | 426.4954 | 427.3471 | 460.4664 | 440.0577 | 1 |
| LEPCJ | 432.8959 | 433.7475 | 466.8668 | 446.4582 | 10 |
| LEPA | 430.5849 | 431.4365 | 464.5559 | 444.1472 | 8 |
| LPP | 634.9586 | 635.6660 | 665.1550 | 647.0140 | 12 |
| LEPL | 427.5919 | 428.4435 | 461.5629 | 441.1542 | 4 |
| LEPR | 633.7501 | 634.6017 | 667.7211 | 647.3124 | 11 |
| LEPLo | 428.4645 | 429.3170 | 462.4363 | 442.0276 | 5 |
| LPZ | 429.4645 | 430.1719 | 459.6609 | 441.5199 | 6 |
| LPSU | 432.6906 | 433.3980 | 462.8870 | 444.7460 | 9 |
| LEPI | 426.5270 | 427.3786 | 460.4979 | 440.0893 | 2 |
| LPI | 430.2170 | 430.9244 | 460.4134 | 442.2724 | 7 |
| LEW | 426.5323 | 427.3839 | 460.5033 | 440.0946 | 3 |
| Dist | c | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| LEPS | 0.32055 | 0.39854 (0.17345) |
4.52354 (0.35328) |
-0.01763 (0.00445) |
-0.30804 (0.12678) |
0.08840 (0.11187) |
-0.53958 (0.31905) |
-0.43946 (0.15208) |
-0.05539 (0.18159) |
| LEPCJ | 0.28569 | 0.44464 (0.12469) |
4.03788 (0.31162) |
-0.01460 (0.00377) |
-0.26641 (0.10794) |
0.05634 (0.10103) |
-0.40018 (0.30172) |
-0.38661 (0.14027) |
-0.06365 (0.16069) |
| LEPA | 0.86502 | 1.02188 (0.47811) |
3.38640 (1.03469) |
-0.01789 (0.00392) |
-0.34401 (0.13128) |
0.09313 (0.12089) |
-0.44848 (0.34812) |
-0.50329 (0.15598) |
-0.00147 (0.20885) |
| LPP | - | 1.34315 (0.08866) |
3.68414 (0.32038) |
-0.02804 (0.00429) |
-0.45720 (0.14211) |
0.12111 (0.13263) |
-0.59199 (0.35996) |
-0.60786 (0.16355) |
-0.28410 (0.22410) |
| LEPL | 0.51725 | 0.55772 (0.23260) |
4.29864 (0.41692) |
-0.01771 (0.00405) |
-0.32000 (0.12351) |
0.09596 (0.11470) |
-0.50055 (0.32494) |
-0.45724 (0.15254) |
-0.02007 (0.19166) |
| LEPR | 0.08776 | 1.30970 (0.08555) |
3.64433 (0.31309) |
-0.02701 (0.00418) |
-0.45200 (0.13917) |
0.11142 (0.12970) |
-0.59003 (0.35738) |
-0.58702 (0.16277) |
-0.27204 (0.21963) |
| LEPLo | 11.0562 | 0.53888 (0.04311) |
-5.81524 (0.84512) |
0.01826 (0.00414) |
0.34664 (0.12894) |
-0.09095 (0.12057) |
0.50343 (0.33638) |
0.48175 (0.15694) |
0.01736 (0.19969) |
| LPZ | - | 1.11805 (0.07670) |
3.27079 (0.29615) |
-0.01817 (0.00390) |
-0.34904 (0.13435) |
0.09141 (0.12386) |
-0.44806 (0.34622) |
-0.51847 (0.16116) |
-0.00658 (0.21319) |
| LPSU | - | 1.49635 (0.08426) |
1.99343 (0.28684) |
-0.01785 (0.00365) |
-0.33588 (0.13137) |
0.09619 (0.12081) |
-0.40231 (0.33385) |
-0.50443 (0.15288) |
0.01387 (0.21289) |
| LEPI | 0.21330 | 0.39922 (0.20624) |
4.42438 (0.41197) |
-0.01755 (0.00391) |
-0.30067 (0.12971) |
0.08156 (0.11068) |
-0.51081 (0.32332) |
-0.42436 (0.15583) |
-0.07581 (0.17826) |
| LPI | - | 1.16293 (0.07608) |
3.25318 (0.30392) |
-0.01902 (0.00398) |
-0.35417 (0.13681) |
0.10365 (0.12661) |
-0.45484 (0.34889) |
-0.52951 (0.16079) |
-0.00731 (0.21907) |
| LEW | 0.53288 | 0.27088 (0.14772) |
4.67512 (0.35132) |
-0.01737 (0.00446) |
-0.28274 (0.12487) |
0.08807 (0.11101) |
-0.53446 (0.31753) |
-0.42685 (0.15148) |
-0.08440 (0.17681) |
| Parameter | LEPS | LEPCJ | LEPA | LPP | LEPL | LPR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Upper | Lower | Upper | Lower | Upper | Lower | Upper | Lower | Upper | Lower | Upper | |
| c | -0.0111 | 0.6522 | 0.0837 | 0.4877 | -0.6538 | 2.3838 | -0.0868 | 1.1213 | -1967.2710 | 1967.4460 | ||
| 0.0573 | 0.7398 | 0.1993 | 0.6899 | 0.0813 | 1.9625 | 1.1687 | 1.5176 | 0.1001 | 1.0153 | 1.1414 | 1.4780 | |
| 3.8285 | 5.2186 | 3.4248 | 4.6509 | 1.3508 | 5.4220 | 3.0538 | 4.3144 | 3.4784 | 5.1189 | 3.0284 | 4.2603 | |
| -0.0264 | -0.0089 | -0.0220 | -0.0072 | -0.0256 | -0.0102 | -0.0365 | -0.0196 | -0.0257 | -0.0097 | -0.0352 | -0.0188 | |
| -0.5575 | -0.0586 | -0.4788 | -0.0541 | -0.6023 | -0.0857 | -0.7368 | -0.1776 | -0.5630 | -0.0770 | -0.7258 | -0.1782 | |
| -0.1317 | 0.3085 | -0.1424 | 0.2551 | -0.1447 | 0.3310 | -0.1398 | 0.3820 | -0.1297 | 0.3216 | -0.1438 | 0.3666 | |
| -1.1673 | 0.0881 | -0.9938 | 0.1934 | -1.1333 | 0.2364 | -1.3002 | 0.1162 | -1.1398 | 0.1387 | -1.2931 | 0.1131 | |
| -0.7387 | -0.1403 | -0.6626 | -0.1106 | -0.8102 | -0.1964 | -0.9296 | -0.2861 | -0.7573 | -0.1571 | -0.9072 | -0.2668 | |
| -0.4126 | 0.3019 | -0.3798 | 0.2525 | -0.4124 | 0.4094 | -0.7250 | 0.1568 | -0.3971 | 0.3570 | -0.7041 | 0.1601 | |
| Parameter | LPL | LPZ | LEPSU | LEPI | LPI | LEW | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Upper | Lower | Upper | Lower | Upper | Lower | Upper | Lower | Upper | Lower | Upper | |
| c | -18.2400 | 40.3524 | -0.0547 | 0.4813 | -0.0000 | 1.0658 | ||||||
| 0.4541 | 0.6237 | 0.9671 | 1.2689 | 1.3306 | 1.6621 | -0.0065 | 0.8049 | 1.0133 | 1.3126 | 0.0503 | 0.6315 | |
| -7.4779 | -4.1526 | 2.6882 | 3.8534 | 1.4291 | 2.5577 | 3.6139 | 5.2349 | 2.6553 | 3.8511 | 3.9840 | 5.3663 | |
| 0.0101 | 0.0264 | -0.0258 | -0.0105 | -0.0250 | -0.0107 | -0.0253 | -0.0099 | -0.0268 | -0.0112 | -0.0261 | -0.0086 | |
| 0.0929 | 0.6003 | -0.6134 | -0.0847 | -0.5943 | -0.0774 | -0.5559 | -0.0455 | -0.6233 | -0.0850 | -0.5284 | -0.0371 | |
| -0.3282 | 0.1463 | -0.1523 | 0.3351 | -0.1415 | 0.3339 | -0.1362 | 0.2993 | -0.1454 | 0.3527 | -0.1303 | 0.3065 | |
| -0.1583 | 1.1652 | -1.1292 | 0.2331 | -1.0591 | 0.2545 | -1.1469 | 0.1253 | -1.1412 | 0.2316 | -1.1592 | 0.0902 | |
| 0.1729 | 0.7905 | -0.8355 | -0.2014 | -0.8052 | -0.2037 | -0.7309 | -0.1178 | -0.8459 | -0.2132 | -0.7249 | -0.1288 | |
| -0.3755 | 0.4102 | -0.4260 | 0.4128 | -0.4050 | 0.4327 | -0.4265 | 0.2749 | -0.4383 | 0.4237 | -0.4323 | 0.2634 | |
| 1.43 | 0.11 | 0.71 | 0.77 | 2.63 | 1.49 | 3.46 | 2.46 | 0.59 | 0.74 |
|---|---|---|---|---|---|---|---|---|---|
| 1.23 | 0.94 | 4.36 | 0.40 | 1.74 | 4.73 | 2.23 | 0.45 | 0.70 | 1.06 |
| 1.46 | 0.30 | 1.82 | 2.37 | 0.63 | 1.23 | 1.24 | 1.97 | 1.86 | 1.17 |
| 0.70570244 | 0.65946256 | 0.62801346 | 0.6143952 | 0.61453596 | 0.59540885 | 0.61190438 |
|---|---|---|---|---|---|---|
| 0.56040019 | 0.53945593 | 0.52641369 | 0.55652406 | 0.56615856 | 0.50050448 | 0.49723726 |
| 0.47911586 | 0.3270769 | 0.34298934 | 0.35461942 | 0.37625366 | 0.41652161 | 0.45295061 |
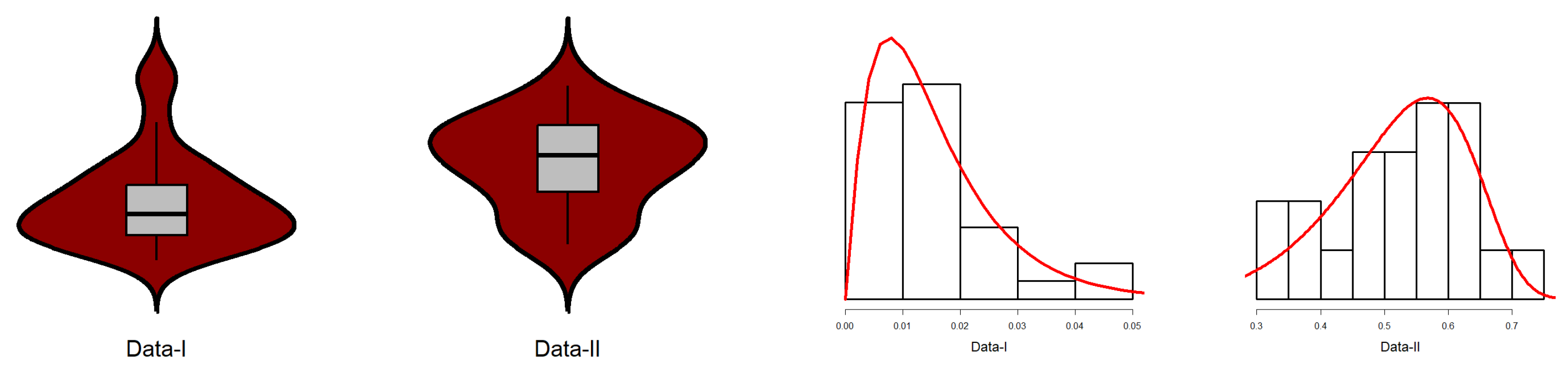
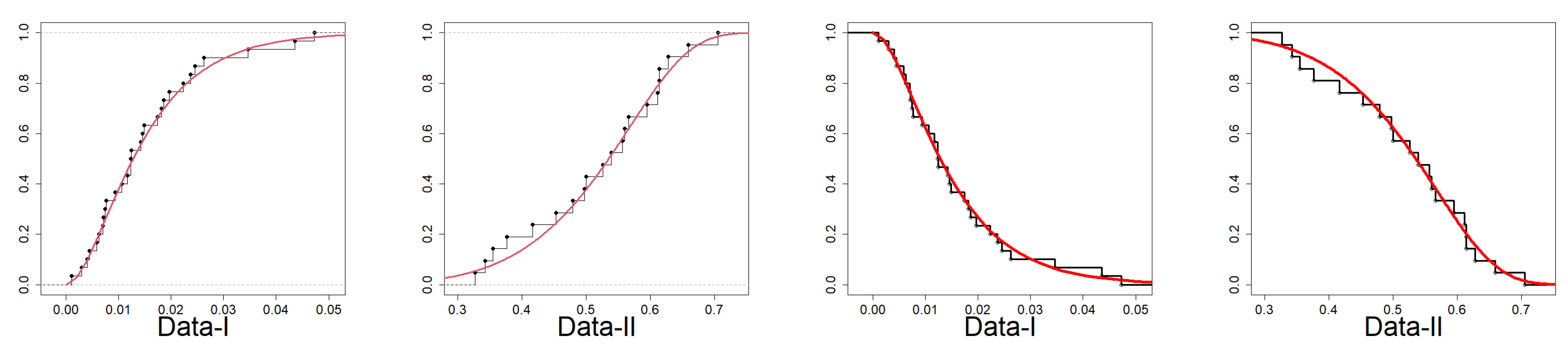
| Data-I | Data-II | |
|---|---|---|
| n | 30 | 21 |
| 0.0072 | 0.4530 | |
| 0.0194 | 0.6119 | |
| IQR | 0.0123 | 0.1590 |
| Outlier | 0.0436, 0.0473 | - |
| Mean | 0.0154 | 0.5203 |
| Median | 0.0124 | 0.5395 |
| Var | 0.0001 | 0.0119 |
| SD | 0.0113 | 0.1090 |
| Range | 0.0462 | 0.3786 |
| Skewness | 1.2955 | -0.3335 |
| Kurtosis | 4.3192 | 2.1101 |
| Distribution | Parameter | Data-I | Data-II | ||
|---|---|---|---|---|---|
| MLE | Standard Error | MLE | Standard Error | ||
| EPS | c | 2.02704 | 2.01553 | 0.53153 | 0.54852 |
| 107.73256 | 161.86640 | 77.82167 | 173.8626 | ||
| 1.02418 | 0.50546 | 8.80975 | 6.35813 | ||
| NGLXTE | 0.95548 | 0.14244 | 0.23295 | 0.04141 | |
| 36.67111 | 4.51186 | 1.22582 | 0.04716 | ||
| Logistic-Weibull | 0.30937 | 2.93717 | 1.70673 | 55.05655 | |
| 3.90162 | 50.42695 | 3.05404 | 109.99449 | ||
| 7.26999 | 69.02284 | 4.59278 | 148.15444 | ||
| Power Zeghdoudi | 125.35135 | 67.87865 | 20.37515 | 7.51274 | |
| 0.98946 | 0.13455 | 3.78107 | 0.64425 | ||
| Power Ishita | 385.28497 | 302.30205 | 28.73580 | 16.17704 | |
| 1.46339 | 0.20284 | 5.84443 | 1.02779 | ||
| Power Prakaamy | 385.19264 | 302.05889 | 28.72744 | 16.18301 | |
| 1.46334 | 0.20273 | 5.84413 | 1.02807 | ||
| Power Rama | 385.40469 | 302.79412 | 28.71725 | 16.14841 | |
| 1.46342 | 0.20310 | 5.84763 | 1.02518 | ||
| Power Lomax | 0.00268 | 0.00061 | 10.36019 | 100.65774 | |
| 3.60831 | 1.70345 | 300.34300 | 2898.00826 | ||
| 1.71697 | 0.13879 | 5.85607 | 1.03083 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





