Conditional Domain Adaptation with α-Rényi Entropy Regularization and Noise-Aware Label Weighting

1. Introduction

A primary challenge in the development of artificial intelligence systems is ensuring that models maintain reliable performance under conditions that differ from those observed during training [1]. Such discrepancies may arise due to changes in the operational environment, variations in acquisition devices, or differences in user population characteristics [2]. These shifts, though often subtle, can significantly impact model behavior and compromise generalization capabilities, even when the underlying task remains unchanged [3]. This vulnerability becomes particularly critical in real-world applications, where it is infeasible to anticipate all possible future scenarios, thus limiting the scalability and trustworthiness of deployed solutions [4]. In this context, validation within the source domain alone proves insufficient to guarantee consistent performance in heterogeneous settings, prompting the development of strategies to mitigate such discrepancies. Among these, domain adaptation has emerged as a key approach, enabling the reuse of pre-trained models in new environments by aligning distributions across domains, thereby reducing the need for extensive data collection and annotation in the target domain [5]. The latter not only enhances the efficiency of knowledge transfer, but also supports the creation of more robust and sustainable systems in dynamic and uncertain environments.

Despite the progress achieved through domain adaptation, the problem of generalizing to unseen domains remains only partially resolved. Domain shifts can take complex forms that go beyond marginal discrepancies, affecting the internal structure of learned representations and leading to systematic performance degradation in the target domain [6]. Consequently, adapted models frequently exhibit degraded or inconsistent performance when deployed in unfamiliar environments, especially under shifts in input distributions that are structural and semantic in nature [7]. This limitation arises primarily from the inability to preserve domain-invariant features under covariate shifts, where noise in input features, biased samples, or insufficient representations can degrade the alignment across domains and compromise the stability of the learned models [8]. Second, generalization is further hindered when the learned features lack discriminative power, particularly in the presence of concept shift and noisy labels. These factors distort latent representations and decision boundaries, making it difficult to maintain semantic clarity in the target domain [9]. Third, the absence of interpretability mechanisms impedes the reliable evaluation of whether predictions are based on meaningful semantic signals or on spurious correlations inherited from the source domain [10]. Collectively, these challenges hinder the development of domain-adaptive systems that are accurate, robust, and interpretable.

In response to the challenges inherent in domain adaptation, numerous classical approaches have been proposed, most of which rely on linear transformations to align source and target distributions. These strategies aim to mitigate distributional discrepancies through statistical alignment techniques. Methods such as Correlation Alignment (CORAL) and Subspace Alignment (SA) reduce marginal discrepancy by aligning covariance matrices or projecting data onto orthonormal subspaces [11,12]. Despite their effectiveness under controlled conditions, their reliance on original feature spaces or linear projections makes them susceptible to distortions, noise, and domain-specific biases, hindering the extraction of invariant representations [13]. To address these limitations, geometrically inspired extensions such as Geometric Transfer Learning (GTL) have been developed, incorporating structural constraints between domains [14]. Nonetheless, they depend on linear subspace representations, which fail to adequately preserve the support of the target domain in the presence of data heterogeneity or limited representational capacity [15]. In addition, techniques such as Transfer Joint Matching (TJM), Transfer Component Analysis (TCA), and Maximum Independence Domain Adaptation (MIDA) seek to align both marginal and conditional distributions via linear projections [16,17,18]. Yet, they do not guarantee class separability in the latent space, particularly under concept shift or class imbalance, resulting in ambiguous decision boundaries and diminished discriminative performance [19]. A comparable deficiency is noted in Joint Distribution Adaptation (JDA), which, despite modeling joint alignment, assumes uniform relevance across classes and lacks adaptive mechanisms to address intra-class heterogeneity or instance-level significance [20].

Due to the structural constraints of traditional domain adaptation techniques, particularly the decoupling of feature transformation and prediction phases, deep learning methods have emerged as a more cohesive solution for preserving domain-invariant features across the representation space [21]. These approaches leverage the expressive capabilities of deep neural networks to jointly optimize feature extraction and domain alignment, enhancing adaptability under covariate shift [22]. Adversarial training-based models, including Domain-Adversarial Neural Networks (DANN) and its extensions, have demonstrated considerable effectiveness in aligning marginal distributions within a shared latent space [23,24]. Still, while these methods reduce global disparities, they often struggle to maintain class separability, as they do not explicitly model conditional structures or discriminative boundaries [25]. To overcome these limitations, hybrid models have emerged that integrate deep learning architectures with statistical alignment objectives, enabling end-to-end optimization for improved domain adaptation performance [26]. These approaches aim to preserve both predictive accuracy and domain invariance by combining supervised losses with the minimization of statistical discrepancies across multiple network layers [27,28]. However, hybrid methods also face challenges, such as gradient conflicts between classification and alignment objectives, and semantic misalignment caused by noisy pseudo-labels [29]. In summary, deep learning models represent a significant advancement in preserving domain-invariant features, yet their ability to ensure discriminative consistency in the target domain remains limited [30].

Despite significant advancements in deep learning techniques aimed at extracting domain-invariant features, these methods often fall short in preserving a well-defined, discriminative class structure within the target domain. To mitigate this issue, transfer-based strategies include fine-tuning, teacher–student models, meta-learning frameworks, and asymmetric architectures such as Adversarial Discriminative Domain Adaptation (ADDA) have been proposed [21,25,31,32,33]. These approaches aim to enhance inter-class separation through adaptive training or auxiliary supervision; however, they exhibit notable limitations, including degradation of pretrained features and susceptibility to noise [34,35]. Additionally, ADDA variants lack explicit modeling of class boundaries, often resulting in ambiguous latent representations [36]. In contrast, conditional alignment techniques—particularly Conditional Adversarial Domain Adaptation (CDAN) and its extensions—integrate classifier outputs into the discriminator to capture class-conditional dependencies [37]. While these techniques improve multimodal alignment, they are vulnerable in scenarios with class imbalance or low prediction confidence, potentially distorting decision boundaries and compromising semantic clarity [30].

In addition to generalization and discriminability, interpretability has become a pivotal aspect of domain adaptation, especially in high-stakes applications where understanding model behavior is essential for fostering trust, transparency, and accountability [38]. In this context, latent space analysis has proven valuable for examining the structure of learned representations. Linear techniques such as Principal Component Analysis (PCA) offer computational efficiency but fall short in capturing the nonlinear relationships relevant across multiple domains [39]. In contrast, nonlinear methods like t-distributed Stochastic Neighbor Embedding (t-SNE) and Uniform Manifold Approximation and Projection (UMAP) are more effective in representing complex inter-domain structures [40]. UMAP, in particular, stands out for its ability to preserve both local and global structures, maintain stability under parameter variation, and scale efficiently—making it especially useful for visualizing semantic alignment across domains [41,42]. Besides, interpretability is especially crucial in sensitive applications. Among post hoc methods, Gradient-weighted Class Activation Mapping (Grad-CAM) generates attention maps that highlight regions influencing model predictions, while its extension, Grad-CAM++, improves spatial resolution through higher-order derivatives, though it remains limited by nonlinear activation functions [43,44,45]. In domain adaptation, Grad-CAM++ has proven effective not only as an explainability tool but also for visually assessing semantic consistency across domains [46]. Other approaches, such as Layer-wise Relevance Propagation (LRP) and SHapley Additive exPlanations (SHAP), provide quantitative insights by assigning relevance scores to input features, aiding the identification of spurious patterns or conflicting decision rules [47]. The lack of interpretability methods specifically designed for transfer learning and domain adaptation remains a significant limitation, highlighting the need for more robust explanatory tools tailored to cross-domain scenarios [48].

Here, we propose Conditional Rényi $\alpha$-Entropy Domain Adaptation (CREDA), a novel domain adaptation framework designed to simultaneously preserve domain-invariant representations, enforce class-conditional alignment, and mitigate the effect of noisy pseudo-labels. The core idea of CREDA is to regularize deep feature alignment using a differentiable, matrix-based formulation of Rényi’s quadratic entropy, which provides a non-parametric and robust estimate of class-wise distributional similarity. CREDA is implemented as an end-to-end trainable architecture comprising three key stages:

–

Deep Feature Extraction: A shared ResNet-18 backbone encodes samples from both source and target domains into a latent representation space.

–

Noise-Aware Label Weighting: An entropy-derived confidence score is used to down-weight low-confidence pseudo-labels in the target domain, improving robustness against noisy or ambiguous predictions.

–

Class-Conditional Alignment via Rényi-based entropy: A novel entropy-based regularization term is applied over kernel Gram matrices to minimize divergence between class-wise source and target feature distributions.

We evaluate CREDA on three widely used visual domain adaptation benchmarks for image classification: Digits, ImageCLEF-DA, and Office-31. We also compare its performance against state-of-the-art approaches such as DANN, ADDA, and CDAN+E. The results consistently demonstrate that CREDA achieves superior performance in terms of classification accuracy, semantic alignment, and interpretability, with improvements of average accuracy across benchmarks. Qualitative analyses using UMAP and Grad-CAM++ further confirm that CREDA maintains both inter-class separability and cross-domain semantic coherence, highlighting its potential for deployment in real-world, label-scarce environments.

The remainder of this paper is organized as follows: Section 2 introduces the materials and methods. Section 3 and Section 4 discuss the experiments and results. Finally, Section 5 outlines the concluding remarks.

2. Materials and Methods

2.1. Kernel Methods Fundamentals

Kernel methods provide a powerful framework for developing non-linear algorithms. The core idea is to implicitly map the input data from its original space $\mathcal{X}$ into a high-dimensional, or even infinite-dimensional, feature space $\mathcal{H}$ via a non-linear mapping $\Phi :\mathcal{X}\to \mathcal{H}$. The space $\mathcal{H}$ is a special type of Hilbert space known as a Reproducing Kernel Hilbert Space (RKHS), and the mapping $\Phi$ is chosen such that complex patterns in the data may become simpler, e.g., linearly separable $\mathcal{H}$ [49].

Explicitly computing the coordinates of the mapped data points $\Phi \left(x\right)$ is often computationally expensive or infeasible. Then, the kernel trick allows us to bypass this by defining a kernel function $\kappa :\mathcal{X}\times \mathcal{X}\to \mathbb{R}$ that computes the inner product between two points in the feature space:

$$\kappa (x_i,x_j)={\langle \Phi \left(x_i\right),\Phi \left(x_j\right)\rangle }_{\mathcal{H}}.$$

(1)

Then, we work directly with the kernel function without ever needing to know the explicit form of $\Phi$ or the structure of $\mathcal{H}$. Indeed, an RKHS is uniquely defined by this property, ensuring that all computations can be performed using the kernel [50]. In practice, a common choice for the kernel function is the Gaussian kernel:

$${\kappa }_{\sigma }(x_i,x_j)=exp\left({\displaystyle \frac{-\parallel x_i-x_j{\parallel }^2}{2{\sigma }^2}}\right),$$

(2)

which corresponds to an infinite-dimensional feature space, with $\sigma \in {\mathbb{R}}^{+}$. Still, its mathematical tractability and intuitive notion of similarity make it a commonly used approach [51].

2.2. Kernel-based $\alpha$-Rényi’s Entropy Estimation

Let X be a continuous random variable with a probability density function (PDF) $f\left(x\right)$, $x\in X$, the Rényi’s $\alpha$-order entropy is defined as [52]:

$$H_{\alpha }\left(X\right)={\displaystyle \frac{1}{1-\alpha }}log{\int }_{\mathcal{X}}f{\left(x\right)}^{\alpha }dx,$$

(3)

where $\alpha >0$ and $\alpha \ne 1$. A primary challenge in applying this definition is that in most practical scenarios, especially with high-dimensional data like deep features, the underlying PDF $f\left(x\right)$ is unknown [53]. To circumvent this, a Parzen-window method, also known as Kernel Density Estimation (KDE) can be employed. Namely, given a finite set of N samples ${\{x_i\in X\}}_{i=1}^N$, the PDF at any point x can be estimated as the average of kernel functions centered at each sample [54]:

$$\widehat{f}\left(x\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\kappa }_{\sigma }(x,x_i),$$

(4)

where the Gaussian kernel is selected for its mathematical simplicity and desirable smoothing behavior (see equation 2). In particular, when $\alpha =2$ in equation 3, we focus on the special case of Rényi’s entropy, known as quadratic entropy. Indeed, the integral term in equation (3), $\int f{\left(x\right)}^{2}dx$, is known as the Information Potential (IP) [55], a measure of the average information contained in the distribution. Substituting the KDE estimator $\widehat{f}\left(x\right)$ into the IP integral, yields:

$$\begin{array}{cc}\hfill {\widehat{V}}_2\left(X\right)=\int \widehat{f}{\left(x\right)}^{2}dx=& \int \left({\displaystyle \frac{1}{N}}\sum _{i=1}^N{\kappa }_{\sigma }(x,x_i)\right)\left({\displaystyle \frac{1}{N}}\sum _{j=1}^N{\kappa }_{\sigma }(x,x_j)\right)dx,\hfill \\ \hfill {\widehat{V}}_2\left(X\right)=& {\displaystyle \frac{1}{N^2}}\sum _{i=1}^N\sum _{j=1}^N\int {\kappa }_{\sigma }(x,x_i){\kappa }_{\sigma }(x,x_j)dx.\hfill \end{array}$$

(5)

A significant advantage of using a Gaussian kernel is that the integral in equation (5) has a closed-form solution based on the convolution property of Gaussians [56]:

$$\int {\kappa }_{\sigma }(x,x_i){\kappa }_{\sigma }(x,x_j)dx={\kappa }_{\sqrt{2}\sigma }(x_i,x_j).$$

(6)

The latter simplifies the IP estimator to a practical, sample-based formula that depends only on pairwise interactions between samples, completely bypassing the need for explicit PDF estimation:

$${\widehat{V}}_2\left(X\right)={\displaystyle \frac{1}{N^2}}\sum _{i=1}^N\sum _{j=1}^N{\kappa }_{\sqrt{2}\sigma }(x_i,x_j).$$

(7)

Next, let $\mathbf{K}\in {\mathbb{R}}^{N\times N}$ be a Gram matrix whose elements are the pairwise kernel evaluations, ${\mathbf{K}}_{ij}={\kappa }_{\sqrt{2}\sigma }(x_i,x_j)$. The sum of all elements in this matrix can be computed as ${\mathbf{1}}^T\mathbf{K}\mathbf{1}$, where $\mathbf{1}$ is a column vector of ones. This gives a matrix-based estimator for the IP:

$${\widehat{V}}_2\left(X\right)={\displaystyle \frac{1}{N^2}}{\mathbf{1}}^{\top }\mathbf{K}\mathbf{1}$$

(8)

Recently, a $\alpha$ -Rényi matrix-based operator extractss from the IP expression in equation 8. More generally, Rényi’s entropy can be defined directly over the eigenspectrum of a normalized Gram matrix. If we define a normalized Gram matrix $\mathbf{A}=\mathbf{K}/\mathrm{tr}\left(\mathbf{K}\right)$, where $\mathrm{tr}(·)$ is the trace operator, the entropy is given by [57]:

$$H_{\alpha }\left(\mathbf{A}\right)={\displaystyle \frac{1}{1-\alpha }}log\left(\mathrm{tr}\left({\mathbf{A}}^{\alpha }\right)\right)={\displaystyle \frac{1}{1-\alpha }}log\left(\sum _i{\breve{\lambda }}_i{\left(\mathbf{A}\right)}^{\alpha }\right),$$

(9)

where ${\breve{\lambda }}_i\left(\mathbf{A}\right)$ are the eigenvalues of $\mathbf{A}$. For our work with $\alpha =2$, we use a computationally stable form based on the Frobenius norm: $H_2\left(\mathbf{A}\right)=-log\left(\mathrm{tr}\left({\breve{\mathbf{A}}}^{\top }\breve{\mathbf{A}}\right)\right)$, where $\breve{\mathbf{A}}=\mathbf{A}/\mathrm{tr}\left(\mathbf{A}\right)$, $\mathrm{tr}\left(\breve{\mathbf{A}}\right)=1,$ and ${\parallel \mathbf{A}\parallel }_F^2=\mathrm{tr}\left({\mathbf{A}}^{\top }\mathbf{A}\right).$ This matrix-based formulation is essential for deep learning due to several key properties:

–

Non-parametric: It makes no prior assumptions about the underlying data distribution, making it highly suitable for the complex and high-dimensional feature spaces learned by neural networks.

–

Differentiable: The entropy loss is a function of the Gram matrix elements, which are themselves differentiable functions of the feature vectors produced by a given network. This allows gradients to be backpropagated through the kernel computations to the network’s parameters, enabling end-to-end training.

–

Robust: The entropy is calculated based on the collective geometric structure of the data, as captured by all pairwise interactions in the Gram matrix. This makes the measure inherently robust to outliers, which would have a limited impact on the overall sum of kernel values.

The matrix-based entropy framework in equation 9 can be extended to measure relationships between two random variables, X and Y, represented by paired feature vectors ${\{{\mathbf{f}}_{X,i},{\mathbf{f}}_{Y,i}\}}_{i=1}^N$. This is achieved by defining a joint Gram matrix using the Hadamard (element-wise) product, as follows:

–

Joint Entropy - (JE). Let ${\mathbf{K}}_X\in {\mathbb{R}}^{N\times N}$ and ${\mathbf{K}}_Y\in {\mathbb{R}}^{N\times N}$ be the Gram matrices computed from the feature sets of X and Y, respectively. The joint entropy based on the $\alpha$-Rényi estimator is defined as [58]:

$$H_{\alpha }({\mathbf{K}}_X,{\mathbf{K}}_Y)={\displaystyle \frac{1}{1-\alpha }}log\left(\mathrm{tr}{\left({\breve{\mathbf{K}}}_{X,Y}\right)}^{\alpha }\right),$$

(10)

where ${\mathbf{K}}_{XY}={\mathbf{K}}_X\odot {\mathbf{K}}_Y$, ${\breve{\mathbf{K}}}_{X,Y}={\mathbf{K}}_{X,Y}/\mathrm{tr}\left({\mathbf{K}}_{X,Y}\right),$ and ⊙ denotes the Hadamard product. Of note, the joint matrix ${\mathbf{K}}_{XY}$ captures the similarity between pairs of samples in the joint feature space.

–

Mutual Information - (MI). It quantifies the statistical dependence between two variables. In the matrix-based framework, it is defined in analogy to its classic information-theoretic definition:

$$I_{\alpha }({\mathbf{K}}_X;{\mathbf{K}}_Y)=H_{\alpha }\left({\mathbf{K}}_X\right)+H_{\alpha }\left({\mathbf{K}}_Y\right)-H_{\alpha }({\mathbf{K}}_X,{\mathbf{K}}_Y),$$

(11)

where each entropy term is computed from its respective (normalized) Gram matrix. Maximizing MI is a common objective in representation learning, as it encourages a representation to retain information about a relevant variable.

–

Conditional Entropy - (CE). It measures the remaining uncertainty in a variable X given that Y is known. It is defined as:

$$H_{\alpha }\left({\mathbf{K}}_X\right|{\mathbf{K}}_Y)=H_{\alpha }({\mathbf{K}}_X,{\mathbf{K}}_Y)-H_{\alpha }\left({\mathbf{K}}_Y\right)$$

(12)

Minimizing conditional entropy is equivalent to making X more predictable from Y.

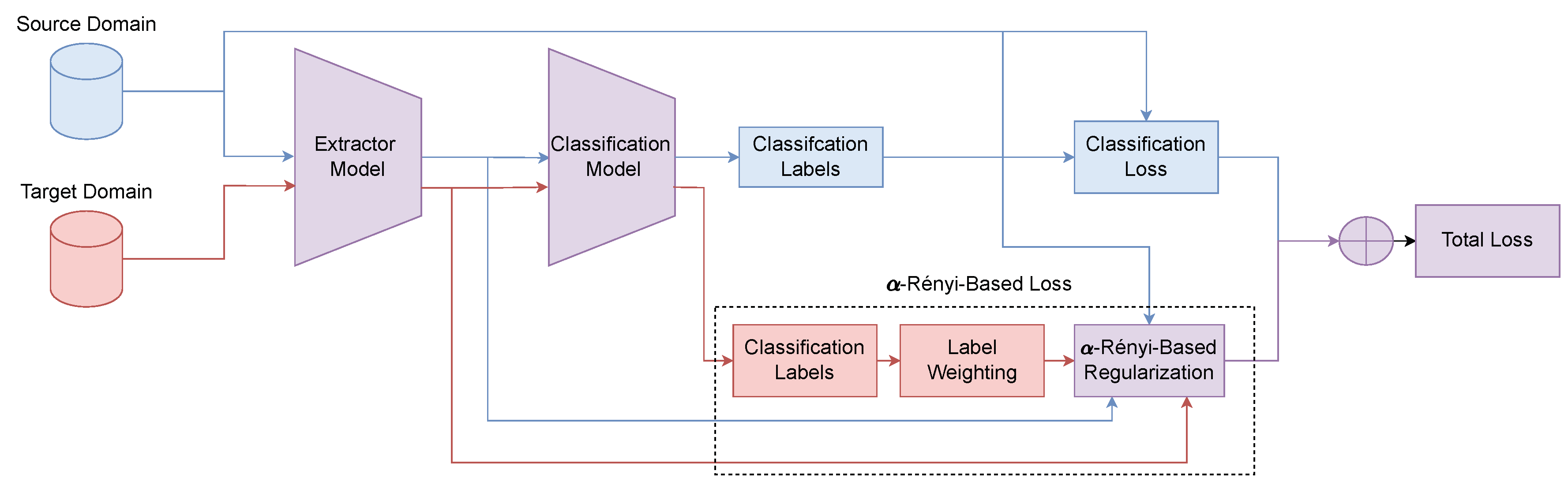
2.3. Domain Adaptation with $\alpha$-Rényi Entropy-based Label Weighting and Regularization

Our proposed method, Conditional $\alpha$-Rényi’s Entropy Regularization (CREDA), is designed for end-to-end training in unsupervised domain adaptation. The framework leverages a deep feature extractor $\mathcal{F}:\mathcal{X}\to {\mathbb{R}}^d$ that maps an input image $\mathbf{x}\in {\mathbb{R}}^{\breve{H}\times \breve{W}\times \breve{C}}$, with $\mathcal{X}\subseteq {\mathbb{R}}^{p^{\prime }},$$p^{\prime }=\breve{H}\times \breve{W}\times \breve{C},$ to a d-dimensional feature vector $\mathbf{f}\in {\mathbb{R}}^d$, as:

$$\mathbf{f}=\mathcal{F}\left(\mathbf{x}\right)=({\breve{f}}_L\circ {\breve{f}}_{L-1}\circ \dots \circ {\breve{f}}_1)\left(\mathbf{x}\right),$$

(13)

where ${\breve{f}}_l(·)$ stands for the l-th feature extractor layer ($l\in L$) and ∘ is the function composition operator. Besides, a classifier $\mathcal{G}:{\mathbb{R}}^d\to {[0,1]}^C$ that predicts class-probability vector $\mathbf{g}\in {[0,1]}^C,$ is defined as follows:

$$\mathbf{g}=\mathcal{G}\left(\mathbf{f}\right)=({\breve{g}}_{\breve{L}}\circ {\breve{g}}_{\breve{L}-1}\circ \dots \circ {\breve{g}}_1)\left(\mathbf{f}\right),$$

(14)

with ${\breve{g}}_{l^{\prime }}(·)$ as a given classifier layer ($l^{\prime }\in \breve{L}$), ${\sum }_{c=1}^C{g}_c=1$ and $g_c\in \mathbf{g}.$

In practice, we are given a labeled source domain ${\mathcal{D}}^s={\{{\mathbf{x}}_i^s\in {\mathbb{R}}^{p^{\prime }},{\mathbf{y}}_i^s\in {\{0,1\}}^C\}}_{i=1}^{N_s},$ with ${\sum }_{c=1}^C{y}_{i,c}^s=1$, $y_{i,c}^s\ne y_{i,c^{\prime }}^s$, $c,c^{\prime }\in C$, and $y_{i,c}^s,y_{i,c^{\prime }}^s\in {\mathbf{y}}_i^s$. Also, an unlabeled target domain is provided as ${\mathcal{D}}^t={\{{\mathbf{x}}_j^t\in {\mathbb{R}}^{p^{\prime }}\}}_{j=1}^{N_t}$. For each class c, we compute the source, target, and source-target kernel-based matrices ${\mathbf{K}}_c^s\in {\mathbb{R}}^{n_c^s\times n_c^s}$, ${\mathbf{K}}_c^t\in {\mathbb{R}}^{n_c^t\times n_c^t},$ and ${\mathbf{K}}_c^{st}\in {\mathbb{R}}^{n_c^t\times n_c^s},$ as follows:

$$\begin{array}{cc}\hfill {\mathbf{K}}_c^s=\left[{\kappa }_{{\sigma }_s}({\mathbf{f}}_i^s,{\mathbf{f}}_{i^{\prime }}^s)\right],& \forall i,i^{\prime }\in n_c^s:{\mathbf{f}}_i^s=\mathcal{F}\left({\mathbf{x}}_i^s\right),y_{i,c}^s=1\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\mathbf{K}}_c^t=\left[{\kappa }_{{\sigma }_t}({\mathbf{f}}_j^t,{\mathbf{f}}_{j^{\prime }}^t)\right],& \forall j,j^{\prime }\in n_c^t:{\mathbf{f}}_j^t=\mathcal{F}\left({\mathbf{x}}_j^t\right),arg\underset{c^{\prime }}{max}{g}_{j,c^{\prime }}^t=c\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\mathbf{K}}_c^{st}=\left[{\kappa }_{{\sigma }_{st}}({\mathbf{f}}_i^s,{\mathbf{f}}_j^t)\right],& \forall i\in n_c^s,j\in n_c^t:y_{i,c}^s=1,arg\underset{c^{\prime }}{max}{g}_{j,c^{\prime }}^t=c,\hfill \end{array}$$

(17)

where $g_{j,c}^t\in {\mathbf{g}}_j^t$ and ${\mathbf{g}}_j^t=\mathcal{G}\left({\mathbf{f}}_j^t\right)$ . Moreover, $n_c^s$ is the number of samples in ${\mathcal{D}}^s$ where $y_{i,c}^s=1$. Likewise, $n_c^t$ holds the number of target inputs satisfying $arg{max}_{c^{\prime }}{g}_{j,c^{\prime }}^t=c$.

To enhance robustness against noisy pseudo-labels in the target set, we propose incorporating a confidence weighting vector ${\mathbf{w}}^t\in {\mathbb{R}}^{N_t}$, derived from a quadratic Rényi entropy estimator (see equation 3) that quantifies the uncertainty in the pseudo-label probability prediction, as follows [59]:

$$w_j^t=1-{\displaystyle \frac{{\widehat{H}}_2\left({\mathbf{g}}_j^t\right)}{log\left(C\right)}},$$

(18)

where $w_j^t\in {\mathbf{w}}^t$ and:

$${\widehat{H}}_2\left({\mathbf{g}}_j^t\right)=-log\left(\sum _{c=1}^C{\left(g_{j,c}^t\right)}^2\right).$$

(19)

Afterward, a target weighting matrix ${\tilde{\mathbf{W}}}_t^c\in {\mathbb{R}}^{n_c^t\times n_c^t}$ can be computed, yielding:

$${\tilde{\mathbf{W}}}_c^t={\tilde{\mathbf{w}}}_c^t{\left({\tilde{\mathbf{w}}}_c^t\right)}^{\top },$$

(20)

where ${\tilde{\mathbf{w}}}_c^t=\{w_j^t:arg{max}_{c^{\prime }}{g}_{j,c^{\prime }}^t=c\}\in {\mathbb{R}}^{n_c^t}$.

The core of our CREDA method lies in a novel regularization term that enforces alignment between the class-conditional distributions of the source and target domains. To achieve this, we employ a kernel-based quadratic Rényi entropy mutual information estimator (see Section 2.2):

$${\tilde{\mathrm{I}}}_2({\mathbf{K}}_c^s;{\tilde{\mathbf{K}}}_c^t)={\displaystyle \frac{1}{2}}\left(H_2\left({\mathbf{K}}_c^s\right)+H_2\left({\tilde{\mathbf{K}}}_c^t\right)\right)-H_2\left({\mathbf{K}}_c^{\mathrm{mix}}\right),$$

(21)

being ${\tilde{\mathbf{K}}}_c^t={\mathbf{K}}_c^t\odot {\tilde{\mathbf{W}}}_c^t$ and:

$${\mathbf{K}}_c^{\mathrm{mix}}=\left(\begin{array}{cc}{\mathbf{K}}_c^s& {\mathbf{K}}_c^{st}\\ {\left({\mathbf{K}}_c^{st}\right)}^{\top }& {\tilde{\mathbf{K}}}_c^t\end{array}\right),$$

(22)

which enables the computation of our MI estimator in equation 21 even when the source and target sample sizes differ, namely, $n_c^t\ne n_c^s$.

Finally, the complete CREDA loss integrates the standard supervised cross-entropy on labeled source data with our proposed mutual information regularizer, based on the quadratic Rényi entropy formulation, as follows:

$${\mathcal{L}}_{\mathrm{CREDA}}=\sum _{i=1}^{N_s}\sum _{c=1}^C{y}_{i,c}^{s}log\left(\mathcal{G}\left(\mathcal{F}\left({\mathbf{x}}_i^s\right)\right)\right)-\lambda \sum _{c\in C}{\tilde{\mathrm{I}}}_2({\mathbf{K}}_c^s;{\tilde{\mathbf{K}}}_c^t),$$

(23)

where $\lambda \in {\mathbb{R}}^{+}$ is a hyperparameter controlling the strength of the domain alignment.

Figure 1 summarizes the core components and training pipeline of our proposed CRERDA model for conditional domain adaptation.

3. Experimental Set-Up

To rigorously evaluate the effectiveness of the proposed CREDA framework for domain adaptation in image classification tasks, we present a comprehensive analysis that includes descriptions of the benchmark datasets, training protocols, comparative baselines, and quantitative and qualitative performance assessments.

3.1. Tested Datasets

To assess the effectiveness and robustness of the proposed domain adaptation method, we conducted extensive experiments on three widely recognized benchmark datasets commonly used in domain adaptation research. Each dataset encompasses visual domains exhibiting substantial distribution shifts, thereby providing a challenging setting for learning domain-invariant representations, as detailed below:

–

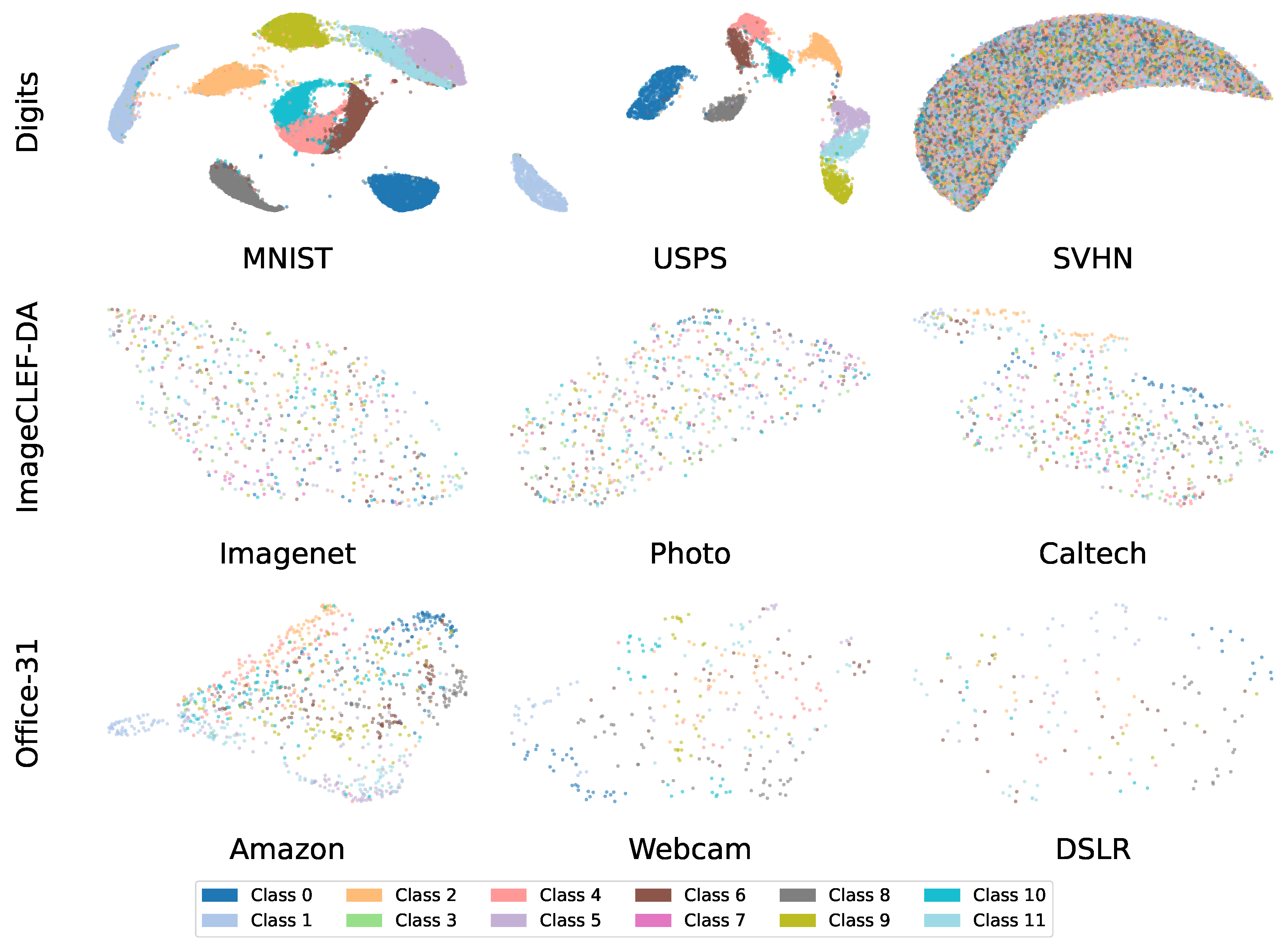
Digits: This benchmark suite is designed for evaluating domain adaptation on digit recognition tasks, spanning both handwritten and natural-scene digits. It comprises three standard datasets: MNIST (M), a large database of handwritten digits; USPS (U), another handwritten digit set characterized by its lower resolution; and SVHN (S), which contains house numbers cropped from real-world street-level images [60]. Notably, the S domain is particularly challenging due to its significant variability in lighting, background clutter, and visual styles compared to M and U (see Figure 2).

–

ImageCLEF-DA: This is a standard benchmark for unsupervised domain adaptation, organized as part of the ImageCLEF evaluation campaign. It comprises 12 common object classes shared across three distinct visual domains: Caltech-256 (C), ImageNet ILSVRC 2012 (I), and Pascal VOC 2012 (P), see Figure 3. Each domain contains 600 images, with a balanced distribution of 50 images per class [61]. All images are resized to $224\times 224$ pixels.

–

Office-31: This is one of the most widely used benchmarks for visual domain adaptation. It consists of 4110 images across 31 object classes, sourced from three domains with distinct visual characteristics: Amazon (A), which features centered objects on a clean, white background under controlled lighting; Webcam (W), containing low-resolution images with typical noise and color artifacts; and DSLR (D), which includes high-resolution images with varying focus and lighting conditions [62]. For this study, we selected a subset of ten shared classes, see Figure 4.

Together, these benchmarks allows evaluating the capacity of domain adaptation methods to generalize across diverse and challenging visual domains.

3.2. Deep Learning Architectures

The architectural components outlined in this section serve as the core modules consistently employed across all experimental configurations. At the heart of the framework lies the feature extractor, which is based on a ResNet-18 convolutional backbone pretrained on ImageNet. To tailor the architecture for domain transfer tasks, the final fully connected layer is removed, while all preceding convolutional and residual blocks are retained. This modification enables the extraction of high-level spatial representations that are robust and transferable across domains [62]. A comprehensive description of the feature extractor’s architecture is provided in Table 1.

The label classifier maps the output of the feature extractor to a vector of class logits corresponding to the C target categories. Its streamlined architecture enables efficient supervised training and facilitates seamless integration into domain adaptation pipelines, as described in Table 2.

To support adversarial training for domain adaptation, the domain discriminator is implemented as a multilayer perceptron. It comprises two fully connected hidden layers with ReLU activations and a final output layer with sigmoid activation. This configuration enables the model to distinguish domain-specific features and promotes the learning of domain-invariant representations. The architecture is summarized in Table 3. The input dimension to this module varies depending on the adversarial method used; for DANN and ADDA, the input is the 512-dimensional feature vector, while for CDAN, it is the 512$\times C$ dimensional joint representation of features and class predictions.

3.3. Assessment and Method Comparison

In all experimental scenarios, we report the classification accuracy and its associated standard deviation in the test set of the target domain. Moreover, during training, model performance is periodically evaluated on validation subsets drawn from both source and target domains to monitor intermediate generalization behavior. In this sense, the Accuracy (ACC) measure is defined as:

$$\mathrm{Acc}(\widehat{\mathbf{y}},\mathbf{y})={\displaystyle \frac{1}{N}}\sum _{i=n}^N\mathbb{I}({\widehat{y}}_n=y_n),$$

(24)

where ${\widehat{y}}_n\in \widehat{\mathbf{y}}$ and $y_n\in \mathbf{y}$ denote the predicted and ground truth labels, respectively. $\mathbb{I}(·)$ is the indicator function that returns 1 if the condition is true and 0 otherwise. The standard deviation is estimated from the batch-wise accuracies, serving as a proxy for model stability during inference. The baseline model is trained solely on labeled samples from the source domain and is directly evaluated in the target domain without any adaptation mechanisms. This setting establishes a lower bound for performance under domain shift conditions.

Moreover, the following domain adaptation strategies are considered for comparison:

–

DANN: The Domain-Adversarial Neural Network incorporates a domain discriminator linked via a Gradient Reversal Layer (GRL), enabling adversarial training of the feature extractor [63]. This configuration encourages the learning of domain-invariant features while preserving class separability.

–

ADDA: The Adversarial Discriminative Domain Adaptation framework separates training into two stages: an initial supervised phase for training the source encoder and classifier, followed by adversarial fine-tuning of the target encoder (initialized with source weights) to align the source and target distributions [64]. The classifier remains fixed during this second phase.

–

CDAN+E: The Conditional Domain Adversarial Network with Entropy Minimization extends adversarial adaptation by feeding the domain discriminator with multilinear features, obtained as the outer product between feature representations and soft classifier predictions [65]. Additionally, an entropy regularization term is applied to the target predictions to encourage confident and well-structured outputs [66].

–

CREDA: Our proposed method integrates a supervised classification loss with a conditional divergence term based on Rényi entropy. The objective is to promote intra-class compactness and inter-domain alignment through class-wise kernel-based weighting schemes, yielding representations that are simultaneously discriminative and domain-invariant.

In addition to quantitative measures, we assess the discriminative quality of the learned feature representations using qualitative techniques. Specifically, we employ the well-known Uniform Manifold Approximation and Projection (UMAP) [41], a non-linear dimensionality reduction technique to project high-dimensional features into a two-dimensional latent space, enabling visual inspection of inter-domain and inter-class separability [67]. This technique facilitates an empirical evaluation of how well the feature extractor captures semantically consistent structures across domains. To further complement this analysis, we apply the GradCAM++ method to the classifier module in order to visualize spatial attention regions associated with individual predictions [68]. These attention maps provide insight into the decision-making process of the model and support a comparative interpretation of class activation patterns across source and target domains.

3.4. Training Details

The training procedure follows the standard protocol for unsupervised domain adaptation: all labeled data from the source domain are used along with the entire set of unlabeled data from the target domain. The latter approach aims to learn domain-invariant representations without requiring explicit supervision in the target domain.

All models are trained using the Adam optimizer, with an initial learning rate set to ${\eta }_0={10}^{-3}$. To promote stable convergence and mitigate early overfitting of the discriminator, a dynamic scheduling scheme is employed for both the learning rate and the adversarial weighting parameter throughout the training process. Both parameters are updated according to the relative training progress $\breve{p}={\displaystyle \frac{\mathrm{epoch}}{\mathrm{total}\text{\_}\mathrm{epochs}}}$, following the expressions:

$$\eta \left(\breve{p}\right)={\eta }_0{(1+\alpha \breve{p})}^{-\beta },\lambda \left(\breve{p}\right)={\displaystyle \frac{1-e^{-\delta \breve{p}}}{1+e^{-\delta \breve{p}}}};$$

(25)

where typical hyperparameter values are $\alpha =10$, $\beta =0.75$, and $\delta =10$ [69].

Next, to maintain class balance during model training and evaluation, an initial partition is performed into training (70%), validation (15%), and test (15%) subsets. This process is conducted independently for both the source and target domains. To ensure representative subsets, stratified sampling is applied within each partition, preserving the internal class distributions of each domain. In particular, the independent construction of the validation sets enables consistent and comparable evaluation conditions across domains, which is essential in domain adaptation scenarios where distributional shifts may introduce evaluation bias.

In addition to stratified sampling, the batch size is dynamically adjusted based on the size of the training set (N) in each domain, according to the following empirical rule:

$$min\left(max\left(16,\lfloor 0.1·N\rfloor \right),64\right).$$

The lower and upper bounds were established empirically. The lower bound ensures the existence of at least 10 mini-batches per epoch, contributing to optimization stability and preventing prohibitively long training times on small datasets. Conversely, the upper bound avoids excessively large batches that could destabilize learning or exceed GPU memory capacity. This configuration strikes an effective trade-off between gradient stability and computational efficiency, especially when handling domains of different sizes.

It is important to note that, since both dataset partitioning and batch size are determined by the number of available samples in each domain, the number of training instances per epoch is not the same across domains. This asymmetry reflects the inherent scale differences between datasets and allows each domain to contribute proportionally to the learning process without enforcing artificial uniformity.

Regarding the optimization objectives, all models rely on cross-entropy loss for supervised classification on labeled source data. For domain alignment, adversarial approaches such as DANN, ADDA, and CDAN+E use binary cross-entropy loss on a domain discriminator. In CDAN+E, this is enhanced through entropy-aware weighting, where per-sample contributions are modulated by prediction uncertainty—removing the need for an explicit entropy regularization term. All alignment-based methods adopt the same dynamic scheduling function $\lambda \left(p\right)$, which progressively increases the weight of the alignment objective throughout training. In the proposed CREDA framework, the adversarial loss is replaced with a divergence-based regularizer that also leverages Rényi entropy for confidence-aware weighting, enabling robust and class-consistent alignment. For all experiments, the kernel bandwidth parameter $\sigma$ used in the estimation of Rényi’s quadratic entropy was fixed to 1. This choice simplifies the training pipeline while maintaining stable alignment behavior across domains.

Besides, to qualitatively assess the discriminative capacity of the learned features, we apply dimensionality reduction using UMAP, leveraging the GPU-accelerated cuML implementation. Unless otherwise stated, the default parameters are set as follows: n_components = 2, n_neighbors = 80, and random_state = 42. Prior to projection, features are normalized with MinMaxScaler, which facilitates visual inspection of inter-class and inter-domain separability in the latent space. Also, we employ the GradCAM++ technique via the torchcam library to visualize class-specific attention regions within the input images. Representative samples for each class are selected from both source and target domains, and the last convolutional layer of the feature extractor is designated as the target layer. The resulting attention masks are normalized and overlaid on the corresponding images, offering a qualitative perspective on the spatial focus of the model during classification.

All experiments are conducted on collaborative computing platforms (Google Colab and Kaggle). The development environment is based on Python 3.11.11, using PyTorch 2.1.2 for model training, cuML 25.02.01 for GPU-accelerated UMAP visualization, and torchcam 0.4.0 for GradCAM++. All source code and datasets are publicly available at: https://github.com/Daprosero/Domain_Adaptation (accessed on 4 July 2025).

4. Results and Discussion

A fundamental objective in domain adaptation is to learn representations that remain invariant under distributional shifts between domains, commonly referred to as covariate shift. A model’s ability to mitigate this challenge is directly reflected in its accuracy on the target domain. To evaluate CREDA’s performance quantitatively, we conducted experiments on the three widely adopted benchmark datasets. In the digit adaptation tasks (see Table 4), CREDA achieves the highest average accuracy (67.69%) and performs exceptionally well in challenging tasks such as M→U (98.17%), characterized by significant visual disparities between domains. This evidences its capacity to align distributions with heterogeneous visual features. While ADDA shows competitive performance in specific cases such as M→S and U→M, its overall performance is less stable compared to our proposed method.

Similarly, on the ImageCLEF-DA dataset (see Table 5), CREDA attains the highest average accuracy (67.56%) and outperforms CDAN+E in particularly demanding tasks such as P→C (80.00%) and C→P (54.44%). These results suggest that the Rényi entropy-based regularization employed in our method more effectively balances domain alignment and the preservation of class discriminability.

Lastly, on the Office-31 benchmark (see Table 6), CREDA confirms its superiority with an average accuracy of 81.07% and perfect performance (100.00%) on the D→W and W→D tasks. In contrast, approaches like ADDA show limited robustness, yielding substantially lower performance in tasks such as D→A (20.14%). Our method, in turn, maintains high consistency across all evaluated settings.

To clarify the reasons for these performance disparities, it is crucial to first examine the inherent complexity of the data domains. Figure 5 presents the 2D UMAP projections of the original feature space, visualized independently for each domain. These plots reveal a fundamental challenge that extends beyond domain shift: the limited class separability within individual domains. This limitation is particularly pronounced in complex datasets such as ImageCLEF-DA and Office-31, where class instances (depicted by distinct colors) exhibit significant entanglement, forming dense and unstructured distributions. Such inherent visual similarity among categories not only complicates classification within the source domain but also serves as a principal source of noisy pseudo-labels in the target domain during unsupervised adaptation. Consequently, a robust domain adaptation strategy must not only align cross-domain distributions but also construct feature representations that enhance inter-class discrimination.

Building upon this analysis, Figure 6 illustrates how different adaptation techniques address these structural challenges, visualized through UMAP projections of the learned latent spaces. The first column depicts the initial state prior to training, highlighting both the domain gap (e.g., M→U) and the poor semantic organization (e.g., P→C). The baseline model, trained exclusively on source data, fails to bridge this gap, maintaining a clear division between domains. In contrast, adversarial methods like DANN and ADDA achieve partial domain alignment, but often at the expense of class coherence, resulting in fragmented and disordered representations. While CDAN+E introduces a degree of structural consistency, significant inter-class dispersion remains. Ultimately, CREDA yields a markedly superior configuration: it not only facilitates seamless domain integration—evidenced by the homogeneous blending of source and target samples—but also preserves, and in some cases enhances, class-wise separability, as demonstrated by the emergence of compact, well-defined clusters. This outcome provides a visual explanation for CREDA’s superior quantitative performance, indicating its ability to balance the removal of spurious domain-specific cues with the preservatio n of underlying semantic structure.

Having established CREDA’s capacity to address covariate shift, we next assess whether the learned representations preserve semantic coherence under concept shift, where object appearance changes substantially across domains. In this context, Figure 7 presents UMAP projections with embedded images to qualitatively examine the model’s ability to cluster semantically related concepts.

The results indicate that CREDA learns a semantically rich feature space that transcends superficial variability. For instance, in the M→U task, the model accurately groups digits despite substantial stylistic differences, as seen in the clusters corresponding to digits 6, 0, and 4. In the P→C task, it effectively clusters objects such as bicycles based on defining visual features, despite background and perspective changes. Similarly, in the W→D task, office-related objects are grouped according to their semantic identity, overcoming differences in image quality. Altogether, these visualizations demonstrate that CREDA not only aligns domains but also constructs a feature space in which proximity reflects conceptual similarity—an essential attribute for robust generalization in real-world applications.

Finally, to reinforce the model’s reliability, it is essential not only to demonstrate high accuracy and semantic coherence, but also to ensure that its predictions are grounded in interpretable reasoning. In other words, it must be verified that decisions are driven by relevant visual cues rather than spurious correlations.

To address this, we employ Grad-CAM++, with the results shown in Figure 8. The heatmaps reveal strong semantic consistency: regardless of the domain, the model focuses attention on canonical and representative regions of the object, such as the face in a portrait or the main structural components of a vehicle. This confirms that CREDA does not rely on superficial distribution alignment, but rather performs deep and meaningful semantic knowledge transfer. These findings not only enhance trust in the model’s predictions but also establish CREDA as a transparent and robust solution for domain adaptation, strengthening the interpretability and reliability of its outputs.

4.1. Limitations

Despite the solid performance of the CREDA framework on unsupervised domain adaptation tasks, several limitations must be acknowledged, which in turn open relevant opportunities for future research. Firstly, its validation has been confined to moderate-scale architectures like ResNet-18; consequently, its scalability and representational capacity on deeper networks, such as ResNet-50 or Transformer-based models, are yet to be explored [70]. Secondly, a single hyperparameter tuning strategy was employed for all tasks, lacking specific optimization per domain pair. Incorporating automated search schemes for adaptation could potentially improve performance and generalization, though this would increase computational cost [71]. Thirdly, the combination of the classification loss and the Rényi divergence-based regularization relies on a static weighting coefficient. Exploring an adaptive normalization method for the loss functions could lead to more stable training by balancing gradient scales. Moreover, given that the regularizer depends on kernel-based estimations, the model’s performance is sensitive to the kernel bandwidth, a parameter that was not dynamically optimized in this work. Finally, while CREDA was conceived for the standard unsupervised adaptation setting, its extension to more demanding scenarios, such as few-shot or source-free adaptation, has not yet been investigated [72]. Overcoming these shortcomings would enhance the robustness of the proposed framework and expand its applicability to more complex transfer learning problems.

5. Conclusions

This work introduced a novel domain adaptation framework, termed Conditional Rényi $\alpha$-Entropy Domain Adaptation (CREDA), a novel deep learning-based strategy integrating kernel-based conditional alignment from a matrix-based formulation of Rényi’s quadratic entropy. CREDA is structured around three key components. First, a deep feature extractor is used to learn domain-invariant representations by leveraging labeled source data and unlabeled target data. Second, an entropy-weighted strategy attenuates the influence of low-confidence pseudo-labels, thereby enhancing robustness in ambiguous regions. Third, a class-conditional alignment loss, expressed as a Rényi divergence, is introduced to promote semantic consistency across domains within the latent representation space. In contrast to supervised or semi-supervised approaches, the proposed method does not require labels in the target domain, making it particularly suitable for scenarios where annotation is costly or unavailable. Besides, our class-wise alignment is formulated in a non-parametric and differentiable manner by leveraging kernel-based information potentials, enabling the preservation of semantic structure across domains.

Experimental results across diverse visual adaptation scenarios demonstrate that CREDA consistently outperforms conventional methods such as DANN, ADDA, and CDAN+E in terms of predictive accuracy, representational quality, and interpretability. Notably, CREDA maintains class separability even under complex distribution shifts and when the predicted labels in the target domain exhibit low confidence. The integration of UMAP- and GradCAM++-based visualizations offers valuable insights into the learned representations, reinforcing its applicability in real-world settings where traceability and semantic coherence are critical. From an implementation standpoint, CREDA does not require modifications to the classification loss function. Its confidence-aware weighting scheme and class-conditional regularization enhance robustness to pseudo-label noise and class imbalance. Moreover, its modular architecture facilitates seamless integration into existing deep learning pipelines.

As future work, we will pursue two major extensions. First, we aim to extend CREDA to multi-source and continual domain adaptation settings, where domain shifts occur either simultaneously or sequentially. Attention-based class-conditioned alignment across multiple source domains has been shown to mitigate negative transfer and effectively address class imbalance [73]. Second, we plan to incorporate class-conditional kernel alignment and attention-guided feature disentanglement to improve both interpretability and discriminative alignment, particularly in contexts characterized by subtle inter-class distinctions or limited labeled data. Recent advances in attention-aware class-conditioned alignment suggest that these mechanisms yield robust feature representations and highlight relevant discriminative regions in multi-source adaptation [74]. Together, these extensions aim to broaden the applicability of CREDA to dynamic and heterogeneous environments, while preserving its core strengths of semantic coherence, interpretability, and transparency.