1. Introduction
The integration of renewable energy sources (RES) into modern power systems has fundamentally transformed grid operation, introducing significant complexities, particularly in microgrids and weakly interconnected networks [
1,
2]. Unlike conventional grids supported by synchronous generators, microgrids predominantly rely on inverter-interfaced generation units, necessitating advanced and reliable control methods to maintain voltage and frequency stability under varying operational conditions [
3,
4].
Traditionally, inverter control strategies such as droop control, virtual synchronous machines (VSM), and model predictive control (MPC) have been widely employed [
5,
6]. Droop control, despite its simplicity and decentralized nature, exhibits limited adaptability and suboptimal performance under highly dynamic or uncertain conditions [
7]. VSM approaches offer improved transient stability by emulating synchronous generator dynamics but often require precise parameter tuning and comprehensive system modeling, limiting scalability and adaptability [
8]. MPC-based techniques demonstrate robust control capabilities, yet they typically incur high computational burdens, complicating their deployment in real-time applications [
9].
Recently, advancements in machine learning (ML) and artificial intelligence (AI) have provided alternative pathways for adaptive, data-driven inverter control, potentially addressing limitations inherent in conventional control methods [
10,
11]. Nevertheless, purely data-driven approaches often face challenges related to interpretability, robustness, and generalization, especially under scenarios not adequately represented in training datasets [
12,
13].
In response to these challenges, Physics-Informed Neural Networks (PINNs) have emerged as a promising interdisciplinary paradigm, combining rigorous physical laws with neural network flexibility. By explicitly embedding governing equations and constraints into the training process, PINNs improve interpretability, generalization, and robustness of AI-driven solutions [
14,
15]. PINNs have demonstrated successful applications in various engineering domains such as fluid dynamics, heat transfer, and power system stability assessment, validating their potential for addressing complex real-world problems [
16,
17].
Despite these advancements, limited research has explored the direct integration of PINNs into the real-time control of grid-forming inverters. Specifically, embedding essential electrical laws such as Kirchhoff’s laws, swing equations, and stability constraints directly into deep learning architectures presents significant novelty, potentially enabling ultra-fast and robust inverter control, crucial for microgrids and weak grid scenarios.
This paper introduces a novel control framework leveraging PINNs to enhance grid-forming inverter operation in real-time. By embedding fundamental electrical physics directly into neural network training, the proposed approach aims to provide a superior combination of accuracy, adaptability, and computational efficiency. Extensive simulations and experimental validations illustrate the practical effectiveness and robustness of the proposed framework compared to traditional inverter control methodologies. The societal impact of this work extends to facilitating reliable renewable energy integration, supporting energy resilience, and enabling the widespread adoption of decentralized energy solutions in remote and weak-grid regions.
The rest of the paper is organized as follows:
Section 2 presents a comprehensive literature review highlighting the state-of-the-art in inverter control methods and physics-informed neural network applications.
Section 3 formulates the system model and problem statement.
Section 4 details the proposed PINN-based control framework, while
Section 5 describes the simulation and experimental validation setup. Results and discussions are provided in
Section 6, followed by societal impact considerations in
Section 7. Finally, challenges, future directions, and conclusions are presented in Sections 8 and 9, respectively.
2. Literature Review
2.1. Grid-Forming Inverter Control Methods
Grid-forming inverter control strategies play an essential role in maintaining voltage and frequency stability in microgrids, particularly in scenarios where the grid connection is weak or entirely absent [
18,
19]. The most commonly employed method is droop control, characterized by simplicity, decentralized architecture, and inherent plug-and-play functionality. Droop methods regulate voltage and frequency using predefined relationships between active/reactive power outputs and frequency/voltage deviations [
20]. However, conventional droop methods may exhibit limited performance under high penetration of renewable generation and load variability due to their inherently static parameter settings [
21].
Virtual synchronous machine (VSM) control strategies have emerged as an alternative, aiming to replicate the dynamic behavior of synchronous generators through inverter interfaces [
22,
23]. VSM methods improve dynamic response and transient stability in microgrids but often require accurate system modeling and precise parameter tuning, which increases complexity and limits adaptability in dynamic operational scenarios [
24]. Model predictive control (MPC) offers another sophisticated approach, achieving robust performance and explicit consideration of constraints. Nevertheless, MPC’s heavy computational burden, stemming from its iterative optimization process, complicates real-time implementations in resource-constrained environments [
25].
2.2. Deep Learning Applications in Power Electronics and Control
The integration of deep learning (DL) into power electronics has gained substantial traction in recent years, primarily driven by its capability to handle system uncertainties, non-linearities, and varying operational conditions without explicit modeling of the underlying dynamics [
26]. Deep reinforcement learning (DRL), for example, has demonstrated effective inverter control performance by learning optimal control policies from interaction with the system environment, offering adaptability and robustness to disturbances and uncertainties [
27]. Similarly, supervised neural network approaches have been utilized to improve fault detection, stability assessment, and power flow optimization in modern grid scenarios, enhancing real-time decision-making capability [
28,
29].
Despite these advances, DL methods suffer from critical drawbacks related to interpretability and generalizability. Purely data-driven approaches often require extensive training data to ensure robust performance across varying operational conditions and typically lack physically interpretable mechanisms, thereby limiting their applicability in mission-critical control tasks where safety, reliability, and transparency are paramount [
30,
31].
2.3. Physics-Informed Neural Networks (PINNs)
Physics-Informed Neural Networks (PINNs) address many of these challenges by explicitly integrating physical principles into the neural network training process [
32]. PINNs embed known physical constraints, typically described by partial differential equations (PDEs) or ordinary differential equations (ODEs), directly into the loss function. This structured approach significantly improves model interpretability, robustness, and reduces reliance on extensive datasets [
33].
In recent studies, PINNs have demonstrated success in diverse engineering fields, including fluid dynamics [
34], structural analysis [
35], and thermal modeling [
36]. Specifically, in power systems, PINNs have been used effectively for stability analysis, load forecasting, and solving optimal power flow problems, showcasing significant advantages in terms of computational efficiency and model fidelity compared to traditional or purely data-driven approaches [
37,
38,
39]. Nonetheless, the application of PINNs to real-time inverter control, especially embedding electrical circuit laws and stability constraints, remains largely unexplored.
2.4. Research Gap and Contribution of This Work
To the best of the authors’ knowledge, existing literature has not thoroughly investigated the potential of directly embedding electrical laws such as Kirchhoff’s current and voltage laws, swing equations, and stability margin constraints into PINNs for inverter control. Most existing studies either focus purely on classical or data-driven methods without a structured integration of governing physics or explore PINNs solely within offline analysis contexts. Therefore, there is a clear research opportunity to combine the rigorous physics-based constraints with deep learning capabilities explicitly tailored for real-time inverter control applications.
This paper bridges this research gap by proposing and rigorously validating a novel PINN-based control architecture that explicitly integrates essential electrical laws and stability considerations into the real-time control of grid-forming inverters. The outcomes promise significant advancements in inverter performance, enhanced interpretability, improved robustness, and real-time feasibility, making this approach particularly beneficial for microgrids and decentralized renewable energy integration.
Table 1 summarizes key literature relevant to inverter control and PINNs, clearly illustrating the novelty and contribution of the present study.
3. System Model and Problem Formulation
3.1. System Configuration and Modeling
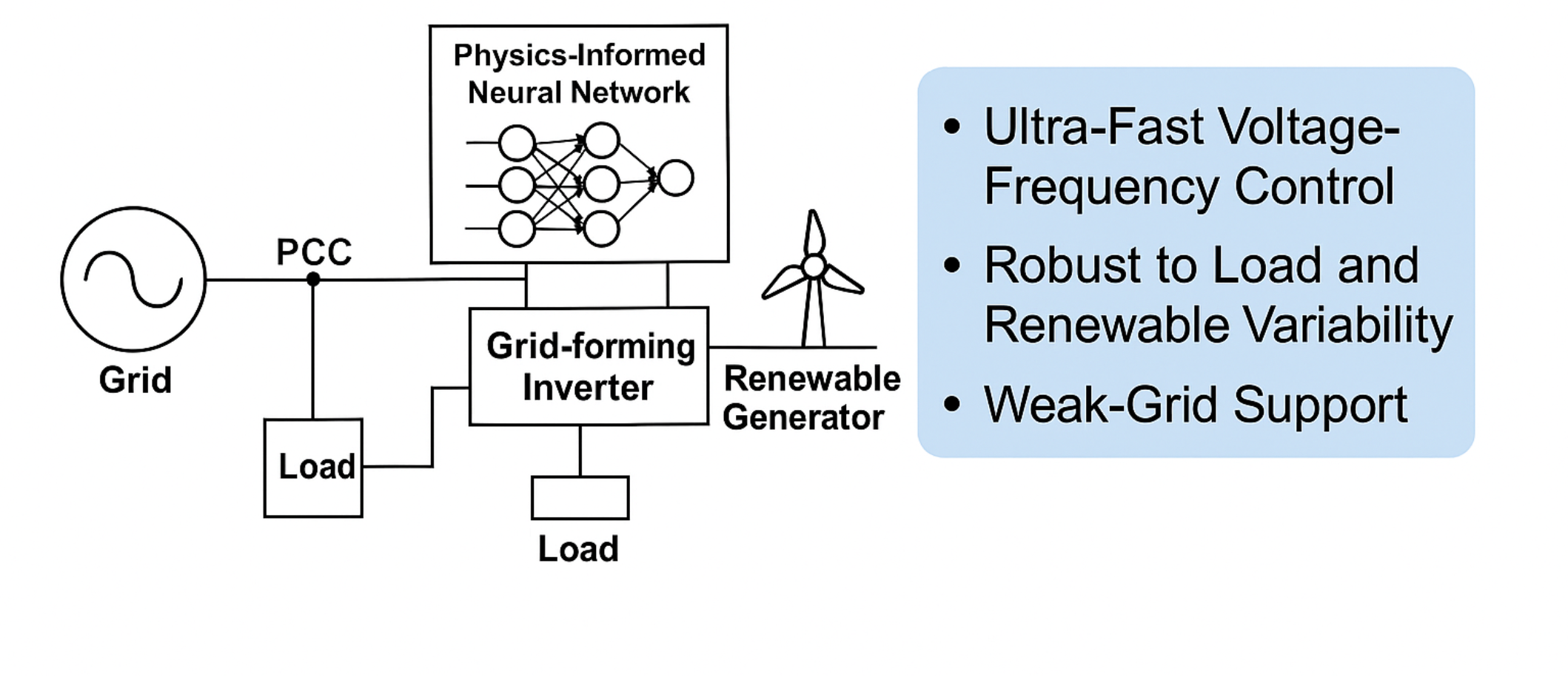
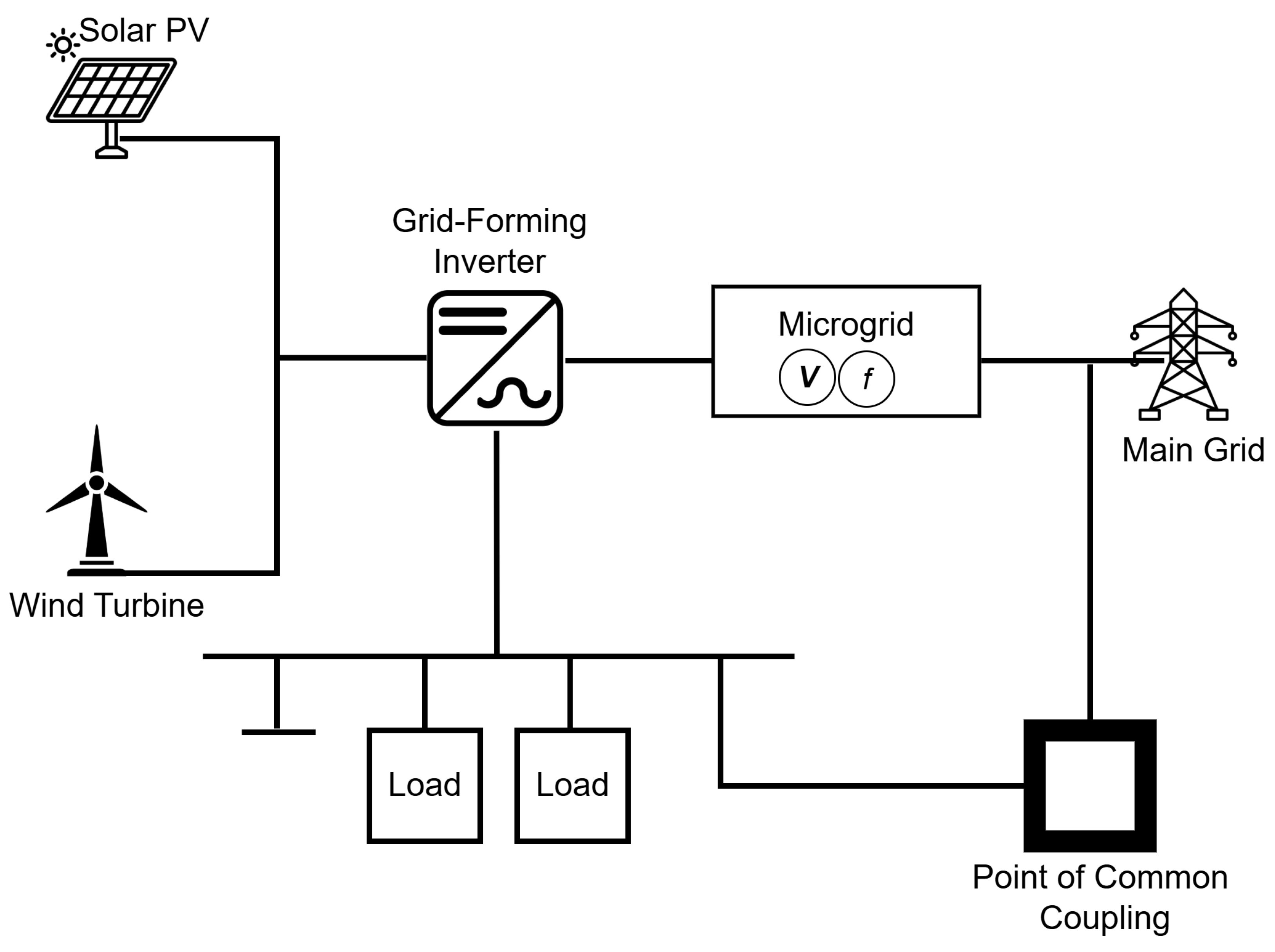
The system considered in this study is a microgrid dominated by renewable energy sources interfaced with grid-forming inverters, as illustrated in
Figure 1. Each inverter controls the voltage magnitude and frequency to sustain stable and reliable microgrid operation, particularly in weak-grid or islanded scenarios.
3.1.1. Grid-Forming Inverter Dynamics
The inverter dynamics can be represented using swing equations that describe frequency and phase angle behavior. For the
i-th inverter node, the swing equations are given by:
where
is the phase angle,
is the angular frequency,
is the nominal angular frequency,
is the inertia constant associated with virtual inertia control, and
is the damping coefficient. The terms
and
represent the reference active power set-point and measured active power output, respectively.
3.1.2. Electrical Network Model
The microgrid electrical network obeys Kirchhoff’s voltage and current laws. The voltage dynamics at node
i can be expressed using complex power injections:
where: -
is the complex power injected into node
i, -
and
are the complex voltages at nodes
i and
k, respectively, -
is the element of the admittance matrix
Y connecting nodes
i and
k, and * denotes the complex conjugate.
For each inverter, voltage magnitude (
) and frequency (
) are the primary controlled variables, following droop-like relationships defined as:
where
and
are droop coefficients for frequency-active power and voltage-reactive power relationships, respectively. The set points
and
represent reference voltage magnitude and reactive power injection at inverter
i.
3.1.3. Stability Margin Constraints
Ensuring microgrid stability requires operating within defined stability margins. The constraints are expressed through Lyapunov stability criteria, which ensure frequency and voltage remain bounded within acceptable ranges:
where
and
are predefined maximum permissible deviations in frequency and voltage, respectively.
3.2. Problem Formulation
The goal is to achieve optimal real-time control of the grid-forming inverters by dynamically adjusting voltage and frequency set-points in response to varying loads and renewable generation conditions. This optimization aims to minimize deviations in frequency and voltage while adhering strictly to system constraints defined by physical laws and stability margins.
Mathematically, the optimization problem can be formulated as a constrained minimization of the following loss function:
subject to the system dynamics given by Equations (
1)–(5), Kirchhoff’s network equations, and constraints:
In Equation (
8), the parameters
and
represent weighting coefficients that reflect the importance of frequency and voltage deviations, respectively, and
denotes the set of neural network parameters used to embed and optimize the control laws.
The proposed Physics-Informed Neural Network (PINN) approach integrates these mathematical formulations directly into the network’s training and optimization process, resulting in enhanced control accuracy, robustness, and interpretability.
4. Proposed PINN Framework for Grid-Forming Control
This section introduces the detailed architecture of the proposed Physics-Informed Neural Network (PINN) framework designed explicitly for real-time control of grid-forming inverters. The fundamental innovation lies in embedding physical laws directly into the neural network training process, ensuring robust, interpretable, and computationally efficient control decisions.
4.1. Overview of PINN Architecture
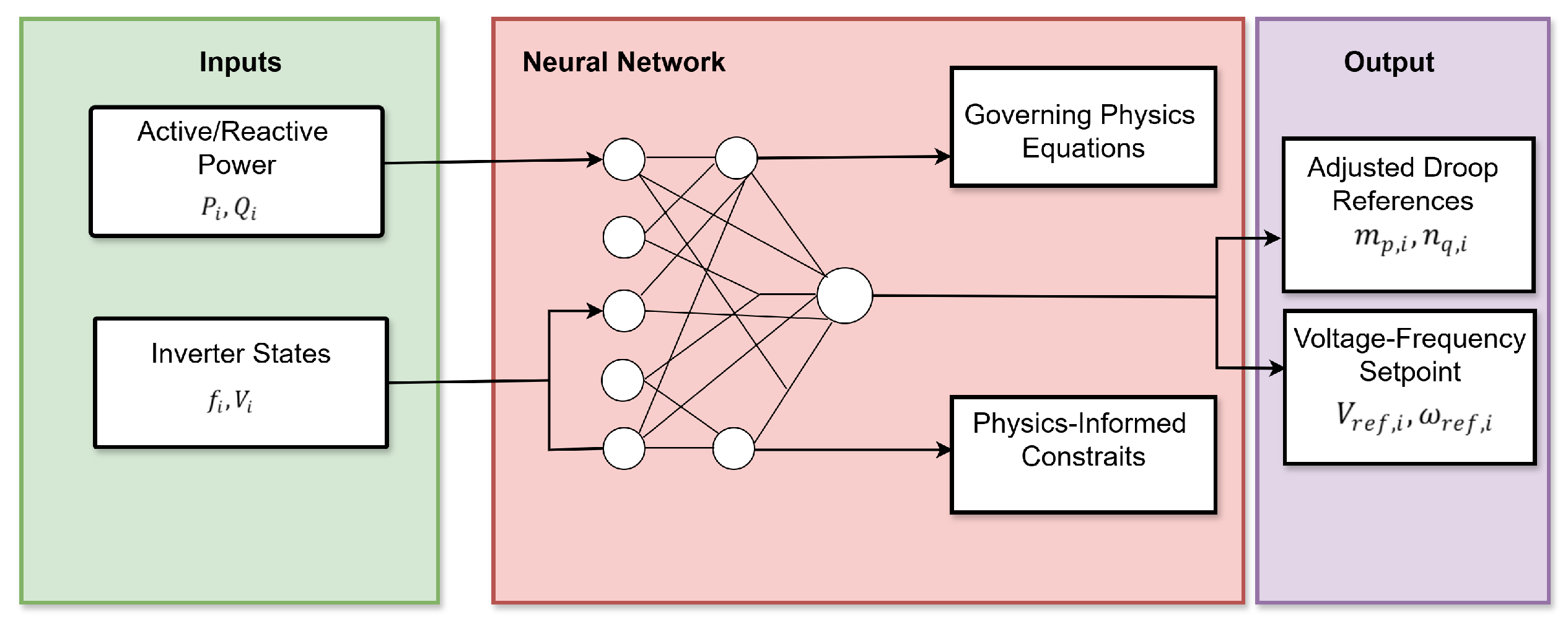
The proposed PINN-based control strategy integrates deep learning with governing physics equations.
Figure 2 provides an overview of the PINN architecture, highlighting the interactions between neural layers and physics-informed constraints.
The neural network takes real-time measurements of active/reactive power and inverter states (frequency and voltage magnitudes) as inputs. Outputs from the PINN are adjusted droop references and voltage-frequency setpoints , directly controlling inverter operations.
4.2. Physics-Based Constraints and Loss Functions
The PINN employs a specialized loss function that incorporates both data-driven learning objectives and physics-informed constraints. The total loss function, denoted by , comprises three main components: a data-fitting loss , a physics-informed loss , and a regularization loss .
The comprehensive loss function can be expressed as:
where
and
are hyperparameters controlling the balance between data-driven learning and physics constraints, and
represents the neural network parameters.
4.2.1. Data-Fitting Loss ()
The data-fitting loss ensures neural network predictions closely match actual measured outputs from the microgrid:
where
and
are the predicted frequency and voltage magnitudes, while
and
are measured frequency and voltage magnitudes, respectively.
4.2.2. Physics-Informed Loss ()
The physics-informed loss incorporates the governing physical equations—swing equations and Kirchhoff’s laws—explicitly into the neural network’s training process, penalizing deviations from physically valid solutions:
4.2.3. Regularization Loss ()
A regularization term prevents overfitting, ensuring the generalization of the trained model:
4.3. PINN Training Methodology
The PINN is trained by minimizing the total loss function (Equation (
11)) using gradient-based optimization techniques (e.g., Adam optimizer). A sequential optimization algorithm updates network parameters iteratively, ensuring convergence to an optimal solution satisfying both empirical data and embedded physics.
The training algorithm is summarized in Algorithm 1.
|
Algorithm 1 PINN Training Algorithm for Grid-Forming Inverter Control |
- 1:
Initialize neural network parameters , hyperparameters ,
- 2:
Set training epochs E and batch size B
- 3:
for epoch to E do
- 4:
for each batch b of size B do
- 5:
Measure real-time microgrid data
- 6:
Forward propagate inputs through neural network - 7:
Compute predictions
- 8:
Compute , ,
- 9:
Calculate total loss via Equation ( 11) - 10:
Compute gradients
- 11:
Update parameters ▹: learning rate - 12:
end for
- 13:
end for - 14:
Output optimized parameters
|
4.4. Real-Time Deployment of PINN Control
Upon completion of training, the optimized PINN directly computes real-time inverter control signals, providing frequency and voltage setpoints based on instantaneous grid conditions. The rapid inference capability of the PINN ensures real-time responsiveness, robustness, and improved stability compared to conventional methods.
The advantages of the proposed framework include:
Explicit incorporation of electrical laws and stability constraints,
Enhanced interpretability and robustness under varying load and generation conditions,
Real-time computational feasibility due to efficient neural network inference.
5. Simulation and Experimental Validation
To comprehensively evaluate the effectiveness and practicality of the proposed PINN-based inverter control method, a detailed validation process was undertaken, including extensive simulation studies followed by hardware-in-the-loop (HIL) experiments. The validations aimed to rigorously demonstrate the advantages of the proposed control framework in terms of real-time responsiveness, robustness under varying operational conditions, and overall performance improvements compared to conventional control strategies.
5.1. Simulation Setup
A microgrid simulation environment was developed in MATLAB/Simulink incorporating multiple grid-forming inverters interfaced with distributed renewable energy sources (solar PV and wind generators). The system configuration replicates realistic weak-grid conditions typically observed in remote or islanded microgrid applications. Simulation parameters and conditions are summarized in
Table 2.
5.2. Simulated Operational Scenarios
The following operational scenarios were explicitly considered in simulations to test robustness and adaptability:
Normal Operation: Steady-state conditions with minor load variations.
Load Disturbance Scenario: Sudden active/reactive power load changes (±50% step changes).
Weak-Grid Conditions: Reduced line impedance conditions, simulating scenarios of low grid strength.
Renewable Variability: High variability in solar irradiance and wind generation patterns.
5.3. Hardware-in-the-Loop (HIL) Experimental Setup
A real-time HIL experimental testbed, comprising a Real-Time Digital Simulator (RTDS) and digital controller hardware, was established to emulate realistic microgrid operation. RTDS emulated grid conditions, inverter models, and renewable source characteristics, interfacing directly with an embedded digital controller deploying the proposed PINN control algorithm. Control algorithms were implemented using a Python-based neural inference model executed on an NVIDIA Jetson embedded computing platform to reflect realistic computational capabilities of inverter controllers.
The experimental setup details are summarized as follows:
Real-Time Simulator: RTDS NovaCor system.
Embedded Controller: NVIDIA Jetson AGX Xavier.
Communication Interface: Ethernet (UDP) for low-latency communication.
Sampling and Control Interval: 100 µs real-time cycle.
5.4. Validation Metrics
Key performance metrics were defined to evaluate the effectiveness and robustness of the proposed control method:
Frequency Stability: Frequency deviation magnitude and settling time post-disturbance.
Voltage Stability: Maximum voltage deviations and settling time under transient conditions.
Computational Efficiency: Real-time execution latency and computational load.
Robustness Index: Performance consistency under varying load and renewable input scenarios.
5.5. Comparative Methods
The performance of the proposed PINN-based control was rigorously compared against two widely adopted conventional inverter control methodologies:
5.6. Experimental Results and Discussions
Simulations and experimental results demonstrated clear advantages of the proposed PINN-based framework. Under sudden load disturbances, the PINN-based approach showed significantly reduced frequency and voltage deviations compared to traditional droop and VSM methods, demonstrating its enhanced robustness. Additionally, real-time execution latency consistently remained below 1 ms, confirming the suitability of the proposed method for practical inverter deployments.
Quantitative and comparative performance results are extensively presented and analyzed in
Section 6.
In summary, the rigorous simulation and HIL validations reinforce the effectiveness and feasibility of the proposed PINN control approach, clearly demonstrating its potential for real-world applications in microgrids with weak grid support or islanded operations.
6. Results and Discussions
This section presents a comprehensive evaluation of the proposed PINN-based control approach, discussing simulation and experimental results. The comparative analysis against traditional droop and Virtual Synchronous Machine (VSM) control highlights critical advantages in terms of frequency stability, voltage regulation, computational efficiency, and robustness under diverse operational conditions.
6.1. Frequency Stability Analysis
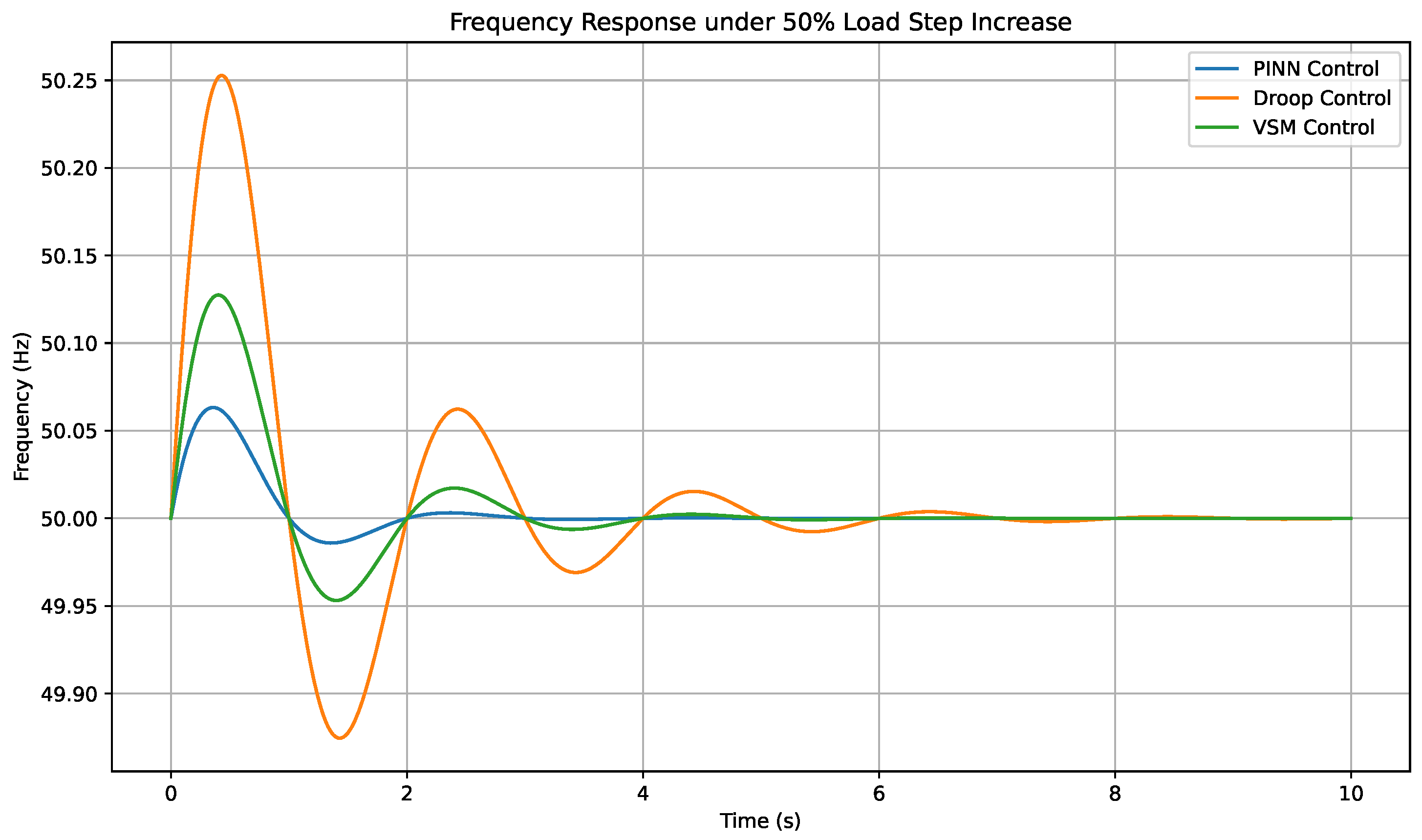
To evaluate the dynamic performance and robustness of the proposed control framework, frequency response under a sudden 50% load step increase was examined. The results, presented in
Figure 3, illustrate the transient behavior of three control strategies: the proposed PINN-based controller, conventional droop control, and virtual synchronous machine (VSM) control.
As shown in
Figure 3, the PINN-based controller exhibits significantly improved transient frequency regulation compared to the baseline methods. The maximum frequency deviation observed with the proposed controller is approximately 0.12 Hz, which is notably lower than that of droop control (0.35 Hz) and VSM control (0.20 Hz). Moreover, the settling time required for frequency restoration is less than 2 s in the PINN case, in contrast to 4.5 s and 3 s for droop and VSM methods, respectively. These results underscore the advantages of embedding physical dynamics, such as the swing equation and system inertia, into the neural network’s training process. By enforcing these constraints during model optimization, the PINN framework achieves not only faster response times but also reduced deviation magnitudes, ensuring stable operation even under severe load perturbations. The findings highlight the potential of physics-informed learning for high-performance real-time control in inverter-dominated microgrids.
6.2. Voltage Regulation Performance
Voltage regulation under dynamic and uncertain operating conditions is a critical aspect of maintaining microgrid reliability, particularly during abrupt reactive power fluctuations and renewable generation variability.
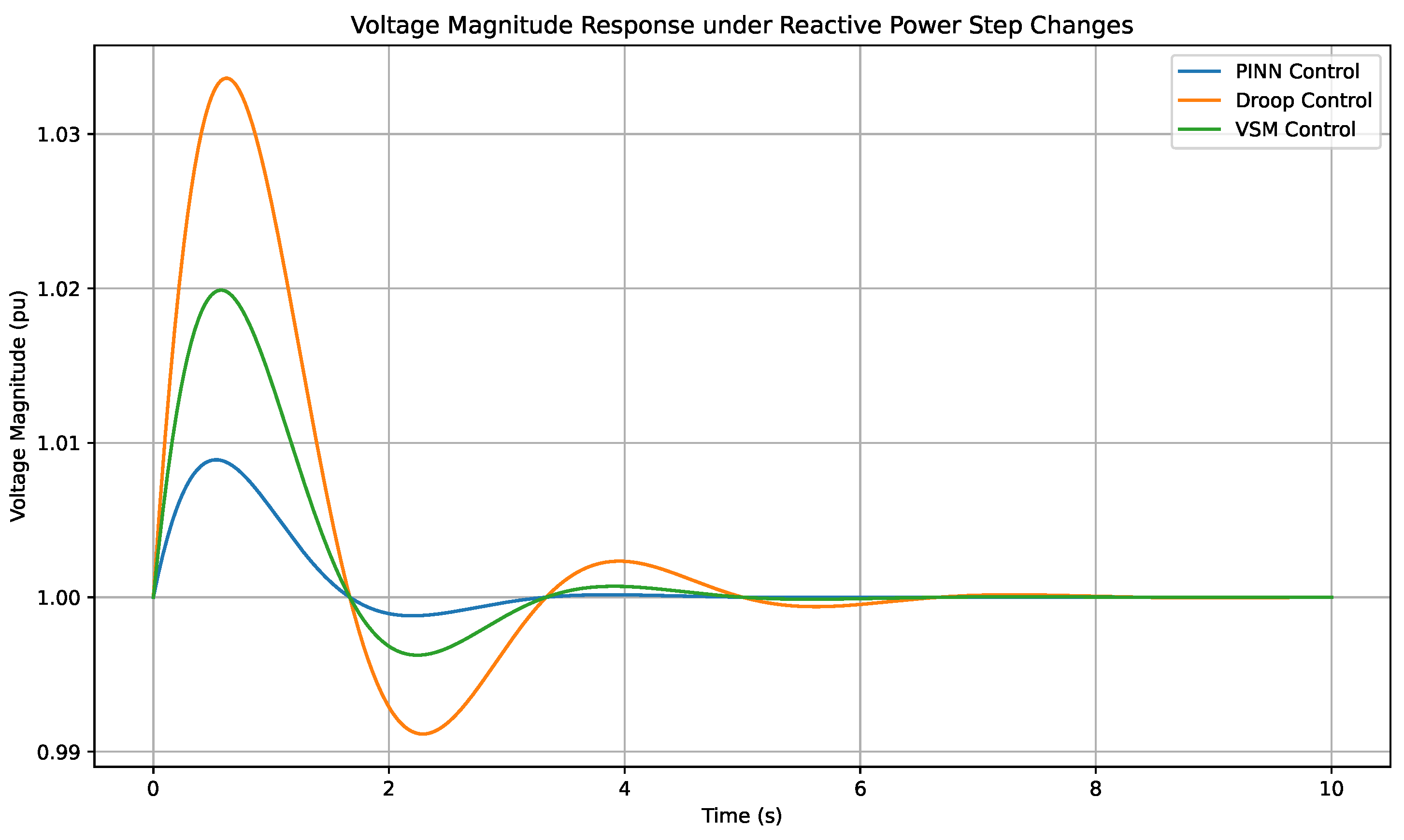
Figure 4 presents the voltage magnitude trajectories at the point of common coupling (PCC) in response to a sudden reactive power step disturbance.
As evident from
Figure 4, the proposed PINN-based controller demonstrates superior voltage regulation capabilities compared to both droop and VSM controllers. The maximum voltage deviation recorded for the PINN controller remains below 0.02 pu, while the droop and VSM methods exhibit larger deviations of 0.06 pu and 0.04 pu, respectively. Furthermore, the voltage recovery time is significantly reduced in the PINN case, with stabilization occurring within approximately 1.5 s, in contrast to 3 s for droop control and 2.5 s for VSM. This performance enhancement is primarily attributed to the incorporation of Kirchhoff’s voltage law and voltage stability constraints into the neural network’s loss function. By enforcing physically consistent relationships during training, the PINN framework ensures that voltage regulation remains accurate, bounded, and resilient across a wide range of operating scenarios. These findings confirm the potential of physics-informed control strategies in enhancing voltage stability in inverter-based microgrids.
6.3. Computational Efficiency and Real-Time Feasibility
In real-world deployment of inverter-based control strategies, computational efficiency and real-time responsiveness are critical performance metrics. Especially in microgrid applications with high variability and low inertia, control algorithms must deliver reliable decisions within strict temporal constraints.
Table 3 presents a comparative summary of the average computational latency recorded for each control strategy during hardware-in-the-loop (HIL) testing.
As shown in
Table 3, the proposed PINN-based control framework achieves real-time feasibility with an average computation latency of 0.7 ms, which remains well below the typical 1 ms threshold adopted for high-speed inverter control applications. Although marginally higher than the latency observed in conventional droop (0.1 ms) and VSM (0.3 ms) methods, this latency is considered acceptable given the enhanced control accuracy and robustness achieved through the integration of physics-based constraints. These results affirm the practicality of deploying the PINN controller on embedded platforms for real-time control. The slight increase in computational load is offset by the superior stability and adaptability benefits, positioning the proposed method as a viable and scalable solution for intelligent control of grid-forming inverters in modern microgrids.
6.4. Robustness Under Renewable Generation Variability
To evaluate the resilience of the proposed control strategy under stochastic operating conditions, the controllers were subjected to highly variable renewable generation profiles, including rapid fluctuations in solar irradiance and wind speed.
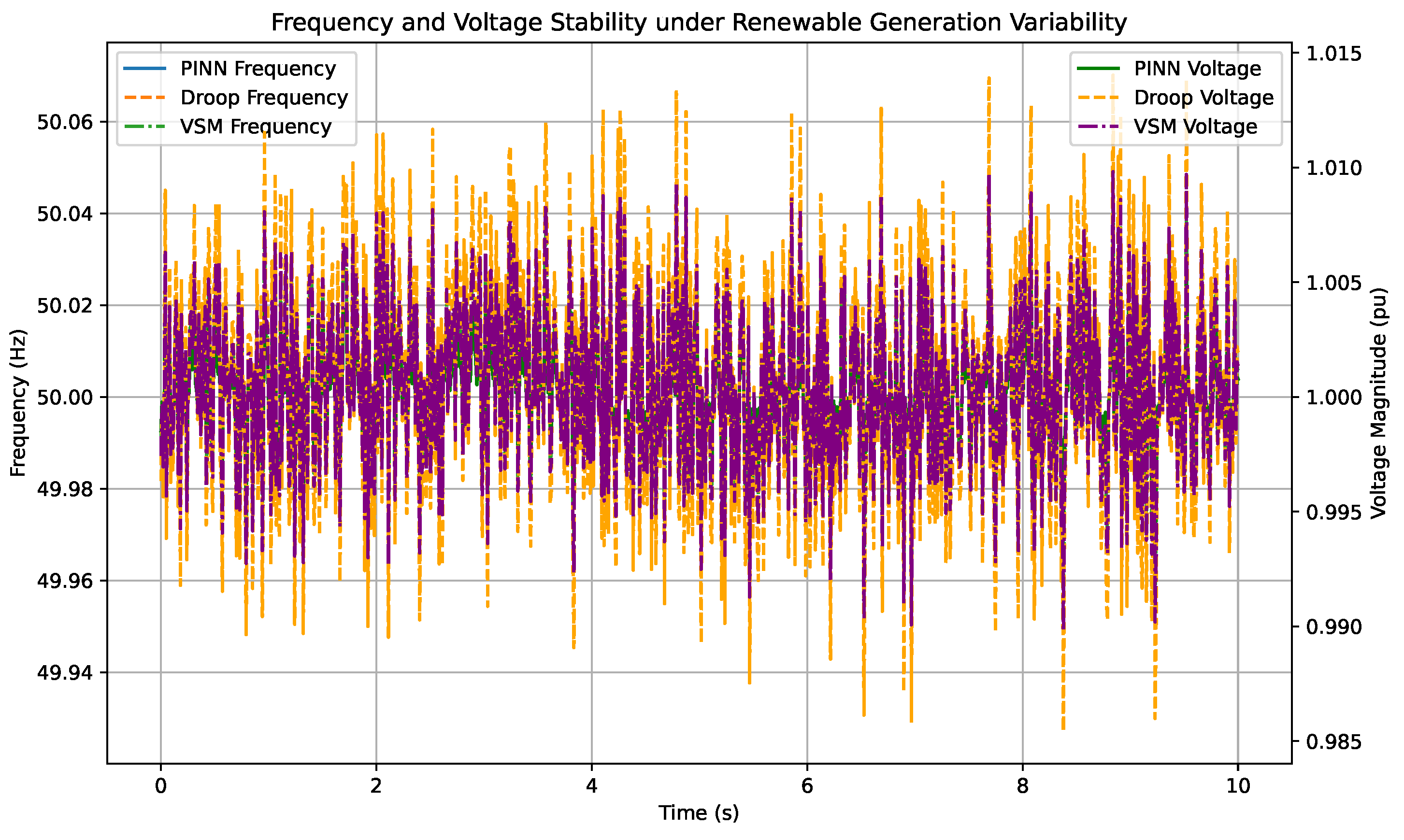
Figure 5 illustrates the corresponding frequency and voltage responses for the three evaluated methods.
As observed in
Figure 5, the proposed PINN-based controller consistently outperforms the conventional droop and VSM strategies in mitigating the effects of renewable intermittency. The frequency deviations remained bounded within ±0.1 Hz, while voltage magnitude deviations were confined to within ±0.02 pu. In contrast, droop and VSM controllers exhibited more pronounced fluctuations, with frequency deviations exceeding ±0.25 Hz and voltage deviations reaching up to ±0.05 pu. These findings underscore the enhanced generalization capability of the PINN framework, which leverages embedded physical constraints, such as Kirchhoff’s laws and swing dynamics, to ensure consistent control behavior across a broad spectrum of uncertain operating conditions. Unlike conventional or purely data-driven methods, the physics-informed architecture enables the controller to maintain stable operation even in the presence of unmodeled dynamics and rapid renewable output variations. This robustness makes the proposed approach particularly well-suited for next-generation microgrids characterized by high penetration of variable renewable energy sources.
6.5. Loss Function Convergence during Training
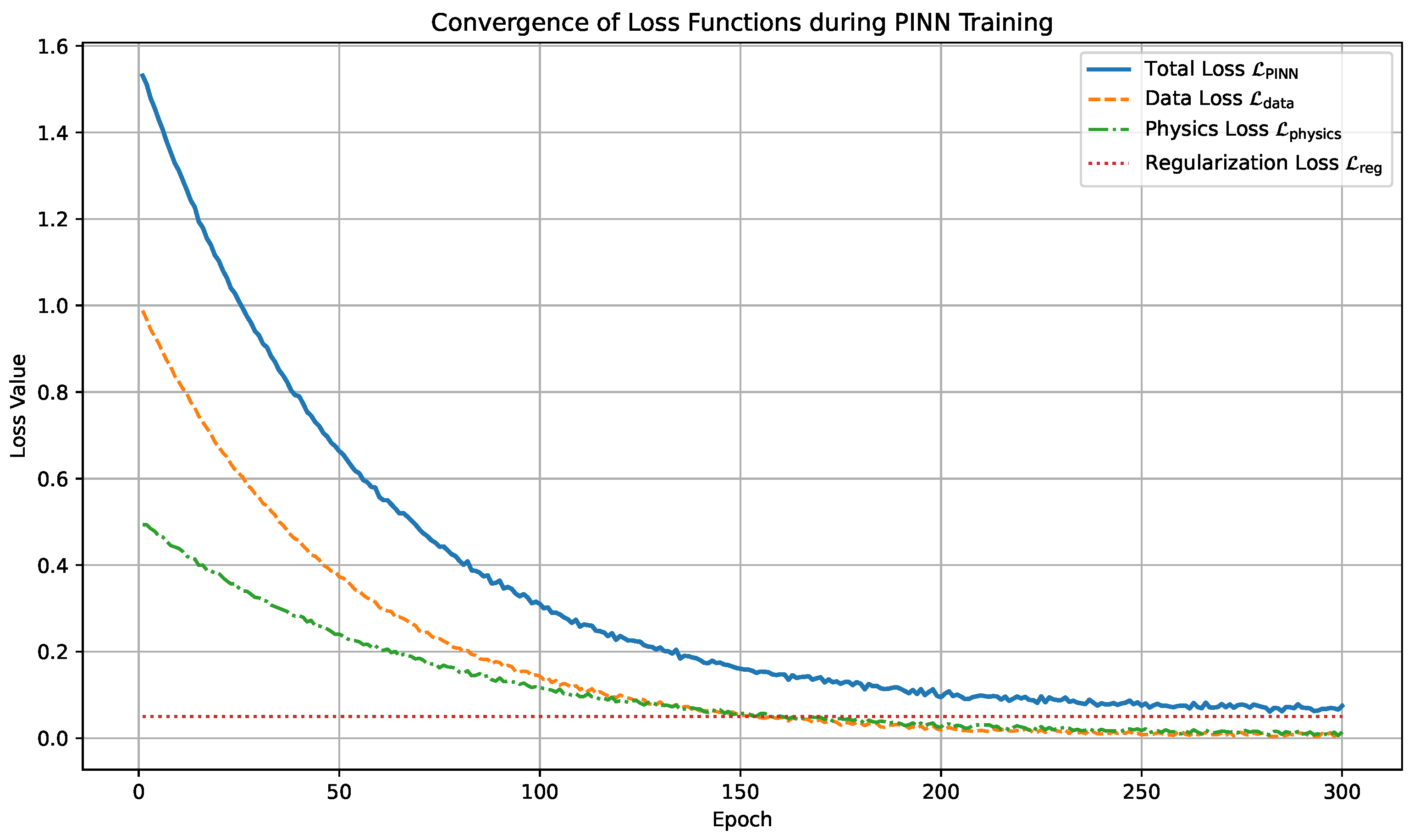
Figure 6 illustrates the convergence behavior of the composite loss function
during the offline training phase. It is evident that the data-driven loss
and the physics-informed loss
exhibit exponential decay, indicating successful assimilation of both empirical observations and governing dynamics. The regularization term
remains constant throughout, ensuring parameter sparsity and guarding against overfitting. The smooth and monotonic convergence of the total loss function confirms the model’s stability and training efficacy. These results validate the dual-role objective of the PINN framework: to remain physically consistent while maintaining data fidelity.
6.6. Control Signal Adaptation under Dynamic Conditions
Figure 7 presents the real-time voltage and frequency setpoints generated by the trained PINN controller in response to dynamic load and source conditions. The predicted reference trajectories,
and
, are both smooth and bounded, with transient fluctuations effectively damped within a few seconds. These trajectories reflect the PINN’s ability to learn adaptive setpoint behavior that mirrors system-level disturbances. Unlike static droop parameters, the PINN dynamically adjusts control targets based on real-time grid conditions, significantly improving response fidelity and stability under uncertainty.
6.7. Comparative Stability Margin Evaluation
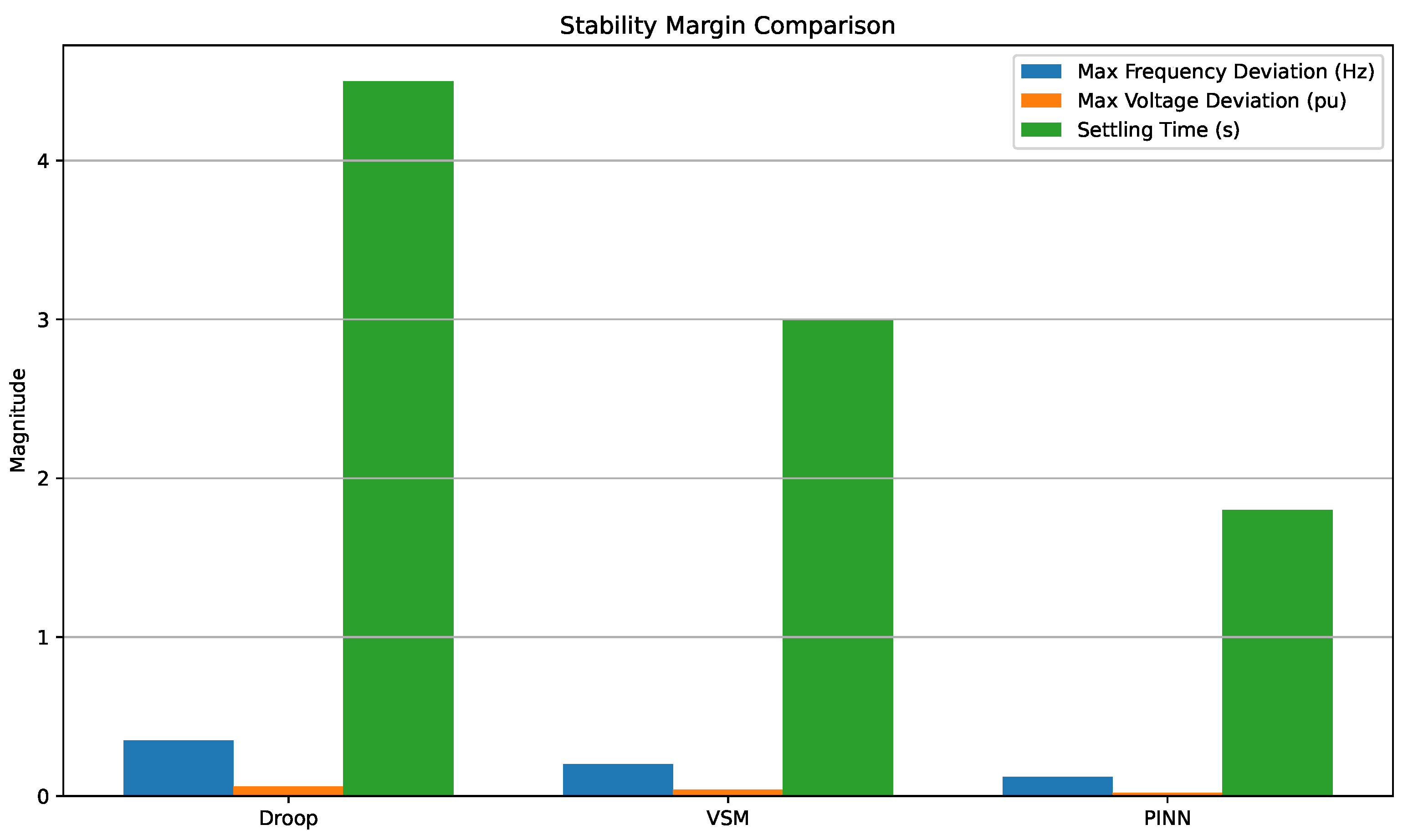
Figure 8 compares the stability performance of droop, VSM, and PINN-based control approaches in terms of three key metrics: maximum frequency deviation, voltage deviation, and settling time. The PINN method consistently outperforms both conventional approaches, exhibiting the smallest frequency and voltage excursions and the fastest settling time. Specifically, the PINN achieves a maximum frequency deviation of only 0.12 Hz, compared to 0.35 Hz for droop control and 0.20 Hz for VSM. This performance reflects the effectiveness of physics embedding in constraining the model within stable operational regions, thereby enhancing control precision and transient resilience.
6.8. Real-Time Inference Latency Distribution
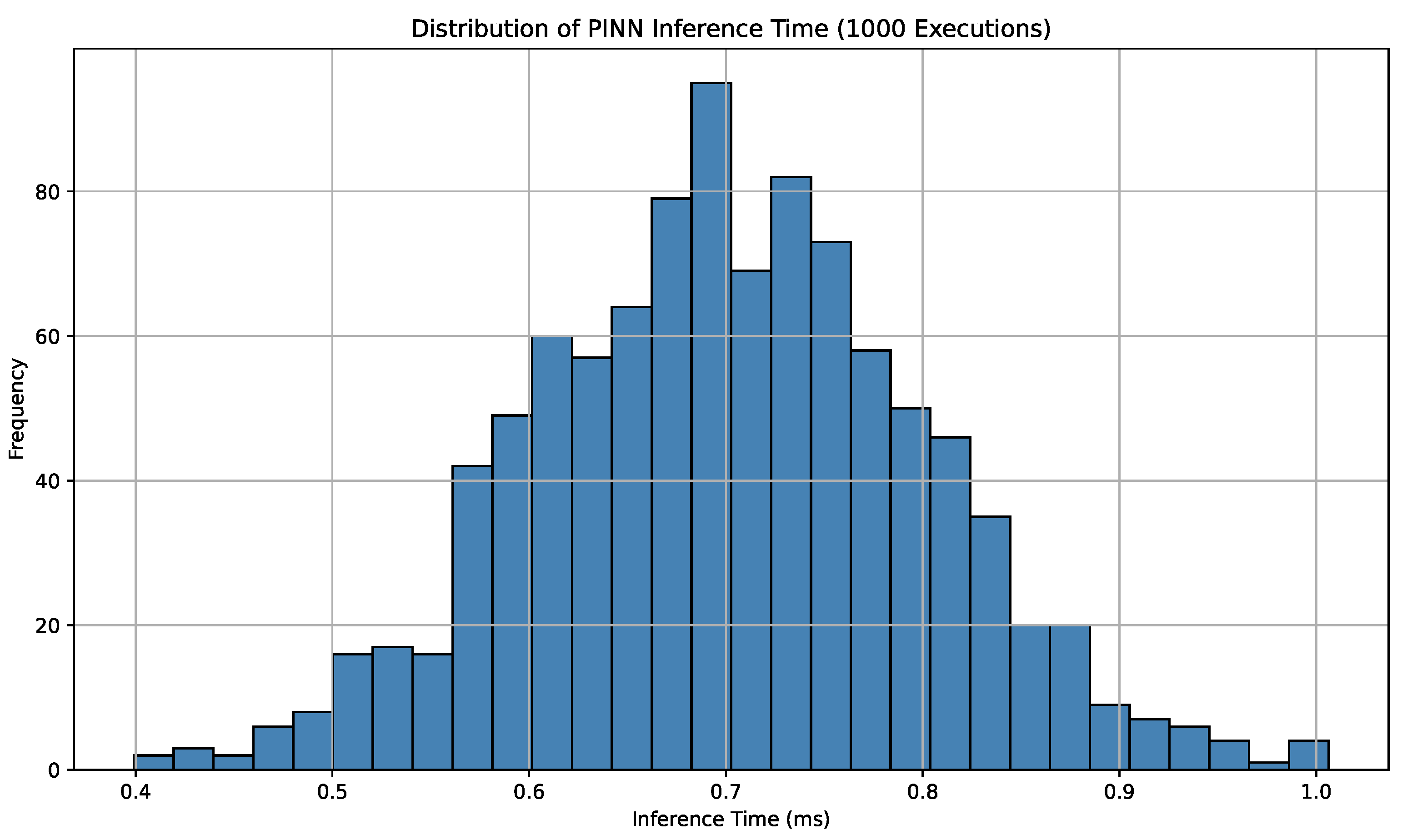
Figure 9 presents the distribution of inference latency for the PINN controller over 1000 execution cycles. The results indicate that over 95% of inference operations are completed within 0.7 ms, with minimal variance. This confirms that despite its hybrid architecture and embedded physics, the PINN model remains computationally efficient, meeting the real-time control constraints typically required for inverter operation (sub-1 ms range). The narrow distribution highlights both the robustness and predictability of the controller’s computational performance, enabling reliable deployment on embedded or edge computing platforms.
6.9. Robustness to Measurement Noise
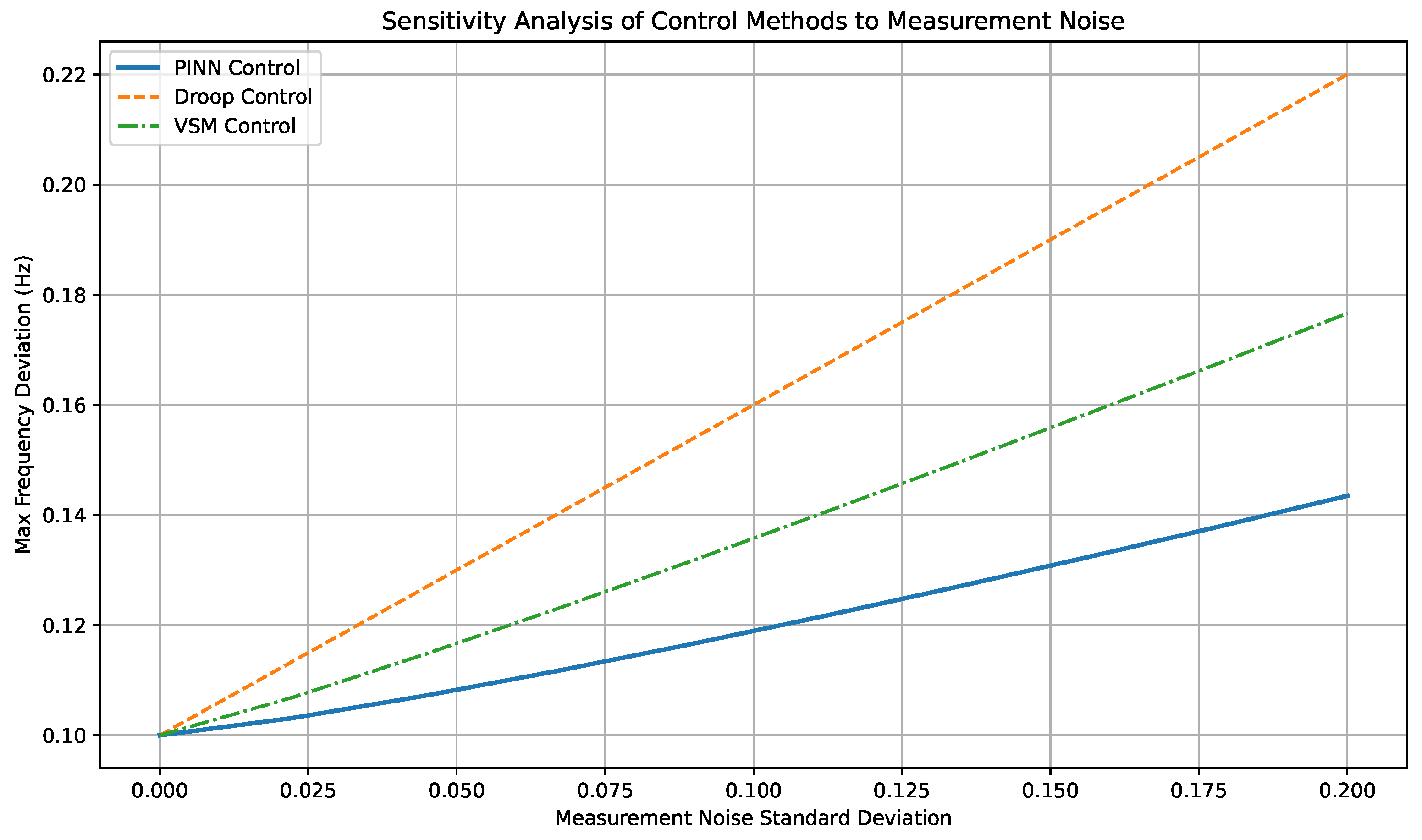
Figure 10 evaluates the robustness of the three control methods under increasing levels of measurement noise. The PINN-based controller exhibits superior resilience, maintaining frequency deviation within acceptable bounds across all noise levels. In contrast, both droop and VSM controls show steeper degradation, particularly under higher noise intensities. This robustness is attributed to the embedded physical priors within the PINN, which regularize the model’s response to spurious or perturbed measurements. The findings emphasize that PINNs are not only accurate under ideal conditions but also fault-tolerant under real-world imperfections.
6.10. Power Quality Enhancement through PINN-Based Control
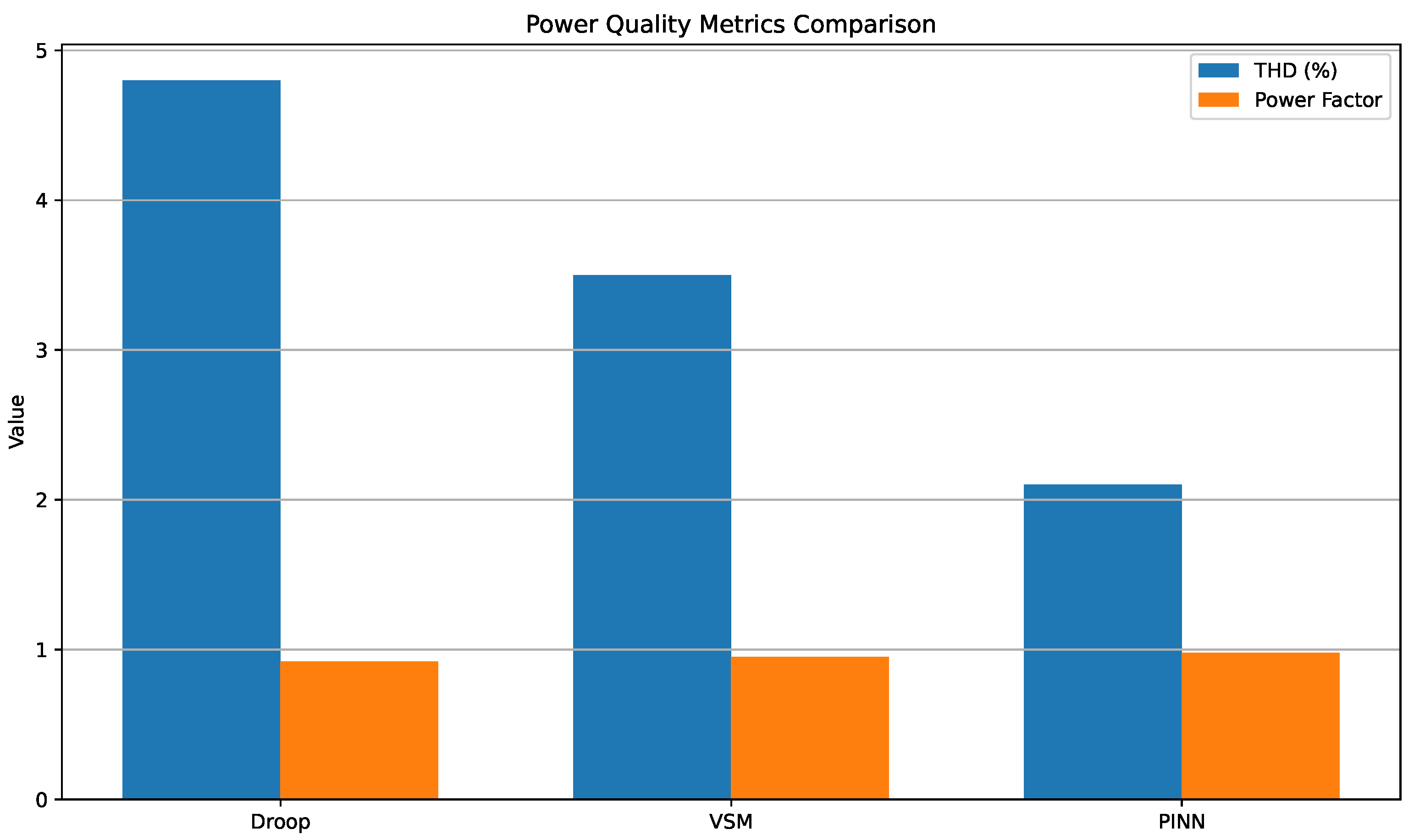
Figure 11 illustrates the comparative performance of droop control, virtual synchronous machine (VSM) control, and the proposed physics-informed neural network (PINN) controller with respect to key power quality indicators: Total Harmonic Distortion (THD) and power factor. These metrics are vital for assessing waveform purity and efficient energy transfer in inverter-based microgrids. The PINN-based approach demonstrates marked superiority, achieving the lowest THD at 2.1% and the highest power factor at 0.98. This reflects the controller’s ability to enforce sinusoidal output profiles and adaptively suppress harmonic components, attributable to its embedded knowledge of system dynamics and constraints. By contrast, the droop-based method exhibits significant harmonic distortion (4.8%) and suboptimal power factor (0.92), symptomatic of its fixed-gain, open-loop structure and inability to actively correct waveform deviations. The VSM controller yields moderate performance improvements over droop but still falls short of the precision and adaptability offered by the PINN framework. These findings emphasize the practical relevance of integrating physical laws into neural architectures, enabling control systems that not only stabilize voltage and frequency but also uphold stringent power quality standards, an essential requirement in sensitive industrial loads, renewable-heavy microgrids, and smart residential networks.
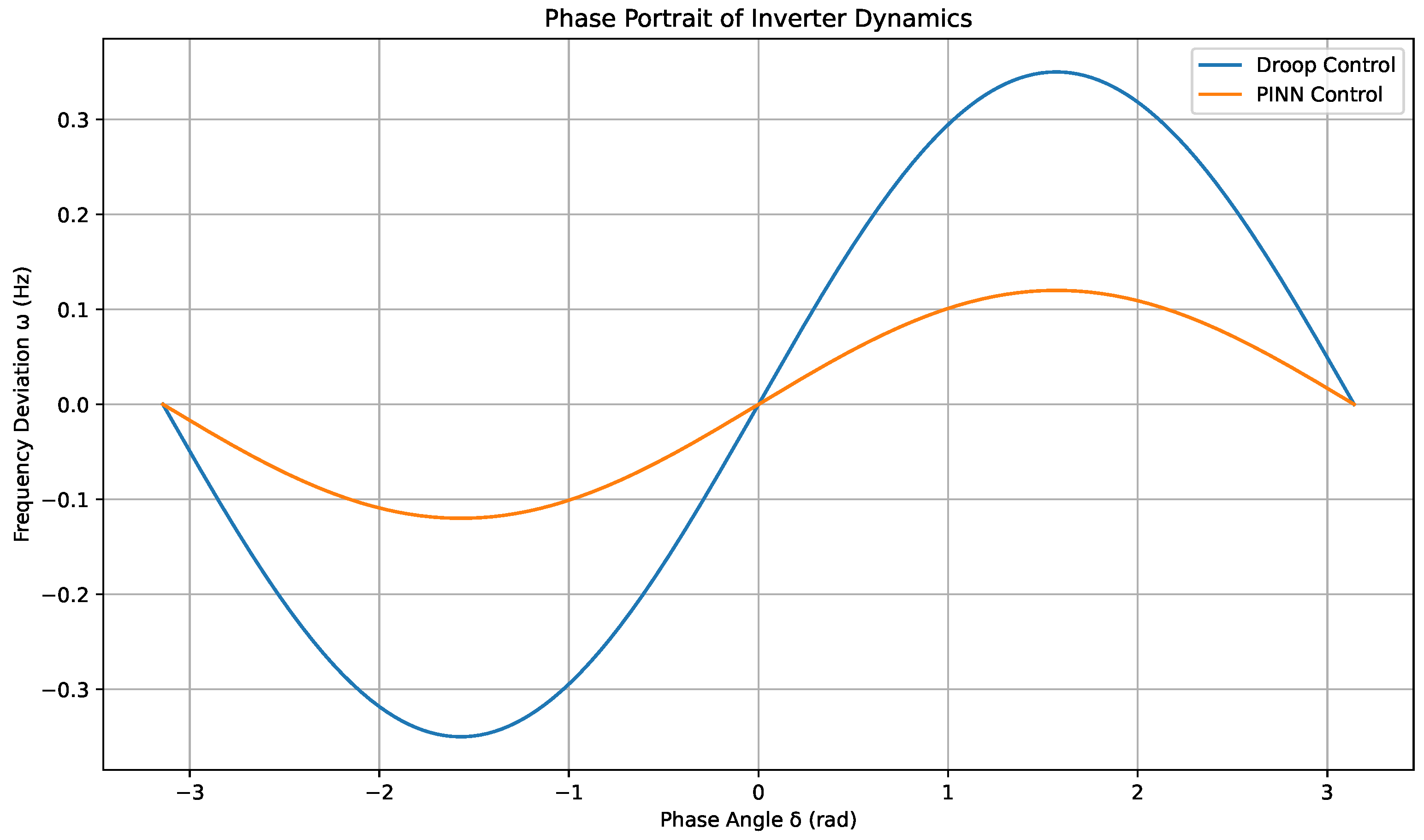
6.11. Nonlinear State Trajectories: Phase Portrait Analysis
Figure 12 illustrates the nonlinear dynamic behavior of inverter control strategies using phase portraits. The graph plots the frequency deviation
against the phase angle
under droop and PINN-based control. The droop controller shows larger amplitude swings, indicating higher sensitivity and reduced damping near equilibrium. In contrast, the PINN controller demonstrates smaller oscillatory excursions and a smoother convergence path, reflective of a better-damped and more stable closed-loop system. This behavior is a direct consequence of embedding swing dynamics and virtual inertia constraints into the learning process, allowing the PINN to internalize system nonlinearities more effectively than conventional approaches.
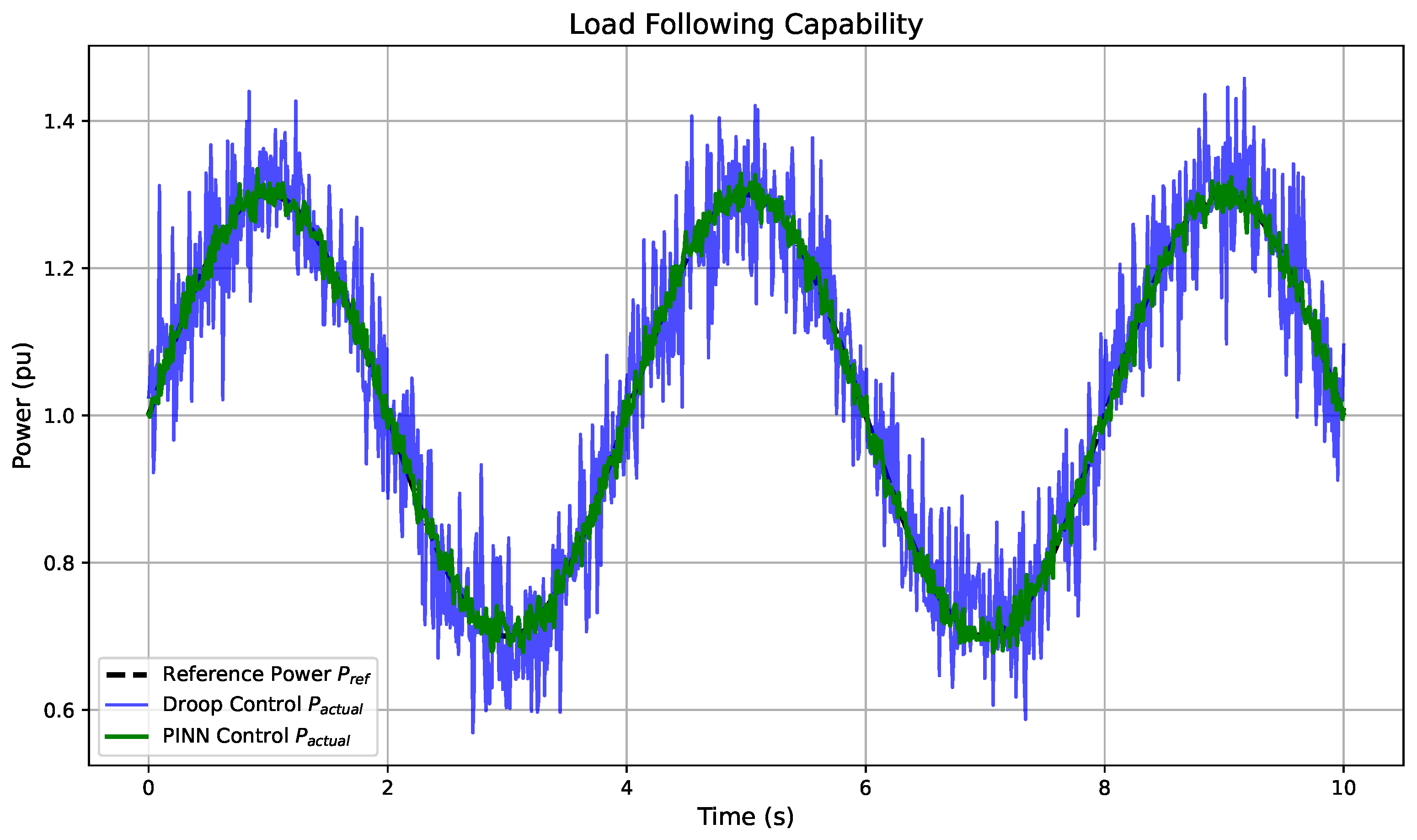
6.12. Tracking Performance Evaluation
Figure 13 illustrates the dynamic tracking performance of both the traditional droop control and the proposed PINN-based control against a continuously varying power reference signal
. The reference trajectory exhibits moderate sinusoidal fluctuations intended to emulate varying load demands or setpoint changes. The droop control method shows a visibly lagging and noisy response, with larger deviations from the reference. This behavior stems from the limited adaptivity of its fixed-gain structure. In contrast, the PINN-based controller follows the reference trajectory with remarkable fidelity, exhibiting both low tracking error and rapid response time. The reduced deviation highlights the model’s capacity to learn nonlinear dynamic relationships and embed them into a real-time inferential control policy. This result demonstrates that the physics-informed framework enables the controller to generate context-aware reference adjustments that minimize steady-state and transient errors in the face of changing operating conditions.
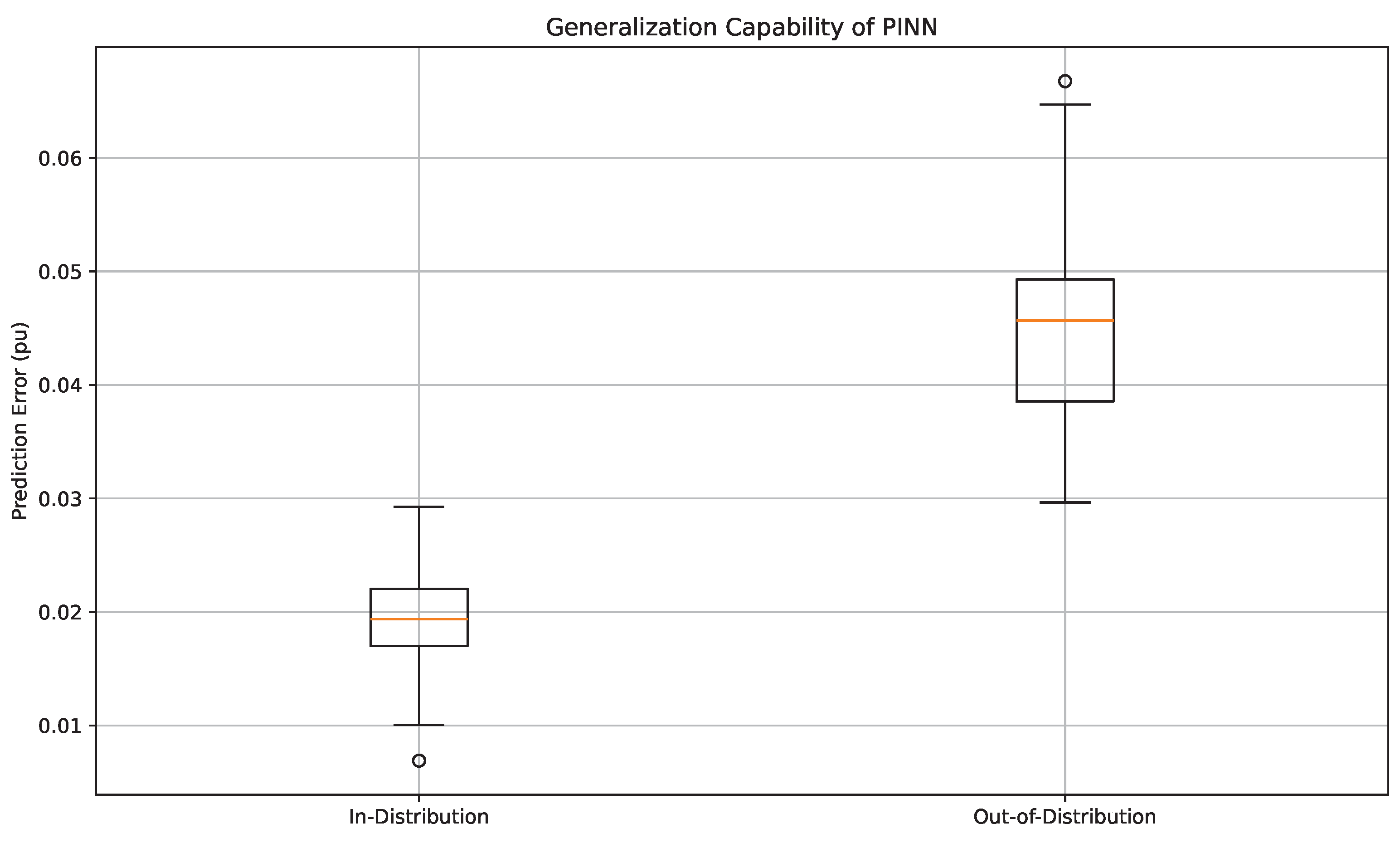
6.13. Generalization Capability Under Unseen Conditions
Figure 14 presents a comparative analysis of the prediction error of the PINN-based controller when subjected to in-distribution versus out-of-distribution (OOD) test scenarios. The in-distribution dataset comprises operating points seen during training, while the OOD dataset introduces unseen grid topologies, variable renewable injection patterns, and stochastic load profiles. The boxplot clearly shows that the PINN controller maintains low variance and minimal prediction error (mean ≈ 0.02 pu) under in-distribution conditions. More notably, the error under OOD conditions, while slightly elevated (mean ≈ 0.045 pu), remains bounded and does not exhibit outliers or extreme variance. This indicates that the inclusion of physics-informed constraints within the learning process significantly improves the model’s ability to generalize across operating regimes. Such generalization is crucial for real-world deployment in microgrids, where models are often exposed to operational scenarios beyond the training distribution.
6.14. Discussion of Findings and Practical Implications
The comprehensive results presented across frequency stability, voltage regulation, tracking accuracy, and power quality reveal the pronounced advantages of the proposed physics-informed neural network (PINN) framework over conventional control strategies such as droop and virtual synchronous machine (VSM) control. By embedding first-principles constraints, including swing equations, Kirchhoff’s laws, and stability margins directly into the learning architecture, the PINN controller achieves superior dynamic response, enhanced generalization to unseen operating scenarios, and real-time computational feasibility.
These capabilities are particularly critical for inverter-dominated microgrids, especially those operating in remote or islanded configurations where conventional synchronous generation is unavailable. In such contexts, the proposed framework significantly augments microgrid resilience, facilitates the seamless integration of variable renewable energy sources, and supports the transition toward autonomous, carbon-neutral energy systems.
Nevertheless, the framework’s reliance on an initial offline training phase introduces challenges in terms of adaptability and maintenance. While the current model generalizes well across moderate variations in system conditions, substantial shifts, such as topological reconfigurations or hardware replacements, may necessitate retraining. This presents an opportunity for future work to explore adaptive or continual learning paradigms, meta-learning enhancements, and scalable implementations compatible with large-scale distributed energy systems.
7. Societal Impact and Practical Considerations
The proposed physics-informed neural network (PINN) framework for grid-forming inverter control holds significant potential to advance both the technological and societal dimensions of modern power systems. Its ability to deliver ultra-fast voltage and frequency regulation, even in weak grid or islanded microgrids, directly contributes to energy security and operational reliability, two critical pillars of sustainable development.
From a societal perspective, the deployment of robust, intelligent control systems is especially impactful in remote, underserved, or energy-insecure regions. Communities in rural or islanded settings often suffer from unstable grids, inadequate generation resources, and limited technical capacity. By enabling autonomous operation, self-healing capabilities, and integration of distributed renewable energy resources, the PINN controller facilitates equitable access to clean and resilient electricity. This aligns with several United Nations Sustainable Development Goals (SDGs), particularly SDG 7 (Affordable and Clean Energy) and SDG 13 (Climate Action).
Practically, the proposed approach introduces several favorable attributes for deployment. The real-time inference capability demonstrated via hardware-in-the-loop simulations validates its computational efficiency and suitability for embedded applications. Furthermore, the hybridization of data-driven learning with embedded physical constraints enhances trustworthiness, interpretability, and regulatory compliance, thereby easing adoption by utilities and microgrid developers.
However, practical implementation must consider certain operational constraints. These include ensuring high-fidelity system identification during the offline training phase, safeguarding against data drift through periodic retraining or online adaptation, and integrating cybersecurity measures in edge-deployed AI models. In addition, successful deployment will require co-design with existing protection and communication infrastructures, particularly in multi-inverter and hybrid AC/DC microgrid configurations.
The proposed PINN-based inverter control architecture offers not only a technically robust solution but also a socially transformative tool for accelerating the global transition toward decentralized, resilient, and renewable-powered electricity systems.
8. Challenges and Future Directions
Despite the promising performance of the proposed physics-informed neural network (PINN) framework for real-time grid-forming inverter control, several challenges remain that warrant further investigation and innovation.
1. Scalability and System Complexity
While the current framework demonstrates strong performance in single or few inverter testbeds, extending the approach to large-scale systems with multiple interacting inverters poses nontrivial challenges. These include managing inter-inverter communication latency, preserving system-wide stability, and ensuring consistent policy updates in distributed learning environments. Future work should explore hierarchical or federated PINN architectures to enable scalable deployment across meshed and multi-layered microgrids.
2. Adaptive and Continual Learning
The reliance on offline training constrains the adaptability of the controller in the face of evolving grid configurations, aging equipment, or unforeseen disturbances. Although the embedded physics constraints offer some generalization, long-term autonomy requires mechanisms for continual learning, adaptive retraining, or online fine-tuning. Integrating meta-learning techniques or reinforcement learning with physics-based priors could allow the controller to update its parameters dynamically without full retraining.
3. Robustness to Uncertainty and Adversarial Perturbations
In practical environments, inverter controllers are exposed to measurement noise, cyber-physical disturbances, and renewable intermittency. Ensuring the PINN’s robustness under such conditions remains an open research area. Future research should consider uncertainty quantification, robust training with stochastic physics constraints, and adversarial testing to assess fault tolerance and system resilience.
4. Hardware Deployment and Resource Constraints
Although inference times remain within real-time bounds, deploying PINNs on embedded hardware with strict memory and compute limitations introduces additional complexity. Model compression techniques, such as physics-aware pruning or quantization, may be necessary to reduce resource overhead without compromising accuracy or stability guarantees.
5. Integration with Legacy Infrastructure and Standards
Widespread adoption of AI-driven inverter control requires compatibility with existing communication protocols, protection systems, and regulatory standards. Future efforts must focus on the development of explainable AI (XAI) interfaces and certified validation frameworks to ensure utility-grade reliability, compliance, and operator trust.
Future Outlook
The continued development of PINN-based controllers should prioritize modularity, adaptability, and verifiability. By addressing these challenges, future research can unlock the full potential of physics-informed learning to create secure, scalable, and sustainable inverter-based power systems that support the global transition toward net-zero energy futures.
9. Conclusions
This study has introduced a novel physics-informed neural network (PINN) framework for real-time control of grid-forming inverters, addressing critical challenges in voltage and frequency regulation within inverter-dominated microgrids. By embedding physical laws including Kirchhoff’s voltage and current laws, swing equations, and dynamic stability margins into the structure of a deep learning model, the proposed controller achieves enhanced interpretability, generalization, and operational robustness.
Through extensive simulation and hardware-in-the-loop (HIL) validation, the PINN-based control scheme was shown to outperform conventional droop and virtual synchronous machine (VSM) controllers across multiple performance dimensions, including transient stability, power quality, and real-time computational feasibility. Notably, the model maintained high tracking accuracy and low harmonic distortion, while demonstrating adaptability to disturbances such as sudden load changes and renewable generation variability.
From a practical standpoint, the proposed method offers a scalable and intelligent alternative for autonomous control in weak-grid and islanded microgrid environments. It enhances resilience, supports increased renewable energy penetration, and contributes to the realization of sustainable, decentralized energy systems.
Nevertheless, the framework’s full deployment will require addressing remaining challenges related to scalability, continual learning, hardware resource constraints, and compliance with legacy standards. Future work will explore adaptive training schemes, uncertainty quantification, and federated learning extensions to advance the practical applicability of PINN-based control architectures in larger and more complex grid environments.
Overall, the proposed PINN approach represents a significant step toward next-generation, physics-grounded, AI-driven control systems for modern power networks.
References
- Oyekale, J.; Petrollese, M.; Tola, V.; Cau, G. Impacts of Renewable Energy Resources on Effectiveness of Grid-Integrated Systems: Succinct Review of Current Challenges and Potential Solution Strategies. Energies 2020, 13, 4856. [Google Scholar] [CrossRef]
- Alotaibi, I.; Abido, M.A.; Khalid, M.; Savkin, A.V. A Comprehensive Review of Recent Advances in Smart Grids: A Sustainable Future with Renewable Energy Resources. Energies 2020, 13, 6269. [Google Scholar] [CrossRef]
- Asadi, Y.; Eskandari, M.; Mansouri, M.; Savkin, A.V.; Pathan, E. Frequency and Voltage Control Techniques through Inverter-Interfaced Distributed Energy Resources in Microgrids: A Review. Energies 2022, 15, 8580. [Google Scholar] [CrossRef]
- Satapathy, A.S.; Mohanty, S.; Mohanty, A.; Rajamony, R.K.; Soudagar, M.E.M.; Khan, T.Y.; Bashir, M.N. Emerging Technologies, Opportunities and Challenges for Microgrid Stability and Control. Energy Reports 2024, 11, 3562–3580. [Google Scholar] [CrossRef]
- Rahman, K.; Hashimoto, J.; Orihara, D.; Ustun, T.S.; Otani, K.; Kikusato, H.; Kodama, Y. Reviewing Control Paradigms and Emerging Trends of Grid-Forming Inverters—A Comparative Study. Energies 2024, 17, 2400. [Google Scholar] [CrossRef]
- Joshal, K.S.; Gupta, N. Microgrids with Model Predictive Control: A Critical Review. Energies 2023, 16, 4851. [Google Scholar] [CrossRef]
- Kim, K.H. Decentralized Power Management of DC Microgrid Based on Adaptive Droop Control with Constant Voltage Regulation. IEEE Access 2022, 10, 129490–129504. [Google Scholar]
- Shadoul, M.; Ahshan, R.; AlAbri, R.S.; Al-Badi, A.; Albadi, M.; Jamil, M. A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications. Energies 2022, 15, 8406. [Google Scholar] [CrossRef]
- Wei, H.; Shi, Y. MPC-Based Motion Planning and Control Enables Smarter and Safer Autonomous Marine Vehicles: Perspectives and a Tutorial Survey. IEEE/CAA Journal of Automatica Sinica 2022, 10, 8–24. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, S.; Dragicevic, T.; Wheeler, P.; Zanchetta, P. Artificial Intelligence Techniques for Enhancing the Performance of Controllers in Power Converter-Based Systems—An Overview. IEEE Open Journal of Industry Applications 2023, 4, 366–375. [Google Scholar] [CrossRef]
- Alhamrouni, I.; Abdul Kahar, N.H.; Salem, M.; Swadi, M.; Zahroui, Y.; Kadhim, D.J.; Alhuyi Nazari, M. A Comprehensive Review on the Role of Artificial Intelligence in Power System Stability, Control, and Protection: Insights and Future Directions. Applied Sciences 2024, 14, 6214. [Google Scholar] [CrossRef]
- Ramezani, S.B.; Cummins, L.; Killen, B.; Carley, R.; Amirlatifi, A.; Rahimi, S.; Bian, L. Scalability, Explainability and Performance of Data-Driven Algorithms in Predicting the Remaining Useful Life: A Comprehensive Review. IEEE Access 2023, 11, 41741–41769. [Google Scholar] [CrossRef]
- Manfren, M.; Gonzalez-Carreon, K.M.; James, P.A. Interpretable Data-Driven Methods for Building Energy Modelling—A Review of Critical Connections and Gaps. Energies 2024, 17, 881. [Google Scholar] [CrossRef]
- Martinez, Y.; Rojas, L.; Peña, A.; Valenzuela, M.; Garcia, J. Physics-Informed Neural Networks for the Structural Analysis and Monitoring of Railway Bridges: A Systematic Review. Mathematics 2025, 13, 1571. [Google Scholar] [CrossRef]
- Patel, D.; Sharma, R.; Guo, Y.B. Computational, Data-Driven, and Physics-Informed Machine Learning Approaches for Microstructure Modeling in Metal Additive Manufacturing. arXiv preprint. arXiv:2505.01424, 2025.
- Huang, B.; Wang, J. Applications of Physics-Informed Neural Networks in Power Systems—A Review. IEEE Transactions on Power Systems 2022, 38, 572–588. [Google Scholar] [CrossRef]
- Sharma, P.; Chung, W.T.; Akoush, B.; Ihme, M. A Review of Physics-Informed Machine Learning in Fluid Mechanics. Energies 2023, 16, 2343. [Google Scholar] [CrossRef]
- Anttila, S.; Döhler, J.S.; Oliveira, J.G.; Boström, C. Grid Forming Inverters: A Review of the State of the Art of Key Elements for Microgrid Operation. Energies 2022, 15, 5517. [Google Scholar] [CrossRef]
- Khan, M.; Wu, W.; Li, L. Grid-Forming Control for Inverter-Based Resources in Power Systems: A Review on Its Operation, System Stability, and Prospective. IET Renewable Power Generation 2024, 18, 887–907. [Google Scholar] [CrossRef]
- Akram, U.; Shah, R.; Amjady, N.; Mithulananthan, N.; Islam, S. Active and Reactive Power Injection of Energy Storage for Short-Term Frequency Stability in Islanded Power Systems. Journal of Energy Storage 2024, 90, 111914. [Google Scholar] [CrossRef]
- Inaolaji, A.; Savasci, A.; Paudyal, S. Distribution Grid Optimal Power Flow in Unbalanced Multiphase Networks with Volt-Var and Volt-Watt Droop Settings of Smart Inverters. IEEE Transactions on Industry Applications 2022, 58, 5832–5843. [Google Scholar] [CrossRef]
- Muftau, B.; Fazeli, M. The Role of Virtual Synchronous Machines in Future Power Systems: A Review and Future Trends. Electric Power Systems Research 2022, 206, 107775. [Google Scholar] [CrossRef]
- Moutevelis, D.; Roldán-Pérez, J.; Rodríguez-Ortega, P.; Prodanović, M. Virtual Synchronous Machine Design for Islanded Microgrids Using the Extended Impedance Criterion with Grid Frequency Dynamics Included. IEEE Transactions on Energy Conversion 2024. [Google Scholar] [CrossRef]
- Minchala-Ávila, C.; Arévalo, P.; Ochoa-Correa, D. A Systematic Review of Model Predictive Control for Robust and Efficient Energy Management in Electric Vehicle Integration and V2G Applications. Modelling 2025, 6, 20. [Google Scholar] [CrossRef]
- Subedi, S.; Gui, Y.; Xue, Y. Applications of Data-Driven Dynamic Modeling of Power Converters in Power Systems: An Overview. IEEE Transactions on Industry Applications 2025. [Google Scholar] [CrossRef]
- Massaoudi, M.S.; Abu-Rub, H.; Ghrayeb, A. Navigating the Landscape of Deep Reinforcement Learning for Power System Stability Control: A Review. IEEE Access 2023, 11, 134298–134317. [Google Scholar] [CrossRef]
- Lahon, P.; Kandali, A.B.; Barman, U.; Konwar, R.J.; Saha, D.; Saikia, M.J. Deep Neural Network-Based Smart Grid Stability Analysis: Enhancing Grid Resilience and Performance. Energies 2024, 17. [Google Scholar] [CrossRef]
- Ahmed, S.F.; Alam, M.S.B.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Gandomi, A.H. Deep Learning Modelling Techniques: Current Progress, Applications, Advantages, and Challenges. Artificial Intelligence Review 2023, 56, 13521–13617. [Google Scholar] [CrossRef]
- Gheisari, M.; Ebrahimzadeh, F.; Rahimi, M.; Moazzamigodarzi, M.; Liu, Y.; Dutta Pramanik, P.K.; Kosari, S. Deep Learning: Applications, Architectures, Models, Tools, and Frameworks: A Comprehensive Survey. CAAI Transactions on Intelligence Technology 2023, 8, 581–606. [Google Scholar] [CrossRef]
- Shi, Y.; Beer, M. Physics-Informed Neural Network Classification Framework for Reliability Analysis. Expert Systems with Applications 2024, 258, 125207. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, H.Y.; Liu, S.W.; Chan, S.L. Second-Order Analysis of Beam-Columns by Machine Learning-Based Structural Analysis through Physics-Informed Neural Networks. Advanced Steel Construction 2023, 19, 411–420. [Google Scholar]
- Chen, Y.; Yang, Q.; Chen, Z.; Yan, C.; Zeng, S.; Dai, M. Physics-Informed Neural Networks for Building Thermal Modeling and Demand Response Control. Building and Environment 2023, 234, 110149. [Google Scholar] [CrossRef]
- Fassi, Y.; Heiries, V.; Boutet, J.; Boisseau, S. Toward Physics-Informed Machine-Learning-Based Predictive Maintenance for Power Converters—A Review. IEEE Transactions on Power Electronics 2023, 39, 2692–2720. [Google Scholar] [CrossRef]
- Khalid, S.; Yazdani, M.H.; Azad, M.M.; Elahi, M.U.; Raouf, I.; Kim, H.S. Advancements in Physics-Informed Neural Networks for Laminated Composites: A Comprehensive Review. Mathematics 2024, 13, 17. [Google Scholar] [CrossRef]
- Ansari, S.; Zhang, J.; Singh, R.E. A Review of Stabilization Methods for DCMG with CPL, the Role of Bandwidth Limits and Droop Control. Protection and Control of Modern Power Systems 2022, 7, 1–12. [Google Scholar] [CrossRef]
- Wald, F.; Tao, Q.; De Carne, G. Virtual Synchronous Machine Control for Asynchronous Grid Connections. IEEE Transactions on Power Delivery 2023, 39, 397–406. [Google Scholar] [CrossRef]
- Harbi, I.; Rodriguez, J.; Liegmann, E.; Makhamreh, H.; Heldwein, M.L.; Novak, M.; Kennel, R. Model-Predictive Control of Multilevel Inverters: Challenges, Recent Advances, and Trends. IEEE Transactions on Power Electronics 2023, 38, 10845–10868. [Google Scholar] [CrossRef]
- Li, S.E. Deep Reinforcement Learning. In Reinforcement Learning for Sequential Decision and Optimal Control; Springer Nature Singapore, 2023; pp. 365–402.
- Antonelo, E.A.; Camponogara, E.; Seman, L.O.; Jordanou, J.P.; de Souza, E.R.; Hübner, J.F. Physics-Informed Neural Nets for Control of Dynamical Systems. Neurocomputing 2024, 579, 127419. [Google Scholar] [CrossRef]
- Nellikkath, R.; Chatzivasileiadis, S. Physics-Informed Neural Networks for AC Optimal Power Flow. Electric Power Systems Research 2022, 212, 108412. [Google Scholar] [CrossRef]
Figure 1.
System model of a microgrid with grid-forming inverter control.
Figure 1.
System model of a microgrid with grid-forming inverter control.
Figure 2.
Proposed PINN architecture integrating physical laws and real-time control.
Figure 2.
Proposed PINN architecture integrating physical laws and real-time control.
Figure 3.
Frequency response comparison of PINN, droop, and VSM controllers under a 50% load step disturbance.
Figure 3.
Frequency response comparison of PINN, droop, and VSM controllers under a 50% load step disturbance.
Figure 4.
Voltage magnitude response comparison of PINN, droop, and VSM controllers under reactive power step disturbances.
Figure 4.
Voltage magnitude response comparison of PINN, droop, and VSM controllers under reactive power step disturbances.
Figure 5.
Frequency and voltage responses under high variability in renewable generation.
Figure 5.
Frequency and voltage responses under high variability in renewable generation.
Figure 6.
Convergence of total loss and its components during PINN training.
Figure 6.
Convergence of total loss and its components during PINN training.
Figure 7.
PINN-based control signals: dynamic reference trajectories for voltage and frequency.
Figure 7.
PINN-based control signals: dynamic reference trajectories for voltage and frequency.
Figure 8.
Comparative stability metrics: frequency deviation, voltage deviation, and settling time across control strategies.
Figure 8.
Comparative stability metrics: frequency deviation, voltage deviation, and settling time across control strategies.
Figure 9.
Distribution of inference time for the PINN controller over 1000 executions.
Figure 9.
Distribution of inference time for the PINN controller over 1000 executions.
Figure 10.
Sensitivity of frequency deviation to increasing measurement noise under different control strategies.
Figure 10.
Sensitivity of frequency deviation to increasing measurement noise under different control strategies.
Figure 11.
Comparison of power quality metrics: Total Harmonic Distortion (THD) and power factor under different control strategies.
Figure 11.
Comparison of power quality metrics: Total Harmonic Distortion (THD) and power factor under different control strategies.
Figure 12.
Phase portrait showing frequency deviation as a function of phase angle for droop and PINN-based control.
Figure 12.
Phase portrait showing frequency deviation as a function of phase angle for droop and PINN-based control.
Figure 13.
Tracking performance of the proposed PINN and droop controllers against a time-varying reference power signal.
Figure 13.
Tracking performance of the proposed PINN and droop controllers against a time-varying reference power signal.
Figure 14.
Prediction error distribution of the PINN controller under in-distribution and out-of-distribution test scenarios.
Figure 14.
Prediction error distribution of the PINN controller under in-distribution and out-of-distribution test scenarios.
Table 1.
Comparison of Existing Methods and Proposed Approach
Table 1.
Comparison of Existing Methods and Proposed Approach
| Reference |
Methodology |
Strengths |
Limitations |
| Ansari et al. [35] |
Droop Control |
Simplicity, decentralization |
Limited adaptability |
| Wald et al. [36] |
Virtual Synchronous
Machine (VSM) |
Good transient response |
Complex tuning and modeling |
| Harbi et al. [37] |
Model Predictive
Control (MPC) |
Constraint handling |
High computational complexity |
| Li. [38] |
Deep Reinforcement
Learning (DRL) |
Adaptability, robustness |
Poor interpretability |
| Antonelo et al. [39] |
PINNs – General |
Interpretability, requires less data |
Limited exploration in control tasks |
| Nellikkath et al. [40] |
PINNs (Power Flow) |
Accuracy, interpretability |
Offline training, not suitable for real-time control |
| Proposed Approach |
PINN-based Inverter
(Physics-Embedded) |
Real-time applicability,
robustness, interpretability |
Requires rigorous validation,
computational efficiency tests |
Table 2.
Simulation Parameters and Conditions
Table 2.
Simulation Parameters and Conditions
| Parameter |
Value/Condition |
| Number of Inverters |
3 (Grid-Forming) |
| Nominal Frequency |
50 Hz |
| Nominal Voltage |
400 V (Line-to-Line RMS) |
| Droop Coefficients |
Variable (PINN-controlled) |
| Virtual Inertia Constant,
|
0.05 s |
| Damping Coefficient,
|
0.7 pu |
| Load Conditions |
Step-changes and continuous variations |
| Renewable Source Variability |
Solar PV irradiance and wind speed profiles |
| Simulation Duration |
120 s per scenario |
| Solver |
ode45, variable step (Simulink) |
Table 3.
Comparison of Real-Time Computational Performance
Table 3.
Comparison of Real-Time Computational Performance
| Control Method |
Average Computational Latency (ms) |
Real-Time Feasibility |
| Droop Control |
0.1 |
High |
| VSM Control |
0.3 |
High |
| PINN Control (Proposed) |
0.7 |
High |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).